Extraction of Stride Events From Gait Accelerometry During Treadmill Walking

Abstract

Objective: evaluating stride events can be valuable for understanding the changes in walking due to aging and neurological diseases. However, creating the time series necessary for this analysis can be cumbersome. In particular, finding heel contact and toe-off events which define the gait cycles accurately are difficult. Method: we proposed a method to extract stride cycle events from tri-axial accelerometry signals. We validated our method via data collected from 14 healthy controls, 10 participants with Parkinson’s disease, and 11 participants with peripheral neuropathy. All participants walked at self-selected comfortable and reduced speeds on a computer-controlled treadmill. Gait accelerometry signals were captured via a tri-axial accelerometer positioned over the L3 segment of the lumbar spine. Motion capture data were also collected and served as the comparison method. Results: our analysis of the accelerometry data showed that the proposed methodology was able to accurately extract heel and toe-contact events from both feet. We used t-tests, analysis of variance (ANOVA) and mixed models to summarize results and make comparisons. Mean gait cycle intervals were the same as those derived from motion capture, and cycle-to-cycle variability measures were within 1.5%. Subject group differences could be similarly identified using measures with the two methods. Conclusions: a simple tri-axial acceleromter accompanied by a signal processing algorithm can be used to capture stride events. Clinical impact: the proposed algorithm enables the assessment of stride events during treadmill walking, and is the first step toward the assessment of stride events using tri-axial accelerometers in real-life settings.

Evaluating stride events are valuable for understanding the changes in walking due to aging and neurological diseases, but, creating the time series necessary for this analysis can be cumbersome. In particular, finding heel contact and toe-off events which define the gait cycles accurately are difficult. We proposed and validated a method to extract stride cycle events from gait accelerometry signals captured via a tri-axial accelerometer positioned over the L3 segment of the lumbar spine. The proposed algorithm enables the assessment of stride events during treadmill walking, and is the first step towards the assessment of stride events using tri-axial accelerometers in real-life settings.

I. Introduction

Walking is one of the most complex, yet most practiced, motor skills [1], [2]. In general, walking arises from complex interactions of cerebellum, the motor cortex, basal ganglia and feedback from vestibular, visual and peripheral receptors [3]. Nevertheless, walking consists of repeatable movement patterns, and thus, it generally exhibits a low level of variability [4]–[6]. Initially, it was believed that observed stride-to-stride variations are a normal random process, but over the years it has been shown that stride interval time series behave more like fractal processes [1], [3]. Depending on the neurological conditions/diseases, previous research has shown that the properties of these fractal processes change [7], [8]. For example, stride intervals become more uncorrelated (random) due to aging and neurological diseases (e.g., [9]–[11]) or to exposure to external cues [12]. Lastly, stride intervals are often useful in the calculation of other gait metrics such as harmonic ratios (e.g., [13], [14]), which quantify the smoothness of walking by assessing step-to-step symmetry within a single stride [14].

Even though stride interval time series are a useful clinical tool, accurately collecting such data is rather difficult and time consuming. A common method for capturing stride interval time series is using an optically-based motion capture system (e.g., [15]–[17]), which utilizes reflective markers positioned at various foot locations. The position signals obtained via these reflective markers are then used to find gait parameters such as heel contact and/or toe-off. However, motion caption systems are usually very expensive, and limit the gait analysis to laboratory settings, which do not necessarily reflect the dynamic nature experienced while walking in non-laboratory settings. To diminish the cost associated with motion caption systems, researchers have often considered systems based on instrumented walkways (e.g., [18], [19]). These are portable sensor arrays typically several meters long that allow researchers to extract multiple gait features simultaneously. While useful, these instrumented walkways limit the number of continuous stride intervals captured during a typical session to maximum of 10-15 strides. Such short time series limit the application of more advanced techniques in order to potentially understand the effects of various diseases on human gait.

Force sensitive resistors (also known as footswitches) are another method used to evaluate stride-to-stride timing. These footswitches are placed on the bottom of shoes or beneath the insoles to capture voltage variations associated with heel strikes and toe-offs (e.g., [20]–[22]). These voltage variations are usually captured by a data logger worn by a participant around the waist. Researchers have used a mixture of custom-made (e.g., [23]–[25]) and commercially available systems to capture these stride intervals time series, and typical walks lasted from a few minutes (100-200 strides) up to hour long walks (a few thousand strides). It should be pointed out that the cost associated with these systems is typically an order of magnitude smaller than the cost associated with motion capture systems and/or instrumented walkways.

The implementation of force sensitive resistors to capture stride interval time series has enabled the study of human gait in more realistic settings and for a smaller cost. However, such systems are prone to several drawbacks. First, a minimum of four sensors are required in order to study heel strikes and toe-offs, as sensors need to be placed on heels and toes of each foot. Second, these sensors usually require tethered connections to a data logger, which can interfere with typical walking patterns of participants, especially when dealing with older adults and/or participants suffering from neurological diseases. Third, researchers and clinicians have often reported a low durability of these sensors (e.g., sensors would break during data collections), which caused data losses and the inability to properly investigate gait events.

To avoid these disadvantages associated with force sensitive resistors, previous contributions have investigated other sensors such as accelerometers and gyroscopes to identify gait events (e.g., [26]–[37]). For an in-depth analysis of some of these algorithms, please refer to [38] and [39], but overall it has been shown that the compared algorithms can generally accurately extract some of the gait parameters. However, many of these contributions, require multiple sensors (accelerometers and gyroscopes), multiple sensor locations, or complex processing techniques to achieve very high accuracies making them difficult to implement in the clinical setting. Furthermore, many of these contributions have investigated their proposed algorithms using only young healthy subjects and/or have not validated their results against the established gait assessment systems. Finally, the remaining algorithms failed to identify all of the critical temporal parameters including toe off.

To avoid the aforementioned shortcomings of the various measurement systems, we developed a method to acquire time estimates for heel strikes and toe-offs for both feet using atri-axial accelerometer worn on the pelvis. An algorithm was developed using the same principles of [40] that more completely analyzes accelerations captured along vertical (V), anterior-posterior (AP) and medial-lateral (ML) axes during walking via a single accelerometer positioned over the L3 segment of the lumbar spine (e.g., [39], [41]). In this paper, we describe this algorithm, and validate its accuracy against the stride interval time series extracted via a motion capture system for healthy and neurotically diseased elderly subjects. Our results show that the typical gait parameters studied in the literature can be accurately extracted from stride interval time series obtained by using the proposed algorithm.

II. Methodology

The data used in the current study were collected from 35 adults who were 65 years of age or older; 14 healthy controls (HC), 10 with Parkinson’s disease (PD) and 11 with peripheral neuropathy (PN). HC participants (4 males, 6 females) were 73.9 ± 5.70 years old with their preferred speed equal to 1.07 ± 0.15 m/s. PD participants (7 males, 3 females) were 66.0 ± 9.70 years old with their group averaged preferred treadmill walking speed equal to 1.02 ± 0.18 m/s. PN participants (5 males, 6 females) were 81.0 ± 5.00 years old with their preferred speed equal to 1.07 ± 0.09 m/s. Details on characteristics of the participants have previously been described in [41], which used the same data and considered the utilization of various accelerometry characteristics to differentiate amongst the three groups. Briefly, all individuals were independently ambulatory and able to continuously walk for at least 3 minutes. Primary exclusion criteria for all subjects were musculoskeletal or cardiopulmonary conditions that would interfere with walking. Healthy subjects with any neurological disorders were excluded. Primary inclusion criteria were intact vibratory sense for HCs and persons with PD (biothesiometer reading 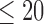), abnormal vibratory sense for persons with PN (biothesiometer reading 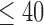), and a minimum of 1 year disease duration for individuals with PD. Individuals with PD were recruited from the university’s Movement Disorder Registry, and older adults (including those with PN) were recruited from the university’s Claude Pepper Center Registry. The diagnosis of idiopathic PD was made by a neurologist using UK PD Society Brain bank criteria [42]. Participants with PD were required to have had a Modified Hoehn and Yahr score between 2-3 (mild-moderate disease). Out 10 PD participants, five participants had a Hoehn and Yahr score of 2, four participants had a Hoehn and Yahr score of 2.5. and one participant had a Hoehn and Yahr score of 3. All participants with PD were on a stable dosing schedule of anti-parkinson medications for at least 3 months prior to testing, and they were tested in their best ON state. In addition to the exclusionary criteria stated in the manuscript, participants were excluded if there were evidence of global cognitive impairment (Folstein 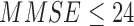). The study protocol was reviewed and approved by the university’s IRB, and informed consent was received from all subjects.

Walking trials were performed on a large custom computer-controlled treadmill (1.2 m wide by 2 m long) with a safety harness system. A 3-D optical motion capture system (Natural Point, Inc) collected heel and toe trajectory data. A tri-axial accelerometer (MMA7260Q, Freescale Semiconductor) secured over the L3 segment of the lumbar spine measured linear accelerations of the body (vertical (V), anterior-posterior (AP) and medial-lateral (ML)), which were recorded using an analog-digital converter. All data were recorded with the same data collection computer in order to properly synchronize the optical and acceleration data. Participants wore their own walking shoes (no sandals, clogs, heels were permitted). The experimenters were experienced physical therapists and biomechanists well-versed in palpation and marker placement. In general, all participants wore mesh or soft-sided athletic shoes which allowed palpation of bony landmarks through the shoes. The accelerometer was secured onto thin elastic belt, fastened at the front of the subjects waist. A larger neoprene lumbar support sleeve was then secured over the accelerometer. Sensor placement was frequently checked/monitored throughout data collection (between all walking conditions, after standing up after any rest breaks). Trunk accelerations and the motion capture system signals were sampled at 100 Hz. Trajectory data from 2 shoe markers (midpoint of proximal interphalangeal of the first digit, and the posterior superior aspect of calcaneous along the midline) were used to extract gait cycle time points [43].

Treadmill familiarization and preferred speed was assessed prior to the start of the protocol, before marker placement. The safety harness was used and participants started off holding on to the treadmill handrail. While holding on we slowly increased treadmill speed (in by 0.05 to 0.10 m/s) until a comfortable walking speed was reported. The subject then established a comfortable walking speed without hand support, similar to [1]. Mindful that we were working with older adults and individuals susceptible to fatigue (PDs), once we re-established comfortable walking speed without hand support the familiarization protocol was terminated. In general, this process took 5-10 minutes.

Each walking trial began with a ramp up period, where the subject’s walking speed was slowly increased until their previously established preferred pace was reached. Subjects completed a 3 minute walking trial at their preferred pace, rested, then completed a 3 minute walking trial at a slower speed (10% reduction from the preferred treadmill speed).

Across groups, the average usual treadmill speed was 1.06 ± 0.014 m/s with a range of m/s. Average reduced treadmill speed was 0.95 ± 0.03 m/s with a range of m/s. The total range of examined speeds was 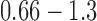m/s, which is wide and representative of persons with limited to independent community ambulation ability [44]; thus the algorithm has potential to be used across a range of gait speeds and clinical populations.

III. Segmentation of Gait Accelerometry Signals

In this section, we first introduce the algorithm for extraction of heel strikes and toe-offs from gait accelerometry signals. Secondly, we describe our approach to validate the accuracy of the proposed algorithm.

A. Proposed Algorithm

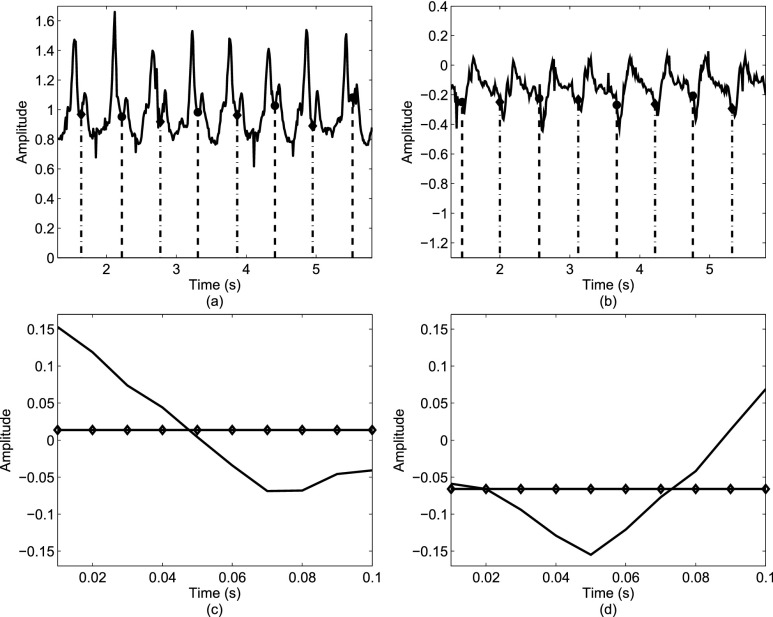
The general approach was to identify events present in the gait accelerometry signals during walking and relate those events to heel strikes and toe-offs on both feet. As shown in Figure 1, such relations can be formed based on accelerations in ML, V and AP directions. For example, the local maximum and minimum values in the AP/V directions appear to be temporally related to heel strikes and toe-offs (i.e., these local maximum/minimum values appear in vicinities of temporal events associated with heel strikes and toe offs). Similarly, as shown in Figures 1(c) and (d), we have observed that based on the average value of first 10 milliseconds of acceleration of a step in the ML direction we can determine whether a person has made a step with left or right leg.

FIGURE 1.

Relationships between gait accelerations and stride events: (a) local minima points in the V direction are related to toe-offs; (b) local minima points in the AP direction are related to heel strikes; (c) if a person stepped first with the right foot then the first 10 ms of acceleration in the ML direction will have a positive mean value (represented by a line with diamonds); (d) if a person stepped first with the left foot then the first 10 ms of acceleration in the ML direction will have a negative mean value (represented by a line with diamonds). Dashed lines represent events related to toe-offs/heel strikes as identified by the motion capture system.

Based on these observations, the proposed algorithm has three stages. In the first stage, we identify possible events from the V direction that represent potential locations of the gait events. The algorithm initially identifies possible events from the V signal; including the heel strikes and toe-offs. In the second stage, potential events are processed to identify the true toe-off events for both feet. Lastly, the third stage works towards the accurate estimation of heel strikes from both feet based on the initial estimates of the gait events.

In the detailed description of the algorithm, 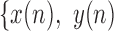, 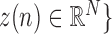will denote samples of gait accelerometry signals in the ML, V and AP directions, respectively. 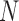represents the length of these vectors representing samples of gait accelerometry signals, and these samples were acquired using a sample frequency 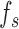. The proposed algorithm is not sensitive to the selection of a sampling frequency, as long as the sampling frequency is greater than twice the Nyquist frequency for gait accelerometry signals (around 10-20 Hz in typical cases) [39], [41]. Hence, the choice of the sampling frequency in here (100 Hz) did not play a significant role.

1). Stage 1 - Identify Events of Interest

The goal of Stage 1 is to identify events of interest, that is, local maximum values in the V and AP directions. To achieve this goal, we adopt the following steps:

• 1)
  Remove any artifact related to the gravity by removing the mean from the acquired signals:

  

  where 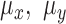and 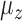represent the calculated mean values for these signals.
• 2)
  Remove impulse-like artifacts unrelated to gait via median filtering:

  

  where 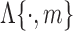represents an 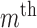order median filtering operation. In this paper, a fifth order filter is utilized.
• 3)
  Normalize the filtered signals to unity amplitudes:

  

  Signal normalization was carried out to reduce the inter-individual variability within groups.
• 4)Determine 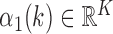representing 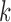local maxima values present in 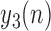under the constraint that successive local maxima have to be at least 0.35 seconds apart and 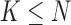, where 0.35 seconds represents a conservative estimate of half of the stance phase during a single stride. Figure 2 depicts that higher peaks are followed by smaller peaks. Here, we seek to identify stronger peaks in order to yield less false positives.
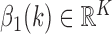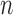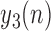• 5)Determine representing the time indices from of 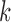local maxima values.
• 6)
  Form a set 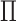representing 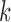values for which 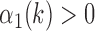. The cardinality of the set will be equal to 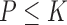. Based on the set 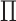, form new vectors:

  

  where .

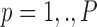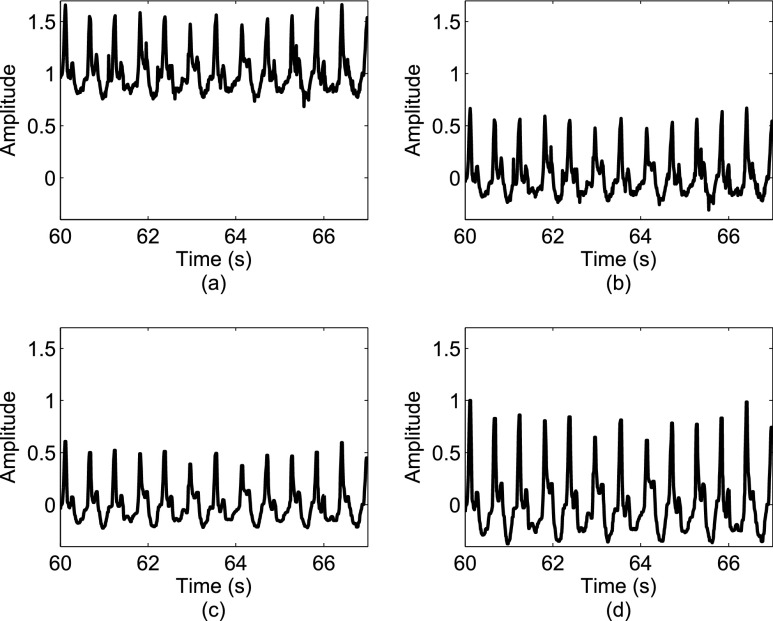
FIGURE 2.

A sample signal in the V direction: (a) a raw acceleration signal; (b) the signal after removing its mean component; (c) the signal after being processed by a median filter; (d) the signal after the amplitude normalization. The amplitude of signals in (a)-(c) is in m/.

Figure 2 depicts the effects of various signal operations on a sample signal from the V direction.

2). Stage 2 - Determining Toe-Offs

The purpose of Stage 2 is to accurately determine the toe-offs based on refining 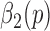values via a closer examination of local minima values in 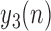. The following steps need to be taken:

• 1)
  Form 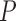sequences based on 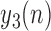, where these sequences are defined as:

  

  where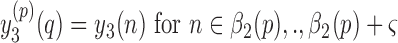 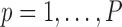and 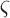represents a time offset. In this paper, we used 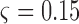seconds (that is, 15 samples), as the double support phase of a stride lasts for about 15% of a stride duration [45]. Therefore, our 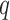values are given by 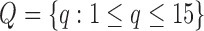. In other words, 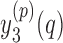represent 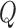points around the 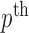maximum found in the Stage 1.
• 2)
  For each sequence , determine 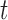representing a location of the minimum value for the sequence. Then, update 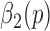to reflect the true location of toe-offs according to the following rule:

  

  with .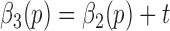
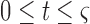• 3)
  Calculate

  

  where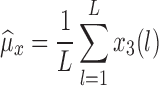 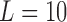is used in this paper.
• 4)
  Based on 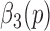and 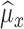, form sequences 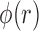and 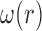representing the time indices of right and left toe-offs, respectively. This can be accomplished via the following rule:

  • Case I
    If 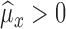, then

    
  • Case II
    If 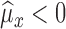, then

    

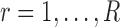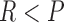    where and for both cases.

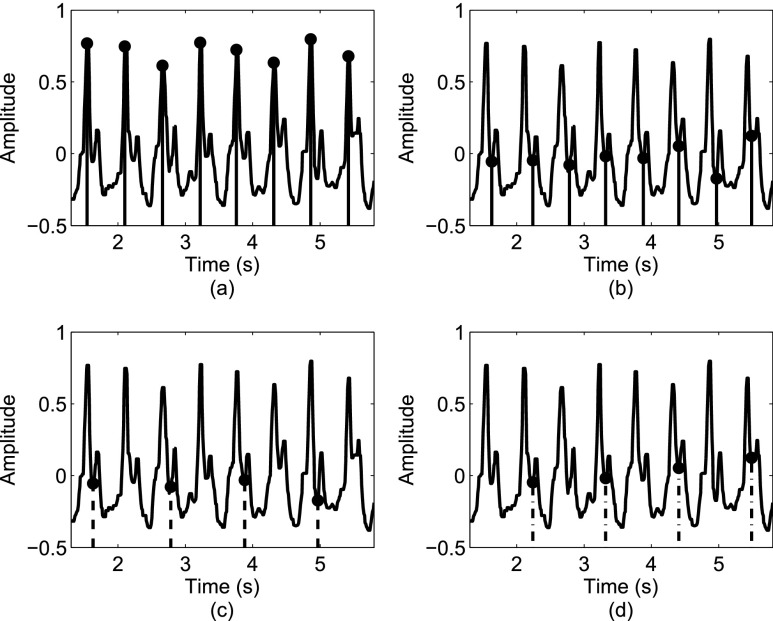
Figure 3 depicts a sample signal, and the outcome of the Stage 2 processing.

FIGURE 3.

Estimating toe-offs: (a) an initial estimate of toe-off events from the V direction; (b) refining the timing of toe-off events; (c) toe-off events identified from acceleration signals for the right foot; (d) toe-off events identified from acceleration signals for the left foot.

3). Stage 3 - Determining Heel Strikes

The purpose of Stage 3 is to accurately determine the heel strikes based on refining 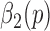values via the first derivative of 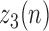. Figure 4 summarizes the steps of this stage. To accomplish this task, the following steps are needed:

• 1)
  Determine 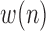representing the absolute value of the first order derivative of :

  
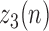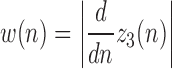
• 2)
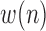  Form sequences based on , where these sequences are defined as:

  

  where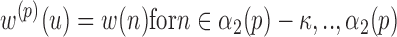 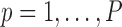and 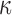represents a time offset. Here, we used 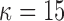samples (that is, 150 ms) which gave us 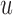values are given by 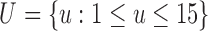. In other words, 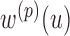represents 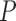points around a local extremum point.
• 3)
  For each sequence 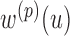, determine 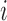representing a location of the minimum value for the sequence. Then, update 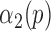to reflect the true location of heel strikes according to the following rule:

  

  with .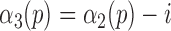
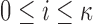• 4)
  Based on 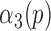and 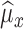from eqn. (14), form sequences 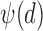and 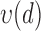representing the time indices of right and left heel strikes, respectively. This can be accomplished via the following rule:

  • Case I
    If 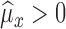, then

    
  • Case II
    If 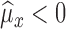, then

    

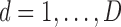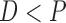    where and for both cases.

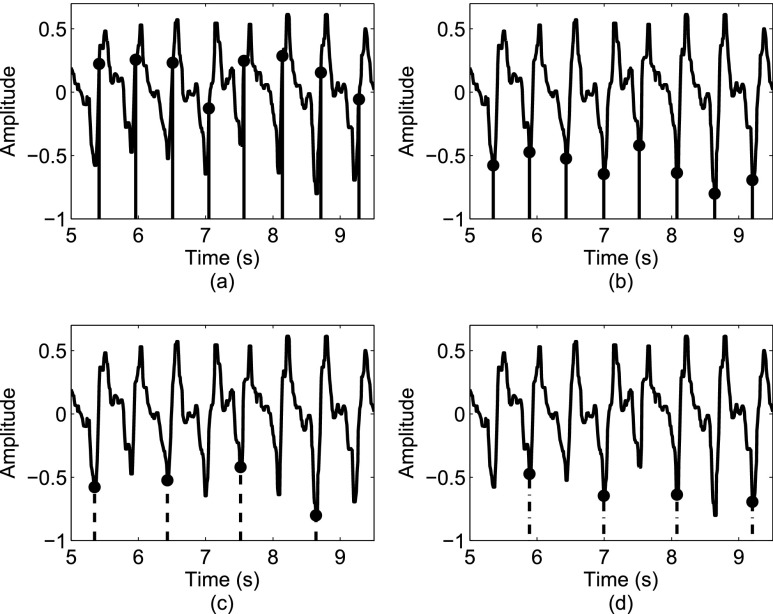
FIGURE 4.

Estimating heel strikes: (a) an initial estimate of heel strike events from the AP direction; (b) refining the timing of heel strike events; (c) heel strike events identified from acceleration signals for the right foot; (d) heel strike events identified from acceleration signals for the left foot.

These three stages will produce time series (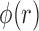, , 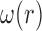, 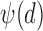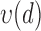) representing time indices of right and left toe-offs and heel strikes. To obtain a stride interval time series, one would need to take the first difference of the obtained time series points and normalize the obtained differences by the sampling frequency used to acquire gait accelerometry signals.

B. Algorithm Evaluation

To evaluate the accuracy of the proposed algorithm, we extracted features from the stride intervals obtained using the proposed algorithm. The extracted features are then compared to the same features extracted from the stride interval time series obtained from reflective markers using the procedure outlined in [43], which has a mean maximal error of 11.9 milliseconds. In particular, we calculated mean stride intervals, coefficients of variations (CoV) (e.g., [5], [46]), but other typical stride features such right and left stances, single and double support times and swing percentages were calculated as well. Also, using these stride time series, harmonic ratios () (e.g., [2], [13], [14], [47], [48]) were calculated based on the acceleration signals. These quantities were calculated in all three anatomical directions considered in this paper from low pass filtered acceleration data over each stride. The filter was a second-order, zero-phase Butterworth filter with a cutoff frequency of 30 Hz. First, we calculated the discrete Fourier transform of the segmented data as follows (e.g., [43], [49]):

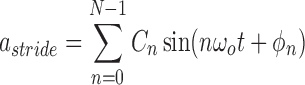where the 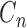is the harmonic coefficient, 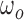is the stride frequency, and 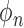is the phase. The first 20 harmonic coefficients are then summed and used to calculate the harmonic ratio, which is defined as:

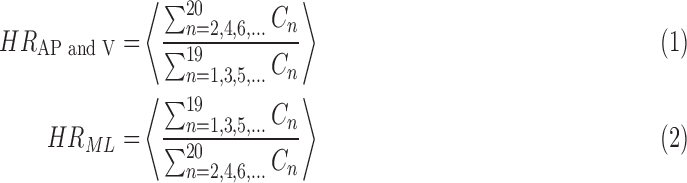where 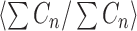denotes the average ratio over all strides. This metric allows us to quantify the step to step asymmetry in the acceleration at the L3/L4, which has been used as a proxy center of mass.

To test statistical significance of our results, we first examined whether there were any differences between features extracted by the algorithm and motion capture method. We conducted a series of paired samples t-tests to compare true and estimated differences under each walking condition in each of the participant groups based on disease/gender. Second, we examined whether the said differences, if any, were different between gender/disease groups using one- and two-way analyses of variance. Finally, we examined whether any finding obtained by comparing different participant groups/conditions would be different if one used estimated features instead of true features. To this end, we fitted a series of linear mixed models with each of the features as the dependent variable; type of value (true/estimated), participant group/condition and their interaction as fixed effects of interest; and a participant random effect to account for multiple measurements from the same set of participants. We constructed appropriate means contrasts to estimate between-group/condition differences under true and estimated measurements separately, and make comparisons between them. We used SAS®version 9.3 (SAS Institute, Inc., Cary, North Carolina) for all statistical analyses.

IV. Results

Mean stride time intervals estimated from the accelerometry data were similar to those calculated from the motion capture system as shown in Table 1, with the differences between the two methods ranging between −0.5 and 2 ms (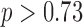). An ANOVA on the differences between the values showed no significant effects of gait speed, group, foot, heel/toe or any interactions. It should be also pointed out that the average value of a mean absolute difference between the true (motion capture) and estimated (algorithm) values was less 0.01 seconds, which is smaller than the temporal resolution of the used instruments. As expected, the mean stride times themselves were significantly affected by speed (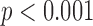), with the averages for the normal and reduced speeds across subjects being 1.11 (s.d. 0.08) and 1.18 (s.d. 0.09) seconds, respectively. There were no effects of group, foot, heel/toe or any interactions on the stride times.

TABLE 1. Motion capture and accelerometry average stride intervals (seconds) as calculated from various points in the gait cycle. † denotes statistical differences between motion capture and accelerometry values within groups. LH left heel strike; RH right heel strike; LT left toe off; RT right toe off; E at the end of the variable name denotes estimated value from accelerometry signals.

	Normal Speed			Reduced Speed
	HC	PN	PD	HC	PN	PD
LH	1.11 ± 0.11	1.10 ± 0.07	1.14 ± 0.08	1.20 ± 0.10$	1.15 ± 0.09	1.19 ± 0.09
LHE	1.11 ± 0.10	1.10 ± 0.07	1.14 ± 0.07†	1.20 ± 0.10	1.15 ± 0.09	1.19 ± 0.09
LT	1.11 ± 0.11	1.10 ± 0.07	1.14 ± 0.08	1.20 ± 0.10	1.15 ± 0.09	1.19 ± 0.09
LTE	1.11 ± 0.10†	1.10 ± 0.07	1.14 ± 0.07†	1.20 ± 0.10	1.15 ± 0.09	1.19 ± 0.09
RH	1.11 ± 0.10	1.10 ± 0.07	1.14 ± 0.08	1.20 ± 0.10	1.15 ± 0.09	1.19 ± 0.09
RHE	1.11 ± 0.10†	1.10 ± 0.07	1.14 ± 0.07	1.20 ± 0.10	1.15 ± 0.09	1.19 ± 0.09
RT	1.11 ± 0.10	1.10 ± 0.07	1.14 ± 0.08	1.20 ± 0.10	1.15 ± 0.09	1.19 ± 0.09
RTE	1.11 ± 0.10	1.10 ± 0.07	1.14 ± 0.07	1.20 ± 0.10	1.15 ± 0.09†	1.19 ± 0.09

Stride time interval variability, as measured by CoV for each subject, was about 1.5% different between the two methods, with the CoV from the accelerometry data being overall greater that the CoV from the motion data as shown in Table 2. However, these numbers still represent typical ranges for CoV values of stride time interval series. The ANOVA investigating the impact of the independent variables showed that speed (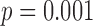) and the interaction of speed and heel strike (or toe-off) events (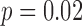) had a small (< 0.3%) but significant impact on the differences between the results obtained with the motion capture system and the proposed method. When using heel contact, there was no significant impact of gait speed on the difference between the two methods. When using the toe, speed did have an impact ( 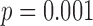for within toe analysis) on the differences. Thus, the accelerometry method resulted in CoVs that were higher than the motion capture data; and when using the heel contact results to define the cycles speed had no effect on the differences between the accelerometry method and the motion data method.

TABLE 2. Motion capture and Aaccelerometry stride interval coefficient of variation (percent) as calculated from various points in the gait cycle for the three subject groups (HC, PN, PD). † denotes statistical differences between motion capture and accelerometry values within groups LH left heel strike; RH right heel strike; LT left toe off; RT right toe off; E at the end of the variable name denotes estimated value from accelerometry signals.

	Normal Speed			Reduced Speed
	HC	PN	PD	HC	PN	PD
LH	2.19 ± 0.56	2.06 ± 0.48	2.16 ± 0.91	2.61 ± 1.12	2.28 ± 0.54	2.43 ± 0.81
LHE	3.37 ± 0.81†	3.73 ± 0.77†	3.77 ± 0.99†	3.86 ± 0.99†	3.98 ± 0.58†	3.95 ± 0.89†
LT	2.32 ± 0.60	2.32 ± 0.54	2.31 ± 0.98	2.78 ± 1.14	2.56 ± 0.60	2.59 ± 0.86
LTE	3.75 ± 1.47†	4.37 ± 1.92†	3.98 ± 1.32†	3.32 ± 1.09†	3.75 ± 1.13†	3.85 ± 1.33†
RH	2.17 ± 0.62	2.09 ± 0.48	2.19 ± 0.89	2.59 ± 1.18	2.33 ± 0.64	2.43 ± 0.75
RHE	3.80 ± 0.64†	3.81 ± 1.03†	3.64 ± 1.03†	3.86 ± 1.06†	3.76 ± 0.47†	3.80 ± 1.03†
RT	2.30 ± 0.53	2.28 ± 0.56	2.34 ± 0.96	2.67 ± 1.06	2.54 ± 0.71	2.54 ± 0.79
RTE	3.36 ± 1.03†	3.63 ± 1.38†	3.84 ± 1.22†	3.31 ± 1.28†	3.75 ± 1.54†	3.71 ± 1.22†

Additionally, we examined other typical stride features as shown in Table 3. Our statistical analysis has shown that any group and sex differences are not affected by the use of the proposed algorithm ().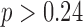

TABLE 3. Typical stride parameters. The variables are expressed in seconds unless a variable is defined as a percentage. RS= right stance; LS= left stance; DSRL = double support (right-left); DSRL= double support (left-right); SSR = right single support; SSL = left single support; SPR = right swing percentage; SPL = left swing percentage. E at the end of the variable name denotes estimated value from accelerometry signals.

	Normal Speed			Reduced Speed
	HC	PN	PD	HC	PN	PD
RS	0.74 ± 0.08	0.73 ± 0.04	0.76 ± 0.04	0.81 ± 0.08	0.78 ± 0.05	0.80 ± 0.05
RSE	0.71 ± 0.06	0.71 ± 0.04	0.72 ± 0.04	0.76 ± 0.07	0.74 ± 0.06	0.75 ± 0.05
LS	0.74 ± 0.08	0.73 ± 0.05	0.76 ± 0.05	0.81 ± 0.08	0.77 ± 0.07	0.80 ± 0.06
LSE	0.71 ± 0.06	0.70 ± 0.06	0.73 ± 0.06	0.76 ± 0.06	0.73 ± 0.07	0.77 ± 0.08
DSRL	0.19 ± 0.03	0.18 ± 0.02	0.19 ± 0.02	0.21 ± 0.03	0.20 ± 0.02	0.21 ± 0.02
DSRLE	0.16 ± 0.02	0.16 ± 0.02	0.16 ± 0.03	0.16 ± 0.03	0.16 ± 0.03	0.16 ± 0.03
DSLR	0.19 ± 0.03	0.18 ± 0.02	0.19 ± 0.02	0.21 ± 0.04	0.19 ± 0.02	0.20 ± 0.02
DSLRE	0.15 ± 0.02	0.15 ± 0.03	0.16 ± 0.03	0.16 ± 0.02	0.16 ± 0.03	0.16 ± 0.02
SSR	0.37 ± 0.03	0.37 ± 0.03	0.38 ± 0.03	0.39 ± 0.03	0.38 ± 0.03	0.38 ± 0.03
SSRE	0.40 ± 0.05	0.40 ± 0.03	0.40 ± 0.03	0.43 ± 0.05	0.43 ± 0.03	0.42 ± 0.03
SSL	0.37 ± 0.03	0.37 ± 0.03	0.38 ± 0.04	0.39 ± 0.03	0.38 ± 0.04	0.39 ± 0.05
SSLE	0.40 ± 0.05	0.39 ± 0.04	0.41 ± 0.05	0.43 ± 0.05	0.41 ± 0.05	0.44 ± 0.05
SPR	33.0 ± 1.83	33.5 ± 1.08	33.3 ± 1.65	33.3 ± 2.04	32.8 ± 1.12	32.6 ± 1.71
SPRE	35.8 ± 2.83	35.5 ± 2.59	36.2 ± 2.82	36.2 ± 2.58	35.6 ± 2.18	36.9 ± 2.14
SPL	33.4 ± 1.44	33.9 ± 1.52	33.4 ± 0.93	32.5 ± 1.51	33.3 ± 1.50	32.6 ± 1.06
SPLE	35.8 ± 1.81	36.6 ± 2.02	35.5 ± 2.30	36.1 ± 2.00	37.1 ± 1.96	35.6 ± 2.46

Harmonic Ratio (HR) estimations from the accelerometry data were calculated using the two methods (accelerometry and motion) to define the gait cycles (see Table 4). For the HR in the ML direction, the HR was smaller for the accelerometry-defined gait cycles compared to the motion-defined cycles. Group (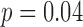) and speed (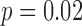) had a small, but significant influence on the differences between the two methods. For the vertical HR, there was again a bias with the accelerometry defined cycles resulting in smaller HRs. Speed influenced the HR for both cycle defining methods with reduced speed having a greater HR than normal speed. The HR in the AP direction showed similar results as the vertical HRs, with the acceleration defined gait cycles having greater HRs than the motion defined gait cycles and lower HRs for reduced speed. On average, the magnitudes of HRs estimated with the proposed algorithm were lower by 5%-10% than the magnitudes of HRs estimated with the motion capture system.

TABLE 4. Harmonic ratios. † denotes statistical differences between the true and estimated values within the group. E at the end of the variable name denotes estimated value from accelerometry signals.

	Normal Speed			Reduced Speed
	HC	PN	PD	HC	PN	PD
LH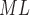	2.24 ± 0.55	1.83 ± 0.46	1.91 ± 0.44	2.45 ± 0.67	1.88 ± 0.41	1.95 ± 0.48
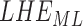	2.12 ± 0.52†	1.78 ± 0.31	1.82 ± 0.42†	2.26 ± 0.57†	1.81 ± 0.29	1.85 ± 0.45†
RH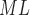	2.35 ± 0.50	1.94 ± 0.42	1.85 ± 0.46	2.44 ± 0.48	1.99 ± 0.39	1.95 ± 0.56
RHE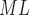	2.13 ± 0.41†	1.86 ± 0.35†	1.80 ± 0.37	2.23 ± 0.44†	1.89 ± 0.29†	1.86 ± 0.45
LH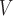	3.27 ± 0.97	2.83 ± 0.38	2.72 ± 0.60	3.12 ± 0.90	2.66 ± 0.43	2.58 ± 0.56
LHE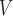	2.95 ± 0.69†	2.56 ± 0.22†	2.44 ± 0.44†	2.76 ± 0.61†	2.42 ± 0.29†	2.30 ± 0.38†
RH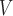	3.26 ± 0.87	3.08 ± 0.47	2.54 ± 0.48	3.05 ± 0.79	2.82 ± 0.50	2.50 ± 0.55
RHE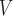	2.81 ± 0.65†	2.70 ± 0.33†	2.38 ± 0.37†	2.68 ± 0.60†	2.54 ± 0.30†	2.28 ± 0.41†
LH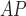	2.87 ± 0.82	2.42 ± 0.49	2.18 ± 0.49	2.65 ± 0.62	2.26 ± 0.35	2.07 ± 0.47
LHE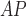	2.67 ± 0.78†	2.19 ± 0.42†	2.06 ± 0.46†	2.42 ± 0.52†	2.08 ± 0.30†	1.93 ± 0.40†
RH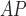	2.95 ± 0.72	2.57 ± 0.55	2.12 ± 0.49	2.68 ± 0.58	2.36 ± 0.41	2.05 ± 0.43
RHE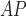	2.64 ± 0.70†	2.29 ± 0.50†	2.00 ± 0.38	2.43 ± 0.52†	2.15 ± 0.31†	1.92 ± 0.36†

The ability of the HR measures to distinguish between groups were similar using the two methods to define gait cycles. For the anteroposterior HRs, a significant difference across groups was found for both the acceleration-defined gait cycles and the motion-defined gait cycles (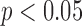). For the vertical HRs, group was not found to be significant in either case (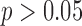). For the mediolateral HR, the acceleration based gait cycles did have a significant group effect (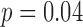), while the motion based gait cycles did not attain statistical significance (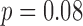). For all HR directions, speed was found to significantly impact the HR when using the acceleration or the motion defined cycles. Similarly, a combination of groups and speed did not significantly impact the HR when using the acceleration or the motion defined cycles.

V. Discussion

High agreement between the stride interval time series obtained with the proposed algorithm and the stride interval time series obtained with the motion capture system can be achieved. Thus, accelerometers can be used to accurately estimate gait cycles from treadmill walking to be used in the analysis of various subject populations. The algorithm extracts heel contact and toe-off from the right and left foot directly from the accelerometry signals themselves and does not require other additional sensors such as foot switches or optical motion capture.

There were some small, but statistically significant differences in the time series when comparing the two methods. Stride interval variability (as measured by the CoV) was overall higher when the heel contact and toe-off events were defined by the acceleration signals. Higher CoV values were due to occasional misidentification of heel-strike/toe-off events, but these higher values of stride variability are still within the previously reported ranges for these groups [4]–[6]. In addition, the higher CoV values were a small bias of between 1 and 1.5% but behaved similarly at different speeds. When the defined time series were used to calculate the HRs, there was also a small bias between the two methods, but both methods resulted in harmonic ratios within the reported ranges for similar groups [13], [47], [48]. Given the similar behaviors in CoV and HR found in the results, we believe that the proposed method can be very useful in the field to define gait cycles directly from the accererometry signals. Finding subject group differences in HR were found to be generally the same for the two methods as well. There was a small difference in the mediolateral HR results, but given the relatively small patient subject sample size, this difference is not considered practically significant.

The proposed algorithm is robust from two main points of view. First, the reduced speed did not affect the gait event detection with the proposed algorithm, as reduced speeds usually introduce greater values for the average stride interval and the stride interval variability [50]. The proposed algorithm maintained its accuracy for both considered speeds. Second, the algorithm accurately extracted stride intervals from gait accelerometry signals in all three considered groups (i.e., HC, PN and PD). The considered groups typically have very different walking patterns [39], [41], but the proposed algorithm maintained any between-group differences.

Having an ability to extract stride interval time series without the utilization of footswitches and/or motion capture system also enables us to possibly move the gait assessment outside well-controlled conditions (e.g., a laboratory setting). This research is the first step in such a direction. Cumbersomeness of the current acquisition techniques is avoided in this case, as we can use a single sensor worn around a waist to acquire needed time series. Similarly, the proposed algorithm enables us to calculate certain gait characteristics such as harmonic ratios [48] in real-life settings as well. Calculation of these characteristics usually required acquisition of stride interval time series and gait accelerometry signals simultaneously. However, the aforementioned cumbersomeness of the equipment often limited researchers and clinicians in their intents to investigate these gait characteristics outside laboratory settings. The proposed algorithm provides us with an opportunity to simply avoid additional sensors and acquire only gait accelerometry signals from the L3 region.

This study used treadmill walking to validate our method of stride cycle events, but the method should be applicable in overground walking as well. Treadmill walking has been shown to decrease stance phase and double support time generally as a consequence of increased cadence (from 110ms to 80ms for double support) [51]. However, the overall characteristics of the acceleration signal are consistent and the characteristic maximums and minimums still exist. Therefore, any changes in stance and double support would merely affect the timing thresholds (i.e., 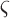values) in Stage 2 of the algorithm similar to varying cadence in the normal population. In fact, the reductions in stance and double support phase would make the threshold choices more conservative and the algorithm more effective.

Additionally, treadmill walking allows for collection of a large amount of continuous strides. Previous research (e.g. [52]) indicates that more than 50 strides are required to reliably measure parameters such as variability during normal walking, and even more are necessary during complex tasks such as dual-task walking, or when performing something other than preferred walking, such as the slow condition in this current study. While we could have collected both motion capture data and direct accelerations during overground walking, due to lab space constraints the strides would either have been non-continuous, or participants would have needed to walk an oval path and thus performing turns. Turning is a different motor task than straight path walking and would have introduced a major confound into the data. In order to achieve the same amount of clean, normal walking data, both options would require the subject to walk for an overall longer time period which may induce fatigue. Fatigue is also known to cause changes in gait characteristics [53]. To avoid these other caveats, we chose to compare groups on the treadmill as opposed to looking at non-continuous or turning conditions.

Treadmill walking has the benefit of allowing for the collection of a large amount of continuous strides while avoiding turning or other path alterations. However, there are differences from overground walking. Because the treadmill acts as an external pacer, treadmill walking can reduce stride time variability, particularly in clinical groups such as Parkinsons disease who benefit from external pacing/cueing. Walking slower than ones preferred pace has been shown to increase variability [13], [54], [55], thus we chose a reduced speed condition to induce variability for the dual purposes of simulating more natural overground variability and to add complexity to test the algorithm.

Determining the timings of toe-offs and heel strike is a key feature of the proposed algorithm that was validated against a motion capture system. The algorithm should be able to detect such events for overground walking in real-life conditions (e.g., walking on a sidewalk) as well. However, real-life conditions can impose additional challenges (e.g., stopping on a red light) which are difficult to reproduce in laboratory settings and change the overall nature of the acceleration signal. Further investigation should be made into starting, stopping and turning events to see if the relevant data can be parsed, or require additional modifications.

In comparison to previous contributions (e.g., [26]–[32], [34], [36], [37], [39]), the proposed algorithm can accurately determine the timings of heel contact and toe off events with a single accelerometer. Furthermore, we validated our algorithm using a motion capture system. Lastly, we examined the performance of the proposed algorithm in healthy older adults and older subjects with neurological disorders including peripheral neuropathy and Parkinsons disease, whereas some of the previous contributions only examined healthy young subjects, which tend to have less obstructed gait than older adults.

A major limitation of the current study is that the motion capture system only allows data collection in a well-controlled environment. Future investigations should investigate the validity of the proposed algorithm in real-world conditions with the understanding that the motion capture data will not be accessible in such conditions. Hence, future studies will probably need to rely on footswitches for comparisons.

VI. Conclusion

An algorithm for extraction of stride cycle events from gait accelerometry signals is described. We validated the proposed algorithm against time series obtained via the motion capture system using data from 35 older adults while walking on a treadmill. Our results demonstrated that the proposed algorithm can accurately extract heel and toe events from gait accelerometry signals. Thus, the proposed algorithm can be utilized to acquire stride cycle events from inexpensive accelerometers while avoiding the limitations and costs of the current acquisition methods.

Biographies

Ervin Sejdić (S’00–M’08) received the B.E.Sc. and Ph.D. degrees in electrical engineering from the University of Western Ontario, London, ON, Canada, in 2002 and 2008, respectively.

He was a Post-Doctoral Fellow with Holland Bloorview Kids Rehabilitation Hospital/University of Toronto and a Research Fellow in medicine with the Beth Israel Deaconess Medical Center/Harvard Medical School. He is currently an Assistant Professor with the Department of Electrical and Computer Engineering (Swanson School of Engineering), the Department of Bioengineering (Swanson School of Engineering), the Department of Biomedical Informatics (School of Medicine), and the Intelligent Systems Program (Kenneth P. Dietrich School of Arts and Sciences) at the University of Pittsburgh, Pittsburgh, PA, USA. His research interests include biomedical and theoretical signal processing, swallowing difficulties, gait and balance, assistive technologies, rehabilitation engineering, anticipatory medical devices, and advanced information systems in medicine.

Dr. SEJDIĆ received prestigious research scholarships from the Natural Sciences and Engineering Research Council of Canada in 2003 and 2005. He also received the Melvin First Young Investigator’s Award from the Institute for Aging Research at Hebrew Senior Life in Boston, MA.

Kristin A. Lowry received the B.S. degree in physical therapy and the M.S degree in kinesiology from the University of Pittsburgh, Pittsburgh, PA, USA, in 1987 and 2002, respectively, and the Ph.D. degree in kinesiology from Iowa State University, Ames, IA, USA in 2010. She joined the Physical Therapy Department, Des Moines University, in 2013, as a Faculty Member, after her post-doctoral training in the School of Medicine, Division of Geriatrics, at the University of Pittsburgh. Her primary research interest is the measurement and retraining of walking skill. Specifically, her work focuses on investigating the control variables and tasks that best capture walking skill, and the development and comparison of gait rehabilitation interventions for older adults with mobility disability and persons with Parkinsons disease.

Jennica Bellanca received the B.S. degree in bioengineering from the University of Pittsburgh, in 2009, and the master’s degrees in bioengineering and mechanical engineering from the University of Pittsburgh, in 2011. She currently works as a part of the technology integration team at the Office of Mine Safety and Health Research, National Institute for Occupational Safety and Health. Her current projects include hazard recognition in stone stand and gravel operations, and the effect of attentional demands on task performance.

Subashan Perera received the Ph.D. degree in statistics from Kansas State University, in 2000. He was a Biostatistician with the Theo and Alfred Landon Center on Aging and an Assistant Professor with the Department of Preventive Medicine and Public Health, University of Kansas Medical Center, and moved to Pittsburgh in 2004. He is a Biostatistician with collaborative research interests in aging. His past research collaborations in aging were in areas of stroke, physical performance measures in the elderly, long-term care, bone health, and back pain. He currently serves as the Co-Director and Senior Statistician of the Data Management and Analysis Core with the Pittsburgh Claude D. Pepper Older Americans Independence Center. He has authored over 151 manuscripts in health science and statistical literature.

Mark S. Redfern received the Ph.D. degree in bioengineering from the University of Michigan, in 1988. He is currently the William Kepler Whiteford Professor with the Department of Bioengineering, University of Pittsburgh, with appointments in the Department of Physical Therapy, Department of Rehabilitation Science and Technology and the Department of Otolaryngology. He conducts research in the areas of human postural control, ergonomics, and injury prevention. He has over 120 peer-reviewed publications, 12 book chapters, and over 200 proceedings and meeting abstracts.

Jennifer S. Brach received the B.S. degree in physical therapy from East Carolina University, in 1992, the M.S. degree in physical therapy from the University of Pittsburgh, in 1994, and the Ph.D. degree in epidemiology from the Graduate School of Public Health, University of Pittsburgh, in 2000. She was a Post-Doctoral Scholar of Aging Research with the Department of Epidemiology and the Division of Geriatric Medicine with the University of Pittsburgh. She is currently an Associate Professor with the Department of Physical Therapy, University of Pittsburgh, Pittsburgh, PA. Her research interests include examining the contributors and consequences of abnormal gait in older adults and developing and testing taskspecific motor learning exercise programs to improve walking in older adults. She was the first nonphysician recipient of the prestigious Paul B. Beeson Career Development Award in Aging from the National Institute on Aging, the American Federation for Aging Research, The Atlantic Philanthropies, and The John A. Hartford Foundation. She was also a recipient of the American Geriatric Society New Investigator Award in 2005.

Funding Statement

This work was supported by the National Institute on Aging through the Pittsburgh Claude D. Pepper Older Americans Independence Center under Grant NIA P30 AG 024827.