An evaluation of constrained randomization for the design and analysis of group-randomized trials

Abstract

In group-randomized trials, a frequent practical limitation to adopting rigorous research designs is that only a small number of groups may be available, and therefore simple randomization cannot be relied upon to balance key group-level prognostic factors across the comparison arms. Constrained randomization is an allocation technique proposed for ensuring balance, and can be used together with a permutation test for randomization-based inference. However, several statistical issues have not been thoroughly studied when constrained randomization is considered. Therefore, we used simulations to evaluate key issues including: the impact of the choice of the candidate set size and the balance metric used to guide randomization; the choice of adjusted versus unadjusted analysis; and the use of model-based versus randomization-based tests. We conducted a simulation study to compare the type I error and power of the F-test and the permutation test in the presence of group-level potential confounders. Our results indicate that the adjusted F-test and the permutation test perform similarly and slightly better for constrained randomization relative to simple randomization in terms of power, and the candidate set size does not substantially affect their power. Under constrained randomization, however, the unadjusted F-test is conservative while the unadjusted permutation test carries the desired type I error rate as long as the candidate set size is not too small; the unadjusted permutation test is consistently more powerful than the unadjusted F-test, and gains power as candidate set size changes. Finally, we caution against the inappropriate specification of permutation distribution under constrained randomization. An ongoing group-randomized trial is used as an illustrative example for the constrained randomization design.

1. Introduction

Group-randomized trials (GRTs) are an attractive research design for evaluating the effect of interventions that target improved health care through modification to the way that providers, clinics, or entire organizations work to treat disease and prevent illness. This design is often used in practice when an individually randomized design is not feasible, possibly because there is potential contamination, or because the investigators wish to study the intervention effect on a group level [1, 2, 3]. In a standard randomized controlled trial (RCT), individuals can be assigned to alternative treatment modalities so that treatment is evaluated by comparing similar subjects across treatment groups within each enrolling clinic. However, many important health care delivery processes operate at the level of the provider, clinic, hospital, or system. For example, health care interventions that seek to deliver “collaborative care” change the structure or operation of an entire clinic by ensuring that various providers work together in a highly coordinated fashion [4]. In order to rigorously evaluate the impact of interventions that apply simultaneously to aggregate groups of subjects such as all patients attending a given clinic, GRTs are necessary. In what follows, we will use the words clinic and group interchangeably, although a group could be any unit under which individuals are considered to be treated similarly.

Frequently a major practical limitation to the use of GRTs is the ability to enlist and study a large number of clinics, and with a limited number of clinics we may not be able to rely on simple randomization to adequately balance important prognostic factors. For example, clinics within a health system may vary with respect to the size of their patient population, whether they treat primarily low income patients, whether they are within a metropolitan area, and other features of the clinics themselves. In addition, patient characteristics could vary over risk factors such as age, race, gender and education. Therefore, statistical methods that can control for important group-level or individual-level factors in the design of a trial or in the analysis are necessary and a comprehensive understanding of the operating characteristics of adjustment methods is needed to appropriately plan a study.

Individually randomized trials generally have sufficient sample sizes so that imbalances due to simple randomization are negligible [5]. In this paper we will refer to prognostic factors that may be imbalanced and therefore distort estimates of treatment effects as “potential confounders”. Foreseen subject-level potential confounders are sometimes handled through stratification [6]. However, potentially confounding factors at the group level are commonly seen in GRTs and these group-level potential confounders are likely to be unevenly distributed under simple randomization due to limited number of groups available in the study. In small GRTs with only a few heterogeneous groups, stratification could also be challenging because of insufficient number of groups to distribute among the many strata formed by a number of group-level potential confounders [7]. However, unlike most individually randomized trials, each participating group in a GRT often can be characterized with respect to these group-level potential confounders prior to randomization. For this situation, covariate-based constrained randomization was proposed as an allocation technique for achieving baseline balance across groups [8]. Briefly, this methodology includes (i) specifying the important potentially confounding factors; (ii) characterizing each prospective group in terms of these factors; (iii) either enumerating all or simulating a large number of potential randomization schemes; (iv) removing the duplicate allocation schemes if any, and (v) selecting a candidate subset of schemes where sufficient balance across potentially confounding covariates is achieved according to some pre-specified balance metric. Ultimately, one scheme is randomly selected out of this smaller candidate subset and the study is implemented using that scheme.

The first purpose of this work was to determine, in the context of small GRTs, whether constrained randomization improves the power of several commonly used tests as compared to simple randomization, while maintaining the size of the test. We also evaluated whether any improvement relied on how to measure the imbalance of group allocation as well as how to constrain the randomization set. In other words, we investigated whether specification of an effective balance metric and a proper candidate set size are crucial design concerns. Balance issues in GRTs were raised by Raab and Butcher [9], who introduced a balance criterion (B) assessing overall balance across covariates between the arms of a trial with illustration on a school-based GRT. This metric was adopted in a recent trial to evaluate obstetrical care [10]. De Hoop et al [11] proposed a “best balance” (BB) metric that led to optimal balance in GRTs. Their empirical findings suggested that constrained randomization with this metric outperformed simple randomization, minimization and matching in terms of quadratic imbalance scores. Building on these recent studies, we adapted the imbalance score (B), proposed by Raab and Butcher to balance group-level potential confounders in this simulation study. To assess whether different metrics impacted statistical inference, we proposed another balance metric, total balance score (TB), corresponding to a slightly modified version of the BB metric for constrained randomization.

Candidate set size is defined to be the number of possible randomization schemes in a specific implementation. Simple randomization draws from the complete set of candidate schemes, while constrained randomization considers a subset of schemes. Tight control with respect to balance naturally limits the size of the candidate set of randomization schemes from which to randomly select the final scheme. Impact of the tightness of control, as evidenced by candidate set size has not yet been detailed by previous studies on GRTs. Carter and Hood [12] extended the work by Raab and Butcher in that they randomized blocks of groups to achieve balance both within and between blocks. Though discussions were put forward in their study on the minimum size of the random component for each block from which the final design is selected, they did not examine the impact of change in the candidate set size at the inference level. We then considered a wide range of candidate set sizes for situations with different randomization space in small GRTs, investigating whether and in what way the constrained randomization space would lead to optimal analyses of the treatment effect.

The remainder of the paper is organized into five sections. In Section 2, we provide background on model-based and permutation methods for data analyses in GRTs. In Section 3, we describe the simulation study used to compare simple versus constrained randomization designs in the context of GRTs. In Section 4, we present the results of the simulation study. In Section 5, we use an ongoing group-randomized trial to illustrate the constrained randomization design. In Section 6, we discuss our findings and offer recommendations.

2. Model-based and Permutation Analyses for GRTs

Mixed-model regression methods are routinely used in the analyses of group-randomized trials since the random effects can account for shared variation at the group level that is in addition to the specific component of variance attributable to individual subjects [1, 2]. Shared random effects induce within-cluster correlation, and the corresponding intra-class correlation coefficient (ICC) measures the degree of similarity among observations taken from subjects within the same group [13]. Estimates of both treatment and covariate effects and variance components or ICCs can be obtained from model-based analyses of GRTs. Murray et al [14] reviewed the model-based methods commonly employed to reflect the design of GRTs. Specifically, mixed-model regression is flexible enough to adjust for covariates that are predictive of the outcome and which may be imbalanced across treatment groups and therefore considered as potential confounders. The linear mixed model is a form of multi-level model and permits covariates at both the group and subject level. In GRTs with continuous endpoints, the conventional model-based hypothesis testing of the fixed treatment effect involves calculating linear mixed model-based F-tests as an extension of standard analysis of variance (ANOVA).

Mixed model F-tests automatically adjust inference for the estimation of regression parameters. Conditional on estimates of random effect variance-covariance parameters, an adjusted treatment effect is estimated based on maximum likelihood or restricted maximum likelihood (REML) assuming normality [15].

When calculating the appropriate denominator degrees of freedom (df) of the F-test, it is critical to determine whether covariates in the regression model are at the group level or subject level [1, 15]. Generally, GRTs with a limited number of randomized groups will not allow estimation of several group-level potential confounding effects. Therefore it may not be possible to a priori specify an adjusted regression model analysis that will control for all group-level potential confounders in small GRTs.

A potential alternative to model-based covariate adjustment is to control for potential confounders by means of a constrained randomization design that purposely balances the distribution of selected measured characteristics across treatment arms. Trials that use constrained randomization may also use model-based analysis but such designs are particularly suited to the use of methods that rely only on the known randomization distribution.

First introduced by Fisher [16], permutation tests present a robust alternative to model-based methods in GRTs. Here, the outcome data are first analyzed based on the actual observed group allocation [17]. Second, the observed test statistic is then referenced against the exact permutational distribution calculated from all other possible allocation schemes. Under the strong null hypothesis of no treatment effect on any group-level means, the type I error rate of the permutation test will not exceed the nominal level [18]. The permutation test can be modified to adjust for group- and subject-level covariates by calculating an adjusted test statistic. When the normality assumption at the subject level in the mixed model is violated in small GRTs, an advantage in power for the permutation test compared to model-based methods was noted in cases when the ICC is large [19]. Edgington [20] provides detailed accounts on implementation of this randomization inference in common practice. In GRTs with only a limited number of groups, the calculation of the permutational distribution based on all possible allocation schemes is feasible with modern computational tools. However, the computational burden becomes nontrivial with increasing number of groups, and Monte Carlo sampling is often employed to approximate the complete randomization space by simulating a large number of allocation schemes.

The properties of alternative design and analysis approaches to covariate control for GRTs have not been sufficiently characterized in the current clinical trial literature and guidance is needed to inform appropriately designed and analyzed trials. In this study, we compared the performance of (i) unadjusted model-based F-test, (ii) unadjusted permutation test, (iii) adjusted model-based F-test, and (iv) adjusted permutation test, each calculated under both simple and constrained randomization. Previous studies [19] have demonstrated that in the case of simple randomization where subject-level potential confounders are present, the permutation test and the model-based F-test, whether unadjusted or adjusted, are similar to each other with regard to their type I error and power. To extend the previous work, we evaluated a more challenging scenario with group-level potential confounders and investigated the impact of constrained randomization in such comparisons by varying the design parameters introduced in Section 1 (namely choice of balance metric, candidate set size, and number of groups).

3. Methods for the Simulation Studies

We conducted a series of simulation studies based on a nested cross-sectional design with a single observation Y_ijk for each subject (k = 1, …, m), nested within each group (j = 1, …, g), nested within treatment arm (i = 1, …, c). The design was limited to c = 2 treatment arms and m = 300 subjects per group, which is typical of school- and worksite-based GRTs [19], and used one-to-one randomization of g groups to each treatment arm. To determine whether the comparison of different tests depends on the number of groups, we varied g using values of 5, 7, 9, 11 and 13. Three levels of the ICC were considered, 0.01, 0.05 and 0.1; this range encompasses the values most often reported for GRTs [2, 14, 21]. We held the number of group-level potential confounders constant for the data generation, but varied the number of these group-level potential confounders used when generating the constrained randomization schemes. For studies focused on the type I error rate, we fixed the treatment effect at zero; for studies focused on power, we fixed the treatment effect at 0.5 standard deviation unit. To ensure stable estimates for the type I error rate and power, we ran 10000 Monte Carlo iterations for each combination of the parameters.

3.1. Outcome Data Generation

To generate the outcome data, we simulated 4 subject-level continuous and 4 group-level binary covariates, each of which represents a “potential” confounder, in that it is constructed to be related to the outcome, but may or may not turn out to be related to treatment, depending on the randomization scheme. Let Y_ijk be the outcome of the kth subject in the jth group nested within ith treatment arm, we generated the outcome measure from the following linear mixed model:

$$Y_{ijk}={\mathit{Z}}_{ijk}^T\mathit{\alpha }+{\mathit{x}}_{ij}^T\mathit{\beta }+\gamma t_i+{\epsilon }_{ijk}$$ (1)

$$i=1,\dots ,c,j=1,\dots ,g,k=1,\dots ,m.$$

Here z_ijk is the vector of 4 subject-level covariates; x_ij is the vector of 4 group-level covariates. Each subject-level covariate was generated from a normal distribution with mean μ_ij and variance ${\sigma }_z^2=4$. Group-level means μ_ij were generated from a uniform distribution supported on (−2, 2). Each group-level covariate was independently simulated from a Bernoulli distribution with probability 0.3 (with a modest probability being either 1 or 0). Creating binary group-level potential confounders represents a pragmatic approach when the number of groups is not large. Examples include whether the group is associated with a teaching hospital, its geographic region (possibly represented by more than one binary covariate), or patient characteristics such as low versus high average age or income. Since their strengths of association were not of major interest, we held both the subject- and group-level coefficient vector α = β = 2_4×1. Let t_i be a binary treatment indicator taking values 0 and 1, depending on the realized randomization scheme. Error term ε_ijk was independently generated from a normal distribution with mean 0 and variance ${\sigma }_{\epsilon }^2=4$. Then the group-specific random effects b_ij were independently generated from a normal distribution with mean μ_b = 1 and variance ${\sigma }_b^2=\rho {\sigma }_{\epsilon }^2/(1-\rho )$.

3.2. Simple versus Constrained Randomization

For simple randomization scenarios, a single randomization scheme was generated and applied, irrespective of information regarding potential confounders. In contrast, the constrained randomization schemes allocated treatment in a subset of randomization schemes where sufficient balance was achieved according to pre-specified balance metrics. We denote S as the number of known group-level potential confounders to be balanced at the randomization stage and created scenarios with S ranges from 1 to 4. Thus in our study at least one group-level potential confounder was balanced under constrained randomization. Throughout, we considered two metrics for balance. The first balance metric, the imbalance score (B), was introduced by Raab and Butcher [9] and defined as:

$$\mathrm{B}=\sum _{l=1}^S{\omega }_l{({\overline{x}}_{0l}-{\overline{x}}_{1l})}^2,$$ (2)

where ω_l is a pre-determined weight for the lth group-level variable and x̄_0l, x̄_1l denote the average of group-level variable means from two treatment arms. Following Raab and Butcher, we adopted the weight for lth variable as the inverse of the variance of the group means. With weight ω_l to determine the relative contribution of each characteristic, the imbalance score seeks overall balance among group-level potential confounders.

De Hoop et al [11] proposed a “best balance” score (BB), which is expressed as a double sum of squared differences across group-level variables and across all levels for each variable:

$$\mathrm{B}\mathrm{B}=\sum _{l=1}^S\sum _{\tau }{(n_{0l\tau }-n_{1l\tau })}^2,$$ (3)

where n_0lτ, n_1lτ are the number of groups assigned to the two different treatment arms that have the τth level of the lth variable. This metric is similar to the imbalance score, but it only accommodates categorical group-level variables. We proposed a slightly modified version of this metric – total balance (TB) score, which is expressed as the sum of maximum absolute differences, where maximum is taken over all levels for each group-level variable as:

$$\mathrm{T}\mathrm{B}=\sum _{l=1}^S{\text{max}}_{\tau }\left|n_{0l\tau }-n_{1l\tau }\right|.$$ (4)

Similar to the BB score, the TB score is designed only to balance group-level variables. In particular, it seeks marginal balance across all group-level characteristics. Different from the imbalance score, the total balance score assumes equal contribution of each group-level potential confounder since no data-driven weights are attached to each variable.

3.3. Candidate Set Size Specification

In constrained randomization, the maximum candidate set size depends on the number of groups in the study. We used g = 5 and g = 7 to emulate extremely small GRTs where only a handful of groups are available to randomize. Under this configuration, a complete enumeration of all possible randomization schemes is computationally feasible. With more groups per arm (g ≥ 9), we simulated 20000 randomization schemes and removed duplicates to approximate the entire randomization space since complete enumeration would lead to intractable computation [22]. The balance metric B (TB) was calculated for each of the resulting randomization schemes. Because the absolute magnitude of B (TB) has no intuitive meaning, we constrained balance by setting the candidate set size and selected those randomization schemes with the smallest values of B (TB). The candidate set sizes were varied, starting at a minimum of 20. The study parameters for each configuration are summarized in Table 1.

Table 1.

Number of groups and candidate set size in constrained randomization. R represents candidate set size.

Scenario	g	Randomization Process	R
(i)	5	Enumerating 252 schemes	20/50/100/200
(ii)	7	Enumerating 3432 schemes	20/100/1000/2000/3000
(iii)	9	Simulating 20000 schemes	20/100/1000/5000/10000
(iv)	11	Simulating 20000 schemes	20/100/1000/5000/10000
(v)	13	Simulating 20000 schemes	20/100/1000/5000/10000

3.4. F-test versus Permutation Test

For both randomization designs, we considered a model-based F-test and a permutation test. To determine whether constrained randomization by itself could provide design-based control of group-level potential confounders, we compared both unadjusted and adjusted tests. Note that the “adjustment” here is with respect to the group-level potential confounders available prior to randomization. The subject-level covariates are collected as patients are recruited, often after group randomization, and they will be controlled for in all of the following analyses. For the unadjusted F-test, we fitted a linear mixed model with all subject-level but no group-level potential confounders. The test for the treatment effect H₀: γ = 0 is given by the usual F-test in linear regression models, conditioning on the restricted maximum likelihood estimate of the error variance [15]. The adjusted F-test additionally incorporated into the model S group-level potential confounders that had already been balanced by constrained randomization. Thus, it included design-based as well as model-based control for group-level potential confounders.

The unadjusted permutation test is adapted from Gail et al. [18]. First assuming subjects are independent, we fit a linear regression model using only subject-level covariates, leading to an estimator

$${\hat{Y}}_{ijk}=\hat{\mu }+{\mathit{z}}_{ijk}^T\hat{\mathit{\alpha }}.$$ (5)

The subject-level residuals were then computed as r_ijk = Y_ijk − Ŷ_ijk. Under the null hypothesis of no treatment effect, these residuals are independent of treatment assignments, and the average residuals of each group ${\overline{r}}_{ij·}=m^{-1}{\sum }_{k=1}^m{r}_{ijk}$ are exchangeable under the condition of equal group size [18]. The resulting test statistic is defined to be:

$$U={\overline{r}}_{2‥}-{\overline{r}}_{1‥}=g^{-1}(\sum _{j=1}^g{\overline{r}}_{2j·}-\sum _{j\prime =1}^g{\overline{r}}_{1j\prime ·})$$ (6)

The permutational (sampling) distribution for U is calculated using the entire randomization space in simple randomization. As discussed later, we found that misspecification of the permutational distribution in constrained randomization will lead to incorrect type I error rates. Therefore, in constrained randomization, the permutational distribution is calculated using only the constrained randomization space, and as a result, the 0.05 level test does not exist when the candidate set size R ≤ 20. The adjusted permutation test is similarly calculated by adding the S group-level confounders that had already been balanced in the constrained randomization to the equation (5).

All data generation and analyses were conducted in R (http://www.r-project.org) [23]. We used two-sided tests throughout the simulation study. For all tests, proportions of false positives and true positives were reported as Monte Carlo type I error rate and power. The nominal type I error was fixed at 0.05

4. Results from the Simulation Studies

4.1. Type I Error

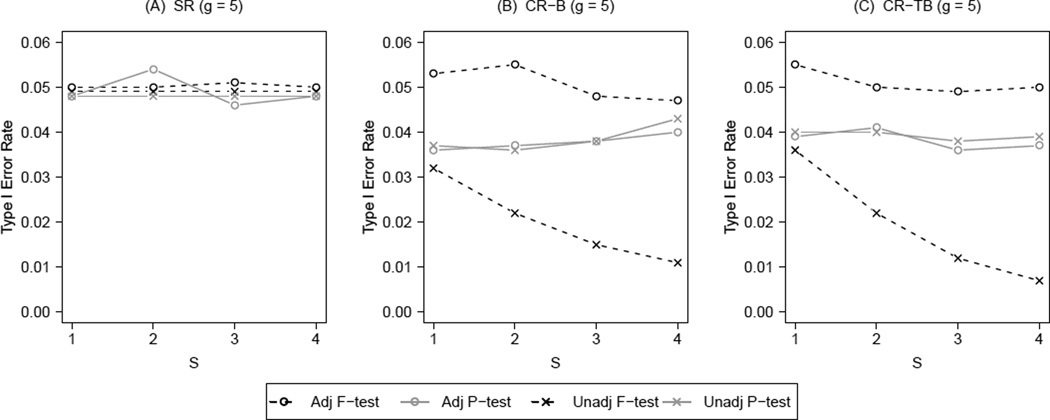
Figure 1 summarizes the results on type I error for the F-test and the permutation test under both simple randomization (SR) and constrained randomization (CR), with g = 5 (the worst case scenario) and different values of S. To simplify the presentation, we held the ICC fixed at 0.05 throughout, and chose candidate set size R = 100 for the constrained randomization. For the SR scenarios, the candidate set is the entire randomization space; no design-based adjustment is utilized. Therefore, any unadjusted test does not involve S and hence has a constant type I error rate against S; the adjusted test takes into account S group-level potential confounders by regression modeling. For the CR scenarios, S further indicates the number of group-level potential confounders adjusted for by the design. Results from CR using the imbalance score (panel B) and the total balance score (panel C) are contrasted with those from SR (panel A). Web Figure 1 to 4 summarizes corresponding results on type I error with g = 7, 9, 11 and 13.

Figure 1.

Type I error rate for F-test and permutation test with different number of group-level potential confounders (S) controlled in constrained randomization (CR) versus simple randomization (SR); B: imbalance score, TB: total balance score, g = 5, ICC = 0.05, R = 100.

With regard to Type I error, all scenarios consistently demonstrated a separation of the methods into three distinct patterns. In particular, there was little to no impact of the balance score and, importantly, the same pattern of results was seen from g = 5 to 13. The most notable pattern was that for the unadjusted F-test under CR. With only design-based adjustment, the unadjusted F-test under CR became more conservative with increasing g and S. In particular, the type I error rate monotonically decreased and actually approached zero when S = 4 and g greater than 7. A different pattern was seen with CR after model-based adjustment; performance in this case was similar to that of the SR F-test and the SR permutation test. They all maintained the desired type I error rate. The third pattern occurred with the unadjusted and adjusted permutation tests under CR, which behaved similarly to each other. However, their associated type I errors were consistently around 4 percent in this case, due to the stepwise nature of the exact p-value within a tightly constrained set. This phenomenon was only observed for small candidate set sizes; both permutation tests maintained their nominal type I error rates at 5 percent when R was at least 1000 (Web Figure 8).

4.2. Power

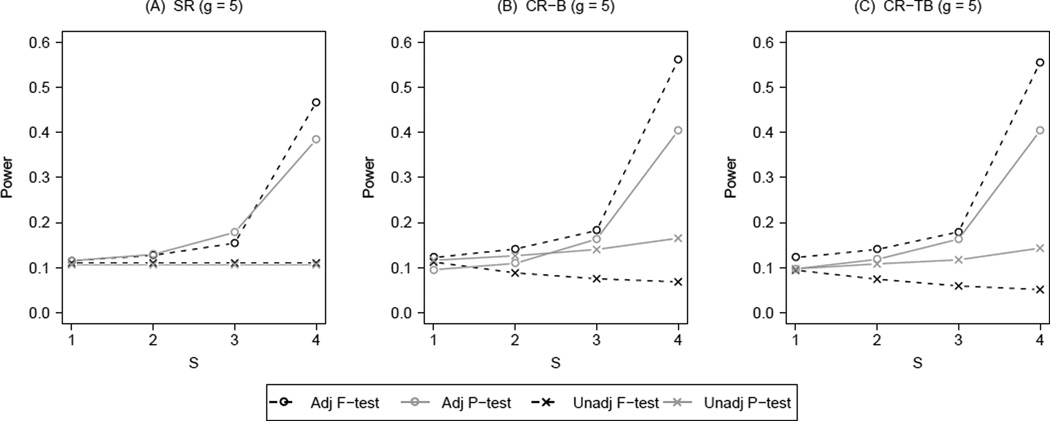
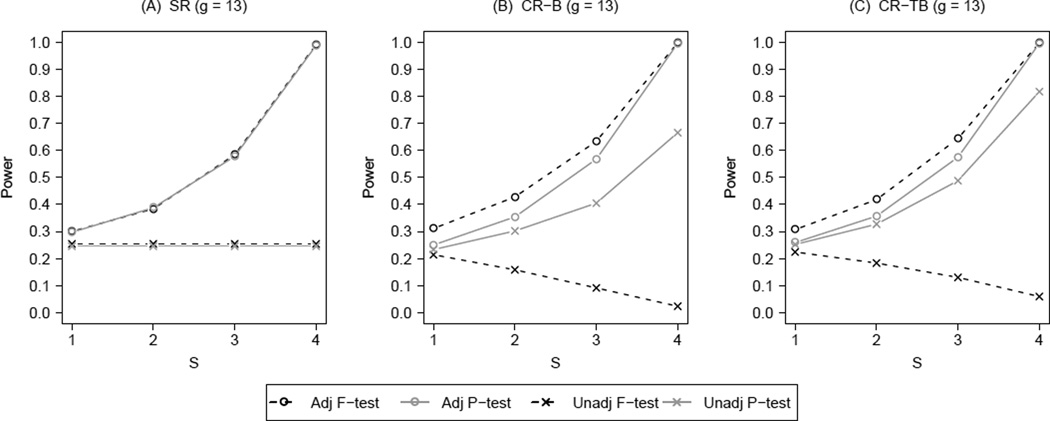
Figure 2 summarizes the results on power corresponding to Figure 1. Similar to Figure 2, Figure 3 presents the power results for g = 13 (the best case scenario). Results for g = 7, 9, 11 are available in Web Figure 5 to 7. Again, three distinct patterns emerged. For either balance metric, the unadjusted F-test under CR demonstrated decreasing power with increasing number of group-level potential confounders adjusted for by the design. Although power for the unadjusted permutation test under CR increased with S, it did not reach the levels attained by any of the adjusted tests. Under SR, the F-test and the permutation test had similar power at S ≤ 3 for all g. When S = 4 at g = 5, 7, 9, F-test was slightly better due to its perfectly correct model assumptions; as g further increased, this difference disappeared since their power reached 1. Under CR, the adjusted permutation test demonstrated similar power to the two simple randomization tests. The highest power was consistently achieved with the adjusted F-test under CR, although the gain over adjusted tests under SR was marginal. By combining design-based and analysis-based control of potential confounders, the two adjusted tests under CR were more powerful than their unadjusted versions. The balance metrics made a difference for the unadjusted permutation test. Of note, CR using the imbalance score (CR-B, S = 4) led to a more powerful unadjusted permutation test at g = 5, 7, while CR using total balance score (CR-TB, S = 4) led to a more powerful such test at g = 11, 13. This difference was as large as 11 percent at g = 7 and 15 percent at g = 13.

Figure 2.

Power for F-test and permutation test with different number of group-level potential confounders (S) controlled in constrained randomization (CR) versus simple randomization (SR); B: imbalance score, TB: total balance score, g = 5, ICC = 0.05, R = 100.

Figure 3.

Power for F-test and permutation test with different number of group-level potential confounders (S) controlled in constrained randomization (CR) versus simple randomization (SR); B: imbalance score, TB: total balance score, g = 13, ICC = 0.05, R = 100.

4.3. Candidate Set Size and Balance Metric

To characterize the impact of the candidate set size for constrained randomization, we present the results on type I error and power for selected tests in Table 2 and Table 3. Table 2 summarizes Monte Carlo type I error rate for both unadjusted and adjusted F-tests as well as permutation tests under different CR scenarios using the imbalance score (B) at g = 7 and g = 11. The different CR scenarios are represented by different candidate set sizes R. The results are compared with SR scenarios, where the candidate set includes all 3432 and 705432 randomization schemes, respectively. In Table 2, all CR scenarios used 4 group-level potential confounders in the balance metric; the adjusted F- and permutation tests controlled for all 4 group-level potential confounders in the regression, i.e., those tests were fully adjusted. Under SR, all tests approximately maintained the nominal type I error at both levels of ICC. Under CR, while the adjusted F-test carried the desired type I error rate at all levels of R and ICC, the unadjusted F-test grew conservative with decreasing R and at both levels of the ICC. In particular, the type I error almost disappeared at R ≤ 100 and ICC = 0.01. The type I error rate for both unadjusted and adjusted permutation tests were around 4 percent at R = 100. With larger candidate set size, the type I error rate for the permutation test held steady at 5 percent at all levels of ICC. Type I error patterns for CR using the total balance score (TB) were similar (Web Table 1).

Table 2.

Type I error rate for the unadjusted and adjusted tests under simple versus constrained randomization using imbalance score (B) with g = 7 and g = 11. All four group-level potential confounders were adjusted in constrained randomization (S = 4) and in any given adjusted test; candidate set size (R) are varied under constrained randomization.

				Type I error rate
	Randomization	ICC	R	Unadj F-test	Unadj P-test	Adj F-test	Adj P-test
g = 7	Constrained	0.01	20	0.000	–	0.050	–
	Constrained	0.01	100	0.000	0.040	0.051	0.039
	Constrained	0.01	1000	0.001	0.050	0.048	0.047
	Constrained	0.01	2000	0.008	0.050	0.047	0.047
	Constrained	0.01	3000	0.032	0.052	0.049	0.051
	Simple	0.01		0.051	0.046	0.049	0.047
	Constrained	0.1	20	0.001	–	0.050	–
	Constrained	0.1	100	0.001	0.038	0.051	0.037
	Constrained	0.1	1000	0.004	0.051	0.049	0.049
	Constrained	0.1	2000	0.012	0.048	0.053	0.049
	Constrained	0.1	3000	0.031	0.052	0.052	0.048
	Simple	0.1	–	0.058	0.048	0.048	0.049
g = 11	Constrained	0.01	20	0.000	–	0.053	–
	Constrained	0.01	100	0.000	0.038	0.052	0.040
	Constrained	0.01	1000	0.000	0.050	0.051	0.051
	Constrained	0.01	5000	0.000	0.050	0.051	0.050
	Constrained	0.01	10000	0.002	0.049	0.050	0.050
	Simple	0.01	–	0.051	0.047	0.052	0.048
	Constrained	0.1	20	0.000	–	0.052	–
	Constrained	0.1	100	0.000	0.040	0.046	0.041
	Constrained	0.1	1000	0.000	0.050	0.051	0.049
	Constrained	0.1	5000	0.002	0.050	0.045	0.050
	Constrained	0.1	10000	0.007	0.052	0.051	0.049
	Simple	0.1	–	0.047	0.047	0.048	0.051

Table 3.

Power for the unadjusted and adjusted tests under simple versus constrained randomization using imbalance score (B) with g = 7 and g = 11. All four potential group-level confounders were adjusted in constrained randomization (S = 4) and in any given adjusted test; candidate set size (R) are varied under constrained randomization.

				Power
	Randomization	ICC	R	Unadj F-test	Unadj P-test	Adj F-test	Adj P-test
g = 7	Constrained	0.01	20	0.013	–	1.000	–
	Constrained	0.01	100	0.015	0.579	1.000	0.999
	Constrained	0.01	1000	0.040	0.270	1.000	0.999
	Constrained	0.01	2000	0.086	0.236	1.000	0.996
	Constrained	0.01	3000	0.123	0.170	0.999	0.980
	Simple	0.01	–	0.148	0.143	0.996	0.946
	Constrained	0.1	20	0.022	–	0.638	–
	Constrained	0.1	100	0.025	0.371	0.631	0.544
	Constrained	0.1	1000	0.046	0.209	0.608	0.576
	Constrained	0.1	2000	0.084	0.196	0.574	0.536
	Constrained	0.1	3000	0.118	0.158	0.546	0.511
	Simple	0.1	–	0.137	0.135	0.516	0.477
g = 11	Constrained	0.01	20	0.007	–	1.000	–
	Constrained	0.01	100	0.010	0.678	1.000	1.000
	Constrained	0.01	1000	0.026	0.719	1.000	1.000
	Constrained	0.01	5000	0.105	0.519	1.000	1.000
	Constrained	0.01	10000	0.153	0.393	1.000	1.000
	Simple	0.01	–	0.223	0.220	1.000	0.999
	Constrained	0.1	20	0.022	–	0.898	–
	Constrained	0.1	100	0.024	0.464	0.896	0.839
	Constrained	0.1	1000	0.041	0.526	0.888	0.882
	Constrained	0.1	5000	0.106	0.413	0.883	0.876
	Constrained	0.1	10000	0.145	0.331	0.875	0.865
	Simple	0.1	–	0.202	0.201	0.827	0.800

Table 3 summarizes the power for the same tests at all levels of R with g = 7 and g = 11. Each cell in Table 3 corresponds to a scenario in Table 2. Four patterns were apparent. First, except for the unadjusted F-test, larger values of ICC led to decreased power for a given test regardless of randomization design. Second, the adjusted tests were much more powerful than their unadjusted counterparts. Third, the unadjusted F-test had low power under either randomization design and power decreased with decreasing candidate set size R. In contrast, the unadjusted permutation test gained power with decreasing R compared with the same test under SR. Finally, the decrease in candidate set size slightly improved the power of both adjusted tests, but not always monotonically for the adjusted permutation test. For instance, at g = 7, 11 and ICC = 0:1 under CR using imbalance score (B), the adjusted permutation test decreased power when R decreased from 1000 to 100. In Web Table 2, this same phenomenon was again seen under CR using total balance score (TB).

Web Table 2 summarizes the power for these tests at all levels of R with g = 7 and g = 11 with total balance score (TB) under CR. Each cell in Web Table 2 corresponds to a scenario in Table 3 and was compared with Table 3. Though little evidence was found in these scenarios to favor one balance metric over the other, major differences in power for the unadjusted permutation test appeared when the candidate set size is relatively small. At g = 7 and both levels of ICC, the unadjusted permutation test was substantially more powerful using imbalance score (B) with R = 100. However at g = 11, CR using total balance score (TB) led to a much more powerful unadjusted permutation test when R = 100. Further, at g = 11 and both levels of ICC, the unadjusted permutation decreased power under CR using imbalance score (B) when R decreased from 1000 to 100, but this test gained power under CR using total balance score (TB) when R decreased from 1000 to 100.

4.4. Number of Groups and Subjects

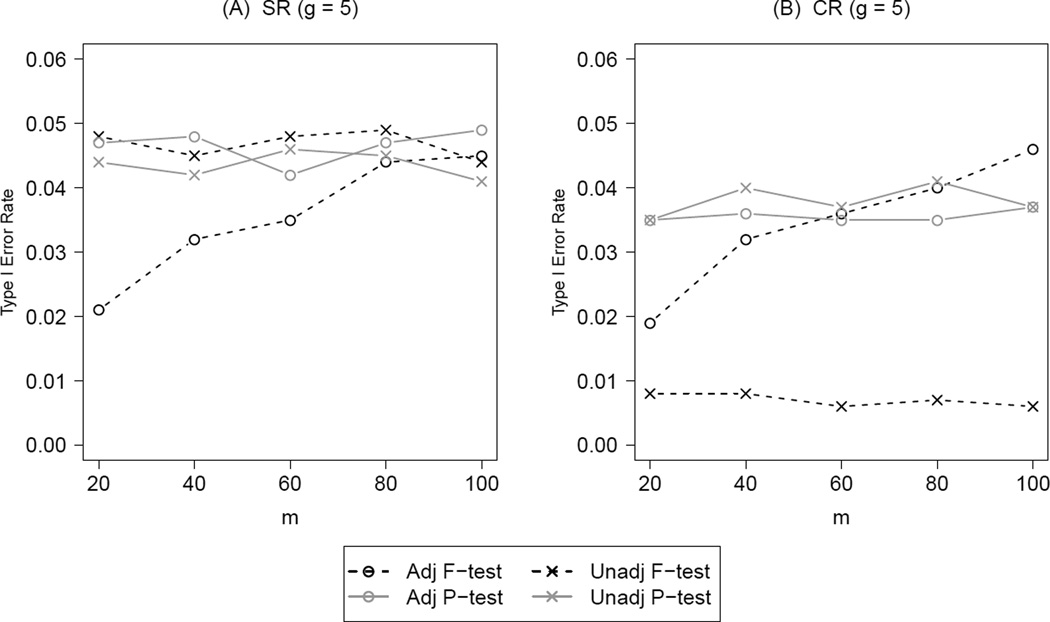
To caution the use of model-based methods in small samples where only a few subjects are available in a group, we compared four tests varying the number of subjects per group at g = 5 and g = 13 (the worst and best case scenarios in terms of the number of groups). The four tests are identical to the ones studied previously, i.e., all four group-level potential confounders were adjusted in constrained randomization and in any given adjusted test. Figure 4 summarizes the results on type I error under both SR (panel A) and CR (panel B) at g = 5 with different values of m, staring at 20. We held the ICC fixed at 0.05 and chose candidate set size R = 100 for CR to simplify the presentation. Under SR, all tests maintained the desired type I error regardless of m except for the adjusted F-test. Although the adjusted F-test was derived from the correct model, its asymptotic properties did not hold if only a few groups with a few subjects were available. The type I error rate for the adjusted F-test at m = 20 was only 2 percent. As m increased to 100, the type I error rate increased to around 5 percent. Under CR with R = 100, the two permutation tests were slightly conservative due to the stepwise nature of the associated p-values within a tightly constrained set; the unadjusted F-test became extremely conservative as before. Just as under SR, the adjusted F-test under CR was conservative with small m and retained its nominal size at m = 100.

Figure 4.

Type I error rate for the unadjusted and adjusted tests under both simple randomization (SR) and constrained randomization (CR) at g = 5, ICC = 0.05 with increasing number of subjects (m) per group. Under CR, the total balance score (TB) metric was used and the candidate set size R = 100. All four potential confounders were adjusted in constrained randomization (S = 4) and in any given adjusted test.

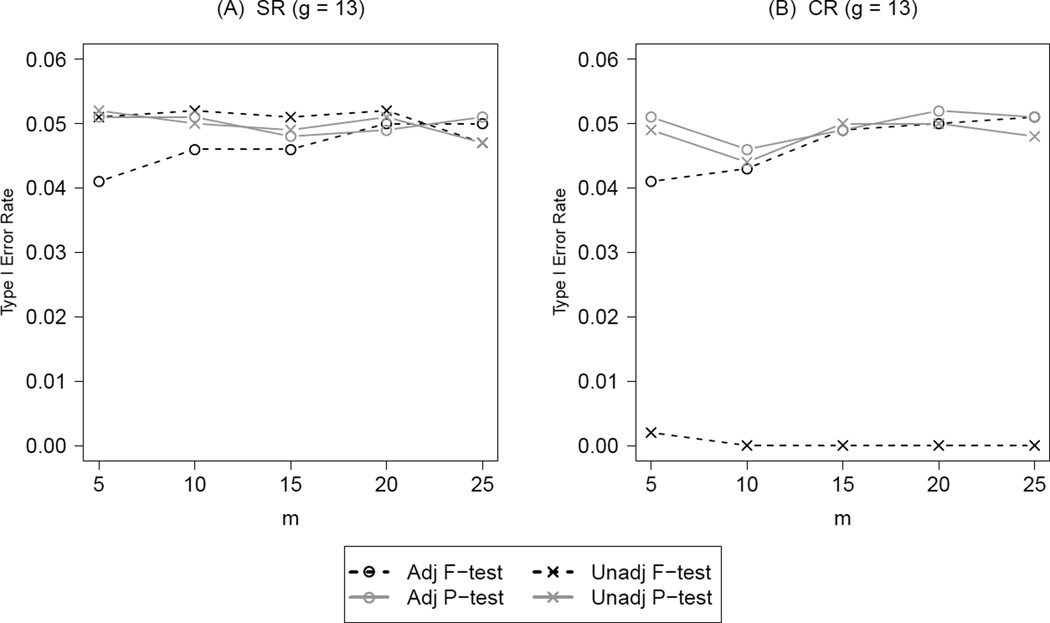
The situation is different when more groups are available even if the number of subjects per group is extremely small. Figure 5 summarizes the results on type I error under both SR (panel A) and CR (panel B) at g = 13 with different values of m, from 5 to 25.We held the ICC fixed at 0.05 and chose candidate set size R = 1000 for CR to simplify the presentation. Unlike Figure 4, the adjusted F-test under SR and CR was slightly conservative (0.04) only at m less than 20. With this larger candidate set size, the two permutation test carried the desired type I error rate regardless of m.

Figure 5.

Type I error rate for the unadjusted and adjusted tests under both simple randomization (SR) and constrained randomization (CR) at g = 13, ICC = 0.05 with increasing number of subjects (m) per group. Under CR, the total balance score (TB) metric was used and the candidate set size R = 1000. All four potential confounders were adjusted in constrained randomization (S = 4) and in any given adjusted test.

4.5. Misspecified Permutation Test

Finally, we caution the use of the permutation test under CR. This permutation test should be performed such that only the constrained subset is used to calculate the permutational (sampling) distribution, rather than using the entire randomization space. Web Figure 9 illustrates the consequences of this misspecification for unadjusted and adjusted permutation tests under CR (using the total balance score) with g = 5 and ICC fixed at 0.05. In each panel, S represents the number of group-level potential confounders controlled for by the design. Notably, the unadjusted misspecified permutation test became more conservative with increasing S and decreasing R. In contrast, the adjusted permutation test carried an inflated type I error rate under misspecification; the inflation grew worse as S increased and R decreased. With increasing S and decreasing R, the unadjusted permutation test became less powerful when using the misspecified permutational distribution, but the adjusted test gained power. The same patterns held for g = 13 (Web Figure 10). The similarity between these results and the unadjusted F-test under CR in Figure 1 and Figure 2 leads us to conjecture that the unadjusted F-test under CR fails to accommodate the change in the randomization space when calculating the sampling distribution of the test statistic.

5. Constrained Randomization Example

We illustrate the constrained randomization procedure using data from an ongoing group-randomized trial [24]. This GRT aims to compare population-based with practice-based reminder-recall (R/R) approaches for increasing up-to-date immunization rate in 19 to 35 month old children from 16 counties in Colorado. Each county is a randomization group; 8 groups are randomized to either R/R approach. The population-based approach relies on the collaborative efforts among primary care physicians and health department leaders to develop a centralized R/R notification, either using telephone or mail, for all parents whose 19-to-35-month-old children were not up-to-date on immunization. On the other hand, eligible parents from the practice-based arm are invited to attend a Webinar training on R/R using Colorado Immunization Information System (CIIS).

At the randomization stage, 9 county-level potential confounders that may be associated with the study outcome are identified. These county-level variables are obtained directly from the U.S. Census and the Colorado Immunization Information System. Among them are whether a county locates in the urban or rural area, number of Community Health Centers (CHCs), ratio of Pediatric to Family Medicine practices (PM-to-FM ratio), percent of children between 0 to 4 months who had over 2 immunization records in CIIS (% in CIIS), number of eligible children, percent up-to-date rate at baseline, percent Hispanic, percent African American and average income. Given the mix of binary and continuous variables, we choose the imbalance score (B) to assess balance and obtain its distribution in Web Figure 11. The arrow indicates the maximum value of the balance score allowed to achieve a candidate set size of 1000. We then compare the group-level variable means from two schemes selected by constrained and simple randomization. The first scheme is randomly selected within the constrained set of size 1000, corresponding to a balance score of 8.51; the other scheme is selected ignoring the covariate information by simple randomization, corresponding to a balance score of 55.31. Table 4 presents the group-level variable information by treatment arm. Unlike the realized scheme from CR, the scheme from SR has assigned one more urban county to the population-based arm; larger mean differences across arms with respect to the continuous group-level variables are seen from the realized scheme by SR.

Table 4.

Group-level variable information by treatment arm from two randomization schemes independently selected from (1) constrained randomization (CR) with B metric and candidate set size 1000; (2) simple randomization (SR). Except for the variable ‘number of urban counties’, all variables are compared with respect to the group-level means by arm.

Variable	CR		SR
	Population-based	Practice-based	Population-based	Practice-based
# of urban county	4 (50%)	4 (50%)	5 (62.5%)	3 (37.5%)
# CHCs	4	5	4	5
PM-to-FM ratio	0.28	0.28	0.25	0.32
% in CIIS	86.9	87.5	88.3	86.1
# of children	3879	4514	2311	6082
% up-to-date at baseline	41.9	39.8	37.0	44.6
% Hispanic	19.0	25.6	27.0	17.8
% African American	2.4	3.4	1.6	4.1
Average income ($1000/yr)	54.6	52.3	50.9	56.1
Imbalance score of the scheme	B = 8.51		B = 55.31

Although this is only a single realization, we observe the potential for imbalance due to SR. At the implementation stage, additional subject-level variables will be collected from each participant. Those subject-level variables believed to be associated with the study outcome, together with the county-level variables adjusted for by the design, should be taken into account in the primary analysis.

6. Discussion

Covariate-adjustment remains a key design and analysis issue for GRTs. Under the context of small GRTs, there are no clear guidelines on when to adjust for important group-level prognostic factors in the current literature. On-going debate exist whether to adjust for these potential confounders at the design stage alone, at the analysis stage alone, or at both the design and analysis stages. In this paper, we provided substantial evidence that the analysis-based adjustment, whether using a model-based or permutation approach, is always necessary even after design-based adjustment, i.e., covariate-based constrained randomization. Throughout, the unadjusted F-test did not have valid size and was the least powerful under constrained randomization, as compared to its adjusted version. The unadjusted permutation test under constrained randomization was also improved using additional analysis-based adjustment.

Similar to previous reports [19], we confirmed there is little evidence to distinguish the F-test and permutation test in terms of their type I error rate and power under simple randomization with normally distributed outcomes, both for unadjusted and adjusted analyses (in terms of group-level covariates). However, our work provided noteworthy extension for the same comparisons under constrained randomization scenarios.

Under constrained randomization, the unadjusted F-test grew conservative and did not gain power, both with respect to increasing the number of group-level potential confounders controlled by design and decreasing the candidate set size. In this case, constrained randomization appears to reduce the standard error of the estimator for treatment effect, leading to smaller regression sum of squares and hence a smaller F-statistic than simple randomization. In the long run, we are much less likely to reject the null hypothesis.

This same behavior was observed for the unadjusted permutation analysis when the sampling distribution ignored the change in the allocation space. There is little practical discussion in the current clinical trial literature on how to implement the permutation test within a constrained randomization space for GRTs. We found in our study that a permutation test should be referenced against the permutational distribution calculated based on the chosen candidate set of balanced treatment allocation schemes. Misspecification of the permutational distribution based on all possible allocations, as would be done with simple randomization, led to an incorrect type I error rate.

Our results further indicate that the unadjusted permutation test, referenced against the constrained distribution space, not only could maintain the nominal type I error rate but also could improve power given an appropriate candidate set size. The candidate set size should not be too small in case that the associated type I error rates are lower than 5 percent; on the other hand, a large candidate set size did not substantially improve power of the permutation tests compared with the those implemented under simple randomization. In our study, we found that in the cases where R = 1000, all permutation tests carried the desired type I error rate and improved power relative to the same tests implemented with a larger candidate set size. However, it is important to realize when g = 5, the maximum candidate set size achievable (under simple randomization) is less than 300. Therefore, any permutation test under constrained randomization is more likely to carry a type I error rate around 4 percent (Web Figure 8).

We believe that constrained randomization by itself can offer design-based control of group-level potential confounders if one uses the unadjusted permutation analysis. The improvement in power is limited when the number of randomization units is small (g = 5) and becomes substantial as the number of randomization units increases (g = 13). However, any unadjusted permutation test can still be improved upon using additional analysis-based adjustment, even under constrained randomization.

The adjusted analysis, whether F- or permutation, gave better power than the corresponding unadjusted analysis under constrained randomization while maintaining the correct type I error rate (as long as the candidate set size is not too small for permutation analysis). However, constrained randomization did not substantially improve the power of the adjusted test over simple randomization, indicating that analysis-based adjustment dominated the power gain. Nevertheless, model-based adjustment sometimes imposes assumptions that may not be realistic. Additionally, mixed-models typically use an iterative algorithm to optimize the likelihood and the algorithm may not always converge. It is likely that in practice investigators may desire to control more group-level characteristics than the available handful of groups will support for a model-based analysis. In these cases, permutation analysis represents a more practical alternative to the mixed-model methods.

The choice of the two balance metrics considered in our study did not make a substantial difference in terms of type I error. However, the imbalance score (B) seemed more effective in improving power of the unadjusted permutation test at certain cases when g = 5 and g = 7 while the total balance score seemed more effective when g is larger. For the most part, the two balance metrics behaved similarly for constrained randomization.

A more critical design element is the candidate set size, which correlated with large differences in power, most typically for the unadjusted permutation analysis. We observed strong design-based control of group-level potential confounders with decreasing size of the randomization space. However, we offer several comments underlying this point. First, an overly restricted randomization subset will not support a permutation analysis for a fixed size. For instance, a 0.05 level permutation test does not exist for R ≤ 20. Second, overly constrained randomization may violate the validity of the design and may raise ethical considerations by limiting the allocation possibility of certain groups [8]. In a different context, Carter and Hood [12] proposed the minimum candidate set size in accordance with the principles of the ICH guidance on randomness [25, 26], stating that R = 100 would be appropriate for g less than 9, and R = 1000 is required for larger g. Third, it is not always the case that both unadjusted and adjusted permutation tests gain power with a smaller candidate set size. In fact, we observed in our study that overly constrained randomization decreased the power of those tests.

It is a well known percept that the number of groups is a more critical design consideration than the number of subjects per group in GRTs. We confirmed this point in our study and further cautioned against the use of model-based methods in small samples. The adjusted F-test, under both randomization designs, did not have valid size at g = 5 and a few subjects per group. As g increased to 13, even though the number of subjects are much fewer, the adjusted F-test remained valid. In contrast, the permutation analysis maintained validity throughout.

Other study parameters had the expected impact on the analysis. For instance, except for the unadjusted F-test, increasing the magnitude of the ICC reduced the effective sample size [2] and hence decreased power for a given test, but the test approximately maintained the nominal size regardless of ICC.

A possible limitation of this study is that our scenarios all had the same number of groups per arm as well as same number of subjects per group. In other words, the simulations were run with a balanced design. Design balance at the group level is commonly seen in GRTs, though there are exceptions where a school or a worksite withdraws from the trial after randomization. Design balance at the subject level is not common, and the number of subjects per group often varies considerably within a single study. Previous work suggests that unbalanced design at the subject level has little effect on the type I error rate or power for either test, so long as the design balance is retained at the group level and the assumption of homogeneity of variance across groups is not too badly violated [18, 19, 27]. The mixed-model methods performed well even when the design is unbalanced at the group level unless the distribution of the group-level errors is extremely skewered or heavy-tailed, g is small, and the ICC is large [28]. The permutation test, however, will not guarantee valid size if the design is unbalanced at the group level [18].

Another limitation is that we only considered binary group-level potential confounders and generated those confounders independently from one another. Multi-category and continuous group-level potential confounders are encountered in practice and need to be addressed for constraining the randomization set. The former is a natural extension of binary potential confounders with dummy variable representation; the latter can be balanced easily by the imbalance score (B), as in the reminder/recall trial for vaccination. Note that in this regard, the total balance score (TB) is likely to be less effective than the imbalance score because (i) categorization of continuous variables is arbitrary and inevitably loses information; and (ii) the data-driven weight term in the imbalance score is designed for better balance among heterogeneous variables [9]. In addition, it is possible for potential confounders to be correlated. Correlation among those confounders, in fact, should not have more serious consequences, as one confounder could always act as a surrogate for the other and a certain level of balance for the other is automatically achieved if either one is balanced.

In our simulations, we generated the outcome data from a linear mixed model and subsequently the fully adjusted F-test was applied to the regression with the correct modeling assumptions. It is therefore expected that the fully adjusted F-test had an advantage over the fully adjusted permutation test. Thus a third limitation is that our exploration did not consider the violation of normality assumptions at both the group and the subject level. However, we believe that violation at the subject-level will yield similar results to our study, as both model-based and permutation analysis are robust to this violation [18, 19, 28]. Previous findings [19, 28] indicate that violation at the group level has more serious consequences but, in general, the linear mixed model is robust to modest violation of normality assumption at the group level as long as the design balance is retained at the group level. When the group-level error distribution is extremely skewed or heavy-tailed, permutation test gained advantage.

Finally, the value for g considered in this investigation ranged from 5 to 13. We allowed small values of g in order to study the performance of the analysis methods with constrained randomization under challenging circumstances. We found throughout the paper that small GRTs limit the efficacy of design-based control of variables. With only a handful of groups available the entire allocation space is not large enough so that any restriction of that space had limited ability to improve the power of a given test. As is widely recognized, smaller studies will have less power than larger studies. ICC values reported for GRTs in public health and medicine often fall in the range 0.01–0.05, and in this range, adequate power for modest treatment effects typically requires 8–12 groups per arm [1]. Previous research [1, 2] advocated that investigators obtain an accurate ICC estimate from their target population so that they can plan a study large enough to accommodate the level of ICC expected in their data. Our results reinforced that recommendation.