Covariance estimators for Generalized Estimating Equations (GEE) in longitudinal analysis with small samples

Abstract

Generalized Estimating Equations (GEE) is a general statistical method to fit marginal models for longitudinal data in biomedical studies. The variance-covariance matrix of the regression parameter coefficients is usually estimated by a robust “sandwich” variance estimator, which does not perform satisfactorily when the sample size is small. To reduce the downward bias and improve the efficiency, several modified variance estimators have been proposed for bias-correction or efficiency improvement. In this paper, we provide a comprehensive review on recent developments of modified variance estimators, and compare their small-sample performance theoretically and numerically through simulation and real data examples. In particular, Wald tests and t–tests based on different variance estimators are used for hypothesis testing, and the guideline on appropriate sample sizes for each estimator is provided for preserving Type I error in general cases based on numerical results. Also, we develop a user-friendly R package “geesmv” incorporating all of these variance estimators for public usage in practice.

1. Introduction

Longitudinal data is commonly encountered in biomedical studies [1, 2, 3, 4]. For example, in a diabetes study, repeated primary efficacy measures on HbA1c were taken over time (baseline and follow-up visits after treatment) for each patient, and the question of interest was to investigate the trend of HbA1c changing over time or the insulin treatment effect on HbA1c [5]. For such a situation, the responses from the same individual turn to be “more alike”, thus incorporating within-subject correlation and between-subject variations into model fitting is necessary to improve the efficiency of the estimation and enhance the power.

To analyze repeated measures, several simple traditional approaches exist (i.e., MANOVA) [6]. However, mixed-effect models (MEM) [2] and Generalized Estimating Equations (GEE) [7] are popularly applied. Of note, MEM is an individual-level approach that is able to adopt random effects to capture the correlation among observations from the same subject [8]; GEE is a population-level model based on the quasi-likelihood function [9, 10]. In this paper, we focus on GEE which holds several defining features: 1) Under mild regularity conditions, the parameter estimates are consistent and asymptotically normal even under the mis-specified “working” correlation structure of the responses; 2) When the inference is intended to be population-based, for instance, the overall treatment effect, GEE treats the variance-covariance matrix of the responses as nuisance parameters [9]; 3) GEE relaxes the distribution assumption, and only requires correct specification of marginal mean and variance as well as the link function between the mean and covariates of interest. GEE has been implemented in statistical software (i.e., SAS, R), and can be directly adopted for analysis.

It is known that the variance estimators of parameters of interest are utilized in hypothesis testing, thus its accuracy is important for valid inference. Under some specific conditions such as small sample size, the traditional GEE with the classic “sandwich” variance estimator does not perform satisfactorily, and considerable downward bias is exhibited [11, 12, 13, 14], in turn leading to inflated type I errors and lower coverage rates of the resulting confidence intervals [15, 16]. Until now, several remedy strategies on modifications of variance estimators have been proposed to improve the finite small-sample performance [13, 17]. To our knowledge, few studies exist to cover various variance estimators including the most recently developed ones on GEE with small samples for comprehensive comparisons, and there is a lack of a guideline on the adequate sample size for preserving Type I error. Note that the recent paper related to this area was discussed by Li and Redden [18] with emphasis on the small sample performance of bias-corrected sandwich estimators particularly for cluster-randomized trials with binary outcomes. However, this work has several limitations: 1) only the scenarios with binary outcomes were considered; 2) the influence of misspecified correlation structure was not explored; 3) The degrees of freedom of the approximate t–distribution did not take the variability of the variance estimator into account [16, 19, 20], but only depended on the number of clusters; 4) limited variance estimators implemented by SAS were considered, but the most recent ones were not. In this paper, we attempt to address these issues and provide a more comprehensive and accurate comparisons of different modified variance estimators. Furthermore, we develop a user-friendly R package including functions for calculating the modified variance estimators as well as the degrees of freedom defined as a function of the variance of the estimator for t–tests [16, 20].

The remainder of the article is organized as follows. In Section 2, we introduce the notations and provide nine variance estimators of GEE as well as their theoretical comparisons. In addition, two types of hypothesis testing, Wald tests and t–tests, are emphasized. Later, in Section 3, we provide extensive simulation to compare the performance of different variance estimators, and identify the suitable sample size for each to ensure their satisfactory performance in controlling Type I error. Importantly, we develop an R package “geesmv” for public use with small samples. Also, we illustrate the application of our R package via a real data example in Section 4. The conclusion with a brief discussion and future work is shown in Section 5.

2. Method

2.1. Notation and GEE

Given longitudinal data consisting of K subjects, denote Y_ij as the j^th response for the i^th subject with n_i observations, i = 1, 2, …, K, j = 1, …, n_i, and X_ij is a p × 1 vector of covariates. Y_i = (Y_i1, Y_i2, …, Y_ini)′ denotes the response vector with the mean vector noted by μ_i = (μ_i1, μ_i2, …, μ_ini)′ where μ_ij is the corresponding j^th mean for subject i. There exists within-subject correlation, but the observations across subjects are assumed to be independent. In addition, the marginal model specifying an association between μ_ij and the covariates of interest X_ij is given by

$$g({\mu }_{ij})={\mathit{X}}_{ij}^{\prime }\mathbf{\beta }$$ (1)

with g as a known link function, β an unknown p × 1 vector of regression coefficients. The conditional variance of Y_ij given X_ij is Var(Y_ij|X_ij) = ν(μ_ij)ϕ with ν as a known variance function of μ_ij and ϕ a scale parameter which may need to be estimated. Of note, ν and ϕ depend on the distributions of outcomes. For example, if Y_ij is a continuous variable, ν(μ_ij) is 1, and ϕ represents the error variance; if Y_ij is a count variable, ν(μ_ij) = μ_ij, and ϕ is equal to 1. Also, the variance-covariance matrix for Y_i is noted by ${\mathit{V}}_i=\varphi {\mathit{A}}_i^{1/2}{\mathit{R}}_i(\mathbf{\alpha }){\mathit{A}}_i^{1/2}$, where A_i = Diag{ν(μ_i1), ⋯, ν(μ_ini)}, and the “working” correlation structure R_i(α) describes the correlation pattern of observations within-subject with α as a vector of association parameters depending on the correlation structure. Several types of “working” correlation structures including independent $(\alpha =0,\mathit{\text{Corr}}(Y_{ij},Y_{ik})=\{\begin{array}{cc}\hfill 1\hfill & \hfill j=k\hfill \\ \hfill 0\hfill & \hfill j\ne k\hfill \end{array})$, exchangeable $(\alpha =\rho ,\mathit{\text{Corr}}(Y_{ij},Y_{ik})=\{\begin{array}{cc}\hfill 1\hfill & \hfill j=k\hfill \\ \hfill \rho \hfill & \hfill j\ne k\hfill \end{array})$, autoregressive (α = ρ, Corr(Y_ij, Y_i,j+m) = ρ^m, j + m ≤ n_i), Toeplitz $(\mathbf{\alpha }={(\theta ,{\theta }_1,{\theta }_2,\dots ,{\theta }_{n_i-1})}^T,\mathit{\text{Corr}}(Y_{ij},Y_{i,j+m})=\{\begin{array}{cc}\hfill 1& m=0\hfill \\ \hfill {\theta }_m& 0<m\le n_i-j\hfill \end{array})$, and also unstructured $(\mathbf{\alpha }={({\theta }_{12},{\theta }_{13},\dots ,{\theta }_{21},{\theta }_{23},\dots ,{\theta }_{n_{i-1}{n}_i})}^T,\mathit{\text{Corr}}(Y_{ij},Y_{ik})=\{\begin{array}{cc}\hfill 1& \hfill j=k\hfill \\ \hfill {\theta }_{jk}& \hfill j\ne k\hfill \end{array})$ ones are commonly used. The estimation of α is based on an iterative fitting process using the Pearson residual $e_{ij}=(y_{ij}-{\hat{\mu }}_{ij})/\sqrt{\nu ({\hat{\mu }}_{ij})}$ given the current value of β; also, the scale parameter ϕ is estimated by $\hat{\varphi }=\frac{1}{N-p}{\sum }_{i=1}^K{\sum }_{j=1}^{n_i}{e}_{ij}^2$ with the total number of observations $N={\sum }_{i=1}^K{n}_i$.

The GEE method yields asymptotically consistent β̂, even when the “working” correlation structure (R_i(α)) is misspecified [7], and β̂ is obtained by the following estimating equation

$$U(\mathbf{\beta })=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}({\mathit{Y}}_i-{\mathit{\mu }}_i)=0,$$ (2)

where ${\mathit{D}}_i=\frac{\partial {\mathbf{\mu }}_i}{\partial \mathbf{\beta }\prime }$. Given the true value of β as β_t and mild regularity conditions, β̂ is asymptotically normally distributed with a mean β_t and a covariance matrix estimated based on the “sandwich” estimator by

$$V_{LZ}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{LZ}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (3)

with

$$M_{LZ}=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}\mathit{\text{Cov}}({\mathit{Y}}_i){\mathit{V}}_i^{-1}{\mathit{D}}_i$$ (4)

by replacing α, β and ϕ with their consistent estimates, where $\mathit{\text{Cov}}({\mathit{Y}}_i)={\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }$ with r̂_i = Y_i − μ̂_i is an estimator of the variance-covariance matrix of Y_i [7, 21]. This “sandwich” estimator is robust in that it is consistent even if the correlation structure is misspecified. Note that if V_i is correctly specified, a consistent estimator for the covariance matrix of β̂ is given by ${\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}$, which is often referred as the model-based variance estimator [7]. Next, we will discuss the small-sample properties of GEE with several modifications on variance estimators and hypotheses testing.

2.2. Modified variance estimators of GEE with small samples

Due to the fact that the fitted value μ̂_i tends to be closer to Y_i than the true value μ_i and when sample size is small, ${\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }$ in V_LZ is biased downward for estimating $E({\mathit{e}}_i{\mathit{e}}_i^{\prime })$, and the bias turns to be larger when the sample is much smaller; meanwhile, a greater variability may arise [16, 22]. Therefore, the hypothesis testing using V_LZ tends to be liberal, and the resulting confidence interval is narrow. Table 1 provides a comprehensive summary of the recent modified variance estimators, and the details of the estimators are provided next.

1. V_MK is the degrees-of-freedom corrected “sandwich” variance estimator proposed by MacKinnon [23]. This estimator incorporates the simplest adjustment by adopting an adjustment factor of $\frac{K}{K-p}$, which is shown by

   $$V_{MK}=\frac{K}{K-p}{V}_{LZ}.$$ (5)

   When K → ∞, V_MK →_p V_LZ. V_MK corrects the bias, but meanwhile increases the variability.
2. V_KC is a bias-corrected “sandwich” variance estimator under the assumption of correctly specified correlation structure proposed by Kauermann and Carroll [24], which is

   $$V_{KC}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{KC}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (6)

   with

   $$M_{KC}=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{({\mathit{I}}_i-{\mathit{H}}_{ii})}^{-1/2}{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }{({\mathit{I}}_i-{\mathit{H}}_{ii}^{\prime })}^{-1/2}{\mathit{V}}_i^{-1}{\mathit{D}}_i$$ (7)

   where I_i is a n_i × n_i identify matrix, and the subject leverage H_ii is a diagonal matrix with the leverage of the i^th subjects, which can be calculated by

   $${\mathit{H}}_{ii}=D_i{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}.$$
3. V_PAN is proposed by Pan [20] given two additional assumptions satisfied: (A1) The conditional variance of Y_ij given X_ij is correctly specified; (A2) A common correlation structure, R_c, exists across all subjects. The modified variance estimator is

   $$V_{PAN}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{PAN}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (8)

   with

   $$M_{PAN}=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}\left\{{\mathit{A}}_i^{1/2}\right(\frac{1}{K}\sum _{i=1}^K{\mathit{A}}_i^{-1/2}{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }{\mathit{A}}_i^{-1/2}\left){\mathit{A}}_i^{1/2}\right\}{\mathit{V}}_i^{-1}{\mathit{D}}_i$$ (9)

   V_PAN pools data across all subjects in estimating Cov(Y_i), which performs more efficient.
4. V_GST made an additional modification on Pan’s estimator by incorporating the bias of ${\mathit{A}}_i^{1/2}\left(\frac{1}{K}{\sum }_{i=1}^K{\mathit{A}}_i^{-1/2}{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }{\mathit{A}}_i^{-1/2}\right){\mathit{A}}_i^{1/2}$ for small K, which was proposed by Gosho et al. [25]. The modified variance estimator is written as:

   $$V_{GST}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{GST}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (10)

   with

   $$M_{GST}=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}\left\{{\mathit{A}}_i^{1/2}\right(\frac{1}{K-p}\sum _{i=1}^K{\mathit{A}}_i^{-1/2}{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }{\mathit{A}}_i^{-1/2}\left){\mathit{A}}_i^{1/2}\right\}{\mathit{V}}_i^{-1}{\mathit{D}}_i$$ (11)

   V_GST also pools data across all subjects in estimating Cov(Y_i). In particular, when K ≫ p and K is large enough, V_GST approximately equals to V_PAN.
5. V_MD is another bias-corrected “sandwich” variance estimator proposed by Mancl and DeRouen [22]. Unlike V_KC, this estimator does not assume a correctly specified correlation structure, and it is written by

   $$V_{MD}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{MD}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (12)

   with

   $$M_{MD}=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{({\mathit{I}}_i-{\mathit{H}}_{ii})}^{-1}{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }{({\mathit{I}}_i-{\mathit{H}}_{ii}^{\prime })}^{-1}{\mathit{V}}_i^{-1}{\mathit{D}}_i$$ (13)

   where I_i and H_ii are defined as the same as V_KC. Note that to correct this bias in finite samples, Mancl and DeRouen [22] relied on the following approximate identity

   $$E({\hat{r}}_i{\hat{r}}_i^{\prime })\approx ({\mathit{I}}_i-{\mathit{H}}_{ii})\mathit{\text{Cov}}({\mathit{Y}}_i)({\mathit{I}}_i-{\mathit{H}}_{ii})\prime ,$$

   but they ignore one term ${\sum }_{j\ne i}{\mathit{H}}_{ij}\mathit{\text{Cov}}({\mathit{Y}}_i){\mathit{H}}_{ij}^T$ from its first order Taylor’s expansion, leading to overcorrection.
6. V_FG indicated by Fay and Graubard [26] made a further adjustment on V_MD by multiplying a scale factor, which is given by

   $$V_{FG}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{FG}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (14)

   with

   $$M_{FC}=\sum _{i=1}^K{\mathit{\eta }}_i^{-1}{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i{\mathit{\eta }}_i^{\prime -1}$$ (15)

   where η_i = I_p − N_i. Note that the jj^th diagnal value of ${\mathit{\eta }}_i^{-1/2}$ equals to (1 − min(b, {N_i}_jj))⁻¹, where ${\mathit{N}}_i={\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i{\left({\sum }_{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}$ for a simple bias correction, and b is prespecified subjectively to avoid extreme adjustments when N_i is quite close to 1.
7. V_MBN is a bias-corrected estimator recommended by Morel et al. [27] by incorporating correlation on the residual cross-products and sample size, provided as

   $$V_{MBN}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{MBN}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (16)

   with

   $$M_{MBN}=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}(k{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }+{\delta }_m\xi {\mathit{V}}_i){\mathit{V}}_i^{-1}{\mathit{D}}_i$$ (17)

   where $k=\frac{N-1}{N-p}\frac{K}{K-1},{\delta }_m=\{\begin{array}{cc}\frac{p}{K-p}\hfill & K>(d+1)p\hfill \\ \frac{1}{d}\hfill & \mathit{\text{otherwise}}\hfill \end{array}$ and $\xi =\mathit{\text{max}}(r,\frac{\mathit{\text{trace}}\left({(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i)}^{-1}{M}_{LZ}\right)}{p})$ with 0 ≤ r ≤ 1. Note that k is a factor to adjust the bias of empirical variance estimator of Cov(Y_i) and δ_m given by Morel can be bounded by 1/d [27]. The default values for d and r are 2 and 1 respectively according to Morel et al. [27].
8. V_WL is a combined variance estimator suggested by Wang and Long [16], which considered both the strength of V_PAN and V_MD for pooling information from all subjects and reducing the bias of the estimate for $e_i{e}_i^{\prime }$. The estimator is below

   $$V_{WL}={\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}{M}_{WL}{\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (18)

   where

   $$M_{WL}=\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{A}}_i^{1/2}\{\sum _{i=1}^K{\mathit{A}}_i^{1/2}{({\mathit{I}}_i-{\mathit{H}}_{ii})}^{-1}{\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }{({\mathit{I}}_i-{\mathit{H}}_{ii}^{\prime })}^{-1}{\mathit{A}}_i^{-1/2}/K\}{\mathit{A}}_i^{1/2}{\mathit{V}}_i^{-1}{\mathit{D}}_i.$$ (19)

   This estimator was confirmed to perform as well as or better than V_PAN and V_M, but the two additional assumptions specified above also need to be satisfied.

Table 1.

Summary of eight modified variance estimators for GEE with small sample

Variance Estimator	Modification	Reference
VMK	Degrees-of-Freedom adjustment	MacKinnon (1985)
VKC	Bias correction	Kauermann and Carroll (2001)
VPAN	Efficiency improvement	Pan (2001)
VGST	Efficiency improvement	Gosho et al. (2014)
VMD	Bias correction	Mancl and DeRouen (2001)
VFG	Bias correction	Fay and Graubard (2001)
VMBN	Bias correction	Morel et al. (2003)
VWL	Bias correction & Efficiency improvement	Wang and Long (2011)

We now present theoretical comparisons among those variance estimators. As shown above, all variance estimators share the same two outside terms, i.e., ${\left(\sum _{i=1}^K{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}{\mathit{D}}_i\right)}^{-1}$. Thus, we focus on assessing and comparing the middle matrix, M, of different variance estimators. The derived covariance matrix for vec(M) are given in Table 2. It has been shown by Wang and Long [16] that Cov(vec(M_LZ)) − Cov(vec(M_WL)) and Cov(vec(M_MD)) − Cov(vec(M_WL)) are non-negative definite with probability 1, while Cov(vec(M_PAN)) − Cov(vec(M_WL)) converges to 0 with probability 1 as K → ∞. For comparisons among the other alternatives,

$$\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{LZ}))-\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{MK}))=\sum _{i=1}^K(1-\frac{K^2}{{(K-p)}^2}){\mathit{S}}_i{\mathit{T}}_i{\mathit{S}}_i^{\prime }$$

$$\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{LZ}))-\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{KC}))=\sum _{i=1}^K{\mathit{S}}_i({\mathit{T}}_i-{\mathit{F}}_i{\mathit{T}}_i{\mathit{F}}_i^{\prime }){\mathit{S}}_i^{\prime }$$

$$\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{LZ}))-\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{GST}))=\sum _{i=1}^K{\mathit{S}}_i({\mathit{T}}_i-{\mathit{E}}_i(\sum _{j=1}^K\frac{1}{{(K-p)}^2}{\mathit{E}}_j^{-1}{\mathit{T}}_j{\mathit{E}}_j^{-1}\left){\mathit{E}}_i\right){\mathit{S}}_i^{\prime }$$

$$\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{LZ}))-\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{FG}))=\sum _{i=1}^K(1-{\mathit{\eta }}_i^{-1}\otimes {\mathit{\eta }}_i^{-1}){\mathit{S}}_i{\mathit{T}}_i{\mathit{S}}_i^{\prime }(1-{\mathit{\eta }}_i^{\prime -1}\otimes {\mathit{\eta }}_i^{\prime -1})$$

$$\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{LZ}))-\mathit{\text{Cov}}(\mathit{\text{vec}}(M_{MBN}))=\sum _{i=1}^K{\mathit{S}}_i({\mathit{T}}_i-{\mathit{N}}_i){\mathit{S}}_i^{\prime }$$

Table 2.

Covariance matrix of the middle part from nine variance estimators for GEE. ${\mathit{T}}_i=\mathit{\text{Cov}}\left(\mathit{\text{vec}}\right({\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime }\left)\right);{\mathit{S}}_i=\left({\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}\right)\otimes \left({\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}\right);{\mathit{F}}_i={({\mathit{I}}_i-{\mathit{H}}_{ii})}^{-\frac{1}{2}}\otimes {({\mathit{I}}_i-{\mathit{H}}_{ii})}^{-\frac{1}{2}}$; G_i = (I_i − H_ii)⁻¹ ⊗ (I_i − H_ii)⁻¹; ${\mathit{E}}_i={\mathit{A}}_i^{1/2}\otimes {\mathit{A}}_i^{1/2};{\mathit{H}}_i=\left({\mathit{\eta }}_i^{-1}{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}\right)\otimes \left({\mathit{\eta }}_i^{-1}{\mathit{D}}_i^{\prime }{\mathit{V}}_i^{-1}\right);{\mathit{N}}_i=\mathit{\text{Cov}}\left(k\mathit{\text{vec}}\right({\hat{\mathit{r}}}_i{\hat{\mathit{r}}}_i^{\prime })+\mathit{\text{vec}}({\delta }_m\xi {\mathit{V}}_i\left)\right)$.

Matrix M	Covariance Matrix of vec(M)
MLZ	${\sum }_{i=1}^K{\mathit{S}}_i{\mathit{T}}_i{\mathit{S}}_i^{\prime }$
MMK	${\sum }_{i=1}^K\frac{K^2}{{(K-p)}^2}{\mathit{S}}_i{\mathit{T}}_i{\mathit{S}}_i^{\prime }$
MKC	${\sum }_{i=1}^K{\mathit{S}}_i{\mathit{F}}_i{\mathit{T}}_i{\mathit{F}}_i^{\prime }{\mathit{S}}_i^{\prime }$
MPAN	${\sum }_{i=1}^K{\mathit{S}}_i\left[{\mathit{E}}_i\right({\sum }_{j=1}^K\frac{1}{K^2}{\mathit{E}}_j^{-1}{\mathit{T}}_j{\mathit{E}}_j^{-1}\left){\mathit{E}}_i\right]{\mathit{S}}_i^{\prime }$
MGST	${\sum }_{i=1}^K{\mathit{S}}_i\left[{\mathit{E}}_i\right({\sum }_{j=1}^K\frac{1}{{(K-p)}^2}{\mathit{E}}_j^{-1}{\mathit{T}}_j{\mathit{E}}_j^{-1}\left){\mathit{E}}_i\right]{\mathit{S}}_i^{\prime }$
MMD	${\sum }_{i=1}^K{\mathit{S}}_i{\mathit{G}}_i{\mathit{T}}_i{\mathit{G}}_i^{\prime }{\mathit{S}}_i^{\prime }$
MFG	${\sum }_{i=1}^K{\mathit{H}}_i{\mathit{T}}_i{\mathit{H}}_i^{\prime }$
MMBN	${\sum }_{i=1}^K{\mathit{S}}_i{\mathit{N}}_i{\mathit{S}}_i^{\prime }$
MWL	${\sum }_{i=1}^K{\mathit{S}}_i\left[{\mathit{E}}_i\right({\sum }_{j=1}^K\frac{1}{K^2}{\mathit{E}}_j^{-1}{\mathit{G}}_j{\mathit{T}}_j]{\mathit{G}}_j^{\prime }{\mathit{E}}_j^{-1}){\mathit{E}}_i]{\mathit{S}}_i^{\prime }$

Based on the above derivations, under mild conditions, Cov(vec(M_LZ)) − Cov(vec(M_MK)), Cov(vec(M_LZ)) − Cov(vec(M_KC)), Cov(vec(M_LZ)) − Cov(vec(M_FG)), and Cov(vec(M_LZ)) − Cov(vec(M_MBN)) will converge to 0 with probability 1, while Cov(vec(M_LZ)) − Cov(vec(M_GST)) is non-negative definite with probability 1 as K → ∞. Hence, these variance estimators are asymptotically equivalent. But when the sample size is small, V_LZ tends to underestimate the variance. Therefore, the modifications through the bias-correction or degrees-of-freedom adjustment are mostly applied (Table 1). On the other hand, the efficiency gain by pooling data across all subjects to improve the estimator of Cov(Y_i) instead of only using data from the i^th subject, is incorporated in V_PAN, V_GST and V_WL. Thus, V_WL is the only estimator that takes into consideration both bias correction and efficiency improvement. Therefore, it is expected intuitively to outperform the other alternatives if the assumptions (A1) and (A2) are satisfied. In Section 3, extensive numerical comparisons via simulations will be conducted for further investigation.

2.3. Hypotheses Testing

For tests of hypotheses in GEE, the Wald test and score test have been popularly applied [16, 20, 28]. However, when the sample size is small, the Wald test leads to inflated type I error, which seems too liberal [20, 28], and score test has smaller test size than the pre-specified nominal level [28]. Therefore, several modifications have been proposed to obtain improved finite performance for GEE, i.e., t–test and modified score test. According to Guo et al. [28], the score test was modified under the context of small sample, which was shown to be less conservative than the t–test via simulation. Currently, we consider t–tests when the sample size is small, and the brief derivation is shown next.

Without generality, a simple univariate hypothesis testing is taken as an example. Suppose in a clinical trial, the mean model is specified as μ_ij = α + β × treatment. The hypothesis of interest for the treatment parameter β is given by H₀ : β = 0 vs H_a : β ≠ 0. Thus, the test statistic for the Wald test is $z=\frac{\hat{\beta }}{\sqrt{\hat{V}(\hat{\beta })}}$, where V̂ (β̂) can be replaced by any estimator mentioned above. For small samples, the t–test was proposed by Pan [20], and was also extensively studied by Wang and Long [16]. Denote κ and ν as the estimated mean and variance of V (β̂). It follows the derivation based on vec operator that the distribution of $\frac{\hat{V}(\hat{\beta })}{c}$ is approximated with a Chi-square distribution ${\chi }_d^2$, where the scale parameter $c=\frac{\nu }{2\kappa }$ and the degrees of freedom $d=\frac{2{\kappa }^2}{\nu }$. The test statistic for t–test is $t=\frac{\hat{\beta }/\sqrt{\kappa }}{\sqrt{\hat{V}(\hat{\beta })/cd}}$, which is the same as the Wald test statistic with the degrees of freedom $d\approx 2\hat{V}{(\hat{\beta })}^2/\widehat{\mathit{\text{Var}}}(\hat{V}(\hat{\beta }))$ [16, 20]. This satterthwaite-type degrees of freedom approximation incorporates the variability of the variance estimator, and thus performs better compared to depending only on the number of clusters in Li and Redden [18]. The outperformance of t–test over the Wald test was identified in the settings with small sample [16, 29].

3. Simulation Studies

In this section, we conduct simulation studies to numerically compare the finite small-sample performance of nine types of variance estimators including the original “sandwich” variance estimator under different settings. Also, we focus on the Wald test and t–test for hypothesis testing to calculate the Type I error rate for each estimator, and further provide the recommendation on suitable sample size for each one to ensure test sizes at the nominal levels. In particular, three scenarios with continuous, count and binary repeated outcomes are considered. The models for data generation are below

$$Y_{ij}={\beta }_0+{\beta }_1\times x_{ij}+b_i+{\epsilon }_{ij}$$

$$\mathit{\text{log}}(u_{ij}|b_i)={\beta }_0+{\beta }_1\times x_{ij}+b_i$$ (20)

$$\mathit{\text{logit}}(u_{ij}|b_i)={\beta }_0+{\beta }_1\times x_{ij}+b_i$$

where β₀ = 0 and β₁ = 0, i = 1, …, K with sample size K = 10, 20, 30, 40, 50 and j = 1, …, n with equal number of observations within-subject (i.e., cluster size) n = 5, 10, 20. The covariate x_ij are independent and identical distributed (i.i.d) from a standard normal distribution N(0, 1). The subject-level random effects b_i’s are i.i.d. from $N(0,{\sigma }_b^2)$ with ${\sigma }_b^2=0.25$, and the random error ε_ij ’s are i.i.d. from $N(0,{\sigma }_{\epsilon }^2)$ with ${\sigma }_{\epsilon }^2=0.8$. The details for each scenarios are listed: 1) For the case with continuous outcomes, b_i and ε_ij are independent with each other, leading to the true exchangeable correlation structure with the correlation parameter as $\alpha ={\sigma }_b^2/({\sigma }_b^2+{\sigma }_{\epsilon }^2)\approx 0.2$; 2) For the case with count outcomes, based on the derivation by Guo et al. [28], the correlation parameter $\alpha \approx {\sigma }_b^2/(1+{\sigma }_b^2)\approx 0.3$; 3) For the case with binary outcomes, the correlation parameter $\alpha \approx \frac{{\sigma }_b^2/16}{E(\frac{1}{1+\mathit{\text{exp}}(-b_i)})[1-E(\frac{1}{1+\mathit{\text{exp}}(-b_i)})]}\approx 0.1$ according to Guo et al. [28].

In particular, 1,000 Monte Carlo data sets are generated for each scenarios, where the parameter estimate β̂₁ along with nine variance estimates are calculated. For each set-up, three types of “working” correlation structures are used, independence, exchangeable and AR-1. The Wald and t–tests are both applied for hypotheses testing, and Type I error is calculated given the significance level of 0.05. Note that the degrees of freedom for t–distribution vary across different variance estimators. For example, the average degrees of freedom for the first scenario with continuous outcomes, K = 10 and n = 5 are rounded by 13, 13, 69, 69, 11, 14, 14, 22, 54 respectively, indicating the variability influence of variance estimators on statistical inference.

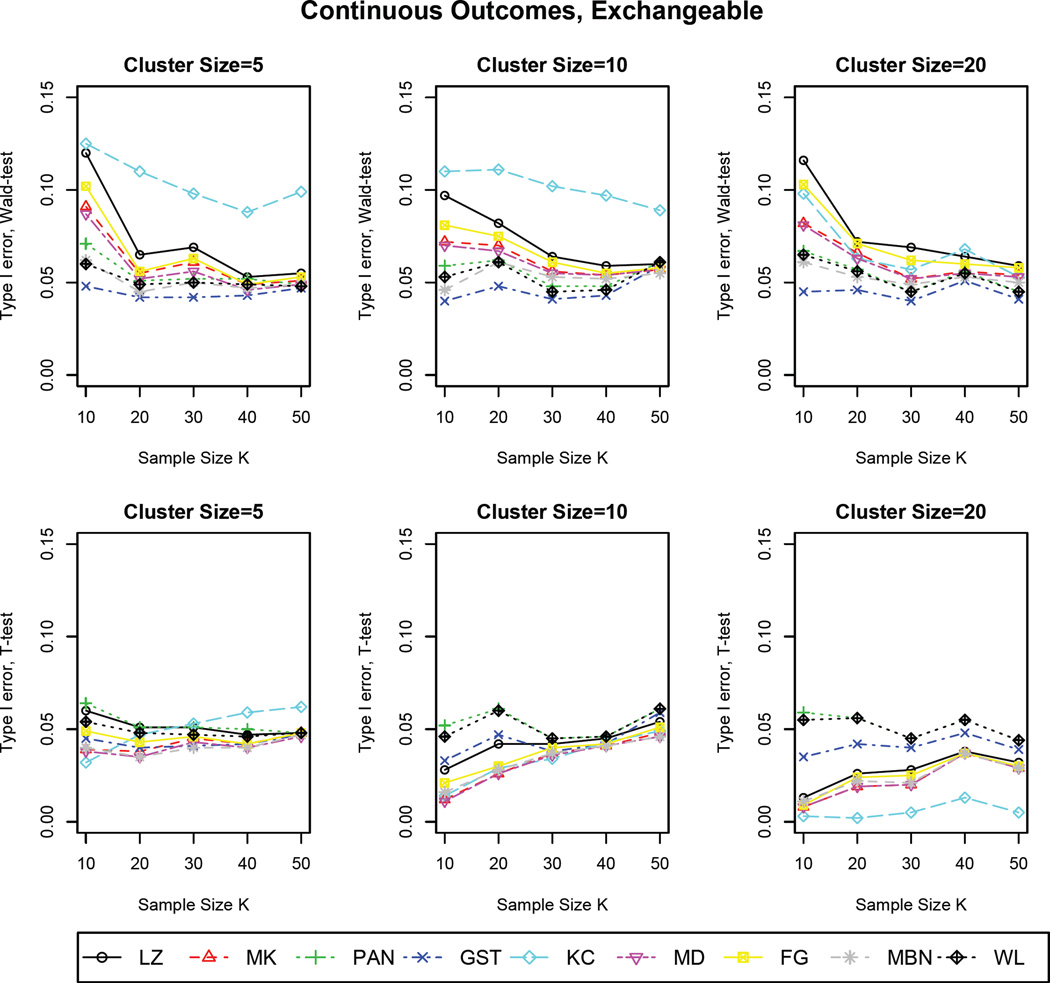
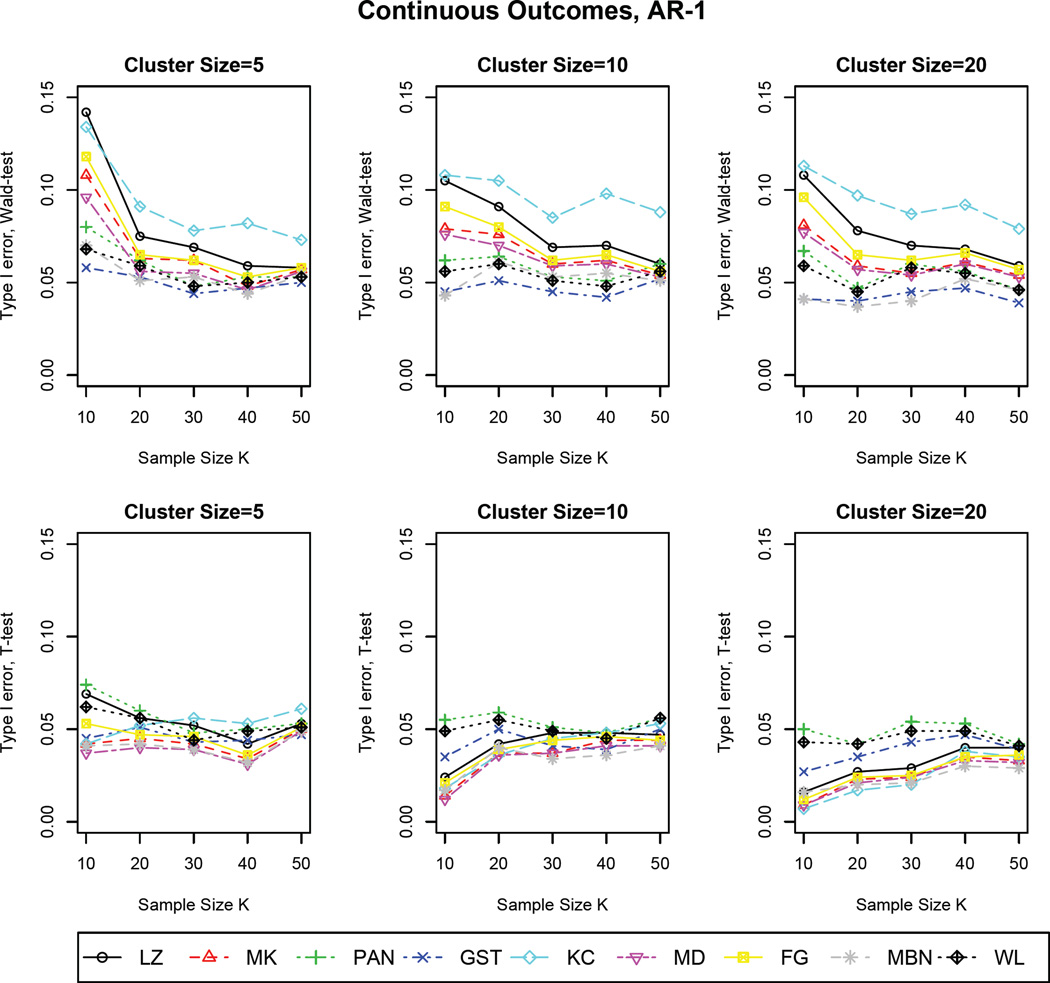
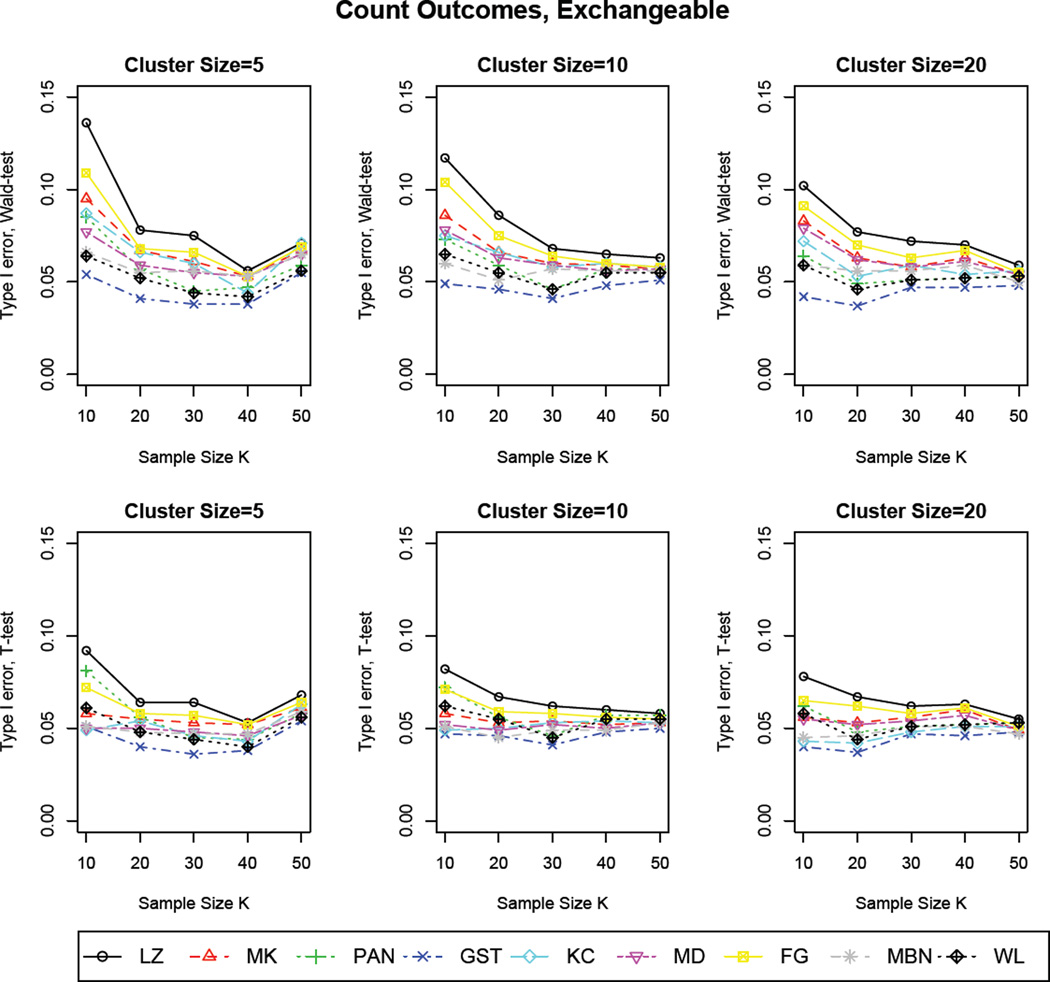
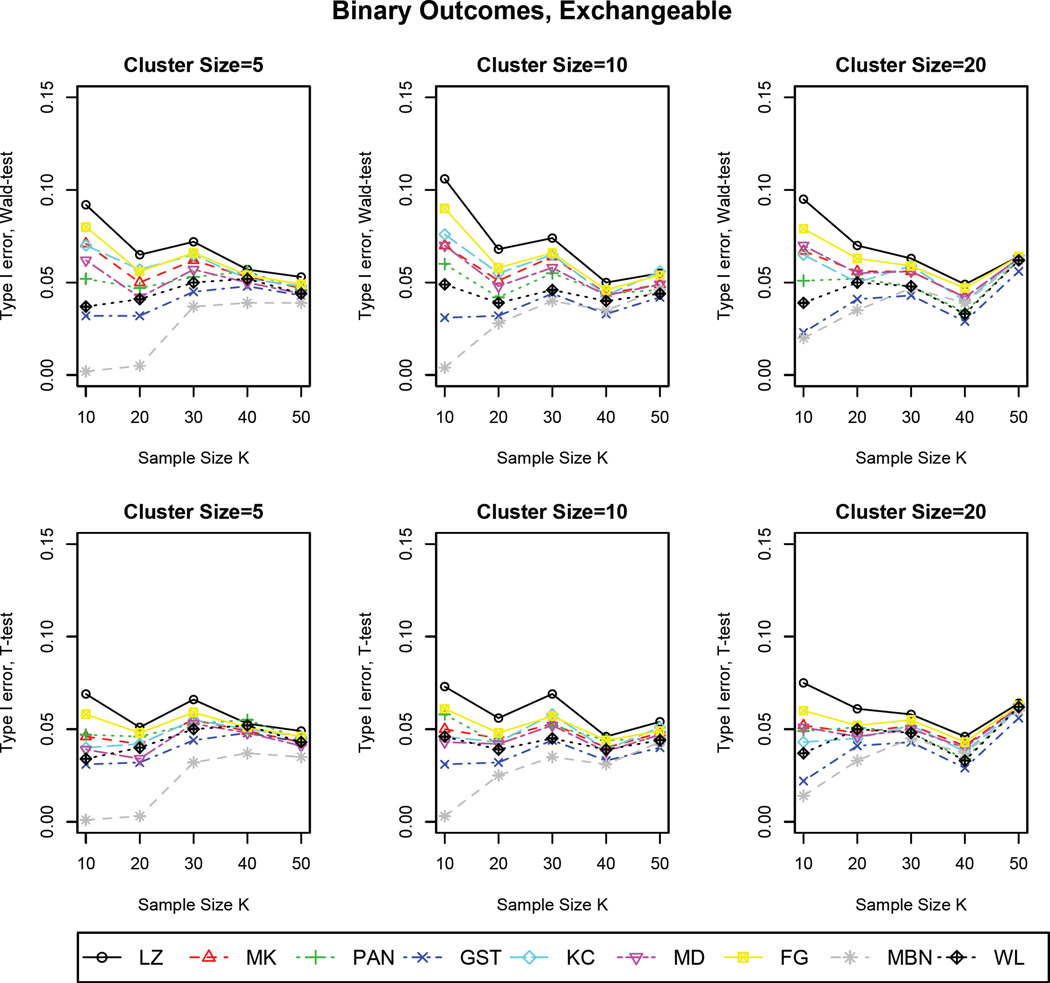
The partial results are shown in Figures 1–6, are summarized as follows: 1) The results based on Wald tests show that the use of robust variance estimator V_LZ always leads to inflated Type I error when the sample size is small (i.e., ≤ 50), which is consistent with our expectation; however, the tests using the other estimators also have inflation to some extent, but the degrees of freedom are relatively smaller with V_WL performing the best; 2) t–tests for hypotheses testing attain better performance than Wald tests in terms of the control of Type I error across all estimators. The estimator V_LZ still leads to some degree of inflation. Interestingly, when the “working” correlation structure is specified correctly, V_LZ achieves satisfactory performance even though the sample size is as small as 10; 3) For t–tests, the performance of variance estimators are substantially influenced by sample size K, while larger cluster size n leads to more conservative results; 4) Note that V_KC performs worse than V_LZ based on Wald tests as indicated by larger inflation on Type I error, but improves with increasing cluster size; In addition, some estimators, such as V_GST and V_MBN, perform conservatively for small samples; 5) Among all nine variance estimators, V_WL has superior performance consistently across a variety of setups. Thus, it is a preferable estimator for GEE even when the sample size is as small as 10. Note that the results on the independent “working” correlation structure are not provided due to the similar trend as AR-1. In the end, according to our current numerical studies as well as literatures [16, 28, 29], we recommend the sample size requirements to preserve Type I error for all variance estimators as follows: V_LZ(≥ 50), V_MK(≥ 40), V_KC(≥ 50), V_PAN(≥ 30), V_GST(≥ 20), V_MD(≥ 30), V_FG(≥ 40), V_MBN(≥ 50), and V_WL(≥ 10). Note that we also investigated the effect of cluster sizes via additional simulations (results available upon request), and found out that the higher cluster size n can somewhat improve the performance in preserving Type I error, but the effect is not as substantial as the sample size K. Due to the fact that in most practical longitudinal designs, the cluster size (i.e., the number of observations within-subject) is usually less than 30 [40, 41]. Thus, our recommendation can be applied in general cases (i.e., n ≥ 5) based on current extensive simulations.

Figure 1.

Type I errors based on Wald and t–tests for continuous outcomes with the true correlation structure as exchangeable

Figure 6.

Type I errors based on Wald and t–tests for binary outcomes with the true correlation structure as AR-1

4. Data examples with small samples

In this paper, we present the results using two real data applications to test our R program and compare the finite performances of different variance estimators under finite sample size, one with continuous outcomes and the other one with count outcomes. The first data is from a study of orthodontic measurements on children, which includes 11 girls and 16 boys measured at ages 8, 10, 12, and 14 [30]. The response is the measurement of the distance (in millimeters) from the center of the pituitary to the pteryomaxillary fissure, and the primary covariates of interest are age (in years) and gender (Male; Female). The objective is to investigate whether there exist statistically significant gender differences in dental growth measurements and their temporal trends as age increases. This example has been analyzed byWang and Long [16] for small-sample properties of several estimators. Here, we conduct comparisons by considering eight types of modified variance estimators in addition to the robust original “sandwich” estimator. Therefore, the mean model of GEE is given by

$$E(y)={\beta }_0+{\beta }_1\times \sqrt{\mathit{\text{Age}}}+{\beta }_2\times \mathit{\text{Gender}}$$ (21)

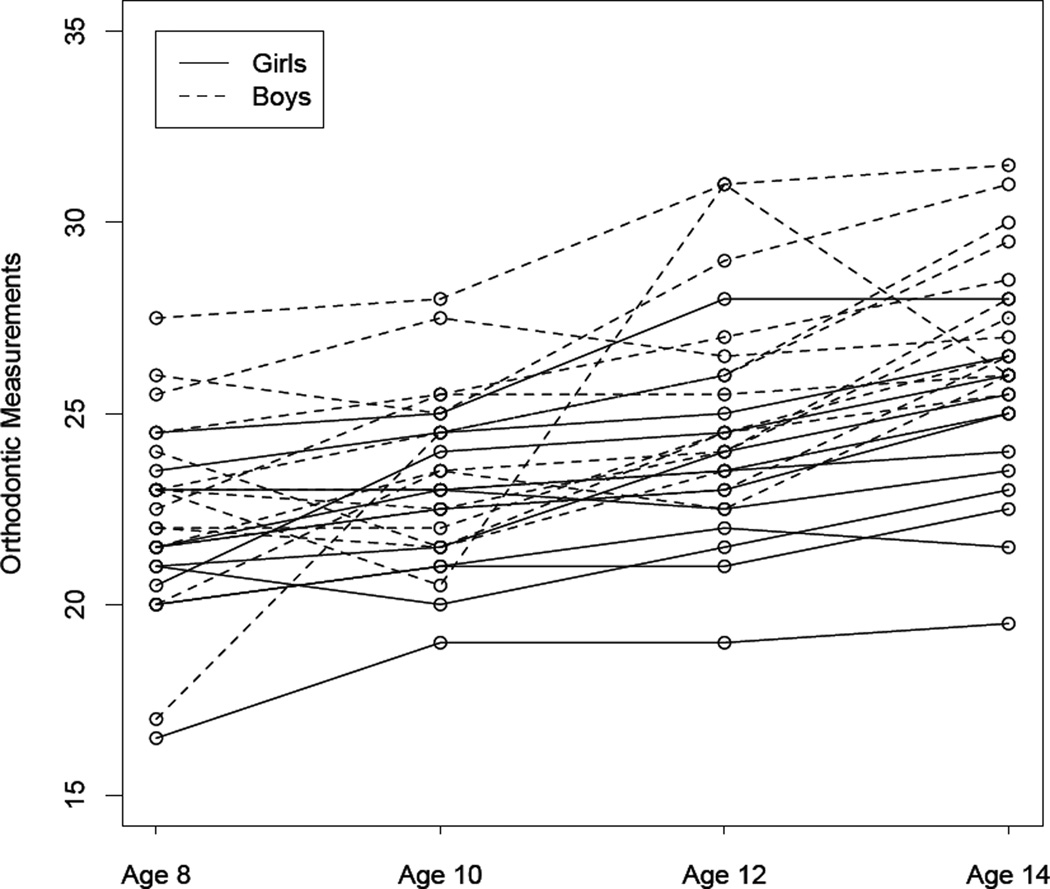
The scatter plot of orthodontic measurements is shown in Figure 7, where the black lines are for girls and the red lines are for boys. It turns out that the boys have higher measurements than the girls on average, and the measurements tend to increase with age. GEE analysis results, including parameter estimates and various variance estimators, are shown in Table 3. Both Wald and t–tests with the significance levels of 0.01 and 0.05 are applied for hypotheses testing. All variance estimators provide comparable results on hypotheses testing of $\sqrt{\mathit{\text{Age}}}$ using Wald tests, but when using t–tests at the significance level of 0.01, different testing conclusions for gender are obtained, indicating that the choice of different small-sample adjustments in variance estimators may affect the testing results.

Figure 7.

Orthodontic measurements by subject over time

Table 3.

Estimation results for the case study of orthodontic measurements

		$\sqrt{\text{Variance Estimator}}$
	β̂	$\sqrt{V_{LZ}}$	$\sqrt{V_{MK}}$	$\sqrt{V_{PAN}}$	$\sqrt{V_{GST}}$	$\sqrt{V_{KC}}$	$\sqrt{V_{MD}}$	$\sqrt{V_{FG}}$	$\sqrt{V_{MBN}}$	$\sqrt{V_{WL}}$
					Independence
$\sqrt{\mathit{\text{Age}}}$	4.32	0.461	0.489	0.461	0.489	0.470	0.479	0.486	0.574	0.479
Gender(=M)	2.32	0.750	0.795	0.733	0.777	0.782	0.816	0.836†	0.803	0.793
					Exchangeable
$\sqrt{\mathit{\text{Age}}}$	4.32	0.461	0.489	0.461	0.489	0.470	0.479	0.469	0.498	0.479
Gender(=M)	2.32	0.750	0.795	0.733	0.777	0.782	0.816	0.836‡	0.818	0.793
					AR-1
$\sqrt{\mathit{\text{Age}}}$	4.25	0.480	0.509	0.480	0.509	0.472	0.499	0.525	0.538	0.499
Gender(=M)	2.41	0.754	0.800	0.734	0.778	0.783	0.821	0.841†	0.813	0.795
					Unstructured
$\sqrt{\mathit{\text{Age}}}$	4.27	0.466	0.495	0.466	0.495	0.516	0.484	0.473	0.507	0.484
Gender(=M)	2.22	0.730	0.774‡	0.713	0.756	0.783‡	0.795‡	0.814†	0.794‡	0.772

All are significant at both significance levels of 0.01 and 0.05 using Wald or t–tests except the ones with the superscripts.

^†: not significant based on either Wald or t–tests at the significance level of 0.01;

^‡: significant based on Wald tests but not on t–tests at the significance level of 0.01.

The second example is from the randomized trial of progabide consisting of 59 individuals [31]. The subjects were randomly assigned to receive the anti-epileptic treatment (progabide) or placebo (control). The outcome is the number of epileptic seizures in each of four consecutive two-week intervals, and the variables recorded include age and baseline epileptic seizure counts (in an eight-week interval) prior to the treatment assignment and the indicator for treatment (Trt, 1=progabide; 0=control). In particular, for modeling fitting, the variable Baseline is noted by the baseline epileptic seizure count rate per week; Time is the number of weeks, which is valued by 2, 4, 6, and 8; Interval duration is the duration of each interval (i.e., 2 weeks), and log(Interval_duration) is treated as an offset variable in the model. The goal of this trial is to evaluate whether the anti-epileptic treatment is effective. We use the complete data set of all 59 subjects and a subset of 30 children, which are randomly drawn from the original complete data without replacement, to perform hypotheses testing and evaluate the small-sample properties of different estimators. Note that the interaction term of Trt and Time is also investigated, but is not significant, thus the final log-linear model for this study is given by

$$\mathit{\text{log}}(E(y))={\beta }_0+{\beta }_1\times \mathit{\text{Baseline}}+{\beta }_2\times \mathit{\text{Trt}}+{\beta }_3\times \mathit{\text{Time}}+\mathit{\text{log}}(\mathit{\text{Interval}}\_\mathit{\text{duration}})$$ (22)

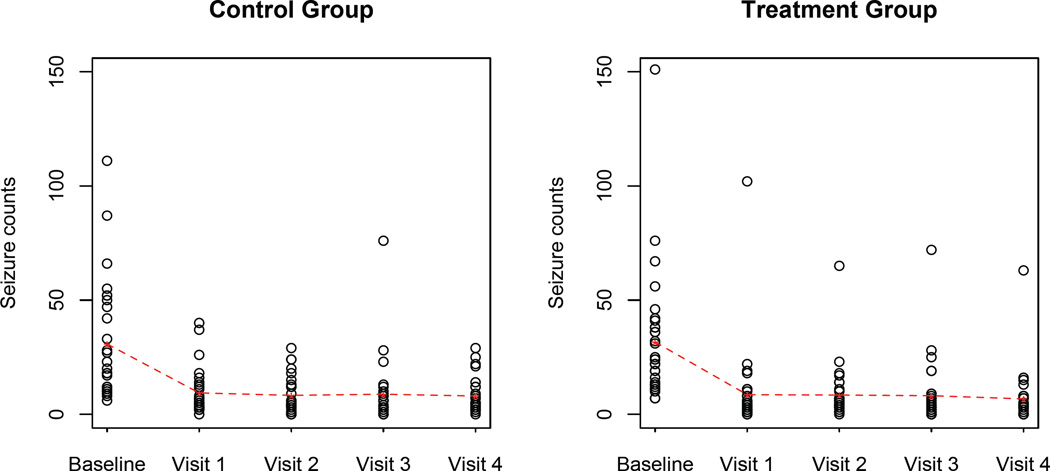
The scatter plots of seizure counts by time intervals for progabide and control groups are shown in Figure 8, and indicate that the counts dramatically decrease after the treatment in the first two weeks and remain stable afterwards for both groups. The GEE-based parameter estimates as well as the square root of various variance estimates are shown in Table 4. No significant (progabide) treatment effect or temporal trend is detected using either complete data or subset data based on all variance estimators, but Baseline has significant effect on the seizure counts throughout. However, for subset data analysis, only slightly different conclusions of significance on temporal trend are obtained depending on the type of tests and the significance level. For instance, the tests of temporal effect using V_GST, V_MD and V_WL are significant at the significance level of 0.05 but not at the significance level of 0.01 based on Wald or t–tests, but V_KC and V_FG are significant only based on Wald tests at the significance level of 0.05. This data example shows that when the sample size is smaller (i.e., ≤ 30), the validity of hypothesis testing could be influenced by the bias of the variance estimators.

Figure 8.

Seizure counts over time for treatment and control groups. The dotted red line is the average number of seizure counts over time

Table 4.

Estimation results for the case study of epileptic seizures

		$\sqrt{\text{Variance Estimator}}$
	β̂	$\sqrt{V_{LZ}}$	$\sqrt{V_{MK}}$	$\sqrt{V_{PAN}}$	$\sqrt{V_{GST}}$	$\sqrt{V_{KC}}$	$\sqrt{V_{MD}}$	$\sqrt{V_{FG}}$	$\sqrt{V_{MBN}}$	$\sqrt{V_{WL}}$
Complete data (K=59)
					Independence
Baseline	0.17	0.008	0.009	0.013	0.014	0.009	0.010	0.009	0.009	0.014
Trt(= 1)†	−0.23	0.176	0.182	0.159	0.165	0.181	0.191	0.180	0.182	0.167
Time†	−0.03	0.017	0.018	0.016	0.016	0.018	0.018	0.018	0.019	0.016
					Exchangeable
Baseline	0.17	0.008	0.009	0.013	0.014	0.009	0.010	0.009	0.009	0.014
Trt(= 1)†	−0.22	0.174	0.180	0.158	0.164	0.182	0.189	0.179	0.181	0.166
Time†	−0.03	0.017	0.018	0.016	0.016	0.019	0.018	0.018	0.018	0.016
					AR-1
Baseline	0.17	0.008	0.009	0.012	0.013	0.010	0.010	0.009	0.009	0.013
Trt(= 1)†	−0.25	0.166	0.172	0.149	0.155	0.185	0.182	0.171	0.173	0.157
Time†	−0.03	0.017	0.018	0.015	0.016	0.018	0.018	0.017	0.018	0.015
Subset data (K=30)
					Independence
Baseline	0.18	0.014	0.015	0.017	0.018	0.014	0.026	0.015	0.015	0.019
Trt(= 1)†	−0.29	0.270	0.290	0.257	0.276	0.293	0.302	0.286	0.289	0.290
Time	−0.05	0.020†	0.021#	0.019#	0.021#	0.023*	0.022#	0.023*	0.025†	0.020#
					Exchangeable
Baseline	0.18	0.013	0.014	0.017	0.019	0.015	0.025	0.015	0.015	0.020
Trt(= 1)†	−0.27	0.288	0.310	0.261	0.281	0.296	0.325	0.305	0.311	0.295
Time	−0.05	0.020#	0.021#	0.019‡	0.021#	0.021*	0.022#	0.021*	0.022†	0.020#
					AR-1
Baseline	0.18	0.013	0.014	0.017	0.018	0.020	0.025	0.015	0.015	0.019
Trt(= 1)†	−0.34	0.279	0.299	0.255	0.274	0.296	0.314	0.295	0.299	0.289
Time	−0.05	0.023#	0.025‡	0.021#	0.023#	0.022*	0.026#	0.026*	0.026†	0.022#

Complete data All are significant at both significance levels of 0.05 and 0.01 using Wald or t–tests except the ones with the superscripts. Subset data: All are significant at both significance levels of 0.05 and 0.01 using Wald or t–tests except the ones with the superscripts. Note that if the notation is put with the variable, the significance result is the same for the whole row.

^†: not significant on either Wald or t–tests at the significance level of either 0.05 or 0.01;

^‡: significant on Wald test, but not significant on t–test at the significance level of 0.01;

^#: significant at the significance level of 0.05 but not at the significance level of 0.01 based on Wald or t–tests;

^*: significant only based on Wald tests at the significance level of 0.05.

5. Conclusions and Discussions

In this paper, we provide a systematic review of recent developments on modified variance estimators for GEE to improve finite small-sample properties, including the formulation of these modifications and their theoretical and numerical comparisons. In addition, to conveniently implement these modifications, we develop the R package “geesmv” which is available at http://cran.r-project.org/web/packages/geesmv/ for free-download and public access. We also discuss two main types of hypothesis testing for GEE,Wald and t–tests, and evaluate their corresponding Type I error when sample size is small. Through extensive simulation studies and two real data examples, we compared the performance of various variance estimators under different scenarios, and provide the guidance of the appropriate sample size for controlling Type I error. As indicated in our simulation study, in general, t–tests based on the variance estimator V_ML perform robustly well across different set-ups. In particular, the degrees of freedom for t–statistic are more accurately approximated as compared to Li and Redden [18]. However, there are still several limitations for this work. First, the modifications discussed here for variance estimation are directly focusing on the “sandwich” variance estimator, but some other methods were also proposed but not covered here (i.e., improving the efficiency and robustness of parameter estimates) [28, 29, 32, 33, 34]; Second, our recommendation on the appropriate sample sizes for each estimator for preserving Type I error is obtained through limited simulation studies under general set-ups (i.e., equal cluster sizes); however, this guideline may not be always applicable, for instance, the cases with unequal cluster sizes; Third, we only evaluate the Type I error, but the Type II error or the power warrants further investigations. It is also worth pointing out that the selection of an appropriate modification method relies on various aspects of the real application (i.e., study design or intra-subject correlation) [2, 4, 35].

In addition to modifications on variance estimators and test statistics, another important issue, power analysis, tends to be challenging, for example, in a cluster randomized trial (CRT) with a small number of clusters [5, 36, 37]. Previous studies on sample size/power calculation included Liu and Liang [38], where the generalized score test was utilized to draw statistical inference and the resulting non-central Chi-square distribution of test statistic under the alternative hypothesis was derived. Afterwards, Shih provided an alternative formula on sample size and power calculation, which relied on Wald tests using the estimates of regression parameters and robust variance estimators [39]. This power analysis is valid only when the V (β̂) is unbiased and asymptotic normality is satisfied. While, when K is small, the estimated power tends to be overestimated. Hence, the modification on the power estimation is necessary to guarantee its unbiasedness, where an approximated t–distribution could be considered. Also, the adjustment of power estimation incorporating the variance estimators in Section 2 for efficiency improvement is expected to be advantageous. In the application of GEE method, other issues such as model selection or missing data under the circumstance of small samples or even with informative cluster sizes are also of interest. Thus, novel methodologies are still necessary and urged to develop for GEE to accommodate various data features for valid inference in real applications.

Figure 2.

Type I errors based on Wald and t–tests for continuous outcomes with the true correlation structure as AR-1

Figure 3.

Type I errors based on Wald and t–tests for count outcomes with the true correlation structure as exchangeable

Figure 4.

Type I errors based on Wald and t–tests for count outcomes with the true correlation structure as AR-1

Figure 5.

Type I errors based on Wald and t–tests for binary outcomes with the true correlation structure as exchangeable