MoCha: Molecular Characterization of Unknown Pathways

Abstract

Automated methods for the reverse-engineering of complex regulatory networks are paving the way for the inference of mechanistic comprehensive models directly from experimental data. These novel methods can infer not only the relations and parameters of the known molecules defined in their input datasets, but also unknown components and pathways identified as necessary by the automated algorithms. Identifying the molecular nature of these unknown components is a crucial step for making testable predictions and experimentally validating the models, yet no specific and efficient tools exist to aid in this process. To this end, we present here MoCha (Molecular Characterization), a tool optimized for the search of unknown proteins and their pathways from a given set of known interacting proteins. MoCha uses the comprehensive dataset of protein–protein interactions provided by the STRING database, which currently includes more than a billion interactions from over 2,000 organisms. MoCha is highly optimized, performing typical searches within seconds. We demonstrate the use of MoCha with the characterization of unknown components from reverse-engineered models from the literature. MoCha is useful for working on network models by hand or as a downstream step of a model inference engine workflow and represents a valuable and efficient tool for the characterization of unknown pathways using known data from thousands of organisms. MoCha and its source code are freely available online under the GPLv3 license.

1. Introduction

Reverse-engineering computational methods can automatically infer regulatory networks directly from experimental data (Hecker et al., 2009; Sirbu et al., 2010; Liu et al., 2012). Taking biological data as input, these algorithms can produce de novo the topology and dynamic parameters of a regulatory network that, when simulated, recapitulates the dynamics of experimental in vivo outcomes. These powerful artificial intelligence methods are paving the way for the discovery of regulatory models of previously puzzling data, readily providing verifiable predictions (Becker et al., 2013).

However, automatically inferred regulatory networks may suggest that there are regulatory nodes that are necessary to explain the data but were not present in the input dataset (not yet implicated by the functional literature). Methods based on regression and metaheuristics for the reverse-engineering from gene expression data from microarrays and quantitative PCR (Yeung et al., 2002; Gardner et al., 2003; Tegner et al., 2003; Kimura et al., 2005; Bonneau et al., 2006; Margolin et al., 2006; Molinelli et al., 2013) as well as from in situ hybridization and immunohistochemical images (Reinitz et al., 1995; Perkins et al., 2006; Fomekong-Nanfack et al., 2007; Crombach et al., 2012; Becker et al., 2013) statistically quantify the fit between the data and model output. Whereas the overall fit can be acceptable, specific components may have a low fit when compared with the experimental data, indicating a possible missing component not included in the input dataset. Furthermore, novel methods for inferring regulatory networks from morphological experimental data can directly predict the existence of unknown products not included in the input datasets, but inferred as functionally necessary by the algorithms for the models to correctly reproduce the results of the input set of experiments (Lobikin et al., 2015; Lobo and Levin, 2015). Characterizing the pathways represented by these unknown components is a necessary step for the experimental validation of the inferred model (Lobo et al., 2013, 2014).

Databases of known molecular interactions represent a valuable resource for identifying the unknown components in these inferred regulatory networks by providing a searchable directory for molecular products and pathways with known similar interactions as in the inferred model. However, searching for candidate molecules represents a significant computational challenge because of both the size of the interaction databases and the fact that a single unknown component can represent a multiprotein subpathway. The STRING database v10 (Szklarczyk et al., 2015) contains more than 2,000 organisms and 1 billion interactions. Indeed, finding candidate pathways by mining this enormous dataset is a demanding task in need of specialized tools. Software technology exists to mine interaction datasets with complex queries (Venkatesan et al., 2014); however, the computational cost of performing these semantically rich searches renders them inefficient for the specific purpose of characterizing partially defined pathways and hence impractical for use with datasets including billions of interactions.

Here, we present MoCha (Molecular Characterization), a highly optimized tool to characterize unknown protein pathway components interacting with a given set of proteins. MoCha can efficiently search within seconds for pathways in a dataset containing more than a billion protein–protein interactions (STRING database v10). The high performance of the algorithm is because of a specific preprocessing of the database, performed once during the configuration of the tool, which allows the subsequent application of very efficient binary search algorithms.

2. Methods

2.1. Database files

MoCha uses the freely available (Creative Commons Attribution 3.0 License) flat-files from the STRING database v10 (Szklarczyk et al., 2015). During the initial configuration of the program with an automated script, the database files are downloaded and preprocessed by ordering them according to different keys (columns) and calculating and storing the line offsets positions of the resultant files. These preprocessed files are then suitable for the application of an efficient binary search algorithm.

2.2. Search algorithm

The main input parameter of MoCha is a set of proteins for which common interactor proteins and pathways are found. Proteins are specified with their common names, and to avoid discrepancies with different protein nomenclatures for different organisms, they are treated as case insensitive. The user can specify the maximum number of links (intermediate interactions) allowed in a pathway, the types of evidence of the links to consider, and the minimum evidence confidence score required for each link. The types of link evidence present in the STRING database and selectable in the MoCha tool include conserved neighborhood, gene fusions, phylogenetic co-occurrence, co-expression, large-scale experiments, database imports, literature co-occurrence, and a combined scored. A pathway score is computed as the residual sum of squares (RSS) of the link scores. Shorter paths have preference over longer paths.

The search algorithm is based on an efficient double deferred binary search, which has O(log n) (Wirth, 1983), to find the lowest and highest indexed matching keys. For each input protein, the algorithm computes the graph with all the proteins connected to that input protein within the specified maximum number of links. The common set of proteins is then calculated by intersecting all the proteins in each graph, and then ordering them according to their average RSS link scores for each graph.

2.3. Implementation

We implemented MoCha in C++ using the Standard Library. A configuration shell script compatible with any UNIX/Linux system is provided to automatically download the necessary database files, process them, and compile the program (Lobo et al., 2016).

3. Results

We created MoCha, a tool for identifying candidate proteins representing unknown nodes in pathways network models. MoCha can efficiently search for proteins and their pathways that interact within a desired maximum path length, evidence type, and confidence score with all the proteins given as an input set (those suggested to be upstream or downstream within the network model). MoCha was designed and optimized for speed, being able to efficiently search within seconds over more than 1 billion interactions from the STRING database.

Figure 1 shows a use case of MoCha: characterizing an unknown pathway from an automatically reverse-engineered regulatory network of planarian regeneration (Lobo and Levin, 2015), an organism studied over a century for its outstanding regenerative capabilities (Lobo et al., 2012). The inferred dynamic network explains the regulation of the planarian body patterning regeneration under different surgical, genetic, and pharmacological perturbations. The networks contain known products defined in the input experiments (β-catenin, wnt1, apc, etc.), as well as two unknown components (labeled “a” and “b”) predicted as necessary by the algorithm. In this use case, we used MoCha to characterize component “a,” using as input for the tool all the proteins that directly interact with the unknown component (β-catenin, wnt1, and wnt11) and specifying combined confidence scores equal to or higher than 0.9 in any organism present in the database. The tool searched through the full database (76 GB of data), finding a total of 18 candidate proteins in the Homo sapiens and Mus musculus organisms. The figure shows the output of the tool containing the found candidate proteins and their pathways ordered according to their average score, with the most likely candidate proteins with the highest confidence listed at the top. The results show how DVL2 is the best candidate protein for the unknown component “a,” with a high relative RSS score of 275, compared with the RSS score of 1481 of the second candidate, FZD7. This search was performed in less than 1 second using a single core in a high-end computer.

FIG. 1.

Using MoCha to characterize the unknown component “a” of a reverse-engineered regulatory network model of planarian regeneration by searching for known pathways in other organisms interacting directly or indirectly with the same known proteins. The tool searched over 1 billion interactions in less than a second, finding and ordering by score 18 candidate proteins and their pathways.

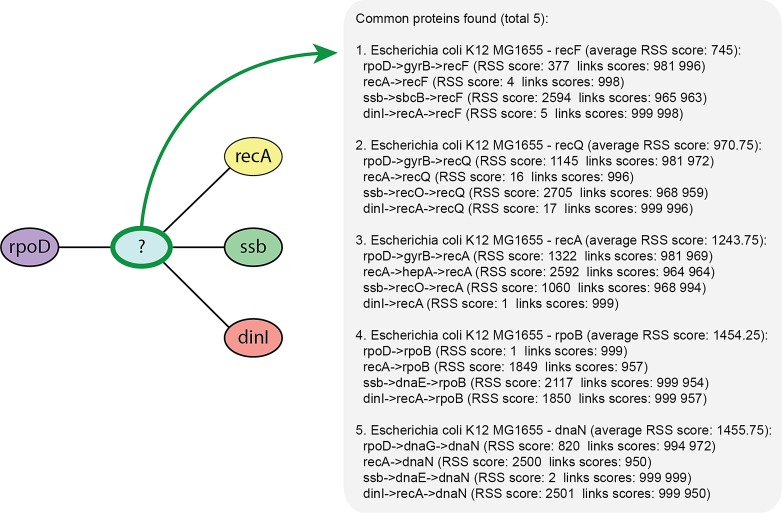
As a second case study, we used MoCha to discover the missing products in an inferred regulatory network from qPCR expression data of the SOS pathway in Eschericha coli (Gardner et al., 2003). This work presented a reverse-engineered model from perturbation data, which suggested the existence of some connections mediated by unknown genes. In particular, the sigma factor rpoD was predicted to indirectly interact with the genes recA, ssb, and dinI. To further investigate these predictions, we used MoCha to find possible interactions and components for these unknown genes (Fig. 2). Indeed, searching with MoCha for a direct link with at least medium confidence score (link confidence score higher than 0.5) did not find any possible candidate, corroborating the article's original conclusion that such interactions must be indirect. We then used MoCha to look for pathways with a maximum of 2 links (and link confidence score higher than 0.95). The algorithm then found five sets of possible interactions in E. coli between all the components, where the set with the best score contained the novel candidate gene recF as a common interactor between the input dataset of genes. This candidate gene can now be validated in vivo, illustrating the capability of our tool to generate predictions that are testable at the bench. The tool performed this search in less than a second.

FIG. 2.

Use example of MoCha for finding a common unknown regulator between four genes from a reverse-engineered regulatory network of Eschericha coli. A search of a common pathway component between the four genes found recF as the most probable candidate directly or indirectly interacting with all the four input components.

4. Discussion and Conclusions

To characterize unknown components in regulatory network models inferred with automated reverse-engineering methods, we need efficient tools that can mine the huge interaction databases to find candidate pathways in known organisms. For this, we presented MoCha, a fast tool for characterizing unknown components interacting with a set of known regulatory proteins. The tool uses STRING database v10 for searching over 1 billion interactions, yet its highly optimized algorithm allows searches to be completed within seconds.

We illustrated the applicability of MoCha with two use cases. First, we used MoCha to search for a candidate gene for an unknown reverse-engineered component in a regulatory network of planarian regeneration. The tool found a common novel gene with a high chance to be a direct common interactor with the other three known components. Second, a predicted but unknown component indirectly interacting with a set of genes from a regulatory network in E. coli was searched with MoCha. The tool confirmed that the interaction was indirect, finding a most likely candidate component and a set of pathways connecting it with all the known components.

MoCha can readily aid in the validation of reverse-engineered regulatory models, characterizing unknown components from interaction data and pathways from other organisms. This is a necessary step in the validation of reverse-engineered models with unknown components, and a further step toward the automation of the generation and validation of scientific hypotheses.

Acknowledgments

We thank the Levin Lab members for valuable discussions and suggestions. This work was supported by National Science Foundation (EF-1124651), National Institutes of Health (GM078484), W.M. Keck Foundation, and G. Harold and Leila Y. Mathers Charitable Foundation. Computation used equipment awarded by Silicon Mechanics.

Author Disclosure Statement

No competing financial interests exist.