Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2015 Dec 2;1(9):488–492. doi: 10.1021/acscentsci.5b00338

Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit

Joseph M Zadrozny †, Jens Niklas ‡, Oleg G Poluektov ‡, Danna E Freedman †,*
PMCID: PMC4827467  PMID: 27163013

Abstract

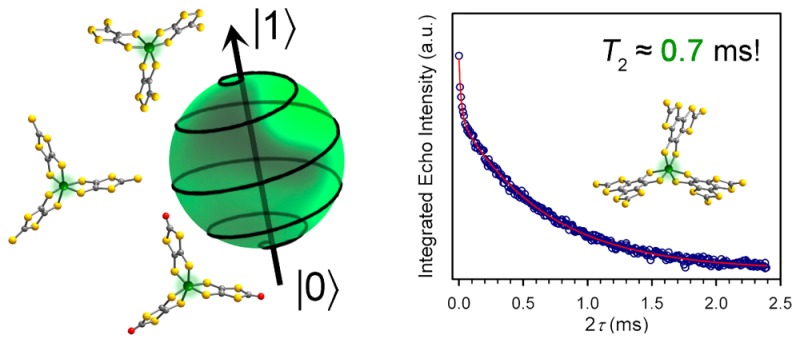
graphic file with name oc-2015-00338q_0007.jpg

Quantum information processing (QIP) could revolutionize areas ranging from chemical modeling to cryptography. One key figure of merit for the smallest unit for QIP, the qubit, is the coherence time (T2), which establishes the lifetime for the qubit. Transition metal complexes offer tremendous potential as tunable qubits, yet their development is hampered by the absence of synthetic design principles to achieve a long T2. We harnessed molecular design to create a series of qubits, (Ph4P)2[V(C8S8)3] (1), (Ph4P)2[V(β-C3S5)3] (2), (Ph4P)2[V(α-C3S5)3] (3), and (Ph4P)2[V(C3S4O)3] (4), with T2s of 1–4 μs at 80 K in protiated and deuterated environments. Crucially, through chemical tuning of nuclear spin content in the vanadium(IV) environment we realized a T2 of ∼1 ms for the species (d20-Ph4P)2[V(C8S8)3] (1′) in CS2, a value that surpasses the coordination complex record by an order of magnitude. This value even eclipses some prominent solid-state qubits. Electrochemical and continuous wave electron paramagnetic resonance (EPR) data reveal variation in the electronic influence of the ligands on the metal ion across 1–4. However, pulsed measurements indicate that the most important influence on decoherence is nuclear spins in the protiated and deuterated solvents utilized herein. Our results illuminate a path forward in synthetic design principles, which should unite CS2 solubility with nuclear spin free ligand fields to develop a new generation of molecular qubits.

Short abstract

We observe a millisecond coherence time for a coordination complex qubit, surpassing the previous record for such a system by an order of magnitude.

By exploiting the inherent properties of quantum species such as spins, quantum information processing (QIP) offers the potential to fundamentally transform our approach to modeling chemical systems and cryptography.1−4 This tantalizing concept relies upon quantum manipulation of the smallest units of a QIP system, qubits. Electronic spins, one of the most intuitive candidate qubit classes, demonstrate promise in a variety of materials and complexes.5−9 Even beyond the well-developed ability to control such qubits10 and their facile synthetic tunability, electronic spin qubits offer the potential to host multiple qubits within a single manifold of spin levels.11,12 Yet, despite decades of research, molecular electronic spin qubits continue to suffer from rapid collapse of their superpositions, a process known as decoherence.13,14 The key variable that describes the lifetime of the superposition, the coherence time, or spin–spin relaxation time T2, is still at least an order of magnitude lower in the best transition metal complex qubits15,16 than required for quantum error correction schemes17 and realistic applications. The rational design of qubits with long coherence times necessitates careful consideration of the chemical variables that contribute to decoherence. One primary factor frequently implicated in decoherence is the interaction of the electronic spin qubit with environmental nuclear spins, within both the complex and external matrix.14,18 To engender long coherence times in transition metal complexes, we are designing nuclear spin-free ligand environments to eliminate the former source of nuclear spins. This approach restricts our ligand selection and design to ligands composed of carbon, oxygen, and sulfur exclusively, which exhibit 98.9, 99.8, and 99.2% natural abundances of nuclear spin-free isotopes, respectively.

We recently communicated a pulsed EPR investigation of the species [V(C8S8)3]2–, which revealed a μs-length T2 that persisted to above the temperature of liquid N2.12 Motivated by these promising results, herein we report a two-part, systematic investigation of synthetically accessible parameters on the lifetime of the qubit formed in the vanadium(IV) trisdithiolate platform: first, a comprehensive study of (Ph4P)2[V(C8S8)3] (1) (Figure 1) and, second, a subsequent evaluation of a series of molecules, where the impact of specific molecular factors on the superposition lifetime could be tested. Incredibly, we observe a 2 order of magnitude range in T2 within this study, including observation of an unrivaled coherence time T2 = 0.7 ms in 1.

Figure 1.

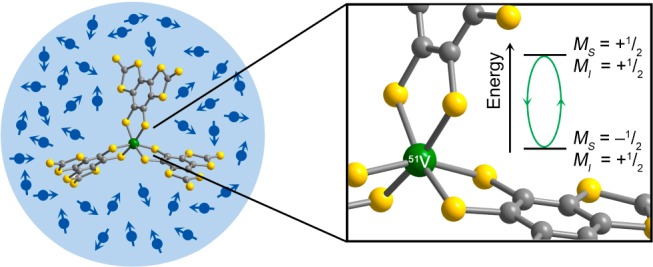
Figure 1

Open in a new tab

Depiction of the immediate environment of [V(C8S8)3]2– in solution, which is high in nuclear spin content, which affects the lifetime of the superpositions of a dissolved electronic spin qubit. The inset denotes the investigated superposition of [V(C8S8)3]2– in this report.

In the initial part of our study, we investigated the stability of the spin superposition of the qubit 1 at the central EPR resonance (Figures 1, S1) by measuring T2 as a function of solvent and temperature (Figure 2). Specifically, we measured 0.5 mM solutions of 1 in four different solvent systems: 1:1 d7-dimethylformamide (DMF)/d8-toluene (Tol), DMF/Tol, DMF/butyronitrile (PrCN), PrCN, and a 0.01 mM solution of (Ph4P)2[V(C8S8)3] (1′) in CS2 (see Figures 2, S2). In all solvents except the nuclear spin-free CS2, T2 remains relatively constant from 10 to 60 K, after which the decay rate displays strong temperature dependence. The temperature independence of T2 at low temperature suggests that nuclear spin-mediated decoherence is significant in this regime, since phonon mediated processes are strongly temperature dependent.18 At higher temperatures the T2 values coalesce toward ≤1 μs, indicating an increasing role of thermal vibrations and spin–lattice relaxation in decoherence, mediated by the spin–orbit coupling of the vanadium(IV) ion.18 The concentration dependence of T2 for 1 was evaluated in PrCN, showing no change in T2 at 10 K from concentrations of 1 to 0.05 mM. On this basis we further conclude that intermolecular interactions are suppressed at the concentrations utilized in this report.

Figure 2.

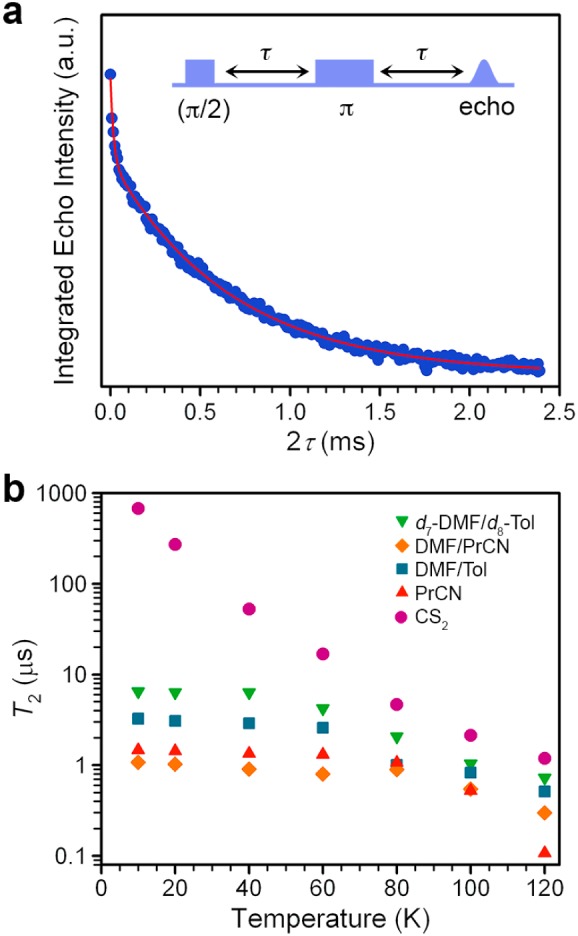
Figure 2

Open in a new tab

Evaluation of the viability of [V(C8S8)3]2– as a qubit in protiated, deuterated, and nuclear spin-free solvents. (a) The Hahn echo decay curve for 1′ at 10 K in CS2 indicates the time frame for the loss of quantum information from the spin qubit. The red line is a biexponential fit that quantifies the time constant for this decay, T2, of 675(7) μs. The fast decay at 2τ < 0.1 ms is attributed to a small percentage of closely spaced [V(C8S8)3]2– moieties that occur due to the inability of CS2 to form a frozen glass. (b) Logarithmic temperature dependence of T2 for [V(C8S8)3]2– in protiated, deuterated, and nuclear spin-free solvents, which illustrates the enormous impact of eliminating nuclear spins on the magnitude of the coherence time.

Elucidation of the phonon contributions to decoherence was accomplished through analysis of the spin–lattice relaxation time, T1, in each of the solvent systems from 10 to 120 K (Figures S3, S4). For [V(C8S8)3]2–, the magnitudes of T1 across all solvents illustrate substantial temperature dependence, decreasing by several orders of magnitude from milliseconds at 10 K (6.5(1)–36.2(2) ms) to under 5 μs at 120 K. The values of T1 are nearly indistinguishable across solvent systems, indicating that analyte–solvent intermolecular interactions are not dominant in dictating spin–lattice relaxation, in accordance with other transition metal complex systems.18 Note, noticeable differentiation occurs at 10 K likely due to differing thermal properties of the frozen glasses.19 In systems where phonon contributions, librational motion,20 or efficient molecular tumbling limit T2, the maximum value of T2 is T1.18 In our system, however, we observe T1 ≫ T2 within the entire low temperature range, which precludes phonon limitation of T2 for [V(C8S8)3]2– in all solvents except CS2. Additionally, the value of T2 at low temperature does not trend with T1, as evidenced by T1(PrCN) > T1(CS2) yet T2(CS2) ≫ T2(PrCN). Further comparison of the T1 and T2 data for the 1:1 DMF/Tol, 1:1 d7-DMF/d8-Tol, and CS2 solvent systems also reveals nearly identical T1 values despite vastly different T2.

Acquisition of data across a range of solvents and temperatures provides us with sufficient evidence to conclude that nuclear spins in the solvent system are the dominant mediator of low temperature decoherence here. The strong influence of nuclear spin on coherence explains the dramatic magnitude of T2 for 1′ in CS2. In this system, T2 demonstrates strong temperature dependence over the entire temperature range, which indicates that, following elimination of nuclear spins, the only remaining sources of decoherence are T1-related effects. Remarkably, at 10 K, the value of T2 is 2 orders of magnitude greater than for the other solvent systems, with T2 = 675(7) μs (∼0.7 ms) in CS2. It is vital to note that previous studies of protiated transition metal qubits in CS2 did not demonstrate this profound enhancement by exclusion of environmental nuclear spins.21 We attribute the magnitudes here to the crucial combination of the nuclear spin free ligand field and environment which together enable the 2 order of magnitude increase.

Based upon this extraordinary result, we pursued nutation experiments designed to determine whether this candidate qubit can be placed into any arbitrary superposition of the states depicted in Figure 1. In these measurements, a variable-length microwave (mw) pulse (a nutation pulse or tipping pulse) was applied to 1′ in CS2 followed by two mw pulses to detect the tipped angle induced by the nutation pulse (Figure 3). Note that the applied dc magnetic field quantizes the alignment of the spin into down (MS = −1/2) and up (MS = +1/2) orientations. Thus, a spin alignment tipped away from the quantized orientations constitutes a superposition of the two levels. The composition of the superposition is dictated by the tipping angle, which is dependent on the power (B1) and length of the mw pulse. With increasing pulse length, these data display a continuous oscillation (a Rabi oscillation), with frequency ΩR (the Rabi frequency), as the composition of the newly created superposition cycles through all possible combinations of the two levels (see Figures 3, S5). Note that the decay of the Rabi oscillation occurs on a time scale considerably shorter than the obtained T2 under the same conditions. This observation does not indicate significant destabilization of the qubit by direct manipulation. Rather, the decay indicates a weakening of the echo intensity due to homogeneous and inhomogeneous broadening mechanisms, as well as a distribution of effective B1 fields experienced across the investigated sample.10

Figure 3.

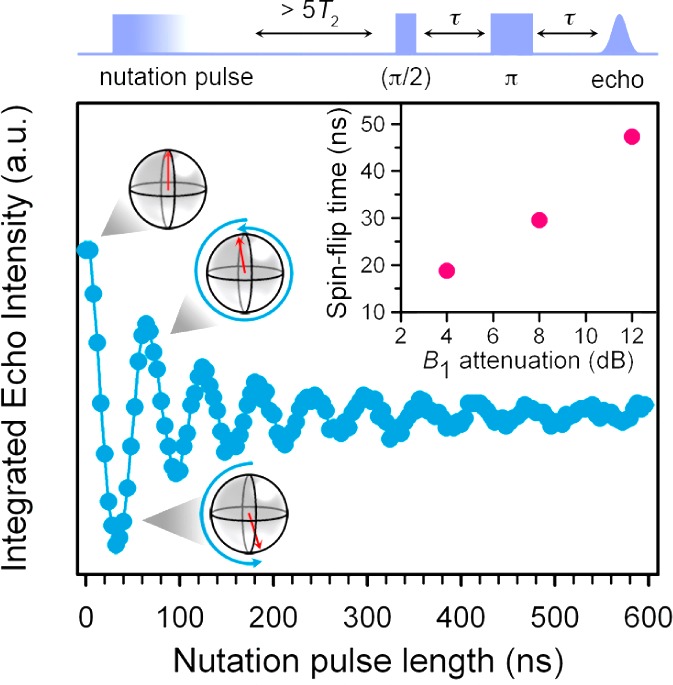
Figure 3

Open in a new tab

Rabi oscillation for 1′ in CS2 at 20 K which shows the ability of [V(C8S8)3]2– to assume any arbitrary superposition of the |±1/2,–1/2⟩ levels. The blue line is a guide for the eye, while spin orientations for specific nutation pulse lengths are depicted. Inset: Spin-flip operation time as a function of B1 attenuation.

The nutation data highlight two important aspects of the quantum control of [V(C8S8)3]2–. Crucially, the time length between adjacent minima and maxima denotes the spin-flip time, which corresponds to a single-qubit NOT computational operation. In 1′ these times fall from 47 to 19 ns with increasing B1 (see Figures 3, S5), with the potential to be even shorter, following instrumental optimization. A useful figure of merit to characterize the qubit, QM, is defined as the ratio of T2/ΩR and represents the number of spin-flip operations that could be performed with a qubit in the time length of T2. In [V(C8S8)3]2– as isolated in CS2, the fastest operation time determined yields QM ≈ 36,000, which is unrivaled by an order of magnitude among candidate transition metal complex qubits. We note that this value is significantly higher than the threshold required for quantum error correction, an important result if an assembly were realized that contained a multitude of these qubits.17 Thus, such a magnitude of QM implies genuine utility for 1′ given the combination of the multiple qubits afforded by the electronuclear hyperfine coupling,12 the access to all superpositions of these qubits, and extremely long T2 values.

To evaluate the universality of the nuclear spin-free design principle and study the tunability of the VS6 platform, we synthesized and studied the complexes (Ph4P)2[V(β-C3S5)3] (2), (Ph4P)2[V(α-C3S5)3] (3), and (Ph4P)2[V(C3S4O)3] (4), each with different nuclear spin-free ligand fields (Figure 4a, Tables S1–S4). Within this set of complexes, electron donation was varied across the series in both σ- and π-orbitals, as evidenced by cyclic voltammetry experiments which suggest a trend of increasing electronic donating behavior from C8S82– < β-C3S52– < α-C3S52– < C3S4O2– (Figure S6). The second factor of potential tunability in 1–4 is the variation in spin delocalization with ligand identity, as indicated by variation in the hyperfine coupling constant A with ligand identity. Analyses of the cw EPR data (see the Supporting Information, Table S5, and Figure S7) suggests localization of the unpaired electrons in vanadium dz2 orbitals, which is further only weakly adjusted by ligand set. Note, the dz2 orbital is energetically distinct from the other 3d orbitals in the pseudo trigonal antiprismatic coordination environments of 1–4.22,23 Thus, small distortions to the coordination geometry of the vanadium(IV) ion, as may occur from molecular vibrations, are hypothesized to be particularly ineffective at modulating the energy of the dz2 orbital. If true, then this aspect of the electronic structure of 1–4 may suppress the ability of the spin–orbit coupling of the vanadium(IV) ion to mediate fast electronic spin decoherence.18,24

Figure 4.

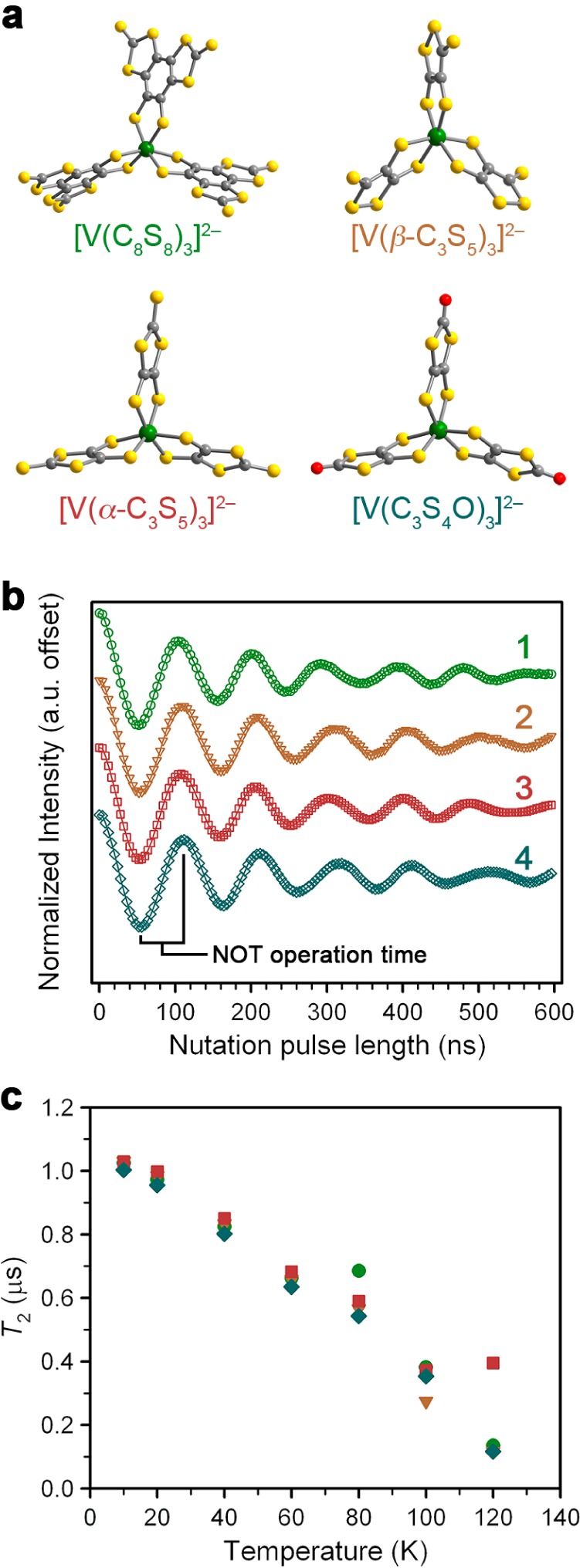
Figure 4

Open in a new tab

Evaluation of a series of VS6 qubits. (a) Molecular structures of the complexes as they appear in the crystal structures of 1–4. Green, yellow, red, and gray spheres represent vanadium, sulfur, oxygen, and carbon atoms, respectively. (b) Nutations for 1–4 that verify quantum control in each member of the series. Data were recorded in 1:1 DMF/Tol at 20 K, and 14 dB attenuation of B1. The spin-flip operation time of 52 ns is highlighted. (c) Temperature dependences of T2 for 1–4 in 1:1 DMF/Tol are nearly indistinguishable.

The impacts of the foregoing electronic structure factors on the viabilities of 1–4 for QIP were evaluated in a preliminary manner by the determination of T2 and T1 (see Tables S6–S9, Figures S9–S13). T1 and T2 are nearly indistinguishable across 1–4 in 1:1 DMF/Tol, 1:1 DMF/PrCN, and 1:1 d7-DMF/d8-Tol except at the lowest temperatures, where slight differences are seen (Figures S10–S13). However, none of the trends implied by the CV or cw-EPR experiments reproduce the trends in T2 or T1 for 1–4. Importantly the temperature dependences of these parameters and the operation times of the complexes (Figures 4, S14, S15) are remarkably similar across the series of complexes. The observed similarity in the data highlight the viability of each of 1–4 as potential qubits, and demonstrate the generalizability of the nuclear spin-free synthetic design principle to a wide range of nuclear spin-free ligand fields. However, the data highlight the overwhelming impact of the environmental nuclear spins on these qubits. On the basis of these results, we conclude that further evaluations of the specific electronic factors that affect coherence in transition metal complexes must first exclude nuclear spins. The insolubility of 2–4 in CS2 precludes the investigation of the coherent spin dynamics in the absence of nuclear spins, and this fact highlights CS2 solubility as an important design parameter for future transition metal qubits.

On the basis of these experiments, we conclude that the solubility in CS2 and the nuclear spin-free ligands cooperate to create exceedingly long coherence times. This synergistic effect offers a blueprint for the future design of tunable, coordination complex-based qubits. Indeed, this relatively high degree of tunability confers special advantages to the present species over nitrogen-doped C60, despite comparable T2 values.25,26 The remarkable lifetime of the spin qubit 1′ in CS2 lifts the achievable limit of tunable, transition metal complex qubits to the range of solid-state qubit candidates, eclipsing some prominent examples such as the nitrogen vacancy center in non-isotopically enriched diamond, defects in silicon carbide, and Er-doped CaWO4.27−30 Electronic and nuclear spin qubits in isotopically purified environments consistently reach T2 values equal to or greater than ms in magnitude31−34 and we anticipate the realization of comparable lifetimes if enrichment were similarly pursued here.

The foregoing results demonstrate a considerable step forward in the design of transition metal complexes useful for studying spin-based quantum computation. Prior to this report, a clear limitation to the use of transition metal complexes for QIP was their generally low coherence times. Importantly, the magnitude of T2 observed here, which eclipses all other transition metal complex qubits, and some solid state candidates (Figure 5),35 demonstrates the broad viability of coordination compounds as qubits. Thus, these results substantially improve the prospects of developing transition metal complexes with coherence times appropriate for more advanced QIP studies, including creating a hybrid electronuclear quantum memory31 with the 51V nuclear spin, or exploiting the full range of transitions within the hyperfine manifold for qubit manipulation.

Figure 5.

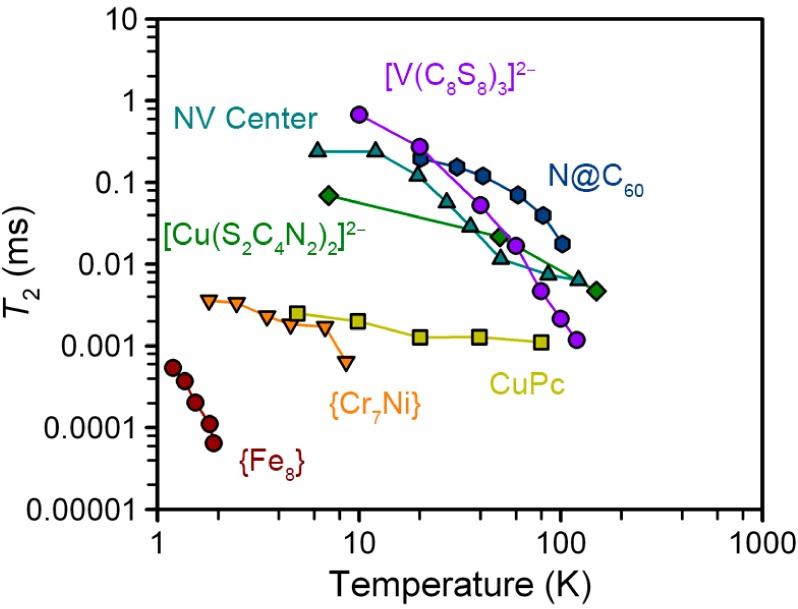
Figure 5

Open in a new tab

Comparison of the highest T2 values of [V(C8S8)3]2– with those of other notable molecular and solid state electronic spin qubits. Data were extracted from refs (14−16), (25−27), and (35). Conditions under which data were collected follow. {Fe8}: single crystal, 240 GHz mw irradiation. {Cr7Ni}: 0.1 mM d8-Tol solution, X-band mw irradiation. CuPc: 0.1% cocrystallization with unmetalated ligand, X-band mw irradiation. (Ph4P)2[Cu(S2C4N2)2]: 1:500 Cu:Ni cocrystallization, X-band mw irradiation. NV center: defects in diamond, 240 GHz mw irradiation. N@C60: <0.8 mM in 3:1 CS2:S2Cl2, X-band mw irradiation.

Acknowledgments

We thank M. S. Fataftah and M. J. Graham for fruitful discussions and experimental assistance. We acknowledge support from Northwestern University, the State of Illinois, and the National Science Foundation for CAREER Award No. CHE-1455017 (J.M.Z. and D.E.F.). This material is based upon work supported by the US Department of Energy Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, under Contract DE-AC02-06CH11357 at Argonne National Laboratory (J.N. and O.G.P.).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.5b00338.

  • Experimental details and spectroscopic, crystallographic, and electrochemical data (PDF)

Author Contributions

All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

oc5b00338_si_001.pdf (9.9MB, pdf)

References

  1. Feynman R. P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. 10.1007/BF02650179. [DOI] [Google Scholar]
  2. Lloyd S. Universal quantum simulators. Science 1996, 273, 1073–1078. 10.1126/science.273.5278.1073. [DOI] [PubMed] [Google Scholar]
  3. Aspuru-Guzik A.; Dutoi A. D.; Love P. J.; Head-Gordon M. Simulated quantum computation of molecular energies. Science 2005, 309, 1704–1707. 10.1126/science.1113479. [DOI] [PubMed] [Google Scholar]
  4. Nielsen M. A.; Chuang I. L.. Quantum Computation and Quantum Information, 10th anniversary ed.; Cambridge University Press: Cambridge, 2010. [Google Scholar]
  5. Ladd T. D.; Jelezko F.; Laflamme R.; Nakamura Y.; Monroe C.; O’Brien J. L. Quantum Computers. Nature 2010, 464, 45–53. 10.1038/nature08812. [DOI] [PubMed] [Google Scholar]
  6. Awschalom D. D.; Bassett L. C.; Dzurak A. S.; Hu E. L.; Petta J. R. Quantum Spintronics: Engineering and Manipulating Atom-Like Spins in Semiconductors. Science 2013, 339, 1174–1179. 10.1126/science.1231364. [DOI] [PubMed] [Google Scholar]
  7. Ochsenbein S. T.; Gamelin D. R. Quantum oscillations in magnetically doped colloidal nanocrystals. Nat. Nanotechnol. 2011, 6, 112–115. 10.1038/nnano.2010.252. [DOI] [PubMed] [Google Scholar]
  8. Troiani F.; Affronte M. Molecular spins for quantum information technologies. Chem. Soc. Rev. 2011, 40, 3119–3129. 10.1039/c0cs00158a. [DOI] [PubMed] [Google Scholar]
  9. Aromí G.; Aguilà D.; Gamez P.; Luis F.; Roubeau O. Design of magnetic coordination complexes for quantum computing. Chem. Soc. Rev. 2012, 41, 537–546. 10.1039/C1CS15115K. [DOI] [PubMed] [Google Scholar]
  10. Schweiger A.; Jeschke G.. Principles of pulse electron paramagnetic resonance; Oxford University Press: Oxford, 2001. [Google Scholar]
  11. Leuenberger M.; Loss D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. 10.1038/35071024. [DOI] [PubMed] [Google Scholar]
  12. Zadrozny J. M.; Niklas J.; Poluektov O. G.; Freedman D. E. Multiple quantum coherences from hyperfine transitions in a vanadium(IV) complex. J. Am. Chem. Soc. 2014, 136, 15841–15844. 10.1021/ja507846k. [DOI] [PubMed] [Google Scholar]
  13. Stamp P. C. E.; Gaita-Ariño A. Spin-based quantum computers made by chemistry: hows and whys. J. Mater. Chem. 2009, 19, 1718–1730. 10.1039/B811778K. [DOI] [Google Scholar]
  14. Takahashi S.; Tupitsyn I. S.; van Tol J.; Beedle C. C.; Hendrickson D. N.; Stamp P. C. E. Decoherence in crystals of quantum molecular magnets. Nature 2011, 476, 76–79. 10.1038/nature10314. [DOI] [PubMed] [Google Scholar]
  15. Warner M.; Din S.; Tupitsyn I. S.; Morley G. W.; Stoneham A. M.; Gardener J. A.; Wu Z.; Fisher A. J.; Heutz S.; Kay C. W. M.; Aeppli G. Potential for spin-based information processing in thin-film molecular semiconductor. Nature 2013, 503, 504–508. 10.1038/nature12597. [DOI] [PubMed] [Google Scholar]
  16. Bader K.; Dengler D.; Lenz S.; Endeward B.; Jiang S.-D.; Neugebauer P.; van Slageren J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. 10.1038/ncomms6304. [DOI] [PubMed] [Google Scholar]
  17. DiVincenzo D. P. The physical implementation of quantum computation. Fortschr. Phys. 2000, 48, 771–783. . [DOI] [Google Scholar]
  18. Eaton S. S.; Eaton G. R. Distance measurements in biological systems by EPR. Biol. Magn. Reson. 2002, 19, 29–154. 10.1007/0-306-47109-4_2. [DOI] [Google Scholar]
  19. Du J.-L.; Eaton G. R.; Eaton S. S. Temperature, orientation, and solvent dependence of electron spin-lattice relaxation rates for nitroxyl radicals in glassy solvents and doped solids. J. Magn. Reson., Ser. A 1995, 115, 213–221. 10.1006/jmra.1995.1169. [DOI] [Google Scholar]
  20. Du J.-L.; Eaton S. S.; Eaton G. R. Effect of molecular motion on electron spin phase memory times for copper(II) complexes in doped solids. Appl. Magn. Reson. 1994, 6, 373–378. 10.1007/BF03162630. [DOI] [Google Scholar]
  21. Schlegel C.; van Slageren J.; Manoli M.; Brechin E. K.; Dressel M. Direct observation of quantum coherence in single-molecule magnets. Phys. Rev. Lett. 2008, 101, 147203. 10.1103/PhysRevLett.101.147203. [DOI] [PubMed] [Google Scholar]
  22. Sproules S.; Weyhermüller T.; DeBeer S.; Wieghardt K. Six-membered electron transfer series [V(dithiolene)3]z (z = 1+, 0, 1–, 2–, 3–, 4−). An X-ray Absorption Spectroscopic and Density Functional Theoretical Study. Inorg. Chem. 2010, 49, 5241–5261. 10.1021/ic100344f. [DOI] [PubMed] [Google Scholar]
  23. Branca M.; Micera G.; Dessi A.; Sanna D.; Raymond K. N. Formation and structure of the tris(catecholato)vanadate(IV) complex in aqueous solution. Inorg. Chem. 1990, 29, 1586–1589. 10.1021/ic00333a030. [DOI] [Google Scholar]
  24. Nuccio L.; Willis M.; Schulz L.; Fratini S.; Messina F.; D’Amico M.; Pratt F. L.; Lord J. S.; McKenzie I.; Loth M.; Purushothaman B.; Anthony J.; Heeney M.; Wilson R. M.; Hernández I.; Cannas M.; Sedlak K.; Kreouzis T.; Gillin W. P.; Bernhard C.; Drew A. J. Importance of Spin-Orbit Interaction for the Electron Spin Relaxation in Organic Semiconductors. Phys. Rev. Lett. 2013, 110, 216602. 10.1103/PhysRevLett.110.216602. [DOI] [PubMed] [Google Scholar]
  25. Morton J. J. L.; Tyryshkin A. M.; Ardavan A.; Porfyrakis K.; Lyon S. A.; Briggs G. A. D. Electron spin relaxation of N@C60 in CS2. J. Chem. Phys. 2006, 124, 014508. 10.1063/1.2147262. [DOI] [PubMed] [Google Scholar]
  26. Morton J. J. L.; Tyryshkin A. M.; Ardavan A.; Porfyrakis K.; Lyon S. A.; Briggs G. A. D. Environmental effects on electron spin relaxation in N@C60. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76, 085418. 10.1103/PhysRevB.76.085418. [DOI] [Google Scholar]
  27. Takahashi S.; Hanson R.; van Tol J.; Sherwin M. S.; Awschalom D. D. Quenching spin decoherence in diamond through spin bath polarization. Phys. Rev. Lett. 2008, 101, 047601. 10.1103/PhysRevLett.101.047601. [DOI] [PubMed] [Google Scholar]
  28. Stanwix P. L.; Pham L. M.; Maze J. R.; Le Sage D.; Yeung T. K.; Cappellaro P.; Hemmer P. R.; Yacoby A.; Lukin M. D.; Walsworth R. L. Coherence of nitrogen vacancy electronic spin ensembles in diamond. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 201201(R). 10.1103/PhysRevB.82.201201. [DOI] [Google Scholar]
  29. Koehl W. F.; Buckley B. B.; Heremans F. J.; Calusine G.; Awschalom D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 2011, 479, 84–87. 10.1038/nature10562. [DOI] [PubMed] [Google Scholar]
  30. Bertaina S.; Gambarelli S.; Tkachuk A.; Kurkin I. N.; Malkin B.; Stepanov A.; Barbara B. Rare-earth solid-state qubits. Nat. Nanotechnol. 2007, 2, 39–42. 10.1038/nnano.2006.174. [DOI] [PubMed] [Google Scholar]
  31. Morton J. J. L; Tyryshkin A. M.; Brown R. M.; Shankar S.; Lovett B. W.; Ardavan A.; Schenkel T.; Haller E. E.; Ager J. W.; Lyon S. A. Solid-state quantum memory using the 31P nuclear spin. Nature 2008, 455, 1085–1088. 10.1038/nature07295. [DOI] [Google Scholar]
  32. Morley G. W.; Lueders P.; Mohammady M. H.; Balian S. J.; Aeppli G.; Kay C. W. M.; Witzel W. M.; Jeschke G.; Monteiro T. S. Quantum control of hybrid nuclear-electronic qubits. Nat. Mater. 2013, 12, 103–107. 10.1038/nmat3499. [DOI] [PubMed] [Google Scholar]
  33. Morley G. W.; Warner M.; Stoneham A. M.; Greenland P. T.; van Tol J.; Kay C. W. M.; Aeppli G. The initialization and manipulation of quantum information stored in silicon by bismuth dopants. Nat. Mater. 2010, 9, 725. 10.1038/nmat2828. [DOI] [PubMed] [Google Scholar]
  34. Tyryshkin A. M.; Tojo S.; Morton J. J. L.; Riemann H.; Abrosimov N. V.; Becker P.; Pohl H.-J.; Schenkel T.; Thewalt M. L. W.; Itoh K. M.; Lyon S. A. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 2012, 11, 143–147. 10.1038/nmat3182. [DOI] [PubMed] [Google Scholar]
  35. Wedge C. J.; Timco G. A.; Spielberg E. T.; George R. E.; Tuna F.; Rigby S.; McInnes E. J. L.; Winpenny R. E. P.; Blundell S. J.; Ardavan A. Chemical engineering of molecular qubits. Phys. Rev. Lett. 2012, 108, 107204. 10.1103/PhysRevLett.108.107204. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc5b00338_si_001.pdf (9.9MB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES