Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2015 Jul 10;1(4):198–205. doi: 10.1021/acscentsci.5b00195

Systematic Computational and Experimental Investigation of Lithium-Ion Transport Mechanisms in Polyester-Based Polymer Electrolytes

Michael A Webb †, Yukyung Jung ‡, Danielle M Pesko ⊥, Brett M Savoie †, Umi Yamamoto †, Geoffrey W Coates ‡, Nitash P Balsara ⊥,§,∥, Zhen-Gang Wang †, Thomas F Miller III †,*
PMCID: PMC4827473  PMID: 27162971

Abstract

graphic file with name oc-2015-001959_0008.jpg

Understanding the mechanisms of lithium-ion transport in polymers is crucial for the design of polymer electrolytes. We combine modular synthesis, electrochemical characterization, and molecular simulation to investigate lithium-ion transport in a new family of polyester-based polymers and in poly(ethylene oxide) (PEO). Theoretical predictions of glass-transition temperatures and ionic conductivities in the polymers agree well with experimental measurements. Interestingly, both the experiments and simulations indicate that the ionic conductivity of PEO, relative to the polyesters, is far higher than would be expected from its relative glass-transition temperature. The simulations reveal that diffusion of the lithium cations in the polyesters proceeds via a different mechanism than in PEO, and analysis of the distribution of available cation solvation sites in the various polymers provides a novel and intuitive way to explain the experimentally observed ionic conductivities. This work provides a platform for the evaluation and prediction of ionic conductivities in polymer electrolyte materials.

Short abstract

Experimental and theoretical methods are combined to study lithium-ion transport in new polymer electrolytes, providing mechanistic insights that inform the design of improved materials.

Introduction

Solvent-free, solid polymeric electrolytes (SPEs)1 are of interest for the development of safe, stable, and cost-effective battery technologies. Candidate SPEs typically require both a strong coordinating affinity for the conducting cation and a suitable distance between coordinating centers.2,3 Consequently, poly(ethylene oxide) (PEO) and PEO-based polymers have been extensively characterized, although ambient temperature ionic conductivities in such polymers are not satisfactory for many practical applications.4,5

Significant theoretical evidence suggests that ion transport in polymers is intrinsically coupled to polymer motion.6−15 In particular, numerous theoretical studies of ion transport in PEO-based SPEs have shown that lithium cations are typically coordinated by 4–7 oxygen atoms (from one or two independent chains) and diffuse via three principal mechanisms: interchain hopping, intrachain hopping, and codiffusion with short polymer chains (<10 000 g/mol). Efforts to improve lithium-ion conductivity in PEO-based polymers have thus mainly focused on disrupting polymer crystallinity and lowering the glass-transition temperature Tg, such as through the use of plasticizing additives,16,17 cross-linked, comb, or graft polymer architectures,18−22 incorporation of comonomers into the PEO backbone,23−30 and polymer blends.31,32 Despite these efforts, ionic conductivities in state-of-the-art, PEO-based SPEs remain limited at ambient temperatures.21

Non-PEO-based polymer architectures provide new opportunities for enhancing ionic conductivity by altering ion–polymer and polymer–polymer interactions and are thus of interest for the design of next-generation SPEs. Ionic conductivity characteristics have been experimentally investigated in several novel polymers that include polyesters, polyphosphazenes, polyamines, polysilanes, polysiloxanes, and polycarbonates.33−40 However, few theoretical studies on the mechanisms of ion transport in such polymers have been performed, and it is not known to what extent the transport mechanisms present in PEO are shared in other polymer architectures. The design of new SPEs requires an improved understanding of the mechanisms that facilitate lithium-ion transport in polymers and the identification of new polymer architectures that efficiently realize these mechanisms.

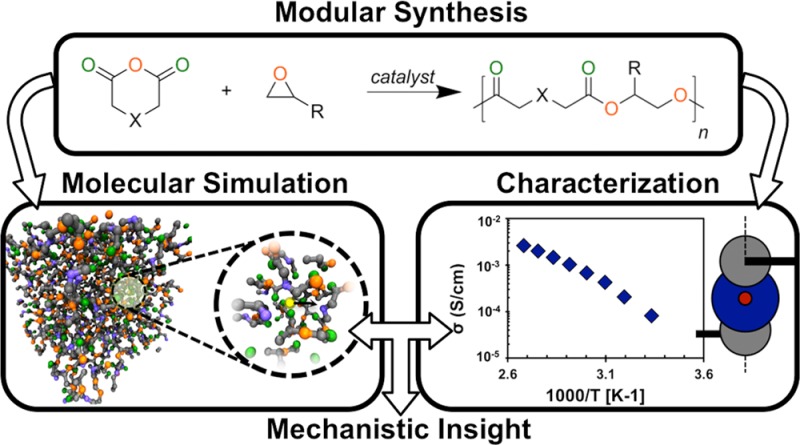
Here, experimental synthesis and electrochemical characterization are combined with long-timescale molecular dynamics (MD) simulations to investigate lithium-ion transport in six new SPEs. Figure 1 illustrates a schematic overview of this approach. Modular synthesis produces six polyesters that have either of two backbone motifs and one of three side chains (Figure 1, top). These polymers are then characterized using both simulation and experiment (Figure 1, middle), which demonstrates the effect of polymer composition and architecture on ionic conductivity (Figure 1, bottom). By comparing experimental observables with the corresponding quantities from simulation, we identify the primary trends regarding polymer architecture and conductivity. Agreement between simulation and experiment then provides a connection between macroscopic properties and molecular-level processes, which enables a detailed theoretical analysis of the molecular processes that give rise to the observed trends. This complementary approach provides a better understanding of ion transport in novel polymer electrolytes than would be obtained from either an independent experimental or theoretical study.

Figure 1.

Figure 1

Open in a new tab

A schematic overview of the study.

Polymer Structures

Six aliphatic polyesters with two different backbone motifs and three different side chains are studied (Figure 2). The repeat unit for each is an ester with a pendant side chain. For ease of reference, the polymers are indexed by number according to the side chain and by letter according to the backbone motif. Polymers are indexed as type-1 for a methyl side chain, type-2 for an allyl side chain, and type-3 for an ethylene-oxide oligomer (n = 2) side chain. The backbone motifs are indexed as type-a for polymers with a methylene between the two carbonyl groups and type-b for polymers with an oxygen between the two carbonyl groups. Comparison between type-a and type-b polymers probes the effect of adding a binding site for the lithium cation in the backbone. Similarly, comparison of type-1, -2, and -3 polymers probes the effect of including additional binding sites in the side chain.

Figure 2.

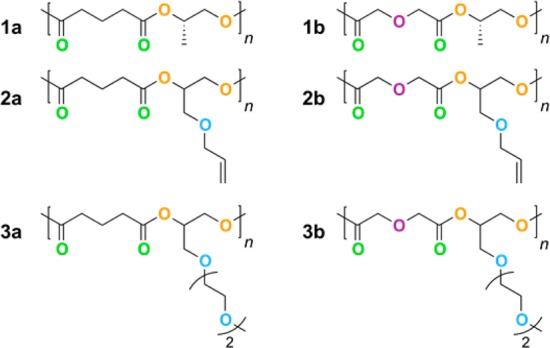
Figure 2

Open in a new tab

Repeat units for polyesters. Oxygen atoms are colored according to type: double-bonded carbonyl oxygens are green, ester oxygens are orange, ether oxygens in the backbone are purple, and ether oxygens in side chains are blue.

Methods

Synthesis

The polyesters are synthesized using the transition metal-catalyzed alternating copolymerization of epoxides and cyclic anhydrides.41−43 See Supporting Information (SI) for details. The polyester backbone structure is varied by copolymerizing glutaric anhydride (type-a) or diglycolic anhydride (type-b) with S-propylene oxide (type-1), allyl glycidyl ether (type-2), or 2-((2-(2-methoxyethoxy) ethoxy) methyl) oxirane (type-3) as shown in Figure 1 (top). Table 1 provides the number-averaged molecular weight ⟨Mn⟩ and polydispersity index (PDI) for each polymer; the polymers in this study exhibit molecular weights that are sufficiently high to expect that variation in ⟨Mn⟩ among the considered samples leads to only minor effects on conductivity and Tg.44,45

Table 1. Polymer Properties for Simulation and Experiment.

  simulation
 experiment
  Mn (kDa) Nca Tg (°C) rb ⟨Mn⟩ (kDa) PDI Tg (°C)
1a 2.54 11 35 0.0062 8.8 1.90 –29
1b 2.57 11 47 0.0062 8.0 1.72 12
2a 2.45 12 37 0.0077 10.4 2.00 –44
2b 2.47 12 49 0.0077 8.9 1.45 –15
3a 2.57 11 39 0.0103 4.2 1.30 –48
3b 2.59 11 41 0.0103 6.1 1.77 –26
PEO 2.38 12 2 0.0139 5c n/a –60
Open in a new tab
a

Number of polymer chains.

b

Number of lithium cations per nine polymer backbone atoms.

c

The measurements for Tg and conductivity in PEO employ molecular masses of 4.6 kDa and 5.0 kDa, respectively.

Simulation

All MD simulations employ a united-atom force field, with bonding parameters taken from CHARMM46 and all other parameters taken from the TraPPE-UA force field;47−50 compatible lithium-ion parameters are obtained from previous simulation studies.51 All simulations are performed using the LAMMPS simulation package52 with GPU acceleration.53,54 The equations of motion are evolved using the velocity-Verlet integrator with a 1 fs time step. Particle–particle–mesh Ewald summation is used to compute all nonbonded interactions beyond a 14 Å cutoff. The Nosé–Hoover thermostat (100 fs relaxation) is used for all NVT simulations, and the Nosé–Hoover barostat (1000 fs relaxation) is used for all NPT simulations. Results in the dilute-ion limit are obtained from simulations of a single lithium cation diffusing in the polymer. Additional details of the simulation protocols and all force-field parameters are provided in the SI.

Characterization

For each polymer, Tg measurements of the neat polymer are made using differential scanning calorimetry. Polymer electrolytes are then prepared by mixing neat polymer sample with lithium bis(trifluoromethanesulfonyl) imide (LiTFSI) salt and anhydrous N-methyl-2-pyrrolidone (NMP) in an argon glovebox until dissolution at 90 °C and drying under a vacuum at 90 °C to remove excess NMP. Ionic conductivities of the polymer electrolytes are determined from ac impedance spectroscopy. Additional details for both the Tg and conductivity measurements are provided in the SI.

Ionic Conductivity Results

Using both simulation and experiment, we examine the ionic conductivities of each polymer in the dilute-ion limit, which minimizes complications associated with ion pairing and aggregation.

Figure 3a–c presents MD simulation results for the mean square-displacement (MSD) of the lithium cation at 363 K. The slopes of the MSDs on a log–log scale are less than unity (Table S5), indicating that the transport is not yet in the fully diffusive regime even after 150 ns. Comparison of polymers 1a and 1b (Figure 3a) reveals that lithium-ion diffusion is slowed by the presence of the ether oxygen on the backbone. However, this effect is largely mitigated by the presence of side chains with oxygen atoms, as seen by comparing polymers 2a and 2b (Figure 3b), and likewise for polymers 3a and 3b (Figure 3c). Comparison of polymers 3a and 1b shows that the differences in polymer architecture considered here at most affect the lithium-ion diffusion by a factor of about 3.75. In contrast, the rate of lithium-ion transport is at least an order-of-magnitude faster in PEO than in any of the polyesters. In particular, the relative span of the subdiffusive regime, which is the near-plateau region in the MSD plots, reveals that the lithium cation is restricted to its local solvation environment for substantially longer times in the polyesters compared to PEO.

Figure 3.

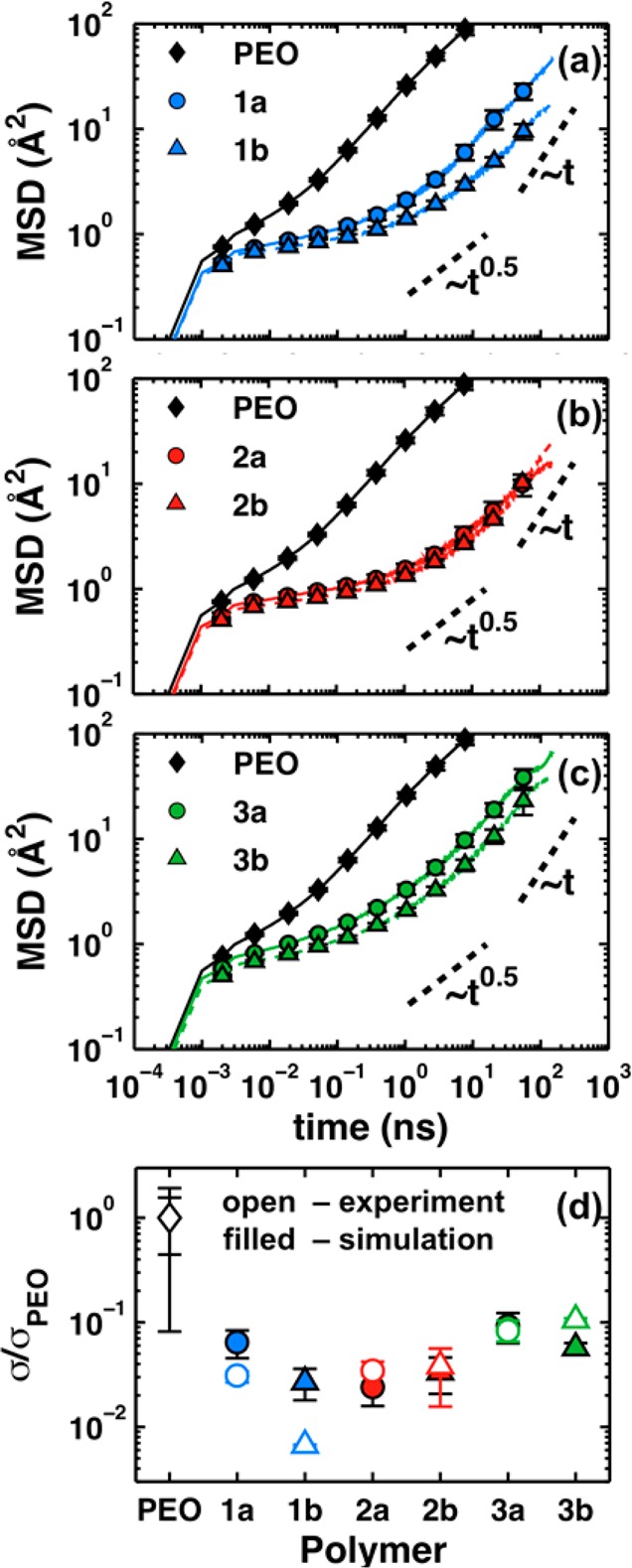
Figure 3

Open in a new tab

Ion transport properties in the dilute-ion limit at 363 K. Lithium-ion mean square-displacement (MSD) from MD simulations in PEO and the (a) type-1 polymers, (b) type-2 polymers, and (c) type-3 polymers. The data for PEO are reproduced in each panel. (d) A comparison of experimental and simulated ionic conductivities; both sets of data are normalized by the corresponding conductivity in PEO. The error bars in (a–c) report the standard error of the mean obtained from block-averaging four 500 ns trajectories for each polymer; error bars in (d) report the sample standard deviation.

For comparison with experiment, the MSD results in Figure 3a–c are used to compute approximate lithium-ion conductivities using the Nernst–Einstein equation55 and the apparent lithium-ion diffusivity6 evaluated at 150 ns (Table S5 and Figure S21). Figure 3d compares these results with experimental dilute ionic conductivities (see SI, section 7) at the same temperature and effective concentration as the simulations (Table 1).

Figure 3d reveals good agreement between dilute-ion conductivities obtained from experiment and those obtained from MD simulations. This correlation for the relative ordering of conductivities suggests that the lithium-ion dynamics are mechanistically similar between simulation and experiment. However, the dilute-ion conductivities obtained from simulation are systematically lower than the corresponding experimental measurements; for example, the conductivity for PEO obtained from simulation is (9 ± 4) × 10–6 compared to (2 ± 1) × 10–4 S/cm. This is possibly because the MD conductivity results reflect only contributions from the lithium cation, whereas the experimental measurements include both cation and anion contributions; of course, it is also possibly due to inaccuracies of the employed MD force field. Furthermore, the molecular weights of the polymer chains are smaller in the simulations than in the experimental samples, though we do not expect this difference to have a substantial effect on conductivity based on our knowledge of the molecular weight-dependence on polymer electrolyte conductivity.44,45 Polymer 1b is the only qualitative outlier in the correlation between experimental and simulation results. This is likely because polymer 1b is notably more solid in experiment, whereas this is not the case for the MD simulations. Even so, the experimental conductivities are all within a factor of 3 and an order-of-magnitude smaller than PEO. Thus, both experimental and simulation results indicate that the effect of varying polymer architecture in the polyesters is somewhat minor compared to the mechanistic advantage that apparently exists for PEO. In the next section, we investigate how differences in Tg affect the conductivity in these polymers.

Correlating Tg with Conductivity

Figure 4a and Table 1 provide both experimental and simulated values of Tg, which is often used as a proxy for the segmental mobility of polymer chains.2,56 Figure 4a illustrates that the experimental and simulation data are qualitatively similar by plotting the data relative to the glass-transition temperature for PEO, Tg,PEO. Consistently, Tg is lower for type-a polymers relative to type-b polymers, which suggests that adding a polar ether oxygen between the two carbonyls decreases segmental mobility. The experimental data also show a weak but consistent side-chain dependence. Namely, increasing side-chain length (type-1 < type-2 < type-3) leads to a slight reduction in Tg, possibly due to a plasticizing effect by the side chains or simply because the flexible side chains constitute a larger volume fraction of the polymer;2,21,57 this particular trend is not as evident in the simulated Tg data.

Figure 4.

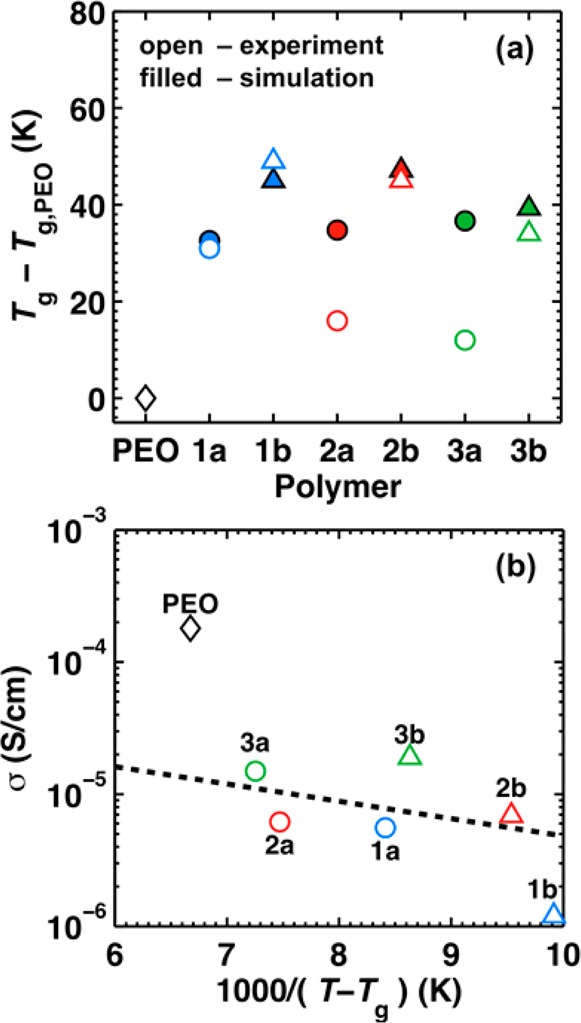
Figure 4

Open in a new tab

(a) Tg obtained via experiment using DSC (open symbols) and via MD using simulated dilatometry (filled symbols). (b) Correlation between dilute-ion conductivity and the inverse temperature difference from Tg at T = 363 K (experimental measurements). The dashed line indicates the linear fit of the data for the polyesters.

For the experimental data, Figure 4b reveals the degree of correlation between ionic conductivity and Tg by plotting the dilute-ion conductivities (on a logarithmic scale) against 1000(T – Tg)−1. This analysis is similar to a typical Vogel–Fulcher–Tammann ionic conductivity plot,2,58 except that a range of polymers (and thus a range of Tg) is examined at a fixed temperature rather than the conductivity of a given polymer over a range of temperatures. The dashed line is the linear fit of the data for the polyesters only. Although there is an overall tendency for polymers with lower Tg to have higher ionic conductivities, the correlation is not well-characterized by a single line. In particular, the figure shows strikingly that PEO exhibits anomalously high conductivity among this set of polymers when only the effects associated with changes in Tg (i.e., polymer segmental mobility) are considered. We emphasize that the corresponding analysis performed using the simulation data yields identical conclusions (Figure S25). In the following section, we demonstrate that this apparent anomaly in the conductivity of PEO can be understood if the connectivity of lithium-ion solvation sites is additionally considered.

Lithium-Ion Coordination Dynamics

Using the results from the MD simulations, we now investigate the mechanistic features of lithium-ion solvation and diffusion in the various polymer electrolytes to better understand the anomalously high conductivity of PEO.

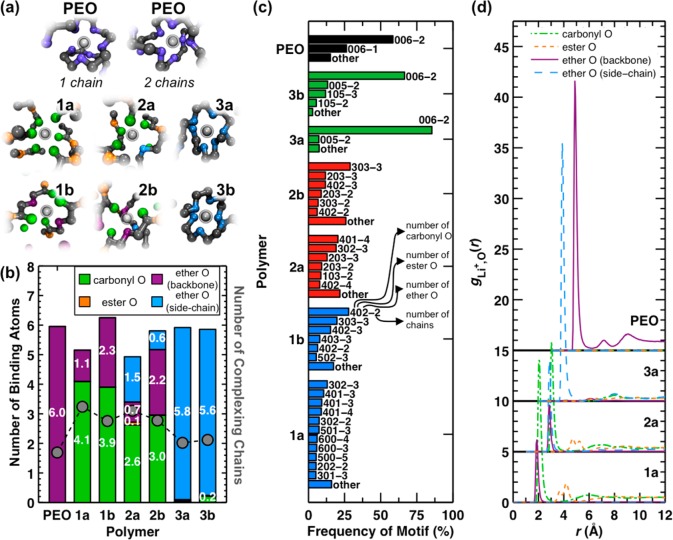
Figure 5 presents an analysis of the lithium-ion coordination environments that are observed in the MD simulations. Representative MD snapshots of common lithium-ion coordination environments are shown in Figure 5a for each polymer. It is well-known from previous MD studies that lithium cations are coordinated by one or two contiguous chain segments in PEO;6,7 examples of both of these binding motifs are shown at the top of Figure 5a. Interestingly, PEO is the only polymer among those studied here for which the lithium cation is frequently solvated by a single contiguous chain segment. This is surprising, given that the backbone composition for the type-b polymers is similar to PEO. Figure 5a also reveals that the ester oxygens on the backbone are not typically present in the lithium-ion solvation shell for any of the polyesters. Comparison of the type-1, -2, and -3 polymers reveals that the side chain can drastically alter how the lithium cation is solvated by the polymer chain. For type-1 polymers, the side chain has no affinity for the lithium cation, and the cation predominantly coordinates with carbonyl oxygens on the polymer backbone. For type-2 and -3 polymers, oxygen atoms on the side chain do interact with the lithium cation. In fact, type-3 polymers coordinate lithium cations entirely with the PEO-like side chains.

Figure 5.

Figure 5

Open in a new tab

Analysis of lithium-ion coordination data from MD simulations at 363 K. (a) Representative snapshots of lithium-ion binding motifs observed in the MD simulations. The lithium cation is shown in silver, carbon atoms are black, and the oxygen atoms are colored according to the scheme in Figures 2 and 5b. (b) The average number of oxygen atoms (left y-axis) and polymer chains (right y-axis) in the first solvation shell of the lithium cation. Vertical bars report the number of different oxygen types; markers report the number of coordinating chains in the solvation shell. Note that backbone ether contributions to the type-a polymers arise due to interactions with the terminal groups of the polymer chains. (c) Frequency of occurrence for lithium-ion binding motifs, where the binding motifs are defined according to the number of each oxygen type and the number of coordinating chains. The first three numbers refer to the number of carbonyl, ester, and ether oxygen atoms, respectively; the number following the dash refers to the number of different contiguous polymer chain segments (i.e., 402-2 indicates a motif with four carbonyl oxygens, zero ester oxygens, and two ether oxygens from two different chains). Only binding motifs that constitute more than 5% of the ensemble are explicitly listed; the remainder are included in “other”. (d) Cation-oxygen radial distribution functions gLi+,o(r) for different oxygen types in the type-a polymers and in PEO. The gLi+,o(r) for each oxygen type is normalized with respect to the total oxygen number density in the polymer. Following the data set for polymer 1a, each subsequent data set is shifted vertically (by 5 units) and horizontally (by 1 Å) for clarity. All statistical properties are calculated from snapshots taken at 100 ps intervals during the MD trajectory. A threshold distance of 3.25 Å from the lithium cation is used to identify constituents of the first lithium-ion solvation shell.

To provide a more quantitative view of the lithium-ion solvation environments, Figure 5b shows the average composition of the lithium-ion coordination environment in each polymer. Interestingly, the statistics for the type-3 polymers are nearly identical to each other and similar to those of PEO. There is also marked similarity between the PEO snapshot with two coordinating chains and the snapshots for the type-3 polymers in Figure 5a. Whereas PEO coordinates the lithium cation with one or two chains, two to four polymer chains typically coordinate the lithium cation in the polyesters. Compared to the other polyesters, the type-3 polymers require fewer chains to coordinate the lithium cation, likely due to the coordinating ability of the PEO-like side chains. Additionally, a comparison of polymer 1a with 1b, and likewise for polymer 2a with 2b, indicates that fewer chains participate in lithium-ion coordination when polymers have an additional oxygen atom in the backbone. It is worth noting that the only ether contribution for the type-a polymers is due to the terminal groups of the polymer chain (see SI, sections 4 and 8). However, additional simulations reveal that this is a minor effect (Figure S24).

To elucidate the compositional differences in the lithium-ion coordination environment for each polymer, Figure 5c presents the frequency with which different lithium-ion binding motifs are observed in the simulations. The binding motifs are identified by the number of each type of oxygen in the lithium-ion solvation shell and by the number of chains that participate in lithium-ion coordination. An array of binding motifs is observed in the type-1 and -2 polymers. In contrast, only one or two binding motifs are observed for polymers 3a, 3b, and also PEO. These results reveal a trend in which lithium cations that coordinate with more polymer chains also have more diversity in the observed binding motifs. It is interesting that the major binding motif for both the type-3 polymers and PEO is 006-2, or six ether oxygen atoms from two different polymer chains, even though PEO exhibits substantially higher conductivity. These results indicate that the composition of the first lithium-ion solvation shell does not fully explain the trends in Figure 3d.

To characterize the lithium-ion solvation environment beyond the first lithium-ion solvation shell, Figure 5d presents pair radial distribution functions (RDFs) for the lithium cation and each type of oxygen atom in the type-a polymers and in PEO; the corresponding RDFs for the type-b polymers are shown in Figure S26. Figure 5d reveals that the types of oxygen atoms that are present in the first peak, which is the lithium-ion solvation shell as discussed for Figure 5a–c, are absent or depleted in the second peak. For the type-1 and -2 polymers, the first peak, which occurs at approximately 2 Å, has only backbone contributions from carbonyl and ether oxygens; the second peak, which occurs at 4–4.5 Å, is mostly comprised of ester oxygens. For type-3 polymers, side-chain ether oxygens are found in the first peak but not in the second. This difference in composition between the first and second solvation shells suggests one reason for the faster lithium-ion diffusion in PEO. Namely, diffusion events in which the lithium cation escapes from its existing coordination environment to a neighboring environment are more likely to occur in PEO because the composition of atoms in the second solvation shell is similar to the first. Consequently, a binding motif comprised of atoms in the first solvation shell is roughly equal in free energy to a binding motif that has some atoms in the first solvation shell exchanged for atoms in the second. In contrast, for the polyesters, atoms in the second peak are not typically represented in the binding motifs enumerated in Figure 5c, which indicates that binding motifs with those atoms are energetically less favorable.

To understand how these differences in lithium-ion solvation affect the conductivity, Figure 6 illustrates the displacement and coordination environment of the lithium cation in a long MD simulation for PEO and for polymer 3b. Figure 6a,b illustrates changes in lithium-ion coordination environment by tracking the indices of oxygen atoms that are within 3.25 Å of the lithium cation. In particular, each oxygen atom in the system is labeled sequentially, starting at one end of a polymer chain and continuing to the end of that chain before proceeding to the next; the oxygen atoms are consecutively labeled from 1 to 648 for PEO and from 1 to 759 for polymer 3b. What appear as solid lines in the figure are actually formed from the markers of contiguous oxygen indices, as seen in the inset; thicker lines typically consist of five or six markers, and thinner lines typically consist of three markers. Figure 7c,d shows changes in the lithium-ion position by tracking the net displacement of the lithium cation from its initial position.

Figure 6.

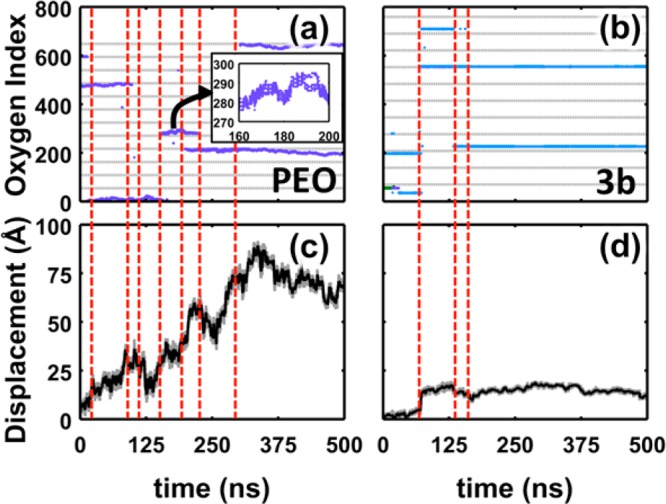
Figure 6

Open in a new tab

Analysis of changes in lithium-ion coordination with changes in lithium-ion position. Lithium-ion coordination environment for (a) PEO and (b) polymer 3b (markers denote coordination with oxygen for at least half of a 100 ps interval). The horizontal gray lines demarcate separate polymer chains. The inset in (a) illustrates the coordination over a 40 ns segment in the trajectory. Lithium-ion displacement from initial position in (c) PEO and (d) polymer 3b. The gray curve indicates the instantaneous displacement from the initial position, and the black curve indicates the rolling average over 100 ps intervals. Vertical, red lines highlight interchain hopping events.

Figure 7.

Figure 7

Open in a new tab

Analysis of lithium-ion solvation sites. (a) Viable solvation sites (green spheres) in representative configurations of polymer 3a, polymer 3b, and PEO. Sites connected by lines if they are within 3 Å to illustrate the relative connectivity. The polymer configuration is shown in the transparent representation. (b) The connectivity density of lithium-ion solvation-site networks for each polymer. Reported data are obtained from averaging over 16 MD trajectory snapshots.

From Figure 6a,b, it is clear that one characteristic of PEO is that the lines fluctuate and drift during the simulation, whereas the lines for polymer 3b are comparatively static. This drift in oxygen indices is a signature of intrachain hopping of the lithium cation to adjacent monomers along the polymer backbone. Notably, PEO is the only polymer studied that illustrates this behavior. Intrachain hopping events are not observed in the type-3 polymers because the lithium cation is localized to the side chains (Figure S27). Similarly, the lithium cation is localized between the two carbonyl groups on the backbone for the type-1 and -2 polymers, which also do not exhibit significant intrachain hopping events (Figure S28).

Because intrachain hopping is not a viable mechanism in the polyesters, lithium cations are limited to diffusion via interchain hopping events and codiffusion with the polymer chains. Changes in coordination that correspond to interchain hopping events are highlighted by the vertical, red dashed lines in Figure 6. Figure 6c,d illustrates that significant lithium-ion displacements often coincide with these events. However, the lithium cation in polymer 3b is limited to local fluctuations during time intervals between interchain hopping events. It is evident that interchain hopping is a rare event that occurs on the 100 ns timescale, even in PEO. Thus, the presence of intrachain hopping in PEO is the primary reason for the faster lithium-ion diffusion compared to the polyesters.

To illustrate why these mechanistic differences arise, Figure 7a shows viable cation solvation sites in polymer 3a, 3b, and PEO, which are obtained from snapshots of the corresponding MD simulations for each polymer. Here, viable solvation sites are considered to be arrangements of atoms in the polymer that are consistent with common binding motifs found in Figure 5c; for the polymers in Figure 7a, sites are defined as the centroid of a set of five or more ether oxygen atoms if each oxygen is also within 3.7 Å of that centroid. Sites are connected in the figure if they are closer than 3 Å to provide a qualitative understanding of available hopping events. It is clear that far fewer viable solvation sites are identified in the type-3 polymers than for PEO; similarly sparse networks characterize the type-1 and -2 polymers (Figure S29). In contrast to the isolated clusters in the polyesters, PEO features a well-connected network of viable solvation sites by virtue of the compositional overlap between first and second solvation shells for the lithium cation (Figure 5d).

To quantify the degree to which the various polymers exhibit connected networks of solvation sites, Figure 7b provides the density of 3 Å connections between solvation sites, termed the connectivity, for each polymer. It is evident that the connectivity for PEO is an order-of-magnitude greater than any of the polyesters. The similarity between Figure 7b and Figure 3d is striking, indicating a strong relationship between connectivity and lithium-ion conductivity. The concept of connectivity provides an intuitive and potentially powerful explanation for the efficiency of the intrachain hopping mechanism in PEO. In an intrachain hopping event, the lithium cation effectively migrates up or down one polymer chain by exchanging a small number of solvating oxygen atoms. Here, this process is represented as a transition along an edge in the solvation-site network. Unlike the polymer architecture of the polyesters, the topology of PEO facilitates these transitions among solvation sites.

Conclusions

This study combines experimental and theoretical approaches to investigate the mechanisms of lithium-ion transport in six new polyester-based polymer electrolytes, as well as PEO.

The modifications to polymer architecture considered are shown to significantly alter the lithium-ion solvation environment and effectively change whether the lithium-ion transport is side-chain- or backbone-mediated. These changes affect the ionic conductivity by a factor of 3. In contrast, the ionic conductivities of the polyesters are about an order of magnitude lower than in PEO (Figure 3d). Because the glass-transition temperature of PEO is only modestly lower than that of some of the polyesters, the observed trends with ionic conductivity are not adequately explained on the basis of polymer segmental mobility (Figure 4b).

To understand the anomalous diffusivity of PEO, the MD simulations are employed to perform an extensive analysis of the lithium-ion solvation and diffusion mechanisms in the various polymers. We find that PEO is the only polymer studied that frequently coordinates a lithium cation with a single chain or exhibits significant intrachain hopping of the lithium cations. This is primarily because the first and second lithium-ion solvation shells differ significantly in composition for all of the polyesters (Figure 5d). Lithium-ion diffusion in the polyesters thus relies upon interchain hopping events, which occur infrequently on the 100 ns timescale, and codiffusion with the polymer chains, which is intrinsically slow (Figure 6).

This analysis reveals that the anomalously high conductivity of PEO (Figure 3d) can be easily understood in terms of a description of lithium-ion diffusion based on the density and proximity of viable solvation sites (Figure 7a). Whereas PEO features a well-connected network of viable solvation sites, the polyesters have isolated clusters of sites that hinder efficient lithium-ion conduction. A simple metric of connectivity predicts an order-of-magnitude higher conductivity for PEO than the polyesters (Figure 7b). Knowledge of the solvation structure, including attributes of the second solvation shell, the connectivity between solvation sites, and the number of chains involved in the coordination appears to provide a powerful tool for the design of future SPEs.

Acknowledgments

This research was supported by the National Science Foundation under DMREF Award Number NSF-CHE-1335486. M.A.W. also acknowledges support from the Resnick Sustainability Institute.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.5b00195.

  • Synthesis details; simulation protocol details; electrochemical characterization details; description of terminal groups in MD simulations; force-field parameters for MD simulations; apparent diffusivities in simulations; dilute-ion conductivity measurement details; discussion of terminal group interactions with lithium cation in type-a polymers; correlation between Tg and conductivity for MD simulations; lithium cation-oxygen radial pair distribution functions for all polymers; coordination plots showing the localization of lithium cation in type-1, -2, and -3 polymers; snapshots of solvation-site networks in all polymers (PDF)

The authors declare no competing financial interest.

Supplementary Material

oc5b00195_si_001.pdf (8MB, pdf)

References

  1. Fenton D. E.; Parker J. M.; Wright P. V. Complexes of Alkali-Metal Ions with Poly(Ethylene Oxide). Polymer 1973, 14, 589–589. [Google Scholar]
  2. Gray F. M.Solid Polymer Electrolytes: Fundamentals and Technological Applications; VCH: New York, 1991. [Google Scholar]
  3. Shriver D. F.; Papke B. L.; Ratner M. A.; Dupon R.; Wong T.; Brodwin M. Structure and Ion-Transport in Polymer-Salt Complexes. Solid State Ionics 1981, 5, 83–88. [Google Scholar]
  4. Meyer W. H. Polymer electrolytes for lithium-ion batteries. Adv. Mater. 1998, 10, 439–448. [DOI] [PubMed] [Google Scholar]
  5. Tarascon J. M.; Armand M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [DOI] [PubMed] [Google Scholar]
  6. Borodin O.; Smith G. D. Mechanism of ion transport in amorphous poly(ethylene oxide)/LiTFSI from molecular dynamics simulations. Macromolecules 2006, 39, 1620–1629. [Google Scholar]
  7. Müller-plathe F.; Vangunsteren W. F. Computer-Simulation of a Polymer Electrolyte - Lithium Iodide in Amorphous Poly(Ethylene Oxide). J. Chem. Phys. 1995, 103, 4745–4756. [Google Scholar]
  8. Neyertz S.; Brown D. Local structure and mobility of ions in polymer electrolytes: A molecular dynamics simulation study of the amorphous PEO(x)NaI system. J. Chem. Phys. 1996, 104, 3797–3809. [Google Scholar]
  9. Siqueira L. J. A.; Ribeiro M. C. C. Molecular dynamics simulation of the polymer electrolyte poly(ethylene oxide)/LiClO4. I. Structural properties. J. Chem. Phys. 2005, 122, 194911. [DOI] [PubMed] [Google Scholar]
  10. Siqueira L. J. A.; Ribeiro M. C. C. Molecular dynamics simulation of the polymer electrolyte poly(ethylene oxide)/LiClO4. II. Dynamical properties. J. Chem. Phys. 2006, 125, 214903. [DOI] [PubMed] [Google Scholar]
  11. Diddens D.; Heuer A.; Borodin O. Understanding the Lithium Transport within a Rouse-Based Model for a PEO/LiTFSI Polymer Electrolyte. Macromolecules 2010, 43, 2028–2036. [Google Scholar]
  12. Duan Y. H.; Halley J. W.; Curtiss L.; Redfern P. Mechanisms of lithium transport in amorphous polyethylene oxide. J. Chem. Phys. 2005, 122, 054702. [DOI] [PubMed] [Google Scholar]
  13. Karo J.; Brandell D. A Molecular Dynamics study of the influence of side-chain length and spacing on lithium mobility in non-crystalline LiPF6 center dot PEOx; x=10 and 30. Solid State Ionics 2009, 180, 1272–1284. [Google Scholar]
  14. Brandell D.; Priimagi P.; Kasemagi H.; Aabloo A. Branched polyethylene/poly(ethylene oxide) as a host matrix for Li-ion battery electrolytes: A molecular dynamics study. Electrochim. Acta 2011, 57, 228–236. [Google Scholar]
  15. Borodin O.; Douglas R.; Smith G. A.; Trouw F.; Petrucci S. MD Simulations and experimental study of structure, dynamics, and thermodynamics of poly(ethylene oxide) and its oligomers. J. Phys. Chem. B 2003, 107, 6813–6823. [Google Scholar]
  16. Croce F.; Persi L.; Scrosati B.; Serraino-Fiory F.; Plichta E.; Hendrickson M. A. Role of the ceramic fillers in enhancing the transport properties of composite polymer electrolytes. Electrochim. Acta 2001, 46, 2457–2461. [Google Scholar]
  17. Johansson P.; Ratner M. A.; Shriver D. F. The influence of inert oxide fillers on poly(ethylene oxide) and amorphous poly(ethylene oxide) based polymer electrolytes. J. Phys. Chem. B 2001, 105, 9016–9021. [Google Scholar]
  18. Nishimoto A.; Watanabe M.; Ikeda Y.; Kohjiya S. High ionic conductivity of new polymer electrolytes based on high molecular weight polyether comb polymers. Electrochim. Acta 1998, 43, 1177–1184. [Google Scholar]
  19. Watanabe M.; Hirakimoto T.; Mutoh S.; Nishimoto A. Polymer electrolytes derived from dendritic polyether macromonomers. Solid State Ionics 2002, 148, 399–404. [Google Scholar]
  20. Matoba Y.; Ikeda Y.; Kohjiya S. Ionic conductivity and mechanical properties of polymer networks prepared from high molecular weight branched poly(oxyethylene)s. Solid State Ionics 2002, 147, 403–409. [Google Scholar]
  21. Buriez O.; Han Y. B.; Hou J.; Kerr J. B.; Qiao J.; Sloop S. E.; Tian M. M.; Wang S. G. Performance limitations of polymer electrolytes based on ethylene oxide polymers. J. Power Sources 2000, 89, 149–155. [Google Scholar]
  22. Khurana R.; Schaefer J. L.; Archer L. A.; Coates G. W. Suppression of Lithium Dendrite Growth Using Cross-Linked Polyethylene/Poly(ethylene oxide) Electrolytes: A New Approach for Practical Lithium-Metal Polymer Batteries. J. Am. Chem. Soc. 2014, 136, 7395–7402. [DOI] [PubMed] [Google Scholar]
  23. Alloin F.; Sanchez J. Y.; Armand M. Electrochemical-Behavior of Lithium Electrolytes Based on New Polyether Networks. J. Electrochem. Soc. 1994, 141, 1915–1920. [Google Scholar]
  24. Andrieu X.; Fauvarque J. F.; Goux A.; Hamaide T.; Mhamdi R.; Vicedo T. Solid Polymer Electrolytes Based on Statistical Poly(Ethylene Oxide-Propylene Oxide) Copolymers. Electrochim. Acta 1995, 40, 2295–2299. [Google Scholar]
  25. Deng Y. L.; Ding J. F.; Yu G.; Mobbs R. H.; Heatley F.; Price C.; Booth C. Preparation and Properties of Stat-Copoly-(Oxyethylene Oxypropylene)-Block-Poly(Oxyethylene). 1. Use of Crown-Ether in the Anionic Copolymerization of Propylene-Oxide and Ethylene-Oxide. Polymer 1992, 33, 1959–1962. [Google Scholar]
  26. Florjanczyk Z.; Krawiec W.; Wieczorek W.; Przyluski J. Polymer Solid Electrolytes Based on Ethylene-Oxide Copolymers. Angew. Makromol. Chem. 1991, 187, 19–32. [Google Scholar]
  27. Ikeda Y.; Masui H.; Matoba Y. Ionic conductivity of polymer solid electrolyte prepared from poly[epichlorohydrin-co-(ethylene oxide)] of high ethylene oxide content. J. Appl. Polym. Sci. 2005, 95, 178–184. [Google Scholar]
  28. Schroers M.; Kokil A.; Weder C. Solid polymer electrolytes based on nanocomposites of ethylene oxide-epichlorohydrin copolymers and cellulose whiskers. J. Appl. Polym. Sci. 2004, 93, 2883–2888. [Google Scholar]
  29. Wolfenson A. E.; Torresi R. M.; Bonagamba T. J.; DePaoli M. A.; Panepucci H. NMR and conductivity studies of ethylene oxide epichloridrine copolymer doped with LiClO4. J. Phys. Chem. B 1997, 101, 3469–3473. [Google Scholar]
  30. Barteau K. P.; Wolffs M.; Lynd N. A.; Fredrickson G. H.; Krarner E. J.; Hawker C. J. Allyl Glycidyl Ether-Based Polymer Electrolytes for Room Temperature Lithium Batteries. Macromolecules 2013, 46, 8988–8994. [Google Scholar]
  31. Nithya H.; Selvasekarapandian S.; Kumar D. A.; Sakunthala A.; Hema M.; Christopherselvin P.; Kawamura J.; Baskaran R.; Sanjeeviraja C. Thermal and dielectric studies of polymer electrolyte based on P(ECH-EO). Mater. Chem. Phys. 2011, 126, 404–408. [Google Scholar]
  32. Tanaka R.; Sakurai M.; Sekiguchi H.; Mori H.; Murayama T.; Ooyama T. Lithium ion conductivity in polyoxyethylene/polyethylenimine blends. Electrochim. Acta 2001, 46, 1709–1715. [Google Scholar]
  33. Watanabe M.; Rikukawa M.; Sanui K.; Ogata N.; Kato H.; Kobayashi T.; Ohtaki Z. Ionic-Conductivity of Polymer Complexes Formed by Poly(Ethylene Succinate) and Lithium Perchlorate. Macromolecules 1984, 17, 2902–2908. [Google Scholar]
  34. Watanabe M.; Togo M.; Sanui K.; Ogata N.; Kobayashi T.; Ohtaki Z. Ionic-Conductivity of Polymer Complexes Formed by Poly(Beta-Propiolactone) and Lithium Perchlorate. Macromolecules 1984, 17, 2908–2912. [Google Scholar]
  35. Blonsky P. M.; Shriver D. F.; Austin P.; Allcock H. R. Complex-Formation and Ionic-Conductivity of Polyphosphazene Solid Electrolytes. Solid State Ionics 1986, 18–19, 258–264.22422014 [Google Scholar]
  36. Harris C. S.; Shriver D. F.; Ratner M. A. Complex-Formation of Poly(Ethylenimine) with Sodium Triflate and Conductivity Behavior of the Complexes. Macromolecules 1986, 19, 987–989. [Google Scholar]
  37. Lee Y. C.; Ratner M. A.; Shriver D. F. Ionic conductivity in the poly(ethylene malonate)/lithium triflate system. Solid State Ionics 2001, 138, 273–276. [Google Scholar]
  38. Zhang Z. C.; Jin J. J.; Bautista F.; Lyons L. J.; Shariatzadeh N.; Sherlock D.; Amine K.; West R. Ion conductive characteristics of cross-linked network polysiloxane-based solid polymer electrolytes. Solid State Ionics 2004, 170, 233–238. [Google Scholar]
  39. Tominaga Y.; Shimomura T.; Nakamura M. Alternating copolymers of carbon dioxide with glycidyl ethers for novel ion-conductive polymer electrolytes. Polymer 2010, 51, 4295–4298. [Google Scholar]
  40. Nakamura M.; Tominaga Y. Utilization of carbon dioxide for polymer electrolytes [II]: Synthesis of alternating copolymers with glycidyl ethers as novel ion-conductive polymers. Electrochim. Acta 2011, 57, 36–39. [Google Scholar]
  41. Jeske R. C.; DiCiccio A. M.; Coates G. W. Alternating copolymerization of Epoxides and cyclic anhydrides: An improved route to aliphatic polyesters. J. Am. Chem. Soc. 2007, 129, 11330–11331. [DOI] [PubMed] [Google Scholar]
  42. DiCiccio A. M.; Coates G. W. Ring-Opening Copolymerization of Maleic Anhydride with Epoxides: A Chain-Growth Approach to Unsaturated Polyesters. J. Am. Chem. Soc. 2011, 133, 10724–10727. [DOI] [PubMed] [Google Scholar]
  43. Longo J. M.; DiCiccio A. M.; Coates G. W. Poly(propylene succinate): A New Polymer Stereocomplex. J. Am. Chem. Soc. 2014, 136, 15897–15900. [DOI] [PubMed] [Google Scholar]
  44. Teran A. A.; Tang M. H.; Mullin S. A.; Balsara N. P. Effect of molecular weight on conductivity of polymer electrolytes. Solid State Ionics 2011, 203, 18–21. [Google Scholar]
  45. Maitra A.; Heuer A.. Cation transport in polymer electrolytes: A microscopic approach. Phys. Rev. Lett. 2007, 98. [DOI] [PubMed] [Google Scholar]
  46. Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; MacKerell A. D. CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Martin M. G.; Siepmann J. I. Novel configurational-bias Monte Carlo method for branched molecules. Transferable potentials for phase equilibria. 2. United-atom description of branched alkanes. J. Phys. Chem. B 1999, 103, 4508–4517. [Google Scholar]
  48. Wick C. D.; Martin M. G.; Siepmann J. I. Transferable potentials for phase equilibria. 4. United-atom description of linear and branched alkenes and alkylbenzenes. J. Phys. Chem. B 2000, 104, 8008–8016. [Google Scholar]
  49. Stubbs J. M.; Potoff J. J.; Siepmann J. I. Transferable potentials for phase equilibria. 6. United-atom description for ethers, glycols, ketones, and aldehydes. J. Phys. Chem. B 2004, 108, 17596–17605. [Google Scholar]
  50. Kamath G.; Robinson J.; Potoff J. J. Application of TraPPE-UA force field for determination of vapor-liquid equilibria of carboxylate esters. Fluid Phase Equilib. 2006, 240, 46–55. [Google Scholar]
  51. Wu H.; Wick C. D. Computational Investigation on the Role of Plasticizers on Ion Conductivity in Poly(ethylene oxide) LiTFSI Electrolytes. Macromolecules 2010, 43, 3502–3510. [Google Scholar]
  52. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular-Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar]
  53. Brown W. M.; Wang P.; Plimpton S. J.; Tharrington A. N. Implementing molecular dynamics on hybrid high performance computers - short range forces. Comput. Phys. Commun. 2011, 182, 898–911. [Google Scholar]
  54. Brown W. M.; Kohlmeyer A.; Plimpton S. J.; Tharrington A. N. Implementing molecular dynamics on hybrid high performance computers - Particle-particle particle-mesh. Comput. Phys. Commun. 2012, 183, 449–459. [Google Scholar]
  55. Newman J. S.; Thomas-Alyea K. E.. Electrochemical Systems, 3rd ed.; Wiley-Interscience: Hoboken, NJ, 2004. [Google Scholar]
  56. Killis A.; Lenest J. F.; Cheradame H.; Gandini A. Ionic-Conductivity of Polyether-Polyurethane Networks Containing NaBPh4 - a Free-Volume Analysis. Makromol. Chem. 1982, 183, 2835–2845. [Google Scholar]
  57. Blonsky P. M.; Shriver D. F.; Austin P.; Allcock H. R. Polyphosphazene Solid Electrolytes. J. Am. Chem. Soc. 1984, 106, 6854–6855. [Google Scholar]
  58. Videa M.; Xu W.; Geil B.; Marzke R.; Angell C. A. High Li+ self-diffusivity and transport number in novel electrolyte solutions. J. Electrochem. Soc. 2001, 148, A1352–A1356. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc5b00195_si_001.pdf (8MB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES