DFTB3 Parametrization for Copper: The Importance of Orbital Angular Momentum Dependence of Hubbard Parameters

Abstract

We report the parametrization of a density functional tight binding method (DFTB3) for copper in a spin-polarized formulation. The parametrization is consistent with the framework of 3OB for main group elements (ONCHPS) and can be readily used for biological applications that involve copper proteins/peptides. The key to our parametrization is to introduce orbital angular momentum dependence of the Hubbard parameter and its charge derivative, thus allowing the 3d and 4s orbitals to adopt different sizes and responses to the change of charge state. The parametrization has been tested by applying to a fairly broad set of molecules of biological relevance, and the properties of interest include optimized geometries, ligand binding energies, and ligand proton affinities. Compared to the reference QM level (B3LYP/aug-cc-pVTZ, which is shown here to be similar to the B97-1 and CCSD(T) results, in terms of many properties of interest for a set of small copper containing molecules), our parametrization generally gives reliable structural properties for both Cu(I) and Cu(II) compounds, although several exceptions are also noted. For energetics, the results are more accurate for neutral ligands than for charged ligands, likely reflecting the minimal basis limitation of DFTB3; the results generally outperform NDDO based methods such as PM6 and even PBE with the 6-31+G(d,p) basis. For all ligand types, single-point B3LYP calculations at DFTB3 geometries give results very close (∼1–2 kcal/mol) to the reference B3LYP values, highlighting the consistency between DFTB3 and B3LYP structures. Possible further developments of the DFTB3 model for a better treatment of transition-metal ions are also discussed. In the current form, our first generation of DFTB3 copper model is expected to be particularly valuable as a method that drives sampling in systems that feature a dynamical copper binding site.

1. Introduction

Transition-metal ions play important roles in chemistry and biology. The unique structural and electronic properties allow them to catalyze complex chemical transformations that are difficult to accomplish using other compounds. Therefore, transition-metal ions are involved in many enzymes and dictate the specific activities of these enzymes.^1,2 Since metal-catalyzed reactions often involve transient species with unique structural and electronic features, computational studies are often required to supplement experimental investigations in mechanistic analysis. The value of closely integrating computations and experiments has been highlighted in many recent studies of complex metalloenzymes, with notable examples such as blue copper proteins,³ cytochrome P450,⁴ photosystem II,⁵ and nitrogenase.⁶

For metalloenzymes that feature well-buried and structurally rigid active sites, insightful computational studies can be conducted using pure quantum mechanical (QM) calculations for active site models⁵ or hybrid QM/MM calculations^4,7 for the realistic system. Since transition-metal ions usually require advanced QM methods such as density functional theory (DFT⁸⁻¹⁰) or correlated ab initio methods,^11,12 QM/MM studies are usually limited to minimum energy path type of calculations⁴ or free-energy simulations with a minimal amount of sampling.^13,14 In some applications, however, the biological system of interest is highly flexible and therefore a meaningful study would require an extensive degree of sampling; examples include metalloenzymes that feature a high degree of catalytic promiscuity,¹⁵⁻¹⁷ metal ion transporters/transcription factors,¹⁸⁻²⁰ proteins involved in the assembly of catalytic metal co-factors,²¹ and peptides/proteins whose (mis)folding and aggregation behaviors are influenced by transition-metal binding.²²⁻²⁵ In these cases, developing a potential function that treats transition-metal ions accurately while still allowing extensive sampling is essential.

The treatment of transition-metal ions using classical force fields has seen major developments in recent years. Contributions particularly important to transition-metal ions such as charge-dipole polarization,^26,27 charge transfer,²⁸⁻³¹ ligand-field effects,³²⁻³⁴ the trans influence³⁵ can be treated at different levels of sophistication and accuracy. To study the chemical processes that involve transition-metal ions in flexible biomolecules, however, an efficient quantum mechanical model is required. Methods in the NDDO framework^36,37 have limited success in this regard. Specific methods such as PM3(TM)³⁸ and AM1*³⁹ target mainly structural properties, and MNDO(d)⁴⁰ has only been parametrized for a few transition-metal ions. Indeed, with Hartree–Fock as the basic framework, it is challenging for the NDDO methods to treat transition-metal ions for which electron correlation is essential to both structural and energetic properties.

Motivated by these considerations, we and others have started to pursue the parametrization and further development of the DFTB method^41,42 for metal ions, with the expectation that it is rooted in DFT and thus potentially better suited for describing metal ions than NDDO methods. These efforts have been fueled in part by the recent success of DFTB methods in studying main group elements, especially in problems where computational efficiency and sampling are particularly important.⁴³⁻⁴⁷ Specifically for transition-metal ions, Elstner, Cui, and co-workers first developed parameters for zinc⁴⁸ in the framework of the second-order DFTB (referred to as Self-Consistent-Charge Density-Functional-Tight-Binding (SCC-DFTB)),⁴⁹ which was found valuable in a range of biological applications.⁵⁰⁻⁵² Morokuma and co-workers developed SCC-DFTB parameters for several first-row transition metals, including Sc, Ti, Fe, Co, and Ni.⁵³ They have shown that the parameters often lead to adequate structural properties, although the energetics are less satisfying; thus, SCC-DFTB was mainly recommended as the intermediate layer in ONIOM calculations of organometallic and metalloenzyme applications.⁵⁴ Recently, Bruschi et al.⁵⁵ developed SCC-DFTB parameters for copper, although their study focused primarily on structural properties of small compounds and very limited benchmarks were reported for energetic properties or larger systems. In the context of materials science, SCC-DFTB parameters have also been developed for several transition metals (e.g., Ti, Zn and Fe) in applications that target metal oxides or nanoparticles.⁵⁶⁻⁵⁸

In our recent work, we have extended the DFTB approach to include third-order contributions,^59,60 leading to the DFTB3 method.⁶¹ We have shown that the third-order terms consider the change of atomic size (and therefore electron–electron interactions) as a function of the atomic charge state, a feature important to the description of many chemical processes. With systematic and careful parametrization, DFTB3 has been shown to often have accuracy comparable to popular DFT-GGA methods with double-ζ-plus-polarization quality basis sets while being 10^2–3 times more efficient; for certain properties of calibrated systems, such as proton affinities, the DFTB3 results can be more accurate. For chemical and biological applications, DFTB3 has been parametrized for a range of main group elements (ONCH⁶²PS,⁶³ halogens⁶⁴) and “simple” metal ions (Na, K, and Ca,⁶⁴ as well as Mg and Zn⁶⁵). In this work, we further extend the DFTB3 approach to complex transition-metal ions that involve open shells.

Using the parametrization for copper as an example, we demonstrate that a balanced treatment of different charge states of the metal ion can be obtained by including the orbital angular momentum (l) dependence of the Hubbard parameter^58,66 and its charge derivative. Copper is selected here because only one of its prevalent oxidation states is open-shell in nature and the Cu ion is an important co-factor in many proteins.^1,2 We show below that rather reliable structural properties can be obtained for both Cu(I) and Cu(II) species with the l-dependent DFTB3 approach; metal–ligand binding energies and ligand proton affinities also show major improvements over NDDO methods such as PM6,⁶⁷ and single-point calculations at DFTB3 geometries in most cases lead to satisfactory energies in comparison to a reference QM method (B3LYP/aug-cc-pVTZ). Therefore, we anticipate that this first generation of DFTB3 parametrization for copper is applicable to many copper protein problems where sampling is important. On the other hand, the parametrization and benchmark studies also highlight the limitations of the current DFTB3 framework, such as the use of a GGA functional (PBE⁶⁸) and a minimal basis set, for treating transition-metal ions and their interactions with polarizable ligands, especially for energetics.

In the following, we first briefly summarize the DFTB3 methodology, especially concerning the treatment of spin polarization for open-shell systems,^58,66 and discuss the introduction of l dependence in the Hubbard parameter and charge derivative. Next, we describe the parametrization protocol for copper, in particular the issue of choosing a reference QM method for calibration. This is followed by a fairly extensive set of benchmark calculations for structural and energetic properties in the gas phase; in a separate study, we report the application to condensed phase problems. Finally, we conclude with a few summarizing remarks, including possible extensions of DFTB3 for improved descriptions of transition-metal ions.

2. Theory

In this section, we first briefly recall the key ingredients of DFTB3,⁶¹ then discuss the treatment of collinear spin polarization, especially concerning the inclusion of orbital angular momentum dependence of the Hubbard parameter.

2.1. DFTB3

To derive the DFTB3 model, one starts by rewriting the DFT total energy expression in the following form. First, replace the electron density ρ by a superposition of a reference density ρ⁰ and a density fluctuation Δρ. Second, expand the energy in a Taylor series of Δρ and truncate at the third order. The total energy then reads

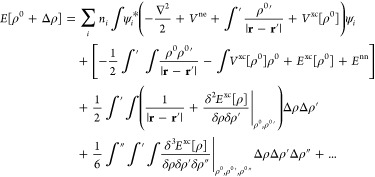1

Approximations that follow include the use of a minimal basis set expansion for the Kohn–Sham orbitals ψ_i and a two-center approximation for the Hamiltonian matrix elements that is dependent only on the reference density (H_μν⁰, which is contained in the first term on the right-hand side (RHS) of eq 1). Furthermore, the electron density fluctuation is approximated by a superposition of spherical charge distributions centered at the nuclei. The second-order kernel⁴⁹ (shown in parentheses in the third term on the RHS of eq 1) is approximated by a function γ that interpolates between the long-range Coulomb interaction of charge fluctuations and the atomic on-site exchange-correlation interaction. The third-order contribution (the fourth term on the RHS of eq 1) accounts for the charge dependence of the γ function.⁵⁹⁻⁶¹ The remaining parts of the total energy expression (the second term on the RHS of eq 1), i.e. the double-counting contributions plus nuclear repulsions, are approximated as pairwise interactions and referred to as the repulsive potentials.⁴⁹ Consequently, the DFTB3 total energy is written as

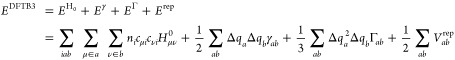2

where Γ_ab is the charge derivative of γ_ab.⁶¹

2.2. Collinear Spin-Polarization

In previous work, the second-order DFTB method has been extended to include spin-polarization effects as derived from an expansion of the spin-polarized Kohn–Sham total energy in a collinear^58,66,69 or noncollinear fashion.⁶⁶ In the present work, we apply the collinear treatment that adds a term to the total energy eq 2, which is given by

3

where p_la = q_la↑– q_la↓ is the difference between the Mulliken spin-populations for orbital angular momentum l_a and W_lal’a are the atomic spin-plarization constants, which can be obtained from DFT calculations^58,66,69 using Janak’s theorem.⁷⁰ Naturally, the spin-up and spin-down electrons are treated with different orbitals; for example, the first term of eq 2 becomes

4

Thus, the Kohn–Sham equations are now solved by diagonalizing the Hamiltonian matrix for up-spin and down-spin electrons separately, which means that the overall computational cost roughly doubles, in comparison to spin-unpolarized DFTB.

2.3. Angular Momentum Dependence of the Hubbard Parameter and Its Charge Derivative

The γ function within DFTB3 describes the electron interaction of the excess charge on one atom and between two atoms. It contains one parameter per element: the Hubbard parameter (U_a). The Hubbard parameter correlates with the size of an atom in an inverse relationship, as has been discussed in detail in refs (59−61). While the spatial extend of 2s and 2p valence orbitals are similar for second-period elements, there is a significant difference between 4s and 3d valence orbitals for the first-row transition metals.⁷¹ Therefore, we suggest to adopt an earlier extension of the second-order DFTB that uses different Hubbard parameters not only for every element but also for each orbital angular momentum l.⁵⁸ The second-order term E^γ in eq 2 then becomes

5

where Δq_la is the Mulliken charge of the l-shell of atom a, and γ becomes l-dependent through the Hubbard parameters. Note that γ_lalb is a shorthand notation for the more precise expression γ_ab,lalb.

Accordingly, for DFTB3, the third-order term E^Γ must be revised to account for the l-dependence of the γ function. Starting from the third-order expression (the last term in eq 1) and rewriting the densities as superpositions of atomic l-dependent charge distributions gives

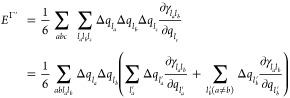6

A rigorous derivation in the framework of DFTB3 would require

where the term ∂γ_lalb/∂U_la can be obtained analytically and the term ∂U_la/∂q_la^′ is a constant parameter that can be calculated with DFT. However, to reduce the number of parameters, we suggest a simplified expression (see the Supporting Information for details):

7

where Γ_lalb is given by

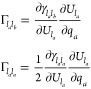8

Note that the approximation in eq 7 lies in considering the charge derivative of the Hubbard parameter within shell l_a. While the rigorous derivation requires different derivatives with respect to the charge of every l_a^′ shell (∂U_la/∂q_la^′), our approximative suggestion requires only derivatives with respect to the total atomic charge (∂U_la/∂q_a). A comprehensive derivation of the total energy expression, as well as Kohn–Sham equations and atomic forces, is provided in the Supporting Information. For example, the Kohn–Sham matrix element (H_μν, μ ∈ a, ν ∈ b) takes the form,

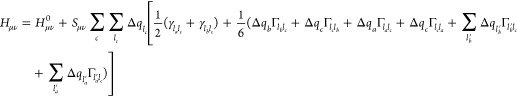9

where S_μν is the overlap matrix element.

As discussed below, taking the Hubbard parameter and its charge derivative to be l-dependent is essential to the successful parametrization of DFTB3 for copper in both oxidation states. Physically, this can be understood as describing the different sizes of 3d and 4s orbitals and responses to the change in atomic charge state.

3. Parameterization

3.1. Choice of the Reference Method

As described in previous work that reported the parametrization of DFTB3 for various main group elements⁶²⁻⁶⁵ (including “simple” metals such as Mg²⁺ and Zn²⁺), although most element-dependent terms in the energy (e.g., H_μν⁰ in eq 2 and W_lala^′ in eq 3) are computed with the PBE functional in atomic calculations (also see below in Section 3.2), a reference QM method is used to parametrize the repulsive potential and calibrate a few other parameters (e.g., the Hubbard derivative and the compression radii used to define the basis functions and reference density, see below). Through this parametrization procedure, the accuracy of the DFTB3 model can go beyond the parent PBE functional with a modest basis set. For main group elements, the reference method is typically chosen as B3LYP/aug-cc-pVTZ for geometries and G3B3⁷²⁻⁷⁴ for energetics (e.g., atomization energies). For transition-metal ions, the choice of the reference method is far from straightforward, since the performance of common QM methods for transition metals is not uniform and can vary significantly among different systems.⁷⁵⁻⁸⁰ For example, while CCSD(T) is generally considered to be the “golden standard” for systems containing main group elements,¹¹ it is well-known that the results can have substantial errors for systems of significant multireference nature,⁸¹ which is not uncommon for transition-metal compounds.^82,83 The performance of DFT methods for transition-metal ions is also rather system-dependent.^79,80,84 The recent studies of Wilson and co-workers⁷⁹ indicated that, for copper and zinc, the B97-1 functional⁸⁵ appears to be more reliable than the popular B3LYP⁸⁶ approach, although the conclusion was drawn based on a rather small number of systems; including a higher amount of exact exchange (e.g., in BH&HLYP) was found to improve the agreement with CCSD(T) in a study of Cu²⁺ binding to water molecules.⁸⁷ Indeed, the challenge for identifying a generally robust reference method is due in part to the lack of extensive sets of highly accurate experimental data in the gas phase, to which QM results can be compared directly. For example, in the recent benchmark calculations by Truhlar et al.^78,80 and Wilson et al.^76,79 for first-row transition-metal ions, there were only a handful cases for copper that involve ligands of any biological relevance.

In Table 1, we summarize the experimental energetics for a set of small Cu(I) compounds and computational results at the B3LYP,⁸⁶ B97-1,⁸⁵ BH&HLYP,⁸⁶ and CCSD(T) levels; scalar relativistic effects are also considered by the one-electron Douglas–Kroll–Hess Hamiltonian.⁸⁸ It is interesting to note that for these molecules, the accuracy of B3LYP and B97-1 is comparable and similar to that of CCSD(T); by comparison, the BH&HLYP approach gives worse results. Even with CCSD(T)-DK, there are cases where the deviation from the experimental value is as large as ∼10 kcal/mol (although for those cases, the experimental values also have large uncertainties; see footnote in Table 1), and analysis of the T₁-norm⁸⁹ indeed indicates that these molecules have significant multireference character (however, see ref (82) for a recent discussion of diagnostics for multireference character for transition-metal wave functions).

Table 1. Experimental Energetic Data and Deviations for DFT and CCSD(T) Methods^a.

				Energetics Data (kcal/mol)
molecule	propertyb	exp (kcal/mol)	ref	derived expc	B3LYPd	B97-1d	BH&HLYPd	CCSD(T)d,e	CCSD(T)-DKe,f	T1h
[Cu(CO)1]+	sBDE	35.6	(90)	37.1	+0.6	+0.0	–7.2	–4.4	–0.5	0.0229
[Cu(CO)2]+	sBDE	41.1	(90)	42.9	–5.1	–5.6	–11.3	–6.6	–3.2	0.0232
[Cu(CO)3]+	sBDE	17.9	(90)	19.0	–1.3	–0.2	–4.0	+0.4	+1.1	0.0237
[Cu(CO)4]+	sBDE	12.7	(90)	14.0	–0.7	+0.6	–2.9	+2.6	+3.2	0.0245
[Cu(NH3)1]+	sBDE	56.6	(91)	59.5	+0.1	–0.9	–5.5	–4.0	–0.2	0.0226
[Cu(NH3)2]+	sBDE	59.3	(91)	62.5	–7.0	–7.4	–11.1	–6.9	–3.2	0.0211
[Cu(NH3)3]+	sBDE	11.0	(91)	12.4	+0.7	+2.0	+2.7	+3.9	+2.2	0.0187
[Cu(NH3)4]+	sBDE	10.8	(91)	12.7	–2.9	–1.9	–1.5	+0.4	–0.4	0.0169
[Cu(H2O)1]+	sBDE	38.4	(92)	40.0	+1.3	+0.1	–1.3	–1.5	+0.5	0.0196
[Cu(H2O)2]+	sBDE	40.7	(92)	42.7	–1.4	–2.6	–4.6	–2.8	+0.2	0.0216
[Cu(H2O)3]+	sBDE	13.7	(92)	15.8	–2.3	–1.5	–0.4	–0.4	+1.4	0.0191
[Cu(H2O)4]+	sBDE	12.8	(92)	14.9	–4.3	–3.3	–2.6	–1.7	–2.8	0.0159
Cu2	ΔHf0/Eat	115.3	(76)	45.8	–3.6	+3.0	–10.9	–3.3	–0.8	0.0287
CuH	ΔHf0/Eat	65.9	(75)	68.7	–5.8	–5.6	–11.3	–6.9	–4.4	0.0392
CuOHg	ΔHf0/Eat	28.0	(76)	169.7	+7.1	+10.3	–7.8	+7.9	+8.5	0.0390
CuOg	ΔHf0/Eat	73.2	(76)	67.0	–2.9	+0.9	–15.8	–5.9	+8.3	0.0787
CuSg	ΔHf0/Eat	75.1	(76)	71.5	–9.2	–2.7	–15.2	–10.3	–13.2	0.0680
Cu	first IP	178.2	(93)	178.2	+7.1	–3.0	–5.4	–6.6	–1.5	0.0251
Cu	second IP	468.0	(93)	468.0	+10.4	+4.5	–12.3	–0.1	–4.0
MADi					2.3	2.2	4.6	3.0	1.6
MAXi					7.0	7.4	11.3	6.9	3.2

^aDeviations are shown with respect to the derived experimental values.

^bThe term “sBDE” denotes sequential bond dissociation energy at 0 K; the nondissociated molecule is listed in the first column. ΔH_f⁰ represents the heat of formation at 298.15 K, E^at is the atomization energy at 0 K, and IP is the ionization potential. If two properties are specified, the one before the slash refers to the actual experiment, the one after refers to the derived experimental value.

^cThe derived experimental values exclude zero-point energy and thermal corrections as calculated from B3LYP/6-31+G(d,p) vibrational frequencies and the classical approximation (see, e.g., ref (94)) for translations ((3/2)RT) and rotation (RT for linear molecules, (3/2)RT otherwise). For the conversions from heats of formation to atomization energy, the PV term is approximated as RT; the enthalpies of formation for gaseous atoms at 0 K and the heat capacity corrections (H²⁹⁸ – H⁰) are taken from refs (95) and (75).

^daug-cc-pVTZ.

^eCalculated at B3LYP/aug-cc-pVTZ geometries.

^faug-cc-pVTZ-DK.

^gExperimental uncertainty larger than 4 kcal/mol.

^hT₁ diagnostic calculated at the CCSD(T)/aug-cc-pVTZ level with Molpro.

ⁱThe error analysis (mean absolute deviation (MAD) and maximal absolute deviation (MAX)) applies only to the Cu(I) compounds.

In Table 2, we compare DFT and CCSD(T) results for several Cu(II) compounds; the amount of experimental data for Cu(II) energetics in the gas phase is very limited. Generally, the difference between the two functionals (B3LYP and B97-1) is small. By contrast, the binding energy of the first ligand differs more between DFT and CCSD(T) results, and, similar to previous observations in the literature,⁸⁷ increasing the amount of exact exchange leads to considerably better agreement with CCSD(T). For the second ligand binding energy, however, the agreement between B3LYP, B97-1, and CCSD(T) is notably better, and BH&HLYP no longer exhibits any notable advantage.

Table 2. Sequential Bond Dissociation Energies, Excluding Zero-Point Corrections, for Several Cu(II) Compounds.

	Sequential Bond Dissociation Energy Data (kcal/mol)
molecule	B3LYPa	B97-1a	BH&HLYPa	CCSD(T)a,b	CCSD(T)-DKb,c	T1d
[Cu(CO)1]2+	93.8	92.3	80.1	82.8	85.4	0.0305
[Cu(CO)2]2+	68.0	67.3	64.3	66.6	68.9	0.0256
[Cu(NH3)1]2+	155.9	153.9	139.9	140.1	142.6	0.0459
[Cu(NH3)2]2+	103.6	103.2	105.1	105.2	108.1	0.0269
[Cu(H2O)1]2+	117.4	114.9	101.8	105.4	107.2	0.0216
[Cu(H2O)2]2+	86.4	84.9	86.7	89.4	91.4	0.0180
[Cu(PH3)1]2+	168.3	164.7	143.9	149.3	149.4	0.0303
[Cu(PH3)2]2+	79.1	79.5	84.6	77.9	83.1	0.0450
[Cu(SH2)1]2+	149.2	146.0	122.4	128.6	123.9	0.0229
[Cu(SH2)2]2+	76.9	76.8	71.7	70.2	74.7	0.0307

^aaug-cc-pVTZ.

^bCalculated at B3LYP/aug-cc-pVTZ geometries.

^caug-cc-pVTZ-DK.

^dT₁ diagnostic calculated at the CCSD(T)/aug-cc-pVTZ level with Molpro.

By considering these observations collectively, we choose to select B3LYP/aug-cc-PVTZ as the reference method for the parametrization of the first generation of DFTB3 model for copper, while recognizing that it has considerable errors in energetics for some cases; this choice is due partly to the consideration that complete ligand dissociation is rarely relevant in biological applications. Our goal here is to capture structural features of Cu(I) and Cu(II) compounds accurately while describing energetic properties at a semiquantitative level. As shown below, these goals are largely met with our parametrization and the energetics can be further improved by single-point energy calculations at DFTB3 structures. In future development, we will consider alternative functional for treating metal ions in the DFTB3 framework (e.g., including a fraction of exact exchange; see Section 5) and the use of a different reference method, such as a double hybrid functional.⁷⁹

3.2. Parameterization Protocols

The parameters for DFTB3 and the fitting procedure have been described in detail for the parametrization of several elements.^{62,63,65,96,97} Here, we briefly discuss our choices for copper and the key parameters are summarized in Table 3; the spin-polarization constants for all elements and parameters for the repulsive potentials are provided in the Supporting Information.

Table 3. Overview of the Electronic Parameters for Copper^a.

parameter	valueb
lmax	2
nmax	2
α0	0.50
α1	1.38
α2	3.81
α3	10.51
α4	29.00
rspwf	2.2
rdwf	3.2
rdens	4.0
ϵs	–0.16311095
ϵp	0.06
ϵd	–0.19159112
Espin	–0.00853636
Usp	0.2383
Ud	0.30
Uspd	–0.0575
Udd	–0.20

^aFor notation, see ref (62). Hubbard and Hubbard derivative parameters for the s and p orbital (U_sp, U_sp^d) are different from those for the d orbitals (U_d, U_d). The optimized parameters are r_sp^wf, r_d, r^dens, ϵ_p, U_d, U_d^d. For the other parameters, ϵ_s, ϵ_d, E^spin, U_sp, U_sp are calculated using the PBE functional, and the remainder follow the standard DFTB choices. For parameters that define the repulsive potential, see Table S1 in the Supporting Information.

^bValues are given in atomic units (a.u.), if not unitless.

The following considerations are taken into account during the parametrization process:

• We determine the Hubbard parameter and its charge derivative for 4s and 4p orbitals as the first and second derivative, respectively, of the eigenvalue of the highest occupied orbital, with respect to its occupation number, using an atomic PBE calculation. The respective parameters of the 3d orbitals, U_d and U_d^d, are chosen such that the experimental oxidation potential Cu(I) → Cu(II) is well reproduced (since this is most relevant to biological applications); the experimental value is 468.0 kcal/mol,⁹³ and DFTB3 gives 469.5 kcal/mol. This choice of U_d and U_d also turns out to be helpful for reproducing the almost-planar coordination of copper in the complex [Cu(NH₃)₄]²⁺.

• The ground state of the Cu atom has the 3d¹⁰4s¹ electron configuration. However, to precalculate the two-center integrals of the charge-independent Hamiltonian H_μν⁰ and overlap integrals, we use the configuration 3d⁹4s², as we find this is particularly advantageous for capturing the geometries of Cu(II) species. By contrast, once the repulsive potentials are adjusted, we find no significant influence on the geometric and energetic properties of Cu(I) species, because of the use of different electron configurations.

• The 4p orbitals in copper are unoccupied. Nevertheless, we choose to include those in our basis set and consider them as polarization functions. Instead of calculating the eigenvalue of the 4p orbital (ϵ_p), as we have done for the occupied atomic 4s and 3d orbitals, we adjust ϵ_p to control the contribution of 4p to bonding. This is particularly helpful for reproducing the almost-planar conformation of [Cu(NH₃)₄]²⁺ and [Cu(SH₂)₄]²⁺.

• The wave function compression radii (r_sp^wf and r_d) are chosen such that qualitative geometrical properties are reproduced for, e.g., the Jahn–Teller distorted octahedral structure of [Cu(H₂O)₆]²⁺ and again the almost-planar coordination of copper in [Cu(NH₃)₄]²⁺ and [Cu(SH₂)₄]²⁺ complexes.

• The density compression (r^dens) is chosen such that the Cu-X repulsive potentials smoothly vanish at the cutoff points without introducing large gradients. r^dens seems extremely small in comparison to those from other elements (e.g., the value is 14 a.u. for Mg²⁺ and 9 a.u. for Zn²⁺⁶⁵), although we do not find any negative impact of the choice here.

• Parameters that define the repulsive potentials are given in Table S1 in the Supporting Information. Reference geometries and energies are calculated from B3LYP/aug-cc-pVTZ. For the fitting procedure, every data point is weighted by 1.0. Note that all data refer to Cu(I) species, with the exception of the geometries of [Cu(H₂O)₆]²⁺ and [Cu(PH₃)]²⁺, to ensure a proper discription of the Cu–O and Cu–P bond lengths, since they are significantly larger in the Cu(II) species, in comparison to their Cu(I) analogues.

4. Benchmark

In the following, we benchmark our new copper parameters and compare the results to DFT and semiempirical methods in the gas phase; in a separate paper, we discuss initial application of DFTB3 in the condensed phase using DFTB3/MM simulations. For DFT, we focus on B3LYP, PBE and B97-1; B3LYP is the reference method, PBE is the parent functional of DFTB3 and B97-1 has been shown to be a promising functional for many transition-metal ions in a recent benchmark.⁷⁶ For semiempirical methods, we focus on PM6, a popular NDDO method that has been recently reparameterized for the entire periodic table;⁶⁷ we also briefly compare structures to AM1*, which has been specifically parametrized to yield good structures for copper and zinc compounds.³⁹ Unless noted otherwise, energetics are given for geometries that are optimized at the respective level of theory. For DFTB3, we always apply the collinear spin-polarization formalism for open shells, and all spin-polarization constants W_la,la^′ are calculated using the PBE functional and are tabulated in the Supporting Information. The l-dependent formalism of the γ-function (Hubbard parameter) and its charge derivative (Γ) is applied to all copper species. For elements CHNOPS, we use the atomic (i.e., l-independent) Hubbard and Hubbard derivative parameters from the 3OB set⁶² for s, p, and d orbitals; i.e., the standard and the l-dependent formalisms are strictly equivalent for molecules containing only CHNOPS. Finally, we note that the ligands tested here are relatively small and therefore, for most cases (except for Sect.4.1), dispersion corrections have not been included for either DFT⁹⁸ or DFTB3^99,100 methods.

All DFTB3 calculations have used our in-house DFTB code, while PM6 and DFT calculations are performed using the Gaussian09 software package;¹⁰¹ CCSD(T) calculations are done with Molpro.¹⁰² To ensure consistent electronic states in the various DFT and CCSD(T) calculations, molecular orbitals are exchanged between them whenever possible.

4.1. Comparison to Experimental Geometries

First, we compare optimized DFTB3 geometries to crystal structures from the Cambridge Structural Database (CSD)¹⁰³ for a list of copper-containing molecules that Kayi and Clark used to calibrate their AM1* method.³⁹ The size of the chosen molecules were in the range of 22–101 atoms and include only those containing ONCHPS in the ligands. For comparison, DFT (B3LYP and B97-1) calculations are also done for some of the molecules that contain relatively small ligands. We note that all geometry optimization is done in the gas phase rather than in the crystalline environment, as done in the previous study.³⁹ The root-mean-square deviations (RMSDs) are calculated using the Quatfit program¹⁰⁴ to superimpose all non-hydrogen atoms. The comparison is summarized in Table 4; detailed values and a visual comparison of the X-ray, DFTB3, and PM6 geometries are given in the Supporting Information.

Table 4. Statistics for the Root Mean Square Deviations of 26 Structures in Comparison to Experimental X-ray Geometries of the Cambridge Structural Database at Different Levels of Theory^a.

	Root Mean Square Deviation, RMSD (Å)
	MAD	MAX
DFTB3(+D3)b	0.53 (0.53)	1.56 (1.42)
AM1*c	0.55	1.34
PM5d	1.02	5.65
PM6d	0.61	1.71
B3LYPe	0.31	0.89
B97-1e	0.30	0.87

^aFor detailed values, see Table S2 in the Supporting Information.

^bNumbers with parentheses are obtained with the D3 dispersion model parametrized for DFTB3.⁹⁹ Without dispersion, geometries are optimized with the in-house DFTB code; with dispersion included, geometries are optimized with CHARMM.

^cData taken from ref (39).

^dABETEH and AYACOS were excluded for PM6, because of unphysical structures after geometry optimization.

^eBasis set is 6-31+G(d,p); due to extensive computational costs only small molecules are considered.

The overall performance for DFTB3 is rather similar to that of AM1* with a MAD in RMSD of 0.53 Å vs 0.55 Å, respectively; for the complexes with smaller ligands, the RMSD values are very close to those for B3LYP and B97-1, which are in the range of 0.3 Å (see below), further supporting the value of DFTB3 for structural analysis of copper compounds. Nevertheless, several systems show notable deviations from the crystal structures. In some cases, the large RMSD values clearly reflect the difference between the gas phase and crystalline environment. For example, the largest RMSDs (∼1.4 Å) are found for ABUXIE and AYACOS. The crystal structure of ABUXIE features a linear S=C=N–Cu arrangement, while DFTB3 shows an angle around the N atom; this is most likely related to the hybridization problem of the N atom with the current DFTB3 model.⁶² More significantly, ABUXIE contains two dimethyl sulfoxides that are bound via one hydrogen bond to the ligands of the copper complex, an arrangement likely promoted by the crystalline environment. With DFTB3 calculations in the gas phase, these dimethyl sulfoxide molecules reorient, leading to a larger RMSD. Similarly, AYACOS consists of a copper thiolate and a doubly protonated bipyridinium, which are not connected via any covalent bond. Thus, DFTB3 optimization in the gas phase leads to rather different relative orientations of the two molecules.

However, there are several cases that exhibit notable differences between DFTB3 and crystal structures, in terms of copper coordination. AJOROG01 contains a pentacoordinated Cu with two oxygen ligands enclosing an angle of ∼83°. With DFTB3, this angle is 164° and one nitrogen ligand is almost dissociated (see below). Substantial differences between experimental and DFTB3 geometries are also found for AWEMAQ and FEJMEN. While experimental structures show an almost-tetrahedral coordination of Cu, DFTB3 reveals a rather trigonal structure with one triphenyl phosphine ligand being coordinated much more loosely. This observation is consistent with the notable errors in the DFTB3 Cu–P bond length, as discussed below. Another general trend concerns the coordination of water to copper, which is often in the range of 2.2 Å in the crystal structures; DFTB3 overestimates this distance by ∼0.2 Å in the case of AQCBCU and ASTMEC. More severely, for AVOQIL, one crystal water is coordinated to Cu in DFTB3 while the water is hydrogen-bonded to the ligands in the crystal structure. In ANCTCU, two formate ions coordinate to the copper in a monodentate fashion in the crystal structure; with DFTB3, one formate coordinates with a crystal water, and the other coordinates to Cu in a bidentate fashion.

The effect of including empirical dispersion is small for most cases, thus DFTB3-D3⁹⁹ gives essentially the same MAD as DFTB3. In several cases that involve large aromatic ligands (e.g., AYACOS), including dispersion improves the agreement with the crystal structure (see Supporting Information); however, in other cases, the deviation actually becomes larger (e.g., FEJMEN), which likely reflects the lack of a crystalline environment in these gas-phase calculations.

Table 4 also shows RMSDs for PM5 (taken from ref (39)), PM6, B3LYP/6-31+G(d,p), and B97-1/6-31+G(d,p). During geometry optimization with PM6, two molecules adopt unphysical geometries: for ABETEH the Cu leaves its central position, while in AYACOS the Cu–S distance shrinks to ∼1.2 Å. Besides these cases, PM6 has an overall similar performance as DFTB3 and AM1*. As to the DFT (B3LYP and B97-1) results, the optimized structures are generally close to the crystal structures (MAD in RMSD is ∼0.3 Å), although only relatively small systems have been optimized here, because of computational cost considerations. For these systems, DFTB3 results are very close to DFT, while both AM1* and PM6 show larger errors in some cases (e.g., AJEVOA). Indeed, the DFTB3 deviations from the crystal structures described above for AJOROG01 and AVOQIL are also reproduced with the DFT calculations, suggesting that these differences are also likely due to the use of gas-phase models, rather than reflecting qualitative errors of DFTB3.

In Table 5, we summarize the deviations in Cu–ligand distances. Structures with major differences (AJOROG01, ANCTCU, AVOQIL, AWEMAQ, FEJMEN) are excluded from the statistics. Generally, all experimental Cu–ligand bonds are shorter than those calculated with DFTB3, most severely for Cu–P with a MAD of 0.186 Å. Considering that we are making comparison between gas-phase calculations and crystal structures, the overall MAD of 0.061 Å indicates that DFTB3 is a viable method for determining geometrical properties. Indeed, even for B3LYP (and the small systems only), an overall MAD of 0.062 Å is found; for more details, see the Supporting Information. In this context, we note that, although the BP86 functional was found to give good structures for copper complexes,⁵⁵ the differences from B3LYP are small.⁵⁵

Table 5. DFTB3 Statistics of Different Bond Types in Comparison to Experimental X-ray Geometries of the Cambridge Structural Database.

		DFTB3 Statistics (Å)
bond type	number of comparisons, N	maximal absolute deviation, MAX	mean signed error, MSE	mean absolute deviation, MAD
rCuC	3	0.068	+0.029	0.031
rCuN	37	0.217	+0.021	0.055
rCuO	25	0.231	+0.026	0.063
rCuP	3	0.237	+0.186	0.186
rCuS	18	0.090	+0.049	0.057
all	86	0.237	+0.034	0.061

4.2. Geometries

In this section, we focus on relatively small Cu-containing molecules in the gas phase and compare more systematically DFTB3 to B3LYP/aug-cc-pVTZ for bond lengths and angles for a set that contains Cu₂, 32 Cu(I) and 42 Cu(II) complexes (summarized in Table S3 in the Supporting Information): ligands considered include CH₃^–, CO, NH₂, NH₃, OH^–, H₂O, PH₂^–, PH₃, SH^–, and SH₂. In addition, complexes with one deprotonated ligand are included as well as CuH, CuH₂, CuO, and CuS. All bond lengths between copper and the closest atom of each ligands are considered, as well as all angles between the ligands (e.g., the O–Cu–O angle within [Cu(H₂O)₂]). Bond lengths within one ligand change only minimally for the free and copper-bound ligands; therefore, these bond lengths have not been considered in the statistics. In total, 165 bond lengths and 157 bond angles are compared. Detailed results are provided in the Supporting Information, and only error statistics are summarized in Tables 6 and 7.

Table 6. Deviation of Bond Lengths and Bond Angles, in Comparison to B3LYP/aug-cc-pVTZ.

	B97-1a,b	B3LYPc	PBEc	PM6d	DFTB3
Cu(I) — Bond Lengths
number of comparisons, N	64	64	64	46	64
mean absolute deviation, MAD (Å)	0.004	0.004	0.039	0.047	0.025
mean signed error, MSE (Å)	+0.000	–0.002	–0.039	+0.025	+0.006
maximal absolute deviation, MAX (Å)	0.014	0.008	0.077	0.158	0.108
Cu(II) — Bond Lengths
number of comparisons, N	98	101	101	74	101
mean absolute deviation, MAD (Å)	0.004	0.003	0.023	0.078	0.031
mean signed error, MSE (Å)	–0.002	–0.002	–0.017	–0.062	–0.016
maximal absolute deviation, MAX (Å)	0.059	0.026	0.085	0.405	0.355
Cu(I) — Bond Angles
number of comparisons, N	44	44	44	29	44
mean absolute deviation, MAD (deg)	0.1	0.2	0.4	0.6	0.9
mean signed error, MSE (deg)	+0.0	+0.0	+0.0	+0.6	+0.5
maximal absolute deviation, MAX (deg)	0.4	1.1	2.3	4.8	4.8
Cu(II) — Bond Angles
number of comparisons, N	110	113	113	85	113
mean absolute deviation, MAD (deg)	0.4	0.5	1.6	12.4	2.2
mean signed error, MSE (deg)	+0.0	+0.1	+0.0	–1.6	+0.1
maximal absolute deviation, MAX (deg)	3.4	10.4	13.1	81.4	30.9

^aBasis set aug-cc-pVTZ.

^b[Cu(SH)₃]⁻ could not be optimized to a similar structure as for B3LYP/aug-cc-pVTZ and, therefore, has been removed from the statistics.

^cBasis set 6-31+G(d,p).

^dBecause of extremely large errors for the Cu–S bonds at the PM6 level of theory, the respective complexes are excluded from the statistics.

Table 7. Deviation of DFTB3 Bond Lengths, in Comparison to B3LYP/aug-cc-pVTZ.

bond type	number of comparisons, N	mean absolute deviation, MAD (Å)	mean signed error, MSE (Å)	maximal absolute deviation, MAX (Å)
Cu(I)
Cu–C	13	0.022	+0.019	0.048
Cu–H	1	0.001	–0.001	0.001
Cu–N	15	0.034	–0.018	0.071
Cu–O	8	0.017	+0.001	0.024
Cu–P	8	0.037	+0.037	0.108
Cu–S	18	0.019	+0.007	0.050
Cu(II)
Cu–C	13	0.034	–0.034	0.090
Cu–H	1	0.019	+0.019	0.019
Cu–N	21	0.044	–0.040	0.355
Cu–O	31	0.023	+0.012	0.071
Cu–P	8	0.024	+0.004	0.062
Cu–S	27	0.033	–0.028	0.124

We note the following trends in the optimized structures at different levels of theory.

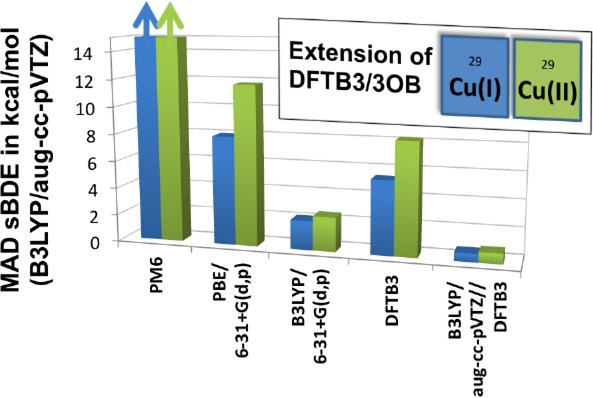
With the aug-cc-pVTZ basis, B97-1 and B3LYP structures are generally very similar, with the only major outlier being [Cu(II) (SH)₃]⁻, for which we do not find the same structure. Copper and sulfur atoms are almost in a plane, and the smallest S–Cu–S angle is 88° for B97-1 and 103° for B3LYP; the Cu–S bond length deviations are also fairly large (0.109 Å). With the same functional, B3LYP, using different basis sets (6-31+G(d,p) vs aug-cc-pVTZ), leads to very small differences in structure: MAD/MAX values of 0.003/0.026 Å for bond lengths, and 0.4°/10.4° for bond angles. Again, the largest deviations are found for [Cu(II) (SH)₃]⁻, whereas all other angles deviate no more than 5°. By contrast, the “parent” functional of DFTB3, PBE, leads to somewhat larger structural differences: MAD/MAX 0.029/0.085 Å for bond lengths, 1.3°/13.1° for bond angles. Therefore, when comparing DFTB3 results to the reference B3LYP, the inherent limitations of PBE should be kept in mind.

For PM6, we note that molecules containing Cu–S bonds within our test set are described quite poorly, and the bond lengths are often underestimated by 0.3 Å and more. Excluding those molecules leads to an overall MAD/MAX for bond lengths of 0.047/0.158 Å for Cu(I) and 0.079/0.405 Å for Cu(II) species. For bond angles, the MAD/MAX values are 0.6°/4.8° for Cu(I) and 12.4°/81.4° for Cu(II). Thus, PM6 is somewhat applicable to Cu(I) species and substantially worse for Cu(II).

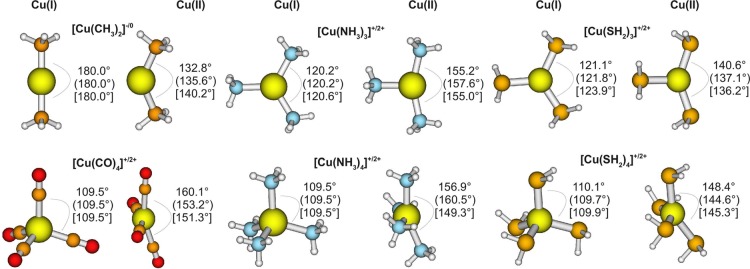
By contrast, with DFTB3, it is rather satisfying that Cu(I) and Cu(II) geometries have comparable accuracy; our efforts indicated that this was difficult to achieve without the l-dependent formalism. The overall MAD for bond lengths is 0.025 Å for Cu(I) and 0.031 Å for Cu(II); the MADs for bond angles are 0.9° and 2.2° for Cu(I) and Cu(II), respectively. Examples for significant structural differences between Cu(I) and Cu(II) species are shown in Figure 1. While tetra-coordinated Cu(I) complexes adopt a (close to) tetrahedral coordination, Cu(II) complexes are nearly square-planar. Complexes with three ligands have a trigonal planar structure with angles between the ligands of ∼120° for Cu(I), but have significantly different angles when oxidized to Cu(II). For [Cu(CH₃)₂]⁺, the linear structure changes to a bend one for [Cu(CH₃)₂]²⁺.¹⁰⁵ All these effects are well described by DFTB3, which shows the largest error of 8.8° for [Cu(CO)₄]²⁺, in comparison to B3LYP/aug-cc-pVTZ; the DFTB3 value in this case is similar to the PBE/6-31+G(d,p) result (see Figure 1).

Figure 1.

Significant structual changes between analogue structures of Cu(I) and Cu(II) species. Bond angles are shown for B3LYP/aug-cc-pVTZ, (PBE/6-31+G(d,p)), and [DFTB3].

Nevertheless, we do see larger MAX errors for Cu(II) than for Cu(I) and also note several limitations of the current DFTB3 model. For example, [Cu(NH₃)₆]²⁺ is a typical complex showing Jahn–Teller distortion with the four equatorial ligands being closer to the central copper than the two axial ligands. With B3LYP, the Cu–N_axial distances are 2.73 and 2.65 Å (the investigated mimimum is a nonsymmetrical structure) and the Cu–N_equatorial distances are ∼2.10 Å. With DFTB3, the equatorial distances (2.11 Å) are similar to those observed for B3LYP, while the axial distances (2.37 Å for both ligands) are significantly shorter than those observed for B3LYP. Another example is [Cu(SH₂)₅]²⁺, in which one Cu–S distance is too short (by 0.124 Å); in [Cu(PH₂)PH₃], the Cu–PH₃ distance is too long (by 0.108 Å). With regard to bond angles, which are generally well-reproduced, the largest difference between DFTB3 and B3LYP is found for [Cu(SH₂)₂]²⁺ with calculated angles of 162.7° (DFTB3) and 131.7° (B3LYP/aug-cc-pVTZ).

Despite these limitations, we note that our first generation of DFTB3 outperforms the second-order parametrization for copper that was reported by Bruschi et al., based on the MIO parameter set for ONCH.⁵⁵ Their model gave satisfying structural results for a set of small copper compounds (in comparison to BP86/TZVP⁵⁵); for larger compounds in our test case, their model has bond-length deviations of 0.15 Å in, for example, [Cu(NH₃)₄]⁺, [Cu(NH₃)₃]⁺, [Cu(NH₃)₆]²⁺, [Cu(NH₃)₄]²⁺, and Cu(II) carbonyl complexes. As a result, for our test set (excluding P- and S-containing systems), their model has a MAD in bond length of 0.089 and 0.100 Å for Cu(I) and Cu(II) species, respectively, which are substantially larger than the DFTB3 values (see Tables 6,7). Qualitative differences from B3LYP/aug-cc-pVTZ are also found for their second-order model. For example, for [Cu(NH₃)₄]²⁺ and [Cu(CO)₄]²⁺, rather than being almost planar (see Figure 1), the two trans ligands show angles of <133°, whereas, with B3LYP, both angles for both molecules are >156°; with DFTB3, the angles are ∼150°. Finally, the second-order model was not systematically tested for energetics in the original parametrization;⁵⁵ for our test set, the mode has much larger errors in ligand dissociation energies than DFTB3, especially for Cu(II).

4.3. Sequential Bond Dissociation Energies

We define sequential bond dissociation energies (sBDEs) corresponding to the reactions

10

11

12

13

for Cu(I) and Cu(II) species with neutral and negatively charged ligands. Results for DFTB3 and other methods in comparison to the reference B3LYP/aug-cc-pVTZ are shown in Table 8 (for detailed values, see Table S4 and S5 in the Supporting Information). We make the following observations.

Table 8. Error Statistics for Sequential Bond Dissociation Energies and Ligand Proton Affinities at 0 K, Excluding ZPE (Deviation from B3LYP/aug-cc-pVTZ^a).

	B97-1b	B3LYPc	PBEc	PM6	DFTB3	B3LYPb//DFTB3d
Cu(I) and Neutral Ligands (eq 10)
MAD (kcal/mol)	1.0	1.7	6.9	22.4	3.1	0.4
MAX (kcal/mol)	1.8	3.6	10.9	121.6	8.5	2.1
Cu(I) and Charged Ligands (eq 11)
MAD (kcal/mol)	1.8	2.8	9.5	37.8	8.7	0.9
MAX (kcal/mol)	2.4	5.6	16.3	135.4	16.7	2.1
Cu(II) and Neutral Ligands (eq 12)
MAD (kcal/mol)	1.4	1.8	9.3	23.2	4.7	0.6
MAX (kcal/mol)	3.6	3.5	20.7	101.5	15.1	4.1
Cu(II) and Charged Ligands (eq 13)
MAD (kcal/mol)	2.5	3.7	15.8	46.6	14.0	1.0
MAX (kcal/mol)	5.2	7.2	23.5	116.7	29.3	3.2
Cu(I) Ligand Proton Affinities
MAD (kcal/mol)	2.1	1.0	6.4	5.4e	6.0f	0.4
MAX (kcal/mol)	3.5	2.5	9.4	9.4e	11.7f	0.8
Cu(II) Ligand Proton Affinities
MAD (kcal/mol)	3.0	1.9	4.8	8.2e	5.7f	1.2
MAX (kcal/mol)	4.5	2.4	9.3	27.7e	15.3f	3.6

^aFor detailed numbers, see Tables S4–S6 in the Supporting Information.

^bBasis set aug-cc-pVTZ.

^cBasis set 6-31+G(d,p).

^dB3LYP single-point calculations on top of the DFTB3 geometries.

^eThe energy of the proton in PM6 is in error by −54 kcal/mol, which has been corrected for the given proton affinities. See discussion at http://openmopac.net/manual/pm6_accuracy.html.

^fNHmod parameters used; for details, see ref (62).

With the aug-cc-pVTZ basis, B3LYP and B97-1 give generally very similar results, as also seen in Section 3.1. Most deviations in our test set are <2 kcal/mol for Cu(I). For bond dissociation energies of Cu(II) complexes with charged ligands, the two functionals differ by up to 5 kcal/mol. Note that these deviations are small, in comparison to those of DFTB3, which supports the argument that the errors for DFTB3 are mainly due to its approximations, rather than due to the specific choice of reference method. With the same B3LYP functional, decreasing the basis set to 6-31+G(d,p) also generally leads to only small deviations. For complexes with charged ligands, as expected, the deviations can be >5 kcal/mol. Finally, comparing PBE/6-31+G(d,p) and B3LYP/aug-cc-pVTZ, PBE results deviate substantially from B3LYP with differences often greater than 10 kcal/mol and become increasingly larger in the order of Cu(I) neutral ligands, Cu(I) charged ligands, Cu(II) neutral ligands, and Cu(II) charged ligands. The differences are particularly large for the first ligand binding energy (i.e., binding to a Cu ion). These trends suggest that one must compensate for part of the inherent limitations of PBE during the parametrization for DFTB3.

With PM6, large deviations for sBDEs, in comparison to B3LYP, are common. Complexes containing sulfur–ligands are not considered, because of unphysical geometries, as discussed above, and very large errors are found for sBDEs of phosphorus–ligands. Even after removing these “outliers” from the statistics, the deviations are still large and errors of >10 kcal/mol are no rarity. Note that, while we compare potential energy differences for all methods, PM6 intrinsically considers heats of formation. Nevertheless, the large errors indicate that PM6 is not suitable for energetic analysis for binding energies to copper in either oxidation state. As also shown in the Supporting Information, errors for AM1* are comparable to those for PM6; for example, for Cu(I), the MADs are 15.6 kcal/mol for neutral ligands and 20.9 kcal/mol for charged ligands.

With DFTB3, the errors are dependent on the charge of the ligand. For charge-neutral ligands, the MADs are 3.1 and 4.7 kcal/mol for Cu(I) and Cu(II) complexes; these values are smaller than those for PBE/6-31+G(d,p), which are 6.9 and 9.3 kcal/mol, respectively. Deviations of >10 kcal/mol are found for dissociations of Cu(II) complexes with only one neutral ligand. For charged ligands, the errors are notably larger, with MAD values of 8.7 and 14.0 kcal/mol for Cu(I) and Cu(II) complexes, respectively. It seems that not only the atomization energies of small anionic systems such as CH₃^– or OH^– are in error as described earlier,⁶² but also their charge-transfer behavior to a cationic metal center requires improvement. Moreover, the polarizability of charged ligands is likely substantially underestimated with DFTB3, because of its minimal basis nature. Solving these issues requires extending the DFTB3 methodology using, for example, the chemical potential equilization approach.¹⁰⁶

Despite these limitations, an encouraging observation from Table 8 is that single-point B3LYP/aug-cc-pVTZ calculations at DFTB3 geometries lead to very reliable binding energies for all ligand types. [Note that, in some cases, the initial guess for the orbitals were taken from the B3LYP/aug-cc-pVTZ optimized geometry in order to calculate the same electronic state.] The MAD values for Cu(I) and Cu(II) complexes with neutral and charged ligands are all <1 kcal/mol, with the largest deviation being ∼4 kcal/mol. These results highlight the close agreements in DFTB3 and B3LYP geometries.

4.4. Proton Affinities

The proton affinities of copper ligands are relevant in many mechanistic studies.^{1,2,107−109} Therefore, we also examine ligand proton affinities at different levels of theory. As shown in Table 8 (for detailed values, see Table S6 in the Supporting Information), the general trends are similar to those observed for the ligand binding energies. The two functionals (B3LYP and B97-1) generally give similar results with an MAD value of 2–3 kcal/mol, and the effect of the basis set for B3LYP is even smaller. PBE/6-31+G(d,p) has larger differences from B3LYP/aug-cc-pVTZ with MADs on the order of 5–6 kcal/mol. PM6 has somewhat larger errors, especially for Cu(II) ligands, for which the MAD is 8.2 kcal/mol. DFTB3 gives results of similar quality as PBE/6-31+G(d,p), reflecting again that the description of anionic ligands (i.e., following deprotonation) is less than ideal in the first generation of the DFTB3 model. Single-point B3LYP/aug-cc-pVTZ energy calculations at DFTB3 structures, however, gives very encouraging results, with MAD values on the order of 1 kcal/mol or less.

4.5. Mixed Ligands

So far, we have only considered complexes with one type of ligands (with the exception of proton affinity calculations, where one ligand is deprotonated). In this subsection, we analyze the properties of copper compounds with different types of ligands and therefore potentially more-complex electronic structures.

The structural comparison is summarized in Table 9, and more details are included in the Supporting Information. As expected, deviations for the different DFT calculations are rather low, the MAD values, in comparison to B3LYP/aug-cc-pVTZ for 102 bond lengths, are 0.009, 0.008, and 0.037 Å for B97-1/aug-cc-pVTZ, B3LYP/6-31+G(d,p), and PBE/6-31+G(d,p), respectively. Bond angles deviate, on average, by 0.5°, 1.0°, and 3.0°, respectively. [One exception is found for PBE, where a large deviation appears for Cu[(H₂O)₂(NH₃)₄]²⁺. While, for the B3LYP/aug-cc-pVTZ set, the four NH₃ ligands are almost planar, PBE predicts them to be more tetrahedral-like. As consequence, the distance from the Cu atom to both water molecules for PBE is significantly larger.]

Table 9. Deviations from B3LYP/aug-cc-pVTZ for Bond Lengths and Angles of the Mixed Ligand Test Set.

		B3LYPa			DFTB3
	number of comparisons, N	mean absolute deviation, MAD	mean signed error, MSE	maximal absolute deviation, MAX	mean absolute deviation, MAD	mean signed error, MSE	maximal absolute deviation, MAX
Cu(I)
rCuN (Å)	3	0.007	–0.007	0.009	0.141	–0.141	0.192
rCuO (Å)	3	0.024	–0.006	0.042	0.142	+0.043	0.174
rCuS (Å)	6	0.017	+0.000	0.038	0.186	+0.149	0.509
angles (deg)	18	2.9	+0.0	8.8	16.4	–2.2	61.3
Cu(II)
rCuN (Å)	41	0.006	–0.005	0.013	0.025	–0.015	0.142
rCuO (Å)	25	0.013	+0.006	0.085	0.056	–0.041	0.277
rCuS (Å)	30	0.005	+0.000	0.016	0.036	–0.029	0.175
angles (deg)	188	0.8	–0.1	9.3	2.5	+0.1	12.8
overall(r)b	108	0.008	–0.001	0.085	0.051	–0.018	0.509
overall(a)c	191	1.0	–0.1	9.3	3.7	–0.1	61.3

^a6-31+G(d,p).

^bOverall statistics for bond lengths (r).

^cOverall statistics for bond angles (a).

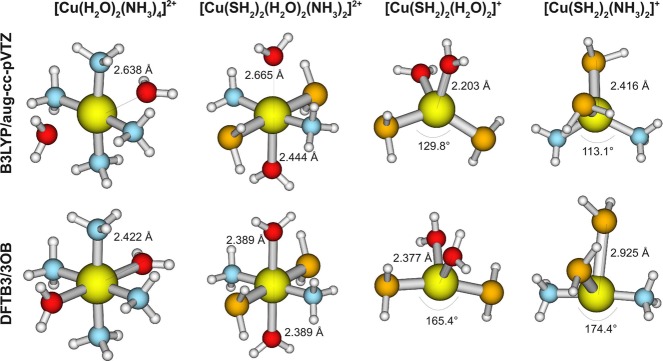
The performance of DFTB3, at first sight, is significantly less satisfying than for complexes with one type of ligands, especially for Cu(I) complexes (compare Table 9 to Tables 6 and 7). In most cases, when large deviations to the B3LYP reference are observed, one particular ligand is predicted to be further away from or closer to the copper. In other cases, bond angles are different; the most significant differences are depicted in Figure 2. For example, the DFTB3-optimized [Cu(SH₂)₂(NH₃)₂]⁺ complex features an almost-linear ammonia–copper–ammonia arrangement, whereas B3LYP predicts a tetrahedral type of structure. As we will demonstrate using single-point energies below, however, the potential energy surface is rather flat along the relevant copper–ligand distances for most cases and therefore the geometrical differences are not likely to lead to major mechanistic impacts. In biological applications, the protein environment can also help avoid major structural deviations for these soft degrees of freedom.

Figure 2.

Most significant differences between DFTB3 and B3LYP/aug-cc-pVTZ within the mixed-ligand test set.

For ligand binding energetics, the performance of DFTB3 is similar to that observed for complexes with a single type of ligands. When a single ligand is removed (see Table S7 in the Supporting Information), the DFTB3 results are slightly worse, compared to DFT methods; the MAD value for DFTB3 is 3.7 kcal/mol, while different DFT methods are usually within 2 kcal/mol. When all ligands are removed, which provide a stringent test, larger differences between methods are observed (see Table 10). For example, with the small 6-31+G(d,p) basis set, B3LYP calculations differ from the reference (B3LYP/aug-cc-pVTZ) by ∼10 kcal/mol, while PBE differs much more with a MAD value of 36.5 kcal/mol. By comparison, DFTB3 has a substantially smaller MAD value of 6.8 kcal/mol, which is a small fraction of the total ligand binding energy. In all cases, single-point B3LYP/aug-cc-pVTZ energies at DFTB3 structures lead to small errors in binding energies. Even for the case of removing all ligands, the MAD value for such single-point energy calculations is 1.6 kcal/mol, clearly highlighting the good quality of DFTB3 for key structural features. The worst cases are those with large structural differences from B3LYP (e.g., those shown in Figure 2), for which the single-point energy differences are ∼4 kcal/mol.

Table 10. Bond Dissociation Energies for Removing All Ligands from the Complex at 0 K, Excluding ZPE (Deviation from B3LYP/aug-cc-pVTZ for Our Mixed-Ligand Test Set).

	Bond Dissociation Energy (kcal/mol)
	B3LYPa	B97-1a	B3LYPb	PBEb	DFTB3	B3LYPa//DFTB3c
[Cu(OH)(H2O) (NH3)2]+	594.6	–1.1	+11.3	+35.5	+3.0	–1.0
[Cu(H2O) (NH3)4]2+	383.8	+0.3	+13.2	+37.6	–16.1	–0.1
[Cu(H2O)2(NH3)2]2+	340.6	–1.8	+10.5	+31.0	–14.1	–0.0
[Cu(H2O)2(NH3)4]2+	398.8	+1.5	+15.2	+41.0	–11.3	–1.0
[Cu(OH) (NH3)3]+	601.3	–0.7	+11.4	+36.4	–0.6	–0.8
[Cu(OH) (NH3)4]+	613.9	+0.7	+13.1	+39.1	+0.7	–1.5
[Cu(SH) (NH3)3]+	572.6	–0.9	+9.6	+38.0	–9.9	–0.4
[Cu(SH) (NH3)4]+	582.9	+1.2	+11.3	+41.1	–6.8	–1.9
[Cu(SH2) (NH3)4]2+	377.5	+1.1	+12.5	+38.9	–15.5	–1.5
[Cu(SH) (SH2) (NH3)2]+	561.2	–0.6	+8.6	+40.2	–7.5	–1.1
[Cu(SH2)2(H2O) (NH3)]2+	321.8	–0.8	+8.4	+35.8	–8.7	–2.1
[Cu(SH2)2(H2O) (NH3)2]2+	355.7	+0.7	+10.9	+39.2	–8.9	–1.1
[Cu(SH2)2(H2O)2(NH3)2]2+	370.0	+2.1	+13.2	+42.1	–3.1	–0.6
[Cu(SH2)2(H2O)2]2+	307.5	–1.5	+8.0	+34.0	–5.0	–2.0
[Cu(SH2)2(H2O)3]2+	330.2	–0.5	+10.1	+36.1	–2.7	–2.4
[Cu(SH2)2(H2O)4]2+	345.3	+0.9	+12.7	+37.7	+2.0	–0.8
[Cu(SH2)2(NH3)2]2+	336.1	–0.3	+8.7	+37.3	–13.3	–1.4
[Cu(SH2)3(NH3)2]2+	351.3	+1.4	+9.9	+41.0	–9.2	–1.9
[Cu(SH2)4(H2O)]2+	324.7	+1.8	+8.6	+41.9	–1.4	–3.0
[Cu(SH2)4(H2O)2]2+	337.8	+3.2	+11.0	+44.3	+5.9	–2.3
[Cu(SH2)2(H2O) (NH3)]+	119.3	+2.0	+7.1	+23.8	+1.8	–1.2
[Cu(SH2)2(H2O)2]+	110.5	+1.5	+6.9	+22.0	+2.1	–4.2
[Cu(SH2)2(NH3)2]+	125.1	+2.1	+7.0	+24.4	+7.1	–4.2
MAD		1.2	10.4	36.5	6.8	1.6
MAX		3.2	15.2	44.3	16.1	4.2

^aaug-cc-pVTZ.

^b6-31+G(d,p).

^cB3LYP single-point calculations on top of DFTB3 geometries.

4.6. Larger Ligand Molecules

Finally, to further test the applicability of our new DFTB3 model, we have compiled another test set that includes more-realistic biological ligands of copper. These include 32 Cu(I) and 32 Cu(II) complexes, and the ligands are methanolate, methanthiolate, methanethiol, N-methylmethanimine, dimethyl sulfide, imidazole, imidazolate, and formaldehyde.

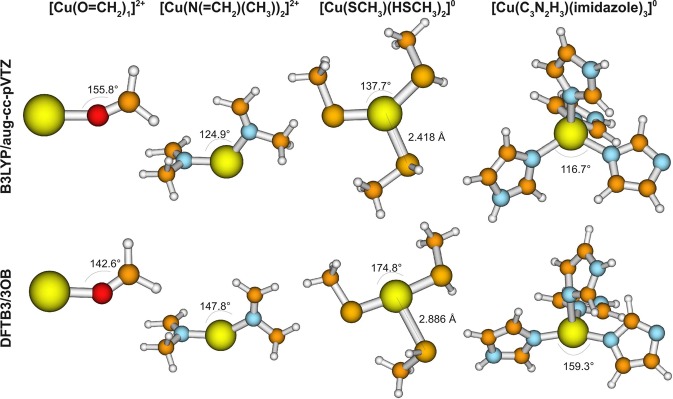
For structures, the general trends are similar to those observed for the mixed-ligand cases. For example, compared to B3LYP/aug-cc-pVTZ optimized structures, B3LYP with the small basis set 6-31+G(d) deviates, on average, by only 0.005 Å and the maximal deviation is 0.060 Å. PBE/6-31+G(d) differs somewhat more with an MAD value of 0.039 Å. Generally, the largest deviations are found for molecules with deprotonated ligands where a neutral ligand has a tendency to dissociate with the double-ζ basis set, whereas it remains covalently bound when using the triple-ζ basis set. However, the relative energy of the geometry with and without dissociated ligand is <3 kcal/mol (at the B3LYP/aug-cc-pVTZ level), showing that the relevant potential energy surface is rather flat. This is particularly true for DFTB3, where the largest error is 0.468 Å, while the MAD value is only 0.035 Å (see Table 11). However, notable differences are found for DFTB3, in comparison to B3LYP/aug-cc-pVTZ, for several cases. As summarized in Figure 3, in Cu(S–CH₃) (HS–CH₃)₂, Cu(C₃N₂H₃) (imidazole)₃, [Cu(S–CH₃) (HS–CH₃)₃]⁺, and [Cu(C₃N₂H₃) (imidazole)₂]⁺, the negatively charged ligand has a tendency to be trans to another neutral ligand, while the remaining neutral ligands coordinate with a much larger copper–ligand distance. This contrasts with the geometry found with B3LYP, which leads to an almost-trigonal planar and tetrahedral structure for three and four ligands, respectively.

Table 11. Deviations from B3LYP/aug-cc-pVTZ for Bond Lengths for the Large-Molecules Test Set.

		PBE/6-31+G(d)			DFTB3
	number of comparisons, N	mean absolute deviation, MAD	mean signed error, MSE	maximal absolute deviation, MAX	mean absolute deviation, MAD	mean signed error, MSE	maximal absolute deviation, MAX
Cu(I)
rCuN	24	0.046	–0.046	0.089	0.064	–0.038	0.171
rCuO	4	0.026	–0.026	0.043	0.021	–0.002	0.030
rCuS	29	0.052	–0.052	0.110	0.035	+0.029	0.468
overall	116	0.039	–0.039	0.138	0.035	–0.006	0.468

Figure 3.

Most significant differences between DFTB3 and B3LYP/aug-cc-pVTZ within the large molecule test set. In the first column, the angle is underestimated; a similar deviation is found for [Cu(O=CH₂)₁]⁺, [Cu(O=CH₂)₂]⁺, [Cu(O–CH₃)₁], [Cu(O–CH₃)₂]⁻, [Cu(O=CH₂)₂]²⁺, [Cu(O–CH₃)₁]⁺, [Cu(O–CH₃)₂], and [Cu(HS–CH₃)₁]²⁺. In the second column, the angle is overestimated. In the third and fourth columns, DFTB3 predicts an almost-linear coordination of “deprotonated ligand–copper–neutral ligand”, instead of an almost-trigonal planar or tetrahedral structure, as B3LYP does. A similar deviation is found for [Cu(S–CH₃) (HS–CH₃)₃]⁺ and [Cu(C₃N₂H₃) (imidazole)₂]⁺.

To further analyze the energetic impact of the different geometries, we calculate the relative energy (at either DFTB3 or B3LYP/aug-cc-pVTZ level) of DFTB3 and B3LYP/aug-cc-pVTZ optimized geometries. As Table S8 in the Supporting Information shows, the relative energies are, overall, quite small at both the DFTB3 and B3LYP levels, with typical values of ∼2 kcal/mol. Nevertheless, larger differences are observed in some cases, with the largest difference being ∼7.6 kcal/mol for [Cu(C₃N₂H₃) (imidazole)₃], in which DFTB3 has a tendency to adopt the conformation with a rather linear “deprotonated ligand–copper–neutral ligand” arrangement.

For additional energetic properties, we analyze the sequential bond dissociation energies (sBDEs) and ligand proton affinities. The detailed results are summarized in Tables S9 and S10 in the Supporting Information. DFTB3 generally performs reasonably well, and large errors are mainly found for species with few and charged ligands. Again, the superb performance of B3LYP single-point energies at DFTB3 geometries (the MAD value is only 0.5 and 0.8 kcal/mol for Cu(I) and Cu(II) bond dissociation energies) indicates the overall consistency of DFTB3 and B3LYP structures. Even for the problematic geometries discussed above, the reaction energies are well-reproduced with single-point calculations, and the largest deviation is 3.1 kcal/mol. For ligand proton affinities, the MAD values for DFTB3 are 7.1 kcal/mol (Cu(I)) and 4.2 kcal/mol (Cu(II)), similar to the values of 6.9 and 5.4 kcal/mol with PBE/6-31+G(d,p). Despite the geometrical differences for the deprotonated structures mentioned above, B3LYP/aug-cc-pVTZ single-point calculations at DFTB3 geometries show excellent results for proton affinities, with the MAD value being <1 kcal/mol for both the Cu(I) and Cu(II) species.

5. Concluding Remarks

Transition-metal ions play various important biological functions, and their uncontrolled activities are also implicated in neurodegenerative diseases and aging. To help better understand the relevant mechanistic details, it is important to develop effective computational methodologies for metal coordination structure, dynamics, and chemistry. For the analysis of systems with considerable structural flexibility, efficient QM/MM methods that strike the proper balance between accuracy and computational efficiency are particularly valuable. Motivated by these considerations and encouraged by success in applications that involve main group elements and simple metal ions (e.g., zinc), we explore the applicability of the DFTB3 method to transition-metal ions in biomolecules.

We start by studying copper, which is important in biology and, in most cases, features only two oxidation states. We show that, by including the orbital angular momentum (l) dependence of the Hubbard parameter (U) and its charge dependence (U^d), we are able to parametrize DFTB3 for copper with largely balanced treatments for both Cu(I) and Cu(II) oxidation states; physically speaking, introducing the l dependence in U and U^d allows us to treat the different sizes of the 3d and 4s orbitals and their responses to change in the charge state. Other than the l dependence and explicit consideration of spin polarization, the parametrization of copper is done in a fashion largely consistent with that observed for other elements in the 3OB set. In particular, PBE is the functional and the reference method for the parametrization/calibration is B3LYP with the aug-cc-pVTZ basis. Although we recognize that these functionals generally are not the optimal choices for transition metals, the current “first generation” parametrization should be considered as encouraging, in that the structural and energetic properties outperform NDDO-based methods (e.g., PM6) for a fairly broad set of molecules of biological relevance. Indeed, even for the challenging cases of ligand binding energies of charged ligands, single-point B3LYP calculations at the DFTB3 structures give very small errors (∼1–2 kcal/mol) compared to the reference B3LYP values. Therefore, we expect that the current 3OB set of parameters are already highly valuable in many biological applications involving copper, especially as the method that drives the sampling of a dynamical copper binding site.

On the other hand, the benchmark calculations also help highlight several issues for the current DFTB3 methodology. For example, as we search for a reference QM method, the amount of exact exchange appears essential to the quality of the result, especially for energetics involving Cu(II); this is consistent with findings from the literature. Therefore, it seems essential to go beyond a GGA-based functional in DFTB3 for a reliable description of transition-metal ions; similar considerations have also been made for the calculation of electronically excited states using time-dependent DFTB.^110,111 Second, although B3LYP/aug-cc-PVTZ seems to be a reasonable choice for many Cu(I) and Cu(II) systems analyzed here (see Tables 1 and 2), the limitation of the method for transition metals generally is well-documented. With the limited amount of experimental data, it remains a challenge to establish the most reliable reference method for parametrization and calibration, although progress is being made;^76,82 in this context, embedding methods¹¹² might be useful for extending the size of benchmark systems that can be analyzed with highly correlated ab initio methods.

Another limitation of the current DFTB3 method is the use of a minimal basis, which significantly underestimates polarizability. This is likely one of the reasons why binding energies of charged ligands have systematically larger errors than neutral ligands. Improved description of polarization and charge transfer using chemical potential equilization^100,106 is of considerable interest as future developments. Finally, we note that the choice of several key parameters, such as the wave function compression radius and eigenvalue of 4p orbitals, are determined in a somewhat ad hoc fashion by monitoring the structures of several compounds. An alternative approach is to determine these parameters by directly comparing key electronic structure of copper–ligand interactions at the DFTB3 and reference QM levels in the framework of NBO analysis.¹⁰⁵ Such analysis might be particularly informative for ensuring the proper order of nearby spin states, which does not appear to be a serious issue for copper but has been documented as being problematic for DFTB2 applications to iron-containing systems.⁵⁴ Along this line, treating the charge fluctuations in the d-shell with m_l dependence, such as in the framework of ligand field theory,^32,33 might be required.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.5b00600.

• Additional details regarding molecular geometries and statistics for benchmark systems, as well as detailed derivations of the Kohn–Sham equations and gradient for the l-dependent spin-polarized DFTB3 model (PDF)

• Detailed calculation data for the benchmark sets discussed in the text (XLS)

The authors declare no competing financial interest.