Estimating Modifying Effect of Age on Genetic and Environmental Variance Components in Twin Models

Abstract

Twin studies have been adopted for decades to disentangle the relative genetic and environmental contributions for a wide range of traits. However, heritability estimation based on the classical twin models does not take into account dynamic behavior of the variance components over age. Varying variance of the genetic component over age can imply the existence of gene–environment (G × E) interactions that general genome-wide association studies (GWAS) fail to capture, which may lead to the inconsistency of heritability estimates between twin design and GWAS. Existing parametric G × E interaction models for twin studies are limited by assuming a linear or quadratic form of the variance curves with respect to a moderator that can, however, be overly restricted in reality. Here we propose spline-based approaches to explore the variance curves of the genetic and environmental components. We choose the additive genetic, common, and unique environmental variance components (ACE) model as the starting point. We treat the component variances as variance functions with respect to age modeled by B-splines or P-splines. We develop an empirical Bayes method to estimate the variance curves together with their confidence bands and provide an R package for public use. Our simulations demonstrate that the proposed methods accurately capture dynamic behavior of the component variances in terms of mean square errors with a data set of >10,000 twin pairs. Using the proposed methods as an alternative and major extension to the classical twin models, our analyses with a large-scale Finnish twin data set (19,510 MZ twins and 27,312 DZ same-sex twins) discover that the variances of the A, C, and E components for body mass index (BMI) change substantially across life span in different patterns and the heritability of BMI drops to ∼50% after middle age. The results further indicate that the decline of heritability is due to increasing unique environmental variance, which provides more insights into age-specific heritability of BMI and evidence of G × E interactions. These findings highlight the fundamental importance and implication of the proposed models in facilitating twin studies to investigate the heritability specific to age and other modifying factors.

TWIN studies have been broadly used as a tool to investigate heritability for decades. A recent comprehensive meta-analysis reported 17,804 heritability estimates for various traits based on twin studies (Polderman et al. 2015). Estimation methods and software such as structural equation modeling (SEM) based on the classical twin models consisting of additive genetic, common, and unshared environmental effects have been well established and extensively adopted (Rijsdijk and Sham 2002). Extensions for longitudinal data or time-to-event phenotypes based on the classical twin models have been proposed (Boomsma et al. 1989; Pitkäniemi et al. 2007). Nevertheless, one of the major issues posing potential challenge is that many twin data sets contain individuals across a wide range of age and the variances of genetic and environmental components for many complex traits such as body mass index (BMI) and height change over age (Lajunen et al. 2009; Elks et al. 2012) or birth cohorts (Silventoinen et al. 2000). For example, the variances of genetic and environmental components and thus the heritability of BMI have been found to diverge with age in a Finnish study of adolescent twins (Lajunen et al. 2009) and another of adolescents and young adults (Ortega-Alonso et al. 2012), implying that potential gene–environment (G × E) interactions play a notable role in these complex traits. During childhood when a twin pair is raised in a similar environment, the common environmental effects may be present in early childhood when children are dependent on their parents and then drop after midchildhood when they start to get more independence (Silventoinen et al. 2009). Unfortunately, relying on the classical twin models in these cases may lead to substantially biased results (Purcell 2002; Zyphur et al. 2013). In many studies, information on age at measurements is available for each twin pair, and ignoring how age potentially modifies the genetic and environmental variances would result in problematic estimates especially when age is distributed widely and considerably different between monozygotic (MZ) and dizygotic (DZ) twin samples.

The gap between the heritability estimated from twin studies and genome-wide association studies (GWAS), known as missing heritability, is observed for many complex traits, and so far little is known about its cause (Manolio et al. 2009; Eichler et al. 2010). As an example, compared with a heritability of from nearly 50% up to 80% estimated from different twin studies for BMI (Elks et al. 2012), thus far, a meta-analysis of multiple GWAS data sets has reported that 97 genome-wide significant loci account for <3% of the variance, while all common single-nucleotide polymorphisms (SNPs) account for ∼20% of the variance in which age has been adjusted for linearly (Locke et al. 2015) and ∼17 million variants account for around 27% of the variance (Yang et al. 2015). While literature has suggested that the fundamental assumption of additive genetics in GWAS might be problematic (Nelson et al. 2013), estimates of heritability from the perspective of twin design should also be refined or revised by taking into account moderators such as age. One of the causes for missing heritability probably lies in the G × E interactions. Increasing variance of the genetic component over age implies the existence of G × E interactions that general GWAS are not able to capture. Hence, it would be of vital concern to explore how the genetic and environmental components evolve and to estimate the variance curves on which there is no prior information available.

Exploration of dynamics of variance components over a period of growth by partitioning the phenotypic variance and covariance with quantitative genetic models can date back to W. Atchley in the early 1980s (Atchley and Rutledge 1980; Cheverud et al. 1983; Pletcher and Geyer 1999; Charmantier et al. 2006). Recently, approaches such as functional GWAS (fGWAS) have been proposed to explore time-varying genetic effects of SNPs by utilizing Legendre orthogonal polynomials and longitudinal data (Wu and Lin 2006; Das et al. 2011; Li and Sillanpää 2015). Different from fGWAS and its recent developments (Das et al. 2011; Li et al. 2015), which are based on a varying-coefficient model, in the case of twin study, we aim at modeling variance functions directly. One of the solutions is to divide samples into multiple strata and to estimate the variances within each stratum (Neale and Cardon 1992). The drawbacks of this strategy include that selection of cut points for strata is often unequivocal and difficult in some scenarios and twins measured at different ages are not always in the same strata. It may result in larger uncertainty of estimates due to reduced sample sizes in each stratum. Another option is to adopt an existing parametric G × E interaction model proposed by Purcell in which age can be modeled by adding a moderator in a linear or quadratic form (Purcell 2002). Unfortunately, the variance curves to be estimated in many cases are not necessarily linear or quadratic. Their patterns can often be fluctuant and dramatically change across life span as shown later in this study. A concrete parametric model is often difficult to determine beforehand. Hence, a nonparametric approach to explore the variance curves of these components can give more realistic understanding on the pattern of the moderating effect provided that the number of estimated parameters is not too large. Most recently, Briley et al. (2015) introduced local structural equation modeling (LOSEM), which estimates G × E interactions using a nonparametric approach based on LOWESS and SEM.

The past two decades have seen rapid advances of employing B-splines, particularly penalized B-splines (P-splines) (O’Sullivan 1986; Eilers and Marx 1996), to estimate an unknown function in the context of epidemiology. With the same advantages of the flexibility as LOSEM, P-splines can further optimally choose the best model by penalizing the smoothness and perform various hypothesis tests (Ruppert et al. 2003). In this work, we propose novel twin models that choose as the starting point the standard twin model based on decomposing total variance into the variance components of additive genetics (A), common environment (C), and unique environment (E) (a.k.a. the ACE model). We generalize the component variances as variance functions with respect to age by using B-splines or P-splines in which the ACE model becomes the special case when all spline coefficients within the components share the same value. We construct expectation-maximization (EM) and Markov chain Monte Carlo (MCMC) algorithms to estimate the variance functions together with their pointwise confidence bands and construct an R package based on these models. We then show through simulation studies and a real data analysis that the proposed models along with the estimation are well behaved and are capable of depicting a refined picture of dynamic behavior of the component variances, which provides more insights into the age-specific heritability. Our results from the analysis of a Finnish twin data set indicate that there exist remarkable age-dependent effects on all A, C, and E components for BMI and age should be taken into account when estimating the heritability of BMI.

Methods

Suppose that we have observed zero-mean normally distributed quantitative phenotypic data $Y_M$ (an $n_M\times 1$ vector) and $Y_D$ (an $n_D\times 1$ vector) for $f_M\left(=n_M/2\right)$ MZ and $f_D\left(=n_D/2\right)$ DZ twin pairs, respectively. The phenotypes of each twin pair are measured at the same age $T_M$ (an $f_M\times 1$ vector) and $T_D$ (an $f_D\times 1$ vector). An example of the observed data format is shown in Table 1.

Table 1. An example of the data format used for model specification.

MZ twins			DZ twins
Twin ID	Trait	Age	Twin ID	Trait	Age
1	$Y_{M(1)}$	$T_{M(1)}$	1	$Y_{D(1)}$	$T_{D(1)}$
1	$Y_{M(2)}$		1	$Y_{D(2)}$
2	$Y_{M(3)}$	$T_{M(2)}$	2	$Y_{D(3)}$	$T_{D(2)}$
2	$Y_{M(4)}$		2	$Y_{D(4)}$
$f_M$	$Y_{M(n_M-1)}$	$T_{M(f_M)}$	$f_D$	$Y_{D(n_D-1)}$	$T_{D(f_D)}$
$f_M$	$Y_{M(n_M)}$		$f_D$	$Y_{D(n_D)}$

According to the ACE model, we have a random effect model $Y_{M(i_M,j)}=a_{M(i_M)}+c_{M(i_M)}+e_{(i_M,j)}$ for the MZ twin pair $i_M$ and a model $Y_{D(i_D,j)}=a_{1D(i_D)}+a_{2D(i_D,j)}+c_{D(i_D)}+e_{(i_D,j)}$ for the DZ twin pair $i_D,$ where $i_M\in \left\{1,\dots ,f_M\right\},$ $i_D\in \left\{1,\dots ,f_D\right\},$ and $j=1,2.$ Here we assume that $a_M\sim \mathcal{N}\left(0,\mathbf{ }{\sigma }_{\mathrm{a}}^2\right),$ $a_{1D},a_{2D}\sim \mathcal{N}\left(0, 0.5{\sigma }_{\mathrm{a}}^2\right),$ $c_M,c_D\sim \mathcal{N}\left(0,\mathbf{ }{\sigma }_{\mathrm{c}}^2\right),$ and $e\sim \mathcal{N}\left(0,\mathbf{ }{\sigma }_{\mathrm{e}}^2\right),$ where ${\sigma }_{\mathrm{a}}^2,$ ${\sigma }_{\mathrm{c}}^2,$ and ${\sigma }_{\mathrm{e}}^2\in (0,+\mathrm{\infty })$ are the additive genetic, common, and unique environmental components, respectively. Thus, this model implies that the phenotypes follow the following normal distribution,

$$\left(\begin{array}{c}{\mathbf{Y}}_M\\ {\mathbf{Y}}_D\end{array}\right)\sim \mathcal{N}\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\mathbf{ }\left(\begin{array}{cc}{\mathbf{\Sigma }}_M& 0\\ 0& {\mathbf{\Sigma }}_D\end{array}\right)\right),$$ (1)

where${\mathbf{\Sigma }}_M={\sigma }_{\mathrm{a}}^2{\mathbf{1}}_B^M+{\sigma }_{\mathrm{c}}^2{\mathbf{1}}_B^M+{\sigma }_{\mathrm{e}}^2\mathbf{I}$ (an $n_M\times n_M$ matrix), ${\mathbf{\Sigma }}_D={\sigma }_{\mathrm{a}}^2\mathbf{A}+{\sigma }_{\mathrm{c}}^2{\mathbf{1}}_B^D+{\sigma }_{\mathrm{e}}^2\mathbf{I}$ (an $n_D\times n_D$ matrix), ${\mathbf{1}}_B^M={\mathbf{I}}_{f_M}\otimes {\mathbf{1}}_2,$ ${\mathbf{1}}_B^D={\mathbf{I}}_{f_D}\otimes {\mathbf{1}}_2,$ and $\mathbf{A}={\mathbf{I}}_{f_D}\otimes {\mathbf{A}}_2,$ where ${\mathbf{1}}_2=\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right),$ ${\mathbf{A}}_2=\left(\begin{array}{cc}1& 0.5\\ 0.5& 1\end{array}\right),$ and ⊗ represents the Kronecker product.

Estimation of variance curves using B-splines

We first propose a nonparametric approach, referred to as an ACE(t) model, to estimate the variance curves of the additive genetic and common environmental components using B-splines (de Boor 1978) with a set of evenly distributed knots. We assume that the A and C variances are represented at each time point with their own parameters as follows:

$${\sigma }_{\mathrm{a}}^2\left(t\right), {\sigma }_{\mathrm{c}}^2\left(t\right), t=1,\dots ,T.$$ (2)

Note that at this stage we assume ${\sigma }_{\mathrm{e}}^2\left(t\right)={\sigma }_{\mathrm{e}}^2$ to be constant over time although including an age-dependent unique environmental component can be readily extended. Instead of trying to estimate ${\sigma }_{\mathrm{a}}^2\left(t\right)$ [or ${\sigma }_{\mathrm{c}}^2\left(t\right)$] separately at each time point, we assume that values at adjacent time points are more alike; that is, they can be described as a smooth curve over time. First, values in (2) are expressed using linear combinations of B-spline basis functions as

$${\sigma }_{\mathrm{a}}^2\left(t\right)=e^{{\displaystyle {\sum }_{k=1}^K{\beta }_k^{\mathrm{A}}{B}_k^{\mathrm{A}}\left(t\right)}}$$

and

$${\sigma }_{\mathrm{c}}^2\left(t\right)=e^{{\displaystyle {\sum }_{l=1}^L{\beta }_l^{\mathrm{C}}{B}_l^{\mathrm{C}}\left(t\right)}},$$

where ${\mathbf{\beta }}^{\mathrm{A}}\in {\left(-\mathrm{\infty },+\mathrm{\infty }\right)}^K$ and ${\mathbf{\beta }}^{\mathrm{C}}\in {\left(-\mathrm{\infty },+\mathrm{\infty }\right)}^L$ are the vectors of coefficients. We select K and L B-spline basis functions for the A and C components, respectively. We choose the B-spline basis functions ${\mathbf{B}}^{\mathrm{A}}(t)$ and ${\mathbf{B}}^{\mathrm{C}}(t)$ with a degree $p=2$ (or an order of 3) for the following simulation and real data analyses. The degree $p=2$ is probably appropriate for most traits as the variance curves of the A and C components are generally smooth and do not change sharply within a small age interval. Thus, the numbers of knots for construction of the B-splines for the A and C components are $K+p+1$ and $L+p+1.$ Replacing the variances ${\sigma }_{\mathrm{a}}^2$ and ${\sigma }_{\mathrm{c}}^2$ in the model (1) with their time-dependent counterparts ${\sigma }_{\mathrm{a}}^2\left(t\right)$ and ${\sigma }_{\mathrm{c}}^2\left(t\right)$ leads to the covariance matrices

$${\mathbf{\Sigma }}_M=\mathrm{diag}\left(e^{{\mathbf{B}}_{T_M}^{\mathrm{A}}{\mathbf{\beta }}^{\mathrm{A}}}\right)\otimes {\mathbf{1}}_2+\mathrm{diag}\left(e^{{\mathbf{B}}_{T_M}^{\mathrm{C}}{\mathbf{\beta }}^{\mathrm{C}}}\right)\otimes {\mathbf{1}}_2+{\sigma }_{\mathrm{e}}^2\mathbf{I},$$

$${\mathbf{\Sigma }}_D=\mathrm{diag}\left(e^{{\mathbf{B}}_{T_D}^{\mathrm{A}}{\mathbf{\beta }}^{\mathrm{A}}}\right)\otimes {\mathbf{A}}_2+\mathrm{diag}\left(e^{{\mathbf{B}}_{T_D}^{\mathrm{C}}{\mathbf{\beta }}^{\mathrm{C}}}\right)\otimes {\mathbf{1}}_2+{\sigma }_{\mathrm{e}}^2\mathbf{I},$$

where ${\mathbf{B}}_{T_M}^{\mathrm{A}},$ ${\mathbf{B}}_{T_M}^{\mathrm{C}},$ ${\mathbf{B}}_{T_D}^{\mathrm{A}},$ and ${\mathbf{B}}_{T_D}^{\mathrm{C}}$ are $f_M\times K,$ $f_M\times L,$ $f_D\times K,$ and $f_D\times L$ design matrices of the B-spline basis functions evaluated at $T_M$ and $T_D$ for the MZ and DZ twins and $\mathrm{diag}(.)$ converts a vector to a diagonal matrix with the vector entries as its diagonal elements. The model becomes the classical ACE model when the coefficients share the same value within ${\mathbf{\beta }}^{\mathrm{A}}$ and ${\mathbf{\beta }}^{\mathrm{C}},$ respectively. The estimates $\left(\widehat{{\mathbf{\beta }}^{\mathrm{A}}},\widehat{{\mathbf{\beta }}^{\mathrm{C}}}\right)$ can be obtained using maximum-likelihood estimation (MLE), and the variance curves ${\sigma }_{\mathrm{a}}^2\left(t\right)$ and ${\sigma }_{\mathrm{c}}^2\left(t\right)$ are estimated by $\widehat{{\sigma }_{\mathrm{a}}^2}\left(t\right)=e^{{\displaystyle {\sum }_{k=1}^K\widehat{{\beta }_k^{\mathrm{A}}}{B}_k^{\mathrm{A}}\left(t\right)}}$ and $\widehat{{\sigma }_{\mathrm{c}}^2}\left(t\right)=e^{{\displaystyle {\sum }_{l=1}^L\widehat{{\beta }_l^{\mathrm{c}}}{B}_l^{\mathrm{C}}\left(t\right)}}.$ The detailed derivation of the MLE for the ACE(t) model is described in the Appendix.

The pointwise (not simultaneous) confidence bands for the ACE(t) model can be constructed from a Delta method as previously described (Rosenberg 1995; Mao and Zhao 2003). In this case, according to the Delta method the estimates $\widehat{{\sigma }_{\mathrm{a}}^2}\left(t\right)$ and $\widehat{{\sigma }_{\mathrm{c}}^2}\left(t\right)$ at the time point t follow normal distributions with the variances approximated by $\widehat{\mathrm{Var}}\left(e^{{\displaystyle {\sum }_{k=1}^K\widehat{{\beta }_k^{\mathrm{A}}}{B}_k^{\mathrm{A}}\left(t\right)}}\right)=e^{2\mathrm{·}{\displaystyle {\sum }_{k=1}^K\widehat{{\beta }_k^{\mathrm{A}}}{B}_k^{\mathrm{A}}\left(t\right)}}\mathrm{·}\left({\mathbf{B}}^{\mathrm{A}}(t{)}^{\prime }{\tilde{{\mathbf{H}}_{{\mathbf{\beta }}^{\mathrm{A}}}}}^{-1}{\mathbf{B}}^{\mathrm{A}}(t)\right)$ and $\widehat{\mathrm{Var}}\left(e^{{\displaystyle {\sum }_{l=1}^L\widehat{{\beta }_l^{\mathrm{C}}}{B}_l^{\mathrm{C}}\left(t\right)}}\right)=e^{2\mathrm{·}{\displaystyle {\sum }_{l=1}^L\widehat{{\beta }_l^{\mathrm{c}}}{B}_l^{\mathrm{C}}\left(t\right)}}\mathrm{·}\left({\mathbf{B}}^{\mathrm{C}}(t{)}^{\prime }{\tilde{{\mathbf{H}}_{{\mathbf{\beta }}^{\mathrm{C}}}}}^{-1}{\mathbf{B}}^{\mathrm{C}}(t)\right),$ where ${\tilde{H}}^{-1}$ is the inverse of the estimated Fisher information from the MLE (i.e., the inverse of the Hessian of the negative log-likelihood). The confidence bands can also be estimated using a bootstrap method that is more computationally intensive than the Delta method. A parametric bootstrapping can be performed by first generating the bootstrap phenotypes $\left(Y_M^{\ast }, Y_D^{\ast }\right)$ based on model (1) with the parameters replaced by their estimates $\left(\widehat{{\mathbf{\beta }}^{\mathrm{A}}},\widehat{{\mathbf{\beta }}^{\mathrm{C}}},\widehat{{\sigma }_{\mathrm{e}}^2}\right)$ and fitting the model to obtain the bootstrap replicates $\left(\widehat{{\mathbf{\beta }}^{\mathrm{A}}}\ast ,\widehat{{\mathbf{\beta }}^{\mathrm{C}}}\ast ,\widehat{{\sigma }_{\mathrm{e}}^2}\ast \right)$ from which the confidence bands at the time point t can be derived (Efron and Tibshirani 1994).

Stable estimation of variance curves, using penalized splines

While the estimation and implementation of the ACE(t) model are straightforward and fast, the performance of using B-splines in practice is sensitive to the selection of the number of knots. Fewer knots suffer from large uncertainty while excessive knots can lead to overfitting. A handful of procedures for automatic knot selection have been developed; however, they are generally quite complicated and computationally intensive as pointed out by Ruppert et al. (2003), especially in the context of variance curve estimation based on large-scale twin data. One preferable way is to retain abundant knots and penalize their roughness, which is described as follows.

To reduce the impact of the number of knots, we therefore propose a more stable model using P-splines (O’Sullivan 1986), which we refer to as an ACE(t)-p model. As previously shown, the number of knots in P-splines has small influence on the results and it has been suggested that at most 35–40 knots are generally enough for all sample sizes and for all smooth functions without too many oscillations (Ruppert 2002). We first parameterize the ACE model with three random effects to decompose the covariance matrices and write the subsequent derivations in a matrix form. Specifically, we let ${\mathit{Z}}_{2M}={\mathit{Z}}_{3M}={\mathit{I}}_{f_M}\otimes {\mathbf{1}}_{2\times 1},$ ${\mathit{Z}}_{1D}=\sqrt{0.5}{\mathit{I}}_{n_D},$ ${\mathit{Z}}_{2D}=\sqrt{0.5}{\mathit{I}}_{f_D}\otimes {\mathbf{1}}_{2\times 1},$ and ${\mathit{Z}}_{3D}={\mathit{I}}_{f_D}\otimes {\mathbf{1}}_{2\times 1}$ so that ${\mathit{Z}}_{2M}{{\mathit{Z}}^{\prime }}_{2M}={\mathit{Z}}_{3M}{{\mathit{Z}}^{\prime }}_{3M}={\mathbf{1}}_B^M,$ ${\mathit{Z}}_{3D}{{\mathit{Z}}^{\prime }}_{3D}={\mathbf{1}}_B^D,$ and ${\mathit{Z}}_{1D}{{\mathit{Z}}^{\prime }}_{1D}+{\mathit{Z}}_{2D}{{\mathit{Z}}^{\prime }}_{2D}=\mathit{A},$ where ${\mathbf{1}}_{2\times 1}=\left(\begin{array}{c}1\\ 1\end{array}\right).$ According to the first type of parameterization proposed by Rabe-Hesketh et al. (2008) and following the notation of the spline coefficients and design matrices in the ACE(t) model, the covariance matrices are expressed as

$${\mathbf{\Sigma }}_M={\mathit{Z}}_{2M}diag\left(e^{{\mathit{B}}_{T_M}^A{\mathit{\beta }}^A}\right){{\mathit{Z}}^{\prime }}_{2M}+{\mathit{Z}}_{3M}diag\left(e^{{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C}\right){{\mathit{Z}}^{\prime }}_{3M}+{\sigma }_e^2\mathit{I},$$

$${\mathbf{\Sigma }}_D={\mathit{Z}}_{1D}diag\left(e^{{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\otimes {\mathbf{1}}_{2\times 1}\right){{\mathit{Z}}^{\prime }}_{1D}+{\mathit{Z}}_{2D}diag\left(e^{{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\right){{\mathit{Z}}^{\prime }}_{2D}+{\mathit{Z}}_{3D}diag\left(e^{{\mathit{B}}_{T_D}^C{\mathit{\beta }}^C}\right){{\mathit{Z}}^{\prime }}_{3D}+{\sigma }_e^2\mathit{I}.$$

The approach using P-splines imposes two penalties on ${\mathit{\beta }}^A$ and ${\mathit{\beta }}^C,$ respectively. We add the quadratic penalties ${\lambda }_A{\mathit{\beta }}^A{}^{\prime }{\mathit{D}}_A{\mathit{\beta }}^A$ and ${\lambda }_C{\mathit{\beta }}^C{}^{\prime }{\mathit{D}}_C{\mathit{\beta }}^C$ to the log-likelihood,

$$\left(-2\right)l_{psp}\left({\sigma }_e^2,{\mathit{\beta }}^A,{\mathit{\beta }}^C\right)=\log \left|{\mathbf{\Sigma }}_M\right|+{{\mathit{Y}}^{\prime }}_M {\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M+\log \left|{\mathbf{\Sigma }}_D\right|+{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D+{\lambda }_A{\mathit{\beta }}^A{}^{\prime }{\mathit{D}}_A{\mathit{\beta }}^A+{\lambda }_C{\mathit{\beta }}^C{}^{\prime }{\mathit{D}}_C{\mathit{\beta }}^C,$$

where ${\mathit{D}}_A$ and ${\mathit{D}}_C$ are the penalty matrices constructed from differences between neighboring coefficients according to Eilers and Marx (1996) (refer to the Appendix for the contents of ${\mathit{D}}_A$ and ${\mathit{D}}_C$). The penalizing coefficients ${\lambda }_{\mathrm{A}}$ and ${\lambda }_{\mathrm{C}}$ substantially affect the estimation results, and many strategies of selecting their values have been proposed, including generalized cross-validation (Craven and Wahba 1978) and Akaike’s information criterion (Akaike 1969). P-splines in Bayesian models may be implemented via variational Bayes estimation (Li and Sillanpää 2013) and MCMC methods (Crainiceanu et al. 2005). On the other hand, under a framework of a random effects model, quadratic penalty terms can be regarded as assuming the following zero-mean normal distributions to the spline coefficients

$${\mathit{\beta }}^A\sim \mathcal{N}\left(0,{\sigma }_{{\beta }^A}^2{\mathit{D}}_A^{-}\right),\hspace{1em}{\mathit{\beta }}^C\sim \mathcal{N}\left(0,{\sigma }_{{\beta }^C}^2{\mathit{D}}_C^{-}\right),$$ (3)

where ${\sigma }_{{\beta }^A}^2=1/{\lambda }_A,$ ${\sigma }_{{\beta }^C}^2=1/{\lambda }_C,$ and ${\mathit{D}}_A^{-},$ ${\mathit{D}}_C^{-}$ are the generalized inverses of ${\mathit{D}}_A$ and ${\mathit{D}}_C.$ Expression (3) provides a connection to estimation of variance components by restricted maximum likelihood (REML) in a linear mixed-model context (Ruppert et al. 2003). To estimate $\mathit{\beta }=\left({\mathit{\beta }}^A,{\mathit{\beta }}^C\right),$ we follow a strategy adopted by Kauermann and Wegener (2011) that first estimates $\left({\sigma }_{{\beta }^A}^2, {\sigma }_{{\beta }^C}^2\right)$ by using a marginal likelihood with the spline coefficients β integrated out analytically. Based on this strategy, Krivobokova proposed a unified EM-type iterative procedure (Krivobokova et al. 2008) to estimate the spline coefficients and the penalizing coefficients (now transformed to the variances of random effects in the linear mixed model) simultaneously by estimating the spline coefficients through an iterated weighted least-squares (IWLS) algorithm and employing an approximation algorithm (Breslow and Clayton 1993) to iterate between the estimation of the spline coefficients and minimization of the marginal log-likelihood. More specifically, following the same spirit, the marginal likelihood in our case is

$$L_{psp}\left({\sigma }_e^2,{\sigma }_{{\beta }^A}^2,{\sigma }_{{\beta }^C}^2\right)=\frac{1}{{\sigma }_{{\beta }^A}^{\tilde{K}}{\sigma }_{{\beta }^C}^{\tilde{L}}}\underset{}{\overset{}{{\displaystyle \mathrm{\iint }}}}\frac{1}{{\left|{\mathbf{\Sigma }}_M\right|}^{1/2}{\left|{\mathit{\Sigma }}_D\right|}^{1/2}}{e}^{-\left(1/2\right)\left[ {\mathit{Y}}_M^{\prime }{\mathit{\Sigma }}_M^{-1}{\mathit{Y}}_M+{\mathit{Y}}_M^{\prime }{\mathit{\Sigma }}_D^{-1}{\mathit{Y}}_D+{\mathit{\beta }}^{A\prime }{\mathit{D}}_A{\mathit{\beta }}^A/{\sigma }_{{\beta }^A}^2+{\mathit{\beta }}^C{}^{\prime }{\mathit{D}}_C{\mathit{\beta }}^C/{\sigma }_{{\beta }^C}^2\right]}d{\mathit{\beta }}^{A}d{\mathit{\beta }}^C,$$ (4)

where $\tilde{K}$ and $\tilde{L}$ are the numbers of positive eigenvalues of ${\mathbf{D}}_{\mathrm{A}}$ and ${\mathbf{D}}_{\mathrm{C}}.$ By applying a Laplace approximation to the integrand of (4) with the condition of $K, L\ll n_M+n_D,$ we obtain the −2 log-likelihood

$$\left(-2\right)l_{psp}\left({\sigma }_e^2,{\sigma }_{{\beta }^A}^2,{\sigma }_{{\beta }^C}^2\right)=\tilde{K}\log {\sigma }_{{\beta }^A}^2+\tilde{L}\log {\sigma }_{{\beta }^C}^2+\log \left|{\mathbf{\Sigma }}_M\left\{\widehat{\mathit{\beta }}\right\}\right|+{{\mathit{Y}}^{\prime }}_M {\mathbf{\Sigma }}_M^{-1}\left\{\widehat{\mathit{\beta }}\right\}{\mathit{Y}}_M+\log \left|{\mathbf{\Sigma }}_D\left\{\widehat{\mathit{\beta }}\right\}\right|+{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}\left\{\widehat{\mathit{\beta }}\right\}{\mathit{Y}}_D+\frac{\widehat{{\mathit{\beta }}^A{}^{\prime }}{\mathit{D}}_A\widehat{{\mathit{\beta }}^A}}{{\sigma }_{{\beta }^A}^2}+\frac{\widehat{{\mathit{\beta }}^C{}^{\prime }}{\mathit{D}}_C\widehat{{\mathit{\beta }}^C}}{{\sigma }_{{\beta }^C}^2}+\log \left|g^{″}\left(\widehat{\mathit{\beta }}\right)\right|,$$

where

$$g\left(\mathit{\beta }\right)=\left(1/2\right)\left(\log \left|{\mathbf{\Sigma }}_M\right|+{{\mathit{Y}}^{\prime }}_M {\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M+\log \left|{\mathbf{\Sigma }}_D\right|+{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D+{\mathit{\beta }}^A{}^{\prime }{\mathit{D}}_A{\mathit{\beta }}^A/{\sigma }_{{\beta }^A}^2+{\mathit{\beta }}^C{}^{\prime }{\mathit{D}}_C{\mathit{\beta }}^C/{\sigma }_{{\beta }^C}^2\right),$$

$\left\{\widehat{\mathit{\beta }}\right\}$ represents the replacement of β at $\widehat{\mathit{\beta }}$ in the covariance matrices, and $\widehat{\mathit{\beta }}$ is evaluated to minimize $g\left(\mathit{\beta }\right).$ Instead of IWLS in Krivobokova et al. (2008), we use the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm (Byrd et al. 1995), which does not require evaluating a Hessian matrix explicitly. The following algorithm computes $\widehat{\mathit{\beta }}$ together with $\left(\widehat{{\sigma }_{{\beta }^A}^2}, \widehat{{\sigma }_{{\beta }^C}^2}\right)$ in an iterative way:

1. Give initial values to $\left({\widehat{{\sigma }_e^2}}^{\left(1\right)},{\widehat{{\sigma }_{{\beta }^A}^2}}^{\left(1\right)},{\widehat{{\sigma }_{{\beta }^C}^2}}^{\left(1\right)}\right).$

2. Given the values of $\left({\widehat{{\sigma }_e^2}}^{\left(i-1\right)},{\widehat{{\sigma }_{{\beta }^A}^2}}^{\left(i-1\right)},{\widehat{{\sigma }_{{\beta }^C}^2}}^{\left(i-1\right)}\right)$ from the previous iteration, we find $\left({\widehat{{\mathit{\beta }}^A}}^{\left(i\right)},{\widehat{{\mathit{\beta }}^C}}^{\left(i\right)}\right),$ minimizing $g\left(\mathit{\beta }\right)$ by using the L-BFGS algorithm.

3. We find $\left({\widehat{{\sigma }_e^2}}^{\left(i\right)},{\widehat{{\sigma }_{{\beta }^A}^2}}^{\left(i\right)},{\widehat{{\sigma }_{{\beta }^C}^2}}^{\left(i\right)}\right),$ minimizing $\left(-2\right)l_{psp}\left({\sigma }_e^2,{\sigma }_{{\beta }^A}^2,{\sigma }_{{\beta }^C}^2\right)$ by using the L-BFGS algorithm with $\left({\widehat{{\mathit{\beta }}^A}}^{\left(i\right)},{\widehat{{\mathit{\beta }}^C}}^{\left(i\right)}\right)$ obtained from step 2.

4. Iterate between steps 2 and 3 until convergence.

The details of the derivation for the algorithm are given in the Appendix.

While the proposed algorithm provides a type of estimate for β, the construction of confidence intervals (C.I.’s) is far from straightforward. It has been pointed out that general bootstrap methods for the C.I.’s are overly narrow because they include only variance but not bias, which is substantial in the penalized estimation (Goeman 2010). The C.I.’s constructed under the mixed-model framework or the posterior distribution overcome this issue (Wood 2006; Kauermann et al. 2009). Recall that a best prediction (BP) for random effects in the linear mixed model is defined as the mean of the posterior distribution of random effects given data and the variances (Searle et al. 2009). This does not naturally apply to $\widehat{\mathit{\beta }}$ as the estimated spline coefficient $\widehat{\mathit{\beta }}$ from the above algorithm is the mode of the joint distribution of $\mathit{Y}=({\mathit{Y}}_M, {\mathit{Y}}_D)$ and β rather than a mean $\check{\mathit{\beta }},$ which minimizes the mean square error (MSE) of prediction (Searle et al. 2009). Unlike the best linear unbiased predictions (BLUPs) in the linear mixed model (Henderson 1975; Robinson 1991), the posterior mean $\check{\mathit{\beta }}$ in our case is not a linear function of Y because β is in the variance functions. Thus, we propose an MCMC method to numerically approximate the posterior distribution to obtain $\check{\mathit{\beta }},$ which is the estimated (or empirical) BP of β with $\left(\widehat{{\sigma }_e^2},\widehat{{\sigma }_{{\beta }^A}^2},\widehat{{\sigma }_{{\beta }^C}^2}\right)$ plugged in. From the Bayesian perspective, $\check{\mathit{\beta }}$ is an empirical Bayes predictor of β (Carlin and Louis 1997). Then the C.I.’s can be derived either from the conditional MSE of prediction obtained from the posterior distribution of β approximated by the MCMC method or from the marginal prediction error covariance matrix $Var\left(\check{\beta }-\mathit{\beta }\right)$ (Booth and Hobert 1998; Skrondal and Rabe-Hesketh 2009), which can be estimated by a parametric bootstrap method. The detailed description of how to construct C.I.’s is given in the Appendix.

Implementation and extension

We developed an R package “ACEt” to implement the proposed models for public use (https://r-forge.r-project.org/R/?group_id=2167). One of the attractive points is that both models can be readily implemented using existing R functions. We utilized the “splines” R package for computing the B-spline design matrices and the “optim” R function to perform the minimizations in which the L-BFGS algorithm with box bounds is used. Although the L-BFGS algorithm does not evaluate the Hessian matrices explicitly, the matrix operations would be time consuming and even impractical when thousands of samples are involved. The situation is particularly exacerbated as the twin models often require a larger sample size to obtain a reliable estimate of the variances. Fortunately, as most of the matrices are sparse and block diagonal, we dramatically reduce the running time by partitioning the matrix operations twin-wisely and implementing the optimization functions in C++.

Our proposed models can be easily modified and extended to handle other twin models such as the AE and CE models. We can also estimate the variance curve of the unique environmental component together with the other components. For example, both variances in the AE model can vary over age, which we refer to as the AE(t) and AE(t)-p models. These models have been implemented and included in the ACEt R package. Their application is demonstrated in the following Finnish BMI twin study.

Data availability

The simulation data is included as an example dataset in the R package.

Results

Simulation study

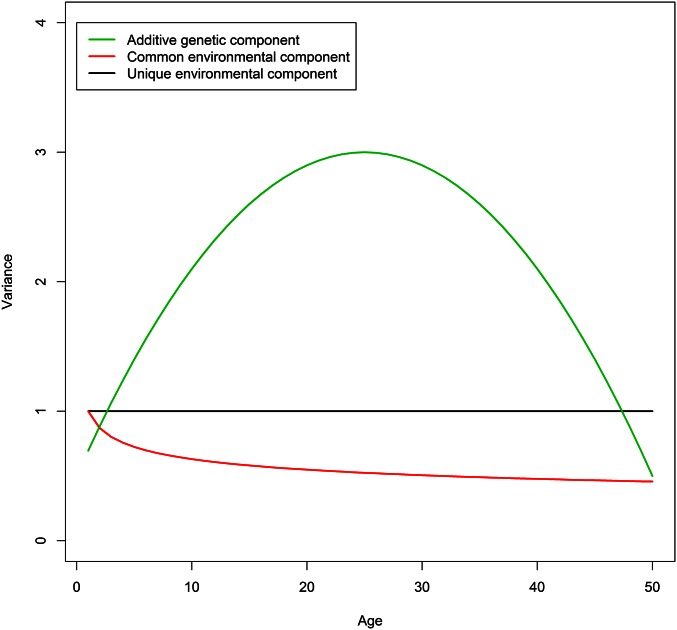
We performed two simulation studies with different sample sizes to provide a rough picture of how many twin pairs are needed for reliable estimates. In these simulations, we also compared the performance among the ACE(t) models with 5 and 8 interior knots and the ACE(t)-p models with 8 and 12 interior knots. We generated phenotypic data for 5000 MZ and 5000 DZ twin pairs in the first simulation and twofold sample sizes in the second one, using R. We first sampled a vector of age T for the twin pairs that was uniformly distributed from 1 to 50. We fixed the variance of the E component at 1 and chose the following quadratic and power variance functions for the A and C components,

$${\sigma }_a^2\left(T\right)=3-10{\left(\frac{T-25}{50}\right)}^2,$$

$${\sigma }_c^2\left(T\right)=T^{-0.2},$$

of which the shapes are depicted in Figure 1. We then simulated the phenotypic data by sampling from bivariate normal distributions based on Equation 1 with ${\sigma }_{\mathrm{a}}^2(T)$ and ${\sigma }_{\mathrm{c}}^2(T)$ plugged into the covariance matrices. The average mean square error (AMSE), which is defined as $AMS{E}_{a,c}=\frac{1}{m}{\displaystyle \sum }_{i=1}^m{\left({\sigma }_{a,c}^2\left(t_i\right)-\widehat{{\sigma }_{a,c}^2\left(t_i\right)}\right)}^2$ and takes into account both bias and variance, was used to evaluate the performance of estimation where we chose the number of evaluated time points $m=500.$ In each scenario, we simulated 200 data sets and fitted them with the proposed ACE(t) and ACE(t)-p models to calculate the AMSEs. For the ACE(t) model, we ran an additional analysis to compare the confidence bands obtained from the Delta method and the bootstrap method with 200 replicates.

Figure 1.

Variance functions of the A, C, and E components investigated in the simulation study.

The results presented in Table 2 show that the AMSEs of the ACE(t) model with 8 knots are larger than those with 5 knots for both components. This suggested that 8 knots seemed excessive and could worsen the performance in terms of AMSE for the relatively smooth functions that we chose to investigate here. In contrast, the ACE(t)-p model had smaller AMSEs than the ACE(t) model in all scenarios, confirming its superiority of tuning the penalty term for optimal estimation as long as a sufficient number of knots is given (Ruppert et al. 2003). The ASMEs from the ACE(t)-p model with a different number of knots were more similar to each other, implying that the estimates from P-splines are much less affected by the choice of knots than those from B-splines. The smaller number of knots in the penalized spline estimator performs better in terms of AMSE, which is in accordance with a previous theoretical finding (Claeskens et al. 2009). The AMSEs decreased almost linearly with increasing sample size in all situations; however, accurate estimates still entailed thousands of twin pairs.

Table 2. The empirical AMSE from the ACE(t) and ACE(t)-p models.

Component	ACE(t) ($5\hspace{0.5em}\text{knots}$)	ACE(t) ($8\hspace{0.5em}\text{knots}$)	ACE(t)-p ($8\hspace{0.5em}\text{knots}$)	ACE(t)-p (12 knots)
$n=20,000$
Additive genetic	0.04020788	0.05683567	0.0290397	0.03235355
Common environmental	0.03416853	0.05224053	0.01837206	0.02278777
$n=40,000$
Additive genetic	0.01770024	0.02705611	0.01339244	0.01574035
Common environmental	0.01588659	0.02550069	0.009042152	0.01346567

The confidence bands from the Delta method were comparable to those from the bootstrap method for both components as plotted in Figure 2. The confidence bands estimated from the bootstrap method were less smooth due to the limited number of resampling (i.e., 200 replicates), which should be adequate for the bootstrap method (Efron and Tibshirani 1994). The confidence bands from these two methods almost coincided, suggesting that the L-BFGS algorithm worked properly as a faster alternative to Newton’s method in this case.

Figure 2.

Confidence bands constructed from the Delta and bootstrap methods for the A (shown in A) and C (shown in B) components.

A Finnish twin study of BMI

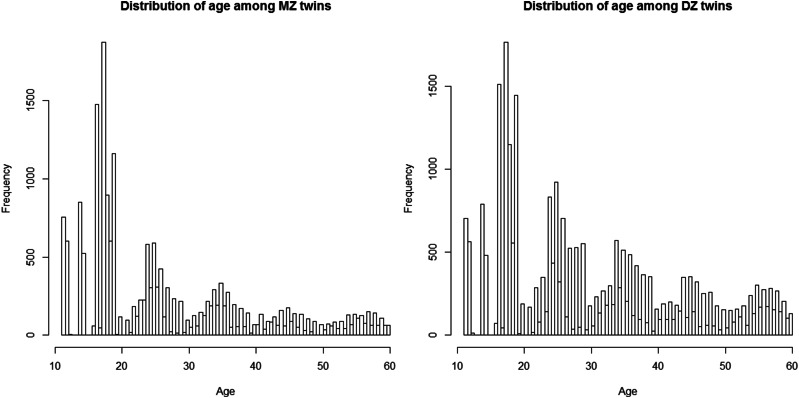
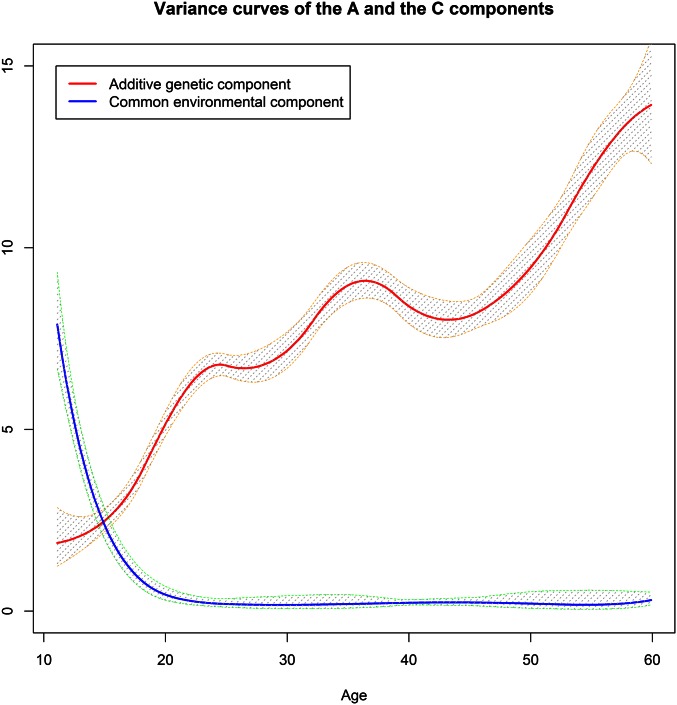
We applied both models to a twin data set retrieved from the Finnish Twin Cohort study to investigate age-dependent genetic and environmental components of BMI. The details on collection of the data were described in previous publications for older (Kaprio and Koskenvuo 2002) and younger cohorts (Kaprio et al. 2002). In this analysis, we included 19,510 MZ and 27,312 DZ same-sex twin individuals together with the information on age at the measurement contributed to the CODATwins project (Silventoinen et al. 2015). The distributions of age at the measurement among the MZ and DZ twins were widespread from 11 years to 60 years as shown in Figure 3. We fitted the data set with a linear regression on sex and age before using the residuals from the regression as the phenotypes for the analysis of variance curves. The variance curves of the genetic and common environmental components estimated from the ACE(t) (with 5 interior knots for either component) and the ACE(t)-p models (with 8 interior knots for either component) are shown in Figure 4 and Figure 5. For the ACE(t)-p model, we included more knots to ensure they were sufficient and excessive knots were affected little in terms of AMSE. The 95% pointwise confidence bands were obtained by using the bootstrap method for the ACE(t) model and the MCMC method described in the Appendix for the ACE(t)-p model. The comparable results from both models suggested that the variance of the additive genetic component started from ∼2 at age 11 years and increased rapidly until age 35 years. After that, it leveled off for ∼10 years before growing again to nearly 15, except that the curve from the ACE(t)-p model had more fluctuations. In contrast, the variance of the common environmental component starting at ∼8 at age 11 years dropped markedly before age 20 years and became almost undetectable after that. The estimated variance of the unique environmental component was 2.25. In contrast, the ACE model using the OpenMX package (Boker et al. 2011) yielded estimates of 7.384, 0.000, and 2.265 for the A, C, and E components, respectively, while the AE model gave nearly the same estimates for the A and E components.

Figure 3.

Distributions of age among MZ and DZ twins.

Figure 4.

The variance curves of the A and C components with the 95% confidence bands estimated from the ACE(t) model.

Figure 5.

The variance curves of the A and C components with the 95% confidence bands estimated from the ACE(t)-p model.

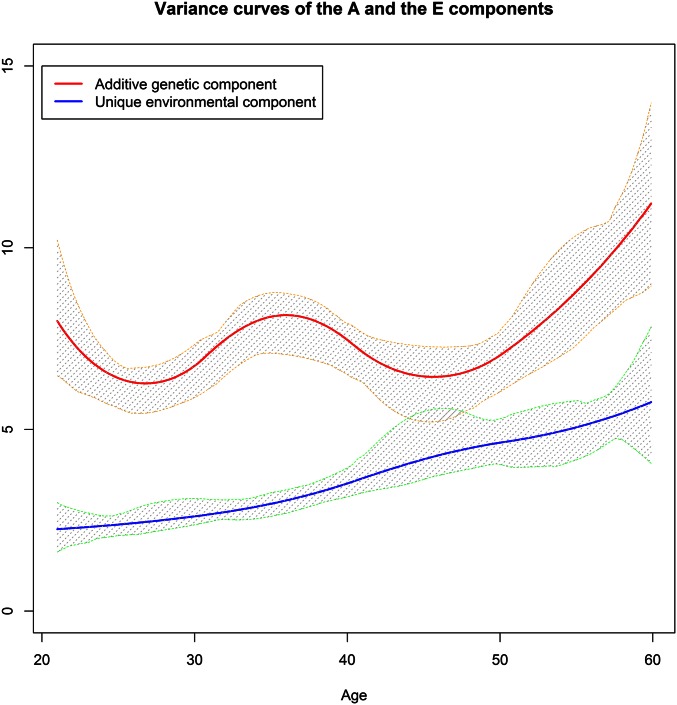
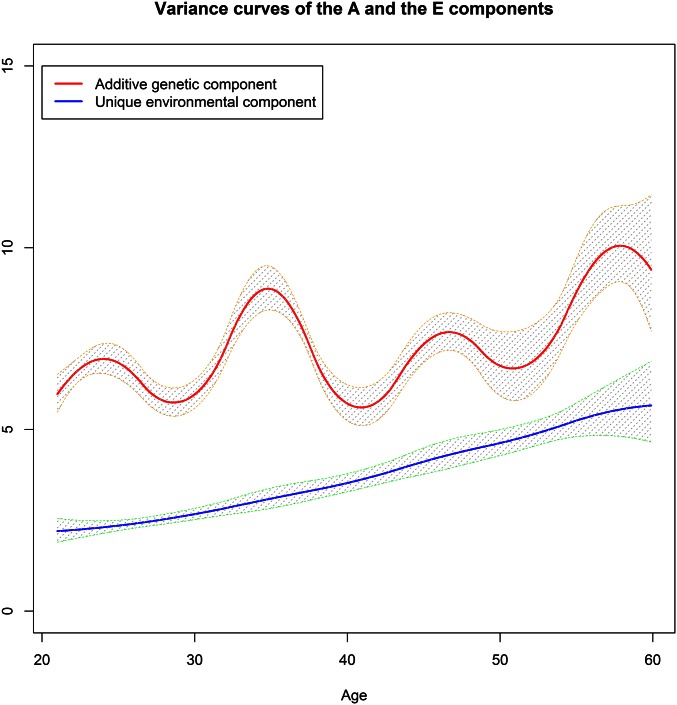
The results revealed that the common environmental factor almost vanished after age 20 years, but the growth of the additive genetic factor might be attributed to an increasing unique environmental variance that was assumed to be constant in the ACE(t) and ACE(t)-p models. Therefore, to verify whether a wrong model was used to fit the data after age 20 years, we employed the AE(t) and AE(t)-p models described in Methods to estimate the variance curves after age 20 years, where we allowed both A and E variance components to change. Consequently, as shown in Figure 6 and Figure 7, the variance of the A component leveled off and moderately fluctuated at ∼7.5 and climbed after age 50 years. In contrast, the variance of the E component initially standing at 2.25 grew almost linearly across the entire age interval. The AE(t) (with five interior knots for either component) and AE(t)-p (with eight interior knots for either component) models generated comparable results for the E component while AE(t)-p produced a more wavy and detailed curve for the A component probably because the number of knots in the AE(t) model was too small to catch the irregular and oscillating curve.

Figure 6.

The variance curves after age 20 years of the A and E components with the 95% confidence bands estimated from the AE(t) model.

Figure 7.

The variance curves after age 20 years of the A and E components with the 95% confidence bands estimated from the AE(t)-p model.

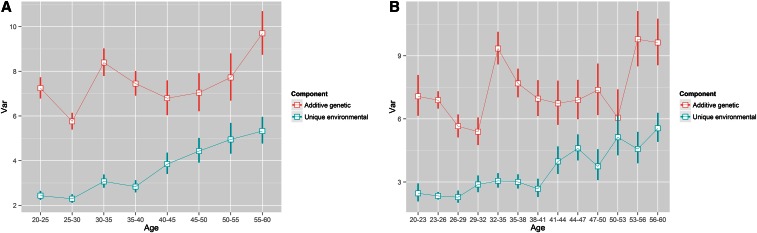
To further verify the periodic pattern of the A component after age 20 years, we performed stratified analyses with 5-year and 3-year intervals based on the AE model. The result based on the 5-year interval (Figure 8A) was very close to that from the AE(t) model (i.e., the B-spline model) and the result based on the 3-year interval (Figure 8B) was more similar to that from the AE(t)-p model (i.e., the P-spline model), which showed more periodic fluctuations. Smaller age intervals offered a refined picture but resulted in larger estimation uncertainty.

Figure 8.

The variance curves after age 20 years of the A and E components with the 95% confidence bands estimated from the stratified analyses. (A) Divided by 5-year intervals. (B) Divided by 3-year intervals.

Discussion

In this work, we have proposed two novel twin models to explore dynamic behavior of the variance components over age or time. The estimated variance functions can be utilized to calculate the age-specific heritability. The results of our BMI study demonstrate that the proposed models provide a more detailed dynamic profile of the A, C, and E variance components than the classical twin models. These models are more flexible than the parametric models (Purcell 2002) as they do not require a prespecified assumption of the function form. Compared to LOSEM, which is an exploratory method and the results of which are heavily dependent on the selection of the width of a weighting distribution (Briley et al. 2015), the proposed models based on P-splines are more adaptive to data and straightforward for model comparison using likelihood-ratio tests.

The ACE(t)-p model is more stable than the ACE(t) model in the sense that it is less sensitive to the number of knots. This amounts to the problem in stratification analyses, that is, how to choose age intervals. The ACE(t)-p model solves this issue by penalizing the smoothness to select the best model. Moreover, the simulation results suggest that the ACE(t)-p model has the advantage of providing better estimates in terms of AMSE; however, the benefit comes from the price of more computational intensity with the same number of knots. It is evident from the simulation study that adding excessive knots in the ACE(t) model worsens the performance for smooth functions. The ACE(t)-p model also performs better with fewer knots provided the number of knots is sufficient but its performance is less affected than that of the ACE(t) model. Thus, assuming that the variance components rarely change drastically within a short period of time, a preferable strategy is to use the ACE(t)-p model and to choose a moderate number of knots [a number of 10 for each component seems enough based on our simulation, although 35-40 is almost adequate for all smooth functions (Ruppert 2002)] to ensure that the model can sufficiently capture the dynamic behavior and in the meantime does not substantially lose performance or increase computational intensity.

The simulation study also indicates that given a sample size of 20,000 and a balanced and widespread distribution of age, both models are able to produce slightly reliable estimates of the functions, which implies that the accurate estimation of variance functions requires a relatively large sample size (at least tens of thousands). Given the current implementation using C++ in the ACEt R package, for a study consisting of 10,000 twin pairs, an Intel i5-3210M laptop takes a few seconds for the ACE(t) model, depending on the number of knots, while it takes around two times longer for the ACE(t)-p model under the same setting. The iterative algorithm for the ACE(t)-p model usually converges within 10 steps.

The trend of the A and C components estimated from the Finnish twin data set for BMI before age 20 years is consistent with that in previous reports (Lajunen et al. 2009; Silventoinen et al. 2009) except that the estimated variance of the C component before age 15 years is higher than that from the stratified study (Lajunen et al. 2009). This is probably caused by the lack of adequate observations at the ages of 13 years and 15 years (Figure 2). It is also possible that the steep decline at the beginning is too rapid for the splines with the order of 3 to capture. Given the absence of the C component, our variance curves of the A and E components indicate that the heritability [estimated as ${\sigma }_a^2(t)/\left({\sigma }_a^2(t)+{\sigma }_e^2(t)\right)$] decreases gradually to <50% until age 50 years. This is in accordance with a previous report in which samples were stratified by 10-year age groups (Korkeila et al. 1991) and a meta-analysis of twin studies showing that the heritability of BMI is higher among adolescents than among adults (Elks et al. 2012). Our estimated variance curves suggest that the decreasing heritability of BMI during middle age is due to the remarkable growth of the unique environmental variance, highlighting the importance of the environmental role in controlling BMI among adults. The variance of the genetic component stabilizes after age 20 years, possibly caused by the end of the physiologically developmental phase that is influenced substantially by genetic factors. It may also relate to the effect size of the SNP rs9939609 in FTO on BMI that rises until around age 20 years and then gradually attenuates into adulthood (Hardy et al. 2010). In contrast, the heritability of 76% from the ACE and AE models is overestimated for age >20 years as our variance curves suggest that the heritability falls below 50% after age 40 years.

Comparing the variance curves from the different models in the Finnish BMI study shows that fitting data using a wrong model may lead to severely misleading results and interpretation. For instance, ignoring the age-dependent effect on the E component inflated the estimation of the variance of the genetic component. As the heterogeneous genetic or environmental effects of age seem ubiquitous for many complex traits, previous twin studies based on the classical twin models (Distel et al. 2011; Elks et al. 2012; Sas et al. 2012) might produce an inaccurate estimate of heritability. Explicitly modeling the variance functions is a necessary action if we want to know more about their strength. Our proposed models provide unprecedentedly refined details for the evolution of both genetic and environmental factors, which pave the way to explore the age-specific heritability function. Identification of the dynamic behavior of the genetic factor likely implies the interaction with age of some key genes related to the phenotype such as FTO for BMI. Our results provide support for the need to further investigate time-dependent effects of significantly associated SNPs identified in GWAS. In fact, multiple significant SNPs have been found to affect BMI with different temporal patterns during middle age (Das et al. 2011).

Future work of the proposed models can be focused on the extension to other types of traits such as binary and categorical traits. A full Bayesian method may be utilized to obtain a more accurate estimate and C.I.’s. Moreover, the proposed models can also be utilized to investigate other timescales and other moderators shared by a twin pair such as birth year. Similar to LOSEM, a major limitation is that the age has to be measured at the twin level (Briley et al. 2015). Further generalization to the variance–covariance matrices using covariance functions (Pletcher and Geyer 1999) is necessary to extend the models to investigate other continuous environmental moderators that may differ within a twin pair, for example education, incomes, or some physical environmental factors.

In conclusion, we have proposed two novel twin models that estimate dynamic behavior of the variance components in the classical twin models with respect to age. As an alternative and generalization to the classical twin models, we have demonstrated the performance of these models through the simulation and the Finnish BMI studies. Our results have emphasized the importance and implications of these models in facilitating twin studies to investigate the age-specific heritability. Given the evidence of the important influence of age on both genetic and environmental factors, previous studies on heritability estimated from the classical twin models may need further review. It should be noted that in addition to age the proposed models can be used to study other environmental moderators as well, which will remarkably broaden their application.

Appendix

Detailed Derivation of the Estimation in the ACE(t) Model

According to model (1), the estimation of ${\sigma }_e^2,$ ${\mathit{\beta }}^A,$ and ${\mathit{\beta }}^C$ is straightforward by minimizing the −2 log-likelihood,

$$\left(-2\right)l=\log \left|{\mathbf{\Sigma }}_M\right|+{{\mathit{Y}}^{\prime }}_M {\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M+\log \left|{\mathbf{\Sigma }}_D\right|+{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D.$$

The score functions are obtained by calculating the partial derivatives with respect to the parameters,

$$\frac{\partial \left(-2\right)l}{\partial {\sigma }_e^2}=tr\left({\mathbf{\Sigma }}_M^{-1}\right)-{{\mathit{Y}}^{\prime }}_M{\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M+tr\left({\mathbf{\Sigma }}_D^{-1}\right)-{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D,$$

$$\frac{\partial \left(-2\right)l}{\partial {\mathit{\beta }}^A}={\left({\mathit{B}}_{T_M}^A\otimes {\mathbf{1}}_{2\times 1}\right)}^{\prime }diag\left(e^{{\mathit{B}}_{T_M}^A{\mathit{\beta }}^A}\otimes {\mathbf{1}}_{2\times 1}\right)d\left({\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^M-{\mathbf{1}}_B^M{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}\right){\mathbf{1}}_{n_M\times 1}+{\left({\mathit{B}}_{T_D}^A\otimes {\mathbf{1}}_{2\times 1}\right)}^{\prime }diag\left(e^{{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\otimes {\mathbf{1}}_{2\times 1}\right)d\left({\mathbf{\Sigma }}_D^{-1}\mathit{A}-\mathit{A}{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}\right){\mathbf{1}}_{n_D\times 1},$$

$$\frac{\partial \left(-2\right)l}{\partial {\mathit{\beta }}^C}={\left({\mathit{B}}_{T_M}^C\otimes {\mathbf{1}}_{2\times 1}\right)}^{\prime }diag\left(e^{{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C}\otimes {\mathbf{1}}_{2\times 1}\right)d\left({\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^M-{\mathbf{1}}_B^M{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}\right){\mathbf{1}}_{n_M\times 1}+{\left({\mathit{B}}_{T_D}^C\otimes {\mathbf{1}}_{2\times 1}\right)}^{\prime }diag\left(e^{{\mathit{B}}_{T_D}^C{\mathit{\beta }}^C}\otimes {\mathbf{1}}_{2\times 1}\right)d\left({\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D-{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}\right){\mathbf{1}}_{n_D\times 1},$$

where $d(·)$ is the matrix with only its diagonal elements. The Hessian matrix $H_{\left({\mathit{\beta }}^A,{\mathit{\beta }}^C,{\sigma }_e^2\right)}$ can be obtained by further calculating the partial derivatives of the score functions with respect to the parameters. Thus, the MLEs $\widehat{{\sigma }_e^2},$ $\widehat{{\beta }_k^A},$ and $\widehat{{\beta }_l^c}$ can be obtained by using numerical methods such as the Newton–Raphson method. Practically, it would be time-consuming because the estimation of variance generally requires a relatively large sample size so that the large-scale computations for the Hessian matrix would be inevitably involved. Alternatively, we minimize the log-likelihood function without directly calculating the Hessian matrix by using the limited-memory L-BFGS algorithm (Byrd et al. 1995) for bound constrained optimization, which is in the family of quasi-Newton methods. In this algorithm, the approximated Hessian matrix $\tilde{\mathit{H}}$ is computed in a way that is much faster than the Newton–Raphson method.

Detailed Derivation of the Estimation in the ACE(t)-p Model

We use the difference matrix of the second order (Eilers and Marx 1996) to construct ${\mathit{D}}_A={\mathbf{\Delta }}_A^T{\mathbf{\Delta }}_A$ and ${\mathit{D}}_C={\mathbf{\Delta }}_C^T{\mathbf{\Delta }}_C,$ where

$${\mathbf{\Delta }}_A={\left(\begin{array}{ccc}\begin{array}{ccc}1& -2& 1\end{array}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & \begin{array}{ccc}1& -2& 1\end{array}\end{array}\right)}_{\left(K-2\right)\times K}$$

and

$${\mathbf{\Delta }}_C={\left(\begin{array}{ccc}\begin{array}{ccc}1& -2& 1\end{array}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & \begin{array}{ccc}1& -2& 1\end{array}\end{array}\right)}_{\left(L-2\right)\times L}.$$

Given the target function

$$g\left({\mathit{\beta }}^A,{\mathit{\beta }}^C\right)=\left(1/2\right)\left(\log \left|{\mathbf{\Sigma }}_M\right|+{{\mathit{Y}}^{\prime }}_M{\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M+\log \left|{\mathbf{\Sigma }}_D\right|+{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D+{\mathit{\beta }}^A{}^{\prime }{\mathit{D}}_A{\mathit{\beta }}^A/{\sigma }_{{\beta }^A}^2+{\mathit{\beta }}^C{}^{\prime }{\mathit{D}}_C{\mathit{\beta }}^C/{\sigma }_{{\beta }^C}^2\right),$$

the L-BFGS algorithm in step 1 can be performed using the following score functions:

$$\frac{\partial g\left({\mathit{\beta }}^A,{\mathit{\beta }}^C\right)}{\partial {\mathit{\beta }}^A}=\frac{1}{2}\left({\mathit{B}}_{T_M}^{A^{\prime }}diag\left(e^{{\mathit{B}}_{T_M}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{2M}{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{2M}-{{\mathit{Z}}^{\prime }}_{2M}{\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M{{\mathit{Y}}^{\prime }}_M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{2M}\right){\mathbf{1}}_{f_M\times 1}+0.5{\left({\mathit{B}}_{T_D}^A\otimes {\mathbf{1}}_{2\times 1}\right)}^{\prime }diag\left(e^{{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\otimes {\mathbf{1}}_{2\times 1}\right)d\left({\mathbf{\Sigma }}_D^{-1}-{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}\right){\mathbf{1}}_{n_D\times 1}+{\mathit{B}}_{T_D}^{A^{\prime }}diag\left(e^{{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{2D}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{2D}-{{\mathit{Z}}^{\prime }}_{2D}{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{2D}\right){\mathbf{1}}_{f_D\times 1}+\frac{\left({\mathit{D}}_A+{{\mathit{D}}^{\prime }}_A\right){\mathit{\beta }}^A}{{\sigma }_{{\beta }^A}^2}\right),$$

$$\frac{\partial g\left({\mathit{\beta }}^A,{\mathit{\beta }}^C\right)}{\partial {\mathit{\beta }}^C}=\frac{1}{2}\left({\mathit{B}}_{T_M}^{C^{\prime }}diag\left(e^{{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C}\right)d\left({{\mathit{Z}}^{\prime }}_{3M}{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}-{{\mathit{Z}}^{\prime }}_{3M}{\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M{{\mathit{Y}}^{\prime }}_M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}\right){\mathbf{1}}_{f_M\times 1}+{\mathit{B}}_{T_D}^{C^{\prime }}diag\left(e^{{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C}\right)d\left({{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}-{{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}\right){\mathbf{1}}_{f_D\times 1}+\frac{\left({\mathit{D}}_C+{{\mathit{D}}^{\prime }}_C\right){\mathit{\beta }}^C}{{\sigma }_{{\beta }^C}^2}\right).$$

Through straightforward matrix operations, it follows that the second derivative after applying expectation over (${\mathit{Y}}_M,{\mathit{Y}}_D$) by recalling that $E\left({\mathit{Y}}^{\prime }\mathit{P}\mathit{Y}\right)=tr(\mathit{P}\mathbf{\Sigma })$ for a nonstochastic matrix P is

$$g^{″}({\mathit{\beta }}^A,{\mathit{\beta }}^C)=\frac{1}{2}\left(\begin{array}{cc}{\mathit{G}}_{11}& {\mathit{G}}_{12}\\ {\mathit{G}}_{12}^{’}& {\mathit{G}}_{22}\end{array}\right),$$

$${\mathit{G}}_{11}={\sigma }_{{\beta }^A}^{-2}d\left({\mathit{D}}_A+{{\mathit{D}}^{\prime }}_A\right)+{\mathit{B}}_{T_M}^{A^{\prime }}diag\left(e^{2{\mathit{B}}_{T_M}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{2M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{2M}\right){\mathit{B}}_{T_M}^A+0.25{\left({\mathit{B}}_{T_D}^A\otimes {\mathbf{1}}_{2\times 1}\right)}^{\prime }diag\left(e^{2{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\otimes {\mathbf{1}}_{2\times 1}\right)d\left( {\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}\right)\left({\mathit{B}}_{T_D}^A\otimes {\mathbf{1}}_{2\times 1}\right)+{\mathit{B}}_{T_D}^{A^{\prime }}diag\left(e^{2{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\right)\left(d\left({{\mathit{Z}}^{\prime }}_{2D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{2D}\right)+0.5d\left({{\mathit{Z}}^{\prime }}_{2D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{2D}\right)\right){\mathit{B}}_{T_D}^A$$

$${\mathit{G}}_{12}={\mathit{B}}_{T_M}^{C^{\prime }}diag\left(e^{{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C+{\mathit{B}}_{T_M}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{3M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}\right){\mathit{B}}_{T_M}^A+0.5{\mathit{B}}_{T_D}^{C^{\prime }}diag\left(e^{{\mathit{B}}_{T_D}^C{\mathit{\beta }}^C+{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}+{{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}\right){\mathit{B}}_{T_D}^A,$$

$${\mathit{G}}_{22}={\sigma }_{{\beta }^C}^{-2}d\left({\mathit{D}}_C+{{\mathit{D}}^{\prime }}_C\right)+{\mathit{B}}_{T_M}^{C^{\prime }}diag\left(e^{2{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C}\right)d\left({{\mathit{Z}}^{\prime }}_{3M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}\right){\mathit{B}}_{T_M}^C+{\mathit{B}}_{T_D}^{C^{\prime }}diag\left(e^{2{\mathit{B}}_{T_D}^C{\mathit{\beta }}^C}\right)d\left({{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}\right){\mathit{B}}_{T_D}^C.$$

To perform the L-BFGS algorithm in step 2, we calculate the score functions given $\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right),$

$$\frac{\partial \left(-2\right)l_{psp}\left({\sigma }_e^2,{\sigma }_{{\beta }^A}^2,{\sigma }_{{\beta }^C}^2\right)}{\partial {\sigma }_{{\beta }^A}^2}=\left(-{\sigma }_{{\beta }^A}^{-4}\right){\widehat{{\mathit{\beta }}^A}}^{\prime }{\mathit{D}}_A\widehat{{\mathit{\beta }}^A}+\frac{\tilde{K}}{{\sigma }_{{\beta }^A}^2}+tr\left(g^{″}{\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}^{-1}\frac{\partial g^{″}\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}{\partial {\sigma }_{{\beta }^A}^2}\right),$$

$$\frac{\partial \left(-2\right)l_{psp}\left({\sigma }_e^2,{\sigma }_{{\beta }^A}^2,{\sigma }_{{\beta }^C}^2\right)}{\partial {\sigma }_{{\beta }^C}^2}=\left(-{\sigma }_{{\beta }^C}^{-4}\right){\widehat{{\mathit{\beta }}^C}}^{\prime }{\mathit{D}}_C\widehat{{\mathit{\beta }}^C}+\frac{\tilde{L}}{{\sigma }_{{\beta }^C}^2}+tr\left(g^{″}{\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}^{-1}\frac{\partial g^{″}\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}{\partial {\sigma }_{{\beta }^C}^2}\right),$$

$$\frac{\partial \left(-2\right)l_{psp}\left({\sigma }_e^2,{\sigma }_{{\beta }^A}^2,{\sigma }_{{\beta }^C}^2\right)}{\partial {\sigma }_e^2}=tr\left({\mathbf{\Sigma }}_M^{-1}\right)-{{\mathit{Y}}^{\prime }}_M{\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M+tr\left({\mathbf{\Sigma }}_D^{-1}\right)-{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D+tr(g^{″}{\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}^{-1}\frac{\partial g^{″}\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}{\partial {\sigma }_e^2}),$$

where

$$\frac{\partial g^{″}\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}{\partial {\sigma }_{{\beta }^A}^2}=-0.5{\sigma }_{{\beta }^A}^{-4}\left(\begin{array}{cc}d({\mathit{D}}_A+{{\mathit{D}}^{\prime }}_A)& 0\\ 0& 0\end{array}\right),$$

$$\frac{\partial g^{″}\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}{\partial {\sigma }_{{\beta }^C}^2}=-0.5{\sigma }_{{\beta }^C}^{-4}\left(\begin{array}{cc}0& 0\\ 0& d({\mathit{D}}_C+{{\mathit{D}}^{\prime }}_C)\end{array}\right),$$

$$\frac{\partial g^{″}\left(\widehat{{\mathit{\beta }}^A},\widehat{{\mathit{\beta }}^C}\right)}{\partial {\sigma }_e^2}=\frac{1}{2}\left(\begin{array}{cc}\frac{\partial {\mathit{G}}_{11}}{\partial {\sigma }_e^2}& \frac{\partial {\mathit{G}}_{12}}{\partial {\sigma }_e^2}\\ {\frac{\partial {\mathit{G}}_{12}}{\partial {\sigma }_e^2}}^{\prime }& \frac{\partial {\mathit{G}}_{22}}{\partial {\sigma }_e^2}\end{array}\right),$$

where

$$\frac{\partial {\mathit{G}}_{11}}{\partial {\sigma }_e^2}=-{\mathit{B}}_{T_M}^{A^{\prime }}diag\left(e^{2{\mathit{B}}_{T_M}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{2M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{2M}^{}+{{\mathit{Z}}^{\prime }}_{2M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{2M}^{}\right){\mathit{B}}_{T_M}^A-0.5{\left({\mathit{B}}_{T_D}^A\otimes {\mathbf{1}}_{2\times 1}\right)}^{\prime }diag\left(e^{2{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\otimes {\mathbf{1}}_{2\times 1}\right)d\left({\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}\right)\left({\mathit{B}}_{T_D}^A\otimes {\mathbf{1}}_{2\times 1}\right)-{\mathit{B}}_{T_D}^{A^{\prime }}diag\left(e^{2{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\right)d\left(2\cdot {{\mathit{Z}}^{\prime }}_{2D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{2D}^{}+{{\mathit{Z}}^{\prime }}_{2D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{2D}^{}+{{\mathit{Z}}^{\prime }}_{2D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{2D}^{}\right){\mathit{B}}_{T_D}^A,$$

$$\frac{\partial {\mathit{G}}_{12}}{\partial {\sigma }_e^2}=-{\mathit{B}}_{T_M}^{C^{\prime }}diag\left(e^{{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C+{\mathit{B}}_{T_M}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{3M} {\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}^{}+{{\mathit{Z}}^{\prime }}_{3M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}^{}\right){\mathit{B}}_{T_M}^A-{\mathit{B}}_{T_D}^{C^{\prime }}diag\left(e^{{\mathit{B}}_{T_D}^C{\mathit{\beta }}^C+{\mathit{B}}_{T_D}^A{\mathit{\beta }}^A}\right)d\left({{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}^{}+{{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}^{}+{{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}^{}\right){\mathit{B}}_{T_D}^A,$$

$$\frac{\partial {\mathit{G}}_{22}}{\partial {\sigma }_e^2}=-{\mathit{B}}_{T_M}^{C^{\prime }}diag\left(e^{2{\mathit{B}}_{T_M}^C{\mathit{\beta }}^C}\right)d\left({{\mathit{Z}}^{\prime }}_{3M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}^{}+{{\mathit{Z}}^{\prime }}_{3M}{\mathbf{\Sigma }}_M^{-1}{\mathbf{1}}_B^M{\mathbf{\Sigma }}_M^{-1}{\mathbf{\Sigma }}_M^{-1}{\mathit{Z}}_{3M}^{}\right){\mathit{B}}_{T_M}^C-{\mathit{B}}_{T_D}^{C^{\prime }}diag\left(e^{2{\mathit{B}}_{T_D}^C{\mathit{\beta }}^C}\right)d\left({{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}^{}+{{\mathit{Z}}^{\prime }}_{3D}{\mathbf{\Sigma }}_D^{-1}{\mathbf{1}}_B^D{\mathbf{\Sigma }}_D^{-1}{\mathbf{\Sigma }}_D^{-1}{\mathit{Z}}_{3D}^{}\right){\mathit{B}}_{T_D}^C.$$

Construction of the Confidence Intervals in the ACE(t)-p Model

Let us denote $\mathit{Y}=({\mathit{Y}}_M,{\mathit{Y}}_D)$ and $\mathit{\beta }=\left({\mathit{\beta }}^A,{\mathit{\beta }}^C\right).$ It has been proposed that treating the P-splines under a framework of a random effects model has the advantages of giving a better estimate of the variance of $\widehat{\mathit{\beta }}$ (Ruppert et al. 2003). In our context, given ${\sigma }_{{\beta }^A}^2$ and ${\sigma }_{{\beta }^C}^2,$ according to the model assumption, $g\left(\mathit{\beta }\right)$ is the logarithm of the joint distribution $f(\mathit{\beta }, \mathit{Y})$ of Y and β. However, when we treat β as random effects, a BP $\check{\beta }$ for the random effects defined as the mean of the posterior distribution given data from the perspective of the Bayesian framework, i.e., $E\left(\mathit{\beta }|y\right),$ has the following desirable properties (Searle et al. 2009),

$$E\left(\check{\mathit{\beta }}\right)=E_y\left(E\left(\mathit{\beta }|y\right)\right)=E\left(\mathit{\beta }\right),$$

$$Var\left(\check{\mathit{\beta }}-\mathit{\beta }\right)=E_y\left(Var\left(\mathit{\beta }|y\right)\right).$$

It is, however, not as straightforward to obtain $E\left(\mathit{\beta }|y\right)$ and $E_y\left(Var\left(\mathit{\beta }|y\right)\right)$ in this case as the BLUP (Henderson 1975) in the linear mixed model because the posterior distribution of β is not available in a closed form. Note that $e^{-g\left(\mathit{\beta }\right)}$ is proportional to the posterior distribution of β. Therefore, various numerical methods can be used to approximate the posterior distribution based on $e^{-g\left(\mathit{\beta }\right)},$ from which the estimated BP $\check{\mathit{\beta }},$ the prediction error $Var\left(\check{\mathit{\beta }}-\mathit{\beta }\right),$ and thus the C.I.’s can be derived.

Here we give a simple Metropolis–Hastings (MH) algorithm (Hastings 1970) to numerically obtain the posterior distribution of β given $\widehat{{\sigma }_{{\beta }^A}^2}$ and $\widehat{{\sigma }_{{\beta }^C}^2},$ which is proportional to the joint distribution of Y and β,

$$e^{-g(\mathit{\beta })}=\exp \left(-\frac{1}{2}\left(\log \left|{\mathbf{\Sigma }}_M\right|+{{\mathit{Y}}^{\prime }}_M{\mathbf{\Sigma }}_M^{-1}{\mathit{Y}}_M+\log \left|{\mathbf{\Sigma }}_D\right|+{{\mathit{Y}}^{\prime }}_D{\mathbf{\Sigma }}_D^{-1}{\mathit{Y}}_D+\frac{{\mathit{\beta }}^{A^{\prime }}{\mathit{D}}_A{\mathit{\beta }}^A}{{\sigma }_{{\beta }^A}^2}+\frac{{\mathit{\beta }}^{C^{\prime }}{\mathit{D}}_C{\mathit{\beta }}^C}{{\sigma }_{{\beta }^C}^2}\right)\right),$$

described as follows:

1. Set the initial value of ${\mathit{\beta }}^{(1)}$ at 0.

2. Propose the next ${\mathit{\beta }}^{(i+1)}$ by sampling from $\mathcal{N}\left({\mathit{\beta }}^{\left(i\right)}, {\sigma }_p^2\mathit{I}\right).$

3. Draw u from $Uni[0, 1].$

4. If $u<e^{-\left(g\left({\mathit{\beta }}^{(i+1)}\right)-g\left({\mathit{\beta }}^{\left(i\right)}\right)\right)},$ accept ${\mathit{\beta }}^{(i+1)}.$ Then go back to step 2.

The variance ${\sigma }_p^2$ of the proposal distribution affects the performance of the MH algorithm in terms of convergence. In our simulation and real data study, we set ${\sigma }_p^2=0.1$ and the trace plots showed the chains mixed quickly. The MCMC samples can give us accurate estimates of $\check{\mathit{\beta }}$ and $Var\left(\mathit{\beta }|y\right)$ under the guarantee of adequate numerical precision. We found in the simulation study that the posterior mean $\check{\mathit{\beta }}$ is often quite close to the mode $\widehat{\mathit{\beta }},$ suggesting that the posterior distribution is highly symmetric. The conditional MSE of prediction $Var\left(\mathit{\beta }|y\right)$ is proposed to be a better estimate of prediction error than $Var\left(\check{\mathit{\beta }}-\mathit{\beta }\right)$ (Skrondal and Rabe-Hesketh 2009), which thus is adopted to compute the C.I.’s in our analyses. Alternatively, a parametric bootstrap method can be used to estimate $E_y\left(Var\left(\mathit{\beta }|y\right)\right)$ by generating a set of bootstrap replicates $y\ast$ from the empirical distribution $\widehat{f}(y)$ according to model (1) with the parameters replaced by their estimates from the EM algorithm. Thus, the variances $\widehat{Var}\left({\mathit{B}}^A\left(t\right){\check{\mathit{\beta }}}^A\right)$ and $\widehat{Var}\left({\mathit{B}}^C\left(t\right){\check{\mathit{\beta }}}^C\right)$ at the time t are expressed as ${\mathit{B}}^A(t{)}^{\prime }\widehat{Var}\left({\check{\mathit{\beta }}}^A-{\mathit{\beta }}^A\right){\mathit{B}}^A(t)$ and ${\mathit{B}}^C(t{)}^{\prime }\widehat{Var}\left({\check{\mathit{\beta }}}^C-{\mathit{\beta }}^C\right){\mathit{B}}^C(t),$ where $\widehat{Var}\left({\check{\mathit{\beta }}}^A-{\mathit{\beta }}^A\right)$ and $\widehat{Var}\left({\check{\mathit{\beta }}}^C-{\mathit{\beta }}^C\right)$ are estimated from the MCMC outputs. It should be pointed out that the estimated variances do not take into account the variability of $\widehat{{\sigma }_{{\beta }^A}^2}$ and $\widehat{{\sigma }_{{\beta }^C}^2},$ which is the price of our Laplace approximation compared to a full Bayesian approach as previously noted (Krivobokova et al. 2008; Skrondal and Rabe-Hesketh 2009). Finally, the C.I.’s can be constructed by assuming the approximate normality of $Var\left(\mathit{\beta }|y\right)$ based on the Bayesian central limit theorem (Carlin and Louis 1997).