Quantification of Global Diastolic Function by Kinematic Modeling-based Analysis of Transmitral Flow via the Parametrized Diastolic Filling Formalism

Abstract

Quantitative cardiac function assessment remains a challenge for physiologists and clinicians. Although historically invasive methods have comprised the only means available, the development of noninvasive imaging modalities (echocardiography, MRI, CT) having high temporal and spatial resolution provide a new window for quantitative diastolic function assessment. Echocardiography is the agreed upon standard for diastolic function assessment, but indexes in current clinical use merely utilize selected features of chamber dimension (M-mode) or blood/tissue motion (Doppler) waveforms without incorporating the physiologic causal determinants of the motion itself. The recognition that all left ventricles (LV) initiate filling by serving as mechanical suction pumps allows global diastolic function to be assessed based on laws of motion that apply to all chambers. What differentiates one heart from another are the parameters of the equation of motion that governs filling. Accordingly, development of the Parametrized Diastolic Filling (PDF) formalism has shown that the entire range of clinically observed early transmitral flow (Doppler E-wave) patterns are extremely well fit by the laws of damped oscillatory motion. This permits analysis of individual E-waves in accordance with a causal mechanism (recoil-initiated suction) that yields three (numerically) unique lumped parameters whose physiologic analogues are chamber stiffness (k), viscoelasticity/relaxation (c), and load (x_o). The recording of transmitral flow (Doppler E-waves) is standard practice in clinical cardiology and, therefore, the echocardiographic recording method is only briefly reviewed. Our focus is on determination of the PDF parameters from routinely recorded E-wave data. As the highlighted results indicate, once the PDF parameters have been obtained from a suitable number of load varying E-waves, the investigator is free to use the parameters or construct indexes from the parameters (such as stored energy 1/2kx_o², maximum A-V pressure gradient kx_o, load independent index of diastolic function, etc.) and select the aspect of physiology or pathophysiology to be quantified.

Download video file ^{(22.3MB, mp4)}

Introduction

Pioneering studies by Katz¹ in 1930 revealed that the mammalian left ventricle initiates filling by being a mechanical suction pump, and much effort since then has been devoted to unraveling the workings of diastole. For many years, invasive methods were the only options available for clinical or research assessment of diastolic function (DF)^2-16. In the 1970s, however, technical advancements and developments in echocardiography finally gave cardiologists and physiologists practical tools for noninvasive characterization of DF.

Without a unifying causal theory or paradigm for diastole regarding how the heart works when it fills, researchers proposed numerous phenomenologic indexes based on correlation with clinical features. The curvilinear, rapidly rising and falling shape of the transmitral blood flow velocity contour during early, rapid filling, for example, was approximated as a triangle and diastolic function indexes were defined from geometric features (height, width, area, etc.) of that triangle. Technical advancements in echocardiography have allowed tissue motion, strain, and strain rate during filling to be measured, for example, and each technical advancement brought with it a new crop of phenomenological indexes to be correlated with clinical features. However, the indexes remain correlative and not causal and many indexes are different measures of the same underlying physiology. It’s not surprising, therefore, that currently employed clinical indexes of DF have limited specificity and sensitivity.

To overcome these limitations the Parametrized Diastolic Filling (PDF) formalism, a causal kinematic, lumped parameter model of left ventricular filling that is motivated by and incorporates the suction-pump physiology of diastole was developed and validated¹⁷. It models diastolic function (as manifested by the curvilinear shapes of transmitral flow contours) in accordance with the rules of damped harmonic oscillatory motion. The equation for damped harmonic oscillatory motion is based on Newton’s Second Law and can be written, per unit mass, as:

    Equation 1

This linear 2^nd order differential equation has three parameters: k- chamber stiffness, c- viscoelasticity/relaxation, and x_o- the oscillator’s initial displacement/preload. The model predicts that the different clinically observed diastolic filling patterns are the result of variation in the numerical value of these three model parameters. Based on the PDF formalism and classical mechanics, E-waves can be classified as being determined by under-damped or over-damped regimes of motion. Numerous studies^17-21 have validated that clinically recorded E-wave contours and PDF model predicted contours show superb agreement and have elucidated the hemodynamic/physiologic analogues of the three PDF parameters²¹. The process for extracting model parameters from clinically recorded E-wave data is detailed in the methods below.

Unlike typical indexes of DF in current clinical use, the PDF model’s three parameters are causality based. As discussed in the methods below, additional indexes of diastolic physiology can be derived from these fundamental parameters and from application of the PDF formalism to aspects of diastole other than transmitral flow. In this work, methods of PDF-based analysis of transmitral flow and the physiologic relations that can be drawn from the PDF approach, its parameters and the derived indexes are described. Additionally, it is shown that the PDF parameters or indexes derived from them can tease apart intrinsic chamber properties from the external effects of load can provide correlates to traditional invasively defined parameters and can differentiate between normal and pathologic groups.

Protocol

The procedure for acquiring echocardiographic images and analyzing them to obtain the PDF parameters is detailed below. Although cardiac catheterization is mentioned in the subject selection portion below, the methodology described applies only to the echocardiographic portion. The description of the catheterization portion was included for independent validation of model based predictions and is unrelated to the analysis of E-waves via the PDF formalism. Prior to data acquisition, all subjects provide signed, informed consent for participation in the study in accordance with the Institutional Review Board (Human Research Protection Office) at Washington University School of Medicine.

NOTE: All software programs (along with tutorials on how to use them) described in this section can be downloaded from http://cbl1.wustl.edu/SoftwareAgreement.htm

1. Subject Selection

NOTE: All subjects in the Cardiovascular Biophysics Laboratory Database had simultaneous echocardiography and cardiac catheterization performed and were referred by their physicians for diagnostic cardiac catheterization. The database inclusion criteria are: 1) absence of any significant valvular abnormalities, 2) absence of wall motion abnormalities or bundle branch block on ECG, 3) presence of a satisfactory echocardiographic window with clearly identifiable E- and A-waves.

2. Echocardiographic Data Acquisition

1. Record a complete 2D/echo-Doppler study for all subjects in accordance with American Society of Echocardiography criteria¹⁶. NOTE: The screening echocardiograms were recorded on a standard clinical imager by a sonographer. If desired, additional transthoracic echocardiographic recording can be performed for verification purposes after a suitable, high fidelity catheter is advanced into the LV to measure LV hemodynamics simultaneously.

2. Image subjects in the supine position. In a nonresearch setting, standard left lateral positioning can be used without loss of generality of the method. Obtain apical four-chamber views using a 2.5 MHz transducer, with the sample volume gated at 1.5-5 mm directed between the tips of the mitral valve leaflets and orthogonal to the MV plane (to minimize alignment effects as seen on color M-mode Doppler), the wall filter set at 1 (125 Hz) or 2 (250 Hz), the baseline adjusted to take advantage of the full height of the display and the velocity scale adjusted to exploit the dynamic range of the output without aliasing.

3. Perform Doppler tissue imaging with the sample volume gated at 2.5 mm and positioned at the lateral and septal potions of the mitral annulus.

4. Save Doppler examinations in DICOM format in the echo machine and record on DVD with simultaneously recorded electrocardiogram (ECG).

3. Doppler Image Processing and Conventional Analysis

NOTE: This section describes two custom MATLAB programs. The first program is described in step 3.1 and the second program is described in steps 3.2-3.5. All software programs (along with tutorials on how to use them) can be downloaded from http://cbl1.wustl.edu/SoftwareAgreement.htm

1. Convert images from the DICOM format and video to bitmap (.bmp) files (using a custom MATLAB program). NOTE: The procedure described below to fit Doppler E-waves and tissue Doppler E’-waves is shown in Figure 1.

2. Load the bitmap image files on another custom MATLAB program to measure conventional transmitral flow parameters such as E_peak, A_peak, E_dur, E’_peak, A’_peak, etc. and crop the images for PDF analysis. Select images with discernible transmitral flow contour and complete cardiac cycle as indicated by ECG for analysis.

3. Mark the time sampling rate (measured in pixels/s on the horizontal axis) and velocity sampling rate (measured in pixels/(m/sec) along the vertical axis) in the images. Identify the complete cardiac cycle by noting and marking consecutive R peaks (or any distinct feature of the ECG) on the image.

4. Mark the transmitral Doppler E- and A-wave or tissue Doppler E’- and A’- wave in the selected cardiac cycle.

   1. Select the Doppler E-wave peak point i.e. E_peak, (or E’_peak) and mark the start of the wave using the line connecting the peak to the start as a guide to match the acceleration slope of the E-wave (or E’-wave). The start of the wave is used to calculate the interval from start to peak flow denoted as the E-wave (or E’-wave) acceleration time (AT).
   2. Mark the end of the E-wave (or E’-wave) using the line connecting the peak to the end as a guide to match the deceleration slope. This is used to calculate the interval from the peak to the baseline denoted as the deceleration time (DT). The interval from start to end of the wave is the duration of the E-wave (E_dur = AT+DT). The program guides the user through the entire process with appropriate instructions.

5. Mark the A-wave using a similar procedure as the E-wave. With both the E- and A-waves marked the program calculates the E_peak/A_peak ratio. NOTE: The program saves the marked waves as cropped images containing the E- and A-waves only. The program also creates a data file with the cropping and measured parameters for each beat.

4. Automated Fitting of Transmitral Flow Using the PDF Formalism

1. The automated fitting of Doppler E- and A-wave and tissue Doppler E’- and A’- wave contours is done using a custom LabView program^18,19.

   1. Load the cropped image, and the program automatically calculates the maximum velocity envelope (MVE). Select the MVE by setting the threshold such that MVE approximates transmitral flow as shown in Figure 1. The onset and termination of the points that define the MVE can be selected along the time-axis by the operator such that only MVE points that provide good correspondence to the actual selected portion of the wave are used as input for the subsequent fitting.

2. NOTE: The user-selected MVE points are the input to the computer program that automatically fits the PDF model solution for velocity as a function of time using a Levenberg- Marquardt (iterative) algorithm. The fitting is accomplished with the requirement that the mean square error between the clinical (input) data (MVE) and the PDF model predicted contour be minimized. Since the model is linear, a unique set of parameters is obtained for each Doppler E-wave derived MVE used as input. Thus numerically unique k, c, and x_o values are generated for each E-wave and k’, c’, and x_o’ for each E’-wave.

3. In the event the fit is obviously suboptimal when the fit is superimposed on the E-wave (or E’-wave) image (i.e. the algorithm attempted to fit noise included in the MVE for example) modify the MVE by using more/less points, thereby modifying the model predicted contour with consequent modification of PDF parameters to achieve a better fit.

Save the data when the appropriate PDF fit has been generated. NOTE: The program is written to automatically save the data in image and text files containing the PDF parameters and the contour information. The PDF parameters obtained from the procedure described above can be used to elucidate new physiology and distinguish between normal and pathological physiology as detailed in the Representative Results section below.

Representative Results

Doppler waveforms representative of the four different types of filling patterns (normal, pseudonormal, delayed relaxation, constrictive-restrictive) using the method detailed above are shown in Figure 2. Figure 2A shows the normal pattern, which, by itself is indistinguishable from the pseudonormal pattern. Figure 2B shows a delayed relaxation and Figure 2C shows a constrictive-restrictive pattern associated with severe diastolic dysfunction. For clarity, the PDF model-predicted fits are overlaid on the images. The conventional echo parameters (E_peak, A_peak, E-wave AT, and E-wave DT) and the PDF parameters (k, c, x_o) are listed below each image. As the figures indicate, the PDF formalism fits (predicts) all three of these filling patterns very well. The PDF parameters also provide information on chamber properties. The delayed relaxation pattern (Figure 2B) typically has higher viscoelasticity/relaxation PDF parameter c than the normal pattern (Figure 2A). Constrictive-restrictive pattern (Figure 2C) typically has a higher stiffness (PDF parameter k) than the normal pattern.

Analysis of Doppler E-waves using the PDF formalism has been used to differentiate between normal and pathological groups and to discover new physiology. Listed below are some selected published results of PDF formalism based DF analysis intended to differentiate between pathologic and normal physiology and selected applications of the PDF formalism to elucidate new physiology.

DIABETES

The method has been shown to quantify the differences in DF between diabetic and age-matched control subjects. While the conventional indexes such as E-wave deceleration time- DT, E_peak or the time constant of isovolumic relaxation were unable to differentiate between the filling patterns of the groups, the PDF viscoelasticity/relaxation parameter c was significantly different between groups²². Additionally, the peak atrio-ventricular pressure gradient, which can be calculated from the PDF parameters as kx_o²³ was significantly higher in the diabetic group. Also, see kinematic filling efficiency, applied to diabetics below.

HYPERTENSION

The method has been used to analyze transmitral filling patterns in hypertensive subjects compared to controls²⁴. Conventional Doppler derived indexes were unable to differentiate between groups but the PDF parameter c was significantly higher in the hypertensive subjects group compared to nonhypertensive controls.

CALORIC RESTRICTION SLOWS CARDIAC AGING

The method assessed the effect of caloric restriction on DF in humans²⁵. DF was assessed in subjects practicing caloric restriction by measuring transmitral flow and comparing to age- matched controls. DF was significantly better in the caloric restriction group as quantified by higher value of E/A and higher early filling (E-wave) fraction. Additionally, the PDF parameter k, representing LV chamber stiffness, and c, representing viscoelasticity, was significantly lower in caloric restriction subjects. Since the E_peak was not significantly different between the two groups, the control group expends more energy to achieve the same peak filling velocity. This revealed that caloric restriction is associated with more efficient DF. Moreover the filling in elderly caloric restricted subjects was comparable to a younger normal cohort, suggesting that caloric restriction slows cardiac aging²⁶.

PRESENCE VS. ABSENCE OF MITRAL ANNULAR OSCILLATIONS

The PDF formalism has also been used to analyze mitral annular oscillations (MAO) after the E’-wave (the E”-wave, E’’’-wave, etc.). This ‘ringing’ of the mitral annulus has been observed in humans²⁰ but characterization of the presence and absence of the subsequent oscillations was lacking. The method allowed the hypothesis to be tested that the absence of MAO is explained by increased viscoelastic effects due to less or slower effective relaxation. By comparing 35 subjects with MAO to 20 subjects without MAO, it was found that the longitudinal stiffness (k’) and the longitudinal viscoelasticity/relaxation (c’) were higher in the group without MAO. The initial recoil force and the stored recoil energy both were higher in the group with MAO. In addition, it was shown that the absence of MAO was concordant with relaxation-related diastolic dysfunction²⁷. Hence the PDF analysis of tissue Doppler E’- waves reveals that the absence of MAO indicates relaxation related diastolic dysfunction.

DIASTATIC STIFFNESS FROM E-WAVE ANALYSIS

While the slope of the end-diastolic pressure-volume relationship (EDPVR) provides the familiar stiffness-based index, the slope (ΔP/ΔV) of the diastatic pressure-volume (P-V) relationship (D-PVR) provides the in-vivo stiffness of the relaxed LV. Echocardiographic, (i.e. Doppler E-wave), analysis can provide only relative, rather than absolute pressure information. Accordingly, it has been shown that the relaxed (diastatic) stiffness of the LV can be computed directly from E-wave analysis alone²⁸. Using the PDF formalism and Bernoulli’s equation pressure and volume at diastasis (end of E-wave) is derived. The derived P, V points when fit via linear regression generate the D-PVR from E-wave analysis (D-PVR_E-wave) whose slope, diastatic stiffness K_E-wave was computed. The results yielded excellent correlation (R²=0.92) between diastatic stiffness from PDF based E-wave analysis (K_E-wave) and the simultaneous gold standard measurement of diastatic stiffness from simultaneous P-V data (K_CATH) in 30 subjects (444 total cardiac cycles) with normal LVEF (LVEF>55%).

KINEMATIC FILLING EFFICIENCY INDEX

From a kinematic modeling perspective, an increased relaxation/viscosity constant c generates increased resistance to filling. Hence a natural choice for idealized ventricular filling is a scenario due to recoil only and complete relaxation, i.e. no damping (c = 0). The kinematic filling efficiency index (KFEI) was defined and derived²⁹ as the dimensionless ratio of actual volume entering the left ventricle (LV) (velocity time integral [VTI] of real E-wave with PDF parameters c, k, x_o) to the ideal volume (VTI of ideal E-wave having same k and x_o but with no resistance filling [c = 0]). In 36 patients with normal ventricular function (17 diabetic and 19 well-matched nondiabetic controls) it was shown that³⁰ KFEI of E-waves in diabetic patients (49.1±3.3%) was significantly lower than in normal patients (55.8±3.3%). This means that even when LVEF is normal, filling efficiency is impaired in diabetics compared to nondiabetics.

FILLING EFFICIENCY DETERIORATES WITH AGE

In light of the ability of kinematic filling efficiency index (KFEI)²⁹ to assess filling in diabetes vs. nondiabetic controls, the age dependence of KFEI was determined. It was shown that KFEI, decreases in magnitude with age and correlates very strongly with age (R²=0.80) by analyzing 72 control subjects with normal LVEF (LVEF>55%) and without cardiovascular pathology³⁰. The age dependence of other conventional parameters of DF was also evaluated. In concordance with other noninvasive DF measures known to decrease with age, KFEI decreases and correlates very strongly with age (R²=0.80). Multivariate analysis showed that age is the single most important contributor to KFEI (p=0.003).

LOAD INDEPENDENT INDEX OF DIASTOLIC FUNCTION

E-wave contours demonstrate beat-by-beat changes in response to respiration and hence demonstrate strong load dependence. Indeed all indexes of DF are load-dependent. This is problematic because it calls into question whether observed differences in DF indexes are the result of load variation or the result of intrinsic chamber property variation. Theoretical prediction and experimental validation of a load independent index of diastolic function (LIIDF) has been a long sought unsolved problem in physiology/cardiology. To address the question of load dependence, the PDF formalism was applied to E-waves measured at variable loads. Through kinematic modeling and mathematical derivation, a load independent index was derived, which is conserved between E-waves measured at different loads. For each measured E-wave, the PDF parameters k and x_o are multiplied to yield kx_o, the model predicted peak force value analogous to the peak instantaneous pressure gradient driving flow, and the PDF parameter c is multiplied by the peak velocity E_peak to yield a value for the peak force resisting filling. Plotting kx_o vs. cE_peak as an ordered pair for each E-wave generates a highly linear relationship whose (dimensionless) slope M is the sought after load independent index and remains conserved despite load generated changes in E-waves.

For validation E-waves recorded while load was varied via tilt table (head up, horizontal, and head down) in 16 healthy volunteers was analyzed. The results³³ yielded the very high correlation (R² = 0.98) between kx_o and cE_peak as predicted. The ability of M to differentiate between normal and diastolic dysfunction subjects was also assessed by analysis of simultaneous cath-echo data in diastolic dysfunction subjects vs. controls. Average M for the diastolic dysfunction group (M = 0.98±0.07) was significantly lower than controls (M = 1.17±0.05, P<0.001)³³.

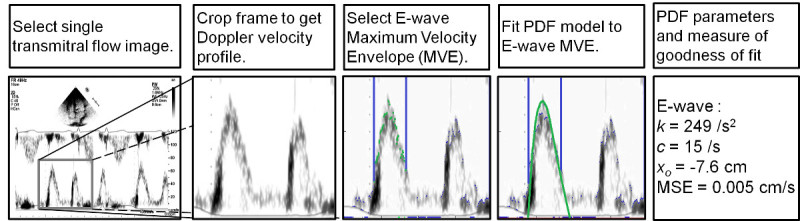Figure 1. Sequence of operational steps for fitting (A) an E-wave and (B) an E’-wave via the PDF formalism. A) From Left to Right- Transmitral flow image is cropped to obtain Doppler velocity profile. E-wave maximum velocity envelope (MVE) to be fit is selected (shown in green with time limits in blue). Error minimizing PDF fit is obtained via Levenberg- Marquardt algorithm resulting in PDF parameters and a measure of goodness of fit. B) Similar procedure for the tissue Doppler image. Image is inverted after cropping. See text for details. Please click here to view a larger version of this figure.

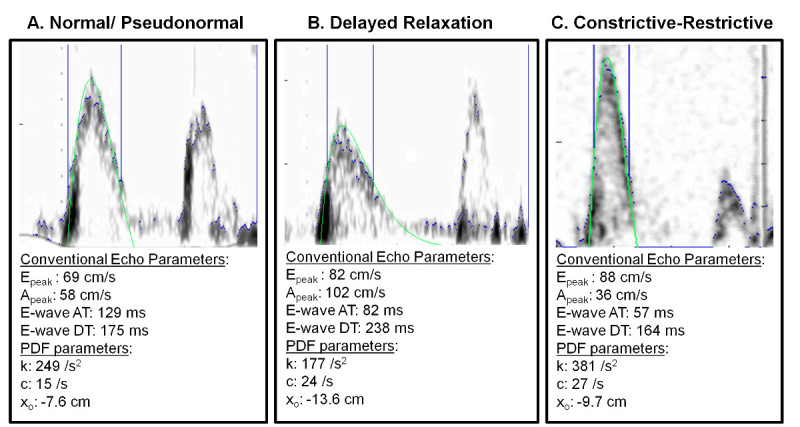Figure 2. Three E-wave patterns with PDF fits. A) Normal/Pseudonormal filling pattern. B) Delayed relaxation pattern. C) Constrictive-restrictive pattern. See text for details. Please click here to view a larger version of this figure.

Discussion

In keeping with our methodologic focus, the key aspects of the methods that facilitate obtaining accurate and meaningful results are highlighted.

ECHOCARDIOGRAPHY

The American Society of Echocardiography (ASE) has guidelines for the performance of transthoracic studies¹⁶. During an echo exam, there are a multitude of factors that affect image quality. Factors that are beyond the control of the sonographer include: technical capabilities of the imager being used, heart rate, patient body habitus, individual variation in the location, orientation of anatomical structures, and quality of ‘echo window’, referring to the characteristics of ultrasound transmission in a given subject’s tissue. Factors that are directly controllable by the sonographer include machine settings, including choice of transducer. Since the fidelity of the PDF analysis is dependent on the echo image quality, care should be taken during the image acquisition process to obtain the best possible images.

For optimal E-wave image quality for PDF analysis, maximizing E-wave size relative to the display and setting the sweep speed to 100 mm/sec are desirable. High sweep speed and use of the full display size in determining maximum velocity scale provides increased temporal resolution (i.e. more points to be fit) along both time and velocity axes. Baseline filter settings can also be better determined with higher sweep speed settings. The number of cardiac cycles recorded is highly variable between echo labs. For meaningful PDF analysis continuous recording through several (3 or 4) respiratory cycles is most desirable. At a typical resting heart rate of 75 beats/min, and 12 respirations/min, 4 respiratory cycles amount to 20 sec of continuous recording that should provide 25 cardiac cycles. Recording this number of cycles is justified because of the load varying consequence of quiet respiration, so that the LIIDF can be computed if desired. Note, that computing values for x_o, c, and k based on the 25 beat average is a legitimate way to characterize diastole. Load variation can also be generated during clinical recording by the Valsalva or Mueller maneuvers, or by passive leg elevation using a 30° foam wedge.

PDF PARAMETER DETERMINATION

ALGORITHMIC DETAILS

The equation of motion for a damped harmonic oscillator and its mathematical solution is standard course content in engineering mathematics, in physics and mechanics³⁴. The choice of computer language (C++, Fortran, LabView, MATLAB, etc.) by which it is implemented is also at the discretion of the user/investigator. Standard numerical methods exist and are well known³⁵. Other groups have implemented the PDF formalism by writing their own numerical algorithm and have independently replicated our results, including numerical values for the PDF parameters³⁶ in a large study involving well over 1,000 patients. While ongoing work includes developing web-based PDF analysis tools, the optimal, broad reaching benefit of the method could be best achieved by incorporation of the PDF formalism into the proprietary analysis package of commercial echocardiographic imagers.

OPERATOR DEPENDENT ASPECTS

Once the E-wave image has been imported and cropped (see Figure 1) determination of the maximum velocity envelope, i.e. the actual set of points to which the solution of damped harmonic oscillatory velocity is to be fit by the method, is determined. As shown by the sequence of panels and operational steps in Figure 1 and discussed above, baseline noise as well as extraneous noise that affects the contour is often part of the image. The operator can determine the continuous set of points to be fit, as shown in Figure 1, by adjusting the position of the vertical blue lines which define the start and end of the points to be fit. The method displays the fit directly over the imported image and the operator can easily assess if it is meaningful or not.

Heart rate has an effect on the duration of diastole and the features of the E-wave³⁷, and care must be taken to interpret the results of the fitting algorithm in the context of patient heart rate. At typical heart rates below 80 beats/min, in sinus rhythm E-and A-waves are separated by a brief period of diastasis. This facilitates inclusion of the deceleration portion of the E-wave. As heart rates increase, diastasis diminishes and disappears, since A-wave onset occurs before E-wave termination. At fast heart rates, above 90 beats/min, the A-wave overlies the deceleration portion of the E-wave and PDF analysis of the E-wave becomes unreliable because of the limited number of MVE points available to be fit. For meaningful analysis at least 1/2 to 2/3 of the total deceleration E-wave waveform should be available for fitting.

Disclosures

The authors have no competing financial interests.