On Vertex Covering Transversal Domination Number of Regular Graphs

Abstract

A simple graph G = (V, E) is said to be r-regular if each vertex of G is of degree r. The vertex covering transversal domination number γ _vct(G) is the minimum cardinality among all vertex covering transversal dominating sets of G. In this paper, we analyse this parameter on different kinds of regular graphs especially for Q _n and H _3,n. Also we provide an upper bound for γ _vct of a connected cubic graph of order n ≥ 8. Then we try to provide a more stronger relationship between γ and γ _vct.

1. Introduction

Hamid [1] introduced independent transversal domination in graphs. It was defined using maximum independent set in a graph. Vasanthi and Subramanian [2] introduced vertex covering transversal domination in graphs using minimum vertex covering set in a graph. The vertex covering transversal domination number of some standard graphs such as K _n, K _m,n, P _n, C _n, and W _n and trees is dealt with in paper [2]. Bounds of γ _vct are also established through various parameters in [2]. Lam et al. [3] worked on independent domination number of regular graphs. In this paper, we investigate our parameter γ _vct for regular graphs. Also we try to provide a more stronger relationship between γ and γ _vct.

A simple graph G = (V, E) is said to be r-regular if each vertex of G is of degree r. A set I⊆V of vertices in G is called an independent set if no two vertices in I are adjacent. Also I is said to be a maximum independent set if there is no other independent set I′ such that |I′| > |I|. The cardinality of a maximum independent set is called the independence number and is denoted by β ₀(G). A set C⊆V of vertices in G is called a vertex covering set (or simply covering set) if every edge of G is incident to at least one vertex in C. Also C is said to be a minimum vertex covering set if there is no other vertex covering set C′ such that |C′| < |C|. The cardinality of a minimum vertex covering set is called the vertex covering number and is denoted by α ₀(G). A set D⊆V of vertices in the graph G is called a dominating set if every vertex in V − D is adjacent to a vertex in D. A dominating set which intersects every minimum vertex covering set in G is called a vertex covering transversal dominating set. The minimum cardinality of a vertex covering transversal dominating set is called vertex covering transversal domination number of G and is denoted by γ _vct(G).

The parameter independent domination number i(G) was introduced by Cockanye and Hedetniemi in [4]. The independent domination number i(G) is the minimum cardinality among all independent dominating sets of G. An independent set is dominating if and only if it is maximal. So i(G) is the minimum cardinality of a maximal independent set in G. In paper [3], the following theorem which gives the upper bound for independent domination number of a connected cubic graph has been proved.

Theorem 1 . —

If G is a connected cubic graph of order n where n ≥ 8, then i(G) ≤ 2n/5.

2. Notations

We use the following notations throughout the paper:

•    α ₀-set to denote minimum vertex covering set,
•    β ₀-set to denote maximum independent set,
•    γ-set to denote a dominating set of minimum cardinality,
•    γ _vct-set to denote a vertex covering transversal dominating set of minimum cardinality,
•    γ(G) to denote domination number of G,
•    γ _vct(G) to denote vertex covering transversal domination number of G,
•    i(G) to denote independent domination number of G,
•    O(G) to denote the order of G,
•   deg_G(u) to denote the degree of a vertex u in G.

3. γ _vct for Regular Graphs

Here, we provide the vertex covering transversal domination number of some standard regular graphs such as complete graphs, complete bipartite regular graphs, cycles, and hypercube Q _n. We also establish γ _vct for certain family of regular graphs defined in [3].

Example 2 . —

K _n is a (n − 1)-regular graph and γ _vct(K _n) = 2 for n ≥ 2.

Example 3 . —

C _n is a 2-regular graph of order n ≥ 3 and

$$\begin{array}{c}{\gamma }_{\text{vct}}\left(C_n\right)=\left\{\begin{array}{cc}\mathrm{2}\hfill & \text{if\hspace{0.17em}\hspace{0.17em}}n=\mathrm{3,4}\hfill \\ \mathrm{3}\hfill & \text{if\hspace{0.17em}\hspace{0.17em}}n=\mathrm{5}\hfill \\ ⌈\frac{n}{\mathrm{3}}⌉\hfill & \text{otherwise}.\hfill \end{array}\right.\end{array}$$ (1)

Example 4 . —

K _n,n is a complete bipartite n-regular graph and γ _vct(K _n,n) = 2.

The following theorem provides the vertex covering transversal domination number of n-dimensional cube or hypercube Q _n defined in [5].

Theorem 5 . —

If Q _n is a hypercube containing 2ⁿ vertices which is n-regular, then

$$\begin{array}{c}{\gamma }_{vct}\left(Q_n\right)=\left\{\begin{array}{cc}\mathrm{2}\hfill & ifn=\mathrm{2}\hfill \\ {\mathrm{2}}^{n-\mathrm{2}}\hfill & ifn\ge \mathrm{3}.\hfill \end{array}\right.\end{array}$$ (2)

Proof —

The n-dimensional cube or hypercube Q _n contains 2ⁿ vertices and is n-regular. Each vertex in Q _n is represented by a n-tuple with 0's and 1's. Two vertices in Q _n are adjacent if and only if the n-tuples differ in exactly one position. Also any v ∈ Q _n is the n-tuple binary number and its complement v ^c is also an n-tuple binary number obtained by replacing 0 by 1 and 1 by 0 in v. The weight of a 0,1 vertex is the number of 1's occurring in it. There are exactly 2ⁿ⁻¹ vertices of odd weight and 2ⁿ⁻¹ vertices of even weight. Each edge of Q _n consists of a vertex of even weight and a vertex of odd weight. The vertices of even weight form an independent set and so do the vertices of odd weight. Therefore Q _n is bipartite with bipartitions S ₁ and S ₂ where S ₁ is the set of all n-tuples of even weight and S ₂ is the set of all n-tuples of odd weight with |S ₁| = |S ₂| = 2ⁿ⁻¹.

Also S ₁ and S ₂ are the only β ₀-sets of Q _n. Since they are complements of each other, S ₁ and S ₂ are the only α ₀-sets of Q _n.

For n = 2, Q ₂ is as shown in Figure 1. Obviously, S ₁ = {00,11} and S ₂ = {10,01} are α ₀-sets of Q ₂. Then D = {00,10} is a γ _vct-set of Q ₂ and so γ _vct(Q ₂) = 2.

Now suppose n ≥ 3.

For n = 3, Q ₃ is the hypercube on 8 vertices which is 3-regular and is represented as in Figure 1. The only two α ₀- sets of Q ₃ are S ₁ = {000,011,110,101} and S ₂ = {001,010,100,111}. Then γ _vct(Q ₃) = 2 since every two-element set of the form {v, v ^c} where v ∈ S ₁ and v ^c ∈ S ₂ is a γ _vct-set.

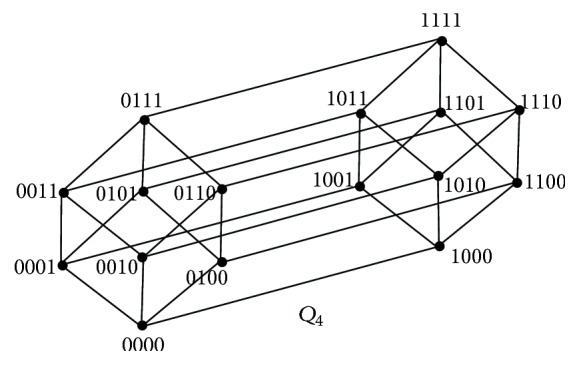
If n = 4, the hypercube Q ₄ contains 2⁴ vertices and is 4-regular as shown in Figure 2. Q ₄ is bipartite with bipartitions S ₁ = {0000,0011,0110,1100,0101,1010,1001,1111} and S ₂ = {0001,0010,0100,1000,0111,1110,1011,1101}. Also S ₁ and S ₂ are the only α ₀-sets of Q ₄.

Let D = {0000,1111,0001,1110}. Then D is a dominating set of Q ₄. Clearly it intersects both S ₁ and S ₂. Therefore D is a vertex covering transversal dominating set and so γ _vct(Q ₄) = 4. Hence it remains to show that D is of minimum cardinality.

Suppose there exists a vertex covering transversal dominating set D′ of cardinality less than 4. It must have at least 2 vertices as it intersects both S ₁ and S ₂. Suppose |D′| = 3. Since each vertex is of degree 4, all the three vertices in D′ may dominate at most 12 vertices. But there are 16 vertices in Q ₄ and so D′ do not dominate at least 1 vertex. This is a contradiction to the assumption that D′ is a vertex covering transversal dominating set.

Also any set containing two mutually complementary vertices from S ₁, say, 1100, 0011, and the other two mutually complementary vertices from S ₂, say, 1000, 0111, form a γ _vct-set. Thus S = {v ₁, v ₁ ^c, v ₂, v ₂ ^c} where v ₁, v ₁ ^c ∈ S ₁ and v ₂, v ₂ ^c ∈ S ₂ is a γ _vct-set of Q ₄.

If n = 5, the hypercube Q ₅ contains 2⁵ = 32 vertices and the bipartition S ₁ contains 2⁴ vertices and S ₂ contains 2⁴ vertices. Let S = {v ₁, v ₁ ^c, v ₂, v ₂ ^c, v ₃, v ₃ ^c, v ₄, v ₄ ^c} where v ₁, v ₂, v ₃, v ₄ ∈ S ₁ and v ₁ ^c, v ₂ ^c, v ₃ ^c, v ₄ ^c ∈ S ₂. Then S is a γ-set which intersects both S ₁ and S ₂. Hence γ _vct(Q ₅) = 2³.

Thus in general, S = {v 1, v 1 c, v 2, v 2 c,…, v 2n−3−1, v 2n−3−1 c, v 2n−3, v 2n−3 c} is a γ vct-set of Q n. In particular, if n is odd, v 1, v 2,…, v 2n−3 ∈ S 1 and v 1 c, v 2 c,…, v 2n−3 c ∈ S 2. If n is even, v 1, v 1 c, v 2, v 2 c,…, v 2n−4, v 2n−4 c ∈ S 1 and v 2n−4+1, v 2n−4+1 c,…, v 2n−3, v 2n−3 c ∈ S 2. Hence γ vct(Q n) = 2n−2.

Figure 1.

Figure 2.

Theorem 6 . —

If G is a connected regular graph of degree n − 2 and O(G) = n, then γ _vct(G) = 2.

Proof —

Choose any vertex u ∈ V(G). Then deg_G(u) = n − 2; that is, u is adjacent to n − 2 vertices in G. Then there remains exactly one vertex, say, v, which is not adjacent to u. Therefore S = {u, v} is an independent set of G. Also v is adjacent to n − 2 vertices in G except u. Hence no other vertex may be included in S. Therefore S is a maximum independent set of G.

Now let w ∈ V − S. Then w is adjacent to both u and v. Since u dominates every vertex in G except v, and w dominates n − 2 vertices including v, it is obvious that D = {u, w} is a dominating set which intersects every minimum vertex covering set of G. Also D is of minimum cardinality in G. Hence γ _vct(G) = 2.

It is noted that {v, w} is also a γ _vct-set.

Remark 7 . —

In the above theorem, n should be even. For otherwise, if n is odd, then n − 2 is odd which is impossible as the number of vertices of odd degree in a graph is even.

Lemma 8 . —

Given positive integers p ≥ 2 and q ≥ 3, let G(p, q) be the family of graphs such that V = ⋃_i=1 ^p(X _i ∪ Y _i ∪ Z _i) and E = E ₁ ∪ E ₂ ∪ E ₃ ∪ E ₄ with

•    X _i = {x _i1, x _i2,…, x _{i(q − 1)}}, Y _i = {y _i1, y _i2,…, y _iq}, Z _i = {z _i1, z _i2,…, z _iq},
•    E ₁ = ⋃_i=1 ^p{x _ik y _il; 1 ≤ k ≤ q − 1, 1 ≤ l ≤ q},
•    E ₂ = ⋃_i=1 ^p{y _ik z _ik; 1 ≤ k ≤ q},
•    E ₃ = ⋃_i=1 ^p{z _ik z _il; 1 ≤ k, l ≤ q, k ≠ l} − {z _i1 z _iq},
•    E ₄ = {z _iq z _{(i + 1)1}; 1 ≤ i ≤ p − 1} ∪ {z _pq z ₁₁}.

Then

• (i)|V(G)| = p(3q − 1),
• (ii) G(p, q) is connected and q-regular,
• (iii) γ _vct(G(p, q)) = 4p.

Proof —

G(p, q) contains p subgraphs which we shall call blocks each containing 3q − 1 vertices and isomorphic to each other. By the edge set E ₄, we observe that they are connected to each other.

Thus (i) and (ii) are obvious.

For q = 4, two connected blocks of G(p, 4) each consisting of 11 vertices are as shown in Figure 3.

Now I = ⋃_i=1 ^p Y _i is a maximum independent set of G(p, q). Then its complement S = V − I = ⋃_i=1 ^p(X _i ∪ Z _i) is a minimum vertex covering set of G(p, q).

Also I _j = ⋃_i=1 ^p(Y _i − {y _ij}) ∪ {z _ij} and J _j = ⋃_i=1 ^p(X _i) ∪ {z _ij}, 1 ≤ j ≤ q are maximum independent sets in G(p, q). Let S _j and T _j be the complement of each I _j and J _j. Then S _j = ⋃_i=1 ^p((X _i ∪ Z _i) − {z _ij} ∪ {y _ij}) and T _j = ⋃_i=1 ^p((Y _i ∪ Z _i) − {z _ij}), 1 ≤ j ≤ q are minimum vertex covering sets in G(p, q). Now the subgraph G _i induced by X _i ∪ Y _i in each block is a complete bipartite graph K _q−1,q.

Since γ _vct(K _m,n) = 2 if m, n > 1, we have γ _vct(K _q−1,q) = 2. Also each {x _ij, y _ik} for 1 ≤ j ≤ q − 1 and 1 ≤ k ≤ q is a vertex covering transversal dominating set of G _i. Then {x _ij, y _ik, z _i1, z _iq}, 1 ≤ j ≤ q − 1 and 1 ≤ k ≤ q, is a dominating set for each block. Therefore D _jk = ⋃_i=1 ^p{x _ij, y _ik, z _i1, z _iq}, 1 ≤ j ≤ q − 1 and 1 ≤ k ≤ q, is a γ-set which intersects the only α ₀-sets S, S _j and T _j of G(p, q) for each j.

Hence γ _vct(G(p, q)) = 4p.

Figure 3.

Theorem 9 . —

If q ≥ 3, then there exists a connected q-regular graph with γ _vct(G)≥⌈4n/3q⌉ where n is the order of G.

Proof —

Let G = G(p, q) be defined as in Lemma 8. Then γ _vct(G)/n = 4/(3q − 1) ≥ 4/3q. Thus γ _vct(G) ≥ 4n/3q.

Lemma 10 . —

Given positive integers p ≥ 1 and q ≥ 2, let G ^∗(p, q) be the graph (V, E) with V = U ∪ [⋃_i=1 ^2p+1(V _i ∪ W _i)] and E = E ₁ ∪ E ₂ ∪ E ₃ ∪ E ₄ with

•    U = {u ₁, u ₂,…, u _2p+1}, V _i = {v _i1, v _i2,…, v _{i(q + 2p)}}, W _i = {w _i1, w _i2,…, w _{i(q + 2p − 1)}},
•    E ₁ = {u _j u _k; 1 ≤ j < k ≤ 2p + 1},
•    E ₂ = ⋃_i=1 ^2p+1{u _i v _ik; 1 ≤ k ≤ q},
•    E ₃ = ⋃_i=1 ^2p+1{v _i(q+2k−1) v _i(q+2k); 1 ≤ k ≤ p},
•    E ₄ = ⋃_i=1 ^2p+1{v _ik w _il; 1 ≤ k ≤ q + 2p, 1 ≤ l ≤ q + 2p − 1}.

Then

• (i)|V(G)| = 2(2p + 1)(q + 2p),
• (ii) G ^∗(p, q) is connected and (q + 2p)-regular,
• (iii) γ _vct(G ^∗(p, q)) = 2(2p + 1).

Proof —

(i) and (ii) are obvious. If p = 1 and q = 2, the graph G ^∗(1,2) is as shown in Figure 4.

It is clear that each I _j = [⋃_i=1 ^2p+1(W _i)] ∪ {u _j}, j = 1 to 2p + 1, is a maximum independent set in G ^∗(p, q). Therefore its complement J _j = V − I _j = [⋃_i=1 ^2p+1(V _i)]∪[U − {u _j}], j = 1 to 2p + 1, is an α ₀ set in G ^∗(p, q). Further J ₁, J ₂,…, J _2p and J _2p+1 are the only α ₀-sets of G ^∗(p, q). Now each S _jk = ⋃_i=1 ^2p+1{v _ik, w _ij}, j = 1 to q + 2p − 1, k = 1 to q is a dominating set intersecting J ₁, J ₂,…, J _2p and J _2p+1 and also of minimum cardinality 2(2p + 1).

Hence γ _vct(G ^∗(p, q)) = 2(2p + 1).

Figure 4.

Theorem 11 . —

For every r ≥ 4, there exists a connected r-regular graph G of order n such that γ _vct(G) = n/r.

Proof —

Let G = G ^∗(p, q) be defined as in Lemma 10. Then G is a connected r-regular graph with r = q + 2p. Also γ _vct(G)/n = 1/(q + 2p).

Thus γ _vct(G) = n/r.

Remark 12 . —

Theorems 9 and 11 hold good if γ _vct is replaced by γ.

4. γ _vct for Regular Cubic Graphs

In this section, we provide the vertex covering transversal domination number of some regular cubic graphs especially Harary graph H _3,n defined in [6]. We also obtain an upper bound for the vertex covering transversal domination number of a connected cubic graph.

Example 13 . —

Consider the triangular prism graph Y ₃ shown in Figure 5. It is a regular cubic graph.

Figure 5.

Y ₃ has 6 vertices and 9 edges. Assume that the graph Y ₃ is labelled as shown in the diagram. It is clear that {u _imod⁡3, v _{(i + 1)mod⁡3}} and {u _imod⁡3, v _{(i + 2)mod⁡3}} for i = 0,1, 2 are β ₀-sets of Y ₃. Then their complements C _i = {u _{(i + 1)mod⁡3}, u _{(i + 2)mod⁡3}, v _imod⁡3, v _{(i + 2)mod⁡3}} and S _i = {u _{(i + 1)mod⁡3}, u _{(i + 2)mod⁡3}, v _imod⁡3, v _{(i + 1)mod⁡3}} for i = 0,1, 2 are α ₀-sets of Y ₃. Now each D _i = {u _imod⁡3, v _imod⁡3}, i = 0,1, 2 is a γ-set for Y ₃. Clearly it intersects each C _i and S _i. Therefore γ _vct(Y ₃) = 2.

Example 14 . —

Consider Peterson graph which is cubic regular shown in Figure 6.

Figure 6.

Assuming that the graph G is labelled as shown in Figure 6, it is obvious that I _i = {v _imod⁡5, v _{(i + 3)mod⁡5}, u _{(i + 1)mod⁡5}, u _{(i + 2)mod⁡5}}, i = 0,1, 2,3, 4 are β ₀-sets of G. Then their complements C _i = {v _{(i + 1)mod⁡5}, v _{(i + 2)mod⁡5}, v _{(i + 4)mod⁡5}, u _imod⁡5, u _{(i + 3)mod⁡5}, u _{(i + 4)mod⁡5}}, i = 0,1, 2,3, 4 are α ₀-sets of G. Now S _i = {v _imod⁡5, u _{(i + 2)mod⁡5}, u _{(i + 3)mod⁡5}} are γ-sets intersecting each C _i. Hence γ _vct(G) = 3.

Note that S _i = {v _imod⁡5, v _{(i + 3)mod⁡5}, u _{(i + 4)mod⁡5}} are also γ _vct-sets in G.

Theorem 15 . —

If H _3,n is a Harary graph with n ≥ 6, then γ _vct(H _3,n) = ⌊(n + 1)/3⌋.

Proof —

H _3,n is a 3-regular graph and so n is even. By the definition of H _3,n, every vertex v _i ∈ H _3,n is adjacent to the vertices v _i+1, v _i−1, and v _i+k where n = 2k.

Let V(H _3,n) = {v ₀, v ₁, v ₂,…, v _n−1}. The graphs H _3,10 and H _3,12 are shown in Figure 7.

Case  1. Suppose n = 2k where k is odd.

Then C ₁ = {v ₀, v ₂, v ₄,…, v _n−2} and C ₂ = {v ₁, v ₃, v ₅,…, v _n−1} are the only α ₀-sets of H _3,n.

Subcase  1. Let n ≡ 0 (mod⁡3).

Then S = {v ₀, v ₃, v ₆,…, v _n−3} is a γ-set which intersects C ₁ and C ₂ and |S| = n/3.

Subcase  2. Suppose n ≡ 1 (mod⁡3).

Then S = {v ₀, v ₃, v ₆,…, v _n−4} is a γ-set which intersects C ₁ and C ₂ and |S| = (n − 1)/3.

Subcase  3. Suppose n ≡ 2 (mod⁡3).

Then S = {v ₀, v ₃, v ₆,…, v _n−2} is a γ-set which intersects C ₁ and C ₂ with |S| = (n + 1)/3.

Thus in all the subcases of Case  1, γ _vct(H _3,n) = ⌊(n + 1)/3⌋.

Case  2. Suppose n = 2k where k is even.

Then I _i = {v _imod⁡n, v _{(i + 2)mod⁡n},…, v _{(i + k − 2)mod⁡n}, v _{(i + k + 1)mod⁡n}, v _{(i + k + 3)mod⁡n},…, v _{(i + n − 5)mod⁡n}, v _{(i + n − 3)mod⁡n}} is a β ₀-set for each i = 0,1, 2,…, n − 1.

Therefore C _i = {v _{(i + 1)mod⁡n}, v _{(i + 3)mod⁡n},…, v _{(i + k − 1)mod⁡n}, v _{(i + k)mod⁡n}, v _{(i + k + 2)mod⁡n},…, v _{(i + n − 4)mod⁡n}, v _{(i + n − 2)mod⁡n}, v _{(i + n − 1)mod⁡n}} is an α ₀-set for each i = 0,1, 2,…, n − 1.

Subcase  1. Let n ≡ 0 (mod⁡3).

Then S _i = {v _imod⁡n, v _{(i + 3)mod⁡n}, v _{(i + 6)mod⁡n},…, v _{(i + n − 3)mod⁡n}} is a γ-set which intersects each C _i for i = 0,1, 2,…, n − 1.

Subcase  2. Let n ≡ 1 (mod⁡3).

Then S _i = {v _imod⁡n, v _{(i + 3)mod⁡n}, v _{(i + 6)mod⁡n},…, v _{(i + n − 4)mod⁡n}} is a γ-set which intersects each C _i for i = 0,1, 2,…, n − 1.

Subcase  3. Let n ≡ 2 (mod⁡3).

Then S _i = {v _imod⁡n, v _{(i + 3)mod⁡n}, v _{(i + 6)mod⁡n},…, v _{(i + n − 2)mod⁡n}} is a γ-set which intersects each C _i for i = 0,1, 2,…, n − 1.

The γ _vct-sets mentioned in all the subcases of Case  2 are also of cardinality ⌊(n + 1)/3⌋.

Thus γ _vct(H _3,n) = ⌊(n + 1)/3⌋.

Figure 7.

Remark 16 . —

In most of the graphs considered by us, it is observed that γ _vct = γ.

Theorem 17 . —

If G is a connected cubic graph of order n with n ≥ 8, then γ _vct(G)≤⌈2n/5⌉.

Proof —

Let I be an independent dominating set of cardinality i(G). Then I is a maximal independent set of minimum cardinality. Since I is independent, no two vertices of I are adjacent in G. Let J = V − I. Then the vertices in I are adjacent only to the vertices in J.

Case  1. Suppose I itself is a β ₀-set. Then J is an α ₀-set. Let S = I ∪ {v} where v ∈ J. Then S is a vertex covering transversal dominating set of G. Therefore γ _vct(G) ≤ i(G) + 1. Hence γ _vct(G) ≤ 2n/5 + 1 (by Theorem 1 proved in [3]).

Case  2. Suppose I is not a β ₀-set. But I is a maximal independent dominating set of minimum cardinality. We claim that I intersects every α ₀-set of G.

Suppose that I does not intersect an α ₀-set C of G. Then I ⊂ V − C where V − C is a β ₀-set of G. This is a contradiction to the maximality of I.

Hence I itself is a vertex covering transversal dominating set of G. Therefore γ _vct(G) ≤ 2n/5.

Thus Cases  1 and 2 imply that γ _vct(G)≤⌈2n/5⌉.

5. Relation between γ(G) and γ _vct(G)

In this section, we prove a more stronger relationship between γ and γ _vct than that proved in [2]. In view of the results and theorems dealt with in the previous sections, we try to characterize graphs for which γ = γ _vct and γ < γ _vct.

Theorem 18 . —

If G is a simple connected graph, then γ _vct(G) ≤ γ(G) + 1.

Proof —

Let D be a minimum dominating set. If D = V(G), then obviously γ _vct(G) = γ(G). If not, then D ⊂ V(G) and V(G) − D ≠ ϕ. Let u ∈ V(G) − D. Then u is dominated by some vertex v in D. Let S = D ∪ {u}. Since uv is an edge in G, either u or v is included in every minimum vertex covering set of G. This implies that S intersects every minimum vertex covering set in G. Hence γ _vct(G) ≤ γ(G) + 1.

Theorem 19 . —

Let G be a simple connected graph. If there exists a γ-set which is not independent, then γ _vct(G) = γ(G).

Proof —

Let D be a minimum dominating set which is not an independent set of G. Then at least two vertices, say, u, v in D, are adjacent to each other. Therefore uv is an edge in G and hence either u or v lies in every minimum vertex covering set of G. So D intersects every α ₀-set of G. Therefore D itself is a γ _vct-set. Hence γ _vct(G) = γ(G).

Remark 20 . —

The converse is not true. If γ _vct(G) = γ(G), then there may exist a γ-set which is independent also. For example, consider C ₆, the cycle on 6 vertices as shown in Figure 8.

Obviously {v ₁, v ₃, v ₅} and {v ₂, v ₄, v ₆} are the only α ₀-sets of C ₆. Also {v ₁, v ₄} is a γ-set which is independent. Further, it is a γ _vct-set as it intersects both the α ₀-sets of C ₆. Thus there exists a γ-set which is independent in C ₆ even though γ _vct(C ₆) = γ(C ₆).

Figure 8.

Remark 21 . —

Now, the obvious question is “If γ _vct(G) = γ(G), is every γ-set of G a γ _vct-set?” The answer is “not always.” The γ-sets and γ _vct-sets in the graphs Q ₂ and Y ₃ discussed in the previous sections are the best examples for it. So it is noted that this happens if there exists a γ-set which is also a β _o-set. It obviously produces the result that “If γ _vct(G) = γ(G) = β _o(G), then there exists at least one γ-set in G which is not a γ _vct-set.” The next general question is that “What happens if all the γ-sets of G are β ₀-sets?”. The following theorem provides the answer to it.

Theorem 22 . —

Let G be a simple connected graph. If every γ-set of G is a β ₀-set, then γ _vct(G) = γ(G) + 1.

Proof —

Since every γ-set D of G is a β ₀-set, choose a vertex v in its complement. This is possible since D ≠ V(G) as D is a β ₀-set of a connected graph G. Obviously D is not a γ _vct-set as it does not intersect the α ₀-set V(G) − D. Let S = D ∪ {v}. We claim that S intersects every α ₀-set of G. Suppose that S∩C = Φ for some α ₀-set C in G. Then S⊆I where I = V(G) − C is a β ₀-set. This implies that β ₀(G) + 1 ≤ β ₀(G) which is a contradiction. Hence S intersects every α ₀-set of G. Also S is a γ _vct-set of G as it contains exactly one vertex more than that of the γ-set D. Thus γ _vct(G) = γ(G) + 1.

Remark 23 . —

It is easy to conclude that even though γ _vct = γ, there are graphs in which γ-sets do not become γ _vct-sets. This implies that the collection of γ _vct-sets in such graphs is contained in the collection of γ-sets. So this may lead to consider γ _vct-sets in the graphs for which γ _vct = γ when we are in a situation to select a minimum number of γ-sets in such graphs. This approach may affect a new variation in domination theory.

Competing Interests

The authors declare that there are no competing interests regarding the publication of this paper.