Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Apr 12;6:24114. doi: 10.1038/srep24114

Neurons in the inferior colliculus of the rat show stimulus-specific adaptation for frequency, but not for intensity

Daniel Duque 1,*,†, Xin Wang 1,*,‡, Javier Nieto-Diego 1, Katrin Krumbholz 2, Manuel S Malmierca 1,3,4,a
PMCID: PMC4828641  PMID: 27066835

Abstract

Electrophysiological and psychophysical responses to a low-intensity probe sound tend to be suppressed by a preceding high-intensity adaptor sound. Nevertheless, rare low-intensity deviant sounds presented among frequent high-intensity standard sounds in an intensity oddball paradigm can elicit an electroencephalographic mismatch negativity (MMN) response. This has been taken to suggest that the MMN is a correlate of true change or “deviance” detection. A key question is where in the ascending auditory pathway true deviance sensitivity first emerges. Here, we addressed this question by measuring low-intensity deviant responses from single units in the inferior colliculus (IC) of anesthetized rats. If the IC exhibits true deviance sensitivity to intensity, IC neurons should show enhanced responses to low-intensity deviant sounds presented among high-intensity standards. Contrary to this prediction, deviant responses were only enhanced when the standards and deviants differed in frequency. The results could be explained with a model assuming that IC neurons integrate over multiple frequency-tuned channels and that adaptation occurs within each channel independently. We used an adaptation paradigm with multiple repeated adaptors to measure the tuning widths of these adaption channels in relation to the neurons’ overall tuning widths.

Adaptation refers to the suppression of the brain’s response to repeatedly or frequently occurring sensory stimuli. Adaptation has been found from single-neuron to macroscopic population responses and is ubiquitous across sensory systems1,2. Nevertheless, its functional role remains debated. For example, it has been suggested that adaptation might enable the brain to efficiently encode stimuli with time-varying statistical properties3,4. Adaptation tends to be specific to the repeated stimulus and not generalize to other, rare stimuli. This has led to the suggestion that adaptation might facilitate the detection of unexpected deviant events in the environment5,6.

The oddball paradigm involves presentation of rare deviant stimuli interspersed among frequent standard stimuli. In the auditory domain, deviants elicit an enhancement in electroencephalographic response, referred to as the mismatch negativity (MMN)7. The MMN can be elicited with a variety of different deviant features, including sound frequency, duration, complex pitch or sound location8,9,10,11. Importantly, an MMN can be elicited by decrements in sound duration12,13 or sound intensity14 and even by sound omissions15. This behavior is difficult to explain in terms of recruitment of unadapted neural elements by the deviants and has therefore been interpreted to suggest that the MMN represents a deviance detection process16.

Enhanced responses to deviant compared to standard sounds have been observed in individual auditory neurons, both in cortex17,18 and in subcortical stations19,20,21, and are described as stimulus-specific adaptation (SSA22). SSA has been widely proposed as a single-neuron precursor or correlate of the MMN5,17,23. Like the MMN, SSA can be elicited by features other than frequency24,25. However, it remains unclear whether, or to what extent, SSA reflects true deviance sensitivity as observed in the MMN22,26, and, in particular, where in the ascending auditory pathway sensitivity to low-intensity deviants embedded in a sequence of high-intensity standards might first emerge26,27,28,29.

The current study addresses this question by measuring responses to oddball sequences where the standard and deviant have the same frequency but differ in intensity (referred to as intensity oddball sequences) from single inferior colliculus (IC) neurons in anesthetized rats. For comparison, we also measured responses to frequency- and double (frequency and intensity) oddball sequences. We modelled the measured responses assuming that IC neurons integrate over multiple frequency-tuned channels and that adaptation occurs independently within each of these channels (henceforth referred to as adaptation channels22,30). We devised a novel adaptation paradigm with repeated adaptors (repeated adaptation paradigm, or RAP), which allowed us to characterize the tuning widths of the adaptation channels in relation to the neurons’ overall tuning widths. Our results showed no evidence of SSA for low-intensity deviant sounds in the IC. They indicate that SSA in the IC is only generated when the deviant sound activates different frequency-tuned channels than the standard sound and suggest that, at least in this subcortical relay station, SSA is dependent on input-specific adaptation mechanisms31.

Results

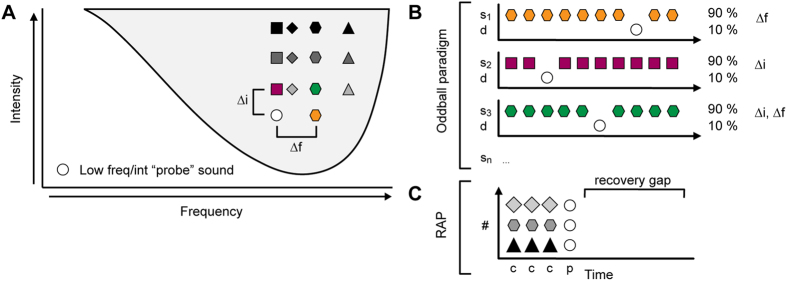
We recorded oddball paradigm responses from 120 single units in the IC of the rat. We determined the frequency response area of each neuron (FRA) and chose a pair of frequencies, f1 and f2, within the FRA to evaluate SSA in a frequency oddball paradigm (Fig. 1A). Then, in order to test whether SSA is generated by intensity-deviants, we fixed the lower of the two frequencies (f1) and tested oddball paradigms where the standards and deviants differed in intensity only, or in both frequency and intensity (intensity and double oddball paradigms, respectively). In the following, we first describe the responses for the frequency oddball paradigm, where the frequency difference between the standards and deviants, Δf, was 0.1 (Fig. 1B). Second, we describe the intensity and double oddball paradigms with the smallest intensity difference of Δi = 10 dB (Fig. 1B). Then, we present the responses for the intensity and double oddball paradigms with larger intensity differences. Finally, we present the data obtained with the repeated adaptation paradigm (RAP; Fig. 1C; see Methods), which was measured in 33 additional units (not contained within the main sample of the 120 units). We use a model to test if adaptation channels in the IC are determined by the tuning properties of the cochlear frequency channels.

Figure 1. Experimental design.

Figure 1

Open in a new tab

(A) Schematic FRA showing the stimuli in the frequency, intensity and double oddball conditions. The lower-frequency/intensity stimulus is shown by the white circle and the different high-frequency/intensity sounds are shown by different colored symbols. (B) Schematic representation of frequency (top), intensity (middle) and double (bottom) oddball paradigms. The color and shape of the symbols is as in (A). In this example, the high-frequency/intensity sound is the as standard. (C) Schematic representation of the repeated adaptation paradigm (RAP). The adaptor (gray symbols) was presented at a wide range of frequencies and intensities throughout the FRA (white circle; see panel (A)).

SSA to frequency and double, but not pure intensity, deviants

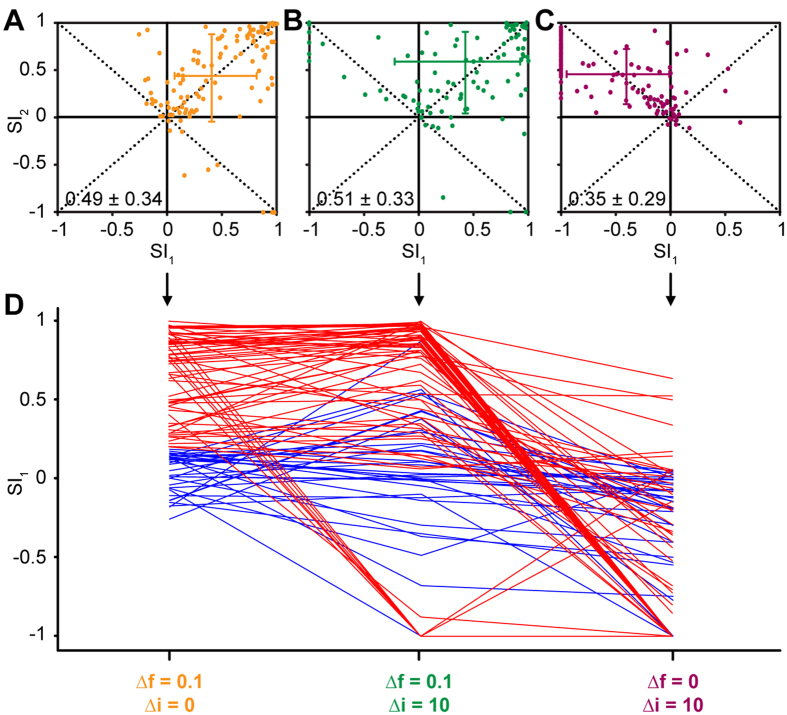
The common SSA index (CSI) was used to quantify SSA in the frequency oddball paradigm (Δf = 0.1, SOA = 250 ms). Across n = 120 neurons, the CSI ranged from −0.09 to 0.99 with a mean of 0.49 ± 0.34 (mean ± S.D.), confirming our previous results19,32,33. Based on these CSI values, we defined two populations of neurons, one with strong SSA and the other with weak SSA, by setting a CSI cutoff criterion of +0.18 (the same value as used in previous studies21). Based on this criterion, 70% of neurons (n = 84) showed strong SSA and 30% (n = 36) showed weak SSA. SSA was also quantified using the frequency-specific SSA index (SI1/2). As expected based on previous results19,32,33,34, in the majority of neurons, both SI values were positive (data points located in the upper right quadrant of Fig. 2A; SI1 = 0.42 ± 0.46 (mean ± S.D.); SI2 = 0.45 ± 0.38). This indicates that the responses to both frequencies (f1 and f2) were more strongly adapted when presented as standard than when presented as deviant, and thus that SSA was present.

Figure 2. IC neurons do not show intensity SSA.

Figure 2

Open in a new tab

(A) Scatter plot of suppression indices (SI) for higher- frequency (SI2) versus lower-frequency (SI1) deviant stimulus in the frequency oddball paradigm (Δf = 0.1). Each dot represents one neuron. The cross indicates the median and interquartile range for each index. The median CSI value and interquartile range at the bottom of the panel. (B) Same as (A) but for the double oddball condition with Δf = 0.1 and Δi = 10 dB. (C) Same as (A,B) but for the intensity oddball condition with Δi = 10 dB. (D) SI1 values for neurons with low (<0.18; blue) or high (≥0.18; red) CSI values in the frequency oddball condition (A), plotted across all three oddball conditions (abscissa).

Figure 2B shows the SI scatter plot for the double oddball condition where Δf was 0.1 as in the frequency oddball condition, but Δi was 10 dB (see green hexagon in Fig. 1A; measured in n = 97 neurons). The CSI values recorded in the double oddball condition ranged from −0.04 to 0.99, with a mean of 0.51 ± 0.33. As for the frequency oddball condition, in the majority of neurons, both SI values were positive (data points in upper right quadrant of Fig. 2B), again indicating SSA (SI1 = 0.48 ± 0.43; SI2 = 0.36 ± 0.57). However, in a small proportion of neurons, SI1 was negative (data points in upper left quadrant), indicating that the lower-frequency/intensity stimulus (f1, i1) elicited a smaller response when presented as deviant than when presented as standard.

Figure 2C shows the SI scatter plot for the intensity oddball paradigm (Δf = 0) with the same intensity difference as in the previous two conditions (Δi = 10 dB; n = 117 neurons). In this condition, the CSI values ranged from −0.04 to 0.92 with a mean of 0.35 ± 0.29. Note that, whilst the CSI values for the intensity oddball condition were smaller than for the frequency and double oddball conditions (Kruskall-Wallis ANOVA on Ranks test; H = 16.70; p < 0.001), the mean CSI value was still positive. This would seem to imply that the intensity oddball condition also elicited SSA. However, the SI scatter plot shows that, in the majority of neurons (n = 95, or 81%), SI1 was negative (data points located in the upper left quadrant; SI1 = −0.48 ± 0.47). This means that the responses to the lower-intensity stimulus were smaller when the stimulus was presented as deviant than as standard. At the same time, SI2 was mostly positive (SI2 = 0.45 ± 0.29), indicating that the responses to the higher-intensity stimulus were generally larger when the stimulus was presented as deviant than as standard. There were 4 neurons (3.4%) with SI1 values larger than +0.18 (the cutoff criterion for strong SSA; see above). However, a bootstrap test (with 1000 within-neuron resamples of trials) showed that the positive SI1 values in these neurons arose, because the lower-intensity stimulus elicited little or no response either as standard or as deviant. When neither the standard nor the deviant elicit a significant response, the SI becomes singular and thus meaningless. Forty-four neurons (37.8%) showed an SI1 value of −1, indicating that the lower-intensity stimulus elicited zero response when presented as deviant.

Figure 2D shows the SI1 values separately for the groups of neurons with strong and weak frequency SSA. The figure shows that neurons with strong frequency SSA (red) generally also showed strong SSA in the double oddball condition, but not SSA for the intensity oddball condition (indicated by negative SI1 values). In contrast, the group with weak frequency SSA (blue) showed SI1 values close to zero in all three conditions.

Responses to higher-intensity standards adapt responses to lower-intensity deviants

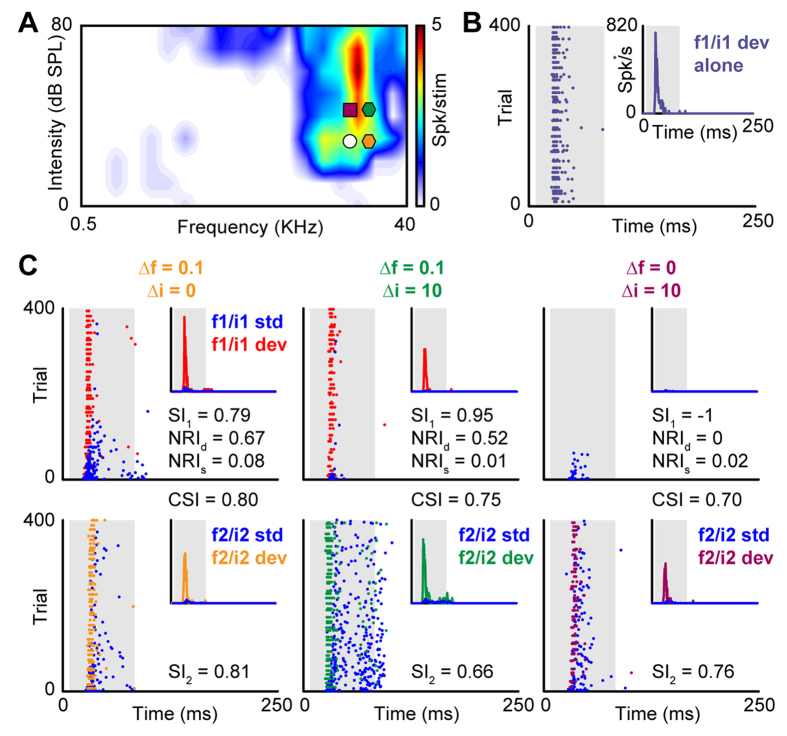
Whilst the CSI works well for frequency oddball paradigms, where the two stimuli are chosen to elicit similar firing rates21, it fails for intensity oddball paradigms, where the firing rates elicited by the two stimuli can be very different. Figure 3 shows a typical example illustrating this effect. In the frequency and double oddball conditions (Fig. 3C, left and middle panels), both the CSI and SI values correctly indicate the presence of SSA. However, in the intensity oddball condition, the CSI wrongly suggests SSA, because it is being biased by the much larger responses to the higher-intensity sound than to the lower-intensity sound (compare right panels in Fig. 3C), which means that the (positive) difference between the higher-intensity deviants and standard responses is often larger than the (negative) difference between the lower-intensity deviants and standard responses.

Figure 3. Single-neuron example of frequency, intensity and double oddball responses and corresponding SSA indices.

Figure 3

Open in a new tab

(A) FRA of the neuron together with stimuli, plotted as in Fig. 1A. (B) Dot raster plot showing the neuron’s responses to the low-frequency/intensity sound (f1/i1; white circle in (A)) in the deviant-alone protocol. The inset shows the corresponding PSTH. The gray-shaded background indicates the timing of the stimulus. (C) Dot raster plots showing the neuron’s responses to the low-frequency/intensity sound (top row) when presented as standard (blue) or as deviant (red; see legend in leftmost panel) in the frequency oddball paradigm (left panel; orange hexagon in (A), the double oddball paradigm with Δf = 0.1 and Δi = 10 dB (right panel; green hexagon in (A) and the intensity oddball paradigm with Δi = 10 dB (right panel; burgundy square in (A). As reference, in the bottom row we show the responses to the high-frequency/intensity sounds (f2/i2) when presented as standard (blue) or as deviant (orange, green or burgundy). All PSTHs shown in this figure have been normalized to the f1/i1 deviant-alone response and are thus shown in relative units. The relevant SI1, NRId and NRIs values are also shown in each panel in the top row. The CSI values, calculated by combining the data from corresponding panels in the top and bottom row are shown between the panels. As reference, SI2 value is shown in the bottom row.

Tradeoff between frequency separation and intensity difference in double oddball paradigms

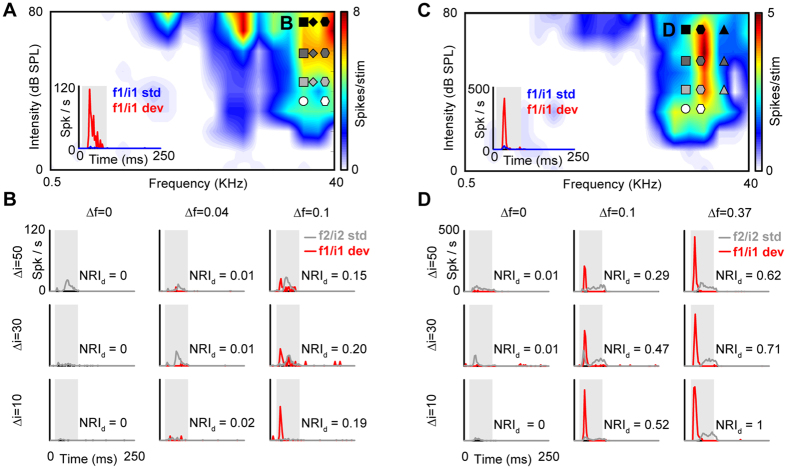
CSI and SI values represent the difference between the deviant and standard responses relative to the summed response. Both indices become singular and thus fail when the summed response is small (as is often the case in intensity oddball paradigms). Here, we devise a new index, referred to as the normalized response index (NRI) to evaluate the degree of adaptation of the deviant and standard responses separately (see Methods). We use the NRI to explore how the degree of adaptation of the deviant response depended on the frequency and intensity separation between the deviants and standards in the intensity and double oddball paradigms. Figure 4 shows deviant responses from two example neurons with strong frequency SSA. In both cases, the response to the lower-intensity deviant was practically completely suppressed (NRId ≈ 0) when the standard was at the same frequency as, and a higher intensity than, the deviant (Fig. 4B,D, left columns). A similar pattern was also observed for the smallest non-zero standard-deviant frequency separation (Δf = 0.04; Fig. 4B, middle column), but for the larger frequency separations (Δf = 0.1 or 0.37; Fig. 4B,D, right columns), the lower-intensity deviant started to elicit a noticeable response (NRId > 0), particularly at the smallest intensity difference (Δi = 10 dB). As the intensity difference increased (Δi = 30 or 50 dB), the deviant response (and thus NRId) tended to decrease.

Figure 4. Two example neuron responses to the intensity and double oddball paradigms.

Figure 4

Open in a new tab

(A,C) FRAs of the two neurons with intensity and double oddball stimuli, plotted as in Fig. 1A. The insets show the PSTHs for the low-frequency/intensity sound (f1/i1; white circle) presented as standard (blue) or deviant (red) in the frequency oddball condition (Δf = 0.1; Δi = 0; see white diamond). (B) PSTHs showing the responses of examples neuron #1 (panel A) to the low-frequency/intensity deviant sound (f1/i1 dev; red line) in nine different intensity and double oddball paradigms, with frequency separations of Δf = 0, 0.04 and 0.1 (rows) and intensity differences of Δi = 10, 30 and 50 dB (columns). For comparison, the gray lines show the corresponding high-frequency/intensity standard responses (f2/i2 std). (D) PSTHs showing the responses of examples neuron #2 (panel C) to the low-frequency/intensity deviant in nine different intensity and double oddball paradigms. In this case, the frequency separations were Δf = 0, 0.1 and 0.37.

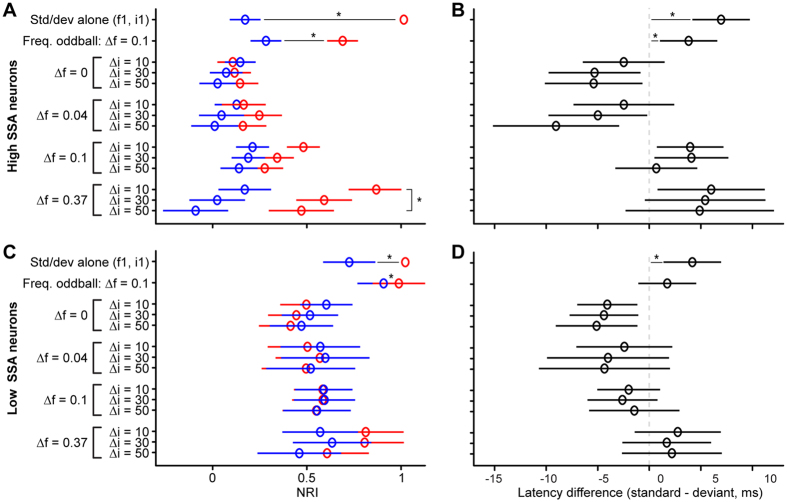
In order to explore these effects further, we analyzed the average NRI values for the groups of neurons with strong and weak frequency SSA (Fig. 5A,C) and measured the average first-spike latency differences between the standard and deviant responses (for the lower-frequency/intensity sound, like the NRI values; Fig. 5B,D). In the frequency oddball condition (Δf = 0.1, Δi = 0; 2nd row in Fig. 5A,C), both groups of neurons showed stronger adaptation of the standards than deviants (sign test of NRIs: strong-SSA, p < 0.001; weak-SSA, p = 0.011), but the difference was much larger for the strong- than weak-SSA neurons (Wilcoxon rank sum test: p < 0.001). This was expected given the way the weak- and strong-SSA neurons were defined. Both neuron groups also showed stronger adaptation in the standard-alone than deviant-alone condition (1st rows in Fig. 5A,C; sign test of NRIs: both p < 0.001), but, again, the difference was much smaller for the weak-SSA than strong-SSA neurons (Wilcoxon rank sum test: p < 0.001). This indicates that, in weak-SSA neurons, adaptation is not only less specific, but the level of adaptation is also overall much weaker. This will be further explored in the modelling section below. The NRI values for the intensity and double oddball conditions were compared with linear mixed-effects models, with Δf, Δi and stimulus type (standard, deviant) as fixed factors and neuron as random intercept. The analysis of the strong-SSA neurons yielded significant main effects of all factors [Δf, Δi, stimulus type; χ2(3) = 110.07, χ2(2) = 30.89, χ2(1) = 80.27, respectively; all p < 0.001], significant two-way interactions [Δf × Δi: χ2(6) = 21.21; Δf × stim: χ2(3) = 132.56; Δi × stim: χ2(2) = 7.36; p ≤ 0.025] and a significant three-way interaction [χ2(6) = 19.58, p = 0.003]. The two-way interaction between Δf and stimulus type shows that the difference between the standard and deviant NRIs increased with increasing standard-deviant frequency separation. The three-way interaction was caused by a significant Δi by stimulus type interaction for Δf = 0.37 [χ2(2) = 18.72, p < 0.001], a marginal interaction for Δf = 0.1 [χ2(2) = 5.39, p = 0.068], but non-significant interactions for Δf = 0.04 and 0 [χ2(2) = 3.73, p = 0.155]. These results confirm that, in the strong-SSA neurons, there was a tradeoff between frequency separation and intensity difference, with greater deviant responses for larger frequency separation, but smaller responses for greater intensity differences. In contrast to the strong-SSA neurons, the weak-SSA neurons showed significant main effects of Δf and Δi [χ2(3) = 23.75, χ2(2) = 10.71; p ≤ 0.005], but not of stimulus type [χ2(1) < 0.01, p = 0.957]. In addition to the main effects, only the Δf by stimulus type interaction was significant [χ2(3) = 29.99; p < 0.001]. The interaction arose because of significant main effects of stimulus type for Δf = 0 and 0.37 [χ2(1) = 16.30, χ2(1) = 11.66, respectively; both p < 0.001], but not for Δf = 0.04 and 0.1 [χ2(1) = 0.40, χ2(1) = 0.78, respectively; both p ≥ 0.38]. For Δf = 0, NRId was generally smaller than NRIs, whereas, for Δf = 0.37, NRId was larger than NRIs. This shows that, even for the weak-SSA neurons, the standard-deviant frequency separation had a small, but noticeable effect on the standard and deviant responses.

Figure 5. Opposing effects of frequency separation and intensity difference in double oddball paradigms.

Figure 5

Open in a new tab

(A,C) Normalized response indices (NRIs) for the deviant (NRId: red) and standard (NRIs: blue), averaged across neurons with strong (A) and weak (C) frequency SSA. Different oddball conditions are shown in different rows (see ordinate). The first row shows the deviant- and standard-alone conditions and the second row, the frequency oddball condition (Δf = 0.1, Δi = 10 dB). The error bars show the 95% confidence intervals of the means. Asterisks (*) show statistical differences. (B,D) First-spike latency differences between standard and deviant responses (std–dev: positive values mean that the deviant response has a shorter latency) for the same conditions and neurons as the NRI values shown in panels (A,C).

The first-spike latency differences (Fig. 5B,D) were consistent with the NRI values, in that conditions where NRId was larger than NRIs (the deviant response was less adapted than the standard response) tended to yield positive latency differences (shorter deviant than standard latencies), whereas conditions where NRId was smaller than NRIs tended to yield negative latency differences (longer deviant than standard latencies). In the strong-SSA neurons, the largest positive latency differences were observed between the standard- and deviant alone conditions and for the frequency oddball condition (1st and 2nd rows in Fig. 5B; Wilcoxon rank sum: both p < 0.001). Positive latency differences were also observed for the larger frequency separations (Δf = 0.1 and 0.37) in the double oddball conditions, particularly at the smaller intensity differences, whilst negative latency differences were observed for the intensity oddball condition (Δf = 0) and the double oddball condition with the smallest frequency separation (Δf = 0.04). The weak-SSA neurons showed a similar pattern of results, but with latency differences that were generally closer to zero than for the strong-SSA neurons. Statistical analyses using linear mixed effects models with Δf and Δi as fixed factors and neuron as random intercept revealed a significant main effect of Δf for both the strong- [χ2(3) = 40.92; p < 0.001] and weak-SSA neurons [χ2(3) = 22.07; p < 0.001], and a marginal main effect of Δi for the strong-SSA neurons [χ2(2) = 5.41; p = 0.067], but not for the weak-SSA neurons [χ2(2) = 0.37; p = 0.831]. The Δf by Δi interaction was non-significant for both groups [strong-SSA: χ2(6) = 3.84; weak-SSA: χ2(6) = 0.86; both p ≥ 0.699].

Absence of intensity SSA even in neurons with non-monotonic rate-intensity functions

In marmoset monkey auditory cortex, intensity-tuned neurons (i.e., neurons with non-monotonic rate-intensity functions) can adapt to frequent loud sounds whilst at the same time maintaining their sensitivity to rare fainter sounds28,29. Here, we tested whether the same was true for IC neurons with non-monotonic rate-intensity functions. For that, we first classified the neurons using the monotonicity index35 (MI; see Methods), dividing them into monotonic (MI ≥ 0.75) and non-monotonic groups (MI < 0.75). If the non-monotonic neurons maintained responsiveness to the lower-intensity deviants, the lower-intensity deviant response should be less suppressed compared to the unadapted response, and so, NRId for intensity and double oddball conditions should be larger in the non-monotonic, compared to the monotonic, neurons. We compared the NRId values for all intensity and double oddball conditions tested (all intensity differences and frequency separations), but found no significant differences in NRId between the monotonic and the non-monotonic neurons in any condition (Mann-Whitney rank sum test with a Holm-Bonferroni correction, p > 0.1 in all cases).

Neurons with strong frequency SSA have narrowly-tuned adaptation channels

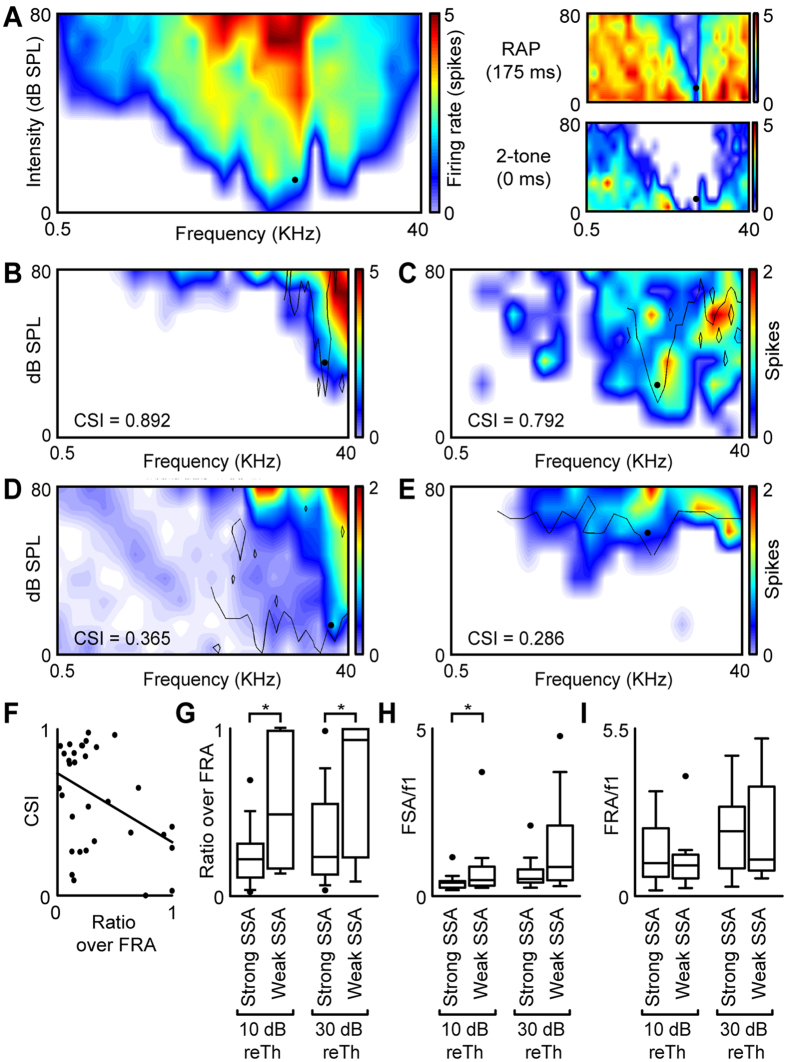
The results so far are consistent with the idea that frequency SSA in the IC is caused by independent adaptation within convergent frequency-tuned input channels (adaptation channels) to the IC neurons. Here, we developed a repeated adaptation paradigm (RAP) to measure the widths of the adaptation channels in relation to the neurons’ overall tuning widths (reflected by the FRA). The RAP measures the suppression of the response to a “probe” stimulus when the probe is preceded by an “adaptor” stimulus, presented repeatedly to mimic the conditions of the oddball paradigm (see Methods and Fig. 1C). Figure 6A shows the FRA of an example neuron (large panel on the left) together with the area of frequencies and intensities within which the adaptor caused suppression of the probe response (referred to as frequency suppression area, or FSA; upper right panel). The FSA obtained with the RAP was much narrower than that obtained with a forward-suppression paradigm36,37 (lower right panel). In forward-suppression paradigms, the adaptor is presented only once and the gap between the adaptor and probe is usually short. We tested such a forward-suppression protocol (with a 0-ms gap between the adaptor and probe) in 7 of the 33 neurons in which we tested the RAP. The suppression area obtained with the forward-suppression protocol typically covered the whole of the FRA. This is consistent with the findings by Scholes et al.37, who reported forward-suppression areas that were typically as wide as the FRA.

Figure 6. Properties of adaptation channels as measured by the repeated adaptation paradigm (RAP).

Figure 6

Open in a new tab

(A) Left panel: FRA of an example IC neuron showing the probe sound used in the RAP as a black dot. For the same neuron, the upper right panel shows the probe responses in the RAP, and the bottom right panel in a forward-suppression paradigm. (B,C) FRAs of two neurons with strong frequency SSA and corresponding FSAs (black lines). (D,E) FRAs of two neurons with weak frequency SSA and corresponding FSAs. (F) Relationship between CSI and the FSA-to-FRA ratio at 10 dB above the probe level. (G) FSA-to-FRA ratio in the neurons with strong and weak frequency SSA at 10 and 30 dB above the probe level. (H,I) FSA (H) and FRA (I) width relative to the probe frequency, again evaluated for neurons with strong and weak frequency SSA and at 10 and 30 dB.

Of the 33 neurons tested with the ROP, neurons with strong frequency SSA tended to show FSAs that were narrow in relation to their FRAs (see Fig. 6B,C for two examples), whereas neurons with weak frequency SSA tended to show FSAs that were broader (see Fig. 6D,E). For the neurons with strong SSA (CSI ≥+0.18; see above), of which there were 21, the FSA covered barely a quarter of the FRA, on average, at both 10 and 30 dB above the probe intensity. In contrast, for the neurons with weak SSA (n = 12), the FSA covered around half of the FRA at 10 dB and almost all the FRA at 30 dB (Fig. 6F). A Wilcoxon rank sum test showed that this difference was significant (p = 0.0247 and 0.0312, respectively; Fig. 6G). The narrower relative width of the FSA compared to the FRA for the strong-SSA neurons could be because, either the suppression area was narrower, or the FRA was wider in strong- than weak-SSA neurons. To test which, we also calculated the widths of the FSA and FRA separately relative to the best frequency of the neuron (inverse of the respective Q-values). The relative width of the FSA was significantly smaller in the strong- than weak-SSA neurons at 10 dB above probe intensity (Wilcoxon rank sum test, p = 0.0494), and marginally smaller at 30 dB (p = 0.0793; Fig. 6H). In contrast, the relative width of the FRA was not significantly different between strong- and weak-SSA neurons (at either level; Wilcoxon rank sum tests: all p ≥ 0.443; Fig. 6I). This suggests that strong-SSA neurons have narrower adaptation channels than weak-SSA neurons.

The width of adaptation channels is frequency-dependent

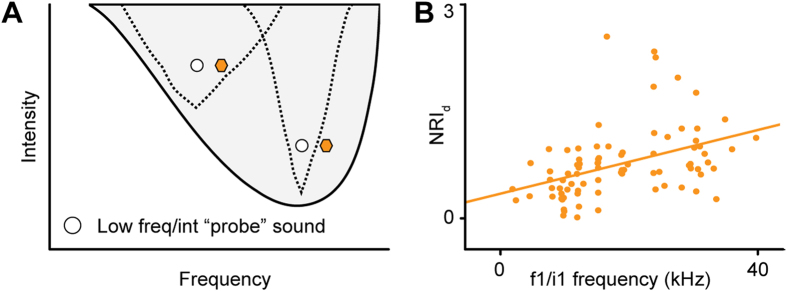
Recent results by Duque and colleagues32 have shown that SSA tends to be stronger at low intensities and at the high-frequency edge of the FRA. The results from the previous section suggest that strong frequency SSA is associated with narrower adaptation channels. In light of this finding, the results by Duque and colleagues suggests that (i) adaptation channels are narrower when the sound intensity is low, and (ii) adaptation channels tuned to higher frequencies are also narrower (Fig. 7A). To test whether the current data support this hypothesis, we analyzed the dependence of NRId on the frequency (f1) and intensity (i1) of the deviant stimulus. We applied a linear regression model and ANOVA, with f1 and i1 as fixed covariates, to the data from the frequency oddball paradigm (Δf = 0.1, Δi = 0). As in the study by Duque and colleagues32, the analysis was limited to neurons with strong frequency SSA (CSI ≥ +0.18; see above). It revealed a significant main effect of f1 on NRId [F(1,116) = 14.21, p < 0.001], with greater NRId values being associated with higher f1 values (Fig. 7B; Pearson’s r2 = 0.172, p < 0.001). This confirms that the relative width of the adaptation channels decreases with increasing frequency. However, we didn’t find any effect of deviant intensity.

Figure 7. Adaptation specificity decreases with increasing frequency.

Figure 7

Open in a new tab

(A) Schematic FRA showing the adaptation channels (dashed lines) for two frequency oddball conditions (white and colored symbols), one where the low-frequency/intensity sound (white circle) is set at a low frequency (left) and where it is set at a higher frequency (right). (B) Relationship between the NIAd values in the frequency oddball paradigm (Δf = 0.1, Δi = 10 dB) and the frequency of the low-frequency/intensity sound (f1/i1 frequency). The solid line shows the regression line.

Adaptation channel model

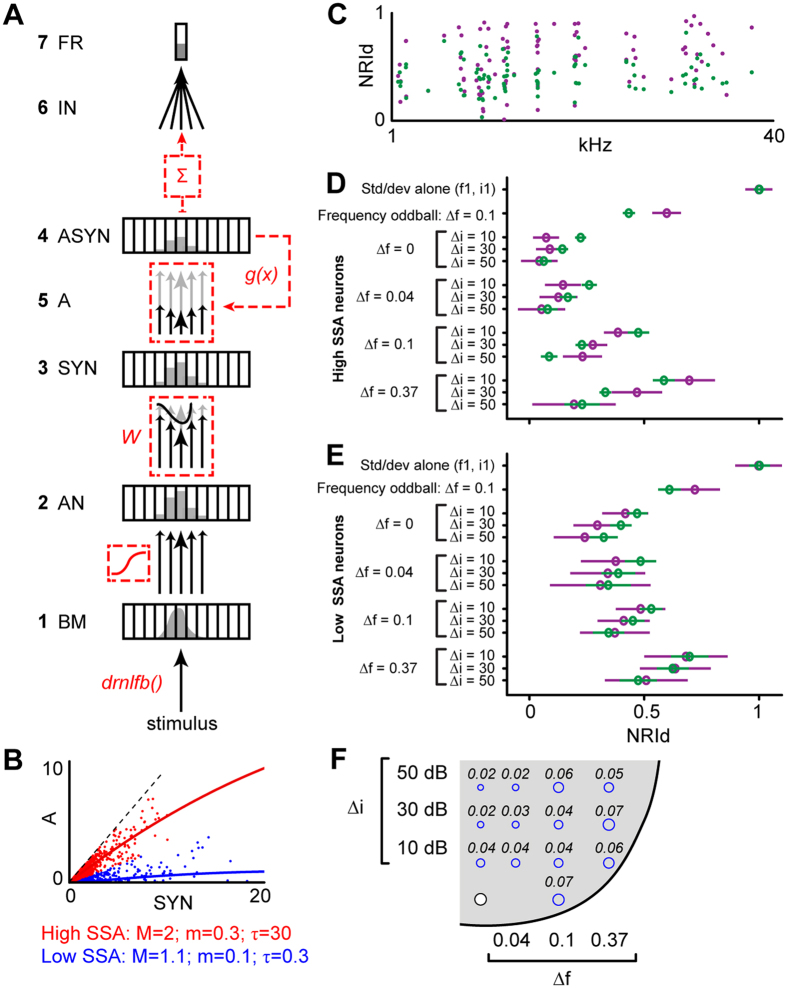
Here, we test whether the current data are consistent with a simple model based on the assumption that SSA in the IC arises as a result of adaptation that occurs independently within the auditory frequency channels formed in the cochlea. Adaptation was assumed to arise as a result of activity-dependent synaptic depression. Each adapting synapse was assumed to be activated by a single cochlear frequency channel (Fig. 8A, for details, see Methods). The tuning of the cochlear channels was modeled with a non-linear filterbank model38. The amount of adaptation within each synapse was assumed to increase with increasing activation of that synapse and recover over time, and was subtracted from the new activation by the next stimulus. The new activation causes new adaptation, which was added to the remaining adaptation from previous trials. Adaptation was assumed to be generally proportional to activation, but in order to accommodate the possibility that adaptation properties differ between low- and high-threshold auditory nerve fibers, the proportionality constant (see Methods) was allowed to differ between low (M) and high (m) levels of synaptic activity. Figure 8B shows population values of M and m, fitted to all weak- (blue) or strong- (red) SSA neurons. In line with the results from the NRI values (see above), these population fits suggest that the same amount of synaptic activity (estimated by the deviant-alone responses) caused much lower levels of adaptation (estimated by the difference between the standard- and deviant-alone responses) in the weak- than strong-SSA neurons. Figure 8C shows the simulated individual NRId values for one example condition (frequency oddball, ∆f = 0.1). The simulated data points (green dots) cover generally the same range as the measured data points (burgundy dots). Figure 8D,E shows the simulated average NRId values for all measured conditions, plotted separately for weak- and strong-SSA neurons as in Fig. 5A,C. In line with the data, the model showed no SSA for intensity oddball conditions, and for double oddball conditions with small frequency separations or large intensity differences. Moreover, the model also replicated the differences in the pattern of NRId values between the strong- and weak-SSA neurons (compare Fig. 8D,E). Overall, the model explained about 60% of the variability in the data, with similar accuracy across all conditions (Fig. 8F).

Figure 8. Comparison between adaptation model results and data.

Figure 8

Open in a new tab

(A) Summary of the computational model of synaptic adaptation used to simulate the measured oddball responses. (B) Relationship between adaptation (estimated by difference in firing rate between standard-alone and deviant-alone conditions) and synaptic activity (estimated from firing rate for deviant-alone condition), shown separately for low- (blue) and strong-SSA neurons (red). (C) Comparison of experimental (burgundy) and simulated (green) NIAd values of individual neurons in the frequency oddball condition (∆f = 0.1). (D,E) Comparison of average experimental (burgundy) and simulated (green) NRId values for all oddball conditions, plotted as in Fig. 5. As in Fig. 5, the NRId values were averaged across the strong- (D) and weak-SSA (E) neurons separately. (F) Mean squared deviation between experimental and simulated NIAd for each oddball condition. The size of the deviation is indicated by the size of the blue circles. The white circle shows the position of the lower-frequency-intensity stimulus with the stimulus space.

Discussion

The current results show that, while neurons in the IC exhibit strong SSA to frequency deviants, they fail to show SSA to pure intensity deviants. This was true even for neurons with non-monotonic rate-intensity functions. The response to low-intensity deviants among high-intensity standards was strongly suppressed or abolished unless the deviants and standards also differed in frequency. This suggests that, in the IC, SSA arises as a result of independent adaptation within the IC’s frequency-tuned input channels. The current results show that the relative width of these adaptation channels decreases with increasing frequency and that neurons with strong frequency SSA integrate over multiple such channels.

Two previous studies measured responses to intensity oddball paradigms in the mammalian auditory cortex17,26. Like the current study, both found enhanced responses to high- but not low-intensity deviants. Despite finding similar results, one study concluded the presence of intensity SSA17, whereas the other concluded the opposite26. Interpretations as to whether or not SSA is present can depend on the metric by which SSA is measured. The current study used the normalized response index (NRI), which measures the degree of adaptation of the standard and deviant responses separately and is particularly suited for conditions where the standards and deviants elicit different-sized responses. The current NRI results are consistent with the interpretation by Farley and colleagues26 and suggest the absence of intensity SSA also in the IC. However, results by Reches and Gutfreund39 indicate that neurons in optic tectum gaze control system in the barn owl do show SSA to low-intensity deviants, suggesting that they exhibit deviance sensitivity similar to the MMN. This is consistent with their functional role in exogenous attentional orienting40.

An interesting aspect of the current results was that, whilst most of the neurons with strong frequency SSA showed a complete, or close to complete, suppression of the low-intensity deviant response in the intensity oddball paradigm, neurons with weak frequency SSA showed low-intensity deviant responses that were often similar in size to the low-intensity standard responses. The NRI values suggest that this was, because weak-SSA neurons were generally much less adapted than strong-SSA neurons (i.e., the same amount of synaptic activity caused much less adaptation in weak- than strong-SSA neurons). A speculative interpretation of this finding is that the IC contains a subset of neurons specialized in frequency-specific adaptation. The current data suggest that there is no corresponding subset of IC neurons specialized in intensity-specific adaptation, because even neurons with non-monotonic rate-intensity functions failed to show intensity SSA. This finding is consistent with the idea that non-monotonicity arises at, rather than before, the level of the IC, for instance through intra-collicular inhibitory projections65,66. Previous results suggest that inhibition within the IC is not involved in the generation of SSA53. In contrast to the IC, it has been shown that some non-monotonic neurons in auditory cortex adapt specifically to high-intensity sounds, whilst preserving their sensitivity to low-intensity sounds28,29. Such neurons might receive convergent input from lower-level non-monotonic neurons with different intensity response ranges.

Previous modeling work has shown that gain adaptation within a single layer of frequency-tuned neurons is unable to explain all aspects of SSA30,41, and that more complicated networks of adapting neurons are needed to explain some of the effects observed in previous data42,43. However, the current results are largely consistent with the idea that SSA in the IC arises as a result of independent adaptation within narrowly frequency-tuned channels. The results from the RAP showed that neurons with strong frequency SSA integrate over multiple narrowly frequency-tuned channels, whereas neurons with weak frequency SSA receive input from fewer and wider channels. The data from the oddball paradigms were broadly consistent with a simple gain adaptation model based on the assumption that adaptation occurs independently within the auditory frequency channels. The model replicated the finding that responses to low-intensity deviants were adapted by high-intensity standards, because frequency-tuned channels responsive to a low-intensity sound will also respond to, and thus be adapted by, a high-intensity sound at the same frequency. The model was also consistent with the data from the double oddball conditions: as the frequency separation between the standard and deviant increased, the standard and deviant activated more disparate frequency channels, and so, the deviant response became less adapted; as the intensity difference increased, the standard activated a greater range of channels, including those responsive to the deviant, and so, the deviant response became more adapted. However, gain adaptation within a single layer of frequency-tuned neurons cannot explain the current finding that the adaptation channels measured with the RAP were narrower than those measured with a forward-suppression paradigm. Forward suppression refers to the reduction in the response to a probe stimulus when preceded by a single adaptor36,37. Comparison between the RAP and forward suppression results suggest that the degree of adaptation specificity increases with repeated exposure to the adapting sound. The current forward suppression paradigm used a shorter gap between the adaptor and probe than the RAP. However, a recent electroencephalographic study has demonstrated a higher degree of adaptation specificity with repeated than with single adaptors, even when all stimuli were separated by the same, long gap41. These findings, suggest that adaptation mechanisms change with repeated exposure to the adapting sound. Mill and colleagues42 have shown that increased adaptation specificity for repeated adaptors can be explained with a two-layered adaptation model. Mill et al.’s model consists of a first layer of sharply-tuned converging synapses, similar to the adapting synapses in the current model, but then contains another layer of synapses, which are more broadly tuned as a result of the convergence in the first layer. The second layer enables the model to explain the change in adaptation specificity between single and repeated adaptors. In the RAP, each probe was preceded by only three adaptors. In the current oddball paradigms, the number of standards preceding each deviant was typically much larger (9:1 ratio). This suggests that adaptation channels were even narrower during the oddball paradigm than measured with the RAP.

The double oddball conditions never yielded stronger SSA than the frequency oddball condition. This was, because IC neurons showed little or no intensity SSA. Previous studies have shown that the MMN is also no larger for double deviants than for pure frequency deviants44,45,46. However, in contrast to SSA in the IC, the MMN can be elicited by pure intensity deviants, and so, the finding that the MMN to double deviants is no larger than to frequency deviants indicates that the MMN is non-additive, and thus, that it processes information from different deviant types (frequency and intensity) together rather than independently (see, however, Althen et al.47).

Using intensity oddball sequences similar to the current ones, Jacobsen and colleagues10 found that lower-intensity deviants elicited an MMN, but no enlarged N1 response. The N1 is thought to reflect stimulus-driven activity within non-primary auditory cortical areas63,64, and so, the finding that the N1 is insensitive to intensity deviants would suggest that MMN-like deviance sensitivity first emerges at higher levels of non-primary auditory cortical processing. However, Althen and colleagues27 measured electroencephalographic middle-latency responses (MLRs) to intensity oddball sequences and found a slight shift in the transition between the Na and Pa peaks in response to low-intensity deviants versus standards. This shift caused a small negative deflection in the difference wave between the deviant and standard responses, which Althen and colleagues interpreted as an early component of the intensity-change MMN. Given that the MLR is thought to be generated in between the thalamus and the primary auditory cortex65,66,67, one might suggest that MMN-like deviance sensitivity first emerges at or before the level of primary auditory cortical processing. However, rather than representing an early MMN component, the observed shift in the transition between the Na and Pa may also have been caused by a suppression in the amplitude, and/or a prolongation in the latency, of the Pa response to the low-intensity deviant. The latter suggest that intensity oddball effects in the MLR are similar to those observed here in IC single-neuron responses (responses to low-intensity deviants were suppressed had longer first-spike latencies). This would be consistent with the N1 results by Jacobson and colleagues suggesting that MMN-like deviance sensitivity emerges only at later stages of non-primary auditory cortical processing.

The oddball paradigm represents a special case of a random stimulus distribution, in which the stimulus can take one of only two discrete values (standard and deviant). A wide range of previous studies on neural adaptation have used continuous, rather than discrete, stimulus distributions, where the stimulus can take one of a whole range of different values2. These studies have shown that, when the stimulus is varied along a dimension that elicits a monotonic stimulus-response function, the response range tends to adjust to both the mean and variance of the stimulus distribution in a way that enhances the encoding of the most commonly occurring sounds (referred to as dynamic-range adaptation3,48,49). Dean and colleagues48 presented sounds at a wide range of intensities, all with the same, low probability of occurrence, apart from a narrow high-probability range. They found that the response range of neurons in the IC shifted towards the high-probability intensities. As a result, the responses to low-probability low intensities were all but completely suppressed when the high-probability intensities were high, but when the high-probability intensities were low, both low and high intensities produced larger responses. This pattern of result is similar to the current pattern of results for the intensity oddball paradigm, potentially suggesting common underlying mechanisms. However, dynamic range adaptation involves processes with time-scales that would appear to be too fast to affect responses to oddball paradigm stimuli2,50,51. Thus, some of the processes that contribute to dynamic-range adaptation may be shorter-lived than the processes underlying the adaptation effects observed in the current study. Instead, they may be more akin to the processes underlying forward suppression36,37.

In summary, our results demonstrate a lack of SSA for intensity deviant sounds in the IC, although SSA occurred for double-deviants when standard and deviant activate sufficiently disparate frequency channels. Moreover, the current results indicate that gain adaptation within frequency-tuned input channels is an important component of SSA at the level of the midbrain.

Methods

Surgical procedures

Experiments were performed on 37 adult pigmented female rats (Rattus norvergicus, Long-Evans) with body weights between 150 and 260 g. All experimental procedures were carried out at the University of Salamanca using methods conforming to the standards of, and approved by, the University of Salamanca Animal Care Committee. Urethane was used to induce (1.5 g/kg, i.p., 20% solution) and maintain (0.5 g/kg, i.p. given as needed) anesthesia. Urethane was chosen as an anesthetic because its effects on multiple aspects of neural activity (including inhibition, spontaneous firing and SSA52,53) are known to be less than those of barbiturates and other anesthetic drugs54 (generally specific to inhibitory receptors). Details of surgical procedures have been described previously19,55. In brief, the animal was placed in a stereotaxic frame, located inside a sound-attenuated room and with the ear bars replaced by hollow specula to accommodate the sound delivery system. The scalp was incised along the sagittal midline, and the skin reflected laterally before performing a craniotomy to expose the cerebral cortex overlaying the left IC.

Electrophysiological recording

Extracellular single-unit responses were recorded using a tungsten electrode (1–2 MΩ56,68) lowered through the cortex by means of a piezoelectric microdrive (Burleigh 6000 ULN). Electrode positioning was based on stereotaxic coordinates, physiological criteria (tonotopicity and other response properties57,58) and confirmed histologically after experiment termination. The sound stimuli were presented monaurally to the ear contralateral to the recording side. The sound delivery system was the same as described previously19,55. Search stimuli were pure tones or noise bursts delivered using TDT System II hardware and custom software19,58,59. The sound system was calibrated using a ¼” condenser microphone (model 4136, Brüel & Kjær) and a dynamic signal analyzer (Photon+, Brüel & Kjær). The maximum sound system output was flat between 0.3–5 kHz (~100 ± 7 dB SPL) and between 5–40 kHz (~90 ± 5 dB SPL). The system’s frequency output was limited to 40 kHz. Even at the highest output level, the system’s relative distortion level was less than −40 dB. Details about the electrophysiological setup and procedures have been described previously19,55. The spike times were logged with a resolution of ~150 μs. For each neuron, the monaural frequency response area (FRA; i.e., the combination of frequencies and intensities capable of evoking a response) was determined by presenting pure tones (75-ms duration with 5-ms rise and fall times) at a range of different frequencies (from 0.5–40 kHz, in 25 logarithmic steps, presented randomly) and intensities (in 10 dB steps, presented in order from lowest to highest) using an automated procedure. Each frequency and intensity combination was repeated 5 times.

Stimulus presentation paradigms

The FRA was used to set the stimulus parameters for the frequency-, intensity- and double- (frequency and intensity) oddball paradigms. For the frequency oddball paradigm, we choose a pair of frequencies (f1 and f2) that, at the same intensity of i1 = i2 ≈ 10 dB above the best-frequency threshold, elicited a similar firing rate (Fig. 1A). The relative separation of the frequencies, Δf, was fixed at 0.10 (corresponding to 0.141 octaves), where Δf = (f2 − f1)/(f2 · f1)1/2. The two frequencies were presented in a random (“oddball”) sequence consisting of 400 stimuli in total, with the lower frequency (f1) presented in 90% of the trials (“standard”) and the higher frequency (f2) presented in 10% of the trials (“deviant”). The stimulus onset asynchrony (SOA) was 250 ms (corresponding to a 4 Hz stimulus presentation rate). After completion of the first sequence, a second sequence was presented, in which the roles of the two stimuli were reversed (f2 was standard and f1 was deviant). Similar oddball sequences have previously been shown to evoke strong SSA in IC neurons19,32. In addition to the two oddball sequences, we also measured the response to the lower-frequency stimulus (f1) in a deviant-alone and a standard-alone sequence, which were similar to the oddball sequences, but with the standards or deviants replaced by silence, respectively. We assumed that the response in the deviant-alone condition would be largely unadapted, and thus represent the maximum-possible response of the neuron at the relevant frequency and intensity (f1, i1).

For the intensity and double oddball conditions, we fixed the frequency and intensity of the lower-frequency stimulus (f1, i1) and varied the frequency and/or intensity of the higher-frequency stimulus (f2, i2; Fig. 1A), where i2 was always greater than i1, and f2 was greater than or equal to f1. The intensity difference (Δi = i2 − i1) was small (10 dB), medium (20–30 dB) or large (40–50 dB). The frequency separation (Δf) was 0, 0.04, 0.1 or 0.37 (corresponding to 0, 0.057, 0.141 or 0.526 octaves, respectively). As before, two oddball sequences were presented for each condition, one in which the lower-frequency/intensity stimulus (f1, i1) was the deviant and the higher-frequency/intensity stimulus (f2, i2) was the standard, and another in which the roles of the stimuli were reversed. Fixing f1 and i1enabled us to systematically map the effect of a higher-intensity standard on a lower-intensity deviant. Figure 1B shows three example conditions, including the frequency oddball paradigm (Δf = 0.1, Δi = 0 dB; orange hexagon), one of the intensity oddball paradigms (Δi = 10 dB, Δf = 0, burgundy square) and one of the double oddball paradigms (Δf = 0.1, Δi = 10 dB; green hexagon). Data were collected first for the smallest intensity difference (Δi = 10 dB), using at least two different frequency separations. Then, the rest of the intensity differences were measured in ascending order, using the same frequency separations as before. The complete protocol comprised a total of 14 conditions (1 frequency oddball condition +3 intensity differences × 4 frequency separations +1 deviant- and standard-alone condition; Fig. 1A) and took ∼80 min to measure in one neuron. The decision to limit f2 to be greater than or equal to f1 was necessary to achieve a manageable measurement time and was based on the finding that SSA tends to be stronger within the high-frequency part of the neuron’s FRA32.

In addition to the standard oddball paradigms, we also measured responses to a repeated adaptation paradigm (RAP, Fig. 1C). Like the adaptation paradigms used in previous studies36,37, the RAP is a trial-based paradigm. Within each trial, a probe tone, p, with a fixed frequency and intensity equal to those of the lower-frequency/intensity stimulus used in the oddball paradigms (f1, i1), was preceded by three identical adaptor tones, c, to create a discrete oddball sequence, a a a p (Fig. 1C). Within the sequences, the stimuli were presented with an SOA = 250 ms and successive sequences were separated by recovery gap of 1000 ms, making each trial 2000 ms long. The adaptors in the RAP paradigm mimic the standards in the classical oddball paradigm. The fact that the RAP paradigm uses discrete oddball sequences means that the adaptor effect can be mapped out systematically as a function of the adaptor frequency and intensity. The adaptor was presented at the same range of frequencies (0.5–40 kHz, in 25 logarithmic steps, presented randomly) and intensities (in 10 dB steps, presented in order from lowest to highest) as used for the FRA measurements. Each combination of adaptor frequency and intensity was repeated 4 times. The resulting firing rates show the area of frequencies and intensities within which the adaptor suppresses the probe response (frequency suppression areas, FSA). The bandwidth of the FSA was defined as the width of the area corresponding to a criterion level of suppression relative to a baseline, measured at an adaptor level of 10 or 30 dB SPL above the probe level. The baseline was the average probe response following the adaptors at the very lowest adaptor intensities used, where the adaptors elicited little or no discernable response. The criterion suppression was 0.632.

Data analysis

Standard and deviant responses obtained from the oddball paradigms were visualized as dot rasters and expressed in spikes per stimulus (to account for the different numbers of presentations) in a peri-stimulus time histogram (PSTH). SSA was quantified in three different ways. First, we calculated the common SSA index, CSI = [d1 + d2 − s1 − s2]/[d1 + d2 + s1 + s2], where d1/2 and s1/2 are the responses to the lower- and higher-frequency/intensity stimulus (f1/2, i1/2) when presented as deviant or standard. We also calculated the SSA index for each frequency separately, SI1/2 = [d1/2 − s1/2]/[d1/2 + s1/2]. Both of these types of indices have been used previously to quantify SSA for frequency oddball paradigms17,19. They can range from −1 to +1, being positive when the response to the deviant stimulus is greater. SIs and CSIs become unreliable when both the standard and deviant responses are small. Therefore, we also calculated normalized response indices (NRIs) of the deviant and standard responses. The responses to the lower-frequency/intensity stimulus presented as deviant or standard (d1 or s1) were normalized by the corresponding unadapted response, u1 (estimated by the deviant-alone condition), to generate the deviant or standard NRI (NRId = d1/u1, NRIs = s1/u1). The NRI can range between 0 and 1, being 1 if the response to the sound is not adapted and 0 if the response to the sound is completely suppressed.

The monotonicity index35 (MI) was evaluated at the lower stimulus frequency (f1) as the firing rate at the highest intensity used in the FRA measurements, FR(f1,max[i]), divided by the highest firing rate across all lower intensities used, max[FR(f1, i)]: MI(f1) = FR(f1,max[i])/max[FR (f1, i)].

The figures were generated in Sigmaplot 11 (Systat Software) and Matlab (MathWorks). The statistical analyses were conducted in Sigmaplot 11, Matlab and R60. The NRI values were analysed with linear, or linear mixed-effects, regression models using the lm and lmer functions in R (lmer is part of the lme4 package61). When using mixed-effects models, factors were significance-tested using likelihood ratio tests. Main effects were post-hoc tested using the testFactors function of the phia package for R62.

SSA model

Neural responses to frequency, intensity and double oddball sequences were simulated using a model based on the assumption that SSA is generated by synaptic depression within narrowly frequency-tuned, convergent channels. The model consisted of seven stages (Fig. 8A). The first stage (BM) used the dual resonance nonlinear (drnl) filterbank38 to model the basilar membrane velocity within each cochlear frequency channel (BMt in m/s) in response to the stimulus at time t (STIMt): BMt = drnl(STIMt). The drnl filterbank models the human cochlea; therefore all stimulus frequencies were first converted from the rat to the human hearing range. The drnl reproduces the nonlinear changes in the shape and width of the cochlear frequency channels with frequency and intensity. The second stage (AN) computed the auditory nerve activity within each channel (ANt, in spikes per second) from BMt using a typical threshold-saturating in/out neural function [ANt = io(BMt)]. The third stage (SYN) modeled the synaptic activation for each input channel (SYNt, arbitrary units) by multiplying ANt with a fixed synaptic weight vector (W) to mimic the neuron’s frequency tuning [SYNt = W*ANt]. At the fourth stage (ASYN), the synaptic activity generated adaptation, At, according to a monotonic adaptation function, g(x). At the fifth stage (A), the adaptation (At) was subtracted from the synaptic activity (SYNt) to obtain the actual adapted activation of the synapse, ASYNt = SYNt − At. Stages four and five were iterated recursively for each trial, whereby the new adaptation from the current trial was added to the remaining adaptation from previous trials and all adaptation was assumed to decay by a factor, R, from trial to trial; At+1 = (1 − R)*(At + g(ASYNt)). The adaptation for the first trial, A1, was set to zero. At the sixth stage (IN), the synaptic activities of all channels were integrated in order to obtain the total synaptic input, INt = 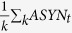Inline graphic (arbitrary units), where k = number of input channels. The seventh and final stage (FR) computed the firing rate of the neuron (FRt) from the integrated synaptic input using a similar threshold-saturating in/out function as used to calculate the auditory-nerve activity [FRt = out(INt)].

The shape of the monotonic adaptation function, g(x) was determined by three parameters, M, m and τ [g(x) = α(x)*x; where α(x) = m + (M − m)*2(−x/τ)], where M and m represent the initial and final slopes of g and τ determines the point where the slope is (M + m)/2. Thus, adaptation [g(x)] was proportional to synaptic activity (x), but with a proportionality constant (α) that could differ between low and high levels of synaptic activity. We estimated population parameters M, m and τ for neurons with high and low SSA, respectively (Fig. 8H), by comparing the adaptation in the standard-alone condition (estimated as the difference in firing rate between the deviant- and standard-alone conditions; FRdeviant-alone − FRstandard-alone) with the unadapted synaptic activity (assumed to be given by FRdeviant-alone). For each individual neuron, the tuning weights (W) and parameters of output function out() were adjusted to mimic the tuning and threshold of that particular neuron and the parameters of the adaptation function (M, m, τ) were fitted through nonlinear least squares regression of the observed and simulated NRId values across conditions. The mean squared error (MSE) was computed to quantify the difference between the observed and the simulated NRId values.

Additional Information

How to cite this article: Duque, D. et al. Neurons in the inferior colliculus of the rat show stimulus-specific adaptation for frequency, but not for intensity. Sci. Rep. 6, 24114; doi: 10.1038/srep24114 (2016).

Acknowledgments

We would like to thank Drs Alan Palmer, Yoram Gutfreund, Israel Nelken and Eric Young for their supportive comments on previous versions of the manuscript. We also thank Dr Enrique López-Póveda for providing the auditory filter bank for the model and David Pérez-González for help with the data analysis. Financial support was provided by the Spanish MEC (BFU2013-43608-P) and JCYL (SA343U14) to MSM and by the intramural funding programme of the Medical Research Council (UK) to KK. DD held a fellowship from the Spanish MEC (BES-2010-035649), from AGAUR (Generalitat de Catalunya) in the frame of the EU COFUND Marie-Curie program (2014BP-A00226) and a fellowship from the Erasmus Mundus ACN program. XW held a fellowship from the National Natural Science Foundation of China (NNSFC-31000493). JN-D held a Ph.D. fellowship from European Social Fund/Spanish JCYL (Operational programme ESF Castilla y León 2007–2013).

Footnotes

Author Contributions The experiments were performed in the Neurobiology of Hearing Laboratory, Institute of Neuroscience of Castilla y León, University of Salamanca, Salamanca, Spain. The contribution of each author to the following aspects of the study is as stated: (1) collection of data: X.W.; (2) conception and design of experiments: D.D., M.S.M.; (3) analysis and interpretation of data: X.W., D.D., J.N.-D., K.K. and M.S.M.; (4) design of the model: J.N.-D. and K.K.; (5) writing of the manuscript: D.D., K.K. and M.S.M. All authors approved the final version of the manuscript.

References

  1. Grill-Spector K., Henson R. & Martin A. Repetition and the brain: neural models of stimulus-specific effects. Trends Cogn Sci 10, 14–23 (2006). [DOI] [PubMed] [Google Scholar]
  2. Wark B., Lundstrom B. N. & Fairhall A. Sensory adaptation. Curr Opin Neurobiol 17, 423–429 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brenner N., Bialek W. & de Ruyter van Steveninck R. Adaptive rescaling maximizes information transmission. Neuron 26, 695–702 (2000). [DOI] [PubMed] [Google Scholar]
  4. Fairhall A. L., Lewen G. D., Bialek W. & de Ruyter Van Steveninck R. R. Efficiency and ambiguity in an adaptive neural code. Nature 412, 787–792 (2001). [DOI] [PubMed] [Google Scholar]
  5. Nelken I. & Ulanovsky N. Mismatch Negativity and Stimulus-Specific Adaptation in Animal Models. J. Psychophysiol. 21, 214–223 (2007). [Google Scholar]
  6. Malmierca M. S., Anderson L. A. & Antunes F. M. The cortical modulation of stimulus-specific adaptation in the auditory midbrain and thalamus: a potential neuronal correlate for predictive coding. Front. Syst. Neurosci. 9, 19 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Näätänen R., Gaillard A. W. & Mantysalo S. Early selective-attention effect on evoked potential reinterpreted. Acta Psychol 42, 313–329 (1978). [DOI] [PubMed] [Google Scholar]
  8. Schroger E. & Wolff C. Mismatch response of the human brain to changes in sound location. Neuroreport 7, 3005–3008 (1996). [DOI] [PubMed] [Google Scholar]
  9. Jacobsen T. & Schroger E. Is there pre-attentive memory-based comparison of pitch? Psychophysiology 38, 723–727 (2001). [PubMed] [Google Scholar]
  10. Jacobsen T. & Schroger E. Measuring duration mismatch negativity. Clin Neurophysiol 114, 1133–1143 (2003). [DOI] [PubMed] [Google Scholar]
  11. Näätänen R., Kujala T. & Winkler I. Auditory processing that leads to conscious perception: A unique window to central auditory processing opened by the mismatch negativity and related responses. Psychophysiology 48, 4–22 (2011). [DOI] [PubMed] [Google Scholar]
  12. Naatanen R., Paavilainen P. & Reinikainen K. Do event-related potentials to infrequent decrements in duration of auditory stimuli demonstrate a memory trace in man? Neurosci Lett 107, 347–352 (1989). [DOI] [PubMed] [Google Scholar]
  13. Paavilainen P., Jiang D., Lavikainen J. & Naatanen R. Stimulus duration and the sensory memory trace: an event-related potential study. Biol Psychol 35, 139–152 (1993). [DOI] [PubMed] [Google Scholar]
  14. Naatanen R., Paavilainen P., Alho K., Reinikainen K. & Sams M. Do event-related potentials reveal the mechanism of the auditory sensory memory in the human brain? Neurosci Lett 98, 217–221 (1989). [DOI] [PubMed] [Google Scholar]
  15. Yabe H., Tervaniemi M., Reinikainen K. & Näätänen R. Temporal window of integration revealed by MMN to sound omission. Neuroreport 8, 1971–1974 (1997). [DOI] [PubMed] [Google Scholar]
  16. Näätänen R. & Picton T. The N1 Wave of the Human Electric and Magnetic Response to Sound: A Review and an Analysis of the Component Structure. Psychophysiology 24, 375–425 (1987). [DOI] [PubMed] [Google Scholar]
  17. Ulanovsky N., Las L. & Nelken I. Processing of low-probability sounds by cortical neurons. Nat Neurosci 6, 391–398 (2003). [DOI] [PubMed] [Google Scholar]
  18. Ulanovsky N., Las L., Farkas D. & Nelken I. Multiple time scales of adaptation in auditory cortex neurons. J Neurosci 24, 10440–10453 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Malmierca M. S., Cristaudo S., Perez-Gonzalez D. & Covey E. Stimulus-specific adaptation in the inferior colliculus of the anesthetized rat. J Neurosci 29, 5483–5493 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Yu X. J., Xu X. X., He S. & He J. Change detection by thalamic reticular neurons. Nat Neurosci 12, 1165–1170 (2009). [DOI] [PubMed] [Google Scholar]
  21. Antunes F. M., Nelken I., Covey E. & Malmierca M. S. Stimulus-specific adaptation in the auditory thalamus of the anesthetized rat. PLoS One 5, e14071 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Nelken I. Stimulus-specific adaptation and deviance detection in the auditory system: experiments and models. Biol Cybern 108, 655–663 (2014). [DOI] [PubMed] [Google Scholar]
  23. Escera C. & Malmierca M. S. The auditory novelty system: an attempt to integrate human and animal research. Psychophysiology 51, 111–123 (2014). [DOI] [PubMed] [Google Scholar]
  24. Reches A. & Gutfreund Y. Stimulus-specific adaptations in the gaze control system of the barn owl. J Neurosci 28, 1523–1533 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Xu X., Yu X., He J. & Nelken I. Across-ear stimulus-specific adaptation in the auditory cortex. Front Neural Circuits 8, 89 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Farley B. J., Quirk M. C., Doherty J. J. & Christian E. P. Stimulus-specific adaptation in auditory cortex is an NMDA-independent process distinct from the sensory novelty encoded by the mismatch negativity. J Neurosci 30, 16475–16484 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Althen H., Grimm S. & Escera C. Fast detection of unexpected sound intensity decrements as revealed by human evoked potentials. PLoS One 6, e28522 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Watkins P. V. & Barbour D. L. Specialized neuronal adaptation for preserving input sensitivity. Nat Neurosci 11, 1259–1261 (2008). [DOI] [PubMed] [Google Scholar]
  29. Watkins P. V. & Barbour D. L. Level-tuned neurons in primary auditory cortex adapt differently to loud versus soft sounds. Cereb Cortex 21, 178–190 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Taaseh N., Yaron A. & Nelken I. Stimulus-specific adaptation and deviance detection in the rat auditory cortex. PLoS One 6, e23369 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Duque D., Ayala Y. A. & Malmierca M. S. Deviance detection in auditory subcortical structures: what can we learn from neurochemistry and neural connectivity? Cell Tissue Res. 361, 215–32 (2015). [DOI] [PubMed] [Google Scholar]
  32. Duque D. et al. Topographic distribution, frequency, and intensity dependence of stimulus-specific adaptation in the inferior colliculus of the rat. J Neurosci 32, 17762–17774 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ayala Y. A. et al. Frequency discrimination and stimulus deviance in the inferior colliculus and cochlear nucleus. Front Neural Circuits 6, 119 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Duque D. & Malmierca M. S. Stimulus-specific adaptation in the inferior colliculus of the mouse: anesthesia and spontaneous activity effects. Brain Struct Funct (2014). doi: 10.1007/s00429-014-0862-1 [DOI] [PubMed] [Google Scholar]
  35. de la Rocha J., Marchetti C., Schiff M. & Reyes A. D. Linking the response properties of cells in auditory cortex with network architecture: cotuning versus lateral inhibition. J Neurosci 28, 9151–9163 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Nelson P. C., Smith Z. M. & Young E. D. Wide-dynamic-range forward suppression in marmoset inferior colliculus neurons is generated centrally and accounts for perceptual masking. J Neurosci 29, 2553–2562 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Scholes C., Palmer A. R. & Sumner C. J. Forward suppression in the auditory cortex is frequency-specific. Eur J Neurosci (2011). doi: 10.1111/j.1460-9568.2010.07568.x [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Lopez-Poveda E. A. & Meddis R. A human nonlinear cochlear filterbank. J. Acoust. Soc. Am. 110, 3107–18 (2001). [DOI] [PubMed] [Google Scholar]
  39. Reches A., Netser S. & Gutfreund Y. Interactions between stimulus-specific adaptation and visual auditory integration in the forebrain of the barn owl. J Neurosci 30, 6991–6998 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Gutfreund Y. Stimulus-specific adaptation, habituation and change detection in the gaze control system. Biol. Cybern. 106, 657–68 (2012). [DOI] [PubMed] [Google Scholar]
  41. Briley P. M. & Krumbholz K. The specificity of stimulus-specific adaptation in human auditory cortex increases with repeated exposure to the adapting stimulus. J Neurophysiol 110, 2679–2688 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Mill R., Coath M., Wennekers T. & Denham S. L. A neurocomputational model of stimulus-specific adaptation to oddball and Markov sequences. PLoS Comput Biol 7, e1002117 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Hershenhoren I., Taaseh N., Antunes F. M. & Nelken I. Intracellular correlates of stimulus-specific adaptation. J Neurosci 34, 3303–3319 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Näätänen R., Tervaniemi M., Sussman E., Paavilainen P. & Winkler I. ‘Primitive intelligence’ in the auditory cortex. Trends Neurosci 24, 283–288 (2001). [DOI] [PubMed] [Google Scholar]
  45. Paavilainen P. et al. Evidence for the different additivity of the temporal and frontal generators of mismatch negativity: a human auditory event-related potential study. Neurosci. Lett. 349, 79–82 (2003). [DOI] [PubMed] [Google Scholar]
  46. Wolff C. & Schroger E. Human pre-attentive auditory change-detection with single, double, and triple deviations as revealed by mismatch negativity additivity. Neurosci Lett 311, 37–40 (2001). [DOI] [PubMed] [Google Scholar]
  47. Althen H., Huotilainen M., Grimm S. & Escera C. Middle latency response correlates of single and double deviant stimuli in a multi-feature paradigm. Clin. Neurophysiol. (2015). doi: 10.1016/j.clinph.2015.04.058 [DOI] [PubMed] [Google Scholar]
  48. Dean I., Harper N. S. & McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat Neurosci 8, 1684–1689 (2005). [DOI] [PubMed] [Google Scholar]
  49. Dahmen J. C., Keating P., Nodal F. R., Schulz A. L. & King A. J. Adaptation to stimulus statistics in the perception and neural representation of auditory space. Neuron 66, 937–948 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Nagel K. I. & Doupe A. J. Temporal processing and adaptation in the songbird auditory forebrain. Neuron 51, 845–859 (2006). [DOI] [PubMed] [Google Scholar]
  51. Dean I., Robinson B. L., Harper N. S. & McAlpine D. Rapid neural adaptation to sound level statistics. J Neurosci 28, 6430–6438 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Duque D., Malmierca M. S. & Caspary D. M. Modulation of stimulus-specific adaptation by GABA(A) receptor activation or blockade in the medial geniculate body of the anaesthetized rat. J Physiol 592, 729–743 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Duque D. & Malmierca M. S. Stimulus-specific adaptation in the inferior colliculus of the mouse: anesthesia and spontaneous activity effects. Brain Struct & Funct 220(6), 3385–3398 (2015). [DOI] [PubMed] [Google Scholar]
  54. Hara K. & Harris R. A. The anesthetic mechanism of urethane: the effects on neurotransmitter-gated ion channels. Anesth Analg 94, 313–8, table of contents (2002). [DOI] [PubMed] [Google Scholar]
  55. Pérez-González D., Malmierca M. S. & Covey E. Novelty detector neurons in the mammalian auditory midbrain. Eur J Neurosci 22, 2879–2885 (2005). [DOI] [PubMed] [Google Scholar]
  56. Merrill E. G. & Ainsworth A. Glass-coated platinum-plated tungsten microelectrodes. Med Biol Eng 10, 662–672 (1972). [DOI] [PubMed] [Google Scholar]
  57. Malmierca M. S. et al. The commissure of the inferior colliculus shapes frequency response areas in rat: an in vivo study using reversible blockade with microinjection of kynurenic acid. Exp Brain Res 153, 522–529 (2003). [DOI] [PubMed] [Google Scholar]
  58. Hernandez O., Espinosa N., Perez-Gonzalez D. & Malmierca M. S. The inferior colliculus of the rat: a quantitative analysis of monaural frequency response areas. Neuroscience 132, 203–217 (2005). [DOI] [PubMed] [Google Scholar]
  59. Faure P. A., Fremouw T., Casseday J. H. & Covey E. Temporal masking reveals properties of sound-evoked inhibition in duration-tuned neurons of the inferior colliculus. J Neurosci 23, 3052–3065 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Core Team. R. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/(2015). [Google Scholar]
  61. Bates D., Maechler M., Bolker B. & Walker S. _lme4: Linear mixed-effects models using Eigen and S4_. R package version 1.1-9, URL : https://CRAN.R-project.org/package= lme4 (2015).
  62. de Rosario-Martinez H. phia: Post-Hoc Interaction Analysis. R package version 0.2-0. http://CRAN.R-project.org/package= phia (2015).
  63. Godey B., Schwartz D., de Graaf J. B., Chauvel P. & Liegeois-Chauvel C. Neuromagnetic source localization of auditory evoked fields and intracerebral evoked potentials: a comparison of data in the same patients. Clin Neurophysiol 112, 1850–1859 (2001). [DOI] [PubMed] [Google Scholar]
  64. Luetkenhoener B. & Steinstrater O. High-precision neuromagnetic study of the functional organization of the human auditory cortex. Audiol Neurootol 3, 191–213 (1998). [DOI] [PubMed] [Google Scholar]
  65. Liégeois-Chauvel C., Musolino A., Badier J. M., Marquis P. & Chauvel P. Evoked potentials recorded from the auditory cortex in man: evaluation and topography of the middle latency components. Electroencephalogr Clin Neurophysiol 92(3), 204–14 (1994). [DOI] [PubMed] [Google Scholar]
  66. Mäkelä J. P., Hämäläinen M., Hari R. & McEvoy L. Whole-head mapping of middle-latency auditory evoked magnetic fields. Electroencephalogr Clin Neurophysiol 92(5), 414–21(1994). [DOI] [PubMed] [Google Scholar]
  67. Yvert B., Crouzeix A., Bertrand O., Seither-Preisler A. & Pantev C. Multiple supratemporal sources of magnetic and electric auditory evoked middle latency components in humans. Cereb Cortex 11(5), 411–23 (2001). [DOI] [PubMed] [Google Scholar]
  68. Ayala Y. A., Pérez-González D., Duque D., Palmer A. R. & Malmierca M. Extracellular Recording of Neuronal Activity Combined with Microiontophoretic Application of Neuroactive Substances in Awake Mice. J. Vis. Exp. e53914, (2016). doi: 10.3791/53914 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES