Dimensional analysis and scaling relevant to flow models of thrombus formation: communication from the SSC of the ISTH

Introduction

Flow chambers are increasingly used to model thrombus formation in (patho)physiologically inspired geometries and conditions. The flexible design enabled by microfluidics and the variety of commercially available devices makes comparisons between flow chambers challenging [1]. There is also a need to make faithful comparisons between these in vitro models and animal models. Dimensional analysis and scaling provide a rigorous method for making these comparisons. Scaling is a mathematical tool used to simplify, characterize and design systems based on their dimensions and dynamics. Scaling arguments to describe biophysical mechanisms that regulate thrombus growth have recently appeared in hematology journals [2,3]. In practise, scaling involves selecting important dimensional and dynamic parameters and forming dimensionless groups that characterize a system [4]. These dimensionless groups determine the relative importance of geometric features, forces and rates. The purpose of this Communication is to provide a primer on scaling and provide recommendations for reporting and calculating relevant dimensionless groups in flow models of thrombus formation.

Dimensional and dynamic similarity

The human vasculature is challenging to model due to the wide range of vessel sizes (5 μm to 1.5 cm) and blood flow velocities (0.03–40 cm s⁻¹) [5,6]. To make accurate predictions, flow chambers that model the (patho)physiological process of thrombus formation need to meet the criteria of dimensional and dynamic similarity. Dimensional similarity means that ratios of the lengths of the scale model must be the same as those for the original model. Dynamic similarity means that the value for each relevant dimensionless group is the same for the scale and original model.

Dimensional similarity

Parallel-plate flow chambers introduced in the 1970s serve as the basis for a proliferation of flow chamber models over the last decade [1,7]. These chambers are typically comprised of a rectangular channel, which makes them easier to image than are tubes, where blood is perfused over a surface coated with prothrombotic proteins. Table 1 describes important geometric ratios required for dimensional similarity in flow models. The first parameter is the channel height relative to the size of a red blood cell (RBC). The hematocrit, and thus the viscosity, of blood decreases with decreasing channel height over the range of 10–300 μm, a phenomenon known as the Fahreus-Lindquist effect [8]. The change in viscosity is sensitive to channel size for dimensions of less than 100 μm. Consider two flow chamber studies performed at the same shear rate; one with a 40-μm height and one with a 100-μm height. The difference in blood viscosity, and thus shear stress, would be ~25% between the two chambers, which could be a significant difference in the importance of VWF-mediated platelet adhesion.

Table 1.

Dimensional and dynamic parameters for scaling in vitro and in vivo flow models

Parameter	Expression	Meaning	Importance	Typical values
Relative channel height	DRBC/H	Size of channel relative to height of RBC	For values of > 0.05 the viscosity of the blood decreases due to reduced hematocrit	0.01–0.2
Aspect ratio	H/W	Height of channel to width of channel for rectangular channels	Values of < 0.2 are recommended to achieve constant shear stresses across the middle of adhesive surfaces	0.1–1
Relative injury size	L/H	Length of thrombotic trigger or injury relative to channel height	Values > 1 enhance the effectiveness of surface reactions	0.1–10
Reynolds number (Re)	ρUH/μ	Inertial forces/viscous forces	Determines the nature of the flow; laminar, recirculation, turbulent	0.001(capillaries) to 4000 (arteries)
Entrance length (Le)	0.057ReDh*	Distance from the channel inlet where flow is well developed	Prothrombotic triggers should be placed at distance greater than Le	1–100 μm (for ~100 μm channels and physiologic shear rates)
Peclet number (Pe)	UciH/D γH2/6D	Convective velocity/diffusive velocity	Determines the relative rates of solute transport by flow and molecular diffusion	0.01 (interstitial flow in thrombi) to 100 000 (coagulation reactions on surfaces)
Dahmköhler number (Da)†	krxnciH/D (low Pe) krxnciδ‡/D (high Pe)	Reaction velocity/diffusive velocity	Determines whether transport of soluble molecules or their reaction is rate limiting.	0.1 (reaction limited) to 10 000 (transport limited)

D_RBC, diameter of red blood cell; H, height of channel; W, width of channel; SA, surface area of injury; V, volume of channel in injured area; L, length of injury; U, average blood velocity; c_i, concentration of component i; D, diffusivity; γ, wall shear rate; k_rxn, rate constant of first order reaction.

^*D_h, hydraulic diameter [2HW/(H + W)].

^†Note that the expression for the Da depends on the order of the reaction and the mass transfer regime [29].

^‡The boundary layer thickness, δ, depends on the Pe and thus the shear rate [δ = (H2L/Pe)^1/3].

Platelets can accumulate by interactions with the surface or with each other. For sufficiently small dimensions, platelet-surface interactions will dominate, which is inconsistent with the platelet-platelet interactions that characterize arterial thrombosis. The transition between situations in which platelet-surface interactions dominate and those in which platelet-platelet interactions dominate is a function of channel size and aspect ratio (height/width) [9].

In rectangular flow chambers, the shear stress on each wall is a parabolic profile, where stresses are zero in the corners and maximum in the center. Aspect ratios ≤ 0.2 give a shear stress, and thus platelet deposition, that is uniform across the middle of the channel [10]. Higher aspect ratios confound data analysis due to high platelet accumulation in the corners.

The area of the thrombotic trigger relative to the channel size determines, in part, how far the thrombus will grow. The area of the thrombotic trigger varies in flow chambers that use micropatterning techniques [1]. The important geometric parameter that regulates growth is the ratio of the length of the trigger in the flow direction divided by the channel height (L/H) [11]. Under static conditions, a sufficiently large L/H will allow coagulation products to accumulate, leading to a burst in thrombin generation [12]. The products of surface-bound reactions catalyzed by tissue factor and thrombomodulin penetrate further across the lumen and downstream with increasing L/H [13,14].

Dynamic similarity

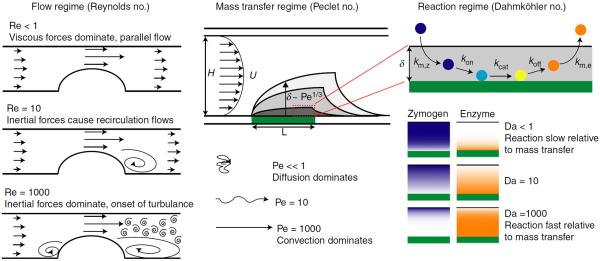
The viscous forces imposed on platelets by flow regulate their adhesion and aggregation [15]. These forces are typically reported as an average wall shear stress. However, inertial forces, those related to the momentum of a fluid, play an important role in recirculating and turbulent flows. The Reynolds number (Re) gives an indication of the relative importance of inertial and viscous forces and is used to characterize the flow regime (Fig. 1). Inertial forces dominate at high Re numbers, which are characteristic of stenosed vessels, bifurcations and valves in large arteries. It is difficult to achieve high Re in flow chambers while maintaining a physiologic wall shear rate owing to the chamber's small size. In other words, supraphysiological shear rates are required to achieve Re > 10. As such, one must cautiously extrapolate conclusions about thrombus formation in large vessels from flow chamber models, as they do not accurately model these inertially driven complex interactions. However, flow chambers are ideal for simulating the hemodynamics of the microvasculature where the Re < 1.

Fig. 1.

Key dimensionless parameters for defining dimensional and dynamic similarity in flow chamber studies. The Reynolds number (Re) determines whether viscous or inertial forces dominate. As a thrombus grows into the lumen, as shown in the left schematic, recirculation flows and turbulence flows appear depending on the Re. The Peclet number (Pe) gives the relative rates of transport by convection (flow) and diffusion. At small Pe solutes move in a random way that becomes increasingly biased towards the flow direction with increasing Pe. At large Pe (dark shading) the boundary layer becomes thinner. The size of the boundary layer, δ, that is enriched in coagulation products and platelet agonists scales as the Pe^1/3. The Dahmköhler number (Da) gives the relative rate of reaction to transport. Da is large if reaction rates are fast relative to transport. Also, a separate Da can be calculated for each transport process and each reaction: mass transfer of the zymogen to and enzyme from the surface (k_m,z, k_m,e), association and dissociation with the surface-bound enzyme complex (k_on, k_off), and catalytic rate (k_cat). Concentration profiles within the boundary layer for the zymogen (blue) and enzyme (orange) are shown at different values of Da.

At a channel or vessel entrance, there exists an entry length, L_e, required for the establishment of well-developed flow (Table 1). Shear stresses and transport rates are different in the developing region upstream of L_e [16]. Therefore, it is important for inter-assay repeatability to observe platelet and fibrin accumulation downstream of L_e and at the same position relative to the channel inlet.

Blood flow regulates coagulation by delivering molecules to the site of an injury and by transporting them away. Here, the concern is the relative rates of transport by convection, transport by diffusion and the rates of the biochemical reactions. Both the relative rates of transport by convection and diffusion, and the relative rate of the reactions and the rate of transport, have strong implications for thrombus development. The Peclet number (Pe) is the ratio of the rate of convection (transport by flow) to the rate of diffusion and is used to characterize the mass transfer regime (Fig. 1). At high Pe, enzymes produced at the wall are confined to a thin boundary layer, δ, near the surface (Fig. 1). The Pe, in combination with the injury length as described above, determines how far solutes move downstream from an injury, and thus regulates the cross-talk between adjacent injuries. A higher Pe reduces downstream transport because solutes diffuse out of the boundary layer more quickly than at low Pe. For example, there is a significant increase in the amount of fibrin accumulating on adjacent 175-μm collagen-TF spots spaced 500 μm apart at a Pe of 1000, but not at a Pe of 10 000 [17]. Therefore, cross-talk between injuries is an important consideration in models that include dense arrays of prothrombotic triggers [18,19].

The Dahmköhler number (Da) is the ratio of the rate of reaction to the rate of transport and is used to characterize the reaction regime (Fig. 1). It tells us whether the rate-limiting step for a solute is its consumption/production by a biochemical reaction or its transport to/from an injury. Take for example the conversion of factor X (FX) to FXa by the TF:FVIIa complex [20]. At Da » 1, transport of FX through the boundary layer is slower than the reaction rate at the wall, thus all FX at the surface is converted to FXa. In this case, FXa production is transport-limited. At Da ⪡ 1, the rate of transport of FX to the surface is faster than the reaction rate, so only a portion of the FX pool in the boundary layer is converted to FXa. In this case, FXa production is reaction-limited. In the reaction-limited regime, the products of surface-mediated reactions are diluted by transport away from the injury, inhibiting coagulation [21,22]. Because the transition between the transport-limited and reaction-limited regimes is sharp for TF-initiated coagulation [13,17,23], small changes in Da can result in significant differences in thrombin generation. Similar arguments hold for platelet aggregation, where platelet accumulation is limited by transport at low shear rates and by the kinetics of GPIbα–VWF interactions at high shear rates [24].

Recommendations for reporting

In the context of scaling, differences in results between flow chamber studies performed at identical shear rates can be attributed to differences in the parameters listed in Table 1. Pe and Da are functions of channel or vessel height (Table 1); therefore, matching only shear rates between different chambers does not ensure the same mass transfer and reaction regime. This is not an exhaustive list and other differences affect results, as reported elsewhere [25–28]. Nevertheless, the reporting of these dimensionless parameters, or at least the important variables that are used to calculate them, provides useful information in making comparisons between flow chambers. Moreover, using the concepts of dimensional and dynamic similarity can aid in the development of new models that seek to better recapitulate physiology in vitro.