The elusive quest for RNA knots

ABSTRACT

Physical entanglement, and particularly knots arise spontaneously in equilibrated polymers that are sufficiently long and densely packed. Biopolymers are no exceptions: knots have long been known to occur in proteins as well as in encapsidated viral DNA. The rapidly growing number of RNA structures has recently made it possible to investigate the incidence of physical knots in this type of biomolecule, too. Strikingly, no knots have been found to date in the known RNA structures. In this Point of View Article we discuss the absence of knots in currently available RNAs and consider the reasons why knots in RNA have not yet been found, despite the expectation that they should exist in Nature. We conclude by singling out a number of RNA sequences that, based on the properties of their predicted secondary structures, are good candidates for knotted RNAs.

The systematic characterization and classification of knots has engaged scientists since the introduction of Tait's knots table, whose first entries are shown in Fig. 1A. It is readily seen that the different types of entanglement are permanently trapped in the closed curves. In fact, any two curves cannot be continuously deformed into one another unless they are cut open, rearranged and resealed.

Figure 1.

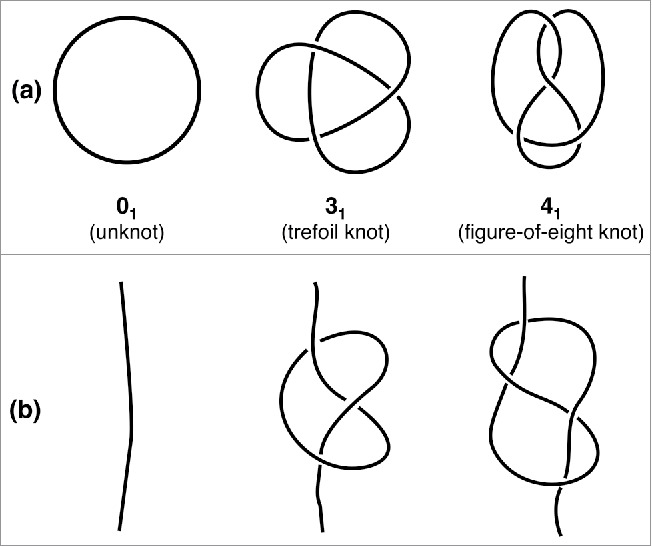
The simplest types of knots. The simplest mathematical knots are shown in panel (a) and are labeled by the number of crossings in the simplest two-dimensional projection followed by a conventional indexing subscript. The corresponding physical knots, which are obtained by opening the closed chains, are shown in panel (b).

In our everyday life, the knots that typically surround us differ from these well-defined mathematical ones because they are tied in open chains (Fig. 1B). These knots are clearly not permanently trapped and hence are termed “physical knots”. Many of the physical knots that we encounter have been purposely introduced in, for example, the yarn of sewn clothes or in ropes secured to anchoring points. Not infrequently, however, we have to deal with their unwanted spontaneous occurrence, as in the earphone cords pulled out of our pocket.

These spontaneous forms of entanglement arise by statistical necessity in microscopic filaments too. As a matter of fact, equilibrated polymers cannot escape the formation of knots, if they are sufficiently long,¹ especially if they are densely packed.^2,3 It is therefore a remarkable fact that the statistical incidence of topological entanglement in biomolecules such as proteins and DNA filaments, which are both long and compact, is substantially smaller than expected for general models of equilibrated polymers with equivalent length and packing conditions.^4-6

The observed limited incidence of knots probably results from evolutionary pressure to limit the likely detrimental implications on the biological viability and functionality of these molecules. For instance, if a protein was as prone as a generic flexible polymer to the stochastic formation of knots, then its folding route would be riddled with kinetic traps and dead ends. It is accordingly plausible, as remarked by Levinthal in more general contexts,^7,8 that protein sequences have evolved to encode not only the thermodynamically-stable native fold, but also the sequence of steps leading to the native structure formation so to minimize the incidence of misfolded states, including knotted ones which would be very challenging to backtrack.

Arguably, the most vivid illustration of the seemingly general aversion to entanglement of biomolecular systems is provided by DNA molecules in higher eukaryotes, where they are hierarchically organized in chromatin fibers and form very long chromosomes. It has long been a puzzle how the chromosomes could dynamically reconfigure through the decondensed interphase configurations and the rod-like mitotic ones without being hindered by the cis- and trans-chromosome entanglement expected to arise from their dense packing in the nucleus.⁹ The complementary advancements in imaging techniques^10,11 and computer modeling ^5,12 have nowadays clarified that the incidence of intra- and inter-chromosome entanglement is kept at a minimum by the fact that the cell cycle lasts only a tiny fraction of the time needed to equilibrate decondensed chromosomes. Consequently, interphase chromosomes are quenched in a state that retains memory of the disentangled mitotic state and are thus efficiently primed for the subsequent recondensation step. These considerations support the long-held notion that biomolecules should typically be free of significant forms of self- and mutual entanglement.¹³

Yet, although expectedly disfavoured, knots do occur both in proteins and in DNA.

For instance, it is known that about 1 − 2% of the proteins in the protein data bank (PDB) contain physical knots.^14-16 Furthermore, electrophoretic experiments have shown that viral dsDNA, once circularised either in bulk or inside viral capsids, is substantially knotted.^17-19 In particular, the incidence of knots in P4 DNA, which is 10kb-long, is at least 95%. ¹⁸ The incidence of knots in longer DNA packed inside viral capsids is expected to be even higher, though at the moment this has not been ascertained yet due to limitations of current topological profiling techniques.

Motivated by these considerations, last year some of us undertook a survey of the occurrence of knots in the RNA structures deposited in the PDB as of June 2014.²⁰ This was motivated by the fact that, since the early study of ref. ²¹, no systematic profiling of RNAs topology had apparently been carried out, despite the rapid increase of the database of publicly available structures. At that time, the PDB contained several thousand RNA entries, spanning a total of 5,466 chains. Assuming a knot incidence comparable to that found in proteins, ∼1%, tens of knotted entries could have been expected. Strikingly, no genuinely-knotted RNA chain was identified in the survey.

For this Point of View article, we considered the reasons why knots in RNA have not yet been found, despite the expectation that they should exist in Nature.

To initiate this query, we first updated our 2014 survey by profiling the RNA structures deposited in the PDB as of August 2015 (Fig. 2 and Supplemental Material). Again, despite the appreciable increase in the number of distinct chains over one year, from 5,466 to 7,013, no genuinely-knotted RNA structure was found. To be precise, the two surveys did return three knotted entries, which are listed in Table 1, but, as already noted in ref. 20 they are most likely artifactual results of cryo-EM reconstructions.

Figure 2.

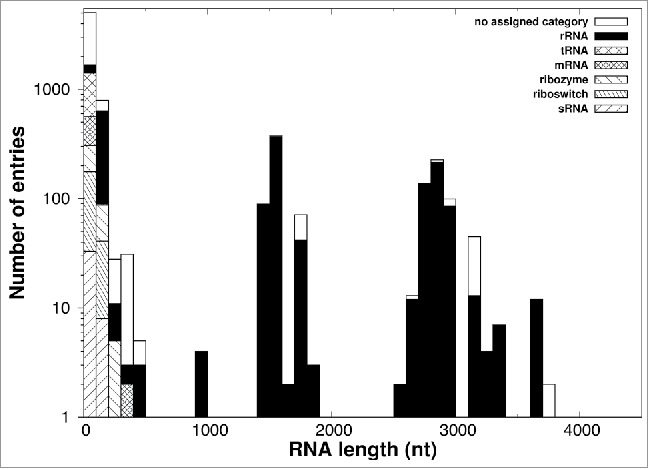
RNA chain length and types. The distribution of lengths (number of phosphates) of all 7,013 RNA molecules with more than five phosphates deposited in the PDB as of August 2015 is shown. The color code describes the contribution of each categorized subdivision to the total amount of chain.

Table 1.

Knotted RNAs in the survey data set. The knots are likely artifactual results of cryo-em reconstruction. The entries are the same as those shown in Table 1 of ref. 20, though some of the PDB codes differ because the PDB introduced a new archiving system of large structures (with no change of atomic coordinates). The overall knot type was established by using the minimally-invasive closing procedure of ref. 46. The # sign in the knot label of the last entry denotes the composition (concatenation) of various prime knots.

Putative knot	Molecule (Organism)	Length (nt)	PDB ID	Suspicious clasp (essential crossings)
41	23S rRNA (E. coli)	2,740	4V4V:B0	G1478-C1480 and C1558-C1561
16124834	26S rRNA (T. lanuginosus)	3,169	4V7H:B5	C618-A622 and A1401-U1405 A710-G714 and U2775-A2780
31#31#41#31	23S rRNA (E. coli)	2,904	1C2W:B	G263-C264 and G363-C364 C1454-G1455 and C1526-G1527  U1476-A1477 and G1514-A1515 U1856-G1857 and C1887-G1888

Though an equal footing comparison with proteins is difficult for the different typical length (number of monomers) of the two types of molecules and the PDB entry redundancy, the total absence of knots in the > 7,000 available RNAs structures is notable.

Assuming that this dataset provides an unbiased representation for naturally-occurring RNAs, it is appealing to speculate on the biological rationale behind the apparent aversion of RNA to knots. A first general consideration regards RNA folding kinetics, particularly its possible co-transcriptional component.^22,23 It appears plausible that newly transcribed nucleotides in a nascent RNA chain could anneal with other nearby nucleotides establishing ephemeral local secondary structures. While these temporary motifs may be traded off for longer range ones at later folding stages, their presence would make it more difficult to develop knots by increasing the effective thickness and local rigidity of the chain. The possible out-of-equilibrium accretion of the RNA chain growing sequentially in layers around the already-transcribed, compact, portion would clearly also push toward entanglement-free structures, too. It is worth noting that the sequential modular growth of RNA chains could be also relevant from an evolutionary point of view. In fact, it has been recently suggested that RNA ribosomal complexes have reached their current large and articulated conformations by the sequential addition of small modular structures.²⁴ Similarly to the kinetic ones, such evolutionary mechanisms should limit the incidence of self-entanglement too.

It also appears plausible that RNA knots, and other forms of entanglement, are not favored thermodynamically. In fact, independent of kinetic considerations, naturally occurring RNAs appear to be primed for acquiring native structures with rather low geometrical complexity. This observation is prompted by the analysis of secondary-structure predictions of algorithms that are exclusively based on the minimization of the (model) free energy of RNA sequences. These phenomenological approaches clearly do not account for any kinetic effects and yet their returned structures are geometrically much simpler than randomly reshuffled variants of the sequences. For instance, even when using structure prediction algorithms based on planar graph representations one observes that viral RNA sequences have a significantly smaller graph diameter, a proxy for three-dimensional size, than their reshuffled versions.^25,26 This point is reinforced by the analysis of the minimum energy structures returned by McGenus.^27,28 Specifically, it is found that the predicted non-planar graphs of the reshuffled variants have a topological complexity, as measured by the graph genus, that is more than an order of magnitude larger than for the wild-type counterparts.²⁰

Although RNA knots may be elusive today, it is conceivable that they were important in earlier evolutionary stages, even during the origins of life. The RNA world concept posits a period of time when RNA, or something chemically similar, was responsible for all living processes including heredity and metabolism. RNA-RNA interactions have often been proposed to be critical to maintaining the physical integrity of networks of distinct sequences.^29-31 Typically these interactions have focused solely on secondary structure interactions, but many environments on an early Earth could have experienced rather extreme temperature fluctuations that could disrupt weak base-pairing. More severe entanglements such as knots – but without covalent bonding – would have been a means to preserve spatial sympatry of RNA network individuals in harsh environments. The observation that many catalytic RNA species have structures that are pseudoknotted seems to hint at closer inter- and intra-molecule associations as one goes back in time.

It is, again, important to recall that these conclusions and considerations are based on the set of currently known RNA structures which, though not negligible, is inevitably still limited. There is also almost certainly a selection effect among the solved RNA structures for molecules that adopt a single stable conformation, meaning that if RNA adopts a knotted conformation as one of multiple conformations or as a misfolding event, then it is less likely to be detected. In this regard, a possible parallel can be drawn with proteins, where the discovery of knotted structures was inextricably tied with the growth of the PDB size. In fact, while the occurrence of a knot in transcarbamylase was reported as early as 1977,³² its genuine character was disputed for its proximity to one of the termini. It was only after the protein database had grown enough that later surveys of Mansfield and Taylor established beyond doubt that genuine, deeply-tied knots were present in naturally occurring proteins.^33,34 It is therefore appealing to speculate that a similar pathway may follow for RNA too. With the number of established structures rapidly increasing, it is possible that genuine knotted RNAs can be found.

The plausibility of knotting in biological RNAs is illustrated strongly by two considerations based on the seminal work of N. Seeman and coworkers. In a remarkable set of experiments,³⁵ they designed synthetic ∼100-nt long RNA sequences that could spontaneously fold in circularised knotted structures and be unknotted by the Top3 bacterial DNA. More recently, the same assay has been used to demonstrate that the human Top3β enzyme also has RNA topoisomerase activity.³⁶ Two important facts emerge from these experiments. First, they vividly demonstrate that even short RNA molecules can be knotted. Secondly, that the molecular machinery of the cell is already predisposed to deal with RNA knots and simplify them. From the principle of biological parsimony, such simplifying action would hardly be expected if complex RNA topologies were not present in vivo, particularly when one considers the exquisite specificity of enzymes that act on nucleic acids for RNA or DNA, but almost never both.

In view of these considerations, the occurrence of knots in naturally occurring RNA appears at least possible, and could be very likely. They would arise from a balance between evolutionary pressures to avoid detrimental entanglement and the functional advantage that knotted RNAs could have in specific, and arguably rare cases. For instance, physical entanglement might allow RNAs to modulate gene expression or to enhance their resilience to in vivo degradation. The latter aspect might be relevant for the recently discovered circRNAs ^37-39 which thanks to their circularised form, could trap long-lived knots, as suggested by Frank-Kamenetskii.⁴⁰ The knotted forms of any RNA would be expected to be only a fraction of total folding space, such that any given genotype could have multiple phenotypes. These could arise from the delicate interplay of folding kinetics and thermodynamics or from the interaction with partner molecules. Perhaps only 5–10% of a ”knottable” RNA is actually knotted in vivo. This could help explain why they have eluded detection so far.

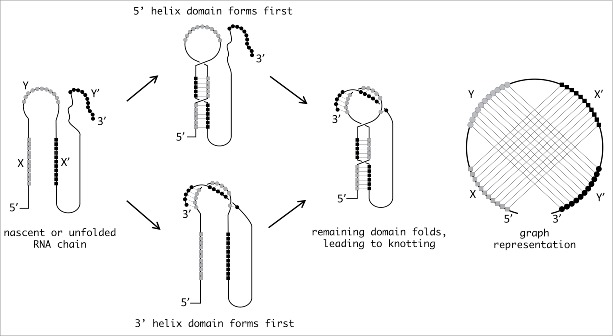
To guide the search for knotted RNA, we carried out specifically for this Point of View article a bioinformatics survey aimed at identifying candidate RNA sequences that could be susceptible to knotting. As the Seeman laboratory elegantly demonstrated,³⁵ nucleic acid sequences designed to contain two self-complementary 11-nucleotide sequences (X, Y, X’, Y’ in which X and X’ pair and Y and Y’ pair) can spontaneously form knots. We have diagrammed this scenario in an example RNA, and show pathways through which knotted structures could form, at least in some sub-population of folded structures (Fig. 3). We note that in addition to forming physical knots, these molecules are also pseudoknotted, in the sense that the strands involved in the two helices are interleaved. Thus, pseudoknotted RNA sequences with relatively long base-pairing stretches appear to be the most likely candidates to form knots. The minimal number of basepairs needed to form a knot can be estimated from a theoretical standpoint, based on the requirement of a minimum of three strand-crossings for the simplest knot. Because ˜10 basepairs are necessary for two strand crossings (a full helical turn), pseudoknotted structures containing multiple helices of at least ten basepairs would be prime candidates for knotting. A review of the RNA pseudoknot database reveals two candidates that approach or meet these criteria (Table 2). Specifically, the plasmid Colib-P9 mRNA (with helices of 18 and 10 basepairs), and Homo sapiens CCR5 PRF (with helices of 25 and 13 basepairs) and telomerase RNA (helices of 22 and 9 basepairs) appear very likely to have at least a slip-knotted structure (in which a free-end has not been completely threaded through a loop). Incidentally we note that such structures have also been observed in proteins.^41-43 These candidate sequences are found within larger RNA molecules, which might seem to preclude the threading events necessary for knotting. In proteins, however, it has been demonstrated in vitro that addition of large structured domains to the N- and C-termini of a knotted protein does not prevent it from adopting its native, knotted conformation so it should not be assumed a priori that longer RNAs cannot form knots.⁴⁴ In addition, we have also identified a number of pseudoknotted RNAs with one helix of 10 or more basepairs and a second helix of seven or more basepairs. Although the lowest energy conformations of these molecules would likely be only pseudoknotted, the potential would seemingly exist for knotting to occur to at least a small extent as an alternative or misfolded conformation (Table 2). As a matter of fact, their secondary structures, as predicted by McGenus,^27,28 are not a priori incompatible with proper knots.

Figure 3.

Possible pathways leading to RNA knotting. The sketch illustrates possible pathways through which two sets of interleaved self-complementary sequences (marked with squares and circles, respectively) can fold and produce a knotted RNA structure. The latter is tied in a figure-of-eight knot and the diagram representing the two helices features the characteristic pseudoknot crossings.

Table 2.

Candidate knot-forming RNA molecules from Pseudoknot database (http://ekevanbatenburg.nl/PKBASE/PKBGETSUM.HTML#TOP; updated November 28, 2014, accessed October 11, 2015).

Molecule	Helix 1 length (nt)	Helix 2 length (nt)
CCR5_PRF (H. sapiens)	13	25
ColIb-P9_repZ (Plasmid ColIb-P9)	18	10
hTER (H. sapiens)	22	9
pMU407_repBA (plasmid pMU407.1 [IncL/M]	19	8
RSV (Rous sarcoma virus)	14	8
Ec_α (E. coli)	12	8
SESV (Seal louse virus)	11	8
Sc_18S-PKE21-7/8 (S. cerevisiae)	10	8
Mm_Edr (M. musculus)	10	9
Bovine coronavirus	8	10
MHV (mouse hepatitis virus)	8	10
Qbeta_PKldX (bacteriophage Q-β)	8	9

The table of RNA sequences we have identified, while not exhausting the repertoire of possible knotted candidates, should nevertheless provide a starting point for a targeted search for knotted RNAs. Previous biochemical analyses raised the possibility that two naturally-occurring RNA intron sequences were capable of adopting knotted conformations, but the presence of a physical knot could not be confirmed irrefutably with the available data.⁴⁵ A significant challenge for the unambiguous confirmation of true knots in RNA is the difficulty associated with solving RNA structures; this challenge could be overcome by the development of an appropriate high-throughput assay to detect knotted RNAs, especially when present as isoforms coexisting with other stable unknotted conformations. The lack of such systematic assays is, at present, the main obstacle toward advancing our understanding of the incidence of physical knots in RNAs.

In conclusion, the lack of physical knots in presently available RNA structures is particularly intriguing and also unexpected by comparison with other biopolymers, such as proteins and encapsidated viral DNA where knots are known to occur. It is possible that the sequence of naturally-occurring RNAs, some of which need to be efficiently translocated through biological pores, have evolved to harness folding kinetics and thermodynamics so as to minimize the incidence of various forms of self-entanglement, including knots, in their native structures. At the same time, the fact that knotted RNAs with as few as ˜100 nucleotides have been successfully designed and synthesized,³⁵ suggests that there is no fundamental reason why relatively short knotted RNAs should not exist in nature, possibly in circularised form where knots could be essential to enhance their mechanical stability. According to this standpoint, the current situation would parallel the historic route taken for proteins, where the occurrence of knots was once deemed implausible, if not impossible, due to the inevitable initial limitations in size and representation bias of the set of available protein structures. To aid the ongoing efforts to detect knotted RNAs we have presented a list of sequences whose predicted native structures are expectedly susceptible to the formation of knots, possibly as isoform competing with other unknotted ones.⁴⁰ We hope that the list of selected candidates will serve as a useful starting point toward the systematic search of RNA knots.

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.

Acknowledgments

We thank Sandro Bottaro and Giovanni Bussi for useful discussions.

Funding

We acknowledge financial support from the Italian Ministry of Education, grant PRIN 2010HXAW77