Abstract
In a previous publication, we presented a new computational model called SLAM (Walker & Hickok, in press), based on the Hierarchical State Feedback Control (HSFC) theory (Hickok, 2012). In his commentary, Goldrick (submitted) claims that SLAM does not represent a theoretical advancement, because it cannot be distinguished from an alternative lexical + post-lexical (LPL) theory proposed by Goldrick and Rapp (2007). First, we point out that SLAM implements a portion of a conceptual model (HSFC) that encompasses LPL. Second, we show that SLAM accounts for a lexical bias present in sound-related errors that LPL does not explain. Third, we show that SLAM’s explanatory advantage is not a result of approximating the architectural or computational assumptions of LPL, since an implemented version of LPL fails to provide the same fit improvements as SLAM. Finally, we show that incorporating a mechanism which violates some core theoretical assumptions of LPL—making it more like SLAM in terms of interactivity—allows the model to capture some of the same effects as SLAM. SLAM therefore provides new modeling constraints regarding interactions among processing levels, while also elaborating on the structure of the phonological level. We view this as evidence that an integration of psycholinguistic, neuroscience, and motor control approaches to speech production is feasible and may lead to substantial new insights.
Introduction
The Semantic-Lexical-Auditory-Motor (SLAM) model of speech production (Walker & Hickok, in press) represents an attempt to evaluate the effects of a theoretically motivated architectural modification of the Semantic-Phonological (SP) model (Foygel & Dell, 2000). The modification involved splitting the phonological layer into two parts: an auditory and a motor component. This was motivated by neuroscience data and motor control theory, which both highlight the importance of sensorimotor interaction in controlling movement, including speech (Hickok, 2012). Part of the neuroscience data that motivated the architecture came from conduction aphasia, which can be conceptualized as a sensorimotor deficit in the linguistic domain, and thus we specifically predicted the SLAM model would provide better fits compared to SP for naming error patterns in this syndrome. Our prediction was confirmed without sacrificing fits for other types of aphasia. Furthermore, we used the clinical description of the conduction syndrome to predict the model configuration that would lead to fit improvements: strong auditory-lexical connections and weak auditory-motor connections. This prediction was confirmed. Moreover, we discovered that this model configuration improved fits for the conduction aphasia group specifically by accounting for sound-related errors via the interaction of the lexical and phonological levels as opposed to dysfunction at the phonological level alone. We took SLAM’s success as support for the idea that an integration of psycholinguistic, motor control, and neuroscience was (is) feasible (Hickok, 2014a, 2014b).
Goldrick (submitted) is unconvinced, however, that SLAM represents any real theoretical progress. He argues instead that SLAM does better than SP because it is an approximation of a lexical + post-lexical phonological theory (henceforth LPL) proposed by Goldrick and Rapp (2007), which he claims provides a better account of the sound-related errors in conduction aphasia by placing their source at the post-lexical level. In partial support of his claim, he presents a regression analysis showing that SLAM's fit improvements over SP for conduction aphasia are correlated with the number of sound-related errors that the patients produced. In reply, we make four points. First, Goldrick is comparing his conceptual model against a computational implementation of a part of our own conceptual framework. His arguments hold no water against our broader theoretical perspective. Second, we extend Goldrick's analysis to show that the SLAM fit improvements correlate with the degree of lexical bias within conduction patients' sound-related errors, thus implicating the involvement of the lexical level in the error pattern in these patients, which LPL does not predict but SLAM does. Third, because Goldrick has not used LPL to make quantitative predictions about the same data as SLAM, there is no objective metric to evaluate the claim that SLAM’s improvement is due to its approximating LPL. Finally, when we implement the LPL theory in a computational model, we find that it fails to provide the same fit improvements as SLAM.
On the relation between SLAM, HSFC, and LPL
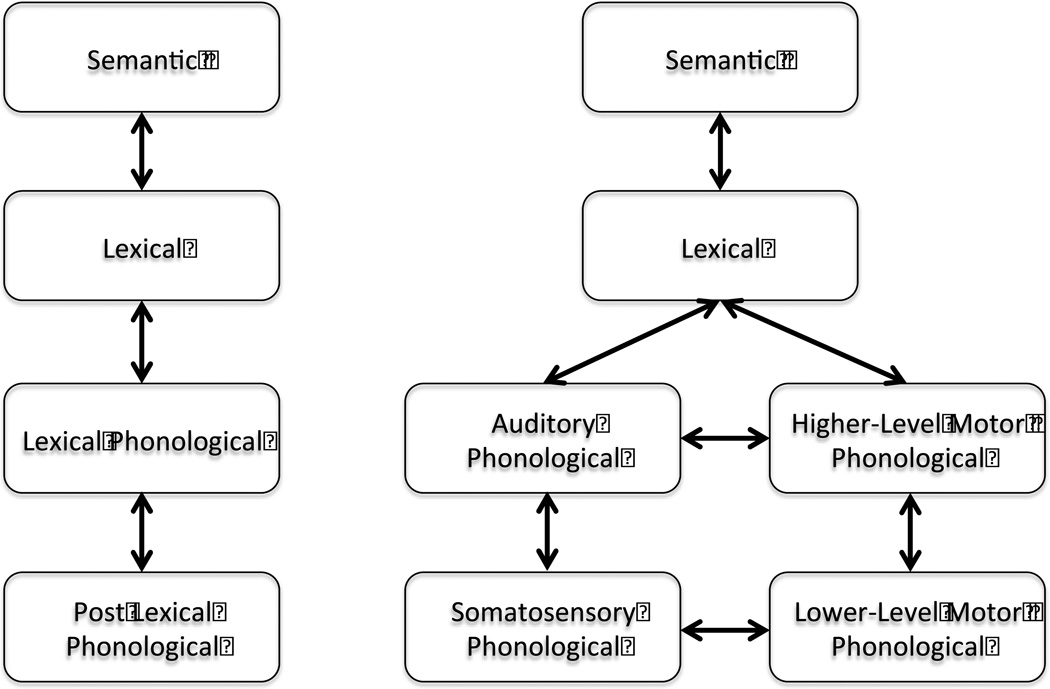
Goldrick begins his commentary by correctly noting that we presented an implementation of aspects of Hickok’s (2012) Hierarchical State Feedback Control (HSFC) theory. He then fails to notice that (a) the unimplemented aspects provide exactly the post-lexical component he calls for and (b) the goal of SLAM was to assess precisely the one bit that we changed, not a full-blown implementation of the entire system as we understand it. In Goldrick’s (submitted) Figure 1, the SLAM architecture is redrawn to show its similarity to the LPL theory and to highlight the difference with respect to the existence of a post-lexical stage of phonological processing, present in LPL and absent in SLAM. But this is misleading with respect to the broader theoretical context in which SLAM is situated. Figure 1 here compares the architectures of the LPL conceptual theory with the HSFC conceptual theory. HSFC proposes the existence of sensorimotor loops that correspond to different hierarchical levels of phonological processing. One could readily map the auditory-phonological loop onto LPL's lexical phonological level and the somatosensory-phonological loop onto the post-lexical level. With this alignment there are no presumed architectural advantages of LPL in terms of selection levels. That is, if we implemented this more complete architecture we would, according to Goldrick’s arguments, provide a better fit to more of the data1. This remains to be seen, of course, but it is an interesting and potentially fruitful direction for further development. And now that we better understand the computational effects of sensorimotor loops in word production models, which was the aim of developing SLAM, we are in a good position to take the next step.
Figure 1.
The lexical + post-lexical (LPL) model (left) compared with the Hierarchical State Feedback Control (HSFC) model (right).
What are the sources of sound-related errors in conduction aphasia?
The symptom complex of conduction aphasia was a major motivation for the development of the dual stream model of language processing (Hickok, 2000, 2001; Hickok et al., 2000; Hickok & Poeppel, 2000, 2004, 2007) and has remained central in recent work, such as the HSFC model, aimed at understanding the computational neuroanatomy of the dorsal, sensorimotor stream (Hickok, 2012, 2014a, 2014b; Hickok, Houde, & Rong, 2011). SLAM was developed specifically to assess the effects of the auditory-motor architecture of the HSFC framework on computational models of speech production. Because the HSFC was developed in part to explain conduction aphasia, we predicted that SLAM should improve the fits in this group by providing an architecture in which the auditory-motor interaction could be weakened while maintaining relatively strong lexical-auditory interaction. Our predictions were confirmed. We did not have further predictions regarding how this computational arrangement would generate the tendency to produce mainly sound-related errors, as is found in conduction aphasia. What we discovered in our analysis of the model, however, is that such errors were not only a function of misselection at the phonological level but also a function of strong auditory-phonological feedback to the lexical level that increased the probability of selecting a sound-related word at that level. The model thus generated a new hypothesis regarding an additional computational source of sound-related errors in conduction aphasia.
Goldrick (submitted) in his commentary presented new evidence linking SLAM’s improvement over SP to a better account of the conduction patients' sound-related errors in particular, extending our analysis in a way that is fully consistent with the assumptions of the HSFC framework. However, Goldrick questions SLAM’s computational explanation of sound-related errors and asserts instead that they arise as a consequence of post-lexical deficits. Quoting Goldrick (2011): "Disruption to post-lexical processing therefore results in the production of phonologically related words as well as nonwords, accounting for the overall performance pattern discussed above … Individuals with deficits to a post-lexical stage, governed by relationships among fully-specified phonological structures, will not be influenced by lexical factors."
One way to test this claim then is to look within the sound-related errors for correlations between lexical factors and SLAM fit improvement. Specifically, if sound-related errors are arising via interactions with the lexical level, then the amount of SLAM fit improvement should correlate with the amount of lexical bias among the sound-related errors. That is, SLAM should provide better fits for patients who produce more sound-related errors that are also real words, as opposed to sound-related errors that result in a non-word. On the other hand, if SLAM is only accounting for post-lexical deficits, fit improvements should be unrelated to the lexical status of the errors. We define the lexical bias for a patient using the empirical logit, i.e., the log-odds that a sound-related error is a word versus a non-word,
The numerator of the odds ratio includes the counts of Formal and Mixed (real word, sound-related) errors, while the denominator includes only the sound-related Non-word errors (i.e., subtracting the Abstruse Neologisms that do not share any phonemes with the target). We examined the responses from 49 of the 50 patients analyzed by Goldrick (submitted); presumably, the excluded patient was added to the online database (Mirman et al., 2010) after our most recent query, and we do not expect data from a single patient to influence our results. We found that the differences in model fit (RMSD) between SP and SLAM significantly correlated with the lexical bias of the sound-related errors (r(47) = .30, p = .03); that is, when conduction patients produced more real-word sound-related errors, SLAM provided better fits. Excluding Mixed errors from the lexical bias definition, under the assumption that these errors could result from earlier semantic processing deficits, increased the correlation (r(47) = .46, p = .001). This does not preclude the possibility that sound-related errors also arise from post-lexical processing deficits in conduction aphasia, but it does show that at least some of the SLAM fit improvement is coming from better modeling of sound-related errors arising via interaction with the lexical level. Goldrick's assumption that the SLAM model is only accounting for post-lexical sound-related errors is therefore unfounded.
How do we know if LPL accounts for the same data as SLAM?
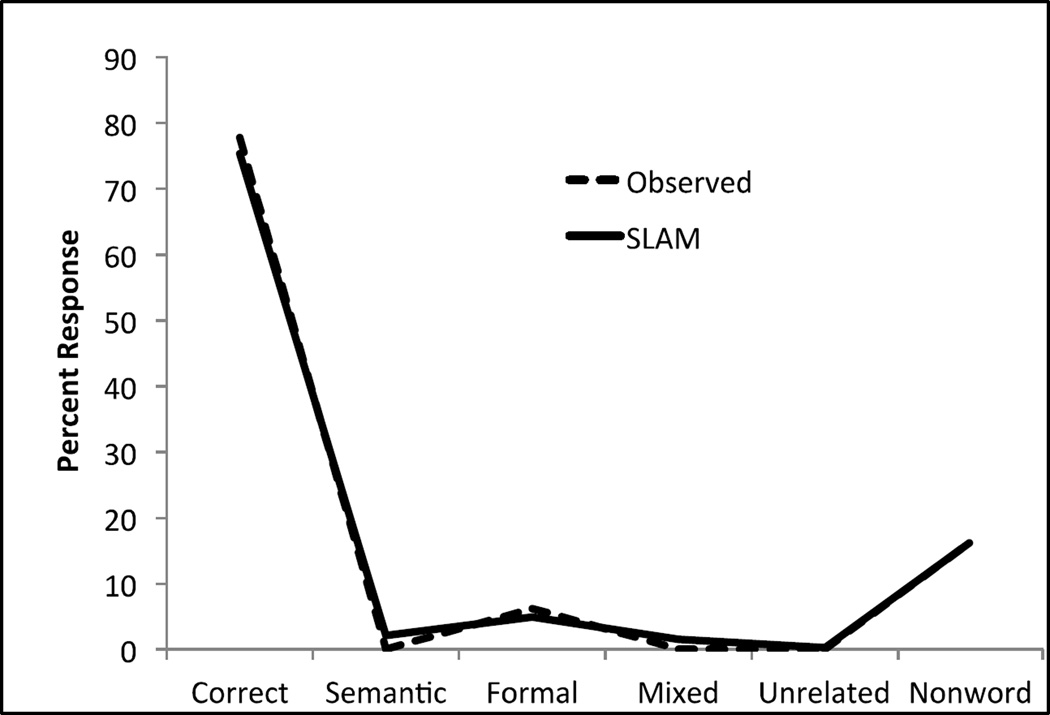
The LPL theory is a conceptual one, not a computational implementation. We can readily compare the amount of variance accounted for by the two computational models we evaluated, SP and SLAM, and apply quantitative metrics to determine which one does a better job. Goldrick does not present a quantitative metric to evaluate the performance of the LPL theory relative to these models, making it impossible to confirm or refute his claim based on his arguments. For example, Goldrick asserts that SLAM has “great difficulty” in accounting for his prototypical case of a patient with only sound-related errors. What we know is that SLAM predictions for this case deviate (using the RMSD metric) from the observed values on average by 1.5% (Figure 2), which is better than the typical fit error values across all patients. Is this a good fit, or is SLAM having great difficulty? The only way to tell is to compare it with the fit of a competitor model. If the competitor’s fit differs by 10%, then SLAM provides a good fit. If the competitor’s fit is off by 0.01%, then indeed SLAM is having great difficulty. Since Goldrick provides no quantitative comparison, his assertions are vacuous.
Figure 2.
Observed response pattern in a patient with no semantic errors and SLAM’s best fit predictions.
The same lack of quantitative comparison undermines Goldrick's critique of our methodological approach. The critique is based on a set of simulations involving the SP model reported previously (Goldrick, 2011). The simulations involved generating artificial datasets with SP as well as two alternative models. Data from the three models were then fit with parameters from the SP model. Goldrick claims that “the degree of fit was equivalent for all three artificial case series.” From this observation, he suggests that model fitting cannot always discriminate between theoretical accounts. However, his statements are misleading and his simulation strategy is inadequate. In order to discriminate models quantitatively, it is not enough to look at fits from a single model and judge them good or poor, equivalent or different. Rather, one needs to evaluate the fits of each model and assess whether one provides a better account of the data than the other.
To demonstrate this point and to evaluate whether our methods can indeed discriminate SP and SLAM, we ran simulations similar to those carried out in Goldrick (2011). Specifically, we generated three artificial data sets using the SP model and three using SLAM. Two of the artificial datasets from each model were generated by simulating 175 naming attempts from each of 1,000 simulated patients, following Goldrick (2011); the third artificial dataset was generated by simulating 175 naming attempts from each of 255 simulated patients (see below). For the first two artificial datasets, a given patient was simulated using a set of model parameters selected randomly from a continuous distribution of parameters. Goldrick (2011) used a single continuous distribution of parameters in his simulations, namely, all weights were independently and normally distributed with a mean of 0.025, a standard deviation of 0.01, and truncated on the interval [0.0001, 0.05]. Since this parameter space distribution is an arbitrary choice, we used two different arbitrary distributions applied to each model (SP and SLAM) to provide a more thorough evaluation of model discriminability. The first was a normal distribution with mean 0.02 and standard deviation 0.01 truncated on the interval [0.0001, 0.04]. These values were selected because we used a maximum weight of 0.04 in our original simulations for both SP and SLAM. Also, in accordance with our original simulations of SLAM, the LM-weight was re-sampled until it was less than the LA-weight (Walker & Hickok, in press). The normal distribution assumes that most aphasic patients will have weights around 0.02, and few will have extreme weight values. In the second simulated dataset, we used a uniform distribution of weight values, that is, a distribution in which any value is equally likely to be selected over the interval [0.0001, 0.04]; again we constrained the LM-weight to be less than the LA-weight for the SLAM simulations. Our third simulation used the empirical distribution of weight configurations in our sample rather than randomly sampling from a continuous distribution of parameter values. For each of the 255 patients in our sample, we generated a new simulated patient with 175 naming attempts using the best fit parameter values from each model. These procedures generated six datasets: three generated by SP and three generated by SLAM. We then fit each dataset with each of the models, using the same maps with 2,321 points and 10,000 naming attempts that we used in our previous studies.
For each data set, we used a paired, two-tailed t-test to assess whether the models produced significantly different fits to the data on average. We note that null hypothesis testing is not the only way to quantitatively compare models, but it provides a familiar frame of reference. Our null hypothesis was that the models have equal fit to the data on average and thus cannot be discriminated with our method. Table 1 shows the average fit of each model to each data set, along with the preferred model if we had enough evidence to reject our null hypothesis and successfully discriminate between them.
Table 1.
Results from paired, two-tailed t-tests comparing mean RMSD for the SP and SLAM models. The data sets that were generated with parametric distributions each have 1,000 simulated patients. The data sets that were generated with empirical distributions each have 255 simulated patients.
| Data set | SP fit (mean RMSD) |
SLAM fit (mean RMSD) |
Preferred model |
p-value |
|---|---|---|---|---|
| SP_normal | 0.0118 | 0.0124 | SP | 0.0021 |
| SP_uniform | 0.0116 | 0.0123 | SP | 0.0006 |
| SP_empirical | 0.0099 | 0.0106 | SP | 0.00006 |
| SLAM_normal | 0.0123 | 0.0117 | SLAM | 0.0155 |
| SLAM_uniform | 0.0120 | 0.0116 | SLAM | 0.0512 |
| SLAM_empirical | 0.0105 | 0.0096 | SLAM | 0.00004 |
In each comparison, the true model that generated the data provided a better fit compared to the alternative model. A statistical test of the difference in fits between the two models shows that the difference is statistically significant in each case (or all but one case if the p = 0.0512 is counted as non-significant). This makes it a non-trivial finding that there are enough individuals from a broad sample of post-acute aphasic patients concentrated in regions of parameter space to detect a difference between the models; if SLAM did not truly improve fits over SP for the aphasia population, then our model comparisons would have indicated this. We note that these effect sizes would be much larger if the analysis was applied to the empirical distribution of only the conduction patients. We also note that our observed effect sizes2 are much smaller than those reported by Goldrick (2011). If we had used Goldrick's (2011) model evaluation method (comparing datasets, not models), we would simply observe that the average fit of the SP model to the SP_normal data is very similar to the average fit of the SP model to the SLAM_normal data, 0.0118 and 0.0123, respectively, and conclude without further analysis that it is impossible to discriminate between the models. This illustrates the importance of comparing different models of the same data.
How does an implemented version of LPL fare?
Goldrick contends that the only reason SLAM improves fits over SP is because SLAM includes an intervening layer between lexical selection and the model's output, accidentally capturing the critical components of the LPL theory. He explains that the SLAM architecture can be converted into an implementation of the LPL theory simply by removing the lexical-motor weight, and more importantly, adding a further selection step at the auditory layer. Indeed, the added selection step is the crucial difference between the theories under consideration. SLAM does not include an extra selection step, so minimizing the LM weight is the best it can do (without becoming a different model) to approximate LPL. But we already demonstrated that restricting this weight for all patients (i.e., approximating LPL) leads to worse predictions (Walker & Hickok, in press). Thus, it is clear that SLAM, as we previously implemented it, does not improve over SP by approximating the structure of LPL. We therefore considered the possibility that a different model that better represents the LPL theory might account for the same data as SLAM.
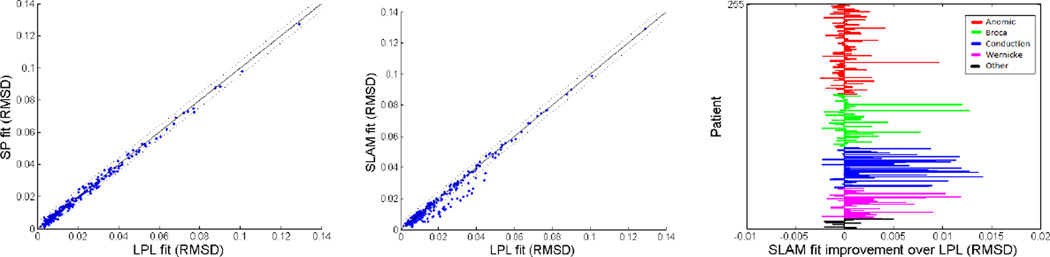
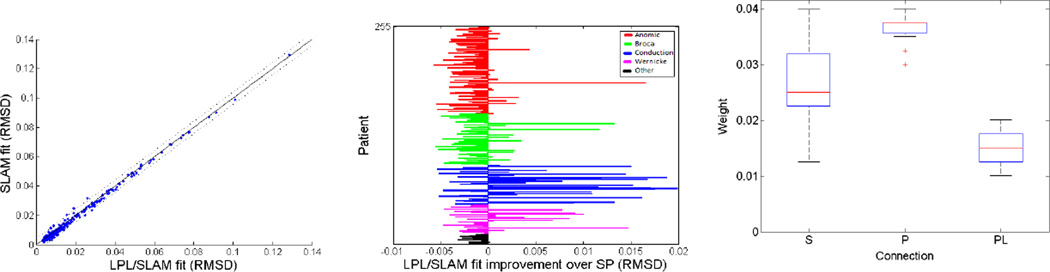
We created a new LPL model by modifying SLAM in accordance with Goldrick's suggestions: removing the lexical-motor weight3, adding a selection step at the auditory layer, and removing the lexical input to phonemes after they are selected. This last modification implements Goldrick’s assumption that post-lexical processing is a distinct stage. Quoting Goldrick (submitted): "Note that this is a distinct stage of production processing in that it follows the explicit selection of an abstract phonological representation. In general, such selection mechanisms serve to reduce interactions across processing levels, increasing the degree to which distinct subprocesses can exhibit distinct patterns of impairment." Thus, by removing lexical input to phonemes after they are selected, we are implementing this theoretical position. In the LPL implementation, the phonological units correspond to SLAM's auditory units, and the phonetic units correspond to the motor units. The phonetic units can be thought of as localist representations of feature bundles, and none of the phonemes in the artificial lexicon share phonetic features. We refer to the connections as S-weights, P-weights, and PL-weights. For the LPL model to be viable, the boost of activation to each phonological unit should be large enough to successfully propagate over a further number of timesteps to produce mostly correct responses in the healthy model. We verified that delivering a boost of 150 to each phonological unit and running the model an additional 8 timesteps with the weights set at the maximum (0.04) was able to approximate the normal pattern (~97% correct). We then used the same procedures that we used previously (Walker & Hickok, in press) to fit the same patient data with our implementation of LPL, using a parameter map that included 2,321 points. As can be seen in Figure 3a, a scatterplot comparing the models' fits (RMSD) shows that LPL offers no improvements over SP: that is, fit differences are within 1SD of the fit difference between SLAM and SP. Figure 3b compares model fits for LPL versus SLAM. Note the cloud of points that fall outside the 1SD range; these indicate SLAM’s fit advantage over LPL. Figure 3c shows that the conduction patients are once again fit better by SLAM compared to LPL. It is clear that SLAM significantly outperforms LPL in the same way that it outperforms SP.
Figure 3.
A) The scatterplot compares model fits (RMSD) for LPL and SP. B) The scatterplot compares model fits (RMSD) for LPL and SLAM. The solid diagonal line represents equivalent fits, and the dotted lines represent 1SD of fit difference between SLAM and SP. C) The bar graph shows SLAM's fit improvements over LPL, grouped by aphasia type
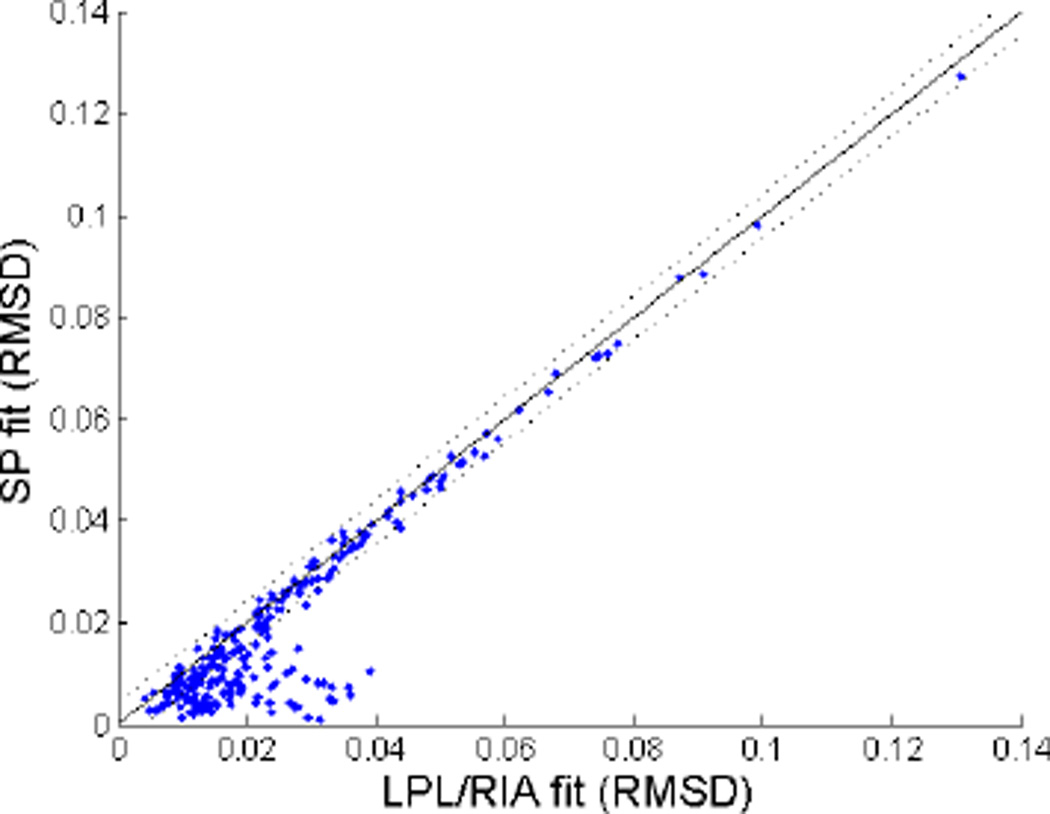
The above simulation shows that SLAM's improvement over SP cannot be accounted for simply by the addition of another processing level. Nevertheless, Goldrick (submitted) proposes a further modification of the SLAM model. He argues that SLAM’s inclusion of strong feedback (following SP) renders the model empirically inadequate. Instead he promotes Rapp and Goldrick's (2000) Restricted Interaction Account (RIA). We tested this assertion computationally by adding the RIA assumptions to the LPL model implementation described above, creating LPL/RIA4. According to RIA, there should be no feedback from the lexical to the semantic layer, and "limited" feedback from the phonological to the lexical layer. Following Ruml, Caramazza, Shelton, and Chialant (2000), who also implemented the RIA assumptions in a computational model to fit patient data, we used a feedback attenuation value of 0.1 for the P-weights, meaning that the connection strength was 1/10 of the value in the reverse direction compared to the forward direction. The PL-weights remained fully interactive5, and again lexical influences were removed during post-lexical processing. The scatterplot (Figure 4) shows that this LPL/RIA model makes worse predictions than the fully interactive SP model.
Figure 4.
The scatterplot compares model fits (RMSD) for LPL/RIA and the (fully interactive) SP. The solid diagonal line represents equivalent fits, and the dotted lines represent 1SD of fit difference between SLAM and SP.
Finally, we hypothesized that our implementation of LPL might be able to approximate SLAM if it incorporated the same mechanism that we previously identified as driving the fit improvements: strong phonological feedback to the lexical level that influences the weak phonological feedforward link to the output layer (Walker & Hickok, in press). The only way we were able to do this was to drop Goldrick’s proposed restrictions on interaction, both with respect to the RIA assumptions and the post-lexical interaction restriction. That is, we allowed lexical representations to influence "post-lexical" processing, in order to capture the effects that SLAM suggests are occurring via interaction with the lexical level, creating LPL/SLAM. To be clear, this is a test of the feedback mechanism as the explanatory factor in model improvement over SP for conduction aphasia, rather than a test of either the LPL or the SLAM models. Due to the interactivity, the lexical layer received a strong boost of feedback activation during phonological selection and, coupled with weak feedforward activation across low PL-weights, this may have the same effect as the two separate phonological sources in SLAM. Although LPL/SLAM still yields a worse fit than SP and SLAM on average, this implementation does capture many of the improvements observed with SLAM, accompanied by strong P-weights and weak PL-weights (Figure 5). The implication is that this mechanism, strong phonological-lexical interaction that influences weak phonological selection, can lead to improved fits for conduction aphasia naming regardless of the other theoretical or computational details of the model. The mechanism provides constraints on assumptions about interactivity of phonological and lexical processing for future models of conduction aphasia.
Figure 5.
A) The scatterplot compares model fits (RMSD) for LPL/SLAM and SLAM. B) The bar graph shows LPL/SLAM's fit improvements over SP, grouped by aphasia type C) The boxplots show the weight configurations for the 19 patients with LPL/SLAM fit improvements over SP greater than .01 RMSD.
Summary
The question raised by Goldrick (submitted) is whether SLAM represents an improvement over his LPL model. He argues that it offers no improvement. We have argued here that it does. First, we pointed out that SLAM implements a portion of a conceptual model (HSFC) that encompasses LPL. Second, we showed that SLAM accounts for a lexical bias among sound-related errors that LPL does not explain. Third, we showed that SLAM’s explanatory advantage is not a result of approximating the architectural or computational assumptions of LPL. Finally, we showed that abandoning some core theoretical assumptions of LPL—making it more like SLAM in terms of interactivity—allowed LPL to capture some of the same effects as SLAM. SLAM therefore provides new modeling constraints regarding interactions among processing levels, while also elaborating on the structure of the phonological level. We view this as evidence that an integration of psycholinguistic, neuroscience, and motor control approaches to speech production is feasible and may lead to substantial new insights (Hickok, 2014a, 2014b).
Acknowledgement
We would like to thank Matt Goldrick and an anonymous reviewer for comments on earlier drafts of this paper. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. 8108915 and by the National Institute of Health under Grant No. DC009659.
Footnotes
Goldrick's primary argument hinges on the claim that SLAM is a limited implementation of HSFC and therefore accidentally captures the details of the LPL theory rather than the intended theory. The criticism implies that Walker and Hickok (in press) overlooked the presence of post-lexical errors in the data, and because SLAM is an approximation of LPL, it is accidentally accounting for these errors in order to improve the fit. We note that, while SP and SLAM are both limited implementations of larger theories, the models both attempt to account for the theoretical notion of post-lexical errors through a practical implementation of lenient scoring. For patients with obvious articulatory-motor impairment, including verbal apraxia (e.g., Romani & Galluzzi, 2005; Romani, Galluzzi, Bureca, & Olson, 2011; Galluzzi, Bureca, Guariglia, & Romani, 2015), scoring is such that responses with a single addition, deletion, or substitution of a phoneme or consonant cluster are scored as correct. This scoring procedure is based on the assumption that the error occurred after the correct selection at the phonological layer of the model (Schwartz et al., 2006). This means that many of the sound-related errors that Goldrick assumes would be better explained by LPL and, by extension, SLAM were actually excluded from the analysis. Nevertheless, according to the LPL theory, any patient has the potential to exhibit a post-lexical processing error. Thus, while the analysis of SLAM clearly did not overlook the potential for post-lexical errors, it is possible that our efforts did not remove these effects from the data entirely (See Goldrick, Folk, and Rapp, 2010 for further discussion). We therefore tried to evaluate Goldrick's claim that SLAM's improvements are in fact due to its approximation of the LPL theory.
Goldrick (2011) reports that the SP model fits the SP-generated dataset with 0.01 mean RMSD and other datasets with 0.017 mean RMSD. Even though this represents a 70% increase in error, and is judged by Goldrick (2011) to be "equivalent", these effect sizes regard the difference in fit between datasets, not the difference in fit between models. These comparisons should not be confused with our effect sizes in fit between models, which is a more clearly interpretable quantity.
In order to reuse our earlier code to map a 4-parameter space, the LM-weight was allowed to vary between 0 and 1e-8, then all points greater than or equal to 5e-9 were removed, as they likely represent duplicate predictions. If an LM-weight was not exactly zero in the final map, it remained several orders of magnitude smaller than the activation levels in the network.
We only implemented assumptions regarding feedback. Other versions of RIA have made different assumptions regarding the size of the lexicon, the implementation of damage as noise, the strength of the boosts, the number of timesteps, and an additional stage of pre-lexical, conceptual processing, which we did not address.
The connections are 1-to-1, so the interactivity has no effect; a stronger boost could simply compensate for reduced feedback.
References
- Foygel D, Dell GS. Models of impaired lexical access in speech production. Journal of Memory and Language. 2000;43(2):182–216. [Google Scholar]
- Galluzzi C, Bureca I, Guariglia C, Romani C. Phonological simplifications, apraxia of speech and the interaction between phonological and phonetic processing. Neuropsychologia. 2015;71:64–83. doi: 10.1016/j.neuropsychologia.2015.03.007. [DOI] [PubMed] [Google Scholar]
- Goldrick M. Integrating SLAM with existing evidence: Comment on Walker and Hickok. Psychonomic Bulletin & Review. doi: 10.3758/s13423-015-0946-9. (submitted). (in press) [DOI] [PubMed] [Google Scholar]
- Goldrick M. Theory selection and evaluation in case series research. Cognitive neuropsychology. 2011;28(7):451–465. doi: 10.1080/02643294.2012.675319. [DOI] [PubMed] [Google Scholar]
- Goldrick M, Folk JR, Rapp B. Mrs. Malaprop’s neighborhood: Using word errors to reveal neighborhood structure. Journal of Memory and Language. 2010;62(2):113–134. doi: 10.1016/j.jml.2009.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldrick M, Rapp B. Lexical and post-lexical phonological representations in spoken production. Cognition. 2007;102(2):219–260. doi: 10.1016/j.cognition.2005.12.010. [DOI] [PubMed] [Google Scholar]
- Hickok G. Speech perception, conduction aphasia, and the functional neuroanatomy of language. In: Grodzinsky Y, Shapiro L, Swinney D, editors. Language and the brain. San Diego: Academic Press; 2000. pp. 87–104. [Google Scholar]
- Hickok G. Functional anatomy of speech perception and speech production: Psycholinguistic implications. Journal of psycholinguistic research. 2001;30:225–234. doi: 10.1023/a:1010486816667. [DOI] [PubMed] [Google Scholar]
- Hickok G. Computational neuroanatomy of speech production. Nature Reviews Neuroscience. 2012;13(2):135–145. doi: 10.1038/nrn3158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickok G. The architecture of speech production and the role of the phoneme in speech processing. Lang Cogn Process. 2014a;29(1):2–20. doi: 10.1080/01690965.2013.834370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickok G. Toward an Integrated Psycholinguistic, Neurolinguistic, Sensorimotor Framework for Speech Production. Lang Cogn Process. 2014b;29(1):52–59. doi: 10.1080/01690965.2013.852907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickok G, Erhard P, Kassubek J, Helms-Tillery AK, Naeve-Velguth S, Strupp JP, et al. A functional magnetic resonance imaging study of the role of left posterior superior temporal gyrus in speech production: implications for the explanation of conduction aphasia. Neuroscience Letters. 2000;287:156–160. doi: 10.1016/s0304-3940(00)01143-5. [DOI] [PubMed] [Google Scholar]
- Hickok G, Houde J, Rong F. Sensorimotor integration in speech processing: computational basis and neural organization. Neuron. 2011;69(3):407–422. doi: 10.1016/j.neuron.2011.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickok G, Poeppel D. Towards a functional neuroanatomy of speech perception. Trends in Cognitive Sciences. 2000;4:131–138. doi: 10.1016/s1364-6613(00)01463-7. [DOI] [PubMed] [Google Scholar]
- Hickok G, Poeppel D. Dorsal and ventral streams: A framework for understanding aspects of the functional anatomy of language. Cognition. 2004;92:67–99. doi: 10.1016/j.cognition.2003.10.011. [DOI] [PubMed] [Google Scholar]
- Hickok G, Poeppel D. The cortical organization of speech processing. Nature Reviews Neuroscience. 2007;8(5):393–402. doi: 10.1038/nrn2113. [DOI] [PubMed] [Google Scholar]
- Mirman D, Strauss TJ, Brecher A, Walker GM, Sobel P, Dell GS, Schwartz MF. A large, searchable, web-based database of aphasic performance on picture naming and other tests of cognitive function. Cognitive neuropsychology. 2010;27(6):495–504. doi: 10.1080/02643294.2011.574112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapp B, Goldrick M. Discreteness and interactivity in spoken word production. Psychological review. 2000;107(3):460. doi: 10.1037/0033-295x.107.3.460. [DOI] [PubMed] [Google Scholar]
- Romani C, Galluzzi C. Effects of syllabic complexity in predicting accuracy of repetition and direction of errors in patients with articulatory and phonological difficulties. Cognitive Neuropsychology. 2005;22(7):817–850. doi: 10.1080/02643290442000365. [DOI] [PubMed] [Google Scholar]
- Romani C, Galluzzi C, Bureca I, Olson A. Effects of syllable structure in aphasic errors: Implications for a new model of speech production. Cognitive psychology. 2011;62(2):151–192. doi: 10.1016/j.cogpsych.2010.08.001. [DOI] [PubMed] [Google Scholar]
- Ruml W, Caramazza A, Shelton JR, Chialant D. Testing assumptions in computational theories of aphasia. Journal of Memory and Language. 2000;43(2):217–248. [Google Scholar]
- Schwartz MF, Dell GS, Martin N, Gahl S, Sobel P. A case-series test of the interactive two-step model of lexical access: Evidence from picture naming. Journal of Memory and language. 2006;54(2):228–264. doi: 10.1016/j.jml.2006.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker GM, Hickok G. Bridging computational approaches to speech production: The semantic–lexical–auditory–motor model (SLAM) Psychonomic Bulletin & Review. doi: 10.3758/s13423-015-0903-7. (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]