Abstract
Chromosome translocations are a well-recognized biological marker of radiation exposure and cancer risk. However, there is uncertainty about the lowest dose at which excess translocations can be detected, and whether there is temporal decay of induced translocations in radiation-exposed populations. Dosimetric uncertainties can substantially alter the shape of dose-response relationships; although regression-calibration methods have been used in some datasets, these have not been applied in radio-occupational studies, where there are also complex patterns of shared and unshared errors that these methods do not account for. In this article we evaluated the relationship between estimated occupational ionizing radiation doses and chromosome translocation rates using fluorescent in situ hybridization in 238 U.S. radiologic technologists selected from a large cohort. Estimated cumulative red bone marrow doses (mean 29.3 mGy, range 0–135.7 mGy) were based on available badge–dose measurement data and on questionnaire-reported work history factors. Dosimetric assessment uncertainties were evaluated using regression calibration, Bayesian and Monte Carlo maximum likelihood methods, taking account of shared and unshared error and adjusted for overdispersion. There was a significant dose response for estimated occupational radiation exposure, adjusted for questionnaire-based personal diagnostic radiation, age, sex and study group (5.7 translocations per 100 whole genome cell equivalents per Gy, 95% CI 0.2, 11.3, P = 0.0440). A significant increasing trend with dose continued to be observed for individuals with estimated doses <100 mGy. For combined estimated occupational and personal-diagnostic-medical radiation exposures, there was a borderline-significant modifying effect of age (P 0.0704), but little evidence (P > 0.5) of temporal decay of induced translocations. The three methods of analysis to adjust for dose uncertainty gave similar results. In summary, chromosome translocation dose-response slopes were detectable down to <100 mGy and were compatible with those observed in other radiation-exposed populations. However, there are substantial uncertainties in both occupational and other (personal-diagnostic-medical) doses that may be imperfectly taken into account in our analysis.
INTRODUCTION
Evaluation of disease risks associated with low-dose exposures to physical, chemical or other environmental agents is difficult. A fundamental difficulty in measuring risks at very low doses is that the signal is often very small compared to the normal background noise in disease rates. An additional complication is the uncertainty in measurement of dose. A crucial component of the exposure assessment is the comparison with a gold standard or other independent type of corroboration (1, 2). Corroborating measurements of exposure that include biological measurements are particularly valuable if repeated over time (3) and if the measurements are biologically meaningful (4).
Directly assessing the risks from occupational radiation exposures at low-to-moderate doses (e.g., up to about 100 mGy) and low dose rates (e.g., up to about 5 mGy/h) (5, 6) is of public health importance and relevant for radiological protection. To date, most of the risk assessment data evaluated in relationship to radiological protection at these doses levels has been limited to cohorts of nuclear workers (7, 8) and other occupationally- and environmentally-exposed groups (9).
A comprehensive historical reconstruction to estimate individual worker doses for a cohort of U.S. radiologic technologists (USRT) was first reported in 2006 (10), and has undergone substantial revision since then (11). New elements include estimation of the more uncertain exposures before 1960 and greater use of period-specific individual work history data (11) (Appendix A). Biodosimetric corroboration of the dosimetry estimates can provide independent confirmation of assumptions made when direct radiation measurements are limited.
Fluorescent in situ hybridization (FISH) with whole-chromosome paints is a well-validated method of detecting chromosome translocations in peripheral blood lymphocytes and has been applied to a number of populations as a means of assessing the degree of radiation exposure (12–15). Translocations measured by FISH painting can detect cumulative radiation exposures occurring more than 50 years previously (15). However there is experimental evidence of temporal decay of induced translocations (16–19), assessment of which has not generally been attempted in previous analyses of chromosome translocations in exposed populations and the ability to assess such trends would possibly have been quite limited. In addition, since translocations decay over time, the studies would have progressively underestimated the true radiation dose a long time after exposure.
Dose measurement errors can alter the shape of dose-response relationships (20, 21). Studies of FISH translocation data in the Japanese A-bomb survivors (15) accounted for dosimetric uncertainties using regression-calibration methods (20). In general, this has not been attempted in populations with occupational radiation exposure (13, 22–25), where complex patterns of shared errors (i.e., the component of dose error that is shared by a group of individuals in a study) and unshared errors (i.e., the component of dose error that is independent of the dose errors in other individuals) would be expected; or in populations where measurements of chemical or environmental exposures may not have been uniformly collected on individuals in the distant past. A distinction is often made between classical measurement error and Berkson error (20, 26). Classical measurement error arises when quantities are measured with error (typically with an imprecise, but unbiased, measuring device). Berkson error arises when groups of individuals are assigned a common representative value that is equal to the mean for the group. Shared (or systematic) errors arise when some aspect of the error is shared between individuals, for example, when a measuring device is biased or when assigned group means are estimated. Shared errors also arise when parameter values in a model-based dosimetry are imprecisely specified (20).
For cancer and related biological effects such as chromosome translocations, scientific committees generally assume, albeit largely for radiological protection purposes, that at low radiation doses there is a positive linear component to the dose response, i.e., that there is no threshold (9, 27, 28). However, this assumption is controversial (29, 30). In addition, and to some extent independent of this question, because of the noise inherent in the measurement process, it has been suggested that a statistically significant excess translocation frequency could not be detected with FISH below 100 mGy (31), but very little human data exists below this dose.
In this article we evaluated the relationship between estimated occupational ionizing radiation doses and chromosome translocation rates using FISH in a subset of the USRT cohort. Although we previously examined chromosome translocations in relationship to occupational dose (22–25) based on our earlier 2006 dose reconstruction (10), the current assessment of stable and unstable chromosomal translocations in relationship to our substantially revised occupational dose reconstruction has three additional features. First, to address issues of possible low-dose risk and dose thresholds, we have assessed the lowest estimated dose at which an excess translocation rate is detectable. Second, to examine effects of decay of chromosome translocations after exposure and temporal changes that might result from changes in radiation energy over time (32), we considered the temporal distribution of estimated dose and its effect on translocation rate. Third, we compared the results obtained using regression-calibration methods (20) with those obtained using more computationally intensive Bayesian Markov Chain Monte Carlo (MCMC) and Monte Carlo maximum-likelihood (MCML) methods (33, 34) that account more fully for the effects of shared and unshared dose uncertainties in relationship to inference about translocation rates. All analyses adjust for the over-dispersion inherent in such data (35, 36).
METHODS
In 1982, the U.S. National Cancer Institute, in collaboration with the University of Minnesota and the American Registry of Radiologic Technologists, initiated a study of cancer incidence and mortality among 146,022 (106,953 female) U.S. radiologic technologists who were certified for at least two years between 1926 and 1982 (37). During 1984–1989, 1993–1998 and 2003–2005, postal surveys were conducted that included detailed questions related to work history as a radiologic technologist and various lifestyle factors and information regarding multiple health outcomes. (Further details on the technologists selected for blood sampling are shown in Appendix B.) We analyzed reciprocal chromosome translocations in two groups of radiologic technologists who provided blood samples in years 1994–1995 [Chromosome Translocation Study I (CTS-I), n = 90] and 2003 [Chromosome Translocation Study II (CTS-II), n = 152], as described previously (22–25) with the current estimated occupational radiation doses (11) (Appendix A). [Note: the CTS-I (22) that previously assessed only 79 subjects, now includes 11 additional subjects for whom we did not previously have sufficient data to estimate doses.] From the combined group we excluded two records in the CTS-I data because of incomplete postal survey information, leaving n = 88; from the CTS-II data (24) another two records were excluded because they were missing CTS-II questionnaires because these individuals had died after giving a blood sample but before the questionnaire could be administered, leaving n = 150. In the CTS-I single-color painting of chromosomes 1, 2 and 4 was performed and in the CTS-II two-color painting was performed, with chromosomes 1, 2 and 4 being painted red and chromosomes 3, 5 and 6 simultaneously painted green. In both studies the number of metaphase cells counted was converted to whole genome cell equivalents (CE), as if the full genome had been scored. The data were described in more detail in Table 1. Unbalanced (nonreciprocal) translocations, for which data are available from the CTS-II (24), were judged a priori not to be as stable a marker of long-term exposure as reciprocal translocations (38, 39), so that most analyses concentrated on the latter. Nevertheless we provide some analysis of various types of unstable aberration (the two dominant types being fragments and dicentrics, in that order) in the CTS-II in Appendix G, Table G1.
TABLE 1.
Distribution of Covariates among Study Subjects, with Mean Translocation Rate and Standard Deviation (SD)
| Mean translocations/100 chromosome equivalentsa |
||||
|---|---|---|---|---|
| Covariates | Number | Percentage | Mean | SD |
| Chromosome translocation study | ||||
| I | 88 | 37.0 | 1.67 | 1.44 |
| II | 150 | 63.0 | 1.37 | 0.80 |
| Age at blood draw (years) | ||||
| <60 | 52 | 21.8 | 1.27 | 1.32 |
| 60–64 | 14 | 5.9 | 1.79 | 1.00 |
| 65–69 | 17 | 7.1 | 2.15 | 1.12 |
| 70–74 | 12 | 5.0 | 1.75 | 2.02 |
| 75–79 | 69 | 29.0 | 1.35 | 0.82 |
| 80–84 | 43 | 18.1 | 1.32 | 0.65 |
| ≥85 | 31 | 13.0 | 1.73 | 1.05 |
| Number of years worked | ||||
| <1 | 3 | 1.3 | 1.62 | 0.83 |
| 1–4 | 30 | 12.6 | 1.32 | 0.95 |
| 5–9 | 28 | 11.8 | 1.22 | 1.43 |
| 10–14 | 22 | 9.2 | 1.30 | 0.79 |
| 15–19 | 27 | 11.3 | 1.17 | 0.88 |
| 20–29 | 50 | 21.0 | 1.59 | 1.26 |
| 30–39 | 59 | 24.8 | 1.66 | 0.99 |
| ≥40 | 19 | 8.0 | 1.86 | 0.99 |
| Sex | ||||
| Male | 103 | 43.3 | 1.62 | 1.24 |
| Female | 135 | 56.7 | 1.37 | 0.94 |
| Smoking period (years) | ||||
| Unknown | 19 | 8.0 | 1.64 | 0.85 |
| 0–0.9 | 103 | 43.3 | 1.46 | 0.95 |
| 1.0–4.9 | 7 | 2.9 | 1.23 | 0.64 |
| 5.0–9.9 | 13 | 5.5 | 1.37 | 1.98 |
| 10.0–19.9 | 24 | 10.1 | 1.82 | 1.24 |
| 20.0–29.9 | 22 | 9.2 | 1.43 | 0.84 |
| 30.0–39.9 | 32 | 13.4 | 1.40 | 1.36 |
| ≥40.0 | 31 | 13.0 | 1.42 | 0.88 |
| Smoking duration and intensity (pack-years) | ||||
| Unknown | 7 | 2.9 | 1.76 | 0.76 |
| 0–0.9 | 166 | 69.7 | 1.53 | 1.19 |
| 1.0–4.9 | 10 | 4.2 | 0.99 | 0.44 |
| 5.0–9.9 | 15 | 6.3 | 1.17 | 0.55 |
| 10.0–19.9 | 8 | 3.4 | 1.02 | 0.56 |
| 20.0–29.9 | 11 | 4.6 | 1.44 | 1.14 |
| 30.0–49.9 | 10 | 4.2 | 1.87 | 1.08 |
| ≥50.0 | 11 | 4.6 | 1.45 | 0.70 |
| Mean estimated occupational dose (Gy) | ||||
| 0–0.004 | 33 | 13.9 | 1.18 | 0.81 |
| 0.005–0.009 | 18 | 7.6 | 0.89 | 0.51 |
| 0.010–0.019 | 44 | 18.5 | 1.62 | 1.38 |
| 0.020–0.029 | 47 | 19.7 | 1.44 | 0.98 |
| 0.030–0.039 | 29 | 12.2 | 1.26 | 0.65 |
| 0.040–0.049 | 30 | 12.6 | 1.87 | 1.48 |
| ≥0.050 | 37 | 15.5 | 1.76 | 0.97 |
| Mean estimated personal-diagnostic-medical dose (Gy) | ||||
| 0–0.009 | 48 | 20.2 | 1.15 | 0.96 |
| 0.010–0.019 | 38 | 16.0 | 1.08 | 0.69 |
| 0.020–0.029 | 37 | 15.5 | 1.43 | 0.88 |
| 0.030–0.049 | 42 | 17.6 | 1.36 | 0.74 |
| 0.050–0.099 | 45 | 18.9 | 1.84 | 1.59 |
| 0.100–0.149 | 16 | 6.7 | 2.25 | 1.05 |
| ≥0.150 | 12 | 5.0 | 2.19 | 0.82 |
Per whole chromosome equivalents, equivalent to the translocation frequency that would be observed if cells were assumed to have full-genome painting done of their nuclear DNA.
To evaluate the relationship between cumulative estimated occupational radiation dose and structural chromosomal translocations, we fitted a linear additive model, in which the expected number of translocations was given by:
| (1) |
where CE is the number of whole genome cell equivalents scored, defined as the number of cells scored if the whole genome had been painted. In both studies the number of metaphase cells counted was converted to whole genome cell equivalents, as if the full genome had been scored (40). The conversion to whole genome equivalent is performed using the formula derived by Lucas et al. (41), i.e., Fp = 2.05 fp(1 – fp)FG where Fp is the measured frequency of translocations detected by FISH, fp is the painted fraction of the genome and FG is the (true) genomic aberration frequency. The multiplier 1/[2.05 fp(1 – fp)] is therefore used to convert measured translocation frequencies to genomic translocation frequencies.
We used estimated cumulative red bone marrow dose from personal-diagnostic-medical (PDM) exposure, Ddiag (in Gy), derived from self-reported radiographic examinations, as described by Bhatti et al. (22–24) and Sigurdson et al. (25). Briefly, this entailed use of self-reported information about medical diagnostic X-ray procedures that technologists received as patients from the first and second cohort surveys to assign weighted red bone marrow dose scores. The doses associated with specific radiographic procedures were assigned midpoint red bone marrow dose values from a comprehensive list of examination types. We used the midpoint doses and, as appropriate, the frequencies to weight the dose scores for the types of radiographic procedures reported by the technologists on the first and second surveys (22–24).
We also used estimates of occupational red bone marrow dose, Doccup (in Gy), using the 2013 dosimetry, cumulative to the end of 1988 for CTS-I and to the end of 1997 (the latest year for which doses have been reconstructed) for CTS-II (i.e., about 6 years before blood sampling in both cases) (11) (Appendix A). This strategy amounts to using estimated dose accumulated with a six-year latent period; we also show sensitivity analyses using latent periods of 0–10 years (Appendix F, Table F1). For the entire cohort, the mean and median estimated occupational/total (occupational + PDM) red bone marrow dose was 29.3/75.1 and 25.0/63.3 mGy, respectively (range 0–135.7/0–356.2). The chromosome translocation rate was adjusted for age, sex, study group (CTS-I or II) and cigarette smoking using the above expression. We used cumulative pack-years smoked as the measure of cigarette smoking, or the total years of cigarette smoking, although smoking duration information was not available for 6 persons in the CTS-II data, and pack-years information was not available for the CTS-I data and 7 persons in the CTS-II data. To stabilize the parameter estimates, age, cigarette smoking years and cigarette pack-years were centered at 71 years, 13 years and 12 pack-years, respectively, which are their approximate mean values in the parts of these data that are not missing; missing values of the smoking variables were set to 0. Additional analyses were also conducted (reported in Appendix Table E1), in which we used total years worked instead of, or as well as, either estimated dose variable, to assess how much extra information the dosimetry added above this simple explanatory variable.
We also conducted analyses using a model that adjusted for estimated occupational dose accumulated in various calendar intervals of follow-up:
| (2) |
where by Doccup,<1959, Doccup,1950–1959, Doccup,1960–1969, Doccup,1970+, are the estimated occupational doses accumulated in the calendar periods <1950, 1950–1959, 1960–1969, 1970+, respectively.
The 2013 occupational dosimetry estimation system has a stochastic design to model shared errors, and to account for missing and uncertain dose-related parameters (Appendix A). Using that system, we produced 1,000 simulations of the posterior distribution of estimated occupational red bone marrow dose for all study subjects.
Table 2 details the model fits to all translocation frequencies, by Poisson maximum likelihood and parameter estimates. Because of indications of significant over-dispersion, in the principal analyses (Tables 2, 3, 5 and Fig. 1) all P values are computed using F tests, derived from quasi-likelihood techniques (42), and the square roots of the associated variance inflation factors (defined by ϕ = deviance/df) are used to scale profile-likelihood confidence intervals in the standard way, i.e., by multiplying the distance of confidence limit to the best estimate by the square root of the inflation factor. The optimal model was selected via analysis of deviance, taking account of over-dispersion (42).
TABLE 2.
Combined Study Data Model Fits and Parameter Estimates for Translocation Rates in Relation to Occupational and Personal-Diagnostic-Medical (PDM) Doses, Using Regression-Calibration Adjusted Occupational Doses, with 95% Profile Likelihood Confidence Intervals, Adjusted for Overdispersiona
| Dose variables | Dose-response modifying variables | P valueb | Linear dose parameter (translocations/100 CEc/Gy) (occupational) | Linear dose parameter (translocations/100 CEc/Gy) (PDM) | Quadratic dose parameter (translocations/100 CEc/Gy2) (occupational) | Quadratic dose parameter (translocations/100 CEc/Gy2) (PDM) |
|---|---|---|---|---|---|---|
| Occupational dose only | - | 0.0188d | 7.0 (1.2, 12.9) | - | - | |
| PDMe dose only | - | <0.0001d | - | 4.4 (2.2, 6.7) | - | |
| Occupational and PDM dose, constrained equal | - | <0.0001d | 4.4 (2.5, 6.5) | 4.4 (2.5, 6.5) | - | |
| Occupational and PDM dose | - | 0.6403e/0.0440f | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) | - | |
| Occupational and PDM dose | Age | 0.0704g | 7.1 (0.1, 14.3) | 5.2 (2.7, 7.8) | - | |
| Occupational and PDM dose | Sex | 0.7166g | 6.0 (0.1, 12.2) | 4.7 (1.5, 8.1) | - | |
| Occupational and PDM dose | Years cigarette smoking | 0.7449g | 5.8 (0.3, 11.4) | 4.3 (2.0, 6.6) | - | |
| Occupational and PDM dose | Pack-years cigarette smoking | 0.9393g | 5.7 (0.1, 11.3) | 4.2 (2.0, 6.6) | - | |
| Occupational and PDM dose | Study group (CTS-I vs. II) | 0.1108g | 4.9 (–0.1, 10.1) | 3.7 (1.7, 6.0) | - | |
| Occupational and PDM dose | Quadratic | 0.0004d | - | - | 49.5 (–5.2, 106.7) | 17.4 (6.8, 28.9) |
| Occupational and PDM dose | Linear-quadratic | 0.0811/0.8965h | 4.1 (–9.0, 16.9) | 5.1 (0.3, 9.9) | 17.6 (–104.6, 146.9) | –4.5 (–25.6, 17.9) |
Background model is adjusted for age, study group (CTS-I vs. II), sex × study group; a 6-year period of latency is assumed.
Unless otherwise indicated the P value refers to the improvement in fit of that line with the model in the line immediately above it in the table.
Per whole chromosome equivalents (CE), equivalent to the translocation frequency that would be observed if cells were assumed to have full- genome painting done of their nuclear DNA.
P value of improvement in fit of this line of table compared with fit of a model without radiation dose terms.
P value of improvement in fit of model with occupational dose and PDM dose unconstrained vs. identical model but with dose coefficients constrained equal.
P value of improvement in fit of model over one with just PDM dose.
P value of improvement in fit of model with occupational dose and PDM dose, unadjusted.
P value of improvement in fit of this line of table compared with model with linear occupational dose and PDM dose terms.
TABLE 3.
Analysis of Calendar Period of Occupational Radiation Exposure, using Regression-Calibration Adjusted Doses Accounting for Personal-Diagnostic-Medical (PDM) Dose, with 95% Profile Likelihood Confidence Intervals, Adjusted for Overdispersiona
| Calendar period (years) | Linear dose parameter (translocations/100 CEb/Gy) (occupational) | P value for heterogeneity |
|---|---|---|
| <1950 | 5.2 (–3.3, 13.8) | 0.9649 |
| 1950–1959 | 9.6 (–6.2, 25.5) | |
| 1960–1969 | 0.6 (–34.9, 37.0) | |
| 1970+ | 4.7 (–27.5, 38.8) |
Background model is adjusted for age, study group (CTS-I vs. II), sex × study group, and with additional adjustment for PDM dose; a 6-year period of latency is assumed.
Per whole chromosome equivalents (CE), equivalent to the translocation frequency that would be observed if cells were assumed to have full-genome painting done of their nuclear DNA.
TABLE 5.
Combined Study Data Model Fits and Slope Estimates in Relationship to Occupational and Personal-Diagnostic-Medical (PDM) Doses, by Limiting to Members of Cohort with Specified Level of Dose, using Regression-Calibration Adjusted Occupational Doses, with 95% Profile Likelihood Confidence Intervals, Adjusted for Overdispersiona
| Dose range used (mGy) (occupational + personal-diagnostic dose) | Occupational linear dose parameter only (translocations/100 CEb/Gy) | P valuec | PDM linear dose parameter only (translocations/100 CEb/Gy) only | P valuec | Occupational + PDM linear dose parameter (constrained equal) (translocations/100 CEb/Gy) | P valuec |
|---|---|---|---|---|---|---|
| Full | 7.0 (1.2, 12.9) | 0.0188 | 4.4 (2.2, 6.7) | <0.0001 | 4.4 (2.5, 6.5) | <0.0001 |
| <250 | 5.9 (–0.3, 12.1) | 0.0607 | 5.0 (2.3, 7.8) | 0.0002 | 5.2 (2.7, 7.7) | <0.0001 |
| <200 | 5.9 (–0.3, 12.1) | 0.0620 | 4.8 (1.9, 7.8) | 0.0011 | 5.1 (2.4, 7.7) | 0.0001 |
| <150 | 6.3 (0.3, 12.4) | 0.0411 | 4.2 (0.6, 7.9) | 0.0210 | 4.8 (1.7, 7.9) | 0.0023 |
| <100 | 9.0 (1.3, 16.7) | 0.0225 | 7.2 (1.5, 13.0) | 0.0137 | 8.4 (3.9, 12.9) | 0.0004 |
| <50 | –4.9 (–16.5, 7.1) | 0.4222 | 13.4 (3.7, 23.4) | 0.0076 | 8.3 (–0.5, 16.9) | 0.0672 |
Background model is adjusted for age, study group (CTS-I vs. II), sex × study group; a 6-year period of latency is assumed.
Per whole chromosome equivalents (CE), i.e., the normalized translocation frequency per 100 cells assumed to have full-genome painting done of their nuclear DNA.
P value refers to the improvement in fit compared with fit of a model without radiation dose terms.
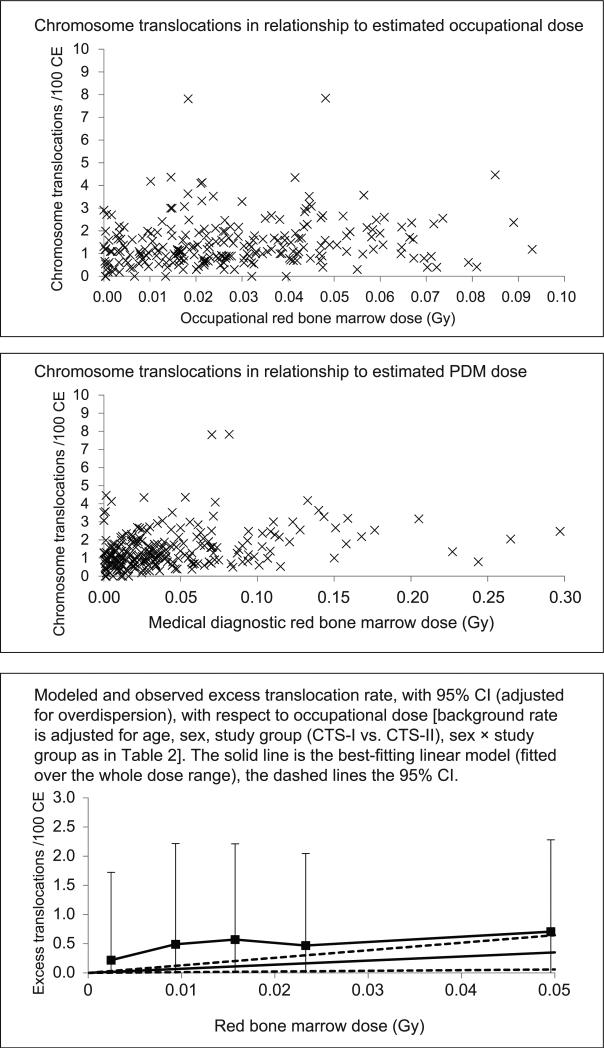
FIG. 1.
Chromosome translocations with respect to occupational and personal-diagnostic-medical (PDM) dose.
Because of the uncertainties in the estimated occupational doses, most analyses (Tables 2, 3, 5 and Fig. 1) used regression-calibration correction (20), a commonly used method of correcting for covariate uncertainty. This was done by using the mean of the 1,000 simulated dose realizations from the Monte Carlo dosimetry (described in Appendix A), which were conditional on the observed film badge doses and other covariates, specifically the frequency of performing X rays, frequency of holding patients during X ray, frequency of conducting fluoroscopy, frequency of performing diagnostic and/or therapeutic radioisotope procedures, frequency of wearing protective lead aprons, full- or part-time work, type of facility worked in (civilian, military, large or small hospital). Two other dose-error correction methods were used: 1. a Bayesian MCMC method (see Appendix C for more details), that samples from the 1,000 dose realizations; and 2. an MCML method in which the posterior average of the likelihood over the dose realizations was computed (33, 34), with parameter estimates and inference based on maximization of the resulting profile likelihood (42). When fitting with Bayesian MCMC or MCML, the over-dispersion must be modeled parametrically. This was done using a negative binomial model, in which the probability of translocations was given by:
| (3) |
where:
| (4) |
So:
| (5) |
| (6) |
RESULTS
As shown in Table 1, the estimated PDM dose substantially exceeded the estimated occupational dose in magnitude. On average the members of the analysis dataset worked 21.2 years, but the number of years worked spanned a wide range, from <1–49 years (Table 1). Mean age at blood draw was 70.9 years, ranging from 34–91 years (Table 1). There were on average 7.3 pack-years of smoking per cohort member, with a range of 0–112.5 pack-years.
The optimal background model (selected by analysis of deviance) is described in Appendix D. As indicated in Table 2, there was a statistically significant dose-response relationship for estimated occupational dose with (P = 0.0440) and without (P = 0.0188) adjustment for estimated PDM dose (see also Fig. 1). There was no significant difference between the dose-response slopes for estimated occupational dose and PDM dose (P > 0.5) (Table 2). Table 2 also shows that there were borderline-significant modifying effects of attained age on the combined (occupational and PDM) dose response (P = 0.0704). There were no significant modifying effects of sex, cigarette smoking or CTS group on the combined (estimated occupational and PDM) dose response (P > 0.1). There were no significant departures from linearity in the combined (estimated occupational and PDM) dose response (P > 0.5).
As can be seen from Table 3, the chromosome translocation occupational dose-response slopes did not differ significantly by time period during which dose was accumulated (P > 0.5), although the data suggested a stronger dose response for estimated doses accumulated in the earlier periods, in particular in the 1950s, than for estimated dose accumulated more recently.
To assess the approximation introduced by regression-calibration, Table 4 shows a comparison of the analyses using regression calibration with those of two full-likelihood methods, Bayesian MCMC and MCML, with similar results obtained for each analysis method. Using regression-calibration, the best estimate of dose-response slope was 7.0 (95% CI 1.2, 12.9) × 10−2 translocations Gy−1, which is comparable to the estimates derived using a negative-binomial model by a Bayesian MCMC model fitting method, 6.9 (95% CI 1.7, 12.2) × 10−2 translocations Gy−1 or by MCML, 7.0 (95% CI 2.3, 10.9) × 10−2 translocations Gy−1.
TABLE 4.
Comparison of Regression-Calibration Adjusted, Bayesian Markov Chain Monte Carlo (MCMC), and Monte Carlo Maximum Likelihood (MCML) Parameter Estimates (and 95% CI) for Translocation Rates in Relation to Occupational and Personal-Diagnostic-Medical (PDM) Doses
| Regression-calibration method, quasi-likelihood model |
Bayesian MCMC method, negative binomial model |
Monte Carlo maximum likelihood, negative binomial model |
|||||
|---|---|---|---|---|---|---|---|
| Model | Dose-response term | Occupational dose | Personal-diagnostic dose | Occupational dose | Personal-diagnostic dose | Occupational dose | Personal-diagnostic dose |
| Occupational dose only, lineara | linear | 7.0 (1.2, 12.9)b | - | 6.9 (1.7, 12.2)b | - | 7.0 (2.3, 10.9)b | - |
| Occupational and PDMc dose, separately, lineara | linear | 5.7 (0.2, 11.3)b | 4.2 (2.0, 6.5)b | 6.5 (1.5,11.4)b | 5.6 (3.0, 8.5)b | 6.4 (1.4, 10.1)b | 4.3 (2.2, 6.5)b |
| Occupational and PDMc dose, separately, pure quadratica | quadratic | 49.5 (–5.2, 106.7)c | 17.4 (6.8, 28.9)c | 51.0 (5.8,104.3)c | 26.3 (10.3, 46.3)c | 47.1 (7.5, 80.0)c | 17.9 (8.0, 28.7)c |
| Occupational and PDMc dose, separately, linear-quadratica | linear | 4.1 (–9.0, 16.9)b | 5.1 (0.3, 9.9)b | 8.1 (–4.8, 21.3)b | 7.6 (2.2, 12.9)b | 1.9 (–7.8, 17.0)b | 5.4 (0.7, 10.0)b |
| quadratic | 17.6 (–104.6, 146.9)c | –4.5 (–25.6, 17.9)c | –14.6 (–148.7, 110.5)c | –10.7 (–34.2, 17.3)c | 37.1 (–75.6, 111.4)c | –4.8 (–25.3, 17.0)c | |
Background model is adjusted for age, study (CTS-I vs. II), sex × study group; a 6-year period of latency is assumed.
FISH translocations/100 chromosome equivalents/Gy, i.e., the normalized translocation frequency per 100 equivalent cells assumed to have full-genome painting done of their nuclear DNA.
FISH translocations/100 chromosome equivalents/Gy2.
Table 5 shows that little difference was made to the magnitude or significance of the regression slopes by considering subsets of the analysis cohort obtained by restricting to persons having total (estimated occupational + PDM) dose less than certain values. Even when restricted to <100 mGy the estimates of slope for estimated occupational or combined, dose were all statistically significant (2-sided P < 0.05), although statistical significance was lost for the occupational or combined (estimated occupational + PDM) doses if estimated doses were restricted to <50 mGy. There was little evidence of the dose-response slope being different over the lower dose range; for example, the occupational dose-response slope only slightly increased from 7.0 (95% CI 1.2, 12.9) × 10−2 translocations Gy−1 over the full dose range, to 9.0 (95% CI 1.3, 16.7) × 10−2 translocations Gy−1 over the <100 mGy estimated dose range.
Using only the total number of years worked instead of either dose variable gave a much worse fit, so that adding the estimated occupational and PDM dose variables (constrained equal) to the model with years worked significantly improved the fit (P < 0.0001) (Appendix Table E1). Adding years worked to a model with the two estimated dose variables (constrained equal) yielded no improvement in fit (P > 0.5) (Appendix Table E1); there were similar findings in relationship to improvements in fit using either estimated occupational dose or PDM dose separately (Appendix Table E1).
All of the above results used estimated occupational radiation dose accumulated with a six-year latent period; sensitivity analyses using latent periods of 0–10 years yielded results that were essentially unchanged (Appendix Table F1).
Analysis of unstable aberrations suggested no significant effects in relationship to occupational dose, for any endpoint (dicentrics, fragments, all aberrations) (Appendix Table G1). However, there were borderline significant increasing trends in relationship to PDM dose for fragments (P = 0.0870) and all unstable aberrations (P = 0.0992). The slopes of the trends with dose were markedly less than for stable aberrations, e.g., for all unstable aberrations, the dose response was 1.2 (95% CI −0.2, 2.7) × 10−2 translocations Gy−1.
DISCUSSION
In our assessment of chromosomal translocation rates in a subset of technologists in the USRT cohort in relationship to a substantially revised 2013 occupational dose reconstruction (Appendix A), we found a significant occupational radiation dose response, irrespective of adjustment for estimated PDM dose. There was little indication that radiation dose response was other than linear, and in particular, the dose-response slope was much the same (and remained statistically significant) even when restricting to <100 mGy (although significance was lost when dose was restricted to <50 mGy). There were no significant differences in excess aberrations per unit dose by calendar time periods, although the dose-response slope was considerably higher for estimated doses accumulated in the 1950s versus other time periods. The comparison of various statistical methods (regression calibration, Bayesian MCMC, MCML) to assess the possible effects of shared and unshared dose uncertainties showed similar findings for each analysis method. We now consider these topics in turn below.
The limitations of our findings should be recognized given the considerable uncertainties in individual dose estimates. As indicated in Appendix A and Table A1, although a substantial proportion of study subjects, over 44%, had 5 or more years of film badge records and for 28% of all years worked there was a film badge measurement, there were few recorded badge dose measurements for these technologists in the years during which they received most of their exposure (i.e., before 1970). Therefore, for this group the dosimetry system relied on questionnaires, a limited number of measurements and literature-based data to estimate typical annual badge doses for those earlier periods. These representative badge dose estimates were adjusted to take into account what was known about each individual's work history [i.e., the frequency of performing X ray, fluoroscopy, diagnostic and therapeutic radioisotope procedures, frequency of holding patients for X rays, use of protective aprons and shields, full- or part-time work and facility type (civilian or military, hospital or physician office)]. The translation of badge dose estimates to red bone marrow absorbed dose estimates introduced additional sources of uncertainty, arising from the individual's ability to reliably answer questions about apron and shield use and dosimeter placement during the years they worked. As detailed in the Methods section, there were also no measurements of the PDM exposures, so that reconstruction of such doses relied on self-reported estimates of personal diagnostic procedures combined with estimated doses from the literature and medical dosimetry experts for a comprehensive list of examination types (22–24). The derivations of shared and unshared errors in dose were largely derived from these questionnaire responses, the moderate amount of directly measured data (Appendix A, Table A1) and certain assumptions made for the Monte Carlo dosimetry, as detailed in Appendix A and at greater length in Simon et al. (11).
Dose Response and Low-Dose Curvature and Possibly Confounding Factors
As noted in Table 6, although there is considerable variation (by nearly an order of magnitude) among the studies, the stable translocation radiation response slope estimates are entirely statistically compatible with those measured in other exposed groups, with large variation in cumulative dose and dose rate. In particular, the results are very close to those of the LSS cohort (15), methodologically among the strongest of the other chromosome aberration datasets. For example, the Techa River cohort (12), the Sellafield nuclear workers (13), the Mayak nuclear workers (14) and the radiologic technologists in the current dataset were all exposed at low-dose rates, although the cumulative doses in the first three of these were substantially higher than the current study. It is not clear why the chromosome aberration dose trend is at least fivefold higher, albeit not statistically significantly so, in the USRT cohort reported here compared with the Sellafield (13) and Mayak (14) nuclear workers or with the Techa River cohort (12), in which radiation dose rates would be similar to those of the current study; but very close to the dose trends observed in the LSS cohort (15), which was exposed at a much higher dose rate and with much higher doses than the current study. As we note below, radiation energy may be a factor, although this would not explain why the LSS dose trends are higher than those of most of the other datasets, which are characterized by much lower (and therefore more biologically effective) radiation energy (32). It is possible that the reduced effect of lower dose rate (compared with the atomic bomb survivors) would offset the increased effect of the lower energy of the radiation exposures in the current cohort, accounting for the similarity of dose trends we assess with those in the atomic bomb survivors (15). Population variations and inter-laboratory differences may also explain some of the discrepancy (43). Uncertainties in the dosimetry in the various datasets should be borne in mind when making comparisons. For example, the current USRT cohort differs from the Sellafield (13) and Mayak (14) nuclear workers, because for those workers, largely complete film badge data exists. By comparison, for the LSS (15) and the Techa River cohorts (12) the dosimetry was largely reliant on historical reconstruction and substantially based on interviews, similar to the USRT cohort. For example, dose estimation in the LSS was by interviews with the survivors, generally 5–15 years after the bombings, combined with reconstructions of radiation transport from the two atomic bombs, although supplemented by much other dosimetric validation, e.g., using activation samples from the two cities (44, 45).
TABLE 6.
Comparison of FISH Regression Coefficients from Comparable Studies in Various Cohorts
| Study | Energy range | Dose rate | FISH regression coefficients (translocations/100 CEa/Sv; 95% CI) |
|---|---|---|---|
| U.S. radiologic technologists | |||
| Occupational radiation dose | |||
| –2013 dose reconstruction adjusted for personal-diagnostic-medical (PDM) dose (current study) | 30–50 KeV | Low | 5.7 (0.2, 11.3) |
| –2006 dose reconstruction adjusted for PDM dose | |||
| >CTS-Ib sample (22) | 30–50 KeV | Low | 30 (–7, 70) |
| >CTS-IIb sample (24) | 30–50 KeV | Low | 9 (–1, 20) |
| U.S. radiologic technologists | |||
| Personal-diagnostic-medical (PDM) dose | |||
| –CTS-I + CTS-IIb PDM dose adjusted for 2013 occupational dose reconstruction (present study) | 30–50 KeV | Low | 4.2 (2.0, 6.5) |
| –CTS-IIb PDM dose adjusted for 2006 occupational dose (25) | 30–50 KeV | Low | 4 (2, 7) |
| Sellafield workers (13) | |||
| –retired workers | 0.1–1.0 MeV | Low | 1.11 (0.74, 1.48) |
| –current workers | 0.1–1.0 MeV | Low | 0.77 (0.34, 1.20) |
| Atomic bomb survivors (15) | |||
| –Hiroshima survivors, coefficient in fit to <1.5 Sv | Mostly 2–5 MeV | High | 6.6 (4.8, 8.4) |
| –Nagasaki survivors, coefficient in fit to <1.5 Sv | Mostly 2–5 MeV | High | 3.7 (2.6, 4.9) |
| Techa River residents (12) | Mostly 90Sr gamma ~0.546 MeV | Low | 0.60 (0.21, 0.99) |
| Mayak workers (14) in relationship to external gamma dose only | Mostly 0.2–1.4 MeV | Low | 0.69 (0.42, 0.96) |
Per whole chromosome equivalents (CE), i.e., the normalized translocation frequency per 100 cells assumed to have full genome painting done of their nuclear DNA.
Chromosome translocation study I (CTS-I) and II (CTS-II).
The borderline significant (P = 0.0992, Appendix Table G1) findings with respect to unstable aberrations and PDM dose are more difficult to compare with those of other exposed groups. There are few human in vivo studies (38, 46) and relatively few ex vivo (47, 48) studies examining unstable aberrations using FISH, although there are more in vivo studies using older methods of ascertaining aberrations, e.g., Giemsa staining (39). Nevertheless, it is plausible that this type of aberration, which would be expected to decay much more rapidly over time after exposure than stable translocations (38, 39), would correlate better with the (probably more recent) PDM exposures than with occupational dose.
We also found borderline significant modifying effects of age on the combined (estimated occupational and PDM) dose response (Table 2). There have been few previous analyses with which the finding can be compared. There was no statistically significant (P = 0.15) variation of translocation dose response with age in a group of Russian nuclear workers at the Mayak nuclear plant (14). Our finding of no significant modifying effect of sex is similar to that in other exposed groups (14, 15).
Our finding of a significant dose response for chromosome translocations below 100 mGy deserves further comment. Tucker and Luckinbill suggested that statistically significant excess translocations for a single exposed individual (n = 1) against a known (unexposed) population could be detected with FISH down to 100 mGy, for largely statistical reasons to do with variability of translocation frequency in exposed and comparison samples (31). This does not contradict our findings of detection of a significant dose-response relationship under 100 mGy.
There were few modifying effects other than radiation exposure, mainly age, sex and study groups (CTS-I vs. CTS-II) (Appendix Table D1), the latter possibly a marker for the different chromosome painting methods used in the two component studies. Although these variables significantly modified the aberration rates, they did not appear to markedly affect the radiation dose response, as modifying factors (P > 0.1, Table 2).
Dose Uncertainties
The problem of allowing for errors in dose assessments when estimating dose-response relationships has been the subject of much interest in biostatistics and epidemiology, with applications in many areas, in particular in nutritional and environmental epidemiology, as reviewed in detail by Carroll et al. (20). Measurement error can substantially alter the shape of the dose-response relationship, and with it, inferred low-dose risk (26). Considerable effort has gone into assessing the impact of dosimetric error for the Japanese atomic bomb survivor data, with much work by Pierce et al. (49, 50) and others (51, 52) using regression-calibration dose-error correction (20), and this method was used for most of our analyses (Tables 2, 3, 5, Appendix Table E1). As emphasized by Carroll et al. (20), it is an approximate method for nonlinear dose-effect relationships. While it leads to reasonable adjusted point estimates of the model parameters it does not fully account for all the variability induced by the measurement (dose estimation) errors.
A Bayesian approach to the measurement-error problem has been developed (53) which rests on the formulation of conditional independence relationships between different model components, following the general structure outlined by Clayton (54). The general advantage of Bayesian methods and other full-likelihood techniques such as MCML (33, 34) is that they take full account of the impact of dose errors on regression estimates, in particular both shared and unshared dose errors which are likely to be a feature of the occupational exposure data considered here. There have been a number of analyses of the Japanese atomic bomb survivor data using Bayesian methods (55, 56).
The minimal difference in dose-response slopes obtained using full-likelihood methods (Bayesian MCMC, MCML) compared to regression-calibration methods (Table 4), implies that dose errors are modest in this cohort. We conclude from this that regression-calibration methods are likely to be adequate for other end points as well (20).
The exposure assessment regression adjustment methods used here are of general applicability. Freedman et al. describe a statistical method for adjusting data on diet and nuclear cataract using an intermediate biomarker (dietary lutein/zeaxanthin) resulting in substantially increased estimates of effectiveness (57). Prentice et al. also apply a regression-calibration approach in conjunction with data on intermediate (urinary) biomarkers (of total energy intake and total protein) to assess effects of energy and protein intake on cancer incidence (58).
Radiation Energy and Biological Effect, Cell Selection and Implications for Temporal Trends
It is well known that higher energy gamma rays are less biologically effective per unit dose than X rays in relationship to a number of experimental end points, in particular chromosome translocations, dicentrics, cell transformation, cell killing, specific locus mutations and various others (32). Our finding that occupational dose accumulated in the earlier time periods (<1960) was slightly [albeit nonsignificantly (P > 0.5)] more effective at producing chromosome translocations than dose accumulated more recently, is probably not related to the increasing use of higher energy radioisotope medical procedures in more recent time periods (59, 60). The changes in energy over time in X-ray imaging in our cohort were due to changes in filtration of the X-ray beam, but the changes were too small to have marked effect, since these changes were not between very low-energy and moderate-energy X rays where the largest difference in biological effect would be expected (32).
There is experimental evidence that cells with translocations can be lost over time as a result of selection (16–19). However, this is controversial, with other researchers observing little or no temporal decay in stable translocation rates (61, 62). Table 3 indicates that there is only modest (and statistically nonsignificant) reduction in chromosome translocation frequencies over time, suggesting that these factors may not have a very pronounced effect in the current study, in agreement with observations in other exposed cohorts (61). However, Table 3 also makes clear that the uncertainties involved are considerable, so that there could well be some effect hidden by these uncertainties.
Other Implications
The occupational doses received by the radiologic technologists, and other radiation workers [e.g., in the Sellafield nuclear plant (13)] were accumulated in small daily increments of <1 mSv. While the effect of any one daily increment is too small to measure, their cumulative effect conforms to expectations derived from other acutely and chronically exposed groups given in Table 6. This suggests, albeit weakly, that such small daily radiation insults result in a cumulative excess of chromosome translocations, indicative of a lack of threshold in the induction of such aberrations.
CONCLUSIONS
In summary, we have demonstrated a statistically significant association of translocation rate with highly fractionated, low-dose estimated occupational radiation exposures to red bone marrow down to <100 mGy, although not if doses are restricted to <50 mGy. There are considerable uncertainties in both estimated occupational and other (PDM) doses, which may have been only imperfectly taken into account in our analysis. Comparison of the findings of regression calibration with full-likelihood (Bayesian MCMC, MCML) methods revealed little evidence that the magnitude of shared errors was substantial enough to modify the dose response. There were no indications of temporal changes in dose response. Dose-response slopes are statistically compatible with those observed in other radiation-exposed populations.
ACKNOWLEDGMENTS
The authors are grateful for the detailed and helpful comments of Professor Jan Tawn, of the Associated Editor and the three referees. This work was supported by the Intramural Research Program of the National Institutes of Health, the National Cancer Institute, Division of Cancer Epidemiology and Genetics. The authors would also like to thank Chris McClure of Research Triangle Institute, Inc. (Research Triangle Park, NC), and Alison Iwan of the University of Minnesota, who organized the in-home phlebotomy, as well as all the participating radiologic technologists in the USRT Study.
APPENDIX A
Summary of Strategy for Estimating Red Bone Marrow Dose for Radiologic Technologists
This Appendix contains a brief description of previously published methods and recent methodological enhancements for reconstructing past red bone marrow doses to U.S. radiologic technologists. The significance of red bone marrow dose is, of course that the fluorescent in situ hybridization (FISH) assay measures the frequency of chromosome translocations in T-lymphocytes and all mammalian stem cells differentiate into specific types of blood cells within the red bone marrow (63). Therefore, the red bone marrow is the most appropriate target tissue to assess the radiation dose-response relationship with respect to translocations in peripheral lymphocytes.
An earlier version of the dosimetry published in 2006 (10) used literature-reported exposure measurements for the years before 1960 and archival personnel monitoring badge data from cohort members through 1984 as the basis to estimate doses for 90,000 radiological technologists. Recent modeling and enhancements and additional personnel monitoring data acquired through 1997 have enabled a more comprehensive assessment of doses for about 110,000 technologists for each year worked from 1916 through 1997 (11).
We obtained 921,134 annual badge dose measurements for 79,959 cohort members between 1960–1997 from the largest commercial personnel dosimetry provider in the U.S., Landauert®, Inc. (N = 899,421 badge measurements for 1977–1997), three branches of the U.S. military (N = 14,825 badge measurements for 1960–1997) and several large civilian employers (N = 2,384 badge measurements for 1960–1976). We also obtained 194 anonymized annual badge doses received by technologists in the years 1949–1960 from a major medical facility, the latter badge doses for workers not in the cohort but used for validation of our estimated doses for those years (11).
Personnel radiation monitoring measurements (film badges and later-era monitoring technologies) are the basis for estimation of red bone marrow dose and were either derived for each technologist on an annual basis from archival databases or simulated from probability density functions derived from the literature to describe the range and likelihoods of exposures in each working year. Those data were used to estimate air kerma, a dosimetric quantity similar to absorbed dose (but pertaining to air), using conversion factors (64) for X-radiation spectra that were tailored to four time periods (<1949, 1949–1954, 1955–1968) and reflected changes in energy and beam filtration, a function of evolving technology and regulations. The absorbed red bone marrow dose was estimated based on the air kerma in the year worked, the protection afforded by the use of protective lead aprons, the body mass index of the technologist in the year worked and conversion coefficients tailored similarly to the time period (64), again reflecting changes in technology and regulation.
Choice of dosimetric parameter values, e.g., the frequency of use of a protective apron, was based on individual questionnaire responses or estimated based on statistical models derived from the cohort and available responses. The statistical models derived considered a variety of types of radiological procedures, e.g., conventional X rays, fluoroscopy and use of radiopharmaceuticals, differentiated into seven time periods from 1940–1997 and questionnaire responses on individual apron usage data.
Each parameter in the dose estimation equations that was used in any of several statistical models was described in terms of a probability density function that was used in a Monte Carlo based algorithm that allowed estimation of a probability density function for the dose for each technologist in each year worked and over their occupational lifetime. Some unknown parameters were specified as “unshared uncertainties” implying that each technologist would receive a random selection of the parameter from the probability density function. Other parameters, e.g., bias factors, were specified as shared uncertainties such that subgroups of technologists could be assigned the same sampled value from the probability density function.
While every technologist's annual dose is estimated as a probability density function to reflect lack-of-knowledge uncertainty about the true dose, the dosimetry system was designed to generate multiple realizations of the entire cohort dose distribution, reflecting shared uncertainties and possible biases in the input data and assumptions used. The system provides multiple realizations of individual annual doses. For these analyses there were 1,000 sets for each year in which the person was believed to have worked. Shared uncertainties introduce some correlation between individual doses across the realizations. The analysis described in the text for the “full likelihood” methods used the ensemble of cohort realizations, numbering 1,000, while the regression-calibration method described used the average of the individual annual dose realizations as an estimate of the expected individual annual dose.
A total of 86/88 (97.7%) individuals in the CTS-I data had any film badge records, and 50/150 (33.3%) individuals in the CTS-II data had any film badge records (Appendix Table A1). The distribution of individuals by numbers of years for which they had records is given in Appendix Table A1, this demonstrates that a substantial proportion of individuals, over 44% of the full cohort, had 5 or more years of film badge records, and for 28.0% of all years worked (1,415 years worked out of 5,052.6) there was a film-badge measurement. Landauer, Inc., is the largest supplier of film badge records, providing 97% of all film badges.
TABLE A1.
Distribution of the Number of Years that Individuals in Cohort have Information on Doses from Film Badges
| CTS-I |
CTS-II |
Total |
||||
|---|---|---|---|---|---|---|
| Years with film-badge dose information | Numbers of individuals | Percentage (%) | Numbers of individuals | Percentage (%) | Numbers of individuals | Percentage (%) |
| 0 | 2 | 2.3 | 100 | 66.7 | 102 | 42.9 |
| 1 | 1 | 1.1 | 5 | 3.3 | 6 | 2.5 |
| 2–4 | 13 | 14.8 | 12 | 8.0 | 25 | 10.5 |
| 5–9 | 25 | 28.4 | 17 | 11.3 | 42 | 17.6 |
| 10–14 | 13 | 14.8 | 7 | 4.7 | 20 | 8.4 |
| 15–19 | 16 | 18.2 | 6 | 4.0 | 22 | 9.2 |
| 20–29 | 17 | 19.3 | 3 | 2.0 | 20 | 8.4 |
| 30+ | 1 | 1.1 | 0 | 0.0 | 1 | 0.4 |
| Total persons with any film badge | 86 | 97.7 | 50 | 33.3 | 136 | 57.1 |
| Total persons without any film badge | 2 | 2.3 | 100 | 66.7 | 102 | 42.9 |
| Total years with film badge | 1,010 | 55.6 | 405 | 12.5 | 1415 | 28.0 |
| Total years worked | 1,815 | 3,237.6 | 5,052.6 | |||
APPENDIX B
Description of Subset Selection for Chromosome Analysis
In this Appendix we outline the criteria used when selecting subjects for blood sampling from within the U.S. Radiologic Technologist cohort (37).
Subject selection and recruitment for the Chromosome Translocation Study I (CTS-I) (22) were based on electronic film badge dose records obtained from a nationwide dosimetry provider (Landauer, Inc.) and spanned the years 1977–1984. A sample of 200 living technologists with high (over 350 mGy) recorded badge doses were randomly selected and approached for participation. Another 130 technologists with low-recorded badge doses (10 mGy or less) who worked for 1 year or less were also randomly sampled. Subjects underwent a brief telephone screening interview to confirm and update their work history information and to exclude subjects with a previous cancer diagnosis or who had undergone radiation therapy for malignancy. Ultimately 62 high-dose and 28 low-dose individuals were recruited and provided a venipuncture blood sample in 1994–1995, 80 samples were analyzed.
Subjects sampled for the Chromosome Translocation Study II (CTS-II) (24) were selected from among a core group of 3,441 cohort members who were known to have started working as technologists prior to 1950 and who were believed to be alive with a known address at the time of sample selection in 2003. To ensure a wide range of doses, we partitioned subjects into groups that were likely to have had high, moderate and low doses of ionizing radiation to the red bone marrow, which was the dose relevant to this study. At the time of recruitment, we used a combination of our estimates of badge doses and work history information to define these groups. Subjects were approached randomly for participation until the targeted quota for each dose group was satisfied. Subjects were excluded if they had a prior cancer diagnosis, a personal or familial history of chromosomal instability disorders (such as Bloom's syndrome or Fanconi's anemia) or reported currently smoking 10 or more cigarettes per day. It is known that familial cancer syndromes such as Bloom's syndrome or Fanconi's anemia are well ascertained, with sensitivity >90% in relationship to cancer in first degree relatives, by survey questionnaires like those administered here (65); in any case it is very unlikely that people with such syndromes would ever be radiologists. Survey data is also a generally very reliable way of ascertaining cancer in a general population with sensitivity >98% (66), and sensitivity would be expected to be even higher among biomedically-trained persons, as here. Smoking is likewise ascertained with high sensitivity (>90%) in survey data (67).
Of the 207 subjects approached for participation, 159 persons (77%) agreed to participate and 48 (23%) declined. Of the 159 participants, 152 gave a blood sample (in 2003) and were analyzed. Further details on cohort selection are given elsewhere (20, 24, 25).
APPENDIX C
Description of Bayesian Model Fitting
We outline a Bayesian Markov Chain Monte Carlo (MCMC) approach to evaluate dose uncertainty. This has the advantage over simpler (e.g., regression calibration) methods because it can consider more complex dosimetry systems and patterns of error, although it is comparable with other full-likelihood methods such as Monte Carlo maximum likelihood (33, 34) in this respect. The dosimetry system produces a number of realizations of the entire set of doses that characterize the state of knowledge about doses for this population. Our main goal was to estimate radiation risk coefficients, θ1 θ2 and their Bayesian credible interval (BCI), accounting for both the usual statistical sampling error and uncertainty in the dosimetry. Our approach can manage various types of outcomes such as continuous, time-to-event and count data. In this application we considered a count outcome variable with Poisson or negative binomial error.
To perform Bayesian inference one must formulate prior distributions on all model parameters. We assumed normal prior distributions for the parameters in expressions (1) and (3). Suppose we had M dose realizations (M = 1,000 here), and let γ be the dose vector index variable in the model. The parameter, γ, is distributed as a multinomial distribution, Mult(1,π). The probability vector, π, has a hyper-prior distribution given by a Dirichlet distribution, Dirichlet(w), with w ≡ 1, so that dose realizations are chosen with equal probability a priori. The Metropolis-Hastings algorithm was then used to produce a sample from the posterior distribution of the parameters of interest. Parameter estimates and their corresponding 95% BCI in Table 4 are based on 20,000 posterior samples after 10,000 burn-in iterations.
APPENDIX D
CTS-I + II Data Background (Nonradiation) Model Fits for Translocation
In this Appendix we outline the optimal background model. As can be seen from Appendix Table D1, translocation rates were highly significantly associated with age (P = 0.0048), sex (P = 0.0065), study group (CTS-I vs. II) (P = 0.0023) and with borderline significant interaction of study group with sex (P = 0.0501), but were not associated with cigarette smoking (P = 0.2750 for years smoked or P = 0.2103 for pack-years smoked). There was no evidence that higher order powers of age than the first are required to explain the increase in background rate with age, once adjustments for gender and study group (CTS-I vs. II) were done (P = 0.9272).
APPENDIX TABLE D1.
CTS-I+II Data Background (Nonradiation) Model Fits and Significance for Translocation, Adjusted for Over-Dispersion
| Baseline variables | Deviance (df) | P valuea |
|---|---|---|
| Constant | 1006.671 (237) | - |
| Constant, age | 973.281 (236) | 0.0048 |
| Constant, age, age2 | 971.190 (235) | 0.4776 |
| Constant, age, age2, age3 | 924.872 (234) | 0.0007 |
| Constant, age, age2, age3, age4 | 912.405 (233) | 0.0757 |
| Constant, age, age2, age3, age4, age5 | 904.471 (232) | 0.1550 |
| Constant, age, age2, age3, age4, age5, age6 | 895.067 (231) | 0.1206 |
| Constant, age, age2, age3, age4, age5, age6 age7 | 895.026 (230) | 0.9183 |
| Constant, age, age2, age3, age4, age5, age6, age7, age8 | 894.777 (229) | 0.8009 |
| Constant, age, age2, age3, age4, age5, age6, sex | 866.612 (230) | 0.0065b |
| Constant, age, age2, age3, age4, age5, age6, sex, years cigarette smoking | 862.105 (229) | 0.2750 |
| Constant, age, age2, age3, age4, age5, age6, sex, pack-years cigarette smoking | 860.680 (229) | 0.2103c |
| Constant, age, age2, age3, age4, age5, age6, sex, study group (CTS-I vs. II) | 831.938 (229) | 0.0023c |
| Constant, study group (CTS-I vs. II) × age, age2, age3, age4, age5, age6, sex, study group | 831.786 (228) | 0.8384 |
| Constant, study group (CTS-I vs. II) × {age, age2, age3, age4, age5, age6}, sex, study group | 806.857 (223) | 0.2335 |
| Constant, age, age2, age3, age4, age5, age6, sex, study group (CTS-I vs. II), sex × study group | 818.019 (228) | 0.0501d |
| Constant, age, study group (CTS-I vs. II), sex × study group | 822.928 (233) | 0.9272e |
| Constant, study group (CTS-I vs. II), sex × study group | 954.514 (234) | <0.0001f |
| Constant, age, study group (CTS-I vs. II) | 852.222 (235) | 0.0296f |
| Constant, age, sex | 927.694 (235) | <0.0001f |
Note. Optimal model shown in boldface.
Unless otherwise indicated the P value refers to the improvement in fit of that line with the model in the line immediately above it in the table.
P value of improvement in fit of this line of table compared with fit of a model with age,. . ., age6.
P value of improvement in fit of this line of table compared with fit of a model with age,. . ., age6, sex.
P value of improvement in fit of this line of table compared with fit of a model with age,. . ., age6, sex, study group (CTS-I vs. II).
P value of improvement in fit of a model with age,. . ., age6, sex, study group (CTS-I vs II), sex study group over a model with age, sex, study group, sex study group.
P value of deterioration of fit of this line of Table compared with fit of a model with age, sex, study group (CTS-I vs. II), sex × study group in the background.
APPENDIX TABLE E1.
Comparison of Dose and Years Worked Model Fits and Parameter Estimates for Translocation Rates in Relationship to Occupational and Personal-Diagnostic-Medical (PDM) Doses, Using Regression-Calibration Adjusted Occupational Doses, with 95% Profile Likelihood Confidence Intervals, Adjusted for Overdispersiona
| Dose and years worked variables | Deviance (df) | P valueb | Linear dose parameter (translocations/100 CEc/Gy) (occupational) | Linear dose parameter (translocations/100 CEc/Gy) (PDM) | Years worked (translocations/100 CEc/1,000 years) |
|---|---|---|---|---|---|
| Years worked only | 812.916 (232) | 0.0923d | - | - | 7.0 (–1.1, 15.1) |
| Occupational dose only | 803.526 (232) | 0.0188d | 7.0 (1.2, 12.9) | - | - |
| PDMe dose only | 765.909 (232) | <0.0001d | - | 4.4 (2.2, 6.7) | - |
| Occupational and PDM dose, constrained equal | 753.256 (232) | <0.0001d | 4.4 (2.5, 6.5) | 4.4 (2.5, 6.5) | - |
| Occupational and PDM dose, unconstrained | 752.543 (231) | 0.6403e/0.0440f | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) | - |
| Years worked and occupational dose | 803.164 (231) | 0.0953g/0.7472h | 6.3 (–1.1, 13.7) | - | 1.7 (–8.5, 11.9) |
| Years worked and PDM dose | 759.938 (231) | <0.0001g/0.1792i | - | 4.3 (2.1, 6.6) | 5.3 (–2.4, 13.0) |
| Years worked and occupational and PDM dose, constrained equal | 752.856 (231) | <0.0001g/0.7264j | 4.3 (2.3, 6.5) | 4.3 (2.3, 6.5) | 1.4 (–6.6, 9.5) |
| Years worked and occupational and PDM dose, unconstrained | 752.513 (230) | 0.0001g/0.9238k | 5.5 (–1.7, 12.7) | 4.2 (2.0, 6.5) | 0.5 (–9.4, 10.4) |
Note. Optimal model shown in boldface.
Background model is adjusted for age, study group (CTS-I vs. II), sex × study group; a 6-year period of latency is assumed.
Unless otherwise indicated the P value refers to the improvement in fit of that line with the model in the line immediately above it in the table.
Whole chromosome equivalents (CE), the equivalent number of cells assumed to have full painting done of their nuclear DNA.
P value of improvement in fit of this line of table compared with fit of a model without years worked or radiation dose terms.
P value of improvement in fit of model with occupational dose and personal-diagnostic dose unconstrained vs. identical model but with dose coefficients constrained equal.
P value of improvement in fit of model over one with just personal-diagnostic dose.
P value of improvement in fit of model with years worked only.
P value of improvement in fit of model with occupational dose only.
P value of improvement in fit of model with personal diagnostic dose only.
P value of improvement in fit of model with occupational and personal-diagnostic dose, constrained equal.
P value of improvement in fit of model with occupational and personal-diagnostic dose, unconstrained.
APPENDIX TABLE F1.
Assessment of Effect of Dose Latency on Parameter Estimates for Translocation Rates in Relationship to Occupational and Personal-Diagnostic-Medical (PDM) Doses, using Regression-Calibration Adjusted Occupational Doses, with 95% Profile Likelihood Confidence Intervals, Adjusted for Overdispersion a
| Latent period (years) | Linear dose parameter (translocations/100 CEb/Gy) (occupational) | Linear dose parameter (translocations/100 CEb/Gy) (PDM) |
|---|---|---|
| 0 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 1 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 2 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 3 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 4 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 5 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 6 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 7 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 8 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 9 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
| 10 | 5.7 (0.2, 11.3) | 4.2 (2.0, 6.5) |
Note. Optimal latency (6 years) is shown in boldface.
Background model is adjusted for age, study group (CTS-I vs. II), sex × study group and with additional adjustment for PDM dose.
Per whole chromosome equivalents (CE), equivalent to the translocation frequency that would be observed if cells were assumed to have full-genome painting done of their nuclear DNA.
TABLE G1.
Analysis of Unstable Aberrations in Relationship to Occupational and Personal-Diagnostic-Medical (PDM) Doses in CTS-II Data, Using Regression-Calibration Adjusted Occupational Doses, with 95% Profile Likelihood Confidence Intervals, Adjusted for Overdispersiona
| Dose and years worked variables | Deviance (df) | P valueb | Linear dose parameter (translocations/100 CEc/Gy) (occupational) | Linear dose parameter (translocations/100 CEc/Gy) (PDM) |
|---|---|---|---|---|
| Dicentrics | ||||
| Occupational dose only | 278.061 (141) | 0.7054d | –0.3 (–1.9, 1.4) | - |
| PDM dose only | 276.235 (141) | 0.3013d | - | 0.3 (–0.3, 1.0) |
| Occupational and PDM dose, constrained equal | 277.114 (141) | 0.4302d | 0.2 (–0.3, 0.8) | 0.2 (–0.3, 0.8) |
| Occupational and PDM dose, unconstrained | 275.457 (140) | 0.3604e/0.1066f | –0.6 (–2.1, 1.2) | 0.4 (–0.3, 1.1) |
| Fragments | ||||
| Occupational dose only | 355.513 (141) | 0.8698d | –0.2 (–2.5, 2.2) | - |
| PDM dose only | 348.246 (141) | 0.0870d | - | 0.8 (–0.1, 1.7) |
| Occupational and PDM dose, constrained equal | 350.084 (141) | 0.1390d | 0.6 (–0.2, 1.4) | 0.6 (–0.2, 1.4) |
| Occupational and PDM dose, unconstrained | 347.831 (140) | 0.3426e/0.0809f | –0.5 (–2.7, 1.8) | 0.8 (–0.1, 1.7) |
| All unstable aberrations (dicentrics, fragments, insertions, rings) | ||||
| Occupational dose only | 510.935 (141) | 0.8040d | –0.5 (–4.2, 3.4) | - |
| PDM dose only | 501.362 (141) | 0.0992d | - | 1.2 (–0.2, 2.7) |
| Occupational and PDM dose, constrained equal | 504.204 (141) | 0.1653d | 0.9 (–0.4, 2.2) | 0.9 (–0.4, 2.2) |
| Occupational and PDM dose, unconstrained | 500.398 (140) | 0.3039e/0.0882f | –1.0 (–4.6, 2.8) | 1.3 (–0.2, 2.8) |
Background model is adjusted for age, age2, age3, age4, age5, sex, smoking pack-years; a 6-year period of latency is assumed.
Unless otherwise indicated the P value refers to the improvement in fit of that line with the model in the line immediately above it in the table.
Whole chromosome equivalents (CE), the equivalent number of cells assumed to have full painting done of their nuclear DNA.
P value of improvement in fit of this line of table compared with fit of a model without radiation dose terms.
P value of improvement in fit of model with occupational dose and personal-diagnostic dose unconstrained vs. identical model but with dose coefficients constrained equal.
P value of improvement in fit of model over one with just occupational dose.
REFERENCES
- 1.Vermeulen R, Coble JB, Lubin JH, Portengen L, Blair A, Attfield MD, et al. The diesel exhaust in miners study: IV. Estimating historical exposures to diesel exhaust in underground non-metal mining facilities. Ann Occup Hyg. 2010;54:774–88. doi: 10.1093/annhyg/meq025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stewart PA, Vermeulen R, Coble JB, Blair A, Schleiff P, Lubin JH, et al. The diesel exhaust in miners study: V. Evaluation of the exposure assessment methods. Ann Occup Hyg. 2012 doi: 10.1093/annhyg/mes020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lagorio S, Ferrante D, Ranucci A, Negri S, Sacco P, Rondelli R, et al. Exposure to benzene and childhood leukaemia: a pilot case-control study. BMJ Open. 2013:3. doi: 10.1136/bmjopen-2012-002275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vermeulen R, Zhang L, Spierenburg A, Tang X, Bonventre JV, Reiss B, et al. Elevated urinary levels of kidney injury molecule-1 among Chinese factory workers exposed to trichloroethylene. Carcinogenesis. 2012;33:1538–41. doi: 10.1093/carcin/bgs191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Muirhead CR, Cox R, Stather JW, MacGibbon BH, Edwards AA, Haylock RGE. Documents of the NRPB. 4. Vol. 4. National Radiological Protection Board; Chilton, Didcot: 1993. Estimates of late radiation risks to the UK population. pp. 15–157. [Google Scholar]
- 6.Wakeford R, Tawn EJ. The meaning of low dose and low dose-rate. J Radiol Prot. 2010;30:1–3. doi: 10.1088/0952-4746/30/1/E02. [DOI] [PubMed] [Google Scholar]
- 7.Muirhead CR, O'Hagan JA, Haylock RG, Phillipson MA, Willcock T, Berridge GL, et al. Mortality and cancer incidence following occupational radiation exposure: Third analysis of the National Registry for Radiation Workers. Br J Cancer. 2009;100:206–12. doi: 10.1038/sj.bjc.6604825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cardis E, Vrijheid M, Blettner M, Gilbert E, Hakama M, Hill C, et al. The 15-country collaborative study of cancer risk among radiation workers in the nuclear industry: estimates of radiation-related cancer risks. Radiat Res. 2007;167:396–416. doi: 10.1667/RR0553.1. [DOI] [PubMed] [Google Scholar]
- 9.Epidemiological studies of radiation and cancer . UNSCEAR 2006 Report. Annex A. United Nations Scientific Committee on the Effects of Atomic Radiation. United Nations; New York: 2008. pp. 13–122. [Google Scholar]
- 10.Simon SL, Weinstock RM, Doody MM, Neton J, Wenzl T, Stewart P, et al. Estimating historical radiation doses to a cohort of U.S. radiologic technologists. Radiat Res. 2006;166:174–92. doi: 10.1667/RR3433.1. [DOI] [PubMed] [Google Scholar]
- 11.Simon SL, Preston DL, Linet MS, Miller JS, Sigurdson AJ, Alexander BH, et al. Radiation organ doses received in a nationwide cohort of U.S. radiologic technologists: methods and findings. Radiat Res. 2014 doi: 10.1667/RR13542.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vozilova AV, Shagina NB, Degteva MO, Edwards AA, Ainsbury EA, Moquet JE, et al. Preliminary FISH-based assessment of external dose for residents exposed on the Techa River. Radiat Res. 2012;177:84–91. doi: 10.1667/rr2485.1. [DOI] [PubMed] [Google Scholar]
- 13.Tawn EJ, Whitehouse CA, Tarone RE. FISH chromosome aberration analysis on retired radiation workers from the Sellafield nuclear facility. Radiat Res. 2004;162:249–56. doi: 10.1667/rr3214. [DOI] [PubMed] [Google Scholar]
- 14.Burak LE, Kodama Y, Nakano M, Ohtaki K, Itoh M, Okladnikova ND, et al. FISH examination of lymphocytes from Mayak workers for assessment of translocation induction rate under chronic radiation exposures. Int J Radiat Biol. 2001;77:901–08. doi: 10.1080/09553000110063386. [DOI] [PubMed] [Google Scholar]
- 15.Kodama Y, Pawel D, Nakamura N, Preston D, Honda T, Itoh M, et al. Stable chromosome aberrations in atomic bomb survivors: results from 25 years of investigation. Radiat Res. 2001;156:337–46. doi: 10.1667/0033-7587(2001)156[0337:scaiab]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 16.Spruill MD, Nelson DO, Ramsey MJ, Nath J, Tucker JD. Lifetime persistence and clonality of chromosome aberrations in the peripheral blood of mice acutely exposed to ionizing radiation. Radiat Res. 2000;153:110–21. doi: 10.1667/0033-7587(2000)153[0110:lpacoc]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 17.Natarajan AT, Santos SJ, Darroudi F, Hadjidikova V, Vermeulen S, Chatterjee S, et al. 137Cesium-induced chromosome aberrations analyzed by fluorescence in situ hybridization: eight years follow up of the Goiania radiation accident victims. Mutat Res. 1998;400:299–312. doi: 10.1016/s0027-5107(98)00021-9. [DOI] [PubMed] [Google Scholar]
- 18.Matsumoto K, Ramsey MJ, Nelson DO, Tucker JD. Persistence of radiation-induced translocations in human peripheral blood determined by chromosome painting. Radiat Res. 1998;149:602–13. [PubMed] [Google Scholar]
- 19.Gardner SN, Tucker JD. The cellular lethality of radiation-induced chromosome translocations in human lymphocytes. Radiat Res. 2002;157:539–52. doi: 10.1667/0033-7587(2002)157[0539:tclori]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 20.Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu CM. A modern perspective. Chapman and Hall/CRC; Boca Raton: 2006. Measurement error in nonlinear models. pp. 1–488. [Google Scholar]
- 21.Kerber RA, Till JE, Simon SL, Lyon JL, Thomas DC, Preston-Martin S, et al. A cohort study of thyroid disease in relation to fallout from nuclear weapons testing. JAMA. 1993;270:2076–82. [PubMed] [Google Scholar]
- 22.Bhatti P, Doody MM, Preston DL, Kampa D, Ron E, Weinstock RW, et al. Increased frequency of chromosome translocations associated with diagnostic x-ray examinations. Radiat Res. 2008;170:149–55. doi: 10.1667/RR1422.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bhatti P, Yong LC, Doody MM, Preston DL, Kampa DM, Ramsey MJ, et al. Diagnostic X-ray examinations and increased chromosome translocations: evidence from three studies. Radiat Environ Biophys. 2010;49:685–92. doi: 10.1007/s00411-010-0307-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bhatti P, Preston DL, Doody MM, Hauptmann M, Kampa D, Alexander BH, et al. Retrospective biodosimetry among United States radiologic technologists. Radiat Res. 2007;167:727–34. doi: 10.1667/RR0894.1. [DOI] [PubMed] [Google Scholar]
- 25.Sigurdson AJ, Bhatti P, Preston DL, Doody MM, Kampa D, Alexander BH, et al. Routine diagnostic X-ray examinations and increased frequency of chromosome translocations among U.S. radiologic technologists. Cancer Res. 2008;68:8825–31. doi: 10.1158/0008-5472.CAN-08-1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Thomas D, Stram D, Dwyer J. Exposure measurement error: influence on exposure-disease relationships and methods of correction. Annu Rev Public Health. 1993;14:69–93. doi: 10.1146/annurev.pu.14.050193.000441. [DOI] [PubMed] [Google Scholar]
- 27.Committee to Assess Health Risks from Exposure to Low Levels of Ionizing Radiation National Research Council . Health risks from exposure to low levels of ionizing radiation: BEIR VII - Phase 2. National Academy Press; Washington DC: 2006. pp. 1–406. [PubMed] [Google Scholar]
- 28.International Commission on Radiological Protection (ICRP) The 2007 recommendations of the international commission on radiological protection. ICRP Publication 103. Ann ICRP. 2007;37:1–332. doi: 10.1016/j.icrp.2007.10.003. [DOI] [PubMed] [Google Scholar]
- 29.Tubiana M, Feinendegen LE, Yang C, Kaminski JM. The linear no-threshold relationship is inconsistent with radiation biologic and experimental data. Radiology. 2009;251:13–22. doi: 10.1148/radiol.2511080671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Little MP, Wakeford R, Tawn EJ, Bouffler SD, Berrington de Gonzalez A. Risks associated with low doses and low dose rates of ionizing radiation: why linearity may be (almost) the best we can do. Radiology. 2009;251:6–12. doi: 10.1148/radiol.2511081686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tucker JD, Luckinbill LS. Estimating the lowest detectable dose of ionizing radiation by FISH whole-chromosome painting. Radiat Res. 2011;175:631–37. doi: 10.1667/RR2506.1. [DOI] [PubMed] [Google Scholar]
- 32.National Council on Radiation Protection and Measurements (NCRP), Report No. 104 . The relative biological effectiveness of radiations of different quality. NCRP; Bethesda: 1990. pp. 1–218. [Google Scholar]
- 33.Stram DO, Kopecky KJ. Power and uncertainty analysis of epidemiological studies of radiation-related disease risk in which dose estimates are based on a complex dosimetry system: some observations. Radiat Res. 2003;160:408–17. doi: 10.1667/3046. [DOI] [PubMed] [Google Scholar]
- 34.Stayner L, Vrijheid M, Cardis E, Stram DO, Deltour I, Gilbert SJ, et al. A Monte Carlo maximum likelihood method for estimating uncertainty arising from shared errors in exposures in epidemiological studies of nuclear workers. Radiat Res. 2007;168:757–63. doi: 10.1667/RR0677.1. [DOI] [PubMed] [Google Scholar]
- 35.Otake M, Prentice RL. The analysis of chromosomally aberrant cells based on beta-binomial distribution. Radiat Res. 1984;98:456–70. [PubMed] [Google Scholar]
- 36.Moore DF. Asymptotic properties of moment estimators for overdispersed counts and proportions. Biometrika. 1986;73:583–88. [Google Scholar]
- 37.Mohan AK, Hauptmann M, Freedman DM, Ron E, Matanoski GM, Lubin JH, et al. Cancer and other causes of mortality among radiologic technologists in the United States. Int J Cancer. 2003;103:259–67. doi: 10.1002/ijc.10811. [DOI] [PubMed] [Google Scholar]
- 38.Fucic A, Zeljezic D, Kasuba V, Kopjar N, Rozgaj R, Lasan R, et al. Stable and unstable chromosome aberrations measured after occupational exposure to ionizing radiation and ultrasound. Croatian Med J. 2007;48:371–7. [PMC free article] [PubMed] [Google Scholar]
- 39.Kleinerman RA, Littlefield LG, Tarone RE, Machado SG, Blettner M, Peters LJ, et al. Chromosome aberrations in peripheral lymphocytes and radiation dose to active bone marrow in patients treated for cancer of the cervix. Radiat Res. 1989;119:176–90. [PubMed] [Google Scholar]
- 40.Tucker JD. Chromosome translocations and assessing human exposure to adverse environmental agents. Environ Mol Mutagen. 2010;51:815–24. doi: 10.1002/em.20561. [DOI] [PubMed] [Google Scholar]
- 41.Lucas JN, Awa A, Straume T, Poggensee M, Kodama Y, Nakano M, et al. Rapid translocation frequency analysis in humans decades after exposure to ionizing radiation. Int J Radiat Biol. 1992;62:53–63. doi: 10.1080/09553009214551821. [DOI] [PubMed] [Google Scholar]
- 42.McCullagh P, Nelder JA. Monographs on statistics and applied probability 37. 2nd ed. Chapman and Hall/CRC; Boca Raton: 1989. Generalized linear models. pp. 1–526. [Google Scholar]
- 43.Sigurdson AJ, Ha M, Hauptmann M, Bhatti P, Sram RJ, Beskid O, et al. International study of factors affecting human chromosome translocations. Mutat Res. 2008;652:112–21. doi: 10.1016/j.mrgentox.2008.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Report of the Joint US-Japan Working Group. Vol. 2005. Radiation Effects Research Foundation; Hiroshima: Reassessment of the atomic bomb radiation dosimetry for Hiroshima and Nagasaki. Dosimetry System 2002. pp. 1–998. [Google Scholar]
- 45.Final Report. Vol. 1. Radiation Effects Research Foundation; Hiroshima: 1987. US-Japan joint reassessment of atomic bomb radiation dosimetry in Hiroshima and Nagasaki. pp. 1–434. [Google Scholar]
- 46.Orjuela MA, Liu X, Miller RL, Warburton D, Tang D, Jobanputra V, et al. Urinary naphthol metabolites and chromosomal aberrations in 5-year-old children. Cancer Epidemiol Biomarkers Prevent. 2012;21:1191–202. doi: 10.1158/1055-9965.EPI-12-0214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lucas JN, Deng W, Oram SW, Hill FS, Durante M, George K, et al. Theoretical and experimental tests of a chromosomal fingerprint for densely ionizing radiation based on F ratios calculated from stable and unstable chromosome aberrations. Radiat Res. 1999;151:85–91. [PubMed] [Google Scholar]
- 48.Johannes C, Horstmann M, Durante M, Chudoba I, Obe G. Chromosome intrachanges and interchanges detected by multicolor banding in lymphocytes: searching for clastogen signatures in the human genome. Radiat Res. 2004;161:540–8. doi: 10.1667/rr3157. [DOI] [PubMed] [Google Scholar]
- 49.Pierce DA, Stram DO, Vaeth M. Allowing for random errors in radiation dose estimates for the atomic bomb survivor data. Radiat Res. 1990;123:275–84. [PubMed] [Google Scholar]
- 50.Pierce DA, Preston DL, Stram DO, Vaeth M. Allowing for dose-estimation errors for the A-bomb survivor data. J Radiat Res (Tokyo) 1991;32(Suppl):108–21. doi: 10.1269/jrr.32.supplement_108. [DOI] [PubMed] [Google Scholar]
- 51.Little MP, Muirhead CR. Evidence for curvilinearity in the cancer incidence dose-response in the Japanese atomic bomb survivors. Int J Radiat Biol. 1996;70:83–94. doi: 10.1080/095530096145364. [DOI] [PubMed] [Google Scholar]
- 52.Little MP. Threshold and other departures from linear-quadratic curvature in the non-cancer mortality dose-response curve in the Japanese atomic bomb survivors. Radiat Environ Biophys. 2004;43:67–75. doi: 10.1007/s00411-004-0244-9. [DOI] [PubMed] [Google Scholar]
- 53.Richardson S, Gilks WR. A Bayesian approach to measurement error problems in epidemiology using conditional independence models. Am J Epidemiol. 1993;138:430–42. doi: 10.1093/oxfordjournals.aje.a116875. [DOI] [PubMed] [Google Scholar]
- 54.Clayton D. The analysis of event history data - a review of progress and outstanding problems. Statist Med. 1988;7:819–41. doi: 10.1002/sim.4780070802. [DOI] [PubMed] [Google Scholar]
- 55.Bennett J, Little MP, Richardson S. Flexible dose-response models for Japanese atomic bomb survivor data: Bayesian estimation and prediction of cancer risk. Radiat Environ Biophys. 2004;43:233–45. doi: 10.1007/s00411-004-0258-3. [DOI] [PubMed] [Google Scholar]
- 56.Little MP, Hoel DG, Molitor J, Boice JD, Jr, Wakeford R, Muirhead CR. New models for evaluation of radiation-induced lifetime cancer risk and its uncertainty employed in the UNSCEAR 2006 report. Radiat Res. 2008;169:660–76. doi: 10.1667/RR1091.1. [DOI] [PubMed] [Google Scholar]
- 57.Freedman LS, Midthune D, Carroll RJ, Tasevska N, Schatzkin A, Mares J, et al. Using regression calibration equations that combine self-reported intake and biomarker measures to obtain unbiased estimates and more powerful tests of dietary associations. Am J Epidemiol. 2011;174:1238–45. doi: 10.1093/aje/kwr248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Prentice RL, Shaw PA, Bingham SA, Beresford SA, Caan B, Neuhouser ML, et al. Biomarker-calibrated energy and protein consumption and increased cancer risk among postmenopausal women. Am J Epidemiol. 2009;169:977–89. doi: 10.1093/aje/kwp008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Mettler FA, Jr, Bhargavan M, Faulkner K, Gilley DB, Gray JE, Ibbott GS, et al. Radiologic and nuclear medicine studies in the United States and worldwide: frequency, radiation dose, and comparison with other radiation sources–1950–2007. Radiology. 2009;253:520–31. doi: 10.1148/radiol.2532082010. [DOI] [PubMed] [Google Scholar]
- 60.Drozdovitch V, Brill AB, Mettler FA, Jr, Beckner WM, Goldsmith SJ, Gross MD, et al. Nuclear medicine practices in the 1950s through the mid-1970s and occupational radiation doses to technologists from diagnostic radioisotope procedures. Health Phys. 2014 doi: 10.1097/HP.0000000000000107. Accepted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lindholm C, Edwards A. Long-term persistence of translocations in stable lymphocytes from victims of a radiological accident. Int J Radiat Biol. 2004;80:559–66. doi: 10.1080/09553000412331283498. [DOI] [PubMed] [Google Scholar]
- 62.Edwards AA, Lindholm C, Darroudi F, Stephan G, Romm H, Barquinero J, et al. Review of translocations detected by FISH for retrospective biological dosimetry applications. Radiat Prot Dosimetry. 2005;113:396–402. doi: 10.1093/rpd/nch452. [DOI] [PubMed] [Google Scholar]
- 63.Janeway CA, Travers P, Walport M, Capra JD. Immunobiology: the immune system in health and disease. 4th ed. Routledge; London: 1999. pp. 1–635. [Google Scholar]
- 64.Simon SL. Organ-specific external dose coefficients and protective apron transmission factors for historical dose reconstruction for medical personnel. Health Phys. 2011;101:13–27. doi: 10.1097/HP.0b013e318204a60a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Acheson LS, Zyzanski SJ, Stange KC, Deptowicz A, Wiesner GL. Validation of a self-administered, computerized tool for collecting and displaying the family history of cancer. J Clin Oncol. 2006;24:5395–402. doi: 10.1200/JCO.2006.07.2462. [DOI] [PubMed] [Google Scholar]
- 66.Gupta V, Gu K, Chen Z, Lu W, Shu XO, Zheng Y. Concordance of self-reported and medical chart information on cancer diagnosis and treatment. BMC Med Res Methodology. 2011;11:72. doi: 10.1186/1471-2288-11-72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wong SL, Shields M, Leatherdale S, Malaison E, Hammond D. Assessment of validity of self-reported smoking status. Health reports / Statistics Canada, Canadian Centre for Health Information = Rapports sur la sante / Statistique Canada, Centre canadien d'information sur la sante. 2012;23:47–53. [PubMed] [Google Scholar]