Abstract
An intriguing question in cell biology is “how do cells regulate their shape?” It is commonly believed that the observed cellular morphologies are a result of the complex interaction among the lipid molecules (constituting the cell membrane), and with a number of other macromolecules, such as proteins. It is also believed that the common biophysical processes essential for the functioning of a cell also play an important role in cellular morphogenesis. At the cellular scale—where typical dimensions are in the order of micrometers—the effects arising from the molecular scale can either be modeled as equilibrium or non-equilibrium processes. In this chapter, we discuss the dynamically triangulated Monte Carlo technique to model and simulate membrane morphologies at the cellular scale, which in turn can be used to investigate several questions related to shape regulation in cells. In particular, we focus on two specific problems within the framework of isotropic and anisotropic elasticity theories: namely, (i) the origin of complex, physiologically relevant, membrane shapes due to the interaction of the membrane with curvature remodeling proteins, and (ii) the genesis of steady state cellular shapes due to the action of non-equilibrium forces that are generated by the fission and fusion of transport vesicles and by the binding and unbinding of proteins from the parent membrane.
Keywords: self-assembly, cell membrane, lipid bilayer, continuum models, Helfrich Hamiltonian, triangulated surfaces, Monte Carlo, curvature remodeling, fission and fusion, detailed balance
1. Introduction
The cell membrane defines the physical boundary of a cell and its organelles. The major constituent of a cell membrane are lipids, which are amphipathic molecules that have a hydrophilic head part and a hydrophobic tail part. A cell membrane can contain one or many types of lipid molecules, with each being different from the other, either through the moieties that constitute the head group or due to differences in the length and saturation of the hydrocarbon chain or both. Eukaryotic and prokaryotic organisms have over 1000 types of lipid molecules [1], and these molecules can be broadly divided into three major classes—namely, glycerol-based lipids, cholesterol, and ceramide based sphingolipids 1. In addition to the lipid molecules, the cell membrane is also home to a number of other macromolecules such as proteins and sugars. While the concentration of membrane associated proteins (both transmembrane and peripheral proteins) can vary between 18% and 75% of the mass of the membrane, depending on the cell type, poly-saccharide molecules are found in lower concentrations, typically in the range of 3% – 10% [2]. These diverse components self assemble into a two dimensional sheet like structure called a membrane bilayer. By virtue of its dimensions (lateral dimensions are in microns while the thickness is approximately 5 – 10 nm), a membrane can effectively be thought of as a two dimensional surface embedded in three dimensional space. From a thermodynamic point of view, the lateral organization of the individual components in such heterogeneous mixtures can be quite complex [3]. The generally accepted model for the lateral organization of the constituents of a multi-component functional membrane is the fluid mosaic model [4], which describes cell membranes as “two-dimensional solutions of lipids and other macromolecules”.
A membrane is selectively permeable to various molecules and ions. As a result, the region encapsulated by the membrane sustains a chemical environment that is expressly different from the bulk. For instance, the extracellular region has a different chemical composition compared to the intracellular region, while the interior of a cell organelle is different from that of the cytoplasm. In spite of being a self assembled structure, the cell membrane is a strong and highly flexible material. It deforms in response to the various stresses caused by the biochemical and biomechanical activities of its constituents and also due to its interactions with other macromolecules in the cell 2. The attributes of semi permeability and flexibility are the key factors that make the cell membrane to effectively function as a barrier. In addition to its primary role as a barrier it is also known to play active roles in mediating a number of biological processes that include endocytosis, exocytosis, cell motility and cell signaling.
Though cell membranes define the boundary of all cells and also of their organelles, the shapes of these interfaces differ from cell to cell and also between organelles within the same cell. These variations can be as diverse as the simple quasi-spherical shape of the plasma membrane to the complex cisternae structure of the golgi. An long standing question in cell biology is “how the morphogenesis of cellular shapes is determined by the molecular organization of the membrane constituents and by the various biophysical processes impacting the membrane? [5, 6]” Purely, from a physical point of view, one may ask a related but perhaps simpler question: “what are the minimal set of parameters required to explain the shapes of cell and cell organelles?” In this chapter, we describe a thermodynamics based computational model for cell membranes and discuss two specific biophysical processes which possibly impact cellular morphogenesis. Specifically, we evaluate (a) the role of protein induced membrane remodeling, and (b) the role of curvature fluctuations caused by the binding-unbinding kinetics of membrane associated proteins and the fission-fusion dynamics of transport vesicles, in regulating cell membrane shapes. While the former is treated as an equilibrium process, where the energetics of the individual components and their cooperativity determine the membrane structure, the latter is treated to be a non-equilibrium phenomenon, in which the observed steady state membrane shapes also depend on the forcing statistics of the active processes.
This chapter is organized as follows. We introduce the elasticity based Canham-Helfrich framework for cellular membranes in Sec. 2, following which in Sec. 3 we give a brief description of the two biophysical processes of interest, namely protein induced membrane curvature and curvature fluctuations due to active binding/unbinding kinetics of proteins and vesicles. We incorporate the biological details in Sec. 4 where we first present the nematic membrane model from a purely equilibrium perspective and discuss its conformational space as a function of protein curvature, concentration and organization. In this section, we also present a thermodynamic integration based method to computationally delineate the free energy landscape of the nematic membrane. The active membrane model, that incorporates non-equilibrium curvature fluctuations, is discussed in Sec. 5, where we show how steady state membrane structures similar to that of the endoplasmic reticulum (ER) and the golgi emerge naturally from our model.
2. Phenomenological theories for membranes
Similar to the length scales in a membrane, the time scales associated with various membrane related biochemical and biophysical processes also extend over a wide range. The presence of such disparate scales provides a major challenge in the experimental investigations of cell membranes. Based on the spatial and temporal resolution of the observed problems, experimental observations can be classified into two broad classes, namely (i) biochemical and (ii) biophysical. In case of the former the focus is to elucidate the chemical details of the system using biochemical tools while the latter aims to generalize the observed phenomenon in terms a minimal number of parameters using a framework drawn mostly from mechanics and thermodynamics. Multiscale approaches are required to establish how the chemistry of the membrane, given in terms of say the lipid and protein compositions, is linked to the various thermodynamic observables that describes it in biophysical experiments. Development of specialized techniques to rigorously bridge the information obtained at various length and time scales is still an ongoing area of research [7–13]. Such bridging techniques are not only useful in the study of membranes but have a wider range of applications in a number of other systems that are categorized as soft matter.
Theoretical and computational modeling can be used as alternative tools to study cell membranes under controlled conditions. They provide a framework to validate experimental findings and can also predict new paradigms that can be verified in future experiments. Owing to the multiscale nature of the problem, as in the case of experiments, theoretical models can also span multiple scales with varying resolutions. All atom and coarse-grained models have atomic resolution and are faithful to the underlying chemistry but are limited by the size of the system that can be investigated. In spite of the advent of faster computer processors and efficient algorithms, membrane system sizes amenable for molecular simulations at present can only go upto a few hundred nm [14]. A simple estimate shows that the total number of atoms, inclusive of both lipids and water, involved in a molecular simulation of a micron sized vesicular membrane is of the order of 1011, which makes the use of molecular models as an all purpose tool computationally infeasible at the present time. The involved number of degrees of freedom is an over representation of the membrane if one is only interested in studying its physical properties at length and time scales separated from and larger than the atomistic scales. To overcome this limitation, coarse grained and thermodynamics based phenomenological models can be used. These models are more suited to study the physical aspects of biological membranes and do not retain the chemical specificity of the underlying membrane constituents —instead, the chemistry is reflected in the choice of the parameters used to characterize the model. Details of the various coarse-grained methods can be found in a number of reviews on this topic [15–21]. In this chapter, we will focus on the elasticity based thermodynamic model for the membrane.
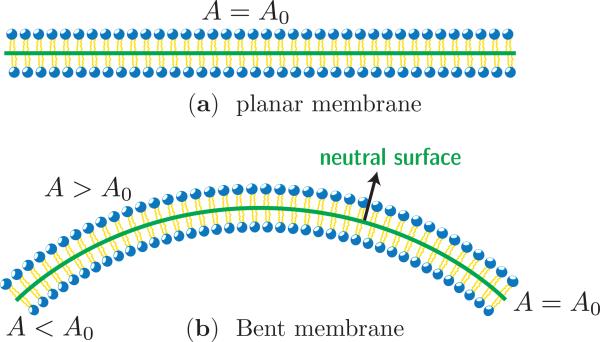
Consider the flat lipid bilayer membrane shown in Fig. 1(a). It can be characterized using three distinct surfaces: (a) the upper monolayer, (b) the lower monolayer, and (c) the mid plane of the bilayer. When the membrane is in its undeformed state all the three surfaces have the same surface area, say A0 for the membrane in Fig. 1(a). Upon bending, the upper monolayer is compressed (with area A < A0) and the inner monolayer is stretched (with area A > A0) while the area of the mid-plane, or in general a neutral surface, remains unchanged, as shown in Fig. 1(b). That is the surface whose area remains constant even in the deformed state is called the neutral surface. Due to the poor solubility of lipids in the surrounding solvent and the slow rate of its flip flop between the monolayers, the number of lipids in a given monolayer of a membrane is nearly constant. Furthermore, the lateral extent of the membrane—for instance the diameter of a vesicle—is large compared to the bilayer thickness . In this limit, a lipid bilayer can be represented as a thin, flexible sheet of constant area; here the sheet is representative of the neutral surface of the bilayer and its shape is governed by the elastic energy given by:
| (1) |
Figure 1.
(a) Cross sectional view of a flat membrane, with surface area A0. (b) When bent, the flat membrane shows stretching (A > A0) in the top monolayer and compression (A < A0) in the bottom monolayer. The neutral surface is the plane in the bent membrane with nearly constant surface area (A = A0). The neutral surfaces in the flat and bent membranes are shown as solid lines.
Here S denotes the surface of the membrane, and H and G are respectively the mean and Gaussian curvature of the membrane. κ is the bending modulus and κG is the deviatoric bending modulus. Various methods to derive this equation can be found in some recent review articles [21, 22]. Since the membrane is a self-assembled system, i.e the relevant energies are comparable to thermal energy , the conformations of a membrane is also governed by thermal fluctuations. Experimental measurements on a wide class of lipid membranes estimate the value of κ to be in the range of 10 – 100kBT, which is roughly three order of magnitude smaller than that for conventional solids. In general, any material with smaller energy density is susceptible to thermal fluctuations and falls into the category of soft matter. The energy functional in eqn. (1) can only capture the bending modes of the surface since it assumes the neutral surface to be incompressible.
However, the morphology of a cell membrane can also be affected by in-plane strains that alter its surface area. These modes can be captured within the thermodynamic framework by coupling the membrane area to its thermodynamic conjugates namely the surface tension, σ, and the area elasticity modulus, . Furthermore, in the case of closed vesicles, an osmotic pressure difference (Δp) between the inside and outside of a vesicle can also drive shape changes. Taking these various contributions into account, eqn. (1) can be written in a more general form, as given by Canham [23] and Helfrich [24] as,
| (2) |
Here, A0 denotes the equilibrium area of the membrane. The geometry of the lipids can impose a preferred equilibrium curvature on the membrane, which is also captured by this energy functional through the local spontaneous curvature H0; more details on the exact form of the spontaneous curvature is given in the next section. The integral in the first term is performed over the entire surface of the membrane1, and the integration in the second term is carried out over the volume (V) enclosed by the surface. The membrane model given in eqn. (2) has been extensively studied in a number of contexts. Details of the various theoretical methods has been described in a number of reviews on this topic [21, 22, 25]. While the analytical methods based on eqn. (2) can be used to study smooth, symmetric membrane shapes they have limited applicability in the study of arbitrary membrane morphologies. Computational methods derived from eqn. (2), on the other hand, can overcome this limitation and hence can be used as generic tools to model cell membranes in the macroscopic scale. Here, we introduce one such computational technique based on the triangulated surface model for two dimensional surfaces and the energy of the triangulated mesh is given by a discretized form of eqn. (2).
Triangulated surfaces as models for membranes
A two dimensional surface like that of a membrane can be discretized into a triangulated surface, which is constituted of T interconnected triangles (faces) intersecting at N vertices (nodes). The position vectors of the N vertices are and denotes the triangulation map. The triangles further define L independent links (edges). The topology of any surface is defined by its Euler characteristics, χ = 2(1 – g) – h [26], where g and h are the number of handles and holes in the surface. For instance, g = 0 for a sphere and g = 1 for a torus, with corresponding Euler characteristic χ = 2 and χ = 0 respectively. In the triangulated surface model, the number of faces, nodes and edges together define the topology of the surface as χ = N + T – L. We limit our discussion to membranes of spherical topology (χ = 2), which is highly relevant to membranes in cells and cell organelles. For fixed topologies, by virtue of the Gauss-Bonnett theorem [26], the deviatoric energy (∫ dS κGG) is a constant and hence will be ignored for the rest of the chapter. The discrete form of the elastic Hamiltonian is thus a sum over the curvature energies at every vertex in the triangulated surface given by,
| (3) |
In the above discretization, the index v denotes a vertex on the triangulated surface and c1,v and c2,v are respectively its principal curvatures, H0,v is the local spontaneous curvature, and Av denotes the surface area associated with the vertex. We follow the method described in Ramakrishnan et. al. [27] to compute surface quantifiers on the triangulated surface. In general, the value of the spontaneous curvature at a vertex is determined as,
| (4) |
where C0 denotes the magnitude of the induced curvature and denotes the functional form of the contribution of the curvature contribution at vertex v′ due to a curvature field at vertex v; see references [21, 28–31] for various forms of in different contexts.
In order to simulate self-avoiding membranes all the vertices on the triangulated surface are subjected to additional self intersecting constraints. If each vertex is treated as a hard core bead of diameter a0 the interaction between any two beads, whose centers are away by r, is hard sphere like and has the form,
| (5) |
This form of the potential defines a lower cutoff for r while the maximum separation of the beads is unconstrained, which can lead to violation of self avoidance. Taking cue from polymer simulations, we solve this problem by treating the edge as a tether whose maximum length is . Hence the condition for self avoidance, in terms of the edge (tether) length , is given by 1. It should be kept in mind that this choice of the self avoidance cutoff endows the system with an implicit area compressibility modulus .
The equilibrium properties of the triangulated surface, i.e of the membrane, is computed by analyzing the total partition function,
| (6) |
The temperature of the system is expressed in units of β = 1/kBT and the integral is carried over all vertex positions and summed over all possible triangulations. A tuple, , represents one particular state of the membrane in its conformational space and the equilibrium state of the system is determined by sampling the various states {η} using Monte Carlo techniques. In our Monte Carlo (MC) studies, a change in state, η → η′, is effected by means of Monte Carlo moves, the rules of which corresponds to importance sampling [32]. The time, in MC simulations, is expressed in units of Monte Carlo steps(MCS).
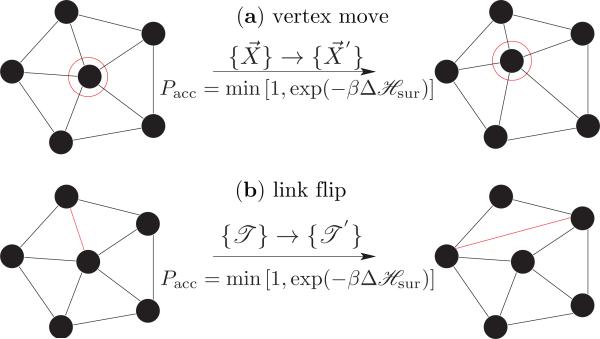
A membrane quenched to a particular thermodynamic state (η) relaxes to its equilibrium conformation, defined by eqn. (3), mainly through thermal fluctuations and in-plane diffusion. A Monte Carlo step captures these modes by performing N attempts to displace a randomly chosen vertex and L attempts to flip a randomly chosen link, as in Fig. 2. N and L are, respectively, the number of vertices and links that constitutes the triangulated surface. The rules of importance sampling and details of each move are as follows:
Figure 2.
Monte Carlo moves involved in equilibrium simulations of a fluid random surface. (a) vertex move emulates thermal fluctuations in the membrane and (b) link flip simulates its fluidity.
(a) Vertex move
The vertex positions of the surface are updated, , by displacing a randomly chosen vertex within a cube of side 2ν around it, with fixed triangulation . As a result, the old configuration of the membrane is updated to a new configuration . The total probability of this MC move obeys the detailed balance condition given by,
| (7) |
Here, P(η) denotes the probability of being in state η. Choosing the attempt probability for forward ω(η → η′) and backward ω(η′ → η) to be equal, i.e., ω(η → η′) = ω(η′ → η) = (8ν3 N)–1, we get the probability of acceptance as
| (8) |
which is the well known Metropolis scheme [33]. The value of ν is chosen appropriately so that the acceptance of vertex moves is close to 50%; this choice results in ν = 0.1 for a system with a0 = 1. It should also be noted that the value of ν depends on bounds on the edge length and it can also modified during runtime by analyzing the acceptance rates at pre-defined intervals.
(b) Link flips
An edge shared between two triangles is flipped to link the previously unconnected vertices of the triangles. Such a move changes the triangulation map from , in the process of which it changes the neighborhood of some vertices, which is effectively a diffusion move. With fixed vertex positions, the old and new configurations in this case are and , respectively. The attempt probability for flipping a link is given by ω(η → η′) = ω(η′ → η) = (L)–1 and the acceptance probability is given by eqn. (8).
3. Membrane remodeling events as equilibrium and non-equilibrium processes
The cell membrane is a dynamic entity. Its surface is continuously remodeled in order to generate ancillary membrane structures, like vesicles1, tubules, and invaginations, that are vital to the functioning of the cell. These ancillary structures are known to drive and also mediate a number of biological processes. For example, vesicular structures are commonly seen as the agents of membrane trafficking since the processes of endocytosis and exocytosis involve the formation and release of cargo loaded transport vesicles, with typical sizes in the range 50-100 nm. The formation of one such vesicle requires approximately 500kBT of energy: this is the bending contribution computed using eqn. (2) for a membrane with bending stiffness κ = 20kBT. Despite being a soft material (see section 2) a membrane cannot spontaneously form such structures merely through thermal fluctuations because the large activation energy will result in very long timescales for spontaneous events. Hence, specialized mechanisms should be invoked to explain how the cell overcomes these large energy barriers and remodel their surface.
Many of these mechanisms can be understood from a purely equilibrium perspective, in that the conformational properties of the cell membrane can be explained by balancing and minimizing the various energy contributions. On the other hand, a number of others are driven processes, in that they consume energy normally through the hydrolysis of ATP or GTP, and hence a non-equilibrium framework is required to discern such systems. The observed properties of the cell membrane is a result of the interplay between the various equilibrium and non-equilibrium forces acting simultaneously on its surface. On the modeling front, these additional membrane reshaping contributions can be represented either explicitly or implicitly. In this chapter, we follow an implicit approach wherein these contributions are recast as spontaneous curvature fields, which were defined in the elastic energy formalism for the membrane given in eqn. (2). Before we proceed to the description of the model it is important to understand that the framework presented here is generic and can be used in a wide range of scenarios. We have chosen to present two class of membrane remodeling problems: (i) protein-induced membrane remodeling as an example for equilibrium processes and (ii) active curvature fluctuations due to fission/fusion of vesicles and binding/unbinding kinetics of proteins as an example for non equilibrium processes.
It has been known [34–47] that membrane associated proteins—BAR domains [48–51], ENTH domains [35, 52–54], Exo70 domains [55] and dynamin [56] to name a few—are primary drivers of cellular remodeling. In addition to the various in vivo assays that establish the role of these proteins, the hypotheses of protein-induced remodeling has also been backed by in vitro observations: an otherwise spherical liposome spontaneously tubulates or vesiculates or invaginates when large concentrations of these protein(s) are introduced into the system [52, 55, 56]. The curvature remodeling aspect of these proteins has also been established using all atom and coarse grained computer simulations [55, 57–63].
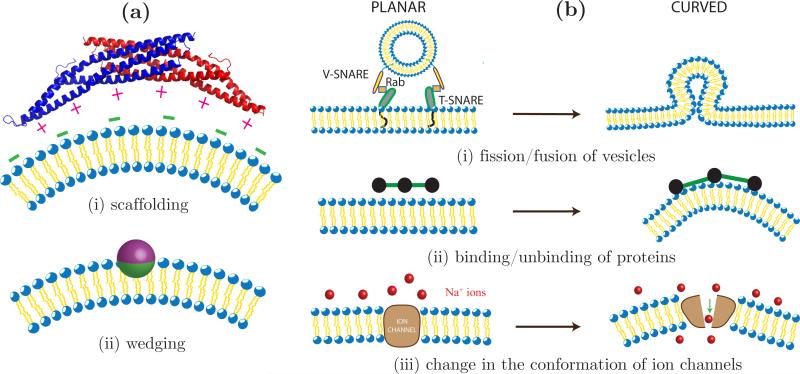
It has been shown that the membrane proteins1 induce curvature either by virtue of their intrinsic geometry or by virtue of their affinity for the membrane microenvironment. The former, called the scaffolding mechanism, is depicted in Fig. 3(a)(i) for the case of a classical Bin/Amphiphysin/Rvs (BAR) domain in which most of the positively charged residues are found on the concave, membrane facing domain [48]. These charged residues have a high affinity for anionic lipids like phosphatidylserine, phosphatidylglycerol, phosphatidic acid and phosphatidylinositol and hence the protein prefers to bind to membrane regions with high concentrations of negatively charged lipids. It is believed that the binding energy of a BAR domain bound to the surface of a membrane is a function of the anionic lipid concentration, protein concentration and membrane stiffness1. The strong electrostatic interactions between the charged residues and lipids deforms the membrane in the vicinity of the protein leading to the formation of a spontaneous curvature as shown in Fig. 3(a)(i). An alternate mechanism by which proteins can induce spontaneous curvature is shown in Fig. 3(a)(ii) wherein a protein asymmetrically buries some of its hydrophobic residues into a monolayer in the membrane. Such an insertion imposes a stress on the monolayer and as a result the whole membrane spontaneously curves at the site of insertion (see [21] for details).
Figure 3.
Equilibrium and non equilibrium processes that remodel membrane curvature. (a) Shown on the left are illustrations of (i) the scaffolding mechanism: a dimer of the classical BAR domain interacts with negatively charged lipids on the membrane, through its positively charged membrane facing residues and (ii) the spontaneous curvature induced by the asymmetric insertion of a protein. (b) Curvature fluctuations in a planar membrane due to (i) fission and fusion of transport vesicles, (ii) binding and unbinding kinetics of membrane associated proteins and (iii) change in the conformation of ion channels.
In order to model how protein induced deformations at the molecular scale affect the conformations of the cell membrane at the cellular scale, it is essential to measure the spontaneous curvature induced by a protein, i.e to measure H0(X), where X denotes the parameterization of the membrane. Experimentally, spontaneous curvature of a protein can be back calculated from the geometry of the remodeled shape, if the protein concentration is known. As an alternate, all atom and coarse grained model can be used to probe the curvature profile at the level of single proteins [13, 20, 55, 57–60, 64]. In general, the curvature profile of most proteins falls under two classes: (a) isotropic and (b) anisotropic. The details of the various formulations can be found in a recent review on this topic [21].
There are a number of cases where the equilibrium framework cannot explain the origin and stability of cell organelle shapes. A case in point being the highly curved cisternae shape of the golgi complex. It is known that a number of curvature remodeling/sensing proteins like Amphiphysins, Endophilins, ARFaptins and ENTH and ANTH domain containing proteins are associated with the membrane of the golgi [65]. Hence it is logical to assume that the sac like structures in the golgi are a result of the membrane sculpting action of these proteins. However, it should be remembered that the golgi is subjected to a continuous flux of transport vesicles due to the retrograde and anterograde trafficking of vesicles from and to the endoplasmic reticulum(ER). The cisternae structure shows an instability on inhibition of this flux: it fragments into spherical and tubular vesicles when the trafficking events are inhibited by addition of Brefeldin A [66] or depletion of ATP [67, 68] or removal of coat protein COPI in the ER [69] or drug induced disruption of microtubules [66, 70] or depletion of PC lipids [71]. Such an instability has also been observed in the telophase of the cell cycle, where normal cellular functions including vesicular traffic are absent [72]. These observations pose two very interesting questions: (i) how does a membrane mediated event, like the vesicular transport, control the morphogenesis of cell organelles and (ii) do the curvature remodeling proteins induce curvature or merely sense and stabilize the curvature generated by other biophysical events? [5, 6] Hence, it is very important to built a framework where the influence of dynamical remodeling processes on membrane morphology can also be assessed.
Spontaneous membrane deformation induced by a dynamical process is in turn coupled to the rates of the process and hence should be treated as a fluctuating quantity, i.e H0 = H0(X, t). This is expressly different from the case of protein induced remodeling where the number of curvactants is held constant during the analysis. The presence of curvature fluctuations can significantly alter the morphology of the cell membrane. In order to construct a physical model for dynamic remodeling, within the framework described in Sec. 2, it is important to recast the problem in terms of spontaneous curvatures. A simplified view of vesicular trafficking is shown in Fig. 3(b)(i). An inbound transport vesicle binds to a cell/organelle membrane through the interactions of the vesicle bound V-SNAREs with the target membrane bound T-SNAREs, with the Rab proteins as an intermediary [73]. Following this docking event, the vesicle fuses into the target membrane and generates a high curvature region, as shown in the right panel of Fig. 3(b)(i). Similarly, the formation of outbound vesicles can be seen as the reverse of vesicle fusion, where a high curvature region, formed by the assembly of coat proteins, fissions off from the parent vesicle leading to a reduction in the membrane curvature. At the cellular scale, the fusion and fission of transport vesicles can be viewed as spontaneous curvature fluctuations on the surface of the parent membrane. Since the curvature is generated and removed with the aid of additional protein machineries these curvature fluctuations should be treated as non-equilibrium processes. In addition to vesicular trafficking, dynamic membrane remodeling is also observed in a number of other cellular processes. Fig. 3(b)(ii) shows how the membrane curvature fluctuates between a planar and curved state when a curvature remodeling protein alternates between the cytoplasm and the membrane microenvironment. The recruitment of membrane bound proteins can be biophysically regulated by curvature [74] or biochemically regulated by specialized lipids such as phosphoinositides [75]. These phosphoinositides themselves are regulated spatiotemporally through kinetic mechanisms in the cell via phosphoinositide metabolism [76]. Membrane embedded ion channels are yet another source of fluctuating curvatures and indeed to complicate the scenario, some of the channel proteins also have curvature sensing abilities [77]. As shown in Fig. 3(b)(iii), for the case of sodium channels, a conformational change of the channel protein from a closed to open state leads to a spontaneous deformation in the membrane. The three examples used here exemplifies the underlying idea of dynamic membrane remodeling but there can be a number of other such contributions that should be considered depending on the problem.
In this section, we have described in detail two key classes of membrane remodeling factors that should be considered when studying membrane morphological transitions. In Sec. 4, we describe the nematic membrane model where the protein induced curvature is treated as an in-plane nematic field and show how the cooperative behaviour of these fields can sculpt complex membrane geometries. Appropriate models to study dynamic remodeling and curvature fluctuations are introduced in Sec. 5 and we demonstrate how flattened sacs and tubules are steady state structures in this model.
4. Nematic membrane model for protein driven membrane remodeling
In a membrane model at the meso- and macroscopic length scales (> 100 nm), the curvature induced by an inclusion on the membrane, like a protein or a nanoparticle, can be captured either through the explicit representation of the inclusion [78–81] or through an implicit representation in terms of its spontaneous curvature field, as done in this chapter. Such an approach requires apriori knowledge of the curvature profile induced by a single protein or by a cluster of proteins, depending upon the characteristic length scales used in the model. The curvature profile can either be determined from experiments, as was described in Sec. 3, or can be estimated using high resolution all atom or coarse grained molecular simulations [20]. In general, the spontaneous curvature profile given by H0(X) can either be isotropic or anisotropic. Examples for the former include curvature fields induced by ENTH domains and a spherical nanoparticle adhering to the membrane surface while curvatures induced by proteins like BAR domains and Exo70 fall into the latter class. The cooperative behavior of isotropic curvactants at the macroscopic scale can be studied within the confines of isotropic elasticity, i.e. using eqn. (2). Details of the formulation and the simulation techniques, including methods to characterize the isotropic curvature field for ENTH domains, can be found in references [13, 21, 30, 31, 82], and these methods are equally applicable to non-isotropic curvactants. In this section, we present an alternative treatment for anisotropic-curvature inducing proteins by treating the spontaneous curvature as an in-plane nematic field. In other words, we set H0,v = 0, ∀v, in eqn. (3) and capture the effect of the protein-membrane interactions through an additional anisotropic elastic Hamiltonian.
It has been recognized for long that cell membranes are inherently anisotropic due to the presence of a number of intrinsic and extrinsic factors like lipid tilt, chirality, anisotropy in the lipid head groups and membrane inclusions [83–89]. Anisotropic elasticity based theoretical models could explain the emergence of complex membrane geometries like tubules [85, 90–94], sponges and egg-cartons [85, 95, 96]. It was first recognized by Iglic̆ and coworkers [97] that the anisotropic elasticity framework can be used to model the curvature modulating effects of membrane associated proteins. Based on this model, they were able to demonstrate that cell membranes can spontaneously tubulate when rod like protein inclusions, which preferentially curve the membrane along the direction of their long axes, are attached to the outer surface of the membrane. Here, we adopt the anisotropic elasticity model proposed by Frank and Kardar [89] to model the cooperative behaviour of membrane proteins and investigate their role in sculpting membranes.
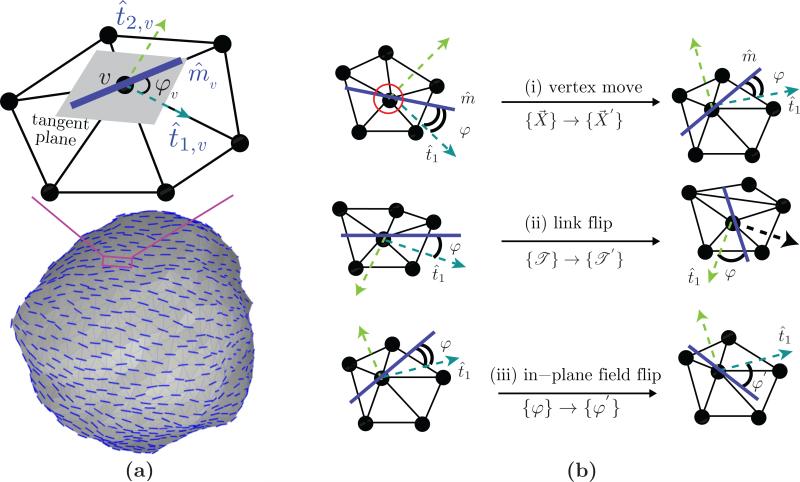
The nematic membrane model starts with the definition of the in-plane nematic field m̂: it is the average orientation of all curvature remodeling proteins on a patch of the membrane. In the case of the triangulated surface model, introduced in Sec. 2, the size of this patch is determined from the area associated with a vertex v, i.e. it depends on the value of a0 in eqn. (5). For computational purposes, a nematic field at vertex v of the triangulated membrane surface is represented as
| (9) |
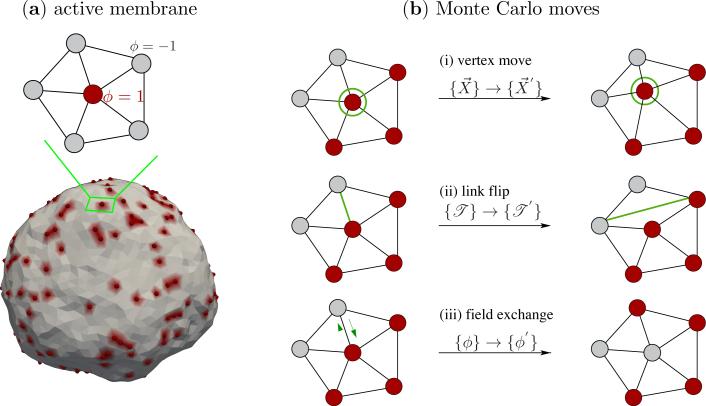
Here, we have used the Darboux gauge [26] which consists of the two principal directions t̂1,v and t̂2,v and the normal direction n̂v —methods to compute the Darboux frame on triangulated surfaces can be found in reference [27]. The nematic field is confined to the tangent plane by setting cv = 0 and unit magnitude is imposed by setting . The coefficient av = cosφv, where φv is the angle between the nematic field m̂v and the maximally curved direction t̂1,v. An illustration of the in-plane nematic field at a vertex along with a snapshot of a membrane surface with nematic field at all vertices is shown in Fig. 4(a). The Monte Carlo moves for a membrane in the presence of a nematic field is shown in Fig. 4(b). Moves (i) and (ii) in Fig. 4(b) are similar to the Monte Carlo moves shown in Fig. 2. In the course of these moves the additional degree of freedom due to the orientations of the in-plane nematic field {φ} is held fixed relative to the principal direction t̂1. The third type of Monte Carlo move (move (iii) in Fig. 4(b)) is designed to sample the conformational space defined by the nematic orientational order: the angle subtended by the nematic field {φ} is randomly perturbed to a new orientation {φ′} and the move is accepted using the Metropolis scheme.
Figure 4.
(a) Illustration of a nematic in-plane field on a patch of the triangulated surface. The unit field m̂v is defined on the tangent plane at vertex v and it subtends an angle ϕv with the maximum curved direction t̂1,v. The three sets of Monte Carlo moves are shown in panel (b). The field orientation φ is preserved during (i) a vertex move (i) and (ii) a link flip while the position and triangulation of the surface is preserved when φ → φ′ as in (iii).
We define the protein concentration through an additional variable ϕv which is defined at every vertex v of the triangulated surface, and it takes a value of ±1; a site with a protein corresponds to +1 and one without the protein corresponds to –1. The total number of proteins on the membrane is defined as,
| (10) |
For example, a membrane with proteins at every site has a value of ϕA = N, where N is the number of vertices on the triangulated surface. The nematic in-plane field, which is representative of a curvature inducing protein, interacts with the membrane in an anisotropic manner and in our model this interaction is given by,
| (11) |
In eqn. (11), we define the elastic parameters on each vertex v as , , and . Here, and are the spontaneous curvatures induced by the nematic field m̂v (i.e. the protein) along the directions parallel and perpendicular to its orientation. While, the gauge invariant measures and are respectively the directional curvatures on the membrane parallel and perpendicular to m̂v. Using the Euler's theorem for directional curvatures [21, 26] and the definition of the principal curvatures given in eqn. (3) it can be shown that and . Furthermore, the presence of the protein also modulates the elasticity of the membrane-protein system [97] and this effect is included into eqn. (11) through the directional bending stiffnesses κ∥ and κ⊥ with their values ≥ 0. For simplicity, we have set κ⊥ = 0 in all the studies presented here.
The simultaneous expression of multiple proteins on the membrane can lead to explicit interactions between the proteins. In the nematic membrane, we model this self interaction as a nematic ordering potential and an aggregation potential, where an in-plane field m̂v interacts with all its neighbours m̂v′ through
| (12) |
The first term represents an orientational interaction and denotes the one constant approximation of the Frank's free energy for liquid crystals [98] and is known the Lebwohl-Lasher potential [99] with εLL being the interaction strength. The second term is the familiar Ising potential which can be tuned to promote the explicit aggregation of the proteins, with J being the exchange interaction strength. The first summation is carried over all the vertices of the surface while the second summation is over all neighbours of v. θvv′ is the difference in the orientations of fields m̂v and m̂v′ with respect to the geodesic that connects them—see Ramakrishnan et. al. [27] for details. In the remainder of this section, we will explore the the role of the various model parameters that contribute to the onset and stability of membrane shapes. The total energy that governs the equilibrium behavior of the nematic-membrane system is then given by
| (13) |
We discuss the phenomenon of how proteins collectively remodel a membrane from two viewpoints: (a) as a result of variations in the elastic moduli that characterize the protein and the membrane, and (b) as a result of the lateral organization and patterning of the nematic field on the membrane.
4.1. Role of the various elastic moduli
The interactions between the lipids and proteins at the molecular scale is a key determinant of the strength of the elastic moduli. The nematic membrane model displays a diverse spectrum of conformations in response to variations in the values of these elastic moduli.
Fig. 5 shows the equilibrium shapes of a fully decorated nematic membrane (ϕA = N) when the anisotropic stiffness (κ∥) is varied from 0 to 5 kBT, with the rest of the parameters fixed to be εLL = 3kBT, J = 0, and κ = 10kBT. When κ∥ = 0 (Fig. 5(a)) the membrane does not respond to the spontaneous curvature induced by the nematic field, i.e. , and as a result its conformation remains quasi-spherical. However, at non-zero values of κ∥ the nematic-membrane interactions collectively remodel the membrane into long tubules as in Fig. 5(b) for κ∥ = 2.5 kBT. With further increase in κ∥, the tubular membrane branches out into a number of short, narrow structures that are connected through a neck like region as can be seen from the snapshot in Fig. 5(c) for κ∥ = 5kBT. While the spontaneous curvature is a measure of the binding affinity of the protein-membrane system, the parameter κ∥ is measure of the fluctuations in : it is small when κ∥ is large and vice versa. The transition from spherical to tubular structures as a function of κ∥ indicates that in order to achieve effective remodeling the spontaneous curvature induced by a protein should be minimally susceptible to fluctuations in its microenvironment.
Figure 5.
Membrane conformations for κ∥=0, 2.5 and 5kBT for a nematic membrane with ϕA = N, εLL = 3kBT, J = 0, and κ = 10kBT. The membrane remains quasi-spherical when κ∥ = 0 (a), which remodels into tubules when κ∥ = 2.5 (b), which then branches out into multiple tubules when κ∥ = 5 (c).
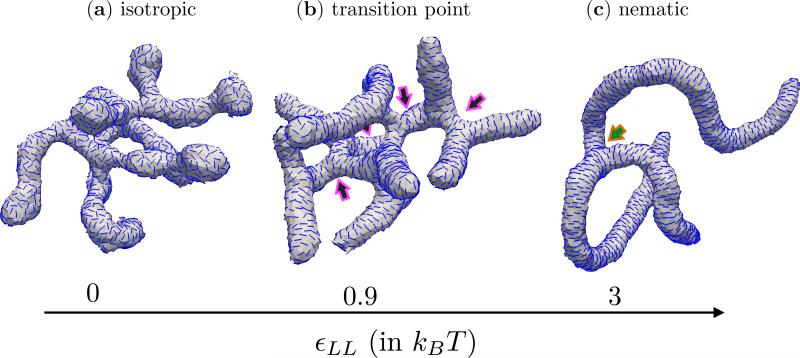
The equilibrium state of the nematic membrane is also influenced by the orientational order in the texture of the in-plane field which is determined by εLL introduced in eqn. (12). The nematic field in our model undergoes an isotropic to nematic transition when εLL ~ 0.89 [99]. In Fig. 6, we have shown the equilibrium configurations of a nematic membrane, with ϕA = N, J = 0, , κ∥ = 5kBT and κ = 10kBT, at three different states of the nematic field. These states correspond to (i) the isotropic phase for εLL = 0 (Fig. 6(a)), (ii) in the vicinity of the transition for εLL = 0.9kBT (Fig. 6(b)) and (iii) the nematic phase for εLL = 3kBT (Fig. 6(c)). Though the underlying membrane conformations for all the three cases are tubular and branched, there are some characteristic features that differentiate these shapes. The first being the orientational order in the in-plane field: the nematics are in an isotropic phase when εLL = 0, i.e. they have random orientations, while they are aligned along a common director when εLL >= 0.89. Another major difference is in the number of neck like structures which is the branching point for the tubules—in Fig. 6 an arrow points to the location of a neck. We observe that the number of necks decreases with an increase in the value of εLL, pointing to the fact that branching is unfavourable when the protein-protein orientational interactions are strong. In case of a fully decorated membrane the nematic texture at the neck region consists of two disclinations, each with a defect charge of –1/2, while the spherical cap at the end of a tubule consists of two +1/2 disclinations. The observed reduction in the number of branches with increase in εLL can be explained based on the energy cost to generate these defects. We refer the interested reader to the relevant discussions on this topic in references [100–105]. The presence of orientational order and the emergence of branched tubules has been recently demonstrated for the case of N-BAR domain proteins [63].
Figure 6.
Tubular membrane structures as a function of the texture of the in-plane nematic field. Shown are (a) the isotropic phase when εLL = 0, (b) in the vicinity of the isotropic-nematic transition when εLL = 0.9kBT and (c) the nematic phase when εLL = 3kBT. The arrows mark the location of the necks from which the branched structures emanate. All data correspond to a fully decorated nematic membrane with J = 0, , κ∥ = 5kBT and κ = 10kBT.
The spontaneous curvature induced by various classes of proteins vary both in their magnitude and direction—in our description, a protein attached to the extracellular side of the cell membrane is said to induce a positive curvature if it curves the membrane into the extracellular side and vice versa.
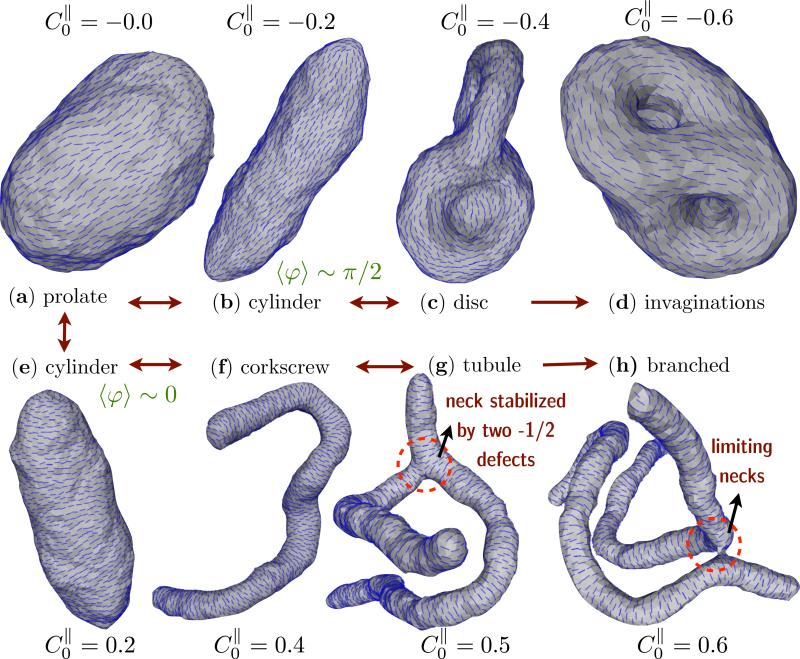
When the in-plane field is in the nematic phase (we set εLL = 3kBT), the nematic membrane model predicts a diverse spectrum of membrane shapes as a function of the anisotropic spontaneous curvature . In Fig. 7, we display the representative equilibrium shapes for values of in the range –0.6 to 0.6. The equilibrium shape of a fully decorated nematic membrane for the case of is a prolate, as in Fig. 7(a), instead of being quasi-spherical as in the case of membranes without nematic field 1. Non zero values of stabilize many shapes ubiquitous in the cell: like tubes (–0.3 to 0.3), corkscrew (0.35 to 0.5), branched shapes (> 0.5), discs (–0.35 to –0.55) and invaginations or caveola (< –0.55). It should be noted that, when the magnitude of is small both positive and negative spontaneous curvatures can stabilize cigar like or cylindrical membrane structures, as shown in Figs. 7(b) and (e) for and 0.2 respectively. A close inspection of the nematic texture reveals the subtle difference in the shapes wherein the average nematic orientation is along the maximally curved direction (〈φ〉 ~ 0) for and is along the minimally curved direction (〈φ〉 ~ π/2) when .
Figure 7.
Membrane conformations as a function of for a nematic membrane with ϕA = N, J = 0, κ∥ = 5kBT and κ = 10kBT. The membrane stabilizes a prolate like shape when (a) which remodels into cylinders (b), discs (c) and invaginations (d) for , and –0.6. Similarly, for positive values of the spontaneous curvature and > 0.5 the observed shapes correspond to cylinder (e), corkscrew (f), branched tubules (g and h). The shapes correspond to a membrane with ϕA = N, J = 0, εLL = 3kBT, κ∥ = 5kBT and κ = 10kBT.
In summary, the spontaneous curvature induced by a protein is the key driver of shape transformations in membrane. In spite of its simplicity, the nematic membrane model predicts the conformational space for the entire repertoire of membrane shapes reported in the literature, especially in experimental studies on protein assisted shape transformation of cellular or model membranes (see references [35, 41, 43, 55, 109]).
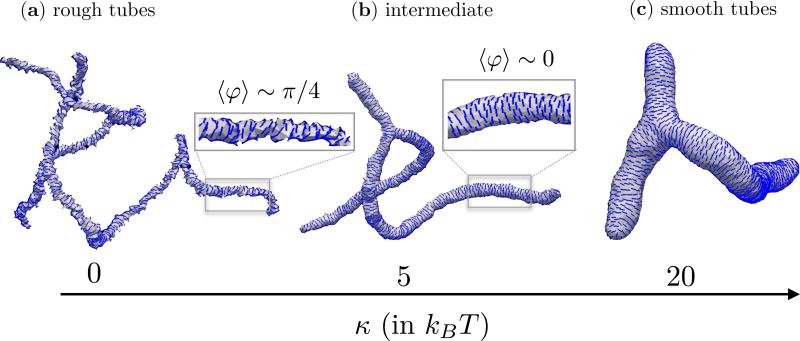
So far we had investigated the role of the various elastic moduli that characterize the proteins and their interactions with the membrane. In addition to κ∥, and εLL, the elasticity of the underlying cell membrane also plays a definitive role in determining the nature of the emergent conformations. The effect of the bending rigidity κ on the equilibrium shapes of a nematic membrane, with ϕA = N, J = 0, εLL = 3kBT, κ∥ = 5kBT and , is shown in Fig. 8. In the absence of the in-plane nematic field, tubular, branched geometries have been shown to be the equilibrium state of a flexible membrane (κ = 0) [110, 111]. This natural state does persist for a nematic membrane with κ = 0 (Fig. 8(a)) but the presence of an orientational order reduces the degree of branching, for similar reasons given in the discussions on Fig. 6. The radius of the tubular region is set by the values of κ, and κ∥ and it has been shown in Ramakrishnan et. al [105] that it follows the relation,
| (14) |
The membrane conformations shown in Figs. 8(b) and (c), for κ = 5kBT and κ = 20kBT, follow this relation as evidenced by the decrease in the tube length as the membrane becomes stiffer. The change in bending rigidity also modulates the nematic texture as seen in the insets to Figs. 8(a) and (b). In case of stiff membranes, the in-plane field orients along the maximally curved direction (〈φ〉 ~ 0), as expected. However, when the membrane is flexible the tubular region is highly constricted (i.e. one or both of its principal curvatures are larger than ) and as a result the system minimizes through modulations in the orientational degree of freedom—this is shown in Fig. 8(a) for κ = 0, where 〈φ〉 ~ π/4. See reference [102] for a detailed discussion on this topic.
Figure 8.
Shapes of a membrane with ordered in-plane field for three value of the bending rigidity, κ = 0 (a), 5kBT (b) and 20kBT (c). The inset to (a) and (b) shows the nematic texture on a small segment on the tubular region. The rest of the parameters are fixed to be ϕA = N, J = 0, εLL = 3kBT, κ∥ = 5kBT and .
So far, we had used the example of a fully decorated nematic membrane and had shown how changes in the model parameters can influence its equilibrium state. However, the concentration and lateral organization of the proteins is another factor that can significantly alter the outcome of protein induced membrane remodeling. In the next section, we briefly touch upon this aspect and show how variations in the nematic density alone is enough to generate non trivial membrane shapes.
4.2. Role of nematic density and patterning
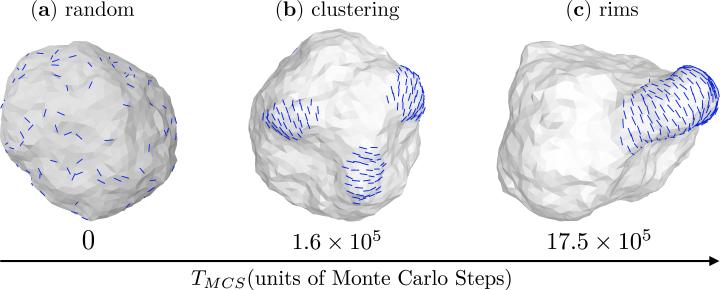
The cell membrane, or in general an elastic surface, can mediate the interactions between the various surface inclusions, such as between proteins [112–116]. The form of this interaction depends on the nature of the deformation field induced by the protein and can either be repulsive or attractive depending the on the elastic moduli of the membrane. Such indirect interactions gain significance in the context of membrane remodeling since they govern how the proteins aggregate into clusters, especially in the absence of specific interactions between them. In Fig. 9 we show how a nematic membrane with 10% field concentration (ϕA = 0.1N) aggregates into a single patch through membrane mediated interactions. The initial state of the membrane with random spatial distribution of the nematic field is shown in Fig. 9(a) and Fig. 9(b) shows its intermediate state at TMCS = 1.6 × 105 Monte Carlo steps where the field aggregates into small local clusters. At much longer times the membrane reaches its equilibrium state wherein the local clusters aggregate into a larger cluster and cooperatively remodels the membrane surface into a rim like structure, a snapshot of the equilibrium state at TMCS = 17.5 × 105 Monte Carlo steps can be seen in Fig. 9(c).
Figure 9.
Membrane mediated self assembly of the in-plane nematic field in a membrane with protein concentration ϕA = 0.1N. Panels from left to right shows (a) the initial state of the membrane with random distribution of the in-plane field, (b) local clustering of the field at intermediate times, TMCS = 1.6 × 105 and (c) aggregation of the smaller clusters and cooperative remodeling of the membrane into a rim like structure. Data shown for membrane parameters ϕA = 0.1N, J = 0, , κ∥ = 5kBT and κ = 10kBT.
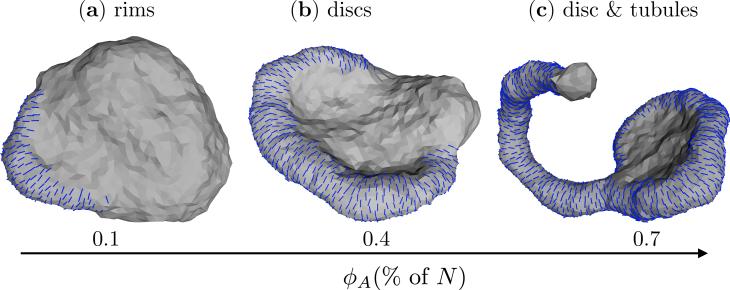
Variations in the field concentration can evoke varied conformational responses in the shapes of the membrane. We demonstrate this feature of membrane remodeling in Fig. 10 for a nematic membrane with J = 0, , κ∥ = 5kBT and κ = 10MkBT for three different values of ϕA = 0.1N, 0.4N and 0.7N. The observed array of shapes are diverse and range from rim like structures for ϕA = 0.1N (Fig.10(a)), to discs for ϕA = 0.4N (Fig. 10(b)), and coexisting state of discs and tubules for ϕA = 0.7N (Fig. 10(c)). With further increase in ϕA the equilibrium shapes of the membrane approaches the state corresponding to a fully decorated membrane, which was earlier shown in Fig. 7. The role of protein concentration and their associated shapes in well exemplified in the endoplasmic reticulum (ER) where DP1 and reticulon class membrane reshaping proteins are involved in the formation of ER discs and tubules [36, 38, 43, 117].
Figure 10.
Conformations of a nematic membrane as a function of field concentration ϕA: (a) rim like structures for ϕA = 0.1N, (b) discs for ϕA = 0.4N, and (c) coexisting disc and tubules for ϕA = 0.7N. Shown data corresponds to J = 0, , κ∥ = 5kBT and κ = 10kBT.
4.3. Free energy methods in nematic membranes
The nematic membrane model or in general the elasticity based membrane models are by construction faithful to the underlying thermodynamics of the system. Hence, such models are excellent candidates to probe the thermodynamic free energy landscapes of the membrane in a number of scenarios. Here, we show how conventional, perturbative and non-perturbative methods can be used to determine the various free energy measures related to protein driven membrane remodeling. A number of methods such as the thermodynamic integration technique [32], the Widom insertion technique [32] and the Bennet acceptance scheme [118] has been earlier used by Agrawal and Radhakrishnan [82, 119], and Tourdot et. al. [13, 31] to study the thermodynamic stability of the membrane conformations remodeled by isotropic curvature inducing proteins. These techniques can also be readily extended to understand the stability of the various conformations observed for the nematic membrane. Here, we briefly describe the thermodynamic integration technique to compute the free energies of highly curved membrane shapes stabilized when .
To perform thermodynamic integration we slowly introduce the effect of the nematic interactions by coupling the Kirkwood coupling parameter λ to the directional bending rigidity κ∥. The nematic membrane interaction, given in eqn.(11), now has the form,
| (15) |
and hence the total energy has the form,
| (16) |
For a given value of the anisotropy parameters κ∥ and , the free energy of the highly curved membrane morphology, observed when λ = 1, with respective to the prolate shapes, seen for λ = 0, can be computed using eqn.(15) as,
| (17) |
| (18) |
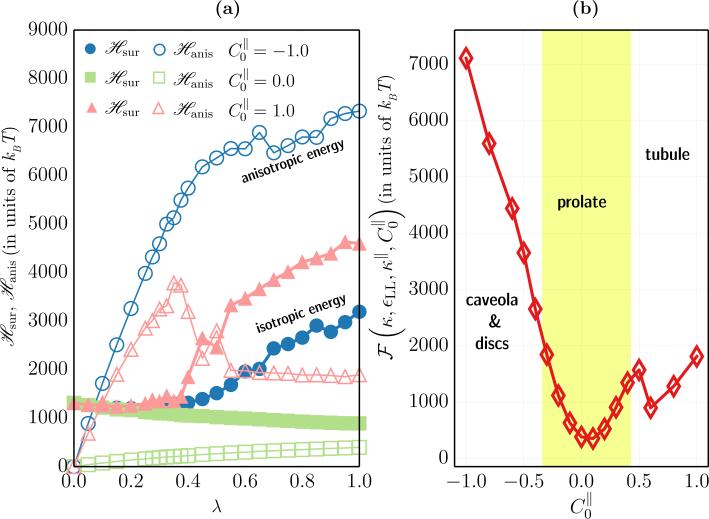
In simulations, the average value of , i.e. the integrand of eqn.(17), is computed for a range of values of λ and these average values are then numerically integrated to compute the relative free energy .
Fig. 11(a) shows the isotropic () and the anisotropic () energy contributions in a fully decorated nematic membrane as a function of the Kirkwood coupling parameter λ, for three different values of , and 1.0. It can be seen that the dominant energy contribution is a function of λ and also a function of . When , is an increasing function of λ since any non-zero curvature on the membrane tends to penalise the anisotropic part, i.e. . This increase is balanced by a corresponding decrease in which indicates that the equilibrium state of the membrane is governed by the complex interplay between the various energy contributions. However, when , increases when λ < λ*, while this contribution is minimum when λ exceeds the threshold value λ*—in the former the nematic field merely senses the membrane curvature while in the latter it also deforms the membrane and imposes the preferred curvature profile. The same cannot be said for the case of curvactants with and particularly for values of that invaginates the membrane surface. Here, the number of invaginations formed by the protein coat is limited by the volume enclosed by the cell membrane and as a result the nematic field in the non-invaginated regions have frustrated textures that lead to higher energy states [102].
Figure 11.
(a) The isotropic elastic energy, (filled symbols), and the anisotropic elastic energy, (open symbols), as a function of λ, for three different values of the anisotropic curvature for a nematic membrane with ϕA = N. (b) The relative thermodynamic free energy as a function of for a fully decorated nematic membrane. Shown alongside are the regions corresponding to the various morphologies shown in Fig. 7.
The relative free energy, , for a fully decorated nematic membrane, with κ = 10kBT, εLL = 3kBT, and κ∥ = 5kBT, is plotted against in Fig. 11(b)—the values of chosen here encompasses all the morphologies shown in Fig. 7. The relatively smooth free energy landscape indicates that the shape transformations in the membrane, as a function of , is a continuous transition with no meta stable states. In other words, an invaginated membrane (say for ) can be transformed into a tubule (say for ) just by increasing the value of the anisotropic spontaneous curvature. A completely tubulated and branched structure, like in panel (g) of Fig. 7, has a higher entropy compared to the rest of the morphologies of the nematic membrane, and this can serve as a marker to determine the state point for the onset of membrane tubulation. The large entropic contributions due to the tubular structures is also captured in Fig. 11(b) which is seen as a small kink at , which coincides very well with the onset values predicted in Fig. 7. Furthermore, also allows us to compute that the relative energy barriers for the various equilibrium shapes; it can be seen that membrane tubulation is less energetic compared to membrane invaginations. More details of the free energy techniques can be found in the review article by Ramakrishnan et. al. [21].
In this section, we have given a brief overview of the role of the various model parameters in reshaping the cell membrane. All the results presented here are purely from an equilibrium perspective: the energetics of the membrane, its interactions with the protein and the interactions amongst the proteins govern the conformational outcome. In the next section, we treat the curvature field and its deformation as a non-equilibrium process and show how such a process can lead to dramatic conformational response in the membrane, even at negligible protein concentrations.
5. Active membrane models for curvature fluctuations
The focus of this section is to study how the modulations in the membrane curvature due to the kinetic events occurring either on its surface or in its vicinity can affect cellular shapes. The class of biophysical processes that also remodel cell membrane curvature had earlier been discussed in Sec. 3 using three specific examples whose illustrations were shown in Fig. 3(b). To reiterate, we are interested in understanding how cellular morphologies are impacted by the rate of spontaneous curvature fluctuations on the cell membrane, which in turn is slaved to the rates of the cellular processes that induce curvature. Before proceeding to the model, it is important to understand the main differences between this approach and that discussed in Sec. 4, where the focus was to study how a fixed number of proteins self-assemble and cooperatively sculpt the membrane. The active membrane model has the following distinctions: (i) the number of curvactants on the membrane surface is not a conserved variable, i.e ϕA(t) ≠ constant, where t denotes time, (ii) the undulations in the number of proteins is governed by an underlying non-equilibrium process, and (iii) the membrane shapes obtained here are steady-state shapes and do not correspond to the true equilibrium state of the system.
The model for a membrane subjected to non-equilibrium curvature inducing processes is also based on the frameworks of membrane elasticity and DTMC introduced in Sec. 2. The location of a protein, as before, is marked by the scalar field ϕ, whose value is ϕ+ when a protein is present and ϕ– when it is not. On a triangulated surface the continuous field ϕ is represented by its discrete representation ϕv which is defined at every vertex v of the discrete surface. If the variables ϕ± take values ±1 then the number of curvature active sites is given by and the number of curvature inactive sites is given N– = N – N+, with N being the total number of the vertices on the triangulated surface. The spontaneous curvature field at a vertex v is related to the scalar variable ϕv as H0(1 + ϕv)/2, where H0 denotes the specific form of the spontaneous curvature measured from experiments or atomistic simulations.
For simplicity, in our discussions we treat H0,v to be a point scalar field by setting in eqn. (4), with δ being the Kronecker delta function: this form of H0,v induces a spontaneous curvature only at the vertex it is associated with. This class of curvatures can be studied using the isotropic curvature model, where the interactions between the spontaneous curvature field and a tensionless membrane surface is given by a modified form of eqn. (3),
| (19) |
An illustration of a triangulated surface with N+ = 0.1N is shown in Fig. 12(a). The self interaction between two neighboring sites () follows the classical Ising Hamiltonian,
| (20) |
which was already introduced in eqn. (12). The exchange interaction strength can either be positive (promoting the formation of protein clusters) or negative (inhibiting the formation of clusters). The thermodynamic state of the active membrane is then governed by the total Hamiltonian given by:
| (21) |
Figure 12.
(a) An active membrane with 10% active curvactants which are modeled as scalar fields with magnitude C0. On a triangulated surface, these curvactants are marked by a vertex with field variable ϕ = +1, as shown in the inset. (b) Shown are three equilibrium Monte Carlo moves to sample both the membrane degrees of freedom and the lateral organization of the scalar field ϕ.
Fig. 12(b) depicts the set of three equilibrium Monte Carlo moves that are used to sample both the protein and membrane degrees of freedom. Of these, the vertex move and link flip are similar to those for a bare membrane, introduced in Sec. 2, but in course of these moves the lateral organization of the curvature field ({ϕ}) is preserved. A third class of Monte Carlo moves, generally called the Kawasaki exchange, is designed to enhance the clustering dynamics of the protein field through the exchange of opposite valued curvature fields (one with ϕ = 1 and the other with ϕ = –1) between two neighbouring vertices on the triangulated surface. This move conserves the scalar field ϕ and the transition probability for a Kawasaki exchange move has been shown to be () [120], where is the energy cost to flip the values of two neighbouring field variables. In the model presented here, the field exchange move ((iii) in Fig. 12(b)) is accepted using the Metropolis scheme with the above mentioned transition probability, but one can also use the probability based on the Boltzmann factor which was earlier described in eqn. (8).
So far, we had focused on the equilibrium aspects of the active membrane and the sampling techniques shown in Fig. 12(b) conform to the rules of the canonical Monte Carlo namely: (i) conservation of the microscopic reversibility of the states, and (ii) the conservation of the number of protein fields N+ during these MC moves. In order to account for the effect of non-equilibrium curvature fluctuations in the membrane, the model should also accommodate for the spatial and temporal fluctuations in the total number of curvactants N+. As stated earlier, such a fluctuation can be caused by a variety of factors which also include the binding/unbinding kinetics of proteins and the onset of curvature inducing/inhibiting physical processes like endocytosis and vesicle fission/fusion.
At every vertex v, the transition probabilities to add or remove a curvactant (ϕv ⇄ –ϕv) are taken to be independent of each other. These probabilities are assumed to be governed by a signaling pathway that is sensitive to the number of curvature inducing units associated with the membrane: it promotes the addition of an active curvactant (a site with ϕ– is converted into a site with ϕ+) when N+ decreases below its preferred steady value and vice versa. In our Monte Carlo method the transitions between curvature active and curvature inactive states are modeled as,
| (22) |
and,
| (23) |
The transition probabilities are only dependent on the preferred asymmetry parameter, , and the fluctuations in N+ is set by the parameter ζ. In case of membranes with N+ ≠ N– the factor ξ ensures that the transitions are attempted with the prescribed rates ε+ and ε–, with ξ = 1 when N+ = N–. Though the transition probabilities shown in eqns. (22) and (23) are applicable to most active remodeling events, it should be applied with care if used to model the effects of vesicle fission and fusion. The given form of the probabilities assumes that the total system size is conserved even when the population of the individual species changes, i.e. it is in a semi grand ensemble. In this context, the results obtained using this model are only valid when the average membrane area remains unaltered during vesicle fission and fusion—this is equivalent to a regime where the area increase due to vesicle fusion is balanced by the area loss due to the budding vesicles. Hence, in order keep our discussions at a generic level we set ε+ = ε– = ε, which denotes the number of attempts per Monte Carlo moves to convert an active species to an inactive one and vice versa.
The above transition probabilities do not depend on the energy change associated with a change in the local configuration, ϕ ⇄ –ϕ hence violating detailed balance. We now explicitly show that this form of transition probabilities do not obey detailed balance, by demonstrating a violation of the Kolmogorov loop condition. The Kolmogorov loop condition states that for every loop in state space, the product of transition probabilities in one direction is equal to the product taken in the reverse direction. Our task is therefore to construct a loop where this condition is violated.
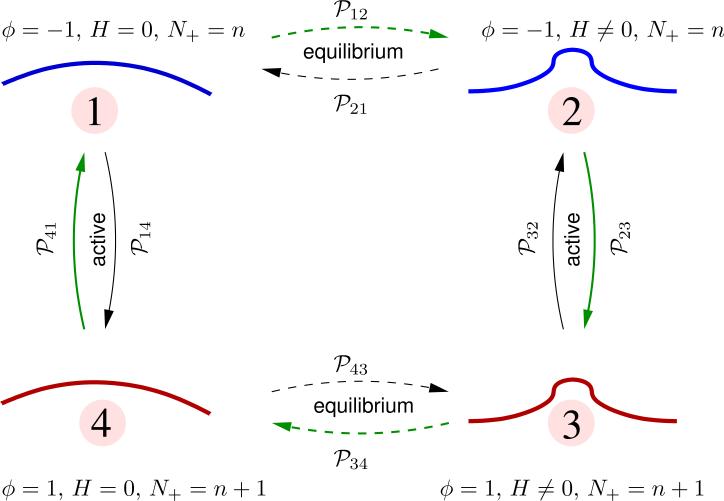
Consider a Kolmogorov loop connecting four distinct states of the continuum membrane, labeled 1 - 4, and characterized by state variables {ϕ, H}, as shown in Table 1
Table 1.
Enumeration of the states considered in the Kolmogorov loop diagram and the associated membrane morphology.
| state | ϕ | H | morphology |
|---|---|---|---|
| 1 | −1 | = 0 | nearly flat |
| 2 | −1 | ≠ 0 | curved |
| 3 | 1 | ≠ 0 | curved |
| 4 | 1 | = 0 | nearly flat |
The transition between any two states with the same value of ϕ is an equilibrium process — here, this corresponds to transitions between 1 ↔ 2 and 3 ↔ 4. Such transitions are characterized by a change in the elastic energy of the membrane , which can either be positive or negative. In perspective, one of these transitions corresponds to a membrane relaxation from a deformed/undeformed state following the unbinding/binding of a curvature-generating vesicle-protein complex. If be the change in energy upon relaxation, it can be shown that the transition probabilities for the various equilibrium transitions are,
| (24) |
The transition between any two states with different values of ϕ is an active process: here, this corresponds to transitions between 2 ↔ 3 and 4 ↔ 1. In our model, we have taken the rates for the transition of the state variable ϕ from 1 → –1 and –1 → 1 to be ε– and ε+, respectively. The probabilities to transition between the various active states can be computed using eqns. (22) and (23) as:
(a) Addition of active species: N+ = n → N+ = n + 1
| (25) |
(b) Removal of active species: N+ = n + 1 → N+ = n
| (26) |
In systems where microscopic reversibility is obeyed, the Kolmogorov loop condition states that the clockwise and counter-clockwise transition probabilities are related by,
| (27) |
From Fig. 13, the difference in the transition probabilities in the clockwise and counter-clockwise directions is non-zero. This is a clear violation of the Kolmogorov loop condition, and hence a violation of the detailed balance. The Kolmogorov loop condition is restored if we set either C0 = 0 or ε = 0. In summary, the binding and unbinding kinetics of curvature remodeling proteins is an active process, since they violate microscopic reversibility.
Figure 13.
A Kolmogorov loop diagram illustrating the transition probabilities between four distinct states of the membrane. The number of active species in states 1 and 2 is N+ = n and in states in 3 and 4 is N+ = n + 1.
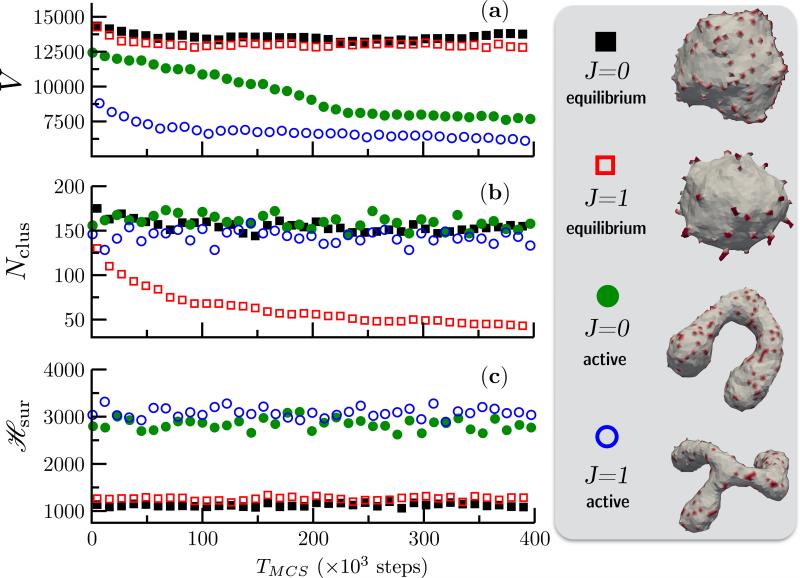
First, it is important to note that the properties of an active membrane is considerably different from that of its equilibrium counterpart. For the purpose of demonstration, starting from the same initial configuration of a membrane, with κ = 20kBT, Δp = 0, , and C0 = 0.7, we simulate four unique systems namely: (i) J = 0 and ε = 0, (ii) J = 1 and ε = 0, (iii) J = 0 and ε = 0.1N/MCS, and (iv) J = 1 and ε = 0.1N/MCS. The first two corresponds to an equilibrium membrane and the rest two represent an active membrane. Three different geometric and thermodynamic measures —(a) V, the volume enclosed by the membrane, (b) Nclus, the number of unique clusters formed by the spontaneous curvature field ϕ and (c) , the elastic energy of the surface computed from eqn. (19)—for the four cases are compared in Fig. 14.
Figure 14.
Shown are (a) the volume V, (b) the number of clusters Nclus, and (c) the elastic energy for four case of equilibrium and active vesicular membranes with κ = 20kBT, Δp = 0, and C0 = 0.7. All simulations start from the same quasi-spherical initial configuration. The conformations of the equilibrium state corresponding to J = 0 ( ) and J = 1 (
) and J = 1 ( ), and the steady state shapes of the active membrane, with ε = 0.1N/MCS, corresponding to J = 0(
), and the steady state shapes of the active membrane, with ε = 0.1N/MCS, corresponding to J = 0( ) and J = 1(
) and J = 1( ) are also shown alongside.
) are also shown alongside.
The first noticeable difference can be seen in the membrane conformations, which are also shown in Fig. 14, where the presence of activity drives an otherwise quasi-spherical membrane into non-trivial shapes like tubes and branched tubes. The implications of this shape transition is also reflected in the membrane volume V (Fig. 14(a)) where the active membranes show consistently smaller volumes. Similarly, the lateral organization of the protein field is significantly altered by non-equilibrium curvature fluctuations. It can be seen from the snapshots of the equilibrium membrane that the affinity of the protein field to aggregate into higher order clusters increases with J, as previously shown by Kumar et. al. [121], and the onset of aggregation is marked by a decrease in the number of protein clusters Nclus as in Fig. 14(b). However, the formation of such clusters is inhibited in an active membrane, even for large values of the parameter J [122]. Finally, the non-equilibrium nature of the active membrane can also be established from the elastic energy of the membrane surface which is shown in Fig. 14(c). It reveals that the energy of the active membrane is at least three times larger compared to its equilibrium state and given that the model only relies on the minimization of the elastic energy it is clear that the large membrane deformations are primarily driven by non-equilibrium curvature fluctuations. At this point, it is instructive to compare the tubular structures stabilized by an active membrane (Fig. 14) to those stabilized by a nematic membrane (see Fig. 10). It can be seen that the threshold protein coverage required to tubulate a membrane is around 70% in case of the latter while this threshold reduces to 10% for the active membrane. This clearly illustrates that the remodeling ability of a given protein not only depends only on its binding energy but also depends on its dynamics in the vicinity of the cell membrane.
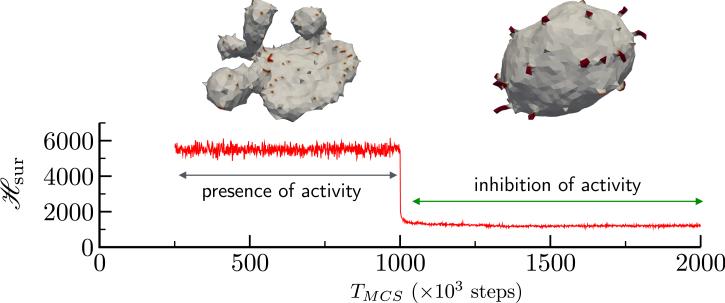
We can verify our hypothesis that non-equilibrium curvature fluctuations lead to highly curved, non trivial membrane shapes by observing the stability of the membrane conformation to changes in the activity rate ε. In Fig. 15 we show how a flattened sac like membrane structure which is the steady state of an active membrane, with κ = 20kBT, Δp = 0, , J = 1 and ε = 0.1N/MCS, rapidly reverts back to its equilibrium state when the activity rate ε is abruptly set to zero at TMCS = 106 steps. Also shown in Fig. 15, is the elastic energy which also shows a rapid decay to its equilibrium value on inhibition of active curvature fluctuations. Furthermore, the proteins aggregate into clusters that are not seen in the case of active membranes. Using this simple experiment, we have shown how the membrane shapes stabilized by the presence of curvature fluctuations are true steady state structures. However, the emergent conformations strongly depends on a number of model parameters. The repertoire of shapes stabilized due to the interplay of J, C0 and ε are shown in Fig. 16. Here, we have investigated how variations in the system parameters can lead to altered morphologies using an active membrane with N = 2030 vertices and .
Figure 15.
The stability of active membrane shapes in response to the inhibition of curvature fluctuations. TMCS = 0 corresponds to the steady state of an active membrane and this steady state persists till activity is abruptly switched off at TMCS = 106 steps. The highly curved sac-like shape of the active membrane disassembles and rapidly goes to the equilibrium shape corresponding to a membrane with κ = 20kBT, Δp = 0, and J = 1.
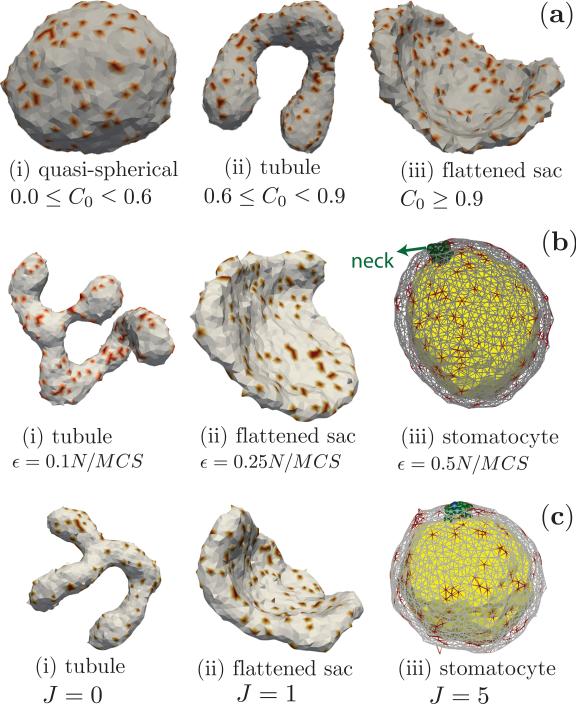
Figure 16.
Shapes of an active membrane. (a) Steady state shapes at ε = 0.1N/MCS and J = 0, as a function of curvature-activity coupling, C0. (b) Steady state shapes at J = 0 and C0 = 0.8, as a function of activity rate, ε. The side of the stomatocyte that is curved-in, is colored differently, for clarity. (c) Steady state shapes at ε = 0.1N/MCS and C0 = 0.8, as a function of cooperativity J between active species. All configurations are obtained with κ = 20, Δp0 = 0 and .
Role of curvature-activity coupling, C 0
The sequence of steady state shapes of the active membrane going from quasi-spherical to tubule to flattened sac on increasing C0, at a fixed activity rate ε = 0.1N/MCS is shown in Fig. 16a(i-iii). These nonequilibrium steady state shapes are distinct from their equilibrium counterparts obtained when the activity rate ε = 0. The membrane remains nearly quasi-spherical when the spontaneous curvature has values in the range 0.0 ≥ C0 < 0.6, but readily deforms into tubular structures when 0.6 ≤ C0 < 0.9. At extremely large values of the curvature-activity coupling, which has been determined to be C0 > 0.9 for an active membrane with , ε = 0.1N/MCS and J = 0, the tubular structures are unstable and leads to the emergence of flattened sac like conformations, that are reminiscent of the sac structures in the golgi.
Role of activity rate, ε
The steady state shapes are very sensitive to the rates of activity and go from tubular to flattened sacs to stomatocyte as the activity rate ε is increased. This effect is displayed in Fig. 16b for three different activity rates, ε = 0.1, 0.25, and 0.5N/MCS, at a fixed value of C0 = 0.8.
Effect of cooperativity, J
Cooperativity between the active species (J > 0), which can be caused due to the presence of export sites [123, 124], promotes the formation of clusters, which in turn enhances the effects of activity and curvature-activity coupling, consistent with results reported in [125] for the case of membrane mediated aggregation of active pumps, and leads to the sequence of shapes depicted in Fig. 16c.
It is now clear that tubules, sacs and stomatocytes are the dominant highly curved shapes within the conformational space of the active membrane and the stability of these shapes are highly sensitive to the various parameters in the model. Interestingly, all the three major shapes of the active membrane can also be stabilized by changing the osmotic pressure difference between the inside and outside of the membrane. It has been shown by Gompper and Kroll that tubules, discs and stomatocytes are the natural states of a closed membrane surface subjected to a deflating pressure [126]. How can one relate two seemingly disparate set of parameters, i.e how to recast the parameters defining the membrane activity (given by the activity rate ε and the curvature activity coupling C0) in terms of a mechanical parameter like the osmotic pressure difference? It has shown by Ramakrishnan et. al [122] that the active processes on the membrane renormalizes its osmotic pressure and this renormalized pressure is related to ε and C0 as ; here, R is the radius of the vesicle in its equilibrium state and the induced pressure is deflating. A closer look at this relation reveals another interesting aspect. The quantity ΔpRR can be thought as the spontaneous tension in the membrane, due to the active processes, and its value is proportional to as predicted by Lipowsky [127] for any contribution C0 within the isotropic framework of membrane elasticity.
In summary, the active membrane model provides an alternative avenue to understand the phenomenon of how curvature remodeling processes can cooperatively affect the macroscopic shapes of cell membranes. It also shows that the non-equilibrium aspects of these processes play a significant role even when the protein concentration is small enough to be negligible.
6. Conclusions
We have presented an elasticity based membrane mechanics model to study the morphogenesis of cell membranes and have shown how the emergent morphologies are influenced by the presence of passive and active remodeling processes that can spontaneously modulate the local curvature of the membrane. In this approach, we represent the interaction between the membrane and the curvactants as effective spontaneous curvature fields, whose values are determined either through experiments or through other high resolution simulation techniques. We have also shown how the Dynamical triangulated Monte Carlo technique provides a computationally less expensive route to study the thermodynamic states of the membranes, with dimensions matching cellular scales. The nematic membrane model was introduced in the context of proteins that deform the cell membrane only along some preferred directions. This anisotropic elasticity based model has been used to show how biologically relevant morphologies are stabilized by the cooperative action of anisotropically curving proteins and the relative stability of the membrane shapes were analyzed using free energy methods based on thermodynamic integration. The active membrane model captures the non-equilibrium curvature fluctuations on the membrane surface caused due to the involvement of the cell membrane in a number of essential biophysical processes like cellular trafficking, cell signaling and motility. The non-equilibrium fluctuations can stabilize a number of non-trivial, steady state membrane shapes even when the concentration of the curvactants is very small. The framework presented in this chapter offers a generic framework to model more complex problems in cell biology where the role of the cell membrane is indispensable.
Acknowledgments
The authors thank Dr. P. B. Sunil Kumar, Dr. John H. Ipsen and Dr. Madan Rao for the works described in Sec. 4.1 and Sec. 5 and for many insightful discussions. The authors acknowledge funding from the US National Science Foundation (CBET-1133267, CBET-1244507, CBET-1236514, DMR-1120901), the US National Institutes of Health (1R01EB006818 and U01-EB016027), and the European Commission (7th programme for research VPH-600841). Supercomputing resources were made available through XSEDE (extreme science and engineering discovery environment, MCB060006).
Footnotes
Even lipids that belong to the same class exhibit large chemical diversity due to variations in the hydrophilic head groups and differences in the number, length and saturation of the hydrocarbon chain (tail). Phospholipids for instance can have a variety of head groups, like phosphatidylcholine (PC), phosphatidylserine (PS), phosphatidylethanolamine (PE), and phospatidylglycerol (PG), and these groups can be uncharged, anionic, cationic, or zwitterionic.
Specifically, these include forces due to molecular binding, cytoskeletal interactions with the cell membrane and long range hydrodynamic interactions mediated by the surrounding fluid
For a parameterization x, the surface area , where is the metric tensor
The bounds on the edge length can be easily determined by considering the scenario where three interconnected spherical beads of diameter a0 are arranged such that their center of masses are on the vertices of an equilateral triangle of length . Any two beads will interpenetrate when the distance between their centers is less than their diameter and this constraint sets the lower bound for the triangle length to be . Similarly when the triangle length the distance between the centroid of the triangle and any of its vertices is exactly a0. This implies that a fourth bead of diameter a0 placed at the centroid of the triangle can freely move in and out the triangular face leading to the violation of self avoidance and this sets the upper bound on the value of to be .
A vesicle is a closed bilayer structure of spherical topology
Most of these proteins do not span the entire bilayer and hence fall under the class of peripheral proteins
For example, in order to remodel a planar membrane into a cylinder a single BAR domain adhering to a 9 nm square membrane patch, with 20% phosphatidylserine and with a bending rigidity of κ = 20kBT, should have a binding energy of at least 12kBT [49]
This transformation occurs due to the implicit coupling between the nematic texture and membrane geometry [106–108].
in case of equilibrium membranes
References
- 1.Escribá PV, González-Ros JM, Goñi FM, Kinnunen PKJ, Vigh L, Sánchez-Magraner L, Fernández AM, Busquets X, Horváth I, Barceló-Coblijn G. Membranes: a meeting point for lipids, proteins and therapies. J Cellular Mol Med. 2008;12:829–875. doi: 10.1111/j.1582-4934.2008.00281.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Guidotti G. Membrane Proteins. Ann. Rev. Biochem. 1972;41:731–752. doi: 10.1146/annurev.bi.41.070172.003503. [DOI] [PubMed] [Google Scholar]
- 3.Israelachvili JN. Intermolecular and Surface Forces. third edition Academic Press; Boston: 2011. [Google Scholar]
- 4.Singer SJ, Nicolson GL. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
- 5.Li R, Gundersen GG. Beyond polymer polarity: how the cytoskeleton builds a polarized cell. Nat. Rev. Mol. Cell Biol. 2008;9:860–873. doi: 10.1038/nrm2522. [DOI] [PubMed] [Google Scholar]
- 6.Bryant DM, Mostov KE. From cells to organs: building polarized tissue. Nat. Rev. Mol. Cell Biol. 2008;9:887–901. doi: 10.1038/nrm2523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lipowsky R. Biomimetic membrane modelling: pictures from the twilight zone. Nature Materials. 2004;3:589–591. doi: 10.1038/nmat1208. [DOI] [PubMed] [Google Scholar]
- 8.Chu JW, Ayton GS, Izvekov S, Voth GA. Emerging methods for multiscale simulation of biomolecular systems. Molecular Physics. 2007;105:167–175. [Google Scholar]
- 9.Ayton GS, Noid WG, Voth GA. Multiscale modeling of biomolecular systems: in serial and in parallel. Current Opinion in Structural Biology. 2007;17:192–198. doi: 10.1016/j.sbi.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 10.Mercker M, Ptashnyk M, Kühnle J, Hartmann D, Weiss M, Jäger W. A multiscale approach to curvature modulated sorting in biological membranes. Journal of Theoretical Biology. 2012;301:67–82. doi: 10.1016/j.jtbi.2012.01.039. [DOI] [PubMed] [Google Scholar]
- 11.Praprotnik M, Site LD, Kremer K. Multiscale Simulation of Soft Matter: From Scale Bridging to Adaptive Resolution. Annu. Rev. Phys. Chem. 2008;59:545–571. doi: 10.1146/annurev.physchem.59.032607.093707. [DOI] [PubMed] [Google Scholar]
- 12.Peter C, Kremer K. Multiscale simulation of soft matter systems – from the atomistic to the coarse-grained level and back. Soft Matter. 2009;5:4357. [Google Scholar]
- 13.Tourdot RW, Bradley RP, Ramakrishnan N, Radhakrishnan R. Multiscale computational models in physical systems biology of intracellular trafficking. IET Systems Biology. 2014;8:198–213. doi: 10.1049/iet-syb.2013.0057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Marrink S-J, de Vries AH, Tieleman DP. Biochimica et Biophysica Acta. BBA - Biomembranes. 2009;1788:149–168. doi: 10.1016/j.bbamem.2008.10.006. [DOI] [PubMed] [Google Scholar]
- 15.Tieleman DP, Marrink S-J, Berendsen HJ. A computer perspective of membranes: molecular dynamics studies of lipid bilayer systems. Biochim Biophys Acta (BBA) -Reviews on Biomembranes. 1997;1331:235–270. doi: 10.1016/s0304-4157(97)00008-7. [DOI] [PubMed] [Google Scholar]
- 16.Saiz L, Bandyopadhyay S, Klein ML. Towards an understanding of complex biological membranes from atomistic molecular dynamics simulations. Biosci. Rep. 2002;22:151–173. doi: 10.1023/a:1020130420869. [DOI] [PubMed] [Google Scholar]
- 17.Venturoli M, Maddalena Sperotto M, Kranenburg M, Smit B. Mesoscopic models of biological membranes. Physics Reports. 2006;437:1–54. [Google Scholar]
- 18.Ayton GS, Voth GA. Multiscale simulation of protein mediated membrane remodeling. Seminars in Cell and Developmental Biology. 2010;21:357–362. doi: 10.1016/j.semcdb.2009.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shinoda W, DeVane R, Klein ML. Computer simulation studies of self-assembling macromolecules. Current Opinion in Structural Biology. 2012;22:175–186. doi: 10.1016/j.sbi.2012.01.011. [DOI] [PubMed] [Google Scholar]
- 20.Bradley RP, Radhakrishnan R. Coarse-Grained Models for Protein-Cell Membrane Interactions. Polymers. 2013;5:890–936. doi: 10.3390/polym5030890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ramakrishnan N, Sunil Kumar PB, Radhakrishnan R. Mesoscale computational studies of membrane bilayer remodeling by curvature-inducing proteins. Physics Reports. 2014;543:1–60. doi: 10.1016/j.physrep.2014.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Deserno M. Fluid lipid membranes: From differential geometry to curvature stresses. Chemistry and Physics of Lipids. 2015;185:11–45. doi: 10.1016/j.chemphyslip.2014.05.001. [DOI] [PubMed] [Google Scholar]
- 23.Canham PB. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970;26:61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 24.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 25.Seifert U. Configurations of fluid membranes and vesicles, Advances in Physics. 1997;46:13–137. [Google Scholar]
- 26.do Carmo MP. Differential geometry of curves and surfaces. Prentice Hall; Engelwood Cliffs, New Jersey: 1976. [Google Scholar]
- 27.Ramakrishnan N, Sunil Kumar PB, Ipsen JH. Monte Carlo simulations of fluid vesicles with in-plane orientational ordering. Phys. Rev. E. 2010;81:041922. doi: 10.1103/PhysRevE.81.041922. [DOI] [PubMed] [Google Scholar]
- 28.Agrawal NJ, Nukpezah J, Radhakrishnan R. Minimal Mesoscale Model for Protein-Mediated Vesiculation in Clathrin-Dependent Endocytosis. PLoS Comput Biol. 2010;6:e1000926. doi: 10.1371/journal.pcbi.1000926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ramanan V, Agrawal NJ, Liu J, Engles S, Toy R, Radhakrishnan R. Systems biology and physical biology of clathrin-mediated endocytosis. Integr. Biol. 2011;3:803. doi: 10.1039/c1ib00036e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu J, Tourdot RW, Ramanan V, Agrawal NJ, Radhakrishanan R. Mesoscale simulations of curvature-inducing protein partitioning on lipid bilayer membranes in the presence of mean curvature fields. Molecular Physics. 2012;110:1127–1137. doi: 10.1080/00268976.2012.664661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tourdot RW, Ramakrishnan N, Radhakrishnan R. Defining the free-energy landscape of curvature-inducing proteins on membrane bilayers. Phys. Rev. E. 2014;90:022717. doi: 10.1103/PhysRevE.90.022717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Frenkel D, Smit B. Understanding Molecular Simulation : From Algorithms to Applications. 2 edition Academic Press; 2001. [Google Scholar]
- 33.Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 34.McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature Cell Biology. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 35.Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nature. 2005;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 36.Shibata Y, Voeltz GK, Rapoport TA. Rough Sheets and Smooth Tubules. Cell. 2006;126:435–439. doi: 10.1016/j.cell.2006.07.019. [DOI] [PubMed] [Google Scholar]
- 37.Voeltz GK, Prinz WA. Sheets, ribbons and tubules - how organelles get their shape. Nat. Rev. Mol. Cell Biol. 2007;8:258–264. doi: 10.1038/nrm2119. [DOI] [PubMed] [Google Scholar]
- 38.Hu J, Shibata Y, Voss C, Shemesh T, Li Z, Coughlin M, Kozlov MM, Rapoport TA, Prinz WA. Membrane Proteins of the Endoplasmic Reticulum Induce High-Curvature Tubules. Science. 2008;319:1247–1250. doi: 10.1126/science.1153634. [DOI] [PubMed] [Google Scholar]
- 39.Sens P, Johannes L, Bassereau P. Biophysical approaches to protein-induced membrane deformations in trafficking. Current Opinion in Cell Biology. 2008;20:476–482. doi: 10.1016/j.ceb.2008.04.004. [DOI] [PubMed] [Google Scholar]
- 40.Devaux PF, Herrmann A, Ohlwein N, Kozlov MM. How lipid flippases can modulate membrane structure. Biochimica et Biophysica Acta (BBA) - Biomembranes. 2008;1778:1591–1600. doi: 10.1016/j.bbamem.2008.03.007. [DOI] [PubMed] [Google Scholar]
- 41.Shibata Y, Hu J, Kozlov MM, Rapoport TA. Mechanisms Shaping the Membranes of Cellular Organelles. Annu. Rev. Cell Dev. Biol. 2009;25:329–354. doi: 10.1146/annurev.cellbio.042308.113324. [DOI] [PubMed] [Google Scholar]
- 42.Doherty GJ, McMahon HT. Mechanisms of Endocytosis. Annu. Rev. Biochem. 2009;78:857–902. doi: 10.1146/annurev.biochem.78.081307.110540. [DOI] [PubMed] [Google Scholar]
- 43.Shibata Y, Shemesh T, Prinz WA, Palazzo AF, Kozlov MM, Rapoport TA. Mechanisms Determining the Morphology of the Peripheral ER. Cell. 2010;143:774–788. doi: 10.1016/j.cell.2010.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Graham TR, Kozlov MM. Interplay of proteins and lipids in generating membrane curvature. Current Opinion in Cell Biology. 2010;22:430–436. doi: 10.1016/j.ceb.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kabaso D, Gongadze E, Elter P, van Rienen U, Gimsa J, Kralj-Iglič V, Iglič A. Attachment of rod-like (BAR) proteins and membrane shape. Mini Rev Med Chem. 2011;11:272–282. doi: 10.2174/138955711795305353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kozlov MM, Campelo F, Liska N, Chernomordik LV, Marrink S-J, McMahon HT. Mechanisms shaping cell membranes. Current Opinion in Cell Biology. 2014;29C:53–60. doi: 10.1016/j.ceb.2014.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Simunovic M, Bassereau P. Reshaping biological membranes in endocytosis: crossing the configurational space of membrane-protein interactions. Biol. Chem. 2014;395:275–283. doi: 10.1515/hsz-2013-0242. [DOI] [PubMed] [Google Scholar]
- 48.Peter BJ, Kent HM, Mills IG, Vallis Y, Butler PJG, Evans PR, McMahon HT. BAR domains as sensors of membrane curvature: the amphiphysin BAR structure. Science. 2004;303:495–499. doi: 10.1126/science.1092586. [DOI] [PubMed] [Google Scholar]
- 49.Zimmerberg J, McLaughlin S. Membrane Curvature: How BAR Domains Bend Bilayers. Current Biology. 2004;14:R250–R252. doi: 10.1016/j.cub.2004.02.060. [DOI] [PubMed] [Google Scholar]
- 50.Dawson JC, Legg JA, Machesky LM. Bar domain proteins: a role in tubulation, scission and actin assembly in clathrin-mediated endocytosis. Trends in Cell Biology. 2006;16:493–498. doi: 10.1016/j.tcb.2006.08.004. [DOI] [PubMed] [Google Scholar]
- 51.Frost A, Perera R, Roux A, Spasov K, Destaing O, Egelman EH, De Camilli P, Unger VM. Structural Basis of Membrane Invagination by F-BAR Domains. Cell. 2008;132:807–817. doi: 10.1016/j.cell.2007.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ford MGJ, Mills IG, Peter BJ, Vallis Y, Praefcke GJK, Evans PR, McMahon HT. Curvature of clathrin-coated pits driven by epsin. Nature. 2002;419:361–366. doi: 10.1038/nature01020. [DOI] [PubMed] [Google Scholar]
- 53.Nossal R, Zimmerberg J. Endocytosis: curvature to the ENTH degree. Current Biology. 2002;12:R770–R772. doi: 10.1016/s0960-9822(02)01289-7. [DOI] [PubMed] [Google Scholar]
- 54.Wendland B. Epsins: adaptors in endocytosis? Nat. Rev. Mol. Cell Biol. 2002;3:971–977. doi: 10.1038/nrm970. [DOI] [PubMed] [Google Scholar]
- 55.Zhao Y, Liu J, Yang C, Capraro BR, Baumgart T, Bradley RP, Ramakrishnan N, Xu X, Radhakrishnan R, Svitkina T, Guo W. Exo70 Generates Membrane Curvature for Morphogenesis and Cell Migration. Developmental Cell. 2013;26:266–278. doi: 10.1016/j.devcel.2013.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hinshaw JE. Dynamin and its role in membrane fission. Annu. Rev. Cell Dev. Biol. 2000;16:483–519. doi: 10.1146/annurev.cellbio.16.1.483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Blood PD, Voth GA. Direct observation of Bin/amphiphysin/Rvs (BAR) domain-induced membrane curvature by means of molecular dynamics simulations. Proc. Natl. Acad. Sci. U.S.A. 2006;103:15068–15072. doi: 10.1073/pnas.0603917103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Arkhipov A, Yin Y, Schulten K. Four-Scale Description of Membrane Sculpting by BAR Domains. Biophys. J. 2008;95:2806–2821. doi: 10.1529/biophysj.108.132563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Arkhipov A, Yin Y, Schulten K. Membrane-Bending Mechanism of Amphiphysin N-BAR Domains. Biophys. J. 2009;97:2727–2735. doi: 10.1016/j.bpj.2009.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yin Y, Arkhipov A, Schulten K. Simulations of Membrane Tubulation by Lattices of Amphiphysin N-BAR Domains. Structure. 2009;17:882–892. doi: 10.1016/j.str.2009.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Cui H, Mim C, Vázquez FX, Lyman E, Unger VM, Voth GA. Understanding the Role of Amphipathic Helices in N-BAR Domain DrivenMembrane Remodeling. Biophys. J. 2013;104:404–411. doi: 10.1016/j.bpj.2012.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lyman E, Cui H, Voth GA. Reconstructing protein remodeled membranes in molecular detail from mesoscopic models. Phys. Chem. Chem. Phys. 2011;13:10430. doi: 10.1039/c0cp02978e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Simunovic M, Mim C, Marlovits TC, Resch G, Unger VM, Voth GA. Protein-Mediated Transformation of Lipid Vesicles into Tubular Networks. Biophys. J. 2013;105:711–719. doi: 10.1016/j.bpj.2013.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Yu H, Schulten K. Membrane Sculpting by F-BAR Domains Studied by Molecular Dynamics Simulations. PLoS Comput Biol. 2013;9 doi: 10.1371/journal.pcbi.1002892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.De Matteis MA, Godi A. Protein–lipid interactions in membrane trafficking at the Golgi complex. Biochimica et Biophysica Acta (BBA) - Biomembranes. 2004;1666:264–274. doi: 10.1016/j.bbamem.2004.07.002. [DOI] [PubMed] [Google Scholar]
- 66.Lippincott-Schwartz J, Donaldson JG, Schweizer A, Berger EG, Hauri HP, Yuan LC, Klausner RD. Microtubule-dependent retrograde transport of proteins into the er in the presence of brefeldin a suggests an er recycling pathway. Cell. 1990;60:821–36. doi: 10.1016/0092-8674(90)90096-w. [DOI] [PubMed] [Google Scholar]
- 67.Cluett EB, Wood SA, Banta M, Brown WJ. Tubulation of golgi membranes in vivo and in vitro in the absence of brefeldin a. The Journal of Cell Biology. 1993;120:15–24. doi: 10.1083/jcb.120.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.del Valle M, Robledo Y, Sandoval IV. Membrane flow through the golgi apparatus: specific disassembly of the cis-golgi network by atp depletion. J Cell Sci. 1999;112(Pt 22):4017–29. doi: 10.1242/jcs.112.22.4017. [DOI] [PubMed] [Google Scholar]
- 69.Lowe M, Nakamura N, Warren G. Golgi division and membrane traffic. Trends Cell Biol. 1998;8:40–4. doi: 10.1016/s0962-8924(97)01189-6. [DOI] [PubMed] [Google Scholar]
- 70.Thyberg J, Moskalewski S. Role of microtubules in the organization of the golgi complex. Exp Cell Res. 1999;246:263–79. doi: 10.1006/excr.1998.4326. [DOI] [PubMed] [Google Scholar]
- 71.Testerink N, van der Sanden MHM, Houweling M, Helms JB, Vaandrager AB. Depletion of phosphatidylcholine affects endoplasmic reticulum morphology and protein traffic at the golgi complex. J Lipid Res. 2009;50:2182–92. doi: 10.1194/jlr.M800660-JLR200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the cell. third edition Garland Publishing; Singapore: 1994. [Google Scholar]
- 73.Søgaard M, Tani K, Ye RR, Geromanos S, Tempst P, Kirchhausen T, Rothman JE, Söllner T. A rab protein is required for the assembly of SNARE complexes in the docking of transport vesicles. Cell. 1994;78:937–948. doi: 10.1016/0092-8674(94)90270-4. [DOI] [PubMed] [Google Scholar]
- 74.Shi Z, Baumgart T. Membrane tension and peripheral protein density mediate membrane shape transitions. Nat Comms. 2015;6:5974. doi: 10.1038/ncomms6974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lemmon MA. Membrane recognition by phospholipid-binding domains. Nature. 2008;9:99–111. doi: 10.1038/nrm2328. [DOI] [PubMed] [Google Scholar]
- 76.Vicinanza M, D'Angelo G, Di Campli A, De Matteis MA. Function and dysfunction of the PI system in membrane trafficking. The EMBO Journal. 2008;27:2457–2470. doi: 10.1038/emboj.2008.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Aimon S, Callan-Jones A, Berthaud A, Pinot M, Toombes GES, Bassereau P. Membrane shape modulates transmembrane protein distribution. Developmental Cell. 2014;28:212–218. doi: 10.1016/j.devcel.2013.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Šarić A, Cacciuto A. Mechanism of Membrane Tube Formation Induced by Adhesive Nanocomponents. Phys. Rev. Lett. 2012;109:188101. doi: 10.1103/PhysRevLett.109.188101. [DOI] [PubMed] [Google Scholar]
- 79.Bahrami AH, Lipowsky R, Weikl TR. Tubulation and Aggregation of Spherical Nanoparticles Adsorbed on Vesicles. Phys. Rev. Lett. 2012;109:188102. doi: 10.1103/PhysRevLett.109.188102. [DOI] [PubMed] [Google Scholar]
- 80.Dasgupta S, Auth T, Gompper G. Wrapping of ellipsoidal nano-particles by fluid membranes. Soft Matter. 2013;9:5473. [Google Scholar]
- 81.Dasgupta S, Auth T, Gompper G. Shape and Orientation Matter for the Cellular Uptake of Nonspherical Particles. Nano Lett. 2014;14:687–693. doi: 10.1021/nl403949h. [DOI] [PubMed] [Google Scholar]
- 82.Agrawal NJ, Radhakrishnan R. Calculation of free energies in fluid membranes subject to heterogeneous curvature fields. Phys. Rev. E. 2009;80:011925. doi: 10.1103/PhysRevE.80.011925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Helfrich W, Prost J. Intrinsic bending force in anisotropic membranes made of chiral molecules. Phys. Rev. A. 1988;38:3065–3068. doi: 10.1103/physreva.38.3065. [DOI] [PubMed] [Google Scholar]
- 84.Schnur JM. Lipid tubules: a paradigm for molecularly engineered structures. Science. 1993;262:1669–1676. doi: 10.1126/science.262.5140.1669. [DOI] [PubMed] [Google Scholar]
- 85.Fournier J-B, Galatola P. Sponges, Tubules and Modulated Phases of Para-Antinematic Membranes. J. de Physique II. 1997;7:1509–1520. [Google Scholar]
- 86.Fournier J-B, Galatola P, Peliti L. On the effects of a nematic phase confined to a membrane. Molecular Crystals and Liquid Crystals Science and Technology. Section A. Molecular Crystals and Liquid Crystals. 1999;332:539–546. [Google Scholar]
- 87.Kralj-Iglič V, Heinrich V, Svetina S, Zeks B. Free energy of closed membrane with anisotropic inclusions. Eur. Phys. J. B. 1999;10:5–8. [Google Scholar]
- 88.Fošnarič M, Bohinc K, Gauger DR, Iglič A, Kralj-Iglič V, May S. The Influence of Anisotropic Membrane Inclusions on Curvature Elastic Properties of Lipid Membranes. J. Chem. Inf. Model. 2005;45:1652–1661. doi: 10.1021/ci050171t. [DOI] [PubMed] [Google Scholar]
- 89.Frank JR, Kardar M. Defects in nematic membranes can buckle into pseudospheres. Phys. Rev. E. 2008;77:041705. doi: 10.1103/PhysRevE.77.041705. [DOI] [PubMed] [Google Scholar]
- 90.Selinger J, Schnur J. Theory of chiral lipid tubules. Phys. Rev. Lett. 1993;71:4091–4094. doi: 10.1103/PhysRevLett.71.4091. [DOI] [PubMed] [Google Scholar]
- 91.Fournier J-B. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys. Rev. Lett. 1996;76:4436–4439. doi: 10.1103/PhysRevLett.76.4436. [DOI] [PubMed] [Google Scholar]
- 92.Selinger J, MacKintosh FC, Schnur J. Theory of cylindrical tubules and helical ribbons of chiral lipid membranes. Phys. Rev. E. 1996;53:3804–3818. doi: 10.1103/physreve.53.3804. [DOI] [PubMed] [Google Scholar]
- 93.Kralj-Iglič V, Iglič A, Gomiscek G, Sevsek F, Arrigler V, Hägerstrand H. Microtubes and nanotubes of a phospholipid bilayer membrane. J. Phys. A: Math. Gen. 2002;35:1533–1549. [Google Scholar]
- 94.Walani N, Torres J, Agrawal A. Anisotropic spontaneous curvatures in lipid membranes. Phys. Rev. E. 2014;89:062715. doi: 10.1103/PhysRevE.89.062715. [DOI] [PubMed] [Google Scholar]
- 95.Dommersnes PG, Fournier J-B. The many-body problem for anisotropic membrane inclusions and the self-assembly of ”saddle” defects into an ”egg carton”. Biophys. J. 2002;83:2898–2905. doi: 10.1016/S0006-3495(02)75299-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Mareš T, Daniel M, Perutková Š, Perne A, Dolinar G, Iglič A, Rappolt M, Kralj-Iglič V. Role of Phospholipid Asymmetry in the Stability of Inverted Hexagonal Mesoscopic Phases. J. Phys. Chem. B. 2008;112:16575–16584. doi: 10.1021/jp805715r. [DOI] [PubMed] [Google Scholar]
- 97.Iglič A, Slivnik T, Kralj-Iglič V. Elastic properties of biological membranes influenced by attached proteins. Journal of Biomechanics. 2007;40:2492–2500. doi: 10.1016/j.jbiomech.2006.11.005. [DOI] [PubMed] [Google Scholar]
- 98.de Gennes PG, Prost J. The Physics of Liquid Crystals (International Series of Monographs on Physics) 2 edition Oxford University Press; USA: 1995. [Google Scholar]
- 99.Lebwohl PA, Lasher G. Nematic-Liquid-Crystal Order-A Monte Carlo Calculation. Phys. Rev. A. 1972;6:426–429. [Google Scholar]
- 100.Vitelli V, Turner A. Anomalous Coupling Between Topological Defects and Curvature. Phys. Rev. Lett. 2004;93:215301. doi: 10.1103/PhysRevLett.93.215301. [DOI] [PubMed] [Google Scholar]
- 101.Vitelli V, Nelson DR. Defect generation and deconfinement on corrugated topographies. Phys. Rev. E. 2004;70:051105. doi: 10.1103/PhysRevE.70.051105. [DOI] [PubMed] [Google Scholar]
- 102.Ramakrishnan N, Ipsen JH, Sunil Kumar PB. Role of disclinations in determining the morphology of deformable fluid interfaces. Soft Matter. 2012;8:3058. [Google Scholar]
- 103.Vitelli V, Nelson DR. Nematic textures in spherical shells. Phys. Rev. E. 2006;74:021711. doi: 10.1103/PhysRevE.74.021711. [DOI] [PubMed] [Google Scholar]
- 104.Bowick MJ, Giomi L. Two-dimensional matter: order, curvature and defects. Advances in Physics. 2009;58:449–563. [Google Scholar]
- 105.Ramakrishnan N, Sunil Kumar PB, Ipsen JH. Membrane-Mediated Aggregation of Curvature-Inducing Nematogens and Membrane Tubulation. Biophys. J. 2013;104:1018–1028. doi: 10.1016/j.bpj.2012.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Park J, Lubensky TC, MacKintosh FC. n-atic order and continuous shape changes of deformable surfaces of genus zero. Euro. Phys. Lett. 1992;20:279. [Google Scholar]
- 107.MacKintosh FC, Lubensky TC. Orientational order, topology, and vesicle shapes. Phys. Rev. Lett. 1991;67:1169–1172. doi: 10.1103/PhysRevLett.67.1169. [DOI] [PubMed] [Google Scholar]
- 108.Ramakrishnan N, Sunil Kumar PB, Ipsen JH. Modeling Anisotropic Elasticity of Fluid Membranes. Macromol. Theory Simul. 2011;20:446–450. [Google Scholar]
- 109.Frost A, Unger VM, De Camilli P. The BAR Domain Superfamily: Membrane-Molding Macromolecules. Cell. 2009;137:191–196. doi: 10.1016/j.cell.2009.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Lipowsky R. The conformation of membranes. Nature. 1991;349:475–481. doi: 10.1038/349475a0. [DOI] [PubMed] [Google Scholar]
- 111.Kroll DM, Gompper G. The conformation of fluid membranes: Monte Carlo simulations. Science. 1992;255:968–971. doi: 10.1126/science.1546294. [DOI] [PubMed] [Google Scholar]
- 112.Kim KS, Neu J, Oster G. Curvature-mediated interactions between membrane proteins. Biophys. J. 1998;75:2274–2291. doi: 10.1016/S0006-3495(98)77672-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Bohinc K, Kralj-Iglič V, May S. Interaction between two cylindrical inclusions in a symmetric lipid bilayer. J. Chem. Phys. 2003;119:7435. [Google Scholar]
- 114.Lewandowski EP, Bernate JA, Searson PC, Stebe KJ. Rotation and Alignment of Anisotropic Particles on Nonplanar Interfaces. Langmuir. 2008;24:9302–9307. doi: 10.1021/la801167h. [DOI] [PubMed] [Google Scholar]
- 115.Lewandowski EP, Bernate JA, Tseng A, Searson PC, Stebe KJ. Oriented assembly of anisotropic particles by capillary interactions. Soft Matter. 2009;5:886–890. [Google Scholar]
- 116.Schweitzer Y, Kozlov MM. Membrane-Mediated Interaction between Strongly Anisotropic Protein Scaffolds. PLoS Comput Biol. 2015;11:e1004054. doi: 10.1371/journal.pcbi.1004054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Shibata Y, Voss C, Rist JM, Hu J, Rapoport TA, Prinz WA, Voeltz GK. The reticulon and DP1/Yop1p proteins form immobile oligomers in the tubular endoplasmic reticulum. J. Biol. Chem. 2008;283:18892–18904. doi: 10.1074/jbc.M800986200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Bennett CH. Efficient Estimation of Free-Energy Differences From Monte-Carlo Data. Journal of Computational Physics. 1976;22:245–268. [Google Scholar]
- 119.Agrawal NJ, Weinstein J, Radhakrishnan R. Landscape of finite-temperature equilibrium behaviour of curvature-inducing proteins on a bilayer membrane explored using a linearized elastic free energy model. Molecular Physics. 2008;106:1913–1923. doi: 10.1080/00268970802365990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Bray AJ. Theory of phase-ordering kinetics. Advances in Physics. 1994;43:357–459. [Google Scholar]
- 121.Sunil Kumar PB, Gompper G, Lipowsky R. Budding Dynamics of Multicomponent Membranes. Phys. Rev. Lett. 2001;86:3911–3914. doi: 10.1103/PhysRevLett.86.3911. [DOI] [PubMed] [Google Scholar]
- 122.Ramakrishnan N, Ipsen JH, Rao M, Sunil Kumar PB. Organelle morphogenesis by active membrane remodeling. Soft Matter. 2015;11:2387–2393. doi: 10.1039/c4sm02311k. [DOI] [PubMed] [Google Scholar]
- 123.Brandizzi F, Barlowe C. Organization of the ER–Golgi interface for membrane traffic control. Nature. 2013;14:382–392. doi: 10.1038/nrm3588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Spang A. Retrograde Traffic from the Golgi to the Endoplasmic Reticulum. Cold Spring Harbor Perspectives in Biology. 2013;5:a013391–a013391. doi: 10.1101/cshperspect.a013391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Ramaswamy S, Toner J, Prost J. Nonequilibrium fluctuations, traveling waves, and instabilities in active membranes. Phys. Rev. Lett. 2000;84:3494–3497. doi: 10.1103/PhysRevLett.84.3494. [DOI] [PubMed] [Google Scholar]
- 126.Gompper G, Kroll DM. Phase-Diagram and Scaling Behavior of Fluid Vesicles. Phys. Rev. E. 1995;51:514–525. doi: 10.1103/physreve.51.514. [DOI] [PubMed] [Google Scholar]
- 127.Lipowsky R. Spontaneous tubulation of membranes and vesicles reveals membrane tension generated by spontaneous curvature. Faraday Discuss. 2013;161:305. doi: 10.1039/c2fd20105d. [DOI] [PubMed] [Google Scholar]