Splitting Methods for Convex Clustering

Abstract

Clustering is a fundamental problem in many scientific applications. Standard methods such as k-means, Gaussian mixture models, and hierarchical clustering, however, are beset by local minima, which are sometimes drastically suboptimal. Recently introduced convex relaxations of k-means and hierarchical clustering shrink cluster centroids toward one another and ensure a unique global minimizer. In this work we present two splitting methods for solving the convex clustering problem. The first is an instance of the alternating direction method of multipliers (ADMM); the second is an instance of the alternating minimization algorithm (AMA). In contrast to previously considered algorithms, our ADMM and AMA formulations provide simple and unified frameworks for solving the convex clustering problem under the previously studied norms and open the door to potentially novel norms. We demonstrate the performance of our algorithm on both simulated and real data examples. While the differences between the two algorithms appear to be minor on the surface, complexity analysis and numerical experiments show AMA to be significantly more efficient. This article has supplemental materials available online.

1 Introduction

In recent years convex relaxations of many fundamental, yet combinatorially hard, optimization problems in engineering, applied mathematics, and statistics have been introduced (Tropp, 2006). Good, and sometimes nearly optimal solutions, can be achieved at affordable computational prices for problems that appear at first blush to be computationally intractable. In this paper, we introduce two new algorithmic frameworks based on variable splitting that generalize and extend recent efforts to convexify the classic unsupervised problem of clustering.

Lindsten et al. (2011) and Hocking et al. (2011) formulate the clustering task as a convex optimization problem. Given n points x₁, …, x_n in ℝ^p, they suggest minimizing the convex criterion

$$F_{\gamma }(\mathbf{U})=\frac{1}{2}{\displaystyle \sum _{i=1}^n{\Vert {\mathbf{x}}_i-{\mathbf{u}}_i\Vert }_2^2+\gamma }{\displaystyle \sum _{i<j}{w}_{ij}\Vert {\mathbf{u}}_i-{\mathbf{u}}_j\Vert },$$ (1.1)

where γ is a positive tuning constant, w_ij = w_ji is a nonnegative weight, and the ith column u_i of the matrix U is the cluster center (centroid) attached to point x_i. Lindsten et al. (2011) consider an ℓ_q norm penalty on the differences u_i − u_j while Hocking et al. (2011) consider ℓ₁, ℓ₂, and ℓ_∞ penalties. In the current paper, an arbitrary norm defines the penalty.

The objective function bears some similarity to the fused lasso signal approximator (Tibshirani et al., 2005). When the ℓ₁ penalty is used in definition (1.1), we recover a special case of the General Fused Lasso (Hoefling, 2010; Tibshirani and Taylor, 2011). In the graphical interpretation of clustering, each point corresponds to a node in a graph, and an edge connects nodes i and j whenever w_ij > 0. Figure 1 depicts an example. In this case, the objective function F_γ(U) separates over the connected components of the underlying graph. Thus, one can solve for the optimal U component by component. Without loss of generality, we assume the graph is connected.

Figure 1.

A graph with positive weights w₁₂, w₁₅, w₃₄ and all other weights w_ij = 0.

When γ = 0, the minimum is attained when u_i = x_i, and each point occupies a unique cluster. As γ increases, the cluster centers begin to coalesce. Two points x_i and x_j with u_i = u_j are said to belong to the same cluster. For sufficiently high γ all points coalesce into a single cluster. Because the objective function F_γ(U) in equation (1.1) is strictly convex and coercive, it possesses a unique minimum point for each value of γ. If we plot the solution matrix U as a function of γ, then we can ordinarily identify those values of γ giving k clusters for any integer k between n and 1. In theory, k can decrement by more than 1 as certain critical values of γ are passed. Indeed, when points are not well separated, we observe that many centroids will coalesce abruptly unless care is taken in choosing the weights w_ij.

The benefits of this formulation are manifold. As we will show, convex relaxation admits a simple and fast iterative algorithm that is guaranteed to converge to the unique global minimizer. In contrast, the classic k-means problem has been shown to be NP-hard (Aloise et al., 2009; Dasgupta and Freund, 2009). In addition, the classical greedy algorithm for solving k-means clustering often gets trapped in suboptimal local minima (Forgy, 1965; Lloyd, 1982; MacQueen, 1967).

Another vexing issue in clustering is determining the number of clusters. Agglomerative hierarchical clustering (Gower and Ross, 1969; Johnson, 1967; Lance and Williams, 1967; Murtagh, 1983; Ward, 1963) finesses the problem by computing an entire clustering path. Agglomerative approaches, however, can be computationally demanding and tend to fall into suboptimal local minima since coalescence events are not reversed. The alternative convex relaxation considered here performs continuous clustering just as the lasso (Chen et al., 1998; Tibshirani, 1996) performs continuous variable selection. Figure 2 shows how the solutions to the alternative convex problem traces out an intuitively appealing, globally optimal, and computationally tractable solution path.

Figure 2.

Cluster path assignment: The simulated example shows five well separated clusters and the assigned clustering generated by the convex clustering algorithm under an ℓ₂-norm. The lines trace the path of the individual cluster centers as the regularization parameter γ increases.

1.1 Contributions

Our main contributions are two new methods for solving the convex clustering problem. Relatively little work has been published on algorithms for solving this optimization problem. In fact, the only other paper introducing dedicated algorithms for minimizing criterion (1.1) that we are aware of is Hocking et al. (2011). Lindsten et al. (2011) used the off-the-shelf convex solver CVX (CVX Research, Inc., 2012; Grant and Boyd, 2008) to generate solution paths. Hocking et al. (2011) note that CVX is useful for solving small problems but a dedicated formulation is required for scalability. Thus, they introduced three distinct algorithms for the three most commonly encountered norms. Given the ℓ₁ norm and unit weights w_ij, the objective function separates, and they solve the convex clustering problem by the exact path following method designed for the fused lasso (Hoefling, 2010). For the ℓ₁ and ℓ₂ norms with arbitrary weights w_ij, they employ subgradient descent in conjunction with active sets. Finally, they solve the convex clustering problem under the ℓ_∞ norm by viewing it as minimization of a Frobenius norm over a polytope. In this guise, the problem succumbs to the Frank-Wolfe algorithm (Frank and Wolfe, 1956) of quadratic programming.

In contrast to this piecemeal approach, we introduce two similar generic frameworks for minimizing the convex clustering objective function with an arbitrary norm. One approach solves the problem by the alternating direction method of multipliers (ADMM), while the other solves it by the alternating minimization algorithm (AMA). The key step in both cases computes the proximal map of a given norm. Consequently, both of our algorithms apply provided the penalty norm admits efficient computation of its proximal map.

In addition to introducing new algorithms for solving the convex clustering problem, the current paper contributes in other concrete ways: (a) We combine existing results on AMA and ADMM with the special structure of the convex clustering problem to characterize both of the new algorithms theoretically. In particular, the clustering problem formulation gives a minimal set of extra assumptions needed to prove the convergence of the ADMM iterates to the unique global minimum. We also explicitly show how the computational and storage complexity of our algorithms scales with the connectivity of the underlying graph. Examination of the dual problem enables us to identify a fixed step size for AMA that is associated with the Laplacian matrix of the underlying graph. Finally, our complexity analysis enables us to rigorously quantify the efficiency of the two algorithms so the two methods can be compared. (b) We provide new proofs of intuitive properties of the solution path. These results are tied solely to the minimization of the objective function (1.1) and hold regardless of the algorithm used to find the minimum point. (c) We provide guidance on how to choose the weights w_ij. Our suggested choices diminish computational complexity and enhance solution quality. In particular, we show that employing k-nearest neighbor weights allows the storage and computation requirements for our AMA method to grow linearly in problem size.

1.2 Related Work

The literature on clustering is immense; the reader can consult the books (Gordon, 1999; Hartigan, 1975; Kaufman and Rousseeuw, 1990; Mirkin, 1996; Wu and Wunsch, 2009) for a comprehensive review. The clustering function (1.1) can be viewed as a convex relaxation of either k-means clustering (Lindsten et al., 2011) or hierarchical agglomerative clustering (Hocking et al., 2011). Both of these classical clustering methods (Sneath, 1957; Sørensen, 1948; Ward, 1963) come in several varieties. The literature on k-means clustering reports notable improvements in the computation (Elkan, 2003) and quality of solutions (Arthur and Vassilvitskii, 2007; Bradley et al., 1997; Kaufman and Rousseeuw, 1990) delivered by the standard greedy algorithms. Faster methods for agglomerative hierarchical clustering have been developed as well (Fraley, 1998). Many statisticians view the hard cluster assignments of k-means as less desirable than the probabilistic assignments generated by mixture models (McLachlan, 2000; Titterington et al., 1985). Mixture models have the advantage of gracefully assigning points to overlapping clusters. These models are amenable to an EM algorithm and can be extended to infinite mixtures (Ferguson, 1973; Rasmussen, 2000; Neal, 2000).

Alternative approaches to clustering involve identifying components in the associated graph via its Laplacian matrix. Spectral clustering (Luxburg, 2007) can be effective in cases when the clusters are non-convex and linearly inseparable. Although spectral clustering is valuable, it does not conflict with convex relaxation. Indeed, Hocking et al. (2011) demonstrate that convex clustering can be effectively merged with spectral clustering. Although we agree with this point, the solution path revealed by convex clustering is meritorious in its own right because it partially obviates the persistent need for determining the number of clusters.

1.3 Notation and Organization

Throughout, scalars are denoted by lowercase letters (a), vectors by boldface lowercase letters (u), and matrices by boldface capital letters (U). The jth column of a matrix U is denoted by u_j. At times in our derivations, it will be easier to work with vectorized matrices. We adopt the convention of denoting the vectorization of a matrix (U) by its lower case letter in boldface (u). Finally, we denote sets by upper case letters (B).

The rest of the paper is organized as follows. We first characterize the solution path theoretically. Previous papers take intuitive properties of the path for granted. We then review the ADMM and AMA algorithms and adapt them to solve the convex clustering problem. Once the algorithms are specified, we discuss their convergence and computational and storage complexity. Practical issues such as weight choice and refinements such as accelerating the algorithms are discussed next. We then present some numerical examples of clustering. The paper concludes with a general discussion.

2 Properties of the solution path

The solution path U(γ) enjoys several nice properties as a function of the regularization parameter γ and the weight matrix W = (w_ij). These properties expedite its numerical computation. The proof of the following two propositions can be found in the Supplemental Materials.

Proposition 2.1

The solution path U(γ) exists, is unique, and depends continuously on γ. The path also depends continuously on the weight matrix W.

Existence and uniqueness of U sets the stage for a well-posed optimization problem. Continuity of U suggests employing homotopy continuation. Indeed, empirically we find great time savings in solving a sequence of problems over a grid of γ values when we use the solution of a previous value of γ as a warm start or initial value for the next larger γ value.

It is plausible that the centroids eventually coalesce to a common point as γ becomes sufficiently large. For the example shown in Figure 1, we intuitively expect for sufficiently large γ that the columns of U satisfy ${\mathbf{u}}_3={\mathbf{u}}_4={\overline{\mathbf{x}}}_{34}$ and ${\mathbf{u}}_1={\mathbf{u}}_2={\mathbf{u}}_5={\overline{\mathbf{x}}}_{125}$, where ${\overline{\mathbf{x}}}_{34}$ is the mean of x₃ and x₄ and ${\overline{\mathbf{x}}}_{125}$ is the mean of x₁, x₂, and x₅. The next proposition rigorously confirms our intuition.

Proposition 2.2

Suppose each point corresponds to a node in a graph with an edge between nodes i and j whenever w_ij > 0. If this graph is connected, then F_γ(U) is minimized by $\overline{\mathbf{X}}$ for γ sufficiently large, where each column of $\overline{\mathbf{X}}$ equals the average $\overline{\mathbf{x}}$ of the n vectors x_i.

We close this section by noting that in general the clustering paths are not guaranteed to be agglomerative. In the special case of the ℓ₁ norm with uniform weights w_ij = 1, Hocking et al. (2011) prove that the path is agglomerative. In the same paper they give an ℓ₂ norm example where the centroids fuse and then unfuse as the regularization parameter increases. This behavior, however, does not seem to occur very frequently in practice. Nonetheless, in the algorithms we describe next, we allow for such fission events to ensure that the computed solution path is truly the global minimizer of the convex criterion (1.1).

3 Algorithms to Compute the Clustering Path

Having characterized the solution path U(γ), we now tackle the task of computing it. We present two closely related optimization approaches: the alternating direction method of multipliers (ADMM) (Boyd et al., 2011; Gabay and Mercier, 1976; Glowinski and Marrocco, 1975) and the alternating minimization algorithm (AMA) (Tseng, 1991). Both approaches employ variable splitting to handle the shrinkage penalties in the convex clustering criterion (1.1).

Let us first recast the convex clustering problem as the equivalent constrained problem

$$\begin{array}{l}\text{minimize}\frac{1}{2}{\displaystyle \sum _{i=1}^n{\Vert {\mathbf{x}}_i-{\mathbf{u}}_i\Vert }_2^2+\gamma }{\displaystyle \sum _{l\in \mathcal{E}}{w}_l\Vert {\mathbf{v}}_l\Vert }\\ \text{subject to}{u}_{l_1}-u_{l_2}-v_l=0.\end{array}$$ (3.1)

Here we index a centroid pair by l = (l₁, l₂) with l₁ < l₂, define the set of edges over the non-zero weights $\mathcal{E}=\{l=(l_1,l_2):w_l>0\}$, and introduce a new variable ${\mathbf{v}}_l={\mathbf{u}}_{l_1}-{\mathbf{u}}_{l_2}$ to account for the difference between the two centroids. The purpose of variable splitting is to simplify optimization with respect to the penalty terms.

Splitting methods such as ADMM and AMA have been successfully used to attack similar problems in image restoration (Goldstein and Osher, 2009). To clarify the similarities and differences between ADMM and AMA, we briefly review how these two methods iteratively solve the following constrained optimization problem

$$\begin{array}{l}\text{minimize}f(\mathbf{u})+g(\mathbf{v})\\ \text{subject to}\mathbf{Au}+\mathbf{Bv}=\mathbf{c},\end{array}$$ (3.2)

which includes the constrained minimization problem (3.1) as a special case. Recall that finding the minimizer to an equality constrained optimization problem is equivalent to the identifying the saddle point of the associated Lagrangian function. Both ADMM and AMA invoke a related function called the augmented Lagrangian,

$${\mathcal{L}}_{\nu }(\mathbf{u},\mathbf{v},\mathbf{\lambda })=f(\mathbf{u})+g(\mathbf{v})+\langle \mathbf{\lambda },\mathbf{c}-\mathbf{Au}-\mathbf{Bv}\rangle +\frac{\nu }{2}{\Vert \mathbf{c}-\mathbf{Au}-\mathbf{Bv}\Vert }_2^2,$$

where the dual variable λ is a vector of Lagrange multipliers and ν is a nonnegative tuning parameter. When ν = 0, the augmented Lagrangian coincides with the ordinary Lagrangian.

ADMM minimizes the augmented Lagrangian one block of variables at a time before updating the dual variable λ. This yields the algorithm

$$\begin{array}{l}{\mathbf{u}}^{m+1}=\underset{\mathbf{u}}{\text{arg min}}{\mathcal{L}}_{\nu }(\mathbf{u},{\mathbf{v}}^m,{\mathbf{\lambda }}^m)\\ {\mathbf{v}}^{m+1}=\underset{\mathbf{v}}{\text{arg min}}{\mathcal{L}}_{\nu }({\mathbf{u}}^{m+1},\mathbf{v},{\mathbf{\lambda }}^m)\\ {\mathbf{\lambda }}^{m+1}={\mathbf{\lambda }}^m+\nu (\mathbf{c}-\mathbf{A}{\mathbf{u}}^{m+1}-\mathbf{B}{\mathbf{v}}^{m+1}).\end{array}$$ (3.3)

AMA takes a slightly different tack and updates the first block u without augmentation, assuming f(u) is strongly convex. This change is accomplished by setting the positive tuning constant ν to be 0. Thus, we update the first block u as

$${\mathbf{u}}^{m+1}=\underset{\mathbf{u}}{\text{arg min}}{\mathcal{L}}_0(\mathbf{u},{\mathbf{v}}^m,{\mathbf{\lambda }}^m),$$ (3.4)

and update v and λ as indicated in (3.3). Later we will see that this seemingly innocuous change pays large dividends in the convex clustering problem. Although block descent appears to complicate matters, it often markedly simplifies optimization in the end. In the case of convex clustering, the updates are either simple linear transformations or evaluations of proximal maps, which we discuss next.

3.1 Proximal Map

For σ > 0 the function

$${\text{prox}}_{\sigma \mathrm{\Omega }}(\mathbf{u})=\underset{\mathbf{v}}{\text{arg min}}\left[\sigma \mathrm{\Omega }(\mathbf{v})+\frac{1}{2}{\Vert \mathbf{u}-\mathbf{v}\Vert }_2^2\right]$$

is a well-studied operation called the proximal map of the function Ω(v). The proximal map exists and is unique whenever the function Ω(v) is convex and lower semicontinuous. Norms satisfy these conditions, and for many norms of interest the proximal map can be evaluated by either an explicit formula or an efficient algorithm. Table 1 lists some common examples. The proximal maps for the ℓ₁ and ℓ₂ norms have explicit solutions and can be computed in $\mathcal{O}(p)$ operations for a vector v ∈ ℝ^p. The proximal map for the ℓ_∞ norm requires projection onto the unit simplex and lacks an explicit solution. However, there are good algorithms for projecting onto the unit simplex (Duchi et al., 2008; Michelot, 1986). In particular, Duchi et al.’s projection algorithm makes it possible to evaluate ${\text{prox}}_{\sigma {\Vert \cdot \Vert }_{\infty }}(\mathbf{v})$ in $\mathcal{O}(\mathit{plogp})$ operations.

Table 1.

Proximal maps for common norms.

Norm	Ω(v)	proxσΩ(v)	Comment
ℓ1	‖v‖1	${\left[1-\frac{\sigma }{\left|v_l\right|}\right]}_{+}{v}_l$	Element-wise soft-thresholding
ℓ2	‖v‖2	${\left[1-\frac{\sigma }{{\Vert \mathbf{v}\Vert }_2}\right]}_{+}\mathbf{v}$	Block-wise soft-thresholding
ℓ∞	‖v‖∞	$\mathbf{v}-{\mathcal{P}}_{\sigma S}(\mathbf{v})$	S is the unit simplex

3.2 ADMM updates

The augmented Lagrangian for criterion (3.1) is given by

$$\begin{array}{l}{\mathcal{L}}_{\nu }(\mathbf{U},\mathbf{V},\mathbf{\Lambda })=\frac{1}{2}{\displaystyle \sum _{i=1}^n{\Vert {\mathbf{x}}_i-{\mathbf{u}}_i\Vert }_2^2+\gamma }{\displaystyle \sum _{l\in \mathcal{E}}{w}_l\Vert {\mathbf{v}}_l\Vert }\\ +{\displaystyle \sum _{l\in \mathcal{E}}\langle {\mathbf{\lambda }}_l,{\mathbf{v}}_l-{\mathbf{u}}_{l_1}+{\mathbf{u}}_{l_2}\rangle +\frac{\nu }{2}{\displaystyle \sum _{l\in \mathcal{E}}{\Vert {\mathbf{v}}_l-{\mathbf{u}}_{l_1}+{\mathbf{u}}_{l_2}\Vert }_2^2}}.\end{array}$$ (3.5)

To update U, we need to minimize the function

$$f(\mathbf{U})=\frac{1}{2}{\displaystyle \sum _{i=1}^n{\Vert {\mathbf{x}}_i-{\mathbf{u}}_i\Vert }_2^2+\frac{\nu }{2}}{\displaystyle \sum _{l\in \mathcal{E}}{\Vert {\stackrel{\sim }{\mathbf{v}}}_l-{\mathbf{u}}_{l_1}+{\mathbf{u}}_{l_2}\Vert }_2^2},$$

where ${\stackrel{\sim }{\mathbf{v}}}_l={\mathbf{v}}_l+{\nu }^{-1}{\lambda }_l$. The gradient of this function vanishes at U satisfying the linear system

$$\mathbf{UM}=\mathbf{X}+\nu {\displaystyle \sum _{l\in \mathcal{E}}{\stackrel{\sim }{\mathbf{v}}}_l{\left({\mathbf{e}}_{l_1}-{\mathbf{e}}_{l_2}\right)}^t,}$$ (3.6)

where $\mathbf{M}=\mathbf{I}+\nu {\displaystyle {\sum }_{l\in \mathcal{E}}({\mathbf{e}}_{l_1}-{\mathbf{e}}_{l_2}){\left({\mathbf{e}}_{l_1}-{\mathbf{e}}_{l_2}\right)}^t}$. If the edge set $\mathcal{E}$ contains all possible edges, then the update for U can be computed analytically as

$${\mathbf{u}}_i=\frac{1}{1+n\nu }{\mathbf{y}}_i+\frac{n\nu }{1+n\nu }\overline{\mathbf{x}},$$ (3.7)

where $\overline{\mathbf{x}}$ is the average column of X and

$${\mathbf{y}}_i={\mathbf{x}}_i+{\displaystyle \sum _{l_1=i}[{\mathbf{\lambda }}_l+\nu {\mathbf{v}}_l]-}{\displaystyle \sum _{l_2=i}[{\mathbf{\lambda }}_l+\nu {\mathbf{v}}_l]}.$$

Detailed derivations of the equalities in (3.6) and (3.7) can be found in the Supplemental Materials.

Before deriving the updates for V, we remark that although a fully connected weights graph allows one to write explicit updates for U, doing so comes at the cost of increasing the number of variables v_l and λ_l. Such choices are not immaterial, and we will discuss the tradeoffs later. To update V, we first observe that the augmented Lagrangian ${\mathcal{L}}_{\nu }(\mathbf{U},\mathbf{V},\mathbf{\Lambda })$ is separable in the vectors v_l. A particular difference vector v_l is determined by the proximal map

$$\begin{array}{l}{\mathbf{v}}_l=\underset{{\mathbf{v}}_l}{\text{arg min}}\frac{1}{2}\left[{\Vert {\mathbf{v}}_l-({\mathbf{u}}_{l_1}-{\mathbf{u}}_{l_2}-{\nu }^{-1}{\mathbf{\lambda }}_l)\Vert }_2^2+\frac{\gamma w_l}{\nu }\Vert {\mathbf{v}}_l\Vert \right]\\ ={\mathrm{prox}}_{{\sigma }_l\Vert \cdot \Vert }({\mathbf{u}}_{l_1}-{\mathbf{u}}_{l_2}-{\nu }^{-1}{\mathbf{\lambda }}_l),\end{array}$$ (3.8)

where σ_l = γw_l/ν. Finally, the Lagrange multipliers are updated by

$${\mathbf{\lambda }}_l={\mathbf{\lambda }}_l+\nu ({\mathbf{v}}_l-{\mathbf{u}}_{l_1}-{\mathbf{u}}_{l_2}).$$

Algorithm 1 summarizes the ADMM algorithm. To track the progress of ADMM, we use standard methods given in (Boyd et al., 2011) based on primal and dual residuals. Details on the stopping rules that we employ are given in the Supplemental Materials.

Algorithm 1 ADMM
Initialize Λ0 and V0.
1:	for m = 1, 2, 3, … do
2:	for i = 1, …, n do
3:	${\mathbf{y}}_i={\mathbf{x}}_i+{\displaystyle {\sum }_{l_1=i}\left[{\mathbf{\lambda }}_l^{m-1}+\nu {\mathbf{v}}_l^{m-1}\right]}-{\displaystyle {\sum }_{l_2=i}\left[{\mathbf{\lambda }}_l^{m-1}+\nu {\mathbf{v}}_l^{m-1}\right]}$
4:	end for
5:	${\mathbf{U}}^m=\frac{1}{1+n\nu }\mathbf{Y}+\frac{n\nu }{1+n\nu }\overline{\mathbf{X}}$
6:	for all l do
7:	${\mathbf{v}}_l^m={\text{prox}}_{{\sigma }_l\Vert \cdot \Vert }\left({\mathbf{u}}_{l_1}^m-{\mathbf{u}}_{l_2}^m-{\nu }^{-1}{\mathbf{\lambda }}_l^{m-1}\right)$
8:	${\mathbf{\lambda }}_l^m={\mathbf{\lambda }}_l^{m-1}+\nu \left({\mathbf{v}}_l^m-{\mathbf{u}}_{l_1}^m+{\mathbf{u}}_{l_2}^m\right)$
9:	end for
10:	end for

3.3 AMA updates

Since AMA shares its update rules for V and Λ with ADMM, consider updating U. Recall that AMA updates U by minimizing the ordinary Lagrangian. In the ν = 0 case, we have

$${\mathbf{U}}^{m+1}=\underset{\mathbf{U}}{\text{arg min}}\frac{1}{2}{\displaystyle \sum _{i=1}^n{\Vert {\mathbf{x}}_i-{\mathbf{u}}_i\Vert }_2^2}+{\displaystyle \sum _{l\in \mathcal{E}}\langle {\mathbf{\lambda }}_l^m,{\mathbf{v}}_l-{\mathbf{u}}_{l_1}-{\mathbf{u}}_{l_2}\rangle }.$$

In contrast to ADMM, this minimization separates in each u_i and gives an update that does not depend on v_l, namely

$${\mathbf{u}}_i^{m+1}={\mathbf{x}}_i+{\displaystyle \sum _{l_1=i}{\mathbf{\lambda }}_l^m}-{\displaystyle \sum _{l_2=i}{\mathbf{\lambda }}_l^m}.$$ (3.9)

Further scrutiny of the updates for V and Λ reveals that AMA does not even require computating V. Applying standard results from convex calculus, it can be shown that Λ has the following update

$${\mathbf{\lambda }}_l^{m+1}={\mathcal{P}}_{C_l}\left({\mathbf{\lambda }}_l^m-\nu {\mathbf{g}}_l^{m+1}\right),$$ (3.10)

where ${\mathbf{g}}_l^m={\mathbf{u}}_{l_1}^m-{\mathbf{u}}_{l_2}^m$, C_l = {λ_l: ‖λ_l‖_† ≤ γω_l}, and ‖·‖_† is the dual norm of the norm defining the fusion penalty. Algorithm 2 summarizes the AMA algorithm. Detailed derivation of this simplification is in the Supplemental Materials. At the termination of Algorithm 2, the centroids can be recovered from the dual variables using equation (3.9).

Algorithm 2 AMA
Initialize λ0.
1:	for m = 1, 2, 3, … do
2:	for i = 1, …, n do
3:	${\mathrm{\Delta }}_i^m={\displaystyle {\sum }_{l_1=i}{\mathbf{\lambda }}_l^{m-1}}-{\displaystyle {\sum }_{l_2=i}{\mathbf{\lambda }}_l^{m-1}}$
4:	end for
5:	for all l do
6:	${\mathbf{g}}_l^m={\mathbf{x}}_{l_1}-{\mathbf{x}}_{l_2}+{\mathrm{\Delta }}_{l_1}^m-{\mathrm{\Delta }}_{l_2}^m$
7:	${\mathbf{\lambda }}_l^m={\mathcal{P}}_{C_l}\left({\mathbf{\lambda }}_l^{m-1}-\nu {\mathbf{g}}_l^m\right)$
8:	end for
9:	end for

Note that Algorithm 2 look remarkably like a projected gradient algorithm. Indeed, Tseng (1991) shows that AMA is actually performing proximal gradient ascent to maximize a dual problem. Since the dual of the convex clustering problem (3.1) is essentially a constrained least squares problem, it is hardly surprising that it can be solved numerically by the classic projected gradient algorithm, a special case of the proximal gradient algorithm. In addition to providing a simple interpretation of the AMA method, the dual problem allows us to derive a rigorous stopping criterion for AMA based on the duality gap, a bound on how much the primal objective evaluated at the current iterate exceeds its optimal value. Due to space limitations, both the dual problem and duality gap computation are covered in the Supplemental Materials. Before proceeding, however, let us emphasize that AMA requires tracking of only as many dual variable λ_l as there are non-zero weights. We will find later that sparse weights often produces better quality clusterings. Thus, when relatively few weights are non-zero, the number of variables introduced by splitting does not become prohibitive under AMA.

4 Convergence

Both ADMM and AMA converge under reasonable conditions. Convergence of ADMM is guaranteed for any ν > 0. Convergence for AMA is guaranteed when ν is not too large. In this section, we show how the specific structure of the convex clustering problem can give stronger convergence results for ADMM and provide guidance on choosing ν in AMA and improve AMA’s rate of convergence in practice. All proofs can be found in the Supplemental Materials.

4.1 ADMM

Under minimal assumptions, it can be shown that the limit points of an ADMM iterate sequence coincide with the stationary points of the objective function being minimized (Boyd et al., 2011). Note, however, this does not guarantee that the iterates U^m converge to U^*. Since the convex clustering criterion F_γ(U) defined by equation (1.1) is strictly convex and coercive, we have the stronger result that the ADMM iterate sequence converges to the unique global minimizer U^* of F_γ(U).

Proposition 4.1

The iterates U^m in Algorithm 1 converge to the unique global minimizer U^* of the clustering criterion F_γ(U).

4.2 AMA

The convergence of Algorithm 2 hinges on the choice of ν, which in turn depends on the connectivity of the associated graph.

Proposition 4.2

Let ${\mathbf{u}}_i^{m+1}={\mathbf{x}}_i+{\displaystyle {\sum }_{l_1=i}{\mathbf{\lambda }}_l^m}-{\displaystyle {\sum }_{l_2=i}{\mathbf{\lambda }}_l^m}$, where ${\mathbf{\lambda }}_l^m$, where ${\lambda }_l^m$ are the iterates in Algorithm 2. Then the sequence U^m+1 converges to the unique global minimizer U^* of the clustering criterion F_γ(U), provided that ν < 2/ρ(L), where ρ(L) denotes the largest eigenvalue of L, the Laplacian matrix of the associated graph.

In lieu of computing ρ(L) numerically, one can bound it by theoretical arguments. In general ρ(L) ≤ n (Anderson and Morley, 1985), with equality when the graph is fully connected and w_ij > 0 for all i < j. Choosing a fixed step size of ν < 2/n works in practice when there are fewer than 1000 data points and the graph is dense. For a sparse graph with bounded node degrees, the sharper bound

$$\rho (\mathbf{L})\le max\{d(i)+d(j):(i,j)\in \mathcal{E}\}$$

applies, where d(i) is the degree of the ith node (Anderson and Morley, 1985). This bound can be computed quickly in $\mathcal{O}(n+\epsilon )$ operations, where ε denotes the number of edges in $\mathcal{E}$. Section 7.2 demonstrates the overwhelming speed advantage AMA on sparse graphs.

5 Computational Complexity

The computational complexity of an optimization algorithm includes the amount of work per iteration, the number of iterations until convergence, and the overall memory requirements. We discuss the first and third components. For the AMA and ADMM convex clustering algorithms, the number of iterations to achieve a desired level of accuracy can be derived from existing complexity results in the literature. Details can be found in the Supplemental Materials.

5.1 AMA

Inspection of Algorithm 2 shows that computing all Δ_i requires p(2ε − n) total additions and subtractions. Computing all vectors g_l in Algorithm 2 takes $\mathcal{O}(\epsilon p)$ operations, and taking the subsequent gradient step costs $\mathcal{O}(\epsilon p)$ operations. Computing the needed projections costs $\mathcal{O}(\epsilon p)$ operations for the ℓ₁ and ℓ₂ norms and $\mathcal{O}(\epsilon \mathit{plogp})$ operations for the ℓ_∞ norm. Finally computing the duality gap costs $\mathcal{O}(np+\epsilon p)$ operations. Details on the duality gap computation appear in the Supplemental Materials. The assumption that n is $\mathcal{O}(\epsilon )$ entails smaller costs. A single iteration with gap checking then costs just $\mathcal{O}(\epsilon p)$ operations for the ℓ₁ and ℓ₂ norms and $\mathcal{O}(\epsilon \mathit{plogp})$ operations for the ℓ_∞ norm.

Total storage is $\mathcal{O}(p\epsilon +np)$. In the worst case ε is $\left(\begin{array}{c}n\\ 2\end{array}\right)$. However, if we limit a node’s connectivity to its k-nearest neighbors, then ε is $\mathcal{O}(kn)$. Thus, the computational complexity of the problem in the worst case is quadratic in the number of points n and linear under the restriction to k-nearest neighbors connectivity. Storage is quadratic in n in the worst case and linear in n under the k-nearest neighbors restriction. Thus, limiting a point’s connectivity to its k-nearest neighbors renders both the storage requirements and operation counts linear in the problem size, namely $\mathcal{O}(\mathit{knp})$.

5.2 ADMM

We have two cases to consider. First consider the explicit updates outlined in Algorithm 1 when the edge set $\mathcal{E}$ is full. By nearly identical arguments as above, the complexity of a single round of ADMM updates with primal and dual residual calculation requires $\mathcal{O}(n^{2}p)$ operations for the ℓ₁ and ℓ₂ norms and $\mathcal{O}(n^2\mathit{plogp})$ operations for the ℓ_∞ norm. Thus, the ADMM algorithm based on the explicit updates (3.7) requires the same computational effort as AMA in the worst case. In this setting both ADMM and AMA also have $\mathcal{O}(p{n}^2)$ storage requirements.

The situation does not improve by much when we consider the more frugal alternative in which $\mathcal{E}$ contains only node pairings corresponding to non-zero weights. In this case, the variables Λ and V have only as many columns as there are non-zero weights. Now the storage requirements are $\mathcal{O}(p\epsilon +np)$ like AMA, but the cost of updating U, the most computationally demanding step, remains quadratic in n. Recall we need to solve a linear system of equations (3.6)

$$\mathbf{UM}=\mathbf{X}+{\displaystyle \sum _{l\in \mathcal{E}}{\stackrel{\sim }{\mathbf{v}}}_l{\left({\mathbf{e}}_{l_1}-{\mathbf{e}}_{l_2}\right)}^t},$$

where M ∈ ℝ^n×n. Since M is positive definite and does not change throughout the ADMM iterations, the prudent course of action is to compute and cache its Cholesky factorization. The factorization requires $\mathcal{O}(n^3)$ operations to calculate but that cost can be amortized across the repeated ADMM updates. With the Cholesky factorization in hand, we can update each row of U by solving two sets of n-by-n triangular systems of equations, which together requires $\mathcal{O}(n^2)$ operations. Since U has p rows, the total amount of work to update U is $\mathcal{O}(n^{2}p)$. Therefore, the overall amount of work per ADMM iteration is $\mathcal{O}(n^{2}p+\epsilon p)$ operations for the ℓ₁ and ℓ₂ norms and $\mathcal{O}(n^{2}p+\epsilon \mathit{plogp})$ operations for the ℓ_∞ norm. Thus, in stark constrast to AMA, both ADMM approaches grow quadratically, either in storage requirements or computational costs, regardless of how we might limit the size of the edge set $\mathcal{E}$.

6 Weights, Cluster Assignment, and Acceleration

We now address some practical issues that arise in applying our algorithms.

Weights

The weight matrix W can dramatically affect the quality of the clustering path. We set the weight between the ith and jth points equal to $w_{ij}={\iota }_{\{i,j\}}^k\exp \left(-\varphi {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }_2^2\right)$, where the indicator function ${\iota }_{\{i,j\}}^k$ is 1 if j is among i’s k-nearest-neighbors or vice versa and 0 otherwise. The second factor is a Gaussian kernel that slows the coalescence of distant points. The constant ϕ is nonnegative; the value ϕ = 0 corresponds to uniform weights. As noted earlier, limiting positive weights to nearest neighbors improves both computational efficiency and clustering quality. Although the two factors defining the weights act similarly, their combination increases the sensitivity of the clustering path to the local density of the data.

Cluster Assignment

We determine clustering assignments as a function of γ by reading off which centroids fuse. For both ADMM and AMA, such assignments can be performed in $\mathcal{O}(n)$ operations using the differences variable V. In the case of AMA, where we do not store a running estimate of V, we compute V via the update (3.8) after the algorithm terminates for a given γ. Once we determine V, we simply apply breadth-first search to identify the connected components of the graph induced by V. This graph identifies a node with every data point and places an edge between the lth pair of points if and only if v_l = 0. Each connected component corresponds to a cluster. Note that the graph described here varies with γ, through the matrix V, and is unrelated to the graph discussed in the rest of this paper, which depends solely on the weights W and is invariant to γ.

Acceleration

Both AMA and ADMM admit acceleration at little additional computational cost (Goldstein et al., 2012). In our timing comparisons, accelerated variants of AMA and ADMM are used. Details on our acceleration techniques can be found in the Supplemental Materials.

7 Numerical Experiments

We now report numerical experiments on convex clustering for a synthetic and real data set. Similar experiments on two additional real data sets (iris and Senate) can be found in the Supplemental Materials. In particular, we focus on how the choice of the weights w_ij affects the quality of the clustering solution. Prior research on this question is limited. Both Lindsten et al. (2011) and Hocking et al. (2011) suggest weights derived from Gaussian kernels and k-nearest neighbors. Because Hocking et al. try only Gaussian kernels, in this section we follow up on their untested suggestion of combining Gaussian kernels and k-nearest neighbors.

We also compare the run times of our splitting methods to the run times of the subgradient algorithm employed by Hocking et al. for ℓ₂ paths. Our attention here focuses on solving the ℓ₂ path since the rotational invariance of the 2-norm makes it a robust choice in practice. Hocking et al. provide R and C++ code for their algorithms. Our algorithms are implemented in R and C. To make a fair comparison, we run our algorithm until it reaches a primal objective value that is less than or equal to the primal objective value obtained by the subgradient algorithm. Specifically, we first run the Hocking et al. code to generate a clusterpath and record the sequence of γ’s generated by their code. We then run our algorithms over the same sequence of γ’s and stop once our primal objective value falls below their value. We also retain the native stopping rule computations employed by our splitting methods, namely the dual loss calculations for AMA and residual calculations for ADMM. Since AMA already calculates the primal loss, this is not an additional burden. Although convergence monitoring creates additional work for ADMM, the added primal loss calculation at worst changes only the constant in the complexity bound. This follows since computing the primal loss requires $\mathcal{O}(np+\epsilon p)$ total operations.

7.1 Qualitative Comparisons

The following examples demonstrate how the character of the solution paths can vary drastically with the choice of weights w_ij.

Two Half Moons

Consider the standard simulated data of two interlocking half moons in ℝ² composed of 100 points each. Figure 3 shows four convex clustering paths computed assuming two different numbers of nearest neighbors (10 and 50) and two different kernel constants ϕ (0 and 0.5). The upper right panel makes it evident that limiting the number of nearest neighbors (k = 10) and imposing non-uniform Gaussian kernel weights (ϕ = 0.5) produce the best clustering path. Using too many neighbors and assuming uniform weights results in little agglomerative clustering until late in the clustering path (lower left panel). The two intermediate cases diverge in interesting ways. The hardest set of points to cluster are the points in the upper half moon’s right tip and the lower half moon’s left tip. Limiting the number of nearest neighbors and omitting the Gaussian kernel (upper left panel) correctly agglomerates the easier points, but waffles on the harder points, agglomerating them only at the very end when all points coalesce at the grand mean. Conversely, using too many neighbors and the Gaussian kernel (lower right panel) leads to a clustering path that does not hedge but incorrectly assigns the harder points.

Figure 3.

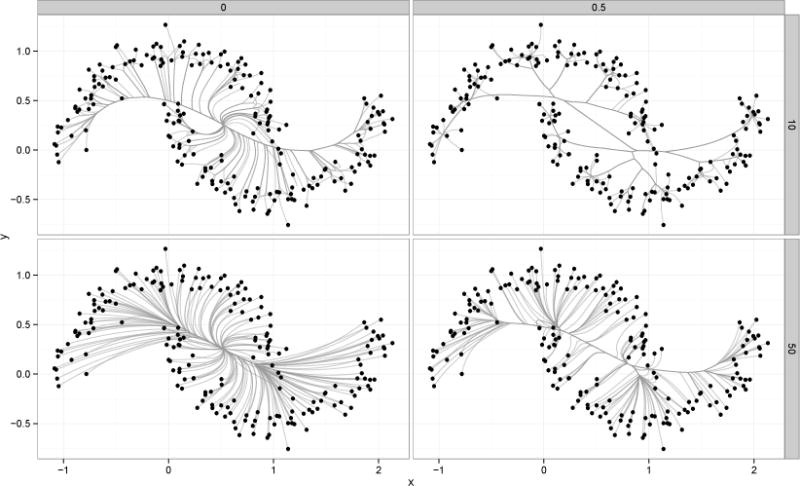
Halfmoons Example: The first and second rows show results using k = 10 and 50 nearest neighbors respectively. The first and second columns show results using ϕ = 0 and 0.5 respectively.

Dentition of mammals

Next we consider the problem of clustering mammals based on their dentition (Hartigan, 1975). Eight different kinds of teeth are tallied for each mammal: the number of top incisors, bottom incisors, top canines, bottom canines, top premolars, bottom premolars, top molars, and bottom molars. We removed observations with teeth distributions that were not unique, leaving us with 27 mammals. Figure 4 shows the resulting clustering paths under two different choices of weights. On the left w_ij = 1 for all i ≠ j, and on the right we use 5-nearest neighbors and ϕ = 0.5. Weights sensitive to the local density give superior results. Since there are eight variables, to visualize results we project the data and the fitted clustering paths onto the first two principal components of the data. The cluster path gives a different and perhaps more sensible solution than a two dimensional principal component analysis (PCA). For example, the brown bat is considered more similar to the house bat and red bat, even though it is closer in the first two PCA coordinates to the coyote and oppossum.

Figure 4.

Clustering path under the ℓ₂ norm for Mammal Data. Panel on the left (Set A) used w_ij = 1 for all i ≠ j. Panel on the right (Set B) used k = 5 nearest neighbors and ϕ = 0.5.

7.2 Timing Comparisons

We now present results on two batches of experiments, with dense weights in the first batch and sparse ones in the second. For the first set of experiments, we compared the run times of the subgradient descent algorithm of Hocking et al. (2011), accelerated ADMM, and accelerated AMA on 10 replicates of simulated data consisting of 100, 200, 300, 400, and 500 points in ℝ² drawn from a multivariate standard normal. We limited our study to at most 500 points because the subgradient algorithm took several hours on a single realization of 500 points. Limiting the number of data points allowed us to use the simpler, but less storage efficient, ADMM formulation given in equation (3.7). For AMA, we fixed the step size at ν = 1/n. For all tests, we assigned full-connectivity weights based on the indicator ${\iota }_{\{i,j\}}^k\equiv 1$ and tuning constant ϕ = −2. The parameter ϕ was chosen to ensure that the smallest weight was bounded safely away from zero. The full-connectivity assumption illustrates the superiority of AMA even under its least favorable circumstances. To trace out the entire clusterpath, we ran the Hocking subgradient algorithm to completion and invoked its default stopping criterion, namely a gradient with an ℓ₂ norm below 0.001. As noted earlier, we stopped our ADMM and AMA algorithms once their centroid iterates achieved a primal loss less than or equal to that achieved by the subgradient algorithm.

Table 2 shows the resulting mean times in seconds. Box-plots showing how the run time scales with the number of data points n can be found in the Supplemental Materials. All three algorithms scale quadratically in the number of points. This is expected for ADMM and AMA because all weights w_ij are positive. Nonetheless, the three algorithms possess different rate constants, with AMA possessing the slowest mean growth. The subgradient and ADMM algorithms performed commensurately, although the ADMM algorithm was almost twice as fast on average when n = 500. Again, to ensure fair comparisons with the subgradient algorithm, we required ADMM to make extra primal loss computations. This change tends to inflates its rate constant. In summary, we see that fast AMA leads to affordable computation times, on the order of minutes for hundreds of data points, in contrast to subgradient descent, which incurs run times on the order of hours for 400 to 500 data points.

Table 2.

Timing comparison under the ℓ₂ norm: Dense weights. Mean run times are in seconds. Different methods are listed on each row. Each column reports times for varying number of points.

	100	200	300	400	500
Subgradient	44.40	287.86	2361.84	3231.21	13895.50
AMA	16.09	71.67	295.23	542.45	1109.67
ADMM	57.82	449.68	1430.05	3432.77	6745.82

In the second batch of experiments, the same set up is retained except for assignments of weights and step length choice for AMA. We used ϕ = −2 again, but this time we zeroed out all weights except those corresponding to the $k=\frac{n}{4}$ nearest neighbors of each point. For AMA we used step sizes based on the bound (4.1). Table 3 shows the resulting mean run times in seconds. As before more detailed box-plot comparisons can be found in the Supplemental Materials. As attested by the shorter run times for all three algorithms, incorporation of sparse weights appears to make the problems easier to solve. In this case ADMM was uniformly better on average than the subgradient method for all n. Even more noteworthy is the pronounced speed advantage of AMA over the other two algorithms for large n. When clustering 500 points, AMA requires on average a mere 7 seconds compared to 5 to 7 minutes for the subgradient and ADMM algorithms.

Table 3.

Timing comparison under the ℓ₂ norm: Sparse weights. Mean run times are in seconds. Different methods are listed on each row. Each column reports times for varying number of points.

	100	200	300	400	500
Subgradient	6.52	37.42	161.68	437.32	386.45
AMA	1.50	2.94	4.46	6.02	7.44
ADMM	3.78	21.35	61.23	139.37	297.99

8 Conclusion & Future Work

In this paper, we introduce two splitting algorithms for solving the convex clustering problem. The splitting perspective encourages path following, one of the chief benefits of convex clustering. The splitting perspective also permits centroid penalties to invoke an arbitrary norm. The only requirement is that the proximal map for the norm be readily computable. Equivalently, projection onto the unit ball of the dual norm should be straightforward. Because proximal maps and projection operators are generally well understood, it is possible for us to quantify the computational complexity and convergence properties of our algorithms.

It is noteworthy that ADMM did not fare as well as AMA. ADMM has become quite popular in machine learning circles in recent years. Applying variable splitting and using ADMM to iteratively solve the convex clustering problem seemed like an obvious and natural initial strategy. Only later during our study did we implement the less favored AMA algorithm. Considering how trivial the differences are between the generic block updates for ADMM (3.3) and AMA (3.4), we were surprised by the performance gap between them. In the convex clustering problem, however, there is a non-trivial difference between minimizing the augmented and unaugmented Lagrangian in the first block update. This task can be accomplished in less time and space by AMA.

Two features of the convex clustering problem make it an especially good candidate for solution by AMA. First, the objective function is strongly convex and therefore has a Lipschitz differentiable dual. Lipschitz differentiability is a standard condition ensuring the convergence of proximal gradient algorithms. Second, a good step size can be readily computed from the Laplacian matrix generated by the edge set $\mathcal{E}$. Without this prior bound, we would have to employ a more complicated line-search.

Our complexity analysis and simulations show that the accelerated AMA method appears to be the algorithm of choice. Nonetheless, given that alternative variants of ADMM may close the performance gap (Deng and Yin, 2012; Goldfarb et al., 2012), we are reluctant to dismiss ADMM too quickly. Both algorithms deserve further investigation. For instance, in both ADMM and AMA, updates of Λ and V could be parallelized. Hocking et al. also employed an active set approach to reduce computations as the centroids coalesce. A similar strategy could be adopted in our framework, but it incurs additional overhead as checks for fission events have to be introduced. An interesting and practical question brought up by Hocking et al. remains open, namely under what conditions or weights are fusion events guaranteed to be permanent as γ increases? In all our experiments, we did not observe any fission events. Identifying those conditions would eliminate the need to check for fission in such cases and expedite computation.

For AMA, the storage demands and computational complexity of convex clustering depend quadratically on the number of points in the worst case. Limiting a point’s connections to its k-nearest neighbors, for example, ensures that the number of edges in the graph is linear in the number of nodes in the graph. Eliminating long-range dependencies is often desirable anyway. Choosing sparse weights can improve both cluster quality and computational efficiency. Moreover, finding the exact k-nearest neighbors is likely not essential, and we conjecture that the quality of solutions would not suffer greatly if approximate nearest neighbors are used and algorithms for fast computation of approximately nearest neighbors are leveraged (Slaney and Casey, 2008). On very large problems, the best strategy might be to exploit the continuity of solution paths in the weights. This suggests starting with even sparser graphs than the desired one and generating a sequence of solutions to increasingly dense problems. A solution with fewer edges can serve as a warm start for the next problem with more edges.

The splitting perspective also invites extensions that impose structured sparsity on the centroids. Witten and Tibshirani (2010) discuss how sparse centroids can improve the quality of a solution, especially when only a relatively few features of data drive clustering. Structured sparsity can be accomplished by adding a sparsity-inducing norm penalty to the U updates. The update for the centroids for both AMA and ADMM then rely on another proximal map of a gradient step. Introducing a sparsifying norm, however, raises the additional complication of choosing the amount of penalization.

Except for a few hints about weights, our analysis leaves the topic of optimal clustering untouched. Recently, von Luxburg (2010) suggested some principled approaches to assessing the quality of a clustering assignment via data perturbation and resampling. These clues are worthy of further investigation.