An “Almost Exhaustive” Search-Based Sequential Permutation Method for Detecting Epistasis in Disease Association Studies

Abstract

Due to the complex nature of common diseases, their etiology is likely to involve “uncommon but strong” (UBS) interactive effects—i.e. allelic combinations that are each present in only a small fraction of the patients but associated with high disease risk. However, the identification of such effects using standard methods for testing association can be difficult. In this work, we introduce a method for testing interactions that is particularly powerful in detecting UBS effects. The method consists of two modules—one is a pattern counting algorithm designed for efficiently evaluating the risk significance of each marker combination, and the other is a sequential permutation scheme for multiple testing correction. We demonstrate the work of our method using a candidate gene data set for cardiovascular and coronary diseases with an injected UBS three-locus interaction. In addition, we investigate the power and false rejection properties of our method using data sets simulated from a joint dominance three-locus model that gives rise to UBS interactive effects. The results show that our method can be much more powerful than standard approaches such as trend test and multifactor dimensionality reduction for detecting UBS interactions.

INTRODUCTION

Epistasis has long been suspected to contribute to the unexplained genetic variance of common complex traits [Maher, 2008; Moore and Williams, 2009], and many statistical methods have been proposed in recent years to identify genetic interactions. Some notable examples include multifactor dimensionality reduction (MDR) [Bush et al., 2006; Moore and Williams, 2009; Ritchie et al., 2001], random forests [Lunetta et al., 2004], and Bayesian epistasis association mapping [Zhang and Liu, 2007]. (Interested readers can see [Cordell, 2009] for a review of these and other existing approaches.) While these methods have led to some interesting findings of genetic interaction, their application to common diseases, so far, has achieved limited success.

The performance of most existing methods for testing disease association rely on an implicit assumption that the underlying allelic combinations of interest contribute to the disease risk of a large proportion of the patients. However, for common diseases, whose etiology involves multiple biological pathways and is influenced by various environmental factors, it is very likely that there exist allelic combinations that are present in only a small fraction of the patients, but when present, incur high disease risk. For example, a particular allelic combination may have a disease risk ratio as high as 4, but is present in only 10% of the patients. For simplicity we refer to these as “uncommon but strong” (UBS) effects. A considerable part of the missing inheritability of common diseases could be due to such effects.

Because each “uncommon” effect pertains to only a small fraction of patients, they often do not exhibit main effects significant enough to withstand multiple testing correction. Thus, methods that rely on recovering interactions from significant marginal effects are not effective in detecting UBS effects. One way to overcome this difficulty is to test marker combinations directly in an exhaustive manner. Some existing methods such as MDR indeed adopt this exhaustive search scheme.

When using an exhaustive search scheme to look for interactions (not just UBS effects but interactions in general), one must be careful about how statistical inference, in particular multiple testing correction, should be carried out. More specifically, multiple testing correction methods such as permutation testing must be adjusted in two important ways for this context. First, correction should be done conditional on the length of the interactions (i.e. the number of markers involved) in that the space of all possible marker combinations expand rapidly with their length. Second, in “correcting” the p-value of any marker combination, the effects of its sub-combinations should be taken into account. These two points have mostly been ignored in existing methods based on exhaustive search. In our later simulation studies, we will demonstrate that this could severely jeopardize the power for detecting interactions.

In this work, we propose a method for testing epistasis that is particularly powerful in detecting UBS effects. The method follows the exhaustive search scheme, but achieves high computational efficiency by skipping in the search procedure parts of the marker combination space that cannot contain detectable signals. (Hence it is “almost” exhaustive.) In addition, it adopts a sequential permutation procedure for multiple testing correction that addresses the two issues mentioned in the previous paragraph. We demonstrate the work of our method in a cardiovascular disease candidate gene study data set with an injected UBS signal. Also, we study the power and false rejection properties of the method using data sets simulated from a three-locus joint dominance model that gives rise to UBS interactive effects.

METHODS

BASIC TERMINOLOGY

We first introduce some basic terms that will be used throughout the rest of the paper. A genetic pattern (or pattern for short) is defined to be a combination of marker-genotypes, and we write them in parentheses. For example, (SNP3=C/G, SNP4=T/T, SNP7=A/T) is a pattern involving three markers. We define the length of a pattern as the number of genetic markers it involves. So the previous pattern is of length three. For simplicity, patterns of length k are called k-patterns. Next, we use “marker combination” (corresponding to a pattern) to mean the set of markers involved in the pattern, and write them in parentheses as well. For instance, (SNP3, SNP4, SNP7) is the corresponding marker combination for the previous pattern. Lastly, the support of a pattern refers to the relative frequency of the pattern among the observations. For example, if 40 out of 1,000 cases and 60 out of 600 controls have the pattern, then it is said to have a case support of 4% and a control support of 10%, as well as an overall support of 6.25%.

EVALUATING THE SIGNIFICANCE OF GENETIC PATTERNS

The simplest way to evaluate the disease association of all possible genetic patterns is to conduct an exhaustive search over the space of all possible patterns up to a given length. However, such an approach wastes a lot of computational power on patterns that occur so rarely among the subjects that even a 100% observed penetrance would not render a p-value significant enough to survive multiple testing correction. For example, suppose a 3-pattern occurs only 1% of the time in a data set of 1,000 cases and 1,000 controls with 600 candidate markers. Even if all of the subjects having this pattern had the disease, corresponding to a nominal p-value of about 10⁻³, this would still not be sufficient evidence to establish an association between this pattern and the disease risk. Therefore, one loses little power by excluding such infrequent patterns in the search for interactions.

Interestingly, making the seeming compromise of leaving the infrequent part of the space of genetic patterns out of the search opens a door to a class of very efficient search algorithms developed in the machine learning literature—the so-called frequent-pattern mining algorithms. In the original frequent-pattern mining setting that motivated the development of those algorithms, the data set is unsupervised, i.e., without a case label, and the goal is to find and count all patterns whose support is above a given threshold, say 2%, among all observations. (These patterns are termed the “frequent patterns.”) The algorithms accomplish this task by utilizing advanced data structures which drastically expedites the search-and-count procedure.

Our current problem of searching for genetic patterns associated with a disease label is slightly more complicated than the standard frequent-pattern mining problem. First, given a case label, we want to find those frequent genetic patterns and count them among the cases and the controls separately. (With these two counts, we can then apply tests, e.g. Fisher's exact test, to evaluate the significance of support difference between cases and controls.) Another difference is that we want to select the frequent patterns based on their support in either the cases alone or the controls alone rather than based on their overall support. This will allow us to capture those patterns that are infrequent overall but frequent among one of the two groups.

Despite these differences, frequent-pattern mining algorithms, with some minor changes, can be applied in our context for testing epistasis. We adopt one of the fastest such algorithms, FP-growth [Borgelt, 2005; Han et al., 2004] for this purpose. (“FP” stands for frequent pattern.) We extended the algorithm to serve our current context and call the new version “supervised FP-growth” to emphasize its key difference from the original version. (See the “Software” section for more information.) In short, the supervised version takes two arguments n and s, and finds all patterns of length up to n whose case support is above s. In addition, it counts each such pattern among cases and controls separately. (Note that by specifying a threshold on the case support instead of the total support, we allow patterns with very low control support to stay in our search space. This leads to the preferential discovery of patterns that increase disease risk. To detect patterns that decrease the risk of disease, we can simply reverse the case/control label.)

With the case and control counts for each frequent genetic pattern, we can apply any one degree of freedom test to measure the significance of its association with disease risk. In this study we use Fisher's exact test. We acknowledge that 1-d.f. tests are not the most powerful in that they do not combine information across patterns involving the same markers. However such tests are extremely attractive computationally in the current setting. Because for any given data set, a pattern's p-value under such a test depends only on its case and control counts, a grid of p-values corresponding to all possible combinations of case and control counts can be precomputed. Each frequent pattern found by supervised FP-growth can then be directly mapped to the corresponding p-value on the grid without being tested on-the-fly. This raises computational efficiency greatly especially when a huge number of patterns are being tested.

MULTIPLE TESTING CORRECTION

Supervised FP-growth provides a means to measure the statistical significance of disease association for individual genetic patterns. While the p-values it generates can serve to rank the patterns in terms of their statistical significance, they cannot be taken at face value due to the large number of tests conducted. In fact, the multiple testing problem is much more serious in the current setting of testing interactions compared to testing main effects because the number of marker combinations is much larger than the number of markers. A common solution to the problem is to use permutation testing.

The appropriate permutation procedure for our problem, however, deviates in two important ways from the standard permutation test. First, p-values for the patterns of different lengths should be tested separately, i.e., using different permutation nulls. As the number of patterns increases combinatorially with their length, there are orders of magnitude more long patterns than short ones. Hence, small p-values are much more likely to appear among longer patterns. If a common permutation null were used for patterns of all lengths, the effect of, say, 2-patterns would be “masked” by the noise of 3-patterns. This problem is amplified as the length of patterns under investigation increases. Second, as we conduct separate permutation testing for patterns of different lengths, the permutation nulls for longer patterns should take into account the significant effects detected among the shorter ones. For example, if a marker combination (SNP1, SNP2) has been determined to be strongly associated with the disease risk, then many 3-patterns that contain this marker combination may also display significant, or even more significant, p-values just due to chance. Those will show up as significant 3-patterns while their effect is, in fact, already accounted for by a subset of the markers they involve. More generally, if the effect of a marker combination can be explained by one or more of its sub-combinations, then we should try to recover such sub-combinations rather than declare the longer one significant. Thus, the significant patterns of length up to n−1 should be considered in constructing the null hypotheses for n-patterns. Our reasoning here is analogous to that used in forward stagewise model selection in the regression setting. In that setting, if certain marginal effects are determined to be significant, one compares an expanded model to the already established model instead of the empty model.

For these reasons we propose a sequential permutation testing procedure. The basic idea is to test the 1-patterns first followed by the 2-patterns using the effects detected in the 1-patterns as the null, and then test the 3-patterns using the effects detected in the 1-patterns and 2-patterns as the null, and so on and so forth. Next we describe this sequential procedure, which we call adaptive marginal effect permutation (AMEP) in an inductive manner.

Suppose we have completed our testing for patterns of length up to n−1, and have arrived at a set, S_n−1, of significant marker combinations up to length n−1. (A marker combination is called significant if one of its corresponding genetic patterns is significant.) To test the n-patterns, we first divide them into G groups in such a fashion that the patterns within each group share exactly the same set of significant marker combinations. The idea is to construct a separate permutation null for each of the G groups. (Note that G depends on both n and S_n−1. To be most precise, we can write G as G(n, S_n−1).) For example, suppose we have tested the 1-patterns and have found two significant markers, S₁ = {(SNP2), (SNP5)}. In testing the 2-patterns, we divide them into G=4 groups—(G1) those that do not contain either SNP2 or SNP5, (G2) those containing SNP2 but not SNP5, (G3) those containing SNP5 but not SNP2, and (G4) those containing both SNP2 and SNP5.

The G permutation nulls, one for each of the G groups, can be constructed simultaneously by permuting the case label together with all the markers in S_n−1. For each permutation, we apply the supervised FP-growth algorithm just as we did for the original data. By pooling the p-values of the patterns belonging to each of the G groups from all the permutations, we obtain a sample of p-values from the permutation null for each of the G groups. The corrected p-value for a pattern can then be computed as the proportion of permutations that generated a more significant p-value in the corresponding group. Those patterns whose corrected p-values pass a significance threshold, e.g. 5%, are declared as significant, and their corresponding marker combinations are joined with S_n−1 to form S_n. A formal algorithm-style description of AMEP is provided in Box 1.

We make two suggestions on applying the AMEP procedure. First, the prescreening threshold α_prescreen used in Step 2a of Box 1 should be as relaxed as the computational resources allow. (Note that α_prescreen = 1 corresponds to no prescreening at all.) Second, the threshold of permutation p-values α used in Step 2g should not be larger than 5% as α controls the family-wise error rate (FWER) for patterns tested using each permutation null. While this criterion may appear stringent, we justify it on the basis that significant patterns passing this threshold affect the null hypotheses for testing longer patterns. We should only allow patterns that demonstrate reasonably strong evidence of association to affect the testing for other patterns.

On the other hand, however, those patterns with moderately significant permutation p-values, though not passing the 5% FWER threshold, may still be of interest. Such patterns should not serve in the permutation nulls for longer patterns, but may still contain evidence for true association. To find such patterns, we extend the AMEP procedure by reporting, in addition to S_n, all patterns whose p-values pass less stringent p-value cutoffs constructed based on controlling the number of false positives (NFP), or alternatively the false discovery rate (FDR). The detail of this extended procedure is presented in Box 2.

In particular, Steps 2i and 2j in Box 2 show how one can estimate the NFP and FDR, as functions of the cutoff p-value, for each of the Gn-pattern groups. In Step 2k we select an appropriate p-value cutoff separately for each group based on the estimated NFP or FDR. For example, one can choose the p-value cutoffs so that the estimated NFP for each group is 0.2. We denote this particular p-value cutoff by p_nfp0.2, which is group specific, and will use it in the following data analytical example.

SIMULATION STUDIES

A REAL DATA SET WITH AN INJECTED UBS SIGNAL

We now demonstrate the work of our method using a real data set—namely the ADVANCE (Atherosclerotic Disease, VAscular function, and genetiC Epidemiology) study data—with an injected signal. ADVANCE is a population based case-control study with a primary aim of identifying novel genetic determinants of coronary artery disease. Between October 28, 2001 and December 31, 2003, a total of 3,179 members of Kaiser Permanente of Northern California were recruited into 3 case cohorts and 2 control cohorts [Assimes et al., 2008]. Case cohorts included members with clinically significant CAD (namely angina, myocardial infarction, or a history of coronary angioplasty or bypass procedures) while control cohorts had no history of clinical CAD. In Phase 1, a small number of cases were sequenced at approximately 100 candidate genes and a subset of sequenced SNPs were then genotyped in all participants. To avoid potential population stratification, we use only the European samples from the two older case cohorts and the older control cohorts. The data set consists of 580 SNP markers in 957 cases and 677 controls. Each of the SNPs is assigned a name (e.g, ABC1_17) indicating its genomic location and corresponding gene. Interested readers can find the rs numbers for all the SNPs as well as other information about the study at http://med.stanford.edu/advance/.

We spike in a three-locus interaction by enforcing a randomly chosen pattern (ABC1_17=A/A, CNTNAP5_500=C/T, ANGPT1_R_3=T/T) to be associated with the disease risk. The only criteria used in choosing this pattern are that (1) its overall support is small, not exceeding 5% and (2) there is no evidence of association for the markers involved in the original data. We inject the signal by flipping the disease labels of 29 randomly chosen controls in the original data that possess this genotypic pattern to cases. Before the flipping, 48 out of the 957 cases and 36 out of the 677 controls had this pattern. After the flipping, 77 out of 986 cases and 7 out of 648 controls have this pattern, corresponding to about 7.9% of the cases and 1.1% of the controls. Note that this mimics a strong interactive effect present in a small fraction of the cases, i.e. a UBS effect.

Before applying our method, we first check what the standard approach, trend test, would reveal about the data. The histogram of the trend test p-values given in Figure 1 shows that none of the three markers involved in our injected signal have a permutation corrected p-value of less than 5% (based on 1,000 permutations). Thus, the standard approach would discard all three at the single marker testing stage, leaving no hope for any follow-up analysis, such as fitting a logistic regression to the significant markers, to uncover the interactive effect.

Fig. 1.

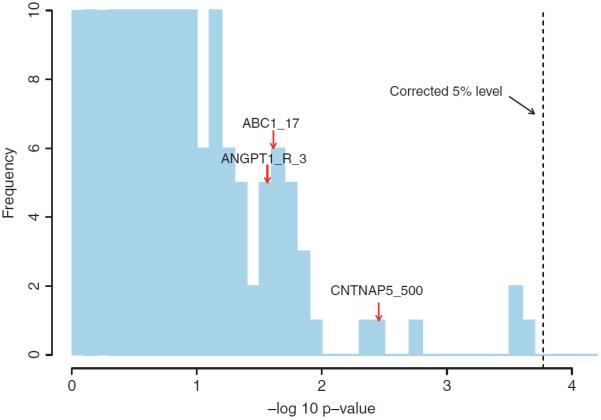
A truncated histogram of the trend test −log₁₀ p-values. The frequency (vertical axis) is truncated at 10. The dashed vertical line indicates the permutation corrected 5% level. The three markers involved in our injected signal fall into the bars indicated by the red arrows.

To apply our method to the data, first we need to specify a few parameters. We set the (within case) support threshold for the supervised FP-growth algorithm s to 2%, and the prescreening threshold α_prescreen to 0.2. (In fact, for a data set of this size the supervised FP-growth algorithm is efficient enough so that no screening is necessary at all for investigating interactions involving up to three markers. Here we apply prescreening to demonstrate our method at work in general. See Discussions for more detail on computational efficiency.) We set N=5,000 as the number of permutations for each pattern length. Finally, we use the conventional level 0.05 for the FWER threshold α, and adopt the p_nfp0.2 level as the p-value cutoff to control the estimated NFP for each permutation null group.

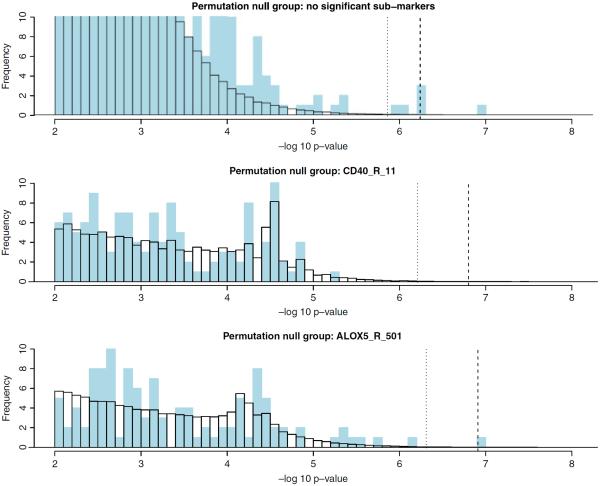
The results for the 1-patterns are summarized in Figure 2 and Table I. Two patterns, namely (CD40_R_11=A/A) and (ALOX5_R_501=A/C), have permutation p-values of less than 5%. Thus for testing the 2-patterns, we permute the case label together with the two markers CD40_R_11 and ALOX5_R_501. The results for 2-patterns are presented in Figure 3 and Table II. We note that (ANGPT1_R_3=T/T, CNTNAP5_500=C/T), which passes the FWER threshold, is a subpattern of our injected signal.

Fig. 2.

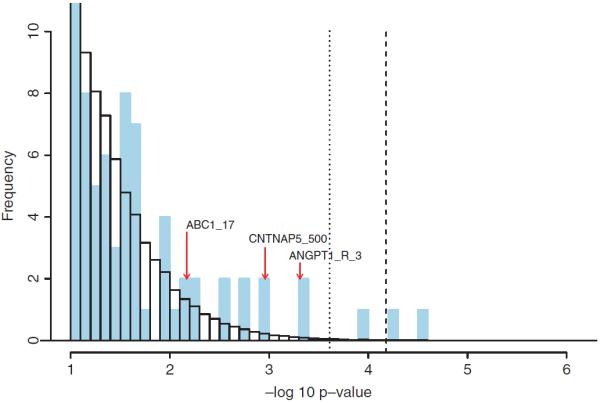
Truncated histogram of −log₁₀ p-values for 1-patterns. The vertical axis is truncated above at 10 and the horizontal axis is truncated below at 1. The blue bars represent 1-patterns observed in the data. The white bars (with black borders) represent the average histogram over all the permuted data sets. The dashed line indicates the 5% corrected p-value cutoff. The dotted line represents p_nfp0.2. The three markers involved in our injected signal fall into the bars indicated by the red arrows.

TABLE I.

1-patterns that passed the p_nfp0.2 threshold

Pattern	−log10P	OR
CD40_R_11=A/A	4.54	2.30
ALOX5_R_9=C/T	3.92	1.39
ALOX5_R_501=A/C	4.27	1.42

The OR column gives the estimated odds ratios. The patterns in bold font has a AMEP corrected p-values of less than 0.05.

Fig. 3.

Truncated histograms of −log₁₀ p-values for 2-patterns. Three permutation null groups are plotted. The vertical axes are truncated above at 10 and the horizontal axes are truncated below at 2. The blue bars represent the 2-patterns observed in the data. The white bars (with black borders) represent the average histogram over all the permuted data sets. The dashed line indicates the 5% corrected p-value cutoff. The dotted line represents p_nfp0.2.

TABLE II.

2-patterns that passed the p_nfp0.2 threshold

Permutation null group	Pattern	−log10P	OR
No significant sub-combinations	*ANGPT1_R_8=C/C CNTNAP5_500=C/T	6.30	2.84
	*ANGPT1_R_8=C/C ABC1_17=A/A	6.09	2.05
	*ANGPT1_R_3=T/T CNTNAP5_500=C/T	6.30	2.84
	*ANGPT1_R_3=T/T ABC1_17=A/A	6.21	2.06
	ALOX5_R_9=C/T CDKN2A_501=G/G	5.93	2.37
	ALOX5_R_9=C/T CNTNAP5_500=C/T	6.91	2.43
ALOX5_R_501	ALOX5_R_501=A/C CDKN2A_501=G/G	6.19	2.41
	ALOX5_R_501=A/C CNTNAP5_500=C/T	6.91	2.43
Others	None

The patterns in bold font have a AMEP corrected p-values of less than 0.05.

^*indicates subpatterns of the injected signal.

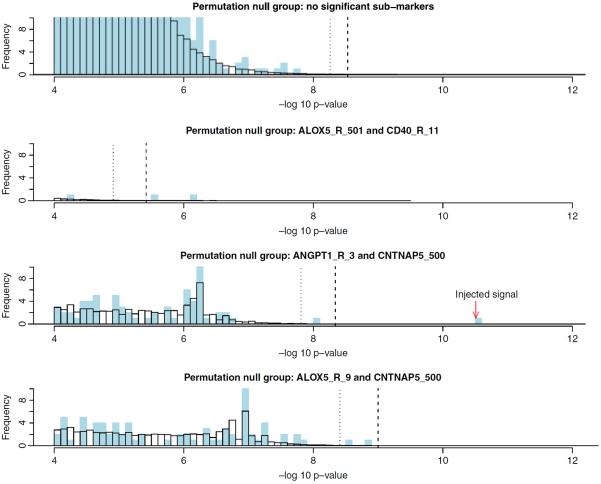
The results for 3-patterns are presented in Figure 4 and Table III. The most important observation is that our injected pattern is detected with absolutely no ambiguity—its −log₁₀ p-value, 10.5, surpasses all −log₁₀ p-values in its permutation null by a large margin. (In fact no patterns in the permutation null have a −log₁₀ p-value of more than 9.6.) Two other 3-pattern passes the 5% FWER threshold: (ALOX5_R_501=A/C, CDKN2A_501=G/G, CD40_R_11=G/G) and (ALOX5_R_501=A/C, CDKN2A_500=G/G, CD40_R_11=G/G). These two patterns effectively represent the same signal due to strong linkage disequilibrium between CDKN2A_500 and CDKN2A_501. They have most likely captured the main effect of the CDKN2A region, which has not been reflected in the analysis of 1-patterns and 2-patterns. (The main effect association between the CDKN2A region and CAD is well established [Wellcome Trust Case Control Consortium, 2007].) These results demonstrate a nice side-product of the our method—it is able to recover biologically relevant markers even when their exact interactive relationships, if any, cannot be determined from the data. (We note that in the current data set the CDKN2A region does not pass the permutation corrected 5% significance level under the trend test. See Figure 1.)

Fig. 4.

Truncated histograms of −log₁₀ p-values for 3-patterns. Four permutation null groups are plotted. The vertical axes are truncated above at 10 and the horizontal axes are truncated below at 4. The blue bars represent the 3-patterns observed in the data. The white bars (with black borders) represent the average histogram over all the permuted data sets. The dashed line indicates the 5% corrected p-value cutoff. The dotted line represents p_nfp0.2.

TABLE III.

3-patterns that passed the p_nfp0.2 threshold

Permutation null group	Pattern	−log10P	OR
ANGPT1_R_8, CNTNAP5_500	*ANGPT1_R_8=C/C CNTNAP5_500=C/T ABC1_17=A/A	10.31	7.21
	ANGPT1_R_8=C/C CNTNAP5_500=C/T WNT4_R_5=T/T	8.06	3.63
ANGPT1_R_3, CNTNAP5_500	*ANGPT1_R_3=T/T CNTNAP5_500=C/T ABC1_17=A/A	10.51	7.30
	ANGPT1_R_3=T/T CNTNAP5_500=C/T WNT4_R_5=T/T	8.06	3.63
ALOX5_R_9, CNTNAP5_500	ALOX5_R_9=C/T CNTNAP5_500=C/T LOX1_2=G/G	8.88	3.35
	ALOX5_R_9=C/T CNTNAP5_500=C/T INSR_R_2=C/C	8.57	3.15
ALOX5_R_501, CD40_R_11	ALOX5_R_501=A/C CDKN2A_500=G/G CD40_R_11=G/G	5.57	3.42
	ALOX5_R_501=A/C CDKN2A_501=G/G CD40_R_11=G/G	6.11	3.46
Others	None

The patterns in bold font have AMEP permutation corrected p-values of less than 0.05.

^*Indicates the injected signal.

POWER AND FALSE REJECTION PROPERTIES

We evaluated the power and multiple testing correction properties of our method using simulation. We simulated retrospectively sampled data sets according to the following scheme. First, we generated the genotypes of 100 SNPs markers for a population of size 50,000. All markers were in Hardy-Weinberg and linkage equilibria with minor allele frequencies being independent uniform draws between 0.1 and 0.4. Then we simulated the disease status according to the following three-locus (joint dominance) model

$$P\left(\text{Disease}\right)=\{\begin{array}{cc}{p}_1\hfill & \mathrm{if}SNP1\ge 1,SNP2\ge 1,\text{and}SNP3\ge 1\hfill \\ p_0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

where “≥1” means that the genotype has at least one minor allele. Under our later choices of p₀ and p₁, this simulation scheme frequently (ranging from 25 to 80% of times) gives rise to populations for which the disease genotypes are present in a small proportion (less than 20%) of the patients. For large values of p₁, these imitate UBS effects. (Note that due to the nonparametric nature of our method, the specific form of the model does not directly affect the performance of our method. This model serves as an example that generates UBS effects.)

We fixed the base line disease risk p₀=0.2, and let the exposure disease risk p₁=0.2, 0.4, 0.6, 0.8 and 1, corresponding to risk ratios 1, 2, 3, 4 and 5. (The null simulation p₁=0.2 was included for our later study of the false rejection properties.) For each value of p₁, we simulated 200 such populations and for each sampled a control group and a case group of sizes N₀ and N₁, respectively. Two sets of sample sizes N₀=N₁=500 and N₀=N₁=1000 were investigated. We then applied our method to each of the simulated case-control data set as we did to the ADVANCE data, except that no prescreening was done here and 200 permutations were used to construct each null.

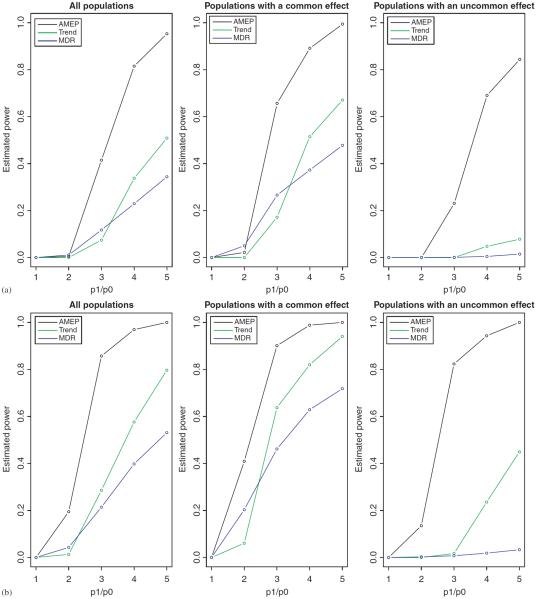
At each p₁ level, we estimated the power of our AMEP method—the probability for the combination (SNP1, SNP2, SNP3) to be in S₃—by the proportion of simulations for which this occurred. For comparison, we estimated the power of the trend test and that of MDR. The power of the trend test was estimated by the fraction of times that all three markers SNP1, SNP2 and SNP3 had trend test p-values significant at the 0.05 level after Bonferroni correction for 100 independent tests. (Of course, the trend test does not actually recover the interactive structure, but only finds the markers with significant main effects.) The power of MDR was estimated by the fraction of times that MDR, using 10-fold cross-validation, declared (SNP1, SNP2, SNP3) to be the best three-locus interaction model. (The software we used for MDR was parallel-MDR introduced in [Bush et al., 2006]. We note that the power of MDR would have been higher if multiple, rather than the single, overall best models had been retained. This function was not yet supported by the latest version of the parallel-MDR software at the time this paper was written.)

Additionally, we divided the simulated populations into two groups, and computed the power estimates separately for each. The two groups are (1) those in which the disease-associated genotype combinations are common, i.e. present in more than 20% of the patients, and (2) those in which the disease-associated combinations are not common. (The 20% “commonness” cutoff was chosen for convenience and the fact that a significant proportion of simulated populations fell into each group under the parameter settings.) Figure 5 presents all the power estimates. We see that in this example our approach outperformed the other two methods, and was particularly more powerful when the causal combinations are uncommon but have large risk ratios (≥3). (As a sidenote, the trend test outpowered MDR for large effect sizes because the model involves main effects.)

Fig. 5.

The power estimates of three different methods for the simulated joint dominance data. Left column: all populations. Middle column: populations in which the causal combinations exist in more than 20% of patients. Right column: populations in which the causal combinations exist in no more than 20% of patients. Two sets of sample sizes: (a) N₀=N₁=500 and (b) N₀=N₁=1000.

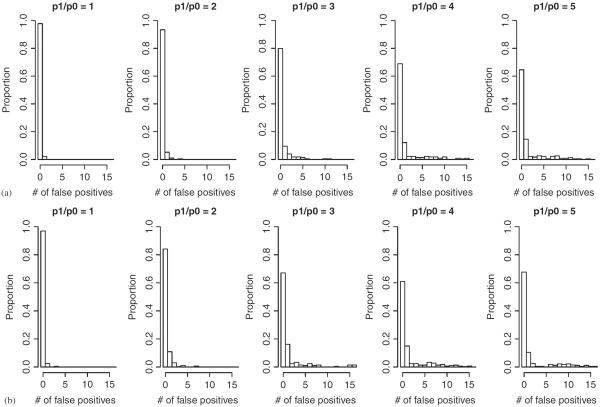
Finally, we investigated whether the AMEP procedure adequately corrects for multiple testing. Histograms of the NFP for the simulated data under different p₁ values and sample sizes are presented in Figure 6. Note that here we have adopted a very strict definition of false positives—any elements in the final set of significant combinations, S₃, that contained any marker other than SNP1, SNP2, and SNP3 were considered false. Almost all of such false rejections contained some of SNP1, SNP2, and SNP3. They were counted as “false” rejections only because they did not recover the exact interactive relation among the three markers. They nonetheless provided rich information about what markers are associated with the disease.

Fig. 6.

Histograms of the number of false rejections produced by AMEP for the simulated data under the three-locus joint dominance model. The x-axes are truncated at 16. Two sets of sample sizes: (a) N₀=N₁=500. (b) N₀=N₁=1000.

By design, the FWER threshold α controls the FWER for each permutation test, and so the FWER for the entire AMEP procedure depends on the actual number of permutation tests conducted. Figure 6 shows that for the simulated data sets, the overall FWER—one minus the height of the first bar in each histogram—can be as high as 40% for some effect size and sample size combinations. (It may seem curious that when N₁=1000, the FWER was smaller for p₁/p₀=5 than for p₁/p₀=4. This happens because when both the sample and the effect size are very large, the relevant SNPs are often detected early in the procedure, reducing the chance that they will later combine with other SNPs to form “false” signals.) On the other hand, the same figure shows that the NFP is typically fairly small (≤10). To summarize, the final set of significant combinations produced by AMEP is likely to include a small number of false rejections, almost all of which contain some of the markers involved in the actual effects.

DISCUSSION

In this work we have introduced a method for testing genetic interactions based on an “almost” exhaustive search strategy over the space of marker combinations, and a sequential permutation testing scheme for multiple testing correction. These two components work independently of each other. Indeed, if we replace supervised FP-growth with any other method for searching through the space of marker combinations, AMEP can still be used for hypothesis testing, and vice versa. Of course, due to the computational nature of any permutation procedure, the applicability of AMEP relies on the effectiveness of the search component.

The frequent-pattern mining algorithms allow us to search the space of marker combinations in a very efficient manner. For example, each permutation for testing 3-patterns on the ADVANCE data was completed by supervised FP-growth in about 10 sec on an Intel Xeon 3.0GHz processor and used approximately 50Mb of memory, mostly for storing the precomputed p-value grid. (The computing time required for 1-patterns and 2-patterns was less than 1 sec per permutation.) Without any prescreening, i.e. using all 580 markers, our method would take about two hours to sweep through the 3-patterns in each permutation. This would also be the time needed to complete the same task on a data set with 5,800 (biallelic) SNPs and similar numbers of cases and controls using a relatively relaxed 10% prescreening threshold. Moreover, because AMEP is a permutation-based procedure, it can be run in parallel on a computer with multiple cores (or multiple computers) to significantly reduce computing time. For example, with 100 processors, AMEP using 1,000 permutations per pattern length can be completed within 1 day to investigate such a 5,800 SNP marker data set for up to 3-pattern interactions.

However, we do acknowledge that our proposed approach is, at its current stage, more suited for large candidate gene studies (those that involve hundreds to thousands of markers) than for genome-wide studies if interactions involving more than two loci are of interest.

Our method is nonparametric—neither supervised FP-growth nor AMEP requires any modeling assumptions. An advantage of nonparametric methods is that they are not limited to detecting statistical interactions, typically defined as deviation from linearity on certain (such as logistic) scales. However, when all markers in a combination demonstrate significant marginal effects, model-free methods often lack a rigorous way to differentiate interaction of these markers from an accumulation of their marginal effects. In the context of our method, for example, if both (SNP2) and (SNP5) are detected to be significant, then by construction (SNP2, SNP5) will also be reported as significant even though there may not actually be any interaction between the two markers. (Note that since both markers are permuted together with the disease label, the corresponding permutation null is essentially degenerate, and such combinations will always be reported as significant due to the design of our method. We call such combinations technical interactions. To avoid distracting the reader, we did not report such “interactions” in Tables I–III, but they were included in the set of significant combinations S_n.) In real applications, however, one can often use information such as allele frequencies and odds ratios to judge whether such an effect is likely to be interactive.

Finally, we note that even though we introduced our method in the context of analyzing data with SNP markers, the method can be applied in exactly the same manner to case-control studies with any predictors of discrete or categorical values. These include other genetic markers, e.g. copy number variation (CNV) markers, environmental variables, e.g. gender and smoking status, as well as other discrete measurements and classifications.

SOFTWARE

The supervised FP-growth software was developed based on an implementation of the original FP-growth by Christian Borgelt, obtained at http://www.borgelt.net/fpgrowth.html. Our source code is available at http://www.stanford.edu/ma2/sFPgrowth.

Box 1. Adaptive marginal effect permutation (AMEP).

1. Initialization: Let M be the marker set under investigation, and S₀=Ø.

2. For n=1, 2,…,max.length,

   1. (Optional) Prescreen the marker set M, retain only those with a trend test p<α_prescreen.
   2. Search and count all patterns whose case support is above a threshold s using supervised FP-growth. This produces a set of frequent genetic patterns C.
   3. For each pattern Pa∈C, compute its Fisher's exact test p-value P(Pa) using its case and control counts.
   4. Classify the patterns into groups C₁, C₂,…,C_G according to the marker combinations in S_n−1 they contain. Let P₁, P₂,…,P_G be the corresponding collections of p-values.
   5. For j=1, 2,…,N, (j is the permutation index and N is the number of permutations.)

      • (i)
        Permute the response label together with the markers involved in S_n−1.
      • (ii)
        Repeat Steps 2a–d to each permuted data set. This produces $C_1^{\left(j\right)},C_2^{\left(j\right)},\dots C_G^{\left(j\right)}$ for permutation j. Let $P_i^{\left(j\right)}$ be the collection of p-values of those patterns in $C_i^{\left(j\right)}$ for i=1, 2,…,G.
   6. For each pattern Pa in C_i, i=1, 2,…,G, the permutation p-value, P*(Pa), is given by $P^{\ast }\left(Pa\right)=\#\{j:\min P_i^{\left(j\right)}<P(Pa\left)\right\}∕N$.
   7. Set S_n = S_n−1⋃ {the corresponding marker combinations of Pa∈C:P*(Pa)<α}, where α is the significance threshold for the corrected p-values.

Box 2. Modified AMEP procedure for controlling NFP or FDR.

1. Initialization: Let M be the marker set under investigation, and S₀=∅.

2. For k=1, 2,…,max.length,

   • a–g
     Same as the original AMEP procedure.
   • h
     Pool the patterns and their p-values from all the permutations according to their classes.
      For i∈{1, 2,…G}, let $C_i^{\left(\mathit{pooled}\right)}={\cup }_{j=1}^N{C}_i^{\left(j\right)}$, and

     $$P_i^{\left(\mathit{pooled}\right)}={\cup }_{j=1}^N{P}_i^{\left(j\right)}.$$
   • i
     For each C_i, $P_i^{\left(\mathit{pooled}\right)}$ gives the empirical permutation null distribution of the Fisher's p-values. Hence, the number of false positives (NFP) as a function of the p-value cutoff for Group i can be estimated as ${\widehat{NFP}}_i\left(p\right)=\#\{\text{elements in}{P}_i^{\left(\mathit{pooled}\right)}\le p\}∕N$, while the number of rejections in the original data is NP_i (p) = #{elements in P_i ≤ p}.
   • j
     The corresponding estimated FDR is ${\widehat{FDR}}_i\left(p\right)={\widehat{NFP}}_i\left(p\right)∕{\mathrm{NP}}_i\left(p\right)$.
   • k
     A p-value cutoff p_i can be chosen for permutation null group i to control ${\widehat{NFP}}_i$ or ${\widehat{FDR}}_i$.
   • l
     Report the patterns in each group whose p-values pass the corresponding p-value cutoff p_i.