Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Apr 14;6:24437. doi: 10.1038/srep24437

Gradient Index Devices for the Full Control of Elastic Waves in Plates

Yabin Jin 1,2, Daniel Torrent 3,a, Yan Pennec 2, Yongdong Pan 1, Bahram Djafari-Rouhani 2
PMCID: PMC4830996  PMID: 27075601

Abstract

In this work, we present a method for the design of gradient index devices for elastic waves in plates. The method allows the design of devices to control the three fundamental modes, despite the fact that their dispersion relation is managed by different elastic constants. It is shown that by means of complex graded phononic crystals and thickness variations it is possible to independently design the three refractive indexes of these waves, allowing therefore their simultaneous control. The effective medium theory required for this purpose is presented, and the method is applied to the design of the Luneburg and Maxwell lenses as well as to the design of a flat gradient index lens. Finally, numerical simulations are used to demonstrate the performance of the method in a broadband frequency region.

The control of the propagating characteristics of mechanical (acoustic and elastic) waves in linear media is a challenging problem with a wide variety of applications, since this control allows the design of acoustic or elastic lenses1,2,3,4,5,6, omnidirectional absorbers7,8,9, cloaking devices10,11,12 or hyperlenses13. The propagation of mechanical waves can be tailored by means of inhomogeneous materials, as it is well known that in these media waves follow curved trajectories that can be properly designed if the position-dependent parameters of the medium are chosen according to specific laws. However, it is obvious that natural materials cannot provide these specific position-dependent parameters. Therefore, their realization has to be achieved artificially.

In this context, the field of phononic crystals14,15 and metamaterials16 provides a promising background for the realization of artificial inhomogeneous materials, as has been widely demonstrated in the literature17,18,19,20,21,22.

The major drawback for the realization of these devices for elastic waves is that, unlike acoustic waves in fluids, the propagation of elastic waves, either in bulk materials or plates, presents three polarizations, which propagate at different speeds. Their design has been done so far for only one of these polarizations, which obviously hinders the full functionality of the devices for applications like cloaking, absorption or even energy harvesting.

The authors have recently developed a design method which allows the simultaneous control of two of the three fundamental plate modes23, namely the anti-symmetric (A0) and symmetric (S0) Lamb modes. This simultaneous control was based on an effective medium theory developed for the A0 mode24 working with Kirchhoff equation25, which is a two-dimensional equation describing the propagation of flexural waves in thin plates. The mentioned theory can be applied as well to the control of the S0 mode given that the refractive indexes of these two modes are related by means of the same elastic constants and the thickness of the plate, however the refractive index of the third plate mode, named the shear horizontal (SH0) mode, cannot be controlled by this approach, given that it depends on different elastic constants that, in general, cannot be changed independently. Due to the extraordinary difficulty required to work on homogenization using plate theories including the shear mode26, we propose in this work an alternate approach, based on the homogenization of the bulk phononic crystal.

In this work a homogenization theory for phononic crystals is developed and applied to the homogenization of phononic crystal plates, which provides the solution of the refractive indexes of the three modes. It is shown then that by means of a complex unit cell, consisting of a circular inclusion with a hole in its center, it is possible to design independently the refractive index of the three fundamental plate modes. The method is applied to the design of a flat gradient index lens, a Luneburg lens and a Maxwell lens working identically for the three modes. Finally, to illustrate the advantage of the method, a more advanced multi-lens device is designed, which works as a Luneburg lens for the S0 and the SH0 modes while it works as a Maxwell lens for the A0 mode. Numerical simulations by COMSOL support their functionality in a broadband frequency region.

Fourier Homogenization of Phononic Crystals and Plates

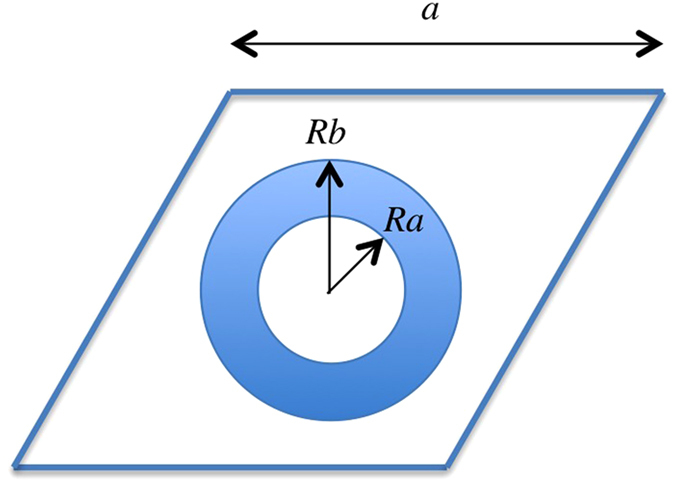
Phononic crystals consist of periodic arrangements of inclusions in an elastic matrix. It is well known that for low frequencies these structures behave like homogeneous materials with some effective parameters (mass density ρ* and stiffness tensor 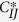Inline graphic). The well known Plane Wave Expansion method can be used to compute the dispersion relation of elastic waves in phononic crystals once we know the Fourier components of the position-dependent elastic constants, and the low frequency analysis of these equations can be used to obtain the effective elastic constants as

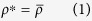graphic file with name srep24437-m2.jpg
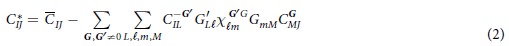graphic file with name srep24437-m3.jpg

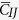where Inline graphic and Inline graphic stands for the unit cell average of the mass density and stiffness tensor components, respectively, and G are the reciprocal lattice vectors of the periodic arrangement, and in all the expressions the term G = 0 is excluded. The quantities 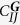Inline graphic are the Fourier components of the position-dependent stiffness tensor components CIJ, for I, J = 1,…6, and the matrix components 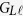Inline graphic and GmM are obtained from the components of the G vector in Voigt notation27. It must be pointed out that the above theory is valid for 1, 2 or 3-dimensional phononic crystals, being the dimensions of the G vector the only difference for each periodicity. Finally, the elements of the 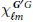Inline graphic matrix are obtained as the inverse of the 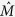Inline graphic matrix defined as27

graphic file with name srep24437-m10.jpg

A phononic crystal plate is a two-dimensional periodic arrangement of inclusions in an elastic plate, and it has also been shown that for low frequencies these structures behave like homogeneous elastic plates. However, the analysis of the dispersion relations of these structures is more complex than that of their bulk counterparts, given that we require additional equations to satisfy boundary conditions, therefore the homogenization of these structures is a more complicated problem28. The authors have recently studied the focalization of the symmetric and antisymmetric Lamb modes in a phononic crystal plate23 assuming that, in the low frequency limit, this plate can be considered a “finite slice” of a two-dimensional phononic crystal, and an excellent agreement was found in the comparison of the respective dispersion curves. Therefore, it is possible to homogenize the bulk phononic crystal by means of equations (1) and (2), and analyze the vibrations of homogeneous plates with the given effective parameters. Although this study was done for the antisymmetric (A0) and symmetric (S0) Lamb modes, here its validity will be demonstrated for the three fundamental Lamb modes.

As an example, let us consider a triangular arrangement with lattice constant a of gold shell-hole structure, with inner radius Ra = 0.2a and outer radius Rb = 0.4a, in an Aluminum matrix (see elastic parameters in Table 1 and schematics of the unit cell in Fig. 1). In the low frequency limit this arrangement of inclusions behaves like a transversely isotropic solid whose effective parameters can be computed using equations (1) and (2) and are given in Table 1. If we take a plate of thickness h of such an effective solid, the dispersion relation of the three fundamental modes in the low frequency limit is isotropic and given by the following equations23

Table 1. Elastic parameters of the materials used in the text.

Material ρ (Kg/m3) C11 (GPa) C12 (GPa) C33 (GPa) C13 (GPa) C66 (GPa)
Aluminum 2.7E3 108.2 51.2 C11 C12 (C11 − C12)/2
Gold 19.5E3 190 161 C11 C12 (C11 − C12)/2
Effective Material 9.63E3 61.1 32.3 79.2 36.6 (C11 − C12)/2
Open in a new tab

Figure 1. Unit cell employed in the design of GRIN devices, consisting of a triangular arrangement of gold inclusions of radius Rb with holes of radius Ra in an Aluminium matrix.

Figure 1

Open in a new tab
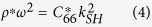graphic file with name srep24437-m11.jpg
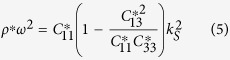graphic file with name srep24437-m12.jpg
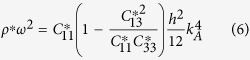graphic file with name srep24437-m13.jpg

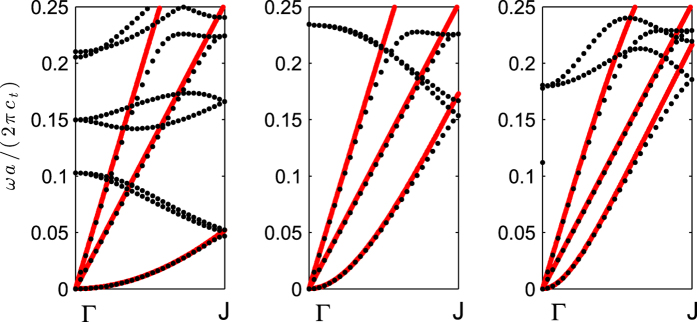
with kX being the wavenumber of the X mode, for X = SH, S, A. Figure 2 shows the comparison of the full dispersion relation of the phononic crystal plate computed with COMSOL (black dots) with the dispersion relation obtained by means of equation (4) (red lines) for plate’s thickness h = 0.1a, 0.5a and h = a in left, center and right panels, respectively. It is clear how in the low frequency limit the plate can be described by the effective medium theory developed for bulk phononic crystals, which in turns simplifies considerably the calculations and also allows for the design of refractive devices, as will be shown in the following section.

Figure 2. Dispersion relations for a phononic crystal consisting of a triangular lattice of gold shell - hole structure with inner radius Ra = 0.2a and outer radius Rb = 0.4a in an aluminum plate of thickness h = 0.1a, h = 0.5a and h = a, corresponding to the left, middle and right panels, respectively.

Figure 2

Open in a new tab

Black dots show the curves calculated by COMSOL and red lines show the dispersion relations obtained by equation (4) with effective parameters in Table 1.

Simultaneous Control of the Fundamental Plate Modes

When a wave passes from a given medium I to a different one II it suffers refraction. The condition for refraction is derived by imposing conservation of the wavenumber in the direction parallel to the plane dividing the two media, and this condition defines the refractive index as the ratio between the wavenumber in the two media29. From expression (4) we find that the refractive indexes of the three fundamental modes are therefore given by

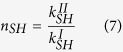graphic file with name srep24437-m14.jpg
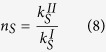graphic file with name srep24437-m15.jpg
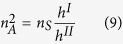graphic file with name srep24437-m16.jpg

where it has been assumed that medium I(II) is a plate with elastic parameters labeled by I(II) and thickness hI (hII). We can see therefore that the thickness of the plate can be used to control the refractive index of the A0 mode independently of the other two modes. Besides, we see that while the elastic constants defining the refractive index of the A0 and S0 mode are the same, the refractive index SH0 mode depends on the 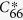Inline graphic component of the stiffness tensor.

The design of gradient index devices is typically done by choosing one material for the background, another for the inclusions, and then the refractive index is a function of the filling fraction (radius) of the inclusions, that is, n = n(R0). In this work we have three refractive indexes to design, however the refractive index of the A0 mode will be designed by changing the relative thickness of the plate and using equation (9), so that actually we have to design only nS and nSH. If we had only one degree of freedom, that is, the radius of the inclusion R0, we could choose for instance nS and then determine the corresponding value of R0, since nS = nS(R0), but then the refractive index of the SH0 mode would be imposed, so that we need an additional degree of freedom to choose independently nS and nSH.

We propose the structure shown in Fig. 1, in which an Aluminum matrix is perforated by a triangular arrangement of gold inclusions of radius Rb with a hole at its center of radius Ra (see materials’ parameters in Table 1). The effective parameters of such a phononic crystal will therefore be a function of both Rb and Ra, which will allow us, as will be explained later, the independent tuning of the three refractive indexes.

Figure 3 shows the “phase diagram” of this material, in which we make a sweep of Rb ∈ (0, 0.5a) and Ra ∈ (0, Rb), with a being the lattice constant of the arrangement. All the possible values that take nS and nSH are shown in this diagram. This diagram can be used as an inverse design tool: We choose a given value for the desired refractive index for the two modes lying in the diagram, then we find the corresponding values for Ra and Rb, to later use expression (9) to determine the thickness of the plate that give us the desired value for nA, so that we are capable of independently tune the three refractive indexes, obviously under the limitations given by the phase diagram depicted in Fig. 3.

Figure 3. Phase diagram showing all the possible values for the effective refractive indexes for the SH0 and S0 modes obtained by varying the radius of the holes and the inclusions.

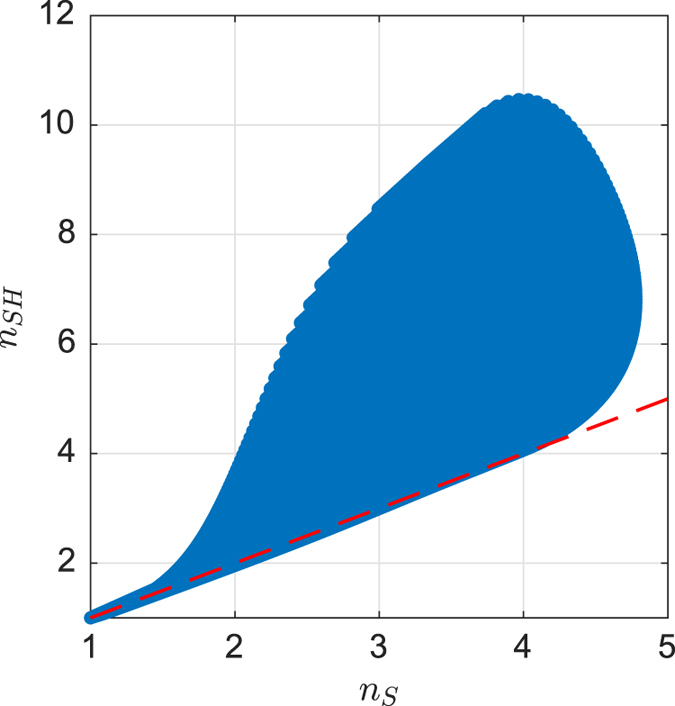
Figure 3

Open in a new tab

The red-dashed line shows the condition nSH = nS, showing that it is possible the design of refractive devices identical for these two modes.

Numerical Examples

This section is devoted to illustrating the power of the presented method to design gradient index devices working simultaneously for all three fundamental plate modes. The design procedure is identical for all these devices: First we decide the device, defined by means of a position-dependent refractive index; second, we define the positions of a cluster of inclusions, according to the device’s geometry (a square slab for a flat GRIN and a circular cluster for a Luneburg or Maxwell lenses), with a large enough number of inclusions to avoid diffractive effects (see discussion below); third, we select the inclusion α and compute the desired radii Ra and Rb. For the computation of these values we need to know the desired refractive indexes for the S0 and SH0 modes at the position rα, and then use the data of the phase diagram shown in Fig. 3 which relates the refractive index with the radius of the hole and inclusion. Finally, once we have selected Ra and Rb, by means of equation (9) we choose the thickness of the plate at that position to obtain the desired refractive index for the A0 mode. It has to be noticed that this design method allows for creating refractive devices for the three modes, but not necessarily the same device for the three modes, given that it can be used to tune independently the three indexes. Therefore, although from the practical point of view it appears better to design devices focusing all the energy at the same point for one kind of lens, we propose in our last example the realization of a multi-lens device working as a Luneburg lens for the S0 and SH0 modes and as a Maxwell lens for the A0 mode.

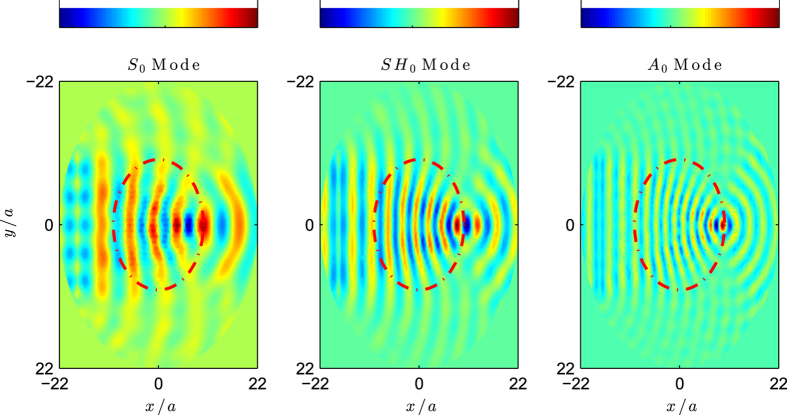
Figure 4 shows a COMSOL simulation of the first example considered in this work. It consists in a long GRIN flat lens as described in several works1,23, in which the refractive index is a function of the distance y to the center of the lens and it is given by

Figure 4. GRIN flat lens made with a slab of 15 rows and 30 columns of gold-hole inclusions in an Aluminum plate of thickness h = a.

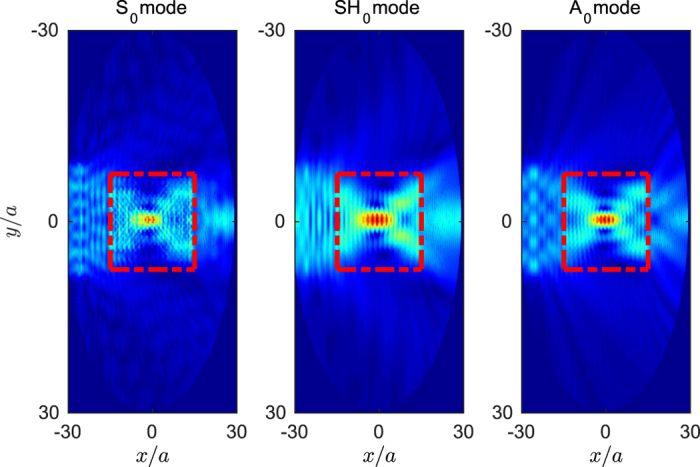
Figure 4

Open in a new tab

Simulations are shown at the same frequency ωa/2πct = 0.178, which corresponds to wavenumbers kSa = 0.65, kSHa = 1.11 and kAa = 1.5, whose corresponding field distributions are shown in left, central and right panels.

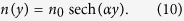graphic file with name srep24437-m18.jpg

In this specific case, the lens is made of 15 rows and 34 columns of inclusions arranged in a triangular lattice, oriented in such a way that the vertical distance between inclusions equals the lattice constant a, therefore it has a height Ly = 15a and a width 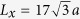Inline graphic. The plate has a thickness h = a in the background (recall that the device has a position-dependent thickness). The simulations show the total displacement field when an external plane wave of a given polarization propagates through the x axis and it arrives to the device. Results shown in the left, central and right panels correspond to the S0, SH0 and A0 modes, respectively, and they are computed at the same frequency ωa/2πct = 0.178, which corresponds to wavenumbers kSa = 0.65, kSHa = 1.11 and kAa = 1.5. The dotted red lines display the size of GRIN flat lens, where the focusing points are demonstrated near the center as expected for all three modes.

We can see how the quality of the focusing point depends on the wavenumber of the incident field, given that it will be limited by diffraction and size effects. Effectively, it is commonly assumed in phononic crystals based devices that the limit of validity is the “low frequency limit”, however in those situations in which we have more than one mode propagating through the material, this limit has to be properly analyzed. The homogenization limit is indeed a propagation regime in which the wavelength of the propagating field is larger than the typical distance between scatterers, so that the field actually detects an average medium and cannot distinguish individual scatterers. Therefore, it is the wavelength of the field and not its frequency the relevant quantity, for this reason, for the same frequency, the different modes will have different wavelengths, and therefore different responses.

In general, there are two physical phenomena relating the validity of the functionality of the device. The upper limit in wavelength is limited by the fact that this wavelength should be smaller than the size of the device, so that the refraction effect dominates over diffraction, this limit can obviously be controlled by increasing the size of the device and, therefore, the number of inclusions; The lower limit in wavelength is determined by the validity of the homogenization theory, which requires a wavelength typically larger than at least 3 or 4 times the lattice constant. These limits are not strictly defined and are only approximate, however it is obvious that for the same device they will be at different frequencies for the three modes, although it is clear that there will be a frequency region in which these conditions hold for the three modes.

The second example considered in this work is a Luneburg lens, which consists of a circular lens in which the refractive index depends on the position to the center of the lens as30

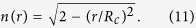graphic file with name srep24437-m20.jpg

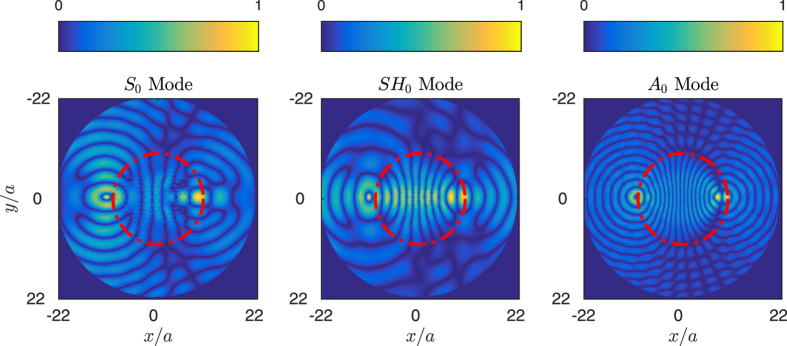
This refractive index is designed in such a way that any plane wave arriving to the lens is focused at the diametrically opposed border of it. It is therefore an omnidirectional device, as it is isotropic and radially symmetric. Its realization is identical to that of the GRIN lens, but this time we use a circular cluster of inclusions of radius Rc = 10a. Figure 5 shows a COMSOL simulation in which a plane wave of a given polarization impinges the cluster from the left, and it is therefore focused at the opposite side of the cluster. The simulations show the real part of the component of the displacement field dominant for each polarization (ux for the S0 mode, uy for the SH0 mode and uz for the A0 mode) and they are performed as in the previous example at the same frequency ωa/2πct = 0.24, corresponding to kSa = 0.87, kSHa = 1.5, and kAa = 1.74, shown in left, central and right panels, respectively. From the simulations it is clear the path followed by the wavefront which is finally focused at the border of the lens, as expected.

Figure 5. Luneburg lens of radius Rc = 10a with about 300 inclusions.

Figure 5

Open in a new tab

Simulations are shown at ωa/2πct = 0.24, which corresponds to wavenumbers kSa = 0.87, kSHa = 1.5, and kAa = 1.74, whose corresponding field distributions are shown in left, central and right panels.

The following example is similar to the previous one, but this time the proposed omnidirectional device is a Maxwell lens30, whose refractive index is given by

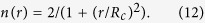graphic file with name srep24437-m21.jpg

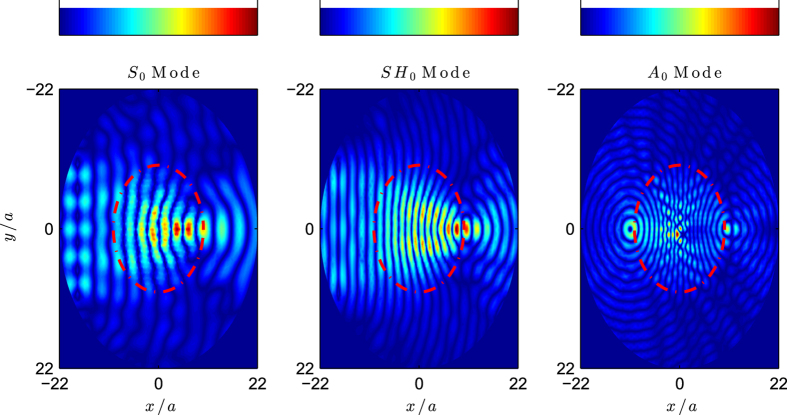
The Maxwell lens is designed in a way that a point source excited at one border of the lens is focused at the opposite side of it. The design method is the same as for the Luneburg lens, and Fig. 6 shows the real part of the results of the simulations performed with COMSOL. The point source for each polarization is excited as a body force in the x, y and z direction for the S0, SH0 and A0 modes, respectively.

Figure 6. Maxwell lens of radius Rc = 10a with about 300 inclusions.

Figure 6

Open in a new tab

Simulations are shown at ωa/2πct = 0.178, which corresponds to wavenumbers kSa = 0.65, kSHa = 1.11, and kAa = 1.5, whose corresponding field distributions are shown in left, central and right panels.

As before, the plots show the real part of the dominant component of the displacement field for each polarization. The source is excited at x = −10a at the same frequency ωa/2πct = 0.178, corresponding to kSa = 0.65, kSHa = 1.11 and kAa = 1.50, shown in left, central and right panels, respectively. The focusing points are identically located at the x = 10a border for the three modes, which shows the good performance of the device.

The above simulations show the performance of the method for the simultaneous control of the three fundamental modes, although the three devices work identically for the three modes. However, the method does not require that the refractive index profile be the same for the three modes, since each refractive index can be tuned independently, which means that a device can be designed as working as one type of lens for one mode and as different one for another mode.

To demonstrate the power of the present method, a multi-lens device is designed to behave as a Luneburg lens for the S0 and SH0 modes and as a Maxwell lens for the A0 mode. Figure 7 shows the real part of the dominant component of the displacement field for each polarization, but this time the simulations were made at the same wavenumber ka = 1.5, in this way it is easier to compare the field distributions and performance of the device. This wavenumber corresponds to reduced frequencies ωa/ct of 0.41, 0.24 and 0.17 for the S0, SH0 and A0 modes respectively. We see how the device behaves as a Luneburg lens for the S0 and SH0 modes while it behaves as a Maxwell lens for the A0 polarization.

Figure 7.

Figure 7

Open in a new tab

Luneburg and Maxwell lens working at the same wavenumber for the three modes ka = 1.5 which corresponds to the frequencies ωa/ct = 0.41, 0.24 and 0.17 for the S0, SH0 and A0 polarizations, respectively.

Summary

In summary, we have presented a method for the design of refractive devices working simultaneously for the three fundamental Lamb modes in thin plates. The method is based on the homogenization of phononic crystal plates, studied here as finite slices of phononic crystals. A complex unit cell is employed to simultaneously control the refractive index of the three modes, together with thickness variations of the plate, the system has therefore enough degrees of freedom to independently tune the refractive indexes of the three modes.

The performance of the method is demonstrated by means of the design of a flat gradient index (GRIN) lens and a circular Luneburg and Maxwell lens working simultaneously for the three modes. Also, a more advanced device is shown which consists in a circular lens working as a Luneburg lens for the S0 and SH0 polarizations and as a Maxwell lens for the A0 one.

Given that the design method is based on a homogenization theory in the quasi-static limit, the devices are shown to work in a broad frequency region, so that the presented method can be efficiently employed to the design of devices for the control or harvesting of mechanical energy, since it allows the full control of vibrations excited in a finite elastic plate. Finally, it must be pointed out that this method can be applied to more complex waves in solids or fluids, being therefore a general approach for the control of multimodal mechanical waves.

Additional Information

How to cite this article: Jin, Y. et al. Gradient Index Devices for the Full Control of Elastic Waves in Plates. Sci. Rep. 6, 24437; doi: 10.1038/srep24437 (2016).

Acknowledgments

This work was supported by the “Agence Nationale de la Recherche (ANR)” and the “Délégation Générale de l’Armement (DGA)” under the project Metactif, Grant No. 443 ANR-11-ASTR-015 and by the LabEx AMADEus (ANR-10- 444 LABX-42) in the framework of IdEx Bordeaux (ANR-10- 445IDEX-03-02), France. Yabin Jin acknowledges a scholarship provided by China Scholarship Council No. 201406260170.

Footnotes

Author Contributions Y.J. designed and performed the simulations. D.T. developed the basis of homogenization method. D.T. and B.D.-R. supervised the research. Y.J., D.T. and B.D.-R. prepared the manuscript. Y.J., D.T., Y.Pennec, Y.Pan and B.D.-R. discussed the results and reviewed the manuscript.

References

  1. Lin S.-C. S., Huang T. J., Sun J.-H. & Wu T.-T. Gradient-index phononic crystals. Phys. Rev. B 79, 094302 (2009). [Google Scholar]
  2. Martin T. et al. Sonic gradient index lens for aqueous applications. Appl. Phys. Lett 97, 113503 (2010). [Google Scholar]
  3. Zigoneanu L., Popa B.-I. & Cummer S. A. Design and measurements of a broadband two-dimensional acoustic lens. Phys. Rev. B 84, 024305 (2011). [Google Scholar]
  4. Zhao J., Marchal R., Bonello B. & Boyko O. Efficient focalization of antisymmetric lamb waves in gradient-index phononic crystal plates. Appl. Phys. Lett 101, 261905 (2012). [Google Scholar]
  5. Torrent D., Pennec Y. & Djafari-Rouhani B. Omnidirectional refractive devices for flexural waves based on graded phononic crystals. J. Appl. Phys 116, 224902 (2014). [Google Scholar]
  6. Climente A., Torrent D. & Sánchez-Dehesa J. Gradient index lenses for flexural waves based on thickness variations. Appl. Phys. Lett 105, 064101 (2014). [Google Scholar]
  7. Climente A., Torrent D. & Sanchez-Dehesa J. Omnidirectional broadband acoustic absorber based on metamaterials. Appl. Phys. Lett 100, 144103 (2012). [Google Scholar]
  8. Umnova O. & Zajamsek B. Omnidirectional graded index sound absorber. In Proceedings of the Acoustics 2012 Nantes Conference, 23–27 April 2012, Nantes, France, 3631 (2012).
  9. Climente A., Torrent D. & Sánchez-Dehesa J. Omnidirectional broadband insulating device for flexural waves in thin plates. J. Appl. Phys 114, 214903 (2013). [Google Scholar]
  10. Cummer S. A. & Schurig D. One path to acoustic cloaking. New J. Phys 9, 45 (2007). [Google Scholar]
  11. Torrent D. & Sánchez-Dehesa J. Acoustic cloaking in two dimensions: a feasible approach. New J. Phys 10, 063015 (2008). [Google Scholar]
  12. Norris A. & Shuvalov A. Elastic cloaking theory. Wave Motion 48, 525–538 (2011). [Google Scholar]
  13. Li J., Fok L., Yin X., Bartal G. & Zhang X. Experimental demonstration of an acoustic magnifying hyperlens. Nat. Mater 8, 931–934 (2009). [DOI] [PubMed] [Google Scholar]
  14. Vasseur J. et al. Experimental and theoretical evidence for the existence of absolute acoustic band gaps in two-dimensional solid phononic crystals. Phys. Rev. Lett 86, 3012 (2001). [DOI] [PubMed] [Google Scholar]
  15. Zhang X. & Liu Z. Negative refraction of acoustic waves in two-dimensional phononic crystals. Appl. Phys. Lett 85, 341–343 (2004). [Google Scholar]
  16. Deymier P. A. Acoustic metamaterials and phononic crystals, vol. 173 (Springer Science & Business Media, 2013). [Google Scholar]
  17. Krokhin A. A., Arriaga J. & Gumen L. N. Speed of sound in periodic elastic composites. Phys. Rev. Lett. 91, 264302 (2003). [DOI] [PubMed] [Google Scholar]
  18. Liu Z., Chan C. & Sheng P. Analytic model of phononic crystals with local resonances. Phys. Rev. B 71, 014103 (2005). [Google Scholar]
  19. Fang N. et al. Ultrasonic metamaterials with negative modulus. Nat. Mater 5, 452–456 (2006). [DOI] [PubMed] [Google Scholar]
  20. Torrent D. & Sánchez-Dehesa J. Acoustic metamaterials for new two-dimensional sonic devices. New J. Phys 9, 323 (2007). [Google Scholar]
  21. Huang H., Sun C. & Huang G. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci 47, 610–617 (2009). [Google Scholar]
  22. Martin T. P., Layman C. N., Moore K. M. & Orris G. J. Elastic shells with high-contrast material properties as acoustic metamaterial components. Phys. Rev. B 85, 161103 (2012). [Google Scholar]
  23. Jin Y., Torrent D., Pennec Y., Pan Y. & Djafari-Rouhani B. Simultaneous control of the s0 and a0 lamb modes by graded phononic crystal plates. J. Appl. Phys 117, 244904 (2015). [Google Scholar]
  24. Torrent D., Pennec Y. & Djafari-Rouhani B. Effective medium theory for elastic metamaterials in thin elastic plates. Phys. Rev. B 90, 104110 (2014). [Google Scholar]
  25. Graff K. F. Wave Motion in elastic solids, 2nd Ed. (Dover, 1991). [Google Scholar]
  26. Vemula C. & Norris A. Flexural wave propagation and scattering on thin plates using mindlin theory. Wave motion 26, 1–12 (1997). [Google Scholar]
  27. Torrent D., Pennec Y. & Djafari-Rouhani B. Resonant and nonlocal properties of phononic metasolids. Phys. Rev. B 92, 174110 (2015). [Google Scholar]
  28. Hsu J.-C. & Wu T.-T. Efficient formulation for band-structure calculations of two-dimensional phononic-crystal plates. Phys. Rev. B 74, 144303 (2006). [Google Scholar]
  29. Born M. & Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light (Cambridge university press, 1999). [Google Scholar]
  30. Šarbort M. & Tyc T. Spherical media and geodesic lenses in geometrical optics. J. Opt 14, 075705 (2012). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES