Precisely parameterized experimental and computational models of tissue organization

Abstract

Patterns of cellular organization in diverse tissues frequently display a complex geometry and topology tightly related to the tissue function. Progressive disorganization of tissue morphology can lead to pathologic remodeling, necessitating the development of experimental and theoretical methods of analysis of the tolerance of normal tissue function to structural alterations. A systematic way to investigate the relationship of diverse cell organization to tissue function is to engineer two-dimensional cell monolayers replicating key aspects of the in vivo tissue architecture. However, it is still not clear how this can be accomplished on a tissue level scale in a parameterized fashion, allowing for a mathematically precise definition of the model tissue organization and properties down to a cellular scale with a parameter dependent gradual change in model tissue organization. Here, we describe and use a method of designing precisely parameterized, geometrically complex patterns that are then used to control cell alignment and communication of model tissues. We demonstrate direct application of this method to guiding the growth of cardiac cell cultures and developing mathematical models of cell function that correspond to the underlying experimental patterns. Several anisotropic patterned cultures spanning a broad range of multicellular organization, mimicking the cardiac tissue organization of different regions of the heart, were found to be similar to each other and to isotropic cell monolayers in terms of local cell–cell interactions, reflected in similar confluency, morphology and connexin-43 expression. However, in agreement with the model predictions, different anisotropic patterns of cell organization, paralleling in vivo alterations of cardiac tissue morphology, resulted in variable and novel functional responses with important implications for the initiation and maintenance of cardiac arrhythmias. We conclude that variations of tissue geometry and topology can dramatically affect cardiac tissue function even if the constituent cells are themselves similar, and that the proposed method can provide a general strategy to experimentally and computationally investigate when such variation can lead to impaired tissue function.

Variability in local tissue organization and geometry is an inherent aspect of normal physiology, but can also be a manifestation of emergent or chronic abnormalities. Understanding what might distinguish ‘normal’ and ‘abnormal’ tissue organization is frequently difficult, as the corresponding differences are often subtle relative to the variability found among healthy individuals, in part due to the substantial robustness of tissue function. It is likely that small changes in relative cell arrangement from the normal tissue organization can be tolerated, and do not result in a pathologic state. However, beyond a critical extent, a change in tissue organization might cross the tolerance threshold and potentially result in abnormal pathological functional behavior, even if the constituent cells are otherwise healthy and unperturbed. Unfortunately, it is currently difficult to quantitatively study the relationship between tissue organization and function, and to measure the degree of change in tissue organization that can lead to pathological behavior. One of the primary reasons for this is that tissue samples are often obtained from patients who display a well developed severe pathologic state, and are likely to be substantially different from tissue samples of normal controls or patients with undiagnosed disease. Thus, it is difficult to determine how the etiology of the disease is correlated with potentially gradual and cumulative alterations in the tissue structure. Furthermore, it is a substantial challenge to achieve consistency in such an analysis, due to distinct histories and sources of the samples. Additionally, while diffusion tensor magnetic resonance imaging (DTMRI) based cell micropatterning provides an excellent first step into studying this structure-function relationship,¹ global descriptions of tissue structure akin to the helical ventricular bands described by Torrent-Guaspe² are lacking. Having this precise control over tissue organization and properties is known to be especially important in cardiac tissue systems where cells are organized in a laminar structure³ and cardiac propagation is a discontinuous process at the cellular level.⁴ To explore whether and how gradual changes in the tissue structure may translate into a serious deviation from the normal function, one can benefit from systematic, systems level methodology allowing gradual and precisely controlled variation of tissue organization on a large scale, while preserving the local cell positioning, coupling and alignment throughout the perturbations.

Mutual positioning and orientation of cells in living tissues are generally non-random, resulting in important structural and functional consequences. For instance, anisotropically shaped cells form local axially aligned ensembles (frequently referred to as fibers), where the fiber structure can increase the effectiveness of muscle contraction, or help to optimally distribute the load in tendons and ligaments. Cell alignment in fluid flow can increase cell resistance to shear stress.⁵ A diverse set of cell types can exhibit spontaneous self-organization into topologically complex patterns in a Petri dish, even if cultured in an initially unstructured way.^6–9 On a larger scale, collective cell orientation can lead to the formation of diverse topological super-structures. For instance, the ventricular myocardium has a helical muscle band structure that results in global and local structural anisotropy of ventricular fibers and other wall constituents.² Such anisotropy provides unique electrical and mechanical properties that contribute to normal physiological function, including electrochemical impulse propagation and the orderly timing of contraction. Spatial variation of this natural anisotropy contributes to the formation of virtual sources during defibrillation,¹⁰ and adaptive remodeling of the myocardial tissue organization on different length scales may lead to conduction failure, wave splitting and attachment of reentrant waves.¹¹ Thus an important question is whether tissues, in which cells preserve local cell alignment in an adaptive fashion, but change at larger scale organization and topology, would possess distinct functional characteristics, possibly leading to pathologic states.

In this report, we describe a method to design families of precisely parameterized cell arrangement patterns that are not only smooth and continuous on a local cellular scale but can also have complex global geometries. We show that the results of this design can be used for both experimental and computational simulations of cell organization patterns and their corresponding functional behavior, yielding a more direct match between experiments and models. We demonstrate how this method can be applied to create three prototypical fiber geometries – linear, curved and splayed – with results suggesting that these or similar variations in cardiac tissue geometry can result in significant alterations of electrophysiological tissue function in both in vitro experimental and computational model systems, with potential relevance to heart disease. At the same time, the methodology proposed can be generally useful for modeling other types of complex cell ensembles and tissue-like structures.

Results

Monolayers of geometrically polarized cells, i.e., cells that have an identifiable axis of orientation, can be abstracted as two-dimensional vector fields, with each vector associated with the direction of an individual cell. Although director rather than vector fields may be more appropriate, as the orientation of the main cell axis may not be associated with front-back polarity,⁷ we will operate with vector notation, for the sake of convenience and familiarity. It is a common observation in natural tissues that the orientation of individual cells is generally continuous and smoothly varying, placing similar constraints on a vector field modeling these cells. Thus, to create parameterized models of multi-cellular geometric organization, one needs the ability to generate extracellular matrix (ECM) patterns that are smooth and continuous on a local scale. At the same time, it is also desirable to have these ECM patterns vary as a function of control parameter(s) on a larger scale, the scale of the overall tissue. Vector fields that can define such ECM patterns are commonly generated during simulation of physical processes, such as the flow of a Newtonian incompressible liquid. In our study, we generated vector fields by simulation of a two-dimensional incompressible isothermal fluid flow determined by the Navier–Stokes equations. We want to stress that this process, although formally not related to how tissues may form, can yield diverse and well defined vector fields that can be used to generate ECM patterns that are then used to develop model tissue structures of desired properties, and can thus be used solely for this purpose (Fig. 1A). The geometry of the resulting vector fields are determined in a precisely parameterized fashion by the initial conditions as well as the boundary conditions imposed on the flow field simulation, including the geometry of the boundaries and the distribution of the flow velocities at these boundaries. Since only the direction of individual vectors, but not their amplitude are typically important for our analysis, we convert the vector fields obtained from solving flow simulations, into corresponding fields whose vectors have the same (e.g., unit) length or amplitude. Accordingly, for the remainder of the manuscript, vector field and flow field are used interchangeably to denote simulation-derived flow fields, where individual vectors are assumed to have the same amplitude.

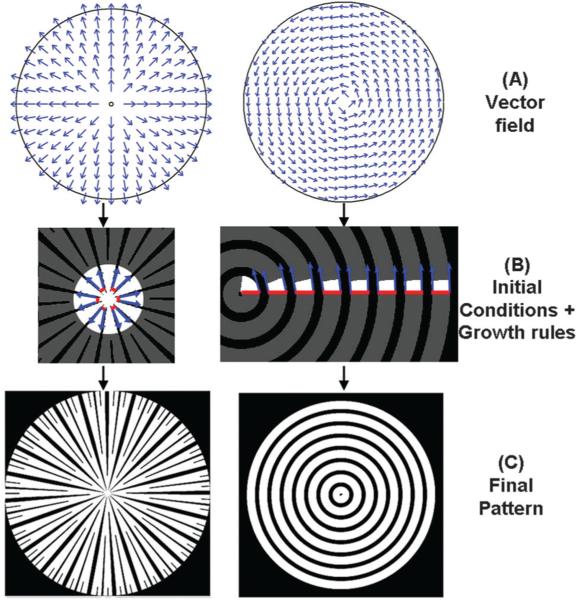
Fig. 1.

Appropriate selection of the initial vector field, the seed pattern and the propagation rules, determines the type of pattern generated. (A) The same circular geometry can give rise to diverse vector fields based on the initial conditions of the simulation, including the positioning of the sources, e.g., at the center (left panel), leading to radially expanding flowlines, or along the radius (right panel), leading to concentrically curved flowlines. (B) The role of the seed pattern is illustrated in the generation of the final pattern. In the left panel, a set of bands (shown in red) and gaps (region between the bands) on the circumference of a small initial circle, form the initial conditions that give rise to a starburst pattern, indicated by the grey bands. The band propagation is indicated by the blue arrows. In the right panel, propagation of the initial conditions defined by alternating bands and gaps along the radius of the circle results in a concentric pattern; (C) the resulting patterns can be used for further analysis of the role of cell patterning. e.g. They can be translated into microfabricated masks and ultimately cell patterns, or be used as inputs into computational models. See additional information in the ESI.†

Vector fields can be used as templates to generate experimental ECM patterns to control cell alignment and communication, where the local ECM orientation specifies the direction of locally parallel microscopic bands of co-oriented cells. Practically, this can be achieved by specifying micro-scale bands of ECM separated by ECM-free gaps (also oriented in the same direction). The widths of the ECM bands and gaps can be varied for different applications, and usually can be optimized to achieve both robust cell alignment and cell–cell interactions across the cell monolayer.^1,12 The initial conditions include a periodic pattern of bands and gaps, which is referred to here as the ‘seed pattern’. The seed pattern typically reflects the desired final pattern and the ratio of widths of bands and gaps in the final pattern. It is an empirical, user defined input used to control the precision of cell orientation, while preserving the desired amount of longitudinal and transverse cell–cell coupling. The vector field can be used to ‘propagate’ the seed pattern, so that as it ‘sweeps’ over the vector field, a final pattern of bands separated by gaps emerges. However, this mapping is not a trivial task in terms of specifying how the bands and gaps (having finite maximum widths) should deform (i.e., bend, branch, appear and disappear), especially in converging and diverging patterns, so as to guarantee both their correspondence to the vector field and seed pattern, and their preservation of a locally parallel and smoothly varying pattern of bands. Below we demonstrate how this challenge can be met in a number of different ways, allowing one to vary the local specification of cell–cell interaction, given a globally complex geometry of cell orientation.

The seed pattern can be first mapped onto an open or closed boundary specified by the sources of the vector field (i.e., the boundary zones where all vectors are directed into rather than out of the area being patterned, e.g., Fig. 1A and B, left; note that a singular, ‘point’ source can be approximated by a finite circle onto which the seed pattern can be mapped). In the case of a rotating concentric flow, the source and the sink are defined to be radial segments connecting the singularity at the concentric center and the circular boundary, and are situated infinitesimally close to each other. The flow lines, which are parallel to the circular boundaries, exit the source and enter the sink, and the seed pattern is mapped on the source radial segment (Fig. 1A and B, right). Following this initial mapping, the seed pattern can then be propagated through the vector field following the local vector directions (i.e., along the field flow-lines), as described in detail in the ESI,† and shown in Fig. 1B and Fig. S1 and S2 (ESI†), giving rise to the ultimate band/gap design (Fig. 1C). One can allow variation of the seed pattern itself as it propagates, e.g., through progressive or selective expansion of the widths of the bands and/or gaps, to analyze the effect of variable cell–cell coupling in the transverse (across the bands and gaps) direction, which can increase the diversity of patterns resulting from the same vector field (Fig. 2A–F). Variation in the direction of the vector field relative to the boundaries and of the number of vector field sources and sinks can further increase the pattern diversity (Fig. 2G–I). In addition, different rules can be formulated for the emergence and disappearance of the resulting gaps and bands during seed pattern propagation, in areas having gradients in flowline density. For instance, new bands and gaps can emerge, or existing bands and gaps can merge, if the local flowlines diverge or converge, respectively (Fig. 2I).

Fig. 2.

Varying the seed pattern and the rules of seed pattern propagation can result in distinct patterns that are based on the same vector field, with further diversity in patterns introduced by generating different underlying vector fields. (A) Direction of simulated fluid flow in a circular region resulting from the initial condition specification, i.e., a source at the center of the circle and a sink at the circumference. (B) The vector field defined by this flow can be used to generate several different patterns. Branching is allowed for both bands and gaps in (C) and (D), but only allowed for the bands in (E) and (F). In (E), the gaps are additionally constrained to not grow beyond a certain maximum width, while in (F) the gaps can grow in an unconstrained fashion. Additionally, varying the relative widths of the bands and gaps in the initial conditions, and the fractional widths of newly generated bands or gaps following a branching, are also conditions that give rise to a diverse range of patterns in (C–F). Changing the boundary conditions during the generation of the vector field, e.g., the direction of the flow to be non-normal to the perimeter of the patterned region, can result in a spiral pattern (G). By defining more than one source, e.g., a line source at the bottom edge of the rectangle and a point source in the center of the rectangle in (H), or by defining a source and a sink as two singularities within the rectangle (I), it is possible to further increase the pattern diversity. As shown in (I), one can define both the emergence and the fusion of adjoining bands (or gaps) depending on whether the local flow lines diverge or converge. See additional information in the ESI.†

Importantly, while the vector fields can be used for generating ECM band patterns, they can also serve as inputs into computational simulations of emergent collective cell behavior, thus providing a convenient tool to create similar experimental and computational tissue models (Fig. 3). Indeed, the underlying ECM patterns derived from the vector fields indicate the degree of local and global anisotropy in the experimental tissue patterns by specifying the distribution of the cell positions and/or their orientations, which is an important determinant of cell–cell interactions, including intercellular chemical signaling and action potential propagation. As the (potentially very complex) vector field used for both computational analysis and cell patterning experiments is the same, the computational and experimental results are expected to achieve a high degree of correlation, yielding further opportunities for model refinement and experimental design. The model parameters can also be controlled by the nature of the seed pattern and the particular way it is propagated over the underlying vector field. Below, we provide examples of such iterative, modeling and experimental analysis.

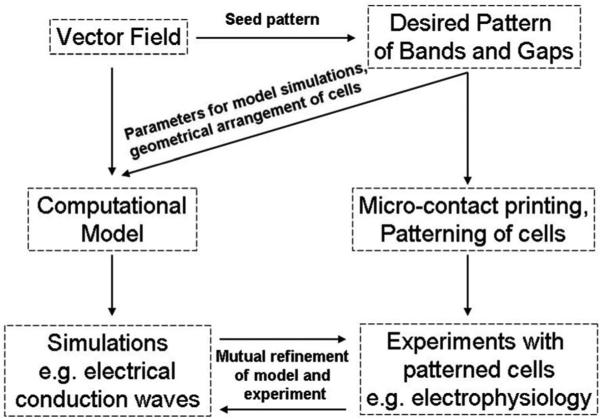
Fig. 3.

Schematic of interplay between modeling and experimental approaches. The vector field is the basis for the generation of a desired pattern of bands and gaps, and can be used to generate a patterned substratum of extracellular matrix, e.g., through microcontact printing. Cells are then patterned on this surface, and biologically relevant experiments, such as electrophysiological studies, are performed. Simultaneously, the vector field is also the basis for the generation of a computational model, which is used to simulate functional consequences of alteration in the model tissue organization, e.g., the electrical conduction. Mutual refinement of the model and experimental design results in a better understanding of the system.

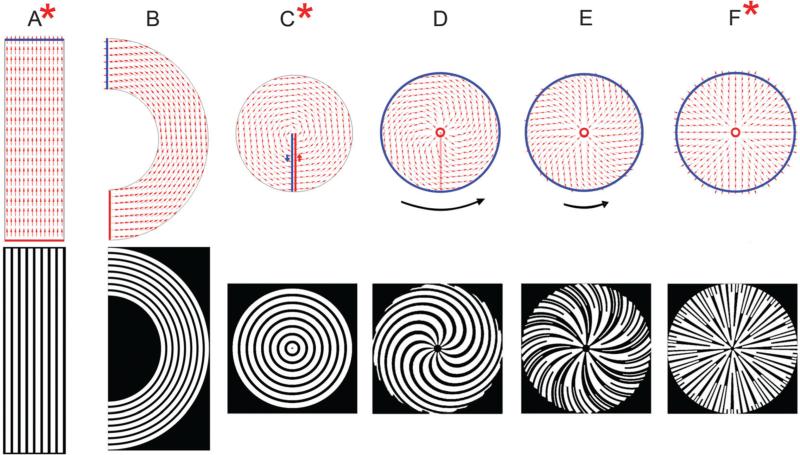
How can one design a set of parametrically defined, progressively changing fields that can not only be infinitely close to each other but also span an extensive range of geometric and topographic diversity? Above, we have shown examples of complex patterns that can be generated by a combination of flow field maps and particular sets of rules defining how a seed pattern can be mapped onto the flow field. Given a seed pattern, the parameters that can be used most conveniently in defining the gradually morphing patterns are the boundary conditions of the flow field. To illustrate this, we explored the effects of the relative positioning and shape of the boundaries and the boundary fluxes yielding progressively more complex geometric patterns, and explored the resulting model tissue properties, both computationally and experimentally (Fig. 4). We started with the pattern most commonly used in 2D tissue patterning studies:¹² a set of parallel stripes designed to generate fields of collinear, locally aligned cells (Fig. 4A). The boundary conditions leading to this organization were two equal linear segments of a ‘source’ and a ‘sink’, parallel to each other, specifying the influx and efflux rates directed normal to the boundaries. The flow field can then be gradually altered by mutual rotation of the horizontal straight segments corresponding to the source and sink, and corresponding modification of the other boundaries to generate a semi-circular pattern (Fig. 4B). The boundaries can then be ultimately rotated and brought to be infinitely close to each other, and offset from the pattern center, resulting in the pattern of flow lines representing concentric circles (the “concentric” pattern) (Fig. 4C). The concentric circles pattern can also be thought of as the limiting case of a family of patterns, wherein the source boundary is shrunk down to the innermost circular edge of a concentric pattern, the sink boundary is expanded to be the outermost circular edge of the concentric pattern (the outermost flow line) and the direction of the flow at the sink boundary is constrained to be at a specific angle (tangential, in the case of concentric circles). Accordingly, we altered the mutual position of the boundaries by allowing the ‘source’ to shrink down to the red circle and the ‘sink’ to expand to the blue circle, as shown in Fig. 4D. If we preserve the magnitude of the overall flow rate of the outermost flow line while changing the direction of the flux at the circular sink boundary, the result is a spiral pattern (Fig. 4D). Progressive variation of the direction of the boundary flux from tangential towards normal at the ‘sink’ boundary, leads to a wide variety of spiral patterns (such as the one shown in Fig. 4E) and eventually yields the ‘‘starburst’’ or splayed pattern where the ‘sink’ boundary flux is normal (Fig. 4F). The starburst pattern shown in (Fig. 4F bottom panel) is a representative pattern, and as shown in Fig. 2, varying the seed pattern and the branching rules can give rise to a range of starburst patterns. As an example, Fig. 2E represents the starburst pattern used for further experimental analysis with live cells. In this analysis, we focused on the most topologically distinct patterns in this progression, the linear, concentric and starburst patterns, to illustrate the versatility of this tissue engineering approach, as described below. We note that many biologically interesting and relevant tissue patterns can be represented as a combination of these three distinct patterns, thus highlighting the power of our approach.

Fig. 4.

Gradual morphing of patterns resulting from variation of the simulation region and the boundary conditions. Vector fields with overlaid boundary conditions, where the red and blue boundaries are the source and sink respectively (above) and their resulting patterns of bands and gaps (below) are displayed. A linear (striped) pattern is generated based on the two horizontal boundaries acting as a source and sink (A). Gradual rotation of the source and sink boundaries as well as the simulation region leads to a semi-circular pattern with concentric rings (B) and eventually a circular pattern with concentric rings (C). The concentric ring pattern can also be generated as the limiting case of a family of patterns, where the source is a small inner circle, the sink is a larger outer circle and the direction of flow is constrained to be at an angle to the sink boundary (tangential for concentric circles). Using these source and sink boundaries, and by progressive variation of the direction of the sink boundary flux from tangential towards normal, we can generate spiral patterns of different shapes (D and E). The black curved arrows next to the flow fields are meant to be a visual aid to represent the degree of curvature of the flow lines (their length is not correlated with actual curl values). When the boundary flux at the sink is normal to the boundary, it leads to a ‘starburst’ pattern (F). The asterisks on (A), (C) and (F) indicate that these vector flows can be used to generate the linear, concentric and starburst patterns, similar to those used in further experimental and computational studies. The starburst pattern in Fig. 2E represents the pattern used for experimental studies.

The flowlines of vector fields can be characterized by their local divergence and curl, which in general may be spatially heterogeneous. Since the vectors in the fields used in our analysis have the same local amplitudes, the two convenient metrics of divergence and curl, can be used for their intuitive characterization, and therefore as a way to visualize the differences between the patterns. It must be noted that the vector fields were generated using the typical parameters specified for a fluid dynamical simulation, rather than by specification of divergence or curl values. As a visualization tool, for such fields, divergence indicates the extent to which adjacent flowlines are non-parallel (i.e., splayed) to each other, whereas the curl characterizes the local ‘vorticity’ or bending of the flowline trajectory. Flowlines that are uniformly oriented in one direction have both divergence and curl equal to zero everywhere. Such a field is the “linear” pattern described above (Fig. 4A, top). An example of a field having flowlines with zero divergence but local curl in regions containing the origin is the “concentric” pattern in the sequence described above (Fig. 4C, top). Finally, a field containing flowlines with zero curl but non-zero divergence in regions containing the origin is the “starburst” pattern (Fig. 4E, top). These three patterns represent the extremes of local organization of vector fields and their flowlines. Any other global pattern of flow-lines will have a combination of zero or non-zero local values of curl and divergence, thus representing a combination of these patterns and highlighting why these three patterns were selected for experimental validation. We therefore set out, first, to characterize the responses of cells organized into the linear, concentric and starburst patterns and determine if the model tissue behavior would vary in a significant way, and, second, to find out whether local values of flow-line curl and divergence might present important control parameters of tissue response. Cardiac myocytes were chosen for this experimental analysis because they are cells which naturally form fiber-based tissue structures that have a high degree of cell–cell coupling and physiologically important structural and functional anisotropy on both global and local scales.

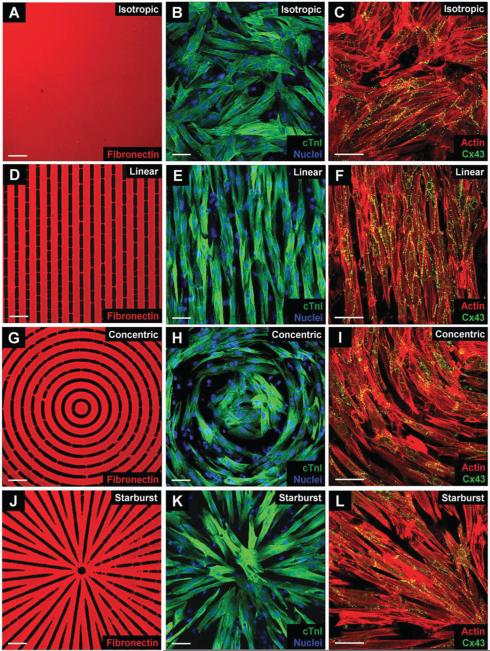
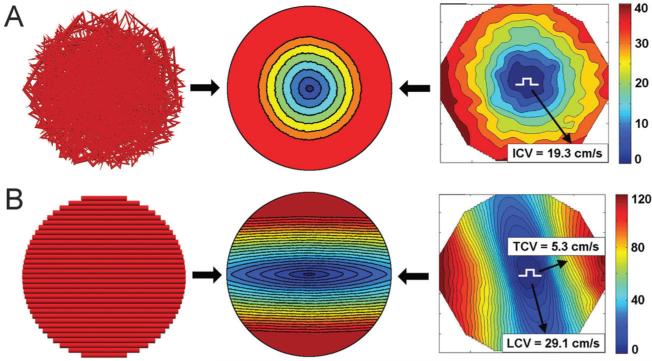
To culture primary neonatal rat ventricular myocytes (NRVMs) into distinct patterns, we microprinted fibronectin in isotropic (Fig. 5A), linear (Fig. 5D), concentric (Fig. 5G) and starburst (Fig. 5J) patterns. The particular seed pattern used (20 μm wide bands separated by 10 μm wide gaps) allowed for optimal and extensive cell–cell contact and for gap junction formation in both the longitudinal and transverse directions, determined from preliminary optimization studies conducted with the linear patterns (not shown). While the linear and concentric patterns have fixed 20 μm wide bands separated by 10 μm wide gaps, the starburst pattern actually has continuously variable bands (typically expanding from 10 to 20 μm wide and then splitting into two 10 μm wide bands repeatedly as the pattern expands outward) and gaps (ranging from 0 to 10 μm wide) throughout the pattern. This capability, along with the selection of the optimal seed pattern by the user, allows for complete control of the patterns desired features for any experimental setup. We found that cells cultured on all 3 anisotropic patterns formed confluent monolayers, with cells locally aligned along their longitudinal axis. Immunolabeling of cardiac troponin I and DAPI nuclear staining in isotropic (Fig. 5B) and anisotropic (Fig. 5E, H, and K for linear, concentric, and starburst patterns, respectively) monolayers showed that the cultures consisted primarily of NRVMs and not of other cell types, e.g., fibroblasts, etc. It needs to be pointed out that fibroblasts can be seen as unstained cells with nuclei in the cardiac troponin image panels (Fig. 5B, E, H and K). These fibroblasts, however, did not appear to affect the continuity of action potentials propagating through the various patterns (Fig. 7 and 8). Additionally, from a qualitative perspective, patterned cell monolayers formed consistently across many trials and each pattern appeared to have similar numbers of fibroblasts (Fig. 5).

Fig. 5.

Characterization of fibronectin transfer and culture properties in isotropic and anisotropic NRVM monolayers. Fibronectin immunostaining (left column), merged cTnI and DAPI (middle column), and merged actin and Cx43 (right column) images of isotropic (A–C), linear (D–F), concentric (G–I), and starburst (J–L) patterned cultures reveal similar cellular morphology, myocyte composition, and levels of Cx43 expression. The linear, concentric, and starburst patterns were constructed by designing microcontact printing masks. Scale bar = 50 μm.

Fig. 7.

Characterization of the conduction properties of isotropic and anisotropic NRVM cultures and optimization of the corresponding computational model. Representative isochronal maps of AP propagation (rightmost panels) in isotropic (A) and linear anisotropic (B) monolayers are matched up with the modeling predictions (middle panels) based on the model fiber orientation (leftmost panels), and model parameters are adjusted to match the experimental measurements. In the isochronal maps, the selected paths of wavefront propagation along which CV was measured are shown by black arrows, and their corresponding values are displayed. The color scales indicate the time values measured in milliseconds. The optimized model was then used for prediction of conduction properties in more complex cellular patterns (Fig. 8), based on alternate vector fields.

Fig. 8.

Contrasting modeling predictions and experimental analysis, based on the initial characterization in Fig. 7. (A) and (F) The geometry of the concentric and starburst fiber patterns based on the vector fields used to generate the corresponding patterns in Fig. 5; (B) and (G) simulations of action potential propagation following a point stimulus at the center of each monolayer pattern shown in (A) and (F) respectively; (C) and (H) simulations of action potential propagation following a point stimulus delivered off-center in each monolayer pattern shown in (A) and (F) respectively; (D) and (I) experimental validation of the predictions in (B) and (G) respectively, using the experimentally constructed patterns, as shown in Fig. 5; (E) and (J) experimental validation of the predictions in (C) and (H) respectively. In the experimental isochronal maps, the selected paths of wavefront propagation along which CV was calculated are shown by black arrows, and their corresponding values are displayed. The color scales indicate time values measured in seconds.

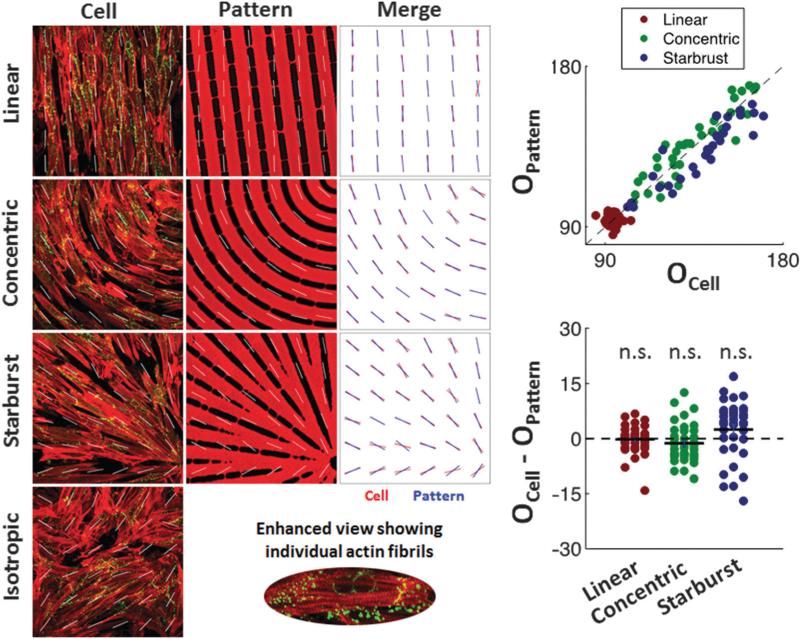
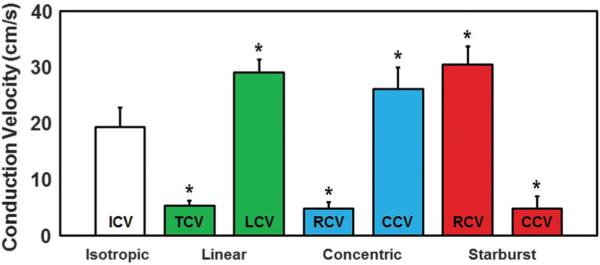
Parallel sarcomere organization was also observed in the anisotropic monolayers. Immunocytochemical analysis using anti-actin and anti-Cx43 antibodies confirmed that both iso-tropic (Fig. 5C) and anisotropic (Fig. 5F, I, and L for linear, concentric, and starburst cases, respectively) monolayers had similar expression patterns of Cx43 localized at cell-to-cell appositions over entire cell lengths, suggesting extensive cell–cell coupling for all patterns. Analysis and quantification of actin orientation (Fig. 6) using a process similar to other groups¹³ was also conducted in order to confirm that the orientation of the patterned myocytes aligned well with the underlying fibronectin patterns, which are based on the orientation of their underlying vector fields. The set of three merged images show that good alignment exists qualitatively, and the two graphs with a t-test shows that the averages of the differences in orientation were not statistically significant, proving this alignment exists quantitatively for each anisotropic pattern. We then analyzed functional characteristics of the patterned NRVM monolayers, which now included curved and splayed fiber geometries (concentric and starburst patterns, respectively). First, we studied the action potential (AP) propagation by multi-site optical mapping of transmembrane potentials in the iso-tropic and linear anisotropic geometries to define the basic parameters of isotropic and anisotropic responses to exogenous pacing. Isochrone maps of AP propagation in isotropic and linear anisotropic monolayers (n = 7) are shown in Fig. 7 (rightmost column). With 2 Hz pacing from a point electrode at the center of the monolayer, isotropic monolayers (Fig. 7A) supported a uniform, smooth AP propagation with isotropic conduction velocity (ICV) of 19.3 ± 3.4 cm s⁻¹ and APD₈₀ (AP duration at 80% repolarization) of 196.2 ± 18.5 ms. In linear anisotropic monolayers (Fig. 7B), with divergence and curl equal to zero everywhere, the longitudinal conduction velocity (LCV) (29.1 ± 2.2 cm s⁻¹) was significantly higher than ICV, and transverse conduction velocity (TCV) (5.3 ± 0.9 cm s⁻¹) was significantly lower than ICV. The anisotropy ratio of CV (AR = LCV/TCV) ranged from 5.6 to 10.2 (7.2 ± 1.6).

Fig. 6.

Analysis and quantification of cellular alignment with their underlying fibronectin patterns. A Sobel filter was used to assign an average orientation for 36 sub-regions for each pattern type based on the orientation of the actin fibrils within the cells or the fibronectin lines. These orientations are indicated by white lines on the patterned cell and fibronectin images. Within each sub-region the orientation from the cell image was then laid on top of the orientation from the fibronectin image into a merged image showing that the actin orientation within the cells qualitatively follows the direction of the underlying fibronectin patterns, which are based on the orientation of their underlying vector fields. To quantitatively prove this, the orientation of each cell sub-region was plotted against that of the fibronectin patterns (top graph), the difference between them was plotted (bottom graph), and a t-test was used to show that the averages of these differences in orientation were not statistically significant for any of the anisotropic patterns (n.s. = not significant).

Using the information from these initial±studies, we then used computational modeling to predict the AP propagation characteristics in the other patterned anisotropic cell mono-layers, using the corresponding vector fields as inputs. Specifically, we simulated two-dimensional cell monolayer models corresponding to the different experimental ECM patterns on a circular simulation domain, with an assumed radius of 10 mm (similar to experimental models). The electrical behavior was modeled by the bidomain equations, which consider the monolayers as composed of intracellular and extracellular spaces coupled electrically via the current that crosses the cell membranes.¹⁴ The membrane properties of individual cells were represented with the updated Luo–Rudy dynamic model of the myocyte AP.¹⁵ AP duration was adjusted to approximately match the results of optical recordings in the isotropic cell monolayers by modifying the time constant of the inactivation gate of the L-type calcium channel; APD₈₀ was thus 160 ms for pacing at 2 Hz. The input vector fields were then mapped onto a regular grid that covered the entire simulation domain. Individual vector components were bilinearly interpolated to the center of each finite element. The resulting vectors were normalized and assigned as the fiber orientations in the corresponding elements. The bidomain conductivity values were determined by approximately matching the experimental LCV and TCV values, 29.1 and 5.3 cm s⁻¹, respectively, to the monolayer with linear patterning (Fig. 7B).

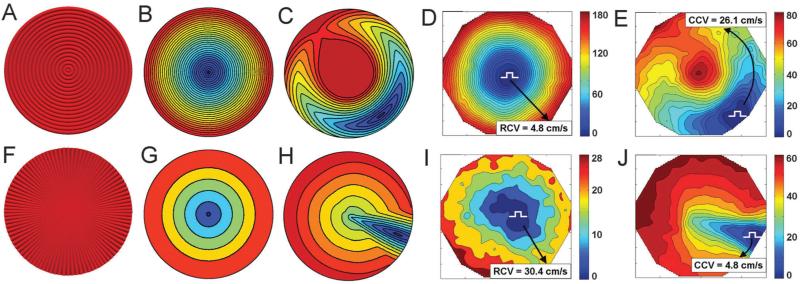
Having established the basic conduction velocity determinants, we computationally predicted AP propagation in simulated concentric (with zero divergence but local curl in regions containing the origin) and starburst (with zero curl but nonzero divergence in regions containing the origin) patterned monolayers which were stimulated both at the center (the singularity positions for both patterns) and off-center of each pattern (Fig. 8). In these simulations, as indicated above, the primary difference between the corresponding models stemmed from different underlying vector fields (Fig. 1A and B), corresponding to those used for the microcontact printed designs in Fig. 5. The models predicted that AP propagation following stimulation of both monolayer types at the center results in uniform expansion of the AP front, albeit with dramatically different CV values. Indeed, in the simulated concentric mono-layer (Fig. 8B), the radial conduction velocity (RCV) at large radial distances (near the edge of the monolayer) was essentially the same as TCV in the linear pattern (5 cm s⁻¹), whereas in the starburst pattern (Fig. 8G), RCV at large radial distances was essentially identical to LCV in the linear pattern (29 cm s⁻¹). Moreover, following off-center stimulation in the concentric pattern (Fig. 8C), the propagating AP front was progressively curved as it traveled with a higher speed along the circumference of the circle centered at the pattern center and lower speed in the radial directions. The complex and novel pattern of propagation ultimately closed on itself, generating two AP waves, one traveling towards the pattern center and the other away from it. AP propagation through the starburst patterned monolayer following off-center stimulation (Fig. 8H) was also novel and rather complex, with the initial wave traveling primarily radially towards the center of the pattern, arriving at the center, and then propagating radially outwards. The circumferential conduction velocity (CCV) near the edge of the monolayer with the concentric pattern was estimated to be close to LCV, while it was found to be close to TCV near the edge of the monolayer with the starburst pattern.

We then tested the model prediction by optical mapping of AP propagation in concentric and starburst patterned cell monolayers (n = 7) (Fig. 7D, E, I, and J); RCV and CCV were measured near the edge of the monolayers. We found that all the on-center and off-center cell stimulation results were in excellent agreement with the model predictions. Indeed, in concentric mono-layers stimulated at the center (Fig. 8D), APs propagated outwardly with a uniform but very slow RCV (4.8 ± 1.1 cm s⁻¹) that was significantly lower than ICV but only slightly lower than the measured TCV (Fig. 9). With stimulation at the edge of the monolayer, where adjacent strands had a more parallel orientation (Fig. 8E), APs initially spread with a curved elliptical wavefront around the circle center, merged with itself, and then split into two waves, one traveling away from and the other traveling towards the center in a retrograde direction. CCV (26.1 ± 3.9 cm s⁻¹) was significantly higher than ICV but only slightly lower than the measured LCV (Fig. 9), APD₈₀ was 205.1 ± 16.2 ms, and AR (CCV/RCV) ranged from 5.0 to 8.1 (6.2 ± 0.9).±In starburst stimulated at the monolayers center (Fig. 8I), APs propagated outwardly with a very fast although irregular RCV (30.4 ± 3.3 cm s⁻¹) that was significantly higher than ICV but only slightly higher than the measured LCV (Fig. 9). With stimulation at the edge of the monolayer (Fig. 8J), APs initially propagated with an elliptical wavefront towards the center of the monolayer, and then spread to the edges of the monolayer in a radial fashion. CCV values (4.8 ± 2.2 cm s⁻¹) were significantly lower than ICV but only slightly lower than the measured TCV (Fig. 9), APD₈₀ values were 198.5 ± 23.3 ms, and AR (CCV/RCV) ranged from 4.5 to 10.4 (7.9 ± 3.2). Thus APD₈₀ was similar among the various tissue patterns, and AR values were similar among the various anisotropic tissue patterns.

Fig. 9.

Bar-plot of average experimental conduction velocities for each pattern. All values were statistically different from the isotropic ICV. Similarities were noted between linear TCV and LCV and their respective concentric and starburst CVs at regions away from the center of the patterns. These similarities also applied to the anisotropy ratio of CV (AR) for all three anisotropic patterns as discussed in the text.

Discussion

How does collective cell behavior yield complex tissue functions? Local cell orientation and organization into fiber-like structures coupled with topologically complex variation of fiber orientation over the scale of thousands of cells can be an important component of coordinated cell behavior. One approach to account for local cell orientation is to use data obtained from diffusion tensor magnetic resonance imaging of intact hearts to obtain fiber orientation throughout the tissue,¹⁶ which can then be realized in microcontact printed cell models¹⁷ or computational models¹⁸ of the heart. However, because of the complex architecture intrinsic to native tissue, it is difficult to establish the precise relationship between tissue organization and function. In this report, we describe a method to extend the analysis of anisotropic cell monolayers to geometrically complex patterns that are precisely parameterized and can be realized both experimentally and computationally in coupled cell models.

The method is based on coupling a vector field generated by simulation of a physical process (e.g., a Newtonian fluid flow in our analysis) and the rules for propagation of the seed pattern to define ECM patterns that are then used to control local cell alignment and communication of patterned tissues. This seed pattern is an empirical input designed by the user which can be adjusted to optimize cell alignment and coupling as presented here or precisely control the degree of cell misalignment and uncoupling to analyze the tolerance of normal tissue function to structural alterations. The use of a vector field for establishing the pattern ensures its local smoothness and continuity, and requires only a small number of parameters to control the corresponding physical processes. For instance, certain variations of parameters can force fluid dynamics to transition into a chaotic regime, the simulation of which can yield a series of gradually changing vector fields that can be used to obtain progressively altered patterned cell arrays, with organization varying from well-ordered to random or chaotic. Changes in cell orientation are characteristic of both normal physiology and pathophysiology, and are closely connected to the structure and function of the heart, e.g., cardiac anisotropy is known to vary with embryological development,¹⁹ the location within the heart,²⁰ aging,²¹ remodeling after infarction,²² and hypertrophic cardiomyopathy.²³ The degree of tissue disorganization that can result in pathologic states²⁴ is now addressable with the methods described here by customizing the input parameters to the model (i.e., altering the seed pattern, etc.). In addition, the vector field can be used to define the geometry of a computational model precisely corresponding to the ECM patterns used to generate the patterned cell monolayers. For example, in the analysis presented, the vector fields that were used to develop the experimental ECM patterns were also fed into a computational model of AP propagation, allowing for a very close comparison of the model and experiment, and, in particular, a more defined analysis of the role of pattern geometry in the behavior of wave propagation. The mapping of the seed pattern onto the vector field by means of propagation from an initial boundary also presents considerable flexibility in determining the details of the pattern. In particular, the details of band branching can define different degrees of transverse cell–cell communication as a function of location within the pattern, even if the underlying vector field is the same (Fig. 2).

In our analysis we focused on three prototypical anisotropic patterns presenting different combinations of local curl and divergence of ECM patterns and the resulting cell orientations. To investigate if these patterns can endow the model tissue with distinct functional properties, we studied the dependence of AP propagation on the structural organization of cardiac cell monolayers. Although linear anisotropy has been extensively studied experimentally in cell cultures and theoretically in computer models, relatively less is known about the properties of AP propagation in curved and splayed fiber geometries. In the curved geometry, cardiac fibers follow circuitous pathways, and have been studied through a cell culture model of field stimulation.²⁵ A similar arrangement is evident at a very early stage of cardiac development¹⁹ and in the apical left ventricular orifice of the adult heart.²⁰ In the splayed ‘starburst’ geometry, fibers diverge or converge, as in papillary muscle insertions in the endocardium and in the right ventricular apex, one of the corners of the ‘triangle of dysplasia’ in arrhythmogenic right ventricular cardiomyopathy.²⁶ In our analysis, we found that the tissue electrophysiology, in terms of AP durations and regional longitudinal and transverse conduction velocities, was similar among all of the anisotropic geometries, yielding however strikingly different and novel patterns of propagating AP waves. As discussed below, this alteration of the pattern of AP propagation, in addition to enhancing our understanding of the variability in normal organization, can be suggestive of pathological states. It is also important to note that while each anisotropic pattern had identical seed pattern constraints, alterations in the topology and geometry of their patterns alone resulted in vastly different outcomes of tissue structure and function.

Alteration of the cardiac fiber geometry is a hallmark of pathological states, including hypertrophic cardiomyopathy²³ and post-infarct myocardial remodeling,²⁷ that might lead to the abnormal self-sustained condition of reentrant AP waves, causing potentially life-threatening arrhythmias. In this context, linear fiber geometry has been well studied in the literature (for review, see ref. 28). Even in this simple fiber arrangement, the degree of cell–cell coupling (something that could be controlled by the seed pattern in our approach) can lead to directional differences in the safety factor of conduction. With premature stimuli in the setting of sparse side-to-side coupling between cells, unidirectional block can occur in the longitudinal direction, while allowing conduction in the transverse direction, and can result in reentry even in millimeter-size areas.²⁹ In this study, we created prototypical examples of alternate forms of tissue structure, including ‘concentric’ and ‘starburst’ fiber geometries, and showed that wavefront propagation in these cases was novel and can differ significantly from that with linear fiber geometry, particularly for off-center stimulation. An increase in wavefront curvature has been cited as one of the possible determining factors in the slowing or stalling of AP waves and ultimately arrhythmia emergence,³⁰ suggesting that the cell patterns explored in this analysis may serve as a model of arrhythmogenesis under structural remodeling arising from pathologic conditions in the heart. Furthermore, we focused our models and experiments on the most topologically distinct patterns, namely linear, concentric and starburst, that each represent an extreme case of divergence and curl properties and have unique and novel electrophysiological wave conduction properties. These findings will therefore encourage future study of biologically interesting and relevant tissue patterns that have their own unique and novel properties and can be represented as a combination of these three distinct patterns in addition to variations in the seed pattern, branching rules, and cell type. For instance, future studies could search for novel insights into cardiac electrical propagation by quickly developing multiple computational models that provide a comprehensive scan of possible parameter ranges, and then validate the results with corresponding experimental studies.

The method described here can be used to create more complex local cell orientation fields on a tissue level scale through the fast and simple generation of printing masks having patterns with varying geometry and topology. The complexity of these designs, which are automatically generated by the algorithm, are in fact difficult to draw by hand, particularly as we explore how changes in specific parameters characterizing the patterns might lead to potentially subtle tissue-level changes in structure and function. These patterns can maintain predefined local properties, e.g., the widths of the ECM coated bands and the gaps separating them, up to the limits placed on them by divergent or convergent behavior. The seed pattern can be selected to maintain optimal axial cell alignment (facilitated by larger gaps and narrower ECM bands) and/or transverse cell contacts and coupling (facilitated by smaller gaps). In our experiments, a seed pattern of 20 μm wide fibronectin bands separated by 10 μm wide gaps led to good cell alignment and both longitudinal and transverse cell coupling, although other seed patterns might be more appropriate for different anisotropic model tissues, or for modeling alterations of cell–cell coupling in pathophysiologic changes, e.g., related to aging,²¹ fibrosis,^31,32 hypertrophic cardiomyopathy,²³ or islands of preserved myocardium surrounded by scar tissue due to post-infarct myocardial remodeling.²⁷ As described elsewhere, micropatterning co-cultures of cardiomyocytes and fibroblasts could potentially be used to study structure–function relationships in fibrotic heart tissue.¹ The proposed method of tissue patterning here has overall similarities to those mentioned previously, and builds on those approaches. In particular, our method is novel in its ability to create continuous, complex ECM structures efficiently with user friendly inputs that provide details down to the cellular level by employing both global and local structural descriptors. These features, which include the ability to create continuous cell bands on a tissue level scale (similar to fiber tractography²⁰), could be used to enforce fiber direction alignment in DTMRI data used in both computational¹⁸ and experimental¹ studies. It needs to be pointed out, however, that DTMRI data is 3D in nature while our current methodology is 2D, which makes translating our model of tissue patterning to this application difficult without further advancements in the technology. The precision of our method also increases the diversity of possible patterns at the cellular level, which could provide insight as to why ventricular tachyarrhythmias arise in the ventricular septum in hypertrophic cardiomyopathy^23,33 or in the right ventricular apex in arrhythmogenic right ventricular cardiomyopathy,²⁶ where there exist sharp direction changes and splaying of fibers. Furthermore, clinical readouts such as DTMRI imaging may be used in the future to develop personalized, computational simulations of a patient's heart and their possible risk for arrhythmias. In fact, DTMRI imaging has already been used to quantify the orientation of myofibrils in healthy and diseased hearts.^34,35 Our work can contribute to this transformation by reducing the complexity of cardiac structural diseases to their global and local parameters, and identifying the electrophysio-logical consequences of different pacemaker placements or ectopic sites of activation. Additionally, it may be possible to incorporate information derived from the global and local parameters of our model to improve the risk stratification for sudden cardiac death in patients with hypertrophic cardiomyopathy. Currently, risk factors for sudden cardiac death include items such as family history, recent syncope, ventricular tachycardia, left ventricular wall thickness, and extent of fibrosis,³³ but more precise information gained from our model about the structure–function relationships of cardiac tissue geometry at multiscale levels may improve this risk stratification in the future.

The patterning method presented here can also be applied to model other highly structured tissues containing ordered arrays of cells, including, but not limited to, the osteocyte rings in the Haversian canals of bone that form concentric circles or the neural pathways in the human brain.³⁶ By combining our cell patterning methodology with cell capture techniques such as dielectrophoresis,^37,38 in which the layout of the electrodes is defined by the pattern used to create the ECM footprint, it may be possible to obtain adjacent arrays of two different cell types. Examples of such arrays can be found in the hepatic lobules, whose cross-sections show radial stripes of hepatocytes interspersed with endothelial cells lining up in the hepatic venules that together form hexagonal, triangular or diamond-shaped super-structures, or in the striped architecture of the renal pyramids with arrays of aligned nephrons closely associated with endothelial cells lining capillaries that together form cone-shaped super-structures (consider Fig. 2H and I with additional sources and sinks and customizable branching and propagation rules for bands and gaps). The complex geometries of these tissues could be computationally and experimentally modeled using the method proposed here if sequential deposition of the cells is enabled, since the directions and widths of the cell stripes can be precisely controlled over arbitrary distances. Furthermore, since vector fields underlying the current method can be easily constructed in 3D, we envision that the presented methodology will be general enough to extend to more realistic three dimensional tissue patterning and therefore in vitro organ development, as long as tissue engineering methods mature sufficiently to achieve the precision required.

The algorithmic nature of defining ECM patterns that control cell distribution and orientation at multiscale levels can facilitate computational analysis of tissue function and mutual refinement of simulation and experimental patterns, e.g., modeling of AP propagation in complex engineered cardiac tissues. Since the vector fields used to create the experimental ECM patterns can be imported directly into the computational model setup, the model can actually be used to make predictions before or alongside the generation of experimental results. As shown in the results, the outcomes of the experimental and modeling analysis are consistent and non-trivial, creating a tight coupling between the model and experiment and suggesting that the model can have considerable predictive power. Multiple experimental designs could be tested in parallel followed by iterative enhancements using the computational model, before time and resources are invested in the final, refined experiments. The computational model could also be used alone, as suggested above with the potential in the future to develop personalized, computational simulations of a patient's heart and their possible risk for arrhythmias, among other potential uses. We foresee that these advantages will make the proposed technology attractive for both fundamental and applied research uses of microcontact printing and computational modeling, yielding novel insights into the role that geometric and topological tissue organization play in controlling biological function and responses.

Materials and methods

Details on Materials and methods, including a more detailed description of the patterning algorithm, are given in the ESI.† Briefly, for experimental analysis, precisely defined anisotropic monolayers of NRVMs were obtained using microcontact printing (μCP) on polydimethyl siloxane (PDMS)-coated glass coverslips. NRVMs were plated at a density of ~263 000/cm². Cultures were characterized by immunostaining for fibronectin, actin, cTnI, Cx43 and DAPI. Six-day old cultured monolayers were stained with 10 μM di-4-ANEPPS and optically mapped. CV and APD at 80% repolarization (APD80) were measured at a 2 Hz pacing rate in a random direction (ICV) for isotropic monolayers, in the longitudinal (LCV) and transverse (TCV) directions for linear anisotropic monolayers, and in the radial (RCV) and circumferential (CCV) directions for concentric and starburst anisotropic monolayers. All experimental CV and APD values have an n = 7. Data were expressed as mean ± SD and compared using the paired Student's t-test. A p-value of <0.05 was considered statistically significant. To quantify the orientation of actin with respect to the underlying fibronectin patterns, immunofluorescent images were divided into sub-regions and each region was analyzed using a modified version of a previously published MATLAB script utilizing pixel gradient analysis.³⁹ The images were passed through Sobel horizontal edge-emphasized filter for horizontal edge detection. Then, this process was repeated with transposed images to extract the vertical edge, and the horizontal and vertical edges were combined to calculate the gradient magnitude of each pixel in the image. Areas of interest in each sub-region of the images were segmented through thresholding, and the orientation of the gradient is measured with respect to the x-axis (0°). Data were compared using the paired Student's t-test.

In the simulations, the bidomain governing equations were solved using the methodology described in.⁴⁰ The computational mesh was of 250 μm resolution, with higher spatial resolution implemented in places where the gradient of the fiber angle was the largest, such as near the centers of the models incorporating concentric and starburst fiber orientations. The algorithm by Roth⁴¹ was then used to relate longitudinal and transverse conduction velocities into bidomain conductivities. The simulations were run on a 120 node Linux cluster, and custom developed software was used for the simulations and visualization.

Insight, innovation, integration.

The paper provides important biological insight into the relationship between tissue geometry and tissue function. Using cardiac tissue as a model system, we show that alterations in tissue geometry on the macroscale can dramatically affect tissue function, even if constituent cells are similar on the microscale. The technological innovation that enables this insight is the development of a novel computational algorithm that creates precisely parameterized, geometrically complex patterns of model tissues and allows for gradual variation of tissue structure. The paper demonstrates the benefit of integrating technology and biology by using an experimental and computational approach to understand patterned tissue systems, allowing mutual refinement of each approach and providing a general strategy to investigate how tissue disorganization leads to dysfunction.