Statistical Issues in Testing Conformance with the Quantitative Imaging Biomarker Alliance (QIBA) Profile Claims

Abstract

A major initiative of the Quantitative Imaging Biomarker Alliance (QIBA) is to develop standards-based documents called “Profiles”, which describe one or more technical performance claims for a given imaging modality. The term “actor” denotes any entity (device, software, person) whose performance must meet certain specifications in order for the claim to be met. The objective of this paper is to present the statistical issues in testing actors’ conformance with the specifications. In particular, we present the general rationale and interpretation of the claims, the minimum requirements for testing whether an actor achieves the performance requirements, the study designs used for testing conformity, and the statistical analysis plan. We use three examples to illustrate the process: apparent diffusion coefficient (ADC) in solid tumors measured by MRI, change in Perc 15 as a biomarker for the progression of emphysema, and percent change in solid tumor volume by CT as a biomarker for lung cancer progression.

Introduction

The Quantitative Imaging Biomarker Alliance (QIBA) initiative is to advance quantitative imaging and the use of quantitative imaging biomarkers (QIBs) in both clinical trials and clinical practice [1]. One effort in this initiative is to develop standards-based quantitative imaging documents called “Profiles”. These Profiles describe the (1) clinical context for the biomarker, (2) one or more technical performance claims for a given imaging modality (e.g. precision of the measurement for CT, MRI, PET or ultrasound), (3) a list of actors including hardware and software that play defined roles in meeting the claims, (4) technical and performance requirements for each of those actors organized by activities they perform for achieving the claims, (5) summaries of the groundwork scientific studies that support the technical performance claims, and (6) procedures for testing conformity to the technical and performance requirements or an overarching claim. The term “actor” is used in QIBA Profiles to denote any entity (device, software, person or site) whose performance must meet certain specifications in order for the claim to be met.

Through a large volunteer effort, two workshops sponsored by QIBA were conducted to develop standard statistical methods for defining technical performance metrics for QIBs [2–6]. These statistical methods provide the framework for comparing technical performances of imaging procedures in the groundwork studies and for characterizing the performance in the Profile claims.

The objective of this paper is to present the statistical issues in testing conformance to the performance requirements in the QIBA Profiles. In particular, we present the general rationale and interpretation of the claims, the minimum requirements for testing whether an actor achieves the performance requirements, the study designs used for testing conformity, and the statistical analysis plan for the test. We use three examples to illustrate the process:

1. Apparent diffusion coefficient (ADC) in solid tumors measured by MRI to gain insight into the microstructural composition of a tumor,

2. Change in Perc 15 (the 15th percentile of the attenuation curve as measured by CT) as a biomarker for the progression of emphysema, and

3. Percent change in solid tumor volume by CT as a biomarker for lung cancer progression.

The paper is organized as follows. First, we discuss the claims, their interpretation, and the rationale used to determine the performance values used in the claims. We then present the minimum requirements needed to evaluate an actor’s performance conformance based on the different types of claims. The steps in testing actors’ precision, bias, and linearity are described using the three examples for illustration. A Discussion follows.

QIBA’s Performance Claims

Understanding the Claim Statements

Claims involve one or more summary statements of the technical performance of the QIB. Currently, there are two kinds of claims: cross-sectional and longitudinal. A cross-sectional claim describes the imaging procedure’s ability to measure the QIB at one time point, while a longitudinal claim describes the ability to measure the change in the QIB over multiple time points. The claim language is patient-centric, describing the quantitative interpretation of the measurements for the individual patient.

The MRI diffusion-weighted imaging (DWI) Profile [7] provides an example of a cross-sectional claim (note that the Profile also includes a longitudinal claim, but for illustration in this paper we will focus on the cross-sectional one). The draft claim states, “For an ADC measurement of X mm²/s in solid tumors greater than 1 cm in diameter or twice the slice thickness (whichever is greater), a 95% confidence interval for the true ADC value is X ± 5 ×10⁻¹⁰ mm²/s.” To understand the claim, suppose that one follows the imaging specifications in the Profile and measures the ADC of a tumor to be 8 × 10⁻¹⁰ mm²/s. Taking into account the known measurement error, we can state the 95% confidence interval for the true ADC to be [3 × 10⁻¹⁰ mm²/s, 13 × 10⁻¹⁰ mm²/s]. The statistical interpretation of the CI is that if we were to measure the ADC multiple times and construct a CI each time, then the subject’s true ADC would be included in 95% of these CIs. A simpler interpretation is that the interval [3 × 10⁻¹⁰ mm²/s, 13 × 10⁻¹⁰ mm²/s] provides a plausible range for the true ADC value with 95% confidence.

The CT lung density Profile [7] has a longitudinal claim: “a decrease in Perc 15 of at least 18 HU without volume adjustment is required for detection of an increase in the extent of emphysema, with 95% confidence” and “for a measured change of Δ HU in Perc15 without volume adjustment, a 95% confidence interval for the true change is [Δ −18 HU, Δ +18 HU].” (HU refers to Hounsfield units, and Perc 15 refers to the 15th percentile of the attenuation curve.) The first part describes the requirement for confirmation that a true change from baseline has occurred (with 5% error rate that no real change from baseline occurred), while the second part characterizes the magnitude of the change with a 95% confidence interval. Note that these steps are similar to statistical hypothesis testing, where we first test the null hypothesis (i.e. “no change”). If there is evidence that change has occurred, then we construct the confidence interval for the magnitude of the change. Also note that since we cannot measure the correlation in the measurements of Perc 15 at the two time points, for a conservative estimate we assume that the correlation is zero. When there is positive correlation between the two measurements, the confidence interval given by the claim is a little too wide (i.e. conservative) (Negative correlation is unlikely.).

In CT Volumetry, from many groundwork projects, there is strong evidence that the precision in tumor volume measurements depends on the magnitude of the volumes, with greater precision for larger tumors. To quantify precision in the CT volumetry Profile [7], therefore, precision is expressed as a percentage of the magnitude of the measurements in the form of the within-tumor coefficient of variation (wCV) [3]. The draft longitudinal claim is “A measured change in tumor volume of % indicates that a true change in the tumor’s volume has occurred if Δ >40%, with 95% confidence” and “if Y₁ and Y₂ are the volume measurements at the two time points, then the 95% confidence interval for the true change is

$$\mathit{(}{Y}_2-Y_1\mathit{)}\pm \mathit{1.96}\times \sqrt{({[Y_1\times 0.15]}^2+{[Y_2\times 0.15]}^2)}$$

,” where the wCV is 0.15. Note that for this confidence interval we assume that the wCV is constant over the relevant range of tumor volumes. If this assumption is too strong, then a look-up table of wCVs can be included in the Profile so that users can insert the wCV appropriate for the measured magnitude of the tumor. Also note again that the correlation between Y₁ and Y₂ is set to zero for a conservative confidence interval.

Consider the following example. Suppose that one follows the imaging specifications of the CT Volumetry Profile and measures the tumor volume at the first time point to be 200 mm³ and 380 mm³ at follow-up. The measured percent change is ((380−200)/200) × 100, or 90%. Since 90% > 40%, we can be 95% confident that a real change has occurred from baseline (analogous to a test of the hypothesis of “no change”). The plausible range for the true change is 180 ± 126 mm³.

Determining Appropriate Values to Use in the Claim Statements

When writing a QIBA Profile it is challenging to determine which values to use in the claim. There are many issues to consider. The main issue, however, is the trade-off between the strictness of the claim (i.e. how narrow the CI is around the measurement) and achieving conformance with the claim. If the claim is too lax, then it provides little value to the clinician trying to incorporate the information into clinical judgment. If the claim is too strict, then it is difficult for an actor to provide sufficient evidence that it conforms to the claim, thereby limiting availability of the biomarker in practice.

Table 1 lists the general steps that are used in QIBA for choosing the most appropriate values for the claims once a suitable QIB has been identified. We discuss each step briefly.

Table 1.

Guidelines for Choosing Values for Claim Statements

Step	Description
1	Choose statistical metric for performance
2	Determine patient and/or tumor characteristics that can degrade performance for the quantitative imaging biomarker
3	Identify plausible set of values for performance
4	Consider clinical requirements for performance
5	Consider the sample size requirements for actors to test their imaging procedure against the claim value
6	Choose the performance value from the plausible set of values in step 3, taking into consideration steps 4–5.

Step 1: Choose Metric

The first step in choosing a value for a claim statement is determining which statistical metric will be used. The choice of statistical metrics depends on: (1) whether the imaging biomarker measurements tend to be biased or unbiased and (2) whether the claim is cross-sectional or longitudinal. In Table 2 we present the statistical metrics used in the claim statements for our three example claims and the rationale. Note that the units for the metrics are chosen to be as clinically relevant as possible. If change over time in absolute units is used clinically, then performance is described in absolute units (e.g. HU or mm³). If change is typically measured as the percent change from baseline, then we express performance as a percentage.

Table 2.

Statistical Metrics Used in the Claim Statements

Example	Rationale	Statistical Metric	Interpretation
ADC in solid tumors	Cross-sectional claim with negligible bias	Within-subject (or within-tumor) Standard Deviation (wSD) × (95% confidence factor)	The variability seen in multiple measurements on a subject when no biologic change has occurred and the same imaging procedures are used for all measurements.
Change in Perc 15 for monitoring emphysema	Longitudinal claim; Same imaging procedures at 2 time points	Repeatability Coefficient (RC)	The difference between any two measurements on a case is expected to fall between −RC and +RC for 95% of replicated measurements. It represents the minimum detectable difference, with 95% confidence.
% change in CT tumor volume	Longitudinal claim; Different imaging procedures at 2 time points	Reproducibility Coefficient (RDC) is used in the claim statement. The Total Deviation Index with 95% coverage for change (TDI95%) is used for testing conformance.	The RDC is a measure of precision that is used when imaging procedures differ at the two time points. It has a similar interpretation as the RC: it is the minimum detectable difference, with 95% confidence. Since it can be measured directly from clinical studies, it is used in the claim statement. When testing conformance, the bias of the imaging procedures at the two time points will likely differ and this must be accounted for. Thus, the TDI is used for conformance testing. It includes components of both precision and bias. 95% of the differences between the measurements and their true value are <TDI95%. The TDI cannot be measured directly; rather, an actor’s bias and precision are estimated in separate studies. See section on Trade-off between Precision and Bias

Step 2: Determine Characteristics which Degrade Precision

When technical performance is affected by patient or tumor characteristics, and if these characteristics are prevalent in the general population, then the performance value used in the claim statement is often limited to apply only to the appropriate subpopulations of tumors or patients. For example, spiculated tumors may be more difficult to measure (i.e. result in less precision) than spherical tumors. Center of mass may be measured with less precision in patients with excessive head movement. The claim values need to account for imprecision in measuring the QIB for these characteristics based on their relative prevalence in the population. In these cases, there are several options: (i) the claim could be modified to specifically articulate any limitations or exclusions as may be needed based on specifics of the biomarker, (ii) the Profile could include separate claims based on the presence or absence of these characteristics, or (iii) the confidence limits for precision expanded to account for the additional error. For example, in the CT volumetry Profile there is discussion that there be one claim statement for spherical tumors and a second claim statement for spiculated tumors.

Step 3: Identify Plausible Set of Values

Data from published papers and groundwork projects are used to identify a set of plausible field performance values. This set might be the 95% confidence interval (CI) of the performance from a meta-analysis of published studies using a variety of imaging vendors under relevant conditions [6]. Alternatively, this set might be based on results from groundwork projects in QIBA [8] or conducted by another outside group. For the Perc 15 Profile, a meta-analysis was performed based on a synthesis of existing test-retest literature. From the meta-analysis a summary measure of the repeatability coefficient (RC) (i.e. a weighted average of the published studies on RC) was calculated and a 95% CI constructed for the summary measure. For the CT volumetry Profile, multiple groundwork challenge projects were performed where various actors were invited to participate in studies involving a common set of images. The reproducibility coefficient (RDC) and bias were estimated from these studies under various scenarios (e.g. different lesion shapes, different subsets of actors) and the results were used to identify sets of plausible performance values.

Once this set of field values is estimated, the next two steps are used to determine which value in the set should be used in the claim statement.

Step 4: Consider Clinical Requirements

When available, the clinical needs for the QIB performance are considered. For example, we ask: How small does tumor perfusion change need to be before medication is changed? How precise does the volume of a lung nodule need to be estimated so suspicious nodules are appropriately biopsied and stable nodules are followed? When possible, these clinical needs are considered in determining the performance value for the claim. For example in the Perc 15 example, the weighted average of the RC from published studies was 11 HU. However, it was noted that 11 HU represents a very small percent change in lung density. Clinical experts in the field advised that a value somewhat larger than 11 HU would be acceptable in the Profile claim statement.

Step 5: Consider Sample Size for Conformance Test

Whereas many of the requirements documented in the Profile are declaratory in nature, a subset of the requirements need to be demonstrated by a given actor which seeks to indicate that they conform. In testing whether an actor conforms to the claim, the following null (H_o) and alternative (H_A) hypotheses must be tested:

$$H_o\mathit{:}\mathit{\text{the actor}}\text{'}\mathit{\text{s performance is worse than the requirement}}\text{vs.}{H}_A\mathit{:}\mathit{\text{the actor}}\text{'}\mathit{\text{s performance is at least as good as the requirement}}$$ [1]

If an actor’s imaging device has precision very close to the required performance value, then very large studies are needed to verify that the actor’s imaging device conforms with the requirement (i.e. to reject H_o). If an actor’s imaging device has performance much better than the required performance value, then smaller studies could be adequate. For example, if groundwork studies have shown that the RC for most actors is about 7% and if the performance requirement in the Profile is set at 10%, then a study with 30 subjects is needed to test the hypotheses in equation 1 (see section on Sample Size Requirements for Testing Conformity and Table 5). Alternatively, if the performance requirement in the Profile was set at 8%, then a study with nearly 200 subjects would be needed to show conformance of such actors. The performance values chosen must take into consideration the practicality of studies needed to test actors for conformity.

Table 5.

Sample Size for Test of Precision Using RC

(θ/δ)2	# cases needed
0.1	4
0.2	7
0.3	11
0.4	17
0.5	29
0.6	51
0.7	102
0.8	256

Step 6: Choose Performance Value

From the plausible set in step 3, and taking into consideration the clinical needs and sample size requirements for testing conformance in steps 4–5, experts from the fields of imaging physics and medicine choose a reasonable performance value for the Profile. For example, for the Perc 15 Profile a HU of 18 was chosen based on the fact that the clinical requirements do not demand detection of very small changes in lung density; furthermore, if most actors can show a RC near 11, then the sample size requirements for testing conformance are quite reasonable (i.e. a test-retest study of <17 cases is needed, based on Table 5).

Minimum Conformance Requirements

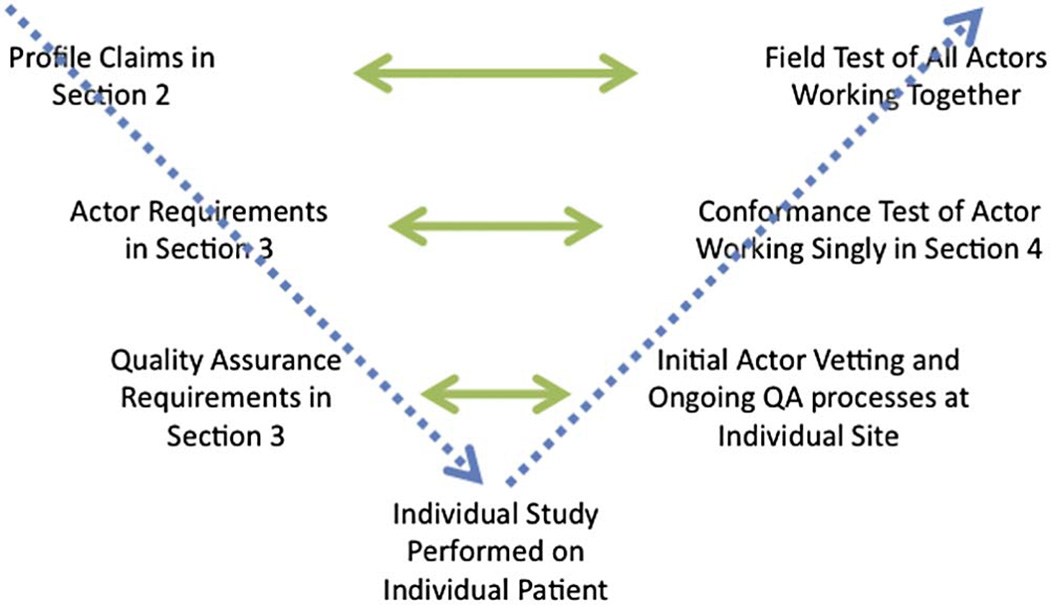
Within each Profile are steps which actors must take to test their conformance with the performance requirements. There are different types of actors (i.e. scanners, software, readers) with different requirements for each. Scanners are usually evaluated on phantoms (i.e., physical test objects) and must conform to scanner-specific requirements. Software algorithms used to measure the biomarker are tested on representative clinical data according to requirements often similar to the claim statements themselves. If human technologists and/or readers are required to perform the scan or run the algorithm, then multiple readers must be included in the conformance testing of the algorithm to ensure that compliance is not reader-dependent. Readers can also be certified as ‘conformant readers’. They can be tested on multiple scanners and/or algorithms; their compliance is specific to the scanners or algorithms they were tested on. The process is illustrated in Figure 1. Note that actors are assessed singly, thus there are no actor-to-actor comparisons just comparisons to the specific stated criteria in the Profile.

Figure 1.

Illustration of the concepts discussed in this paper, with the Profile content identified on the left and the testing identified on the right. Proceeding diagonally down from top left hand side, QIBA Profiles identify Claims in Section 2 of the document template and Requirements for each type of Actor in Section 3 of the document. Section 3 may also articulate requirements for an ongoing QA activity to be conducted at sites if it is judged by Profile authors that stability of the system is not assured. Proceeding from left to right are successive scopes of testing. Whereas at the highest level, the Profile Claims are tested by all Actors working together in a Field Test, Conformance Tests are performed for individual Actors according to the Requirements set for them, and if requirements for QA have been documented, these are further tested. At the bottom of the diagram are individual patient studies themselves.

In some Profiles, one or more datasets are explicitly defined to be used for the conformance testing, but other Profiles articulate statistical criteria as means to document a sufficiently representative test set. Ideally, the test datasets are complex, providing images from multiple (compliant) scanner types and representing the clinically relevant spectrum of disease. When such a rich test dataset is not available, however, the conformance test requirements are more stringent. The rationale is that any lack of trueness or imprecision in an algorithm’s measurements is not only attributable to the algorithm, but also to the scanner and any human reader interaction. This is because the biomarker measurements’ errors are due in part to three main sources of imaging variability: the scanner, reader, and algorithm, along with patient factors, including patient prep. If a test dataset includes images from only one scanner, which had lower intra-scanner variability than other scanners, then we cannot let the algorithm or reader spend the remaining allowable error since the scanner in the test set under-represents error due to scanners. Groundwork studies are performed in QIBA to estimate the percentage of the total variability attributable to different sources of variability so that the spendable error for each source of variability, and potentially interactions between sources, can be allocated in the conformance testing.

The requirements of testing vary from a few simple checks to more involved steps, depending on several factors:

1. Cross-sectional or longitudinal claim,

2. Tendency (if any) for imaging procedure to over- or under-estimate the measurand (i.e. the true value of the biomarker), and

3. For longitudinal claims, whether the imaging systems and scan parameters are the same or different at the two time points.

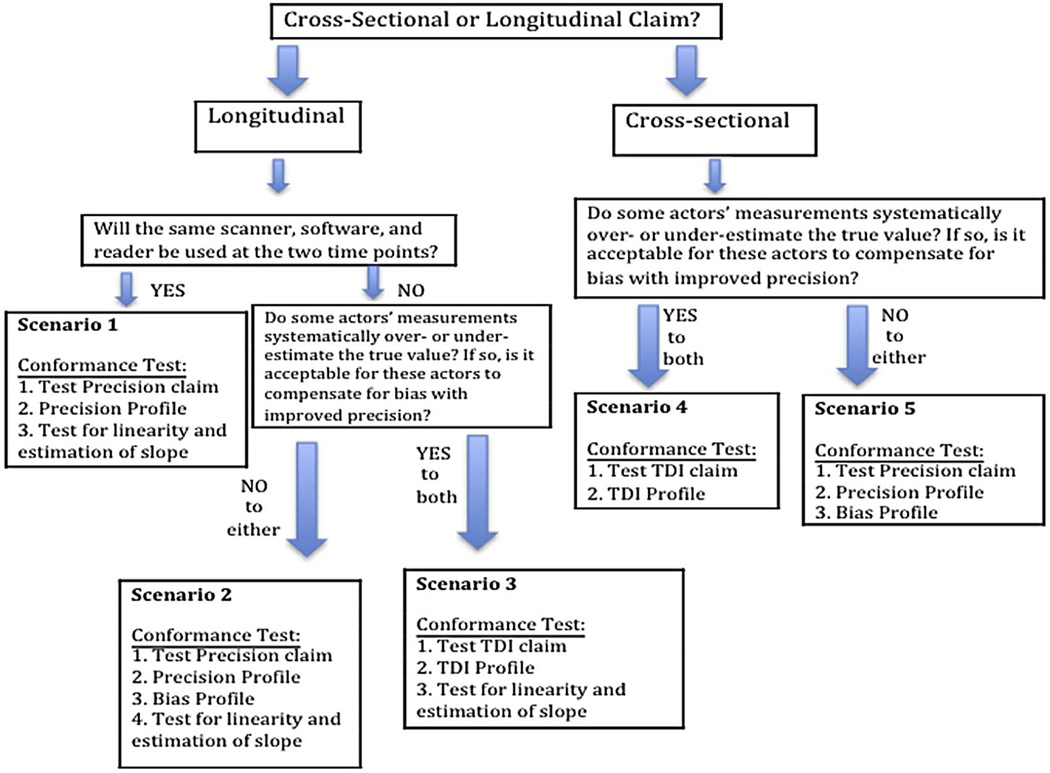
Depending on these factors, there are five test scenarios illustrated in Figure 2. With each scenario a different set of requirements is needed for testing conformance with the claim statement.

Figure 2.

Flow chart of five testing scenarios and minimum testing requirements for each.

The cross-sectional claim for the DWI Profile falls under scenario 5. The requirements needed to support the claim statement are based on the precision of the measurements since any known bias is removed. Conformance to these requirements has three parts: (1) Test that the within-subject (or within-tumor) standard deviation, wSD, of the measurements is non-inferior to (i.e. not larger than) the required performance, (2) Estimate the imaging system’s precision profile to ensure that the precision is acceptable over the range of relevant subject or disease characteristics, and (3) Evaluate the bias to ensure that it is negligible. (Note that a precision profile is a table or plot of precision estimates stratified by one or more variables, e.g. precision estimates grouped by ranges of the magnitude of the measurand [3–5]).

The longitudinal lung density claim falls under scenario 1. The same imaging procedures (i.e., same scanner and scan parameters) will be used at the two time points. The repeatability coefficient (RC) is the statistical metric used in this scenario [3]. Testing conformance involves a statistical test that shows that the RC for these measurements, when estimated under the setting prescribed in the Profile, is non-inferior to the RC stated in the claim statement. In addition, there is a check that the RC is reasonably constant over subject/disease characteristics (precision profile), and a test that any systematic bias in the estimation of the measurand by the imaging system remains constant so that at two time points such bias either cancels out or can be corrected for (i.e. test of linearity and estimation of the slope – discussed in the next section).

The longitudinal CT Volumetry claim falls under scenario 3. Different imaging procedures will be allowed at the two time points, and differential bias in the measurement by the imaging procedures is expected. A statistical metric called the total deviation index with 95% coverage (TDI_95%) is used to evaluate the technical performance of the biomarker. It is an aggregate measure of performance, aggregating both bias and variability into one metric [4]. Testing conformance of scanner hardware is done using a phantom according to tests of such factors as noise content and resolution, which is not considered here. Testing conformance of software algorithms involves three parts. First, a statistical test is needed to show that the software system’s precision is non-inferior to the stated precision in the Analysis sub-section of section 3 in the Profile. If the precision is within the stated requirement, then the second step is to determine the bias of the measurements. Actors with good precision are allowed more bias such that the TDI is still within the requirement (see details in the next section). Last, there is an evaluation of the assumption of linearity to ensure that the bias is proportional over the range of expected tumor volumes.

Testing Conformity

In this section we discuss the statistical steps used in testing conformity of readers and algorithms to the performance requirements in the Profile. In some of the QIBA Profiles, one or more test data sets are identified which actors will use to measure their performance. In other Profiles, actors must conduct a full study in which scanning of new patients and/or phantoms is required to test their performance as part of the conformance test.

Steps in Testing Conformity

The objectives of the conformity test are to determine if an actor’s performance is at least as good as the required performance, and to evaluate relevant assumptions about the measurements (e.g. homogeneity, linearity). In Section 4 of the Profile, specific steps are provided to actors for testing conformity. An example of these steps, using CT Volumetry for illustration, is given in Tables 3 and 4. Since precision can best be estimated in a clinical test-retest study, while bias can only be assessed by a phantom study (because truth must be known), both types of studies are needed to test for conformity for this biomarker. Thus, Table 3 describes the steps for evaluating precision from a test-retest study, while Table 4 describes the steps for evaluating bias and linearity.

Table 3.

Testing Precision using CT Volumetry for Illustration^*

STEP	DESCRIPTION
1. Make measurements on N cases	For each case, measure the tumor volume at time point 1 (denoted Yi1) and at time point 2 (Yi2) where i denotes the i-th case (i=1, 2, …N).
2. For each case, calculate mean and wSD2	For each case, calculate the mean and within-tumor SD: Ȳi = (Yi1 + Yi2)/2 and $wS{D}_i^2={(Y_{i1}-Y_{i2})}^2/2$. (Note that some authors suggest a correction to this wSD estimate [11] or a model-based estimate [12] to account for the small number of replicate measurements.)
3. Estimate wSD or wCV	From the N cases, estimate within-tumor SD (wSD) or CV (wCV): $wSD=\sqrt{{\sum }_{i=1}^{N}wS{D}_i^2/N}$ and $wCV=\sqrt{{\sum }_{i=1}^N(wS{D}_i^2/{\overline{Y}}_i^2)/N}$. (Note that averaging over the N cases is appropriate when we can assume that the wSD is constant over the range of tumor volume values.)
4. Estimate RC or %RC*	Estimate the Repeatability Coefficient (RC) or %RC: $\widehat{RC}=2.77\times wSD$ and $\widehat{\%RC}=2.77\times wCV\times 100$. For the CT volumetry example, %RC is used.
5. Calculate test statistic and assess compliance	The null hypothesis is that the RC does not satisfy the requirement in the Profile (i.e. the RC is too large); the alternative hypothesis is that the RC does satisfy the requirement. The test statistic T is: $T=\frac{N\times ({\widehat{\%RC}}^2)}{{\delta }^2}$, where δ is the performance value from the Profile claim statement (i.e. δ = 40%). Compliance with the claim is shown if $T<{\chi }_{\alpha ,N}^2$, where ${\chi }_{\alpha ,N}^2$ is the α-th percentile of a chi square distribution** with N dfs (for a one-sided test with α type I error rate).
6. Construct precision profile	Estimate %RC as a function of tumor size and check that all %RC ≤ δ.

^*The process above is applicable for testing a reader’s conformance using a specific algorithm or for testing a fully-automated algorithm (no reader interaction). For testing an algorithm that requires manipulation by human readers, usually, 3–5 independent readers not involved in developing the algorithm should be included in the conformance study. Steps 1–4 are repeated for each reader separately. Thus, in step 4 there will be an estimate of the RC for each reader. Instead of using the test in step 5, a different statistical approach is used, which assesses whether the average readers’ RC satisfies the performance requirements in the Profile. A generalized linear model can be built for the RC, treating readers as a random effect nested in cases [5]. From the model, a 95% CI for the mean RC is constructed and used to evaluate the actor’s performance relative to the requirement in the Profile.

^**A chi square distribution is a commonly used probability distribution that is used when constructing a CI for a population standard deviation of a normal distribution, e.g. wSD or RC, from a standard deviation estimated from a sample of size N.

Table 4.

Testing Bias and Linearity using CT Volumetry for Illustration^*

STEP	DESCRIPTION
7: Make measurements from N cases	For each case calculate the tumor volume (denoted Yi), where i denotes the i-th case (i=1, 2, …N).
8. Calculate individual bias	For each case calculate the bias or % bias: bi = (Yi − Xi) and %bi = [(Yi − Xi)/Xi] × 100, where Xi is the measurand value (i.e. true value). For CT volumetry, %b is used.
9. Estimate overall bias and its variance*	Over N cases, estimate the bias: $\hat{b}=\sqrt{{\sum }_{i=1}^N\%b_i/N}$. The estimate of the variance of the bias (i.e. between-case variance) is ${\widehat{\mathit{\text{Var}}}}_b={\sum }_{i=1}^N{(\%b_i-\hat{b})}^2/(N-1)$.
10. Construct 95% CI for b̂	The 95% CI for the bias is $\hat{b}\pm t_{\alpha =0.025,(N-1)df}\times \sqrt{{\widehat{\mathit{\text{Var}}}}_b}$, where tα=0.025,(N−1)df is from the Student’s t-distribution** with α=0.025 and (N−1) degrees of freedom. To test whether the actor’s bias satisfies the performance requirement in the Profile, the smallest and largest values in the 95% CI are examined. If the smallest value is greater than the minimum requirement stated in the Profile and the largest value is less than the maximum requirement stated in the Profile, then the performance requirement for the overall bias is met.
11. Bias Profile	Separate the cases into strata based on covariates known to affect bias (tumor size and density). For each stratum estimate the bias.
12. Perform OLS regression	Fit an ordinary least squares (OLS) regression of the Yi’s on Xi’s. A quadratic term is first included in the model to rule out non-linear relationships: Y = βo + β1X + β2X2. Then a linear model should be fit: Y = βo + β1X where R-squared (R2) >0.90.
13. Construct 95% CI for slope	Let $\widehat{{\beta }_1}$ denote the estimated slope from step 12 (assuming β2 = 0). Calculate its variance as ${\widehat{\mathit{\text{Var}}}}_{{\beta }_1}=\{{\sum }_{i=1}^N{(Y_i-{Ŷ}_{\iota })}^2/(N-2)\}/{\sum }_{i=1}^N{(X_i-\overline{X})}^2$, where Ŷι is the fitted value of Yi from the regression line and X̄ is the mean of the true values. The 95% CI is $\widehat{{\beta }_1}\pm t_{\alpha =0.025,(N-2)df}\sqrt{{\widehat{\mathit{\text{Var}}}}_{{\beta }_1}}$

^*As in Table 3, if multiple readers are studied, then the bias of the average reader must be compared to the performance requirement in the Profile. A generalized linear model can be built for the bias, treating readers as a random effect nested in cases [5]. From the model, a 95% CI for the readers’ mean bias is constructed and used to evaluate the actor’s performance relative to the requirements in the Profile.

^**Student’s t-distribution is a commonly used probability distribution that is used when a statistic, like the bias estimator, is normally distributed but the study sample size is small (sample size of N) and the population standard deviation is unknown and must be estimated from the data.

Precision

Steps 1 and 2 in Table 3 describe the measurements and calculations that must be performed to estimate the biomarker’s precision. In steps 3 and 4 an overall estimate of measurement precision is derived, assuming wSD or wCV is constant across the cases. Following these steps, the actor’s performance can be tested (step 5) for the following set of hypotheses:

$$H_o:\theta >\delta \text{ versus }{H}_A:\theta \le \delta$$

where θ is the actor’s precision (e.g. the actor’s RC, where larger values indicate worse precision) and δ is the precision value from the claim statement. This is a one-side test, i.e. under the null hypothesis the actor’s precision is considered inferior to the Profile claim. If the null hypothesis is rejected, then we conclude that the actor’s precision is at least as good as the performance in the claim statement (alternative hypothesis).

Note that the statistical test described in step 5 relies on asymptotic theory. This test may not always be appropriate for testing conformity because the sample size for clinical test-retest studies are typically small. In a simulation study we found that asymptotic methods worked well for sample sizes of 30 or larger. We also investigated the situation where there are multiple regions of interest (ROIs) (e.g. tumors) per patient and found that the coverage of the asymptotic confidence intervals was reasonable unless the between-ROI correlation was quite high (>0.4). An alternative to the asymptotic test is to construct a bootstrap confidence interval for the precision estimate. In our simulation study we found that the bootstrap method does not provide adequate coverage for the RC unless the sample size is much larger (~120), though this method’s coverage was not affected by correlation between multiple lesions because the resampling is conducted at the patient level.

Step 6 evaluates the assumption of homogeneity in precision descriptively, i.e. that the wSD or RC is fairly constant over the range of disease and subject characteristics. For the CT Volumetry example, tumor size is known to affect precision. Thus, the tumors may be divided into multiple strata based on size, and the RC is estimated separately for each stratum, constituting a precision profile [4–5].

Bias

While a test of an actor’s precision is key to the statistical requirement for assessing conformance with the Profile, an evaluation of bias is also necessary for the claims in both the ADC and the CT Volumetry Profiles. In the ADC cross-sectional claim, the 95% CIs for the bias must be within pre-specified bounds because the ADC claim statement is based on the assumption of negligible bias. Specifically, when measuring an ice-water phantom at isocenter, the ADC measurement should exhibit no more than a 5% bias from the true value of 1.1 × 10⁻⁹ mm²/s. For the Lung Densitometry Profile, there is no assessment of bias, only linearity (see section on linearity below).

For the CT Volumetry Profile, a dataset different from the one used for testing precision is planned to evaluate actors’ bias. The dataset is from a large phantom study involving tumors covering a large spectrum of sizes and shapes. Steps 7 and 8 in Table 4 describe collection of the measurements and estimation of the individual bias. In step 9 the overall bias is estimated and its 95% CI is constructed in step 10 (assuming that the individual bias is similar across cases). Note, however, that when the data is a mixture of different cohorts, it may not make sense to report a single estimate of bias as a conglomeration of the cohort data. Bias across a mixed dataset can be inconsistent with the bias of any individual cohort, for example, when grouping the data produces a distribution with multiple peaks (around individual cohorts) or when large negative and positive biases cancel out to result in an overall zero bias. When this occurs, the bias can fall outside any achievable bias for individual cohorts and likely doesn’t represent achievable performance. In this situation, only a bias profile (step 11) should be reported. A bias profile provides estimates of the bias for subgroups, based on relevant disease and subject characteristics. For example, bias for tumors of different sizes, shapes, and densities would be reported as part of the bias profile for CT volumetry [9]. The bias profile ensures that the bias for relevant disease and subject characteristics is within acceptable parameters.

Linearity

Linearity is a critical assumption in constructing the CI around the amount of change for the longitudinal claims. It is the “ability to provide measured quantity values that are directly proportional to the value of the measurand in the experimental unit” [2]. In other words, the measurements are proportional to the true value by a constant amount (i.e. constant slope) and this constant does not change over the range of true values. To assess linearity, the measurements (Y values) are regressed on the true values (X values). If the relationship between Y and X is well explained by a line, then the assumption of linearity is met (see step 12).

The linearity assumption allows us to estimate the true change as: (Y_(t=1) − Y_(t=2))/β₁, where Y_t=1 and Y_t=2 are the measurements at the two time points, and β₁ is the slope of the regression line of Y on X [3]. For the volumetry Profile, it is specified that β₁ must be sufficiently close to unity so that the measured change of (Y_t=1 − Y_t=2) is an estimate of the true change, (X_t=1 − X_t=2). If β₁ is not sufficiently close to one, then an estimate of β₁ would be needed in order to estimate the true change.

For the Lung Densitometry claim, a metric Perc15, obtained from an area under the whole lung histogram, is one of the main indicators for emphysema quantification. It is assumed that the measured CT Hounsfield Unit (HU) of a given lung region approximates the lung density in that region in g/L. For example, a Perc15 value of −950 HU corresponds to a density of 50 g/L, which signifies that 15% of the lung volume is occupied by regions with a density of approximately 50 g/L or less [10]. The assumption of linearity is assessed via a phantom study by regressing the measured HU value on the known value of density. The phantom study includes calibration using low density foams of known density values representing the range of clinically relevant values considered in the Profile.

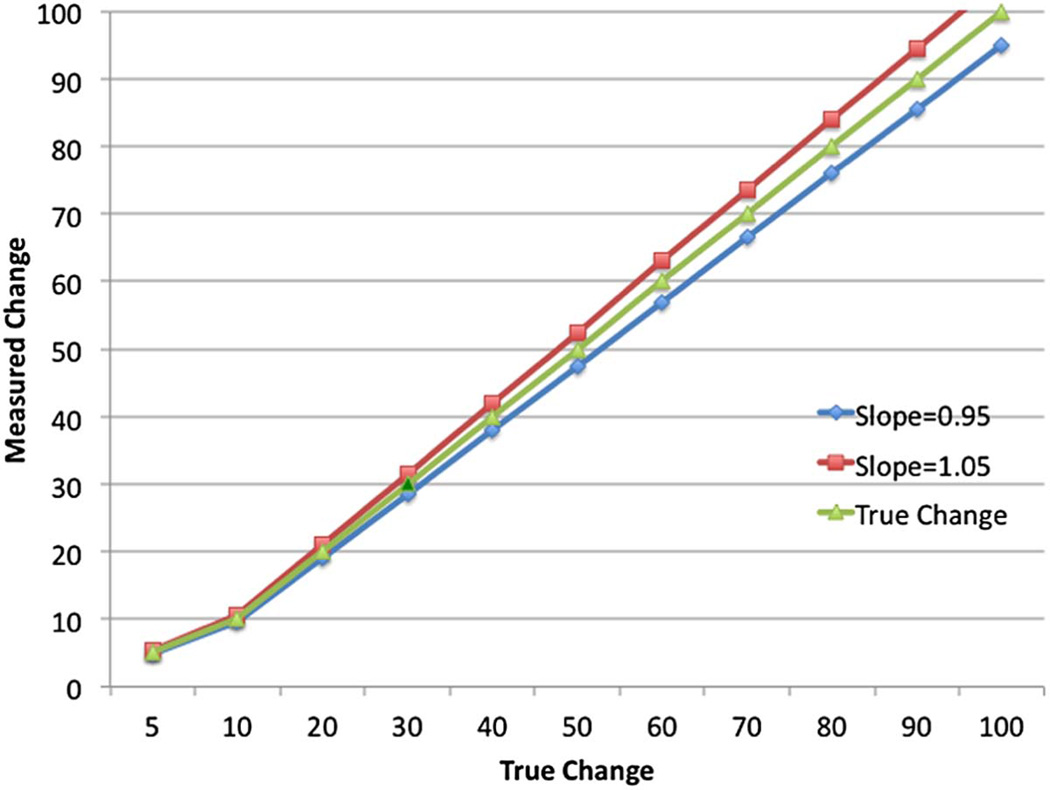
The assumption of linearity with the additional requirement that the slope be close to one is also required for the CT Volumetry example. In order to determine how close to one the slope should be, it is helpful to think about how biased the measurements of change become as the slope departs from one. Figure 3 illustrates the effects of a 5% departure from β₁ = 1 on the estimates of change. The figure shows the estimated change measurement when the slope is 0.95 (blue) and 1.05 (red) in comparison to the desired slope of 1.0 (green). As the magnitude of the change increases, the estimated change becomes increasingly more biased. For example, suppose that a tumor is measured at 20 cm³ at time point 1 and doubles to 40 cm³ at time point 2. The measured change is 20 cm³. When the slope of the regression line of the measured volume on the true volume is unity, 20 cm³ is an unbiased estimate of the true change. However, when the slope is different from unity, say 0.8, this measured change underestimates the true change by 20%. In general, a 5% departure from linearity (i.e. the 95% confidence bounds on the slope are contained in the interval [0.95, 1.05]) may be acceptable.

Figure 3.

Illustration of the Effect of Slope ≠ 1 on Measurements of Change

Trade-off between Precision and Bias

In the Perc 15 example, the Profile specifies that the same imaging procedures will be used at the two time points. Thus, even if the imaging procedure generates biased estimates of Perc 15, as long as linearity holds over the range of interest and the slope is one, the bias in the measurements cancels out when measuring change. In contrast, in the CT Volumetry example different imaging procedures (scanner, software algorithm, and/or reader) may be used at the two time points with each having a potentially different bias. One option in this situation is to require that all actors’ measurements be made without bias. An alternative approach is to allow actors’ measurements to have some bias. However, the bias and imprecision in the measurements must be balanced so that the total error is within the requirement. To balance bias and imprecision, QIBA is using a performance metric called the total deviation index with 95% coverage (TDI_95%). Assume that the difference between the measured value and ground truth follows a normal distribution. Then the TDI_95% is defined as:

$$\widehat{TD{I}_{95\%}}={\mathrm{\Phi }}^{-1}(1-\frac{1-0.95}{2})|\hat{\epsilon }|$$

where Φ⁻¹ is the inverse cumulative normal distribution (i.e. 1.96 for 95% coverage) and ε̂ is the estimate of the root mean square deviation (RMSD):

$$\widehat{MSD}={\hat{\epsilon }}^2={(\mathit{\text{bias}})}^2+s_Y^2,$$

where bias is an estimate of the bias of the measurements (from step 9 in Table 4) and $s_Y^2$ is an estimate of the within-subject (e.g. within-tumor) variance (from step 3 in Table 3).

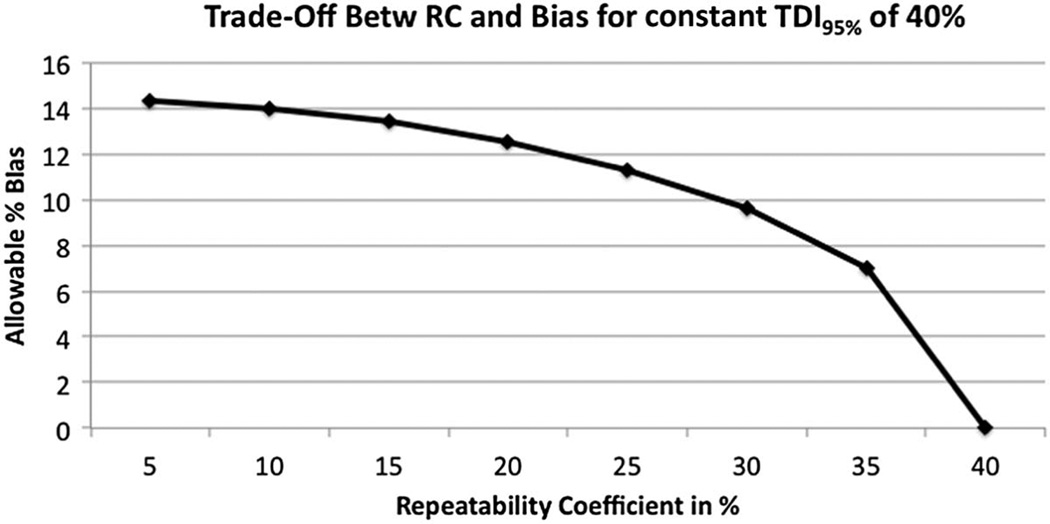
For the CT Volumetry Profile, actors first test that their RC meets the requirements (i.e. Table 3). If these requirements are met, then the actors estimate their measurement bias from Table 4. The actors are allowed some bias, but the magnitude of the bias depends on their RC. The lower the RC, the more bias allowed such that the estimated TDI can still meet the Profile claim. Figure 4 illustrates the trade-off between bias and precision such that the TDI_95% is maintained at a constant 40%. Note that when the actor’s estimated RC approaches 40%, little bias is allowed. In contrast, when the RC is very small, much greater bias is allowed. In this illustration, we expect the RC of most actors to be near 15%, thus allowing for a bias of ≤13.4%.

Figure 4.

Illustration of the trade-off between Precision (expressed as the RC) and Bias for Constant TDI_95% of 40%

Sample Size Requirements for Testing Conformity

The following set of hypotheses is evaluated for testing conformity to the precision requirement:

$$H_o:\theta >\delta \text{ versus }{H}_A:\theta \le \delta$$

where θ is the actor’s precision and δ is the precision value from the claim statement. In order to compute sample size for a study to test this set of hypotheses, the following must be specified:

1. Power: This is the probability that we will reject the null hypothesis when it is incorrect. We typically consider power levels of 80–90%.

2. Type I error rate: This is the probability of rejecting the null hypothesis when it is correct. We set this at 5%.

3. Hypothesized ratio of RCs: If RC is expected to be much smaller than the precision value in the Profile, then a small study suffices. If RC is expected to be very similar in magnitude to the precision value in the Profile, then a much larger study is required.

Table 5 provides sample size requirements for a study with 80% power [13–14]. One must specify the ratio: θ/δ. The table then provides the number of cases needed. Suppose that precision is expressed in the Profile as a RC with a stated claim that RC=10%. Suppose that an actor hypothesizes that his RC is 7%; thus, (θ/δ)²=0.49. Then a sample size of about 29 cases is required to have 80% power (5% type I error) to show that the actor’s RC is ≤ the RC in the Profile claim.

For assessing bias, a phantom study is usually performed where measurements are taken at multiple values over the relevant range of the true value, X. Ideally, 10 nearly equally-spaced values should be chosen [3]. A 95% CI should be constructed for the bias, as described in Table 4. Sample size requirements are given in Table 6 for constructing the CI for bias, as a function of the specified half-width of the CI and the between-case variability. For example, to estimate the bias to within ±1% when the variance between cases is 10%, 42 cases are needed. For estimating the slope of the regression line of Y on X, the sample size requirements depend on the variability in the Y’s around a fixed X and on the desired precision for the slope estimate. For many applications, we have found that 3–4 measurements at each fixed value of X is sufficient to estimate the slope to within ±2% (i.e. total sample size of 30–40). Since linearity is usually assessed from phantom data, these requirements are usually quite workable.

Table 6.

Sample Size for Evaluating Bias

	Half-Width of 95% CI for Bias
	± 1%	± 2%	± 3%	± 4%	± 5%
Varb*=5%	22	8	≤5	≤5	≤5
Varb=10%	42	13	7	≤5	≤5
Varb=15%	61	17	9	7	≤5
Varb=20%	80	22	12	8	6
Varb=25%	99	27	14	9	7

^*The between-case variance (described in Table 4) is represented here as the variance divided by the bias.

Discussion

In this paper we have presented the current status and rationale behind QIBA’s claim statements and corresponding tests of actor conformity with the requirements to support them. Over the last year, the claim statements have evolved from multiple statements about the performance of the imaging procedures (e.g. The %bias is <5%, the %RC is <15%, and the inter-reader RDC is <25%) to a single statement (e.g. For a measured tumor volume of Y, a 95% confidence interval for the true tumor volume is [Y −30%, Y +30%].) The latter does not require familiarity with definitions for bias, repeatability coefficient (RC), and reproducibility coefficient (RDC). Furthermore, it is not left up to the user to determine how to aggregate bias and precision into a single value of performance. The intent of the current verbiage is to provide a more intuitive claim about performance.

The claim statements are written to be patient-centric, focusing on a quantitative interpretation of the measurements for the individual subject. In order to keep this focus, most of the Profiles have used longitudinal claims, where precision and linearity are the key components, rather than bias. For a cross-sectional claim, knowledge of and the ability to test for bias are essential. In order to estimate bias, truth must be known. While simulated data have been used extensively for studying the bias of many QIBs, it is often difficult to simulate the complexities seen in real subjects. Thus, the bias calculated from simulated data often underestimates the bias of measurements on real subjects. For this reason, many of the QIBA Profiles have not made cross-sectional claims. QIBA is investigating several strategies that would enable it to make cross-sectional claims in future Profiles. However, these claims are likely to differ in content from the patient-centric longitudinal claims, focusing more on discrimination performance of the QIB rather than on its calibration performance.

For longitudinal claims where the imaging procedure actors are allowed to vary at the two time points, evaluations of precision and linearity alone are not sufficient for showing compliance. The same imaging procedure with different actors can have different magnitudes of bias; thus, the change measurement may be biased. The TDI_95% is used to account for both bias and imprecision. When bias and precision can be estimated from the same study, TDI can be estimated directly and a 95% CI for it can be constructed. This is often not possible. When estimating the TDI for the CT Volumetry claim, for example, bias and precision are estimated in different studies. Both bias and precision are estimated with uncertainty, and how this uncertainty should be incorporated into the estimate of the TDI is unclear. One approach is to use the upper 95% confidence bound for bias and for precision in calculating the TDI; however, this would seem to be a very conservative approach. Alternatives are being considered in future work.

QIBA Profiles provide data on the technical performance of the QIB that can be used to understand the measurements on an individual patient. They do not, however, provide all of the information that would be needed to plan a clinical trial with the QIB. In a clinical trial the focus is usually on the mean measurement or mean change in the QIB for a specified population of patients. Often, the population is identified by having a certain condition (e.g. lung cancer) and perhaps undergoing a certain treatment. In order to calculate sample size for a clinical trial, one would need an estimate of the precision of each measurement (which is provided in the Profile), and also estimates of the expected effect size and the variability in the QIB measurements between patients in the study population. The latter two estimates are specific to the clinical trial and thus will vary depending on the trial details.

Much of the groundwork for the QIBA Profiles is based on simulated data and literature review. The claim statements, although based on the best available data, are often driven by expert opinion. QIBA is currently designing and conducting several field studies. These studies will be used to evaluate the feasibility of the Profiles and test the adequacy of its claim statements. These are critical studies to the completion of the Profiles.