Abstract
When measuring thresholds, careful selection of stimulus amplitude can increase efficiency by increasing the precision of psychometric fit parameters (e.g., decreasing the fit parameter error bars). To find efficient adaptive algorithms for psychometric threshold (“sigma”) estimation, we combined analytic approaches, Monte Carlo simulations and human experiments for a one-interval, binary forced-choice, direction-recognition task. To our knowledge, this is the first time analytic results have been combined and compared with either simulation or human results. Human performance was consistent with theory and not significantly different from simulation predictions. Our analytic approach provides a bound on efficiency, which we compared against the efficiency of standard staircase algorithms, a modified staircase algorithm with asymmetric step sizes, and a maximum likelihood estimation (MLE) procedure. Simulation results suggest that optimal efficiency at determining threshold is provided by the MLE procedure targeting a fraction correct level of 0.92, an asymmetric 4-down, 1-up (4D1U) staircase targeting between 0.86 and 0.92 or a standard 6D1U staircase. Psychometric test efficiency, computed by comparing simulation and analytic results, was between 41%–58% for 50 trials for these three algorithms, reaching up to 84% for 200 trials. These approaches were 13%–21% more efficient than the commonly-used 3D1U symmetric staircase. We also applied recent advances to reduce accuracy errors using a bias-reduced fitting approach. Taken together, the results lend confidence that the assumptions underlying each approach are reasonable, and that human threshold forced-choice decision-making is modeled well by detection-theory models and mimics simulations based on detection theory models.
Keywords: psychometric curve, psychophysics, efficiency, precision
Introduction
Thresholds provide significant insight into neural processing and are an important part of clinical care (e.g. Fletcher 1923;Valko, Priesol et al. 2012;Ernst and Banks 2002;Lewis, Priesol et al. 2011). Determining thresholds usually involves repeatedly collecting perceptual responses after exposing subjects to stimuli of different amplitudes and/or directions. In many clinical or experimental situations, a certain level of precision is required for a threshold estimate. Although collecting additional responses can improve precision (Taylor and Creelman 1967;Taylor 1971), this takes additional time. Thoughtful selection of stimuli can improve precision without additional responses, which saves time and thus improves efficiency (Wetherill 1963;Kaernbach 1991;Treutwein 1995;Pentland 1980;Harvey 1986;Hall 1968;Hall 1981;Watt and Andrews 1981;Green 1990;Garcia-Perez 1998;Leek 2001;Merfeld 2011;Lim and Merfeld 2012). Indeed, it seems possible to get “something for nothing;” for example, large stimuli to which subjects will consistently respond correctly provide little useful information about threshold, as do tiny stimuli for which subjects are guessing. Adaptive algorithms, which adapt stimulus amplitude based on the subjects’ responses (Leek 2001), are particularly important for threshold testing because thresholds can vary by more than a factor of ten across individuals (Benson, Spencer et al. 1986;Benson, Hutt et al. 1989).
A number of approaches have been used to determine the ideal stimulus amplitudes for precisely estimating threshold, including analytic approaches, Monte Carlo simulations and human experiments. In this paper, we detail a novel analytic approach, and combine and directly compare these three approaches. Our analytic approach for Gaussian distributions is motivated by a previous analysis for logistic distributions (Wetherill 1963). It determines a bound on the lowest possible error given a set of conditions (such as the Cramér-Rao bound1 (Rao 1945;Cramér 1946;Van Trees, Bell et al. 2013)). Comparing the three approaches together is important because analytic approaches do not consider practical issues (Wetherill 1963), and simulation and experimental results do not consider all theory. For example, analytic approaches do not take into account the particulars of the adaptive algorithm used, nor predict whether or how quickly real-world results will converge on theoretical bounds as the number of trials increases2. Our analytic results closely match the previous gold standard, the “omniscient experimenter” Monte Carlo simulation in which the simulated experimenter has perfect information about the subject’s psychometric curve (Taylor and Creelman 1967), providing robust support to both approaches. We performed our analyses for a recognition task (e.g. left vs. right) and focus our results on threshold, which is the spread of the Gaussian psychometric function; while standard, this differs from the definition sometimes used for detection tasks (e.g. stimulus present/not present). Discussion explains why we did not focus on bias.
Our approach allows the calculation of “psychometric test efficiency” (Taylor and Creelman 1967) of sampling schemes, using the theoretic bound as a benchmark which is more robust than simulations (Taylor and Creelman 1967). To demonstrate, we apply our approach to variations of three previously described adaptive sampling schemes to compare their efficiency at threshold determination, although the approach can be used with any sampling scheme. The first is the common parameter estimation by sequential testing (PEST) staircase scheme (Taylor and Creelman 1967). The second is the maximum likelihood estimation (MLE) scheme (Hall 1968;Pentland 1980;Watt and Andrews 1981;Harvey 1986;Green 1990;Treutwein 1995;Leek 2001;Shen, Dai et al. 2015), which fits the psychometric curve after every response and uses the new fit parameters to determine the ideal stimulus level for the next trial. The third is a staircase with different up and down steps sizes (Kaernbach 1991;Garcia-Perez 1998), which allows the experimenter to target the staircase at specific stimulus levels.
Since the assumption that human behavior is well modeled by detection theory is not exhaustively tested, we compare human and analytic predictions, and also extend previous comparisons between human and simulation results (Kollmeier, Gilkey et al. 1988;Garcia-Perez 2000;Garcia-Perez and Alcala-Quintana 2007;Garcia-Perez and Alcala-Quintana 2009). Our human results are consistent with both simulation and analytic results, and confirm that threshold can easily be determined 15% more efficiently compared to the widely used three-down, one-up staircase (e.g. Grabherr, Nicoucar et al. 2008;Valko, Priesol, Lewis, and Merfeld 2012;Agrawal, Bremova et al. 2013;Hartmann, Haller et al. 2014).
Improved efficiency means that either parameter estimation can be done (a) with fewer trials to yield the same precision, (b) more precisely with the same number of trials, or (c) some combination of the two. High-quality patient care relies on clinical testing with high sensitivity and specificity, which are improved by reducing error on parameter estimates. Efficient data collection is particularly important for motion studies (e.g. with visual or vestibular stimuli) because of the time required to present relevant dynamic stimuli for each trial. For example, thresholds for single cycles of 0.1 Hz sinusoidal motion which take 10 seconds to present are different for vestibular migraine subjects compared to other subjects (Lewis, Priesol, Nicoucar, Lim, and Merfeld 2011), and it is often informative to measure thresholds at multiple frequencies (Nakayama and Tyler 1981;Benson, Spencer, and Stott 1986;Benson, Hutt, and Brown 1989;Grabherr, Nicoucar, Mast, and Merfeld 2008;Lewis, Priesol, Nicoucar, Lim, and Merfeld 2011;Soyka, Robuffo et al. 2011;Valko, Priesol, Lewis, and Merfeld 2012;Haburcakova, Lewis et al. 2012;Karmali, Lim et al. 2014).
Methods
Psychometric function
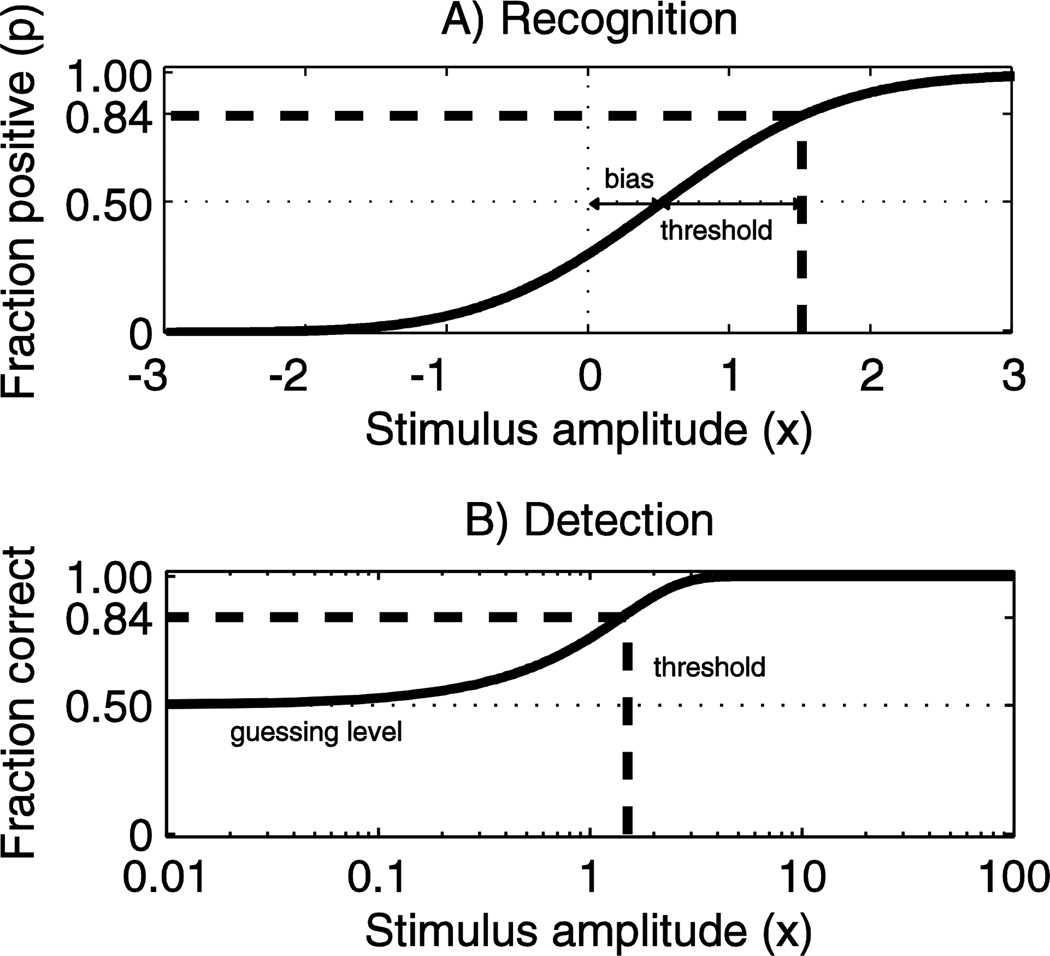
Our psychometric function relates a bidirectional physical stimulus amplitude (magnitude and direction) to the binary subject response (e.g., left/right). We assume that the psychometric function is a cumulative Gaussian distribution, as in many recent experimental studies (e.g. Butler, Smith et al. 2010;MacNeilage, Banks et al. 2010;Soyka, Robuffo, Beykirch, and Bulthoff 2011; Roditi and Crane 2012b). The psychometric fit parameters are the standard deviation and mean of a Gaussian distribution underlying the psychometric function, often referred to as threshold and bias (Merfeld 2011;Garcia-Perez and Alcala-Quintana 2013). We assume a one-interval, two-alternative, direction-recognition (sometimes called discrimination), forced-choice task. Subject responses are binary and are 0 for negative responses (e.g., I perceive I moved to the right) and 1 for positive responses (e.g., I perceive that I moved to the left), meaning that rightward motions would occupy the left side of the abscissa and rightward subject responses would occupy the lower part of the ordinate of the psychometric curve plot (Figure 1A). The linear translation of the psychometric function along the abscissa is referred to as the bias, is represented mathematically as μ, and corresponds to the mean of the underlying Gaussian distribution. The spread of the psychometric function, referred to as the threshold, is related to both the standard deviation of the underlying Gaussian and the function’s slope, and is represented mathematically by σ. For sensory applications, this parameter corresponds to the standard deviation of the equivalent physiological noise (Merfeld 2011), which is often referred to as the threshold. Our estimates of μ and σ will be represented by μ̂ and σ̂ respectively.
Figure 1.
A) An example of a psychometric function (solid line) with an underlying Gaussian distribution, a vestibular bias μ = +0.5 and threshold σ =1. The function corresponds to a bidirectional recognition task, which is common in vestibular and visual studies (e.g. task is to determine if motion is leftward or rightward). In this case a stimulus level of +1.5 (i.e. +1 relative to vestibular bias) corresponds to an average of 84% of responses being positive (dashed lines). B) For comparison, a typical psychometric curve for a 2-alternative force choice detection task is shown, with the threshold defined as the 75% correct level, as is typical.
The following equation defines our psychometric function (ψ):
| (1) |
where Φ is the cumulative standard Gaussian distribution and z is a “dummy” integration variable. Figure 1A shows an example of a psychometric function with μ = 0.5 and σ = 1. This notation is consistent with our earlier papers (Merfeld 2011;Lim and Merfeld 2012;Chaudhuri and Merfeld 2013).
Target level
The target level refers to the location on the psychometric curve that adaptive sampling schemes attempt to place stimuli (Taylor and Creelman 1967). Target level can be defined both in terms of stimulus amplitude and fraction correct. Since the psychometric curve is symmetric, and since we use a bidirectional task, stimuli are usually placed symmetrically about 0, although some algorithms place them symmetrically around μ ^. When we state target level as stimulus amplitude (k), it refers to stimuli at either −k σ̂ or +k σ̂. Note that for our simulations we assume σ = 1 and our experimental data are normalized, but these results generalize to any underlying σ. When we state target level as fraction correct (p), it refers to the corresponding fraction correct for stimuli at −k σ̂ or +k σ̂, which corresponds to a fraction positive of p and 1–p. Since both stimulus amplitude and fraction correct are intuitive and important, many of our results present both.
While adaptive sampling schemes are designed to converge towards a certain target level, actual stimulus amplitudes will generally differ from the target level. This is especially true early in a session, when there is a very imprecise estimate σ̂ ; given that there is a ten-fold range of motion thresholds in the population (Benson, Spencer, and Stott 1986;Benson, Hutt, and Brown 1989), little a priori information about threshold is available. Thus, when our results (and those of others), are related to target level, the distribution of actual stimuli will depend on random variability and the specific scheme used. For sessions having few trials, many stimuli may not be close to the target level. Regardless, for practical purposes, the target level and scheme used are the variables set by the experimenter, and thus are the most appropriate independent variables for analyses and experimental design decisions. The discussion elaborates on how this could explain some small differences between simulations and analytical predictions.
Analytic prediction for limits on efficiency using Fisher Information
We applied an approach similar to that previously used for logistic distributions (Wetherill 1963) to determine the theoretical bounds for the precision of parameters defining the psychometric curve with an underlying Gaussian distribution. Specifically, our analytic approach uses concepts from information theory, a mathematical approach to determine the fundamental limits of signaling channels, which is often used to understand digital communication and neural signaling.. Fisher Information (Fisher 1922;Fisher 1925;Van Trees, Bell, and Tian 2013) provides a measure of the amount of information that a set of responses carry about the parameters of interest (i.e. threshold and bias). We determine the Fisher Information for the Gaussian psychometric curve using a standard maximum likelihood approach below. The Cramér-Rao bound (Rao 1945;Cramér 1946;Van Trees, Bell, and Tian 2013) relates Fisher Information to a theoretical limit on the precision of a parameter estimate. Specifically, the inverse of the Fisher Information provides a lower bound for the variance of a parameter estimate, assuming the parameter estimate is unbiased:
| (2) |
| (3) |
where I [σ] and I[μ] are the Fisher Information for threshold and bias, respectively. In our analyses, we are often interested in the information per trial resulting in the bounds
| (4) |
| (5) |
Note that a lower standard deviation and a higher information per trial correspond to higher efficiency and/or better precision; we use standard deviation rather than variance as it possesses the physical units of direct interest. The units of information per trial are the inverse of the square of the stimulus units. For example, if the stimulus is angular velocity, the units of information per trial will be 1/(°/s)2.
We applied a standard maximum likelihood estimation approach (Wetherill 1963) to determine Fisher Information. The log-likelihood function log ℒfor a general binary response model is:
| (6) |
where x is the stimulus vector, y is the binary response vector and Φ is the cumulative standard Gaussian distribution that underlies the psychometric function ψ (Eq. 1). The maximum likelihood estimate occurs when log ℒ is maximized, i.e. ∇log ℒ = 0. The second derivatives of log ℒ indicate the steepness around the maximum, which reflects the confidence in parameter estimates. The expected values of the second derivatives are:
| (7) |
| (8) |
| (9) |
We assume the case where stimuli are divided into two groups, each placed an equal distance below and above μ. For symmetric distributions (e.g., logistic, Gaussian), when there are the same number of observations above and below the bias located k standard deviations from μ (i.e. x±=μ±kσ),
| (10) |
For the Gaussian distribution, this leads to the following relationships for information per trial for μ and σ:
| (11) |
| (12) |
where φ is the probability density function of the standard Gaussian distribution, and Φ is the cumulative distribution function of the standard Gaussian distribution defined earlier. To estimate the information per trial about both μ and σ, we use the common metric previously used for logistic distributions (Wetherill 1963), the geometric mean of each parameter’s information per trial:
| (13) |
This formulation is one of many possible ways of combining information about the two parameters and other possibilities could be selected, especially if precision of one parameter was of greater importance than that of the other.
By examining the dependence of information per trial on the stimulus level k, we determined the ideal placement of stimuli to efficiently estimate psychometric fit parameters. These relationships are examined in Results.
Adaptive sampling schemes
The estimation of psychometric functions is a common experimental problem with applications in many fields, and, as such, numerous sampling procedures have been developed (Treutwein 1995;Leek 2001). Early contributions included the development of an up-down protocol to analyze sensitivity of explosives (Dixon and Mood 1948) and estimate psychometric function thresholds (Cornsweet 1962), with subsequent work providing a more robust mathematical framework (Wetherill 1963). Adaptive algorithms, which adapt stimulus amplitude based on the subjects’ responses (Leek 2001), are particularly important for threshold testing given that thresholds can vary by more than a factor of ten across individuals (Benson, Spencer, and Stott 1986;Benson, Hutt, and Brown 1989).
We evaluated three classes of adaptive sampling schemes using Monte Carlo simulations. Each scheme adaptively determined stimulus amplitude, and every stimulus had a 50% probability of being positive or negative (e.g. leftward or rightward).
The first adaptive sampling scheme we evaluated was the common parameter estimation by sequential testing (PEST) staircase protocol (Taylor and Creelman 1967). For the remainder of this paper, when we use the term “staircase,” it always refers to the PEST staircase. The staircase converges on a target stimulus level by decreasing stimulus amplitude when a number (N) of responses are correct, and increasing stimulus amplitude when one response is incorrect. For example, in a three-down, one-up staircase (3D1U) the stimulus amplitude decreases after three correct responses and increases when one response was incorrect. We simulated two-, three-, four-, five- and six-down, one-up staircases (2D1U, 3D1U, 4D1U, 5D1U, 6D1U). The PEST rules developed by Taylor and Creelman (1967) were utilized to modulate step size. Briefly, they are: 1) Every time the staircase reverses direction, halve the step size. 2) The first and second steps in a given direction have the same size. 3) The third step in a given direction is the same size, with the exception that if the previous reversal did not have a doubling, then the step size should double. 4) A fourth step in a given direction has a step size double of the previous step. The initial step size was 3.01 dB , the minimum step size was 0.38 dB and the maximum step size to 6.02 dB (i.e. 20log102). The N-down, one-up staircases target the fraction correct level (Taylor and Creelman 1967;Levitt 1971). Thus the 2D1U, 3D1U, 4D1U, 5D1U, 6D1U staircases target the 0.707, 0.794, 0.841, 0.871, 0.891 probability correct level. Simulations were performed for n=50, 100, 150 and 200 trials.
The second adaptive scheme we simulated was the maximum likelihood estimation (MLE) method (Hall 1968;Pentland 1980;Hall 1981;Watt and Andrews 1981;Harvey 1986;Treutwein 1995;Garcia-Perez and Alcala-Quintana 2007;Shen, Dai, and Richards 2015), which fits the psychometric curve after every response and uses the new fit parameters to determine the ideal stimulus level for the next trial. We chose a hybrid approach method which was previously shown to improve efficiency (Hall 1981) by using an initial staircase to roughly estimate threshold before beginning the second phase of the MLE procedure. We performed most simulations with an initial 3D1U staircase with n=25 trials (after pilot simulations showed that 3D1U yielded a more precise estimate of threshold than a 2D1U staircase and was also more responsive and similarly precise compared to 4D1U and 5D1U staircases for small numbers of trials). In the second phase of the MLE procedure, after each response, the psychometric function was fit to all previous responses. The next stimulus amplitude was a fixed ratio (k) of the estimated threshold, and had a 50% probability of being positive or negative (i.e. −kσ̂ or +kσ̂ ). To determine the optimal target stimulus levels, we conducted simulations with fixed ratios that targeted fraction correct levels from 0.50 to 0.99 with steps of 0.01. We also conducted simulations in which the next stimulus amplitude was a fixed ratio of the estimated threshold, but centered around the bias (i.e. −kσ̂+μ̂ or +kσ̂+μ̂).
The third adaptive scheme, which we call the asymmetric staircase, is a modification of the PEST staircase so that the step sizes are different for up and down steps. Our bidirectional implementation is similar to one previously used for non-directional stimuli in a detection task (Kaernbach 1991;Garcia-Perez 1998). The ratio of up/down steps is chosen to target a particular stimulus level. Ideally, the ratio would be chosen to target the optimal stimulus amplitude to efficiently estimate the parameter(s) of interest.
To determine target level from step size, we begin with the equilibrium condition for convergence,
| (14) |
where Sdown and Sup are the down and up step sizes, and pdown and pup are the probability of responses leading to the staircase going down and up. For an N-down, 1-up staircase,
| (15) |
since N correct responses are required to go down, where p is the target fraction correct level. Likewise,
| (16) |
with each term corresponding to an incorrect response preceded by a certain number of correct responses. This is easily simplified to
| (17) |
Thus,
| (18) |
| (19) |
For example, for 3D1U targeting p= 0.895, Sup /Sdown = 2.533 , which means that the upward step size is 2.5 times greater than the downward step size to target p=0.895 for a three-down, one-up staircase.
With the exception of asymmetric step size, our asymmetric staircase was implemented with identical rules to those stated above for the PEST symmetric staircase. Simulations targeted fraction correct levels from 0.70 to 0.99 with steps of 0.01. Simulations were performed for n=50, 100, 150 and 200 trials. Simulations were performed with 2D1U, 3D1U, 4D1U, 5D1U, 6D1U.
Simulations and bias-reduced psychometric curve fits
Simulations were implemented in MATLAB R2011b (The Mathworks, Inc, Massachusetts) on the Harvard Orchestra computation cluster. Simulations were run in parallel on a number of IBM BladeCenter HS21 XMs with 3.16 GHz Xeon processors and 8 GB of RAM.
Monte Carlo simulations were used to estimate precision of parameter estimates for the various sampling procedures. All simulations started with an initial amplitude of 4 σ and set σ = 1. In all cases 2D1U, 3D1U, 4D1U,5D1U and 6D1U were tested. The simulations were performed with μ = 0, μ = 0.2 σ and μ = 0.5 σ . Simulations for MLE were performed with stimuli positioned symmetrically around 0 and around the estimated bias. There were 50 target levels for MLE and 45 for asymmetric staircases. Simulations were performed for n=50, 100, 150 and 200 trials. This resulted in 5×3×4=60 sets of conditions for staircases, 5×3×2×50×4=6000 for MLE and 5×3×45×4=2700 for asymmetric staircases, resulting in 8760 sets of conditions total. Every set of conditions was simulated 10000 times. Each simulation produced estimates of threshold and bias σ̂ and μ̂. The standard deviation across the population was computed to estimate how precisely the parameters were estimated.
We obtained the psychometric function parameter estimates μ̂ and σ̂ using maximum likelihood fits determined using a generalized linear model (GLM) and probit link function. Specifically, we applied a recent innovation to psychometric curve fitting that improves the accuracy of parameter estimation without sacrificing how precisely parameters are estimated (Chaudhuri and Merfeld 2013). This approach responds to the observation that σ is often overestimated when fitting serially-dependent data (Leek, Hanna et al. 1992;Treutwein and Strasburger 1999;Kaernbach 2001;Leek 2001) and applies established techniques for removing bias during estimation with generalized linear models to psychometric curve fitting (McCullagh and Nelder 1989;Firth 1993). These bias-reduced maximum likelihood fits were performed using the brglmfit.m program (Chaudhuri and Merfeld 2013) in Matlab 2011b (The Mathworks, MA, USA). To simplify interpretation of results, we did not perform the scaling of the biased-reduced estimates (Chaudhuri and Merfeld 2013) to further improve accuracy, but this could easily be done in combination with the approaches described in this paper. For simplicity, we opted not to include a nonlinear asymmetry (Roditi and Crane 2012a) or a lapse rate (Wichmann and Hill 2001a), though either could be readily included as independent effects when necessary.
Omniscient experimenter sample scheme
To verify both analytic and simulation approaches, we performed Monte Carlo simulations of an “omniscient experimenter” sampling scheme to show that the simulations converged to predicted theoretical limits, which was previously used to determine the bounds on efficiency for a quasilogistic distribution (Taylor and Creelman 1967). Like the adaptive schemes, the omniscient experimenter sampling scheme targets stimuli at a particular level. However, whereas the adaptive schemes determine stimulus amplitude based on prior trials, the omniscient experimenter scheme uses the known threshold and bias to select stimuli amplitudes. These schemes assume that complete a priori information about the underlying psychophysical distribution is known. 10000 simulations were performed with n=200 trials at 10 target stimulus amplitudes ranging from 0.3 to 2.1 with steps of 0.2.
Measuring psychometric test efficiency
Our analytic approach provides a bound for the best possible precision for a given target level and number of trials. We used this to evaluate the efficiency of adaptive sampling schemes by calculating, for a certain number of trials, the ratio of the variances determined by the simulation and analytic approaches. With the exception that we use a closed-form analytic solution rather than an “omniscient experimenter” as our benchmark, this approach is equivalent to that of Taylor and Creelman (1967) in which the ratio of the sweat factors was determined (Taylor and Creelman 1967), since the number of trials in the numerator and denominator is equal. Since, in this paper, our goal is to determine how to most efficiently determine threshold, we use the theoretic bound at the target level that provides the best precision for a given number of trials.
Experimental human psychophysical task
Human subject thresholds were determined to evaluate the efficiency of different adaptive sampling schemes by testing subjects’ ability to perceive rotation of their body in the dark, which is primarily senses by the vestibular organs, and specifically the semicircular canal (Grabherr, Nicoucar, Mast, and Merfeld 2008). Eight healthy human subjects (5 male, 3 female, 19–54 years old) were recruited to participate in the study. The study was approved by the local institutional review board and was performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki. Each subject was screened using a detailed, standard vestibular diagnostic clinical exam to confirm the absence of undiagnosed vestibular disorders (Grabherr, Nicoucar, Mast, and Merfeld 2008;Valko, Priesol, Lewis, and Merfeld 2012;Chaudhuri, Karmali et al. 2013;Karmali, Lim, and Merfeld 2014). Screening included Hallpike tests, angular vestibuloocular reflex (VOR) evoked via rotation, caloric testing, and posture control measures. Subjects also completed a short health history questionnaire to confirm the absence of vertigo, dizziness, and any other neurological deficits.
Subjects performed a direction-recognition task (i.e. did I move left or right?) in response to upright whole-body yaw rotation, using methods similar to those used in previous studies (Grabherr, Nicoucar, Mast, and Merfeld 2008;Valko, Priesol, Lewis, and Merfeld 2012;Chaudhuri, Karmali, and Merfeld 2013). An adaptive, one-interval, two-alternative, categorical, forced-choice procedure (Treutwein 1995;Leek 2001) was used. In separate counterbalanced sessions of 100 responses each, subjects did (a) a standard, symmetric three-down, one-up staircase which targeted the 0.794 fraction correct level (3D1U) and (b) a modified three-down, one-up staircase with asymmetric step size which targeted the 0.90 fraction correct level (3D1U-90%). A tone began 300 ms before motion commenced and ended simultaneous with motion. After the tone ended, subjects were required to push a button in their right hand if they perceived rightward motion and push a button in their left hand if they perceived leftward motion. If subjects were unsure, they were required to make their best guess. Subjects practiced the task before each session.
Motions were provided by our Eccentric Rotator device (Neurokinetics, Pittsburg, PA, USA). Motions were single cycles of sinusoidal acceleration, as in many other motion threshold studies (Benson, Hutt, and Brown 1989;Benson, Spencer, and Stott 1986;Kolev, Mergner et al. 1996;Grabherr, Nicoucar, Mast, and Merfeld 2008;Zupan and Merfeld 2008;Butler, Smith, Campos, and Bulthoff 2010;Soyka, Robuffo, Beykirch, and Bulthoff 2011;Haburcakova, Lewis, and Merfeld 2012;Roditi and Crane 2012a;Roditi and Crane 2012b;Crane 2012a;Valko, Priesol, Lewis, and Merfeld 2012). In this study, motions always had a frequency f =2 Hz and were defined by the equations:
| (20) |
| (21) |
| (22) |
We attempted to minimize the influence of non-vestibular cues using the same approaches previously used (Grabherr, Nicoucar, Mast, and Merfeld 2008;Valko, Priesol, Lewis, and Merfeld 2012;Chaudhuri, Karmali, and Merfeld 2013;Karmali, Lim, and Merfeld 2014). Briefly, subjects were secured with a five-point harness in a racing-style chair, with their head fixed relative to the chair and platform with a vacuum cushion snugly pressed between two adjustable plates. Gloves and long sleeves reduced wind cues on skin surfaces. Auditory cues were masked with active noise-canceling headphones playing white noise (circa 60 dB). Elevated thresholds measured in patients suffering total vestibular loss (Valko, Priesol, Lewis, and Merfeld 2012) suggest that motion thresholds depend predominantly on vestibular cues.
There was a pause of at least 3 s between motions since bias after-effects extinguish within 3 s in the dark (Crane 2012b). Since a stationary visual scene can help extinguish perceived motion (Guedry, Collins et al. 1961), we tested whether any influence of prior motion on thresholds may be modulated by a stationary visual scene between motions. We did this by testing each condition once in total darkness, and a second time with a stationary full-field scene illuminated by a dim light for at least 1.5 s after subjects responded and before the commencement of the following trial. We found that there was no significant difference in thresholds between sessions with and without a stationary visual scene between motions (paired t-test; p=0.34), and thus we pooled these data when performing statistical tests.
We were primarily interested in estimating the precision (i.e. standard deviation) of the measured threshold for each subject, which we determined using a standard bootstrap approach (Wichmann and Hill 2001b;Chaudhuri and Merfeld 2013). In this approach, for each subject and condition, the psychometric curve was fit to a resampled set of responses 2000 times using the bias-reduced maximum-likelihood fit (Chaudhuri and Merfeld 2013) to calculate a population of fit thresholds and biases. These values were normalized by the subject’s threshold to allow comparison across subjects. The standard deviation of the normalized thresholds and bias were determined (Wichmann and Hill 2001b) to measure their precision.
Results
Analytic limits on efficiency
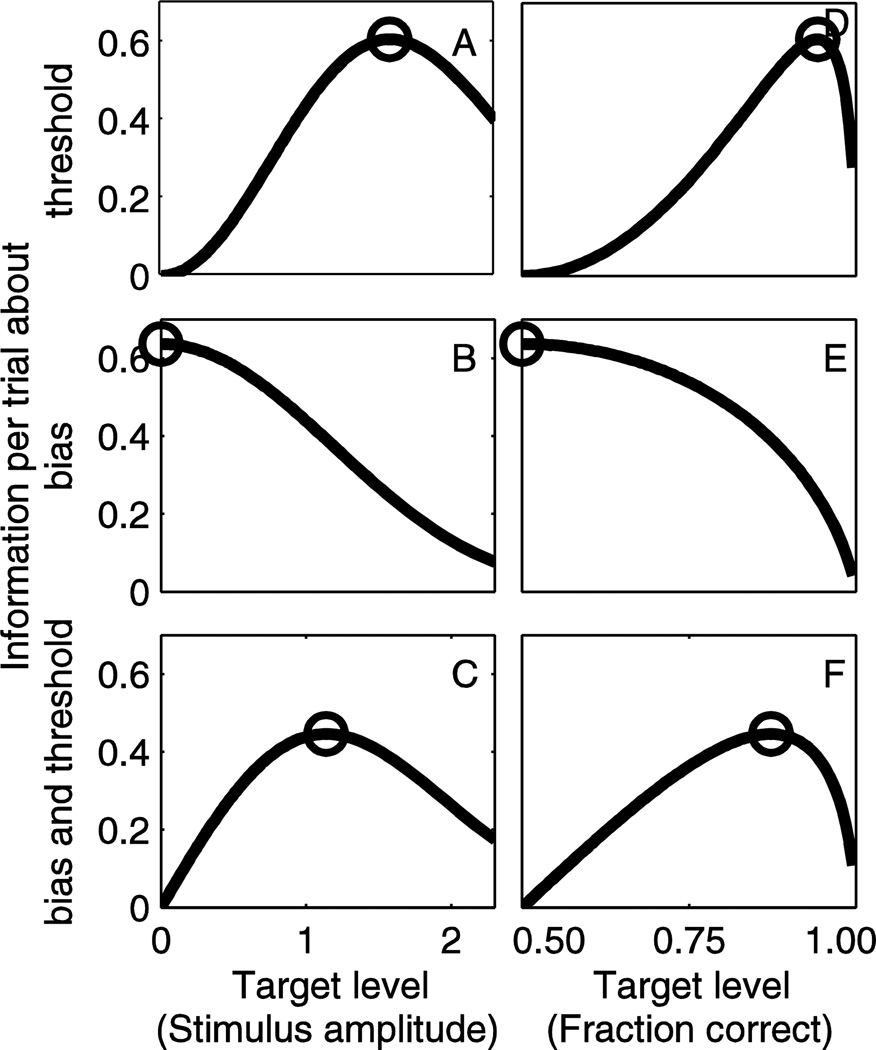
Figure 2 shows the results of analyses that determine the theoretic bound on efficiency. While the majority of our results are presented in terms of the standard deviation of parameter estimates, this figure shows Fisher Information per trial because it is relates directly to the underlying analytic framework. Figure 2A,D show how Fisher Information per trial regarding the threshold (σ) varies as target level changes (Eq. 12). We show results for target level presented both in terms of stimulus level (Figure 2A,B,C) and the corresponding fraction correct (Figure 2D,E,F). We provide both because each provides a different relevant perspective. Figure 2A shows that at small stimulus amplitudes, each response provides almost no additional information about threshold (σ), meaning that it is an unwise choice for stimulus amplitude if threshold is the parameter of interest. Information per trial about threshold (σ) peaks as stimulus amplitude increases to 1.575 (indicated by circle), suggesting that this is the ideal target level to efficiently collect data about threshold. As stimulus amplitude continues to increase, information per trial again decreases. Note that the abscissae are relative to bias, and thus in a subject with a bias, these stimulus amplitudes should be shifted accordingly. Figure 2D shows the information per trial peaks (circle) when the target fraction correct level is 0.9424, which occurs at a stimulus level of 1.575 (e.g., see Figure 2A). The peak information per trial is 0.6084 (both curves). Since the psychometric curve is symmetric, this also includes stimuli placed at −1.575, which corresponds to 0.9424 fraction correct and 1–0.9424=0.0576 fraction positive. Figure 2B,E show the Fisher Information per trial regarding bias μ (Eq. 11). At zero stimulus amplitude, the information per trial is maximized (circle), suggesting that this is the optimal target level to collect information about bias (μ). This corresponds (circle) to a fraction correct of 0.5. As stimulus amplitude increases, the information per trial about bias (μ) decreases, suggesting reduced efficiency. The peak information per trial is 0.6366. Figure 2C,F show the Fisher Information per trial about both threshold and bias, using a formulation that gives the two parameters equal weight (Eq. 13). As expected, when stimulus amplitude is small, there is almost no information provided. As stimulus amplitude increases, information per trial increases until it reaches a peak (circle) at 1.138. This corresponds to a fraction correct (circle) of 0.8725. Note that this target level is between the optimal target levels when only threshold or bias is of interest, which is expected given that both are being optimized. The peak information per trial is 0.4457.
Figure 2.
Information per trial as a function of target level derived from an analytic analysis. Target level is presented both in terms of stimulus level as a ratio of threshold (A,B,C) and corresponding fraction correct (D,E,F); note that while presenting different perspectives, these provide redundant information. We indicate the target level that maximizes information per trial (circle) regarding threshold (A,D), bias (B,E) and bias and threshold together (C,F).
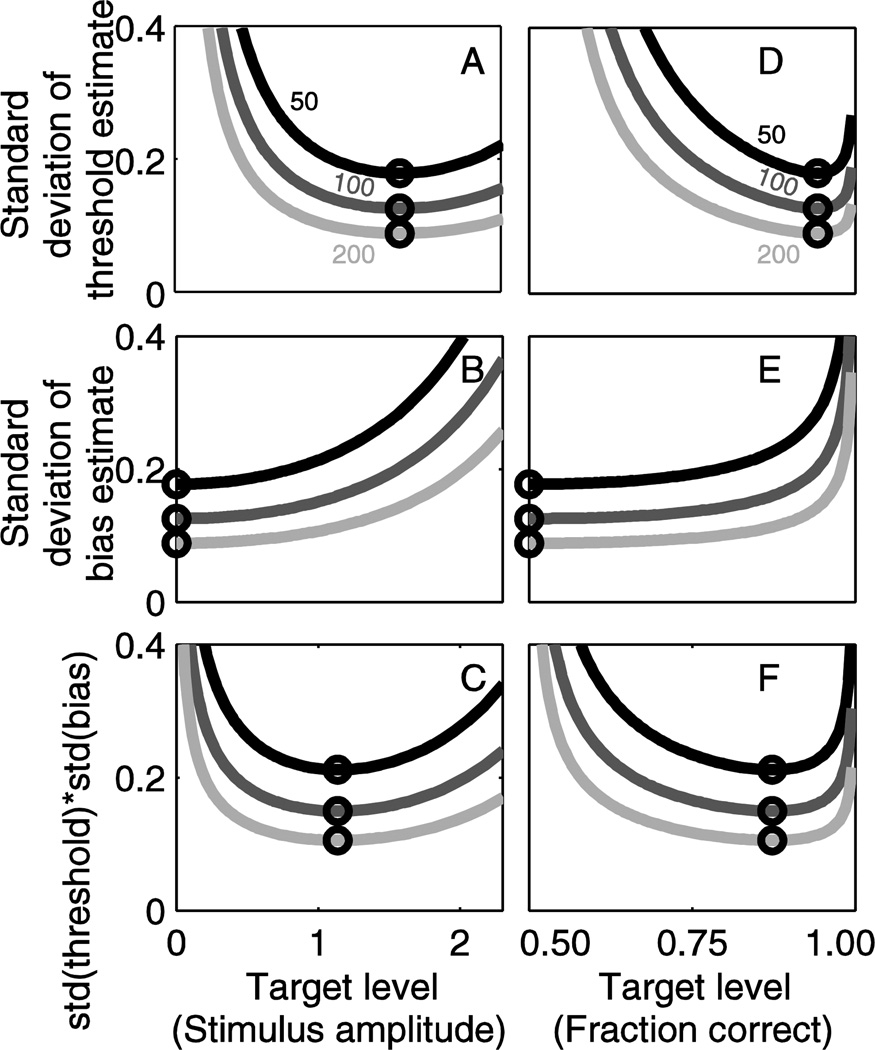
In many cases the overall precision for an experiment, rather than just the information gained from each response, is of interest. In addition, standard deviation is a more intuitive measure of precision since it is formulated in the physical units of interest. Figure 3 and Table 1 show the same analytic results as in Figure 2, but presented as standard deviation of the parameter estimates (Eqs. 4 and Eqs. 5). When shown as standard deviation, the theoretic bound (lines) depends on number of trials; results are shown for 50, 100 and 200 trials. Since more information per trial improves precision, standard deviation is minimized at the same target level that information per trial is maximized, resulting in the most efficient data collection. Since we assume an underlying distribution with σ =1 for all results in this paper, standard deviation is always equivalent to coefficient of variation.
Figure 3.
The same analytic results as in Figure 2, but shown as the standard deviation of the parameter estimates, rather than information per trial. This presentation is of practical use because investigators can see the expected precision of results. When shown as standard deviation, the theoretic limit (lines) depends on number of trials; results are provided for 50, 100 and 200 trials. Since more information per trial improves precision, standard deviation is minimized at the same target level that information per trial is maximized. As in Figure 2, target level is presented both in terms of stimulus level (A,B,C) and corresponding fraction correct (D,E,F). Since we assume an underlying distribution with σ =1 for all results in this paper, standard deviation is always equivalent to coefficient of variation.
Table 1.
Summary of performance at optimal target levels for various adaptive sampling schemes, including analytic predictions, simulations and human experiments. For asymmetric staircases and MLE, the target level yielding the lowest standard deviation of the threshold estimate is shown. Symmetric staircases can target only a single level, and performance is shown for that level. ND1U (e.g. 2D1U) means that the staircase requires N correct responses to decrease stimulus amplitude and 1 incorrect response to increase stimulus amplitude.
| Performance at optimal target
levels for various adaptive sampling schemes | ||||||
|---|---|---|---|---|---|---|
| Optimal target
level |
Standard deviation of
threshold estimate |
|||||
| Scheme | Stimulus amplitude |
Fraction correct |
50 trials | 100 trials | 150 trials | 200 trials |
| Analytic | 1.555 | 0.940 | 0.181 | 0.128 | 0.105 | 0.091 |
| Omniscient experimenter | 1.500 | 0.933 | - | - | - | 0.092 |
| MLE simulations | 1.405 | 0.920 | 0.237 | 0.149 | 0.117 | 0.099 |
| Symmetric 2D1U simulations | 0.545 | 0.707 | 0.366 | 0.246 | 0.195 | 0.167 |
| Symmetric 3D1U simulations | 0.819 | 0.794 | 0.283 | 0.185 | 0.147 | 0.126 |
| Symmetric 4D1U simulations | 0.998 | 0.841 | 0.256 | 0.166 | 0.132 | 0.113 |
| Symmetric 5D1U simulations | 1.129 | 0.871 | 0.250 | 0.160 | 0.126 | 0.108 |
| Symmetric 6D1U simulations | 1.231 | 0.891 | 0.247 | 0.158 | 0.124 | 0.105 |
| Asymmetric 2D1U simulations | 1.103 | 0.865 | 0.279 | 0.177 | 0.142 | 0.120 |
| Asymmetric 3D1U simulations | 1.254 | 0.895 | 0.257 | 0.163 | 0.131 | 0.111 |
| Asymmetric 4D1U simulations | 1.254 | 0.895 | 0.240 | 0.158 | 0.127 | 0.108 |
| Asymmetric 5D1U simulations | 1.282 | 0.900 | 0.238 | 0.154 | 0.123 | 0.105 |
| Asymmetric 6D1U simulations | 1.341 | 0.910 | 0.234 | 0.152 | 0.122 | 0.105 |
| Human symmetric 3D1U | 0.819 | 0.794 | - | 0.211 | - | - |
Omniscient experimenter simulation results approach the theoretical bound
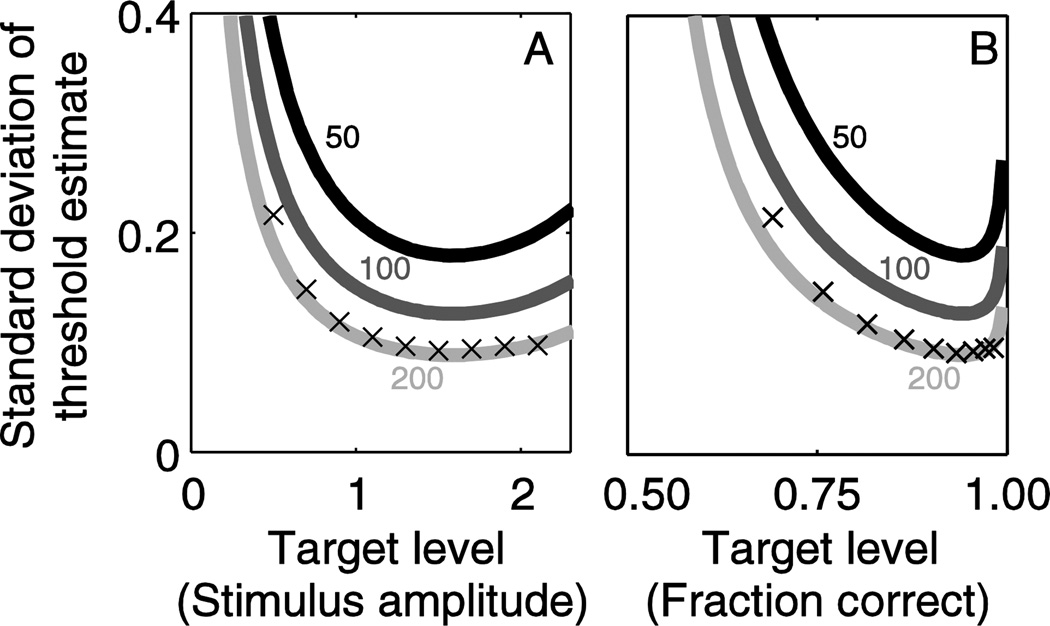
Figure 4 compares simulation results from the omniscient experimenter sampling scheme (Taylor and Creelman 1967) with the theoretic bound. In this scheme, all stimuli are provided at the target level, under the assumption that the sampling scheme has full a priori information about the underlying psychophysical distribution. We focus the remainder of results on threshold (σ) because this is the parameter usually of interest to many groups, and because bias is often considered a nuisance parameter (Garcia-Perez and Alcala-Quintana 2013); however, these results can all be extended to optimizing both bias and a combination of threshold and bias. We present standard deviation both in terms of stimulus level (Figure 4A) and the corresponding fraction correct (Figure 4B), as in Figure 3. Simulation results are the standard deviation of the thresholds calculated in each of 10000 experiments, with each experiment having 200 trials.
Figure 4.
Omniscient experimenter simulation results (x) are similar to the theoretic limits (lines). The analytic results are identical to those presented in Figure 3. Each simulations has 200 responses. Target level is presented in terms of stimulus amplitude (A) and fraction correct (B), as described above.
Figure 4 shows that the relationship between standard deviation and target level is very similar for the omniscient experimenter simulations (x) and analytic approach (thick line). In all cases, a target level slightly above threshold is the optimal target level. The similarity of the results lends support to the assumption underlying both the analytic and simulation approaches. Simulations were also performed (not shown) with 1000 trials; these results converged to be indistinguishable from the corresponding analytic curves (not shown).
Human subject results are consistent with simulation and analytic results
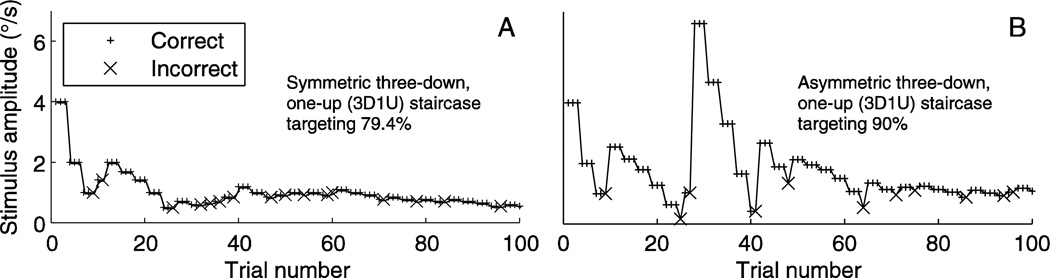
We conducted human psychophysics experiments to examine whether the precision of threshold estimates predicted by analytic analyses and simulations modeled human performance well. We did so by measuring precision for a symmetric 3D1U staircase targeting 79.4% correct and an asymmetric 3D1U staircase targeting 90% correct, both for human subjects and simulations for the same staircases (As a reminder, in this paper, “staircase” always refers to the PEST staircase). Figure 5 shows example staircase tracks from simulations, and highlights the large upward steps after incorrect responses in the asymmetric 3D1U-90% staircase (Figure 5B) in comparison to the symmetric 3D1U staircase (Figure 5A). This results in stimuli being placed at a higher level, which is illustrated by the difference in stimulus amplitude near the ends of the two tracks. Subjects performed 100 trials of a direction-recognition task (did I move left or right) in response to whole-body movement.
Figure 5.
Example staircase tracks from a symmetric 3D1U staircase (A) and asymmetric 3D1U staircase targeting 90% (B). Derived from one simulated experiment each, consisting of 100 trials.
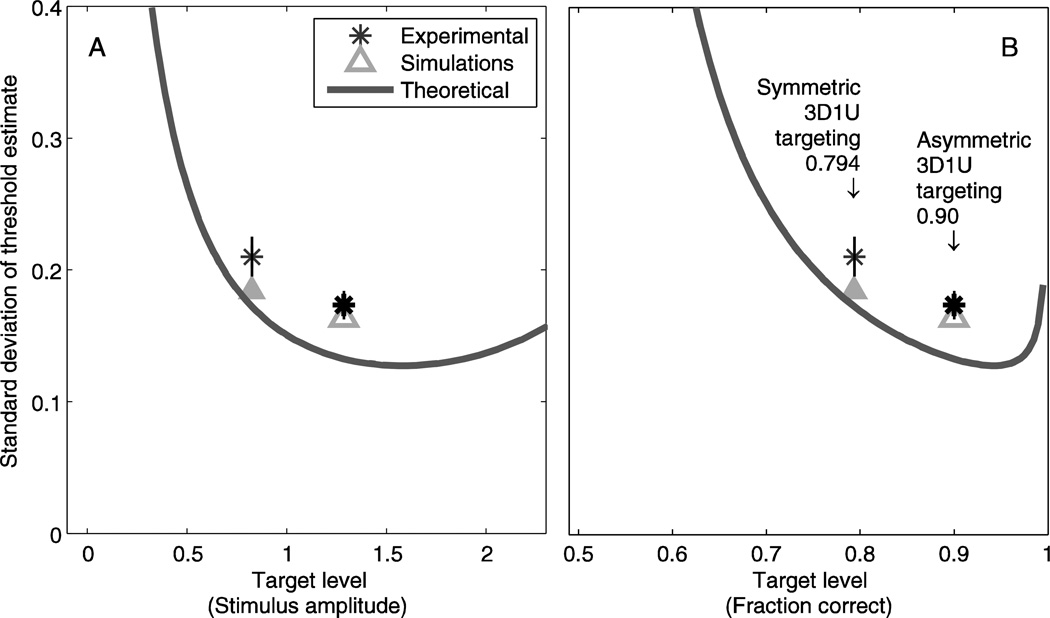
Figure 6 compares human, simulation and analytic results, for the case of 100 trials per session. Broadly, precision of threshold estimates follow the same trend as analytic predictions for both human and simulation results. Human results shown are the standard deviation of threshold measurements for a standard 3D1U staircase (thin asterisk) and an asymmetric 3D1U-90% staircase targeting the 0.90 fraction correct level (thick asterisk), normalized by each subject’s threshold then averaged across subjects. Standard deviation decreases from 0.211 for 3D1U (thin asterisk) to 0.174 for 3D1U-90% (thick asterisks). This 17% improvement is statistically significant (paired t-test, p=0.021). The corresponding simulation (triangles) yield estimates for the precision of threshold estimate that broadly follow the theoretic bound, and show that threshold can be determined 12% more precisely with 3D1U-90% than 3D1U. The simulations are consistent with human performance, with small differences not reaching the level of statistical significance (t-test, p=0.735 for 3D1U-90% and p=0.094 for 3D1U). The theoretic bound (thick line) for 100 trials is replicated from that shown in Figure 4. That both human performance and simulations are similar suggests that the human observers are performing as assumed. That both are somewhat worse than the theoretical bound is indicative of sub-optimal design of the adaptive sampling scheme.
Figure 6.
Precision of threshold estimates in human experiments are consistent with simulations and close to theoretical limits. Human experiments (stars) were performed with a symmetric 3D1U staircase targeting the 0.794 fraction correct level and an asymmetric 3D1U staircase targeting the 0.90 fraction correct level. There were 100 trials in each experiment, and precision was determined for each subject then averaged across subjects, with error bars showing standard error across subjects. Simulations were done for symmetric 3D1U (filled triangle) and asymmetric 3D1U targeting 0.90 (open triangle), and also included 100 trials/simulation. Both human performance and simulations are close to the theoretical limit (line), which means that the symmetric staircase is a reasonably efficient choice of algorithm. Target level is presented in terms of stimulus amplitude (A) and fraction correct (B), as described above.
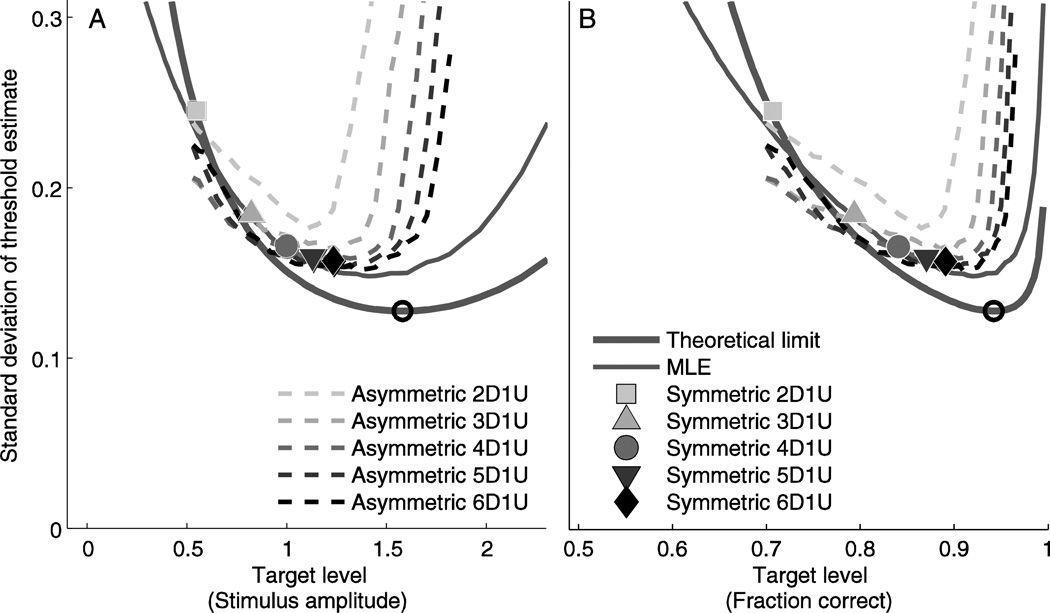
Comparison of efficiency for common adaptive sampling schemes
We now compare three different adaptive sampling schemes to each other, relative to theoretic bounds, for the case of 100 trials per session (Figure 7, Table 1). The theoretic bound (thick line) for 100 trials is replicated from that shown in Figure 4. The simulations for the MLE procedure (thin solid line) yield estimates for the precision of threshold estimate that are broadly similar to the theoretic bound, with some exceptions (discussed below). The MLE procedure most efficiently estimates threshold when the target level is 1.405 (fraction correct of 0.920). The results for standard staircase simulations show that 2D1U, which has the smallest target level, provides the least precise estimate of threshold. Precision increases progressively for 3D1U, 4D1U, 5D1U and 6D1U (Figure 7, solid symbols and Table 1), which corresponds to increasing staircase target level. Simulations of the asymmetric staircases (dashed lines) demonstrate that varying target level changes the precision of the threshold estimate, with a relationship that is broadly similar to the theoretic bound; differences from theory are explained in Discussion. While asymmetric staircases generally follow a similar relationship between precision and target level regardless of whether 2D1U, 3D1U, 4D1U, 5D1U or 6D1U is used, asymmetric 2D1U underperforms and has a lower optimal target level compared to the rest. For example, the 4D1U asymmetric staircase most precisely estimates threshold when the target level is approximately 1.254 (fraction correct of 0.895), although any target level between 1.058 and 1.405 (fraction correct between 0.855 and 0.920) provides precision within 3% of that at its best.
Figure 7.
Precision of common adaptive algorithms compared to theoretical limits (thick line) for a range of target levels. Results presented for 100 responses in each simulation/experiment. Symmetric staircases (solid symbols) have a single target level, while asymmetric staircases (dashed lines) and the MLE procedure (thin line) were simulated at a range of target levels. Target level is presented in terms of stimulus amplitude (A) and fraction correct (B), as described above.
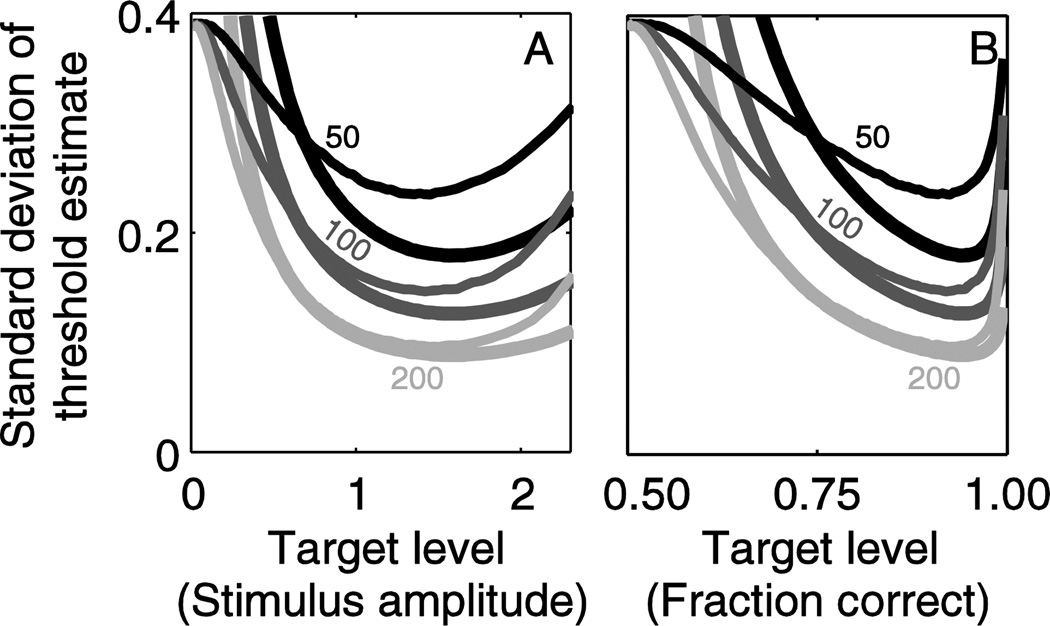
Figure 8 compares the efficiency of the MLE adaptive sampling scheme with the analytic results for experiments with 50, 100 and 200 trials. It shows that the relationship between standard deviation of the threshold estimate and target level is broadly similar for the MLE simulations (thin lines) and theoretic bound (thick line). In all cases, a target level slightly above threshold is the optimal target level. The gap between MLE simulation and the theoretical bound is very small for 200 trials; the larger gap for 100 and especially 50 trials suggests that the MLE procedure is suboptimal for smaller numbers of trials. As expected, the precision of the threshold estimate improves with number of trials for both the analytic and simulation results. For example, the MLE simulations show that the lowest standard deviation at the optimal target level is 0.237 for 50 trials, 0.149 for 100 trials and 0.0984 for 200 trials (Table 1). There are a few notable differences between the MLE procedure and the theoretic bound. First, the best precision occurs at slightly lower stimulus levels for MLE simulations, especially with a small number of trials. Second, the MLE simulations targeting very low levels actually provide better precision than the theoretical bound. These differences are likely because of differences between target stimulus level and actual stimulus level, which is examined in Discussion.
Figure 8.
MLE simulations (thin lines) compared to analytic results (thick lines). Results are shown for 50, 100 and 200 trials, with the same shade used for both results. With 50 trials, the MLE procedure is much less precise than theoretically possible, whereas with 200 trials it functions very close to the theoretical limit. The optimal target level is almost identical regardless of number of trials. Target level is presented in terms of stimulus amplitude (A) and fraction correct (B), as described above.
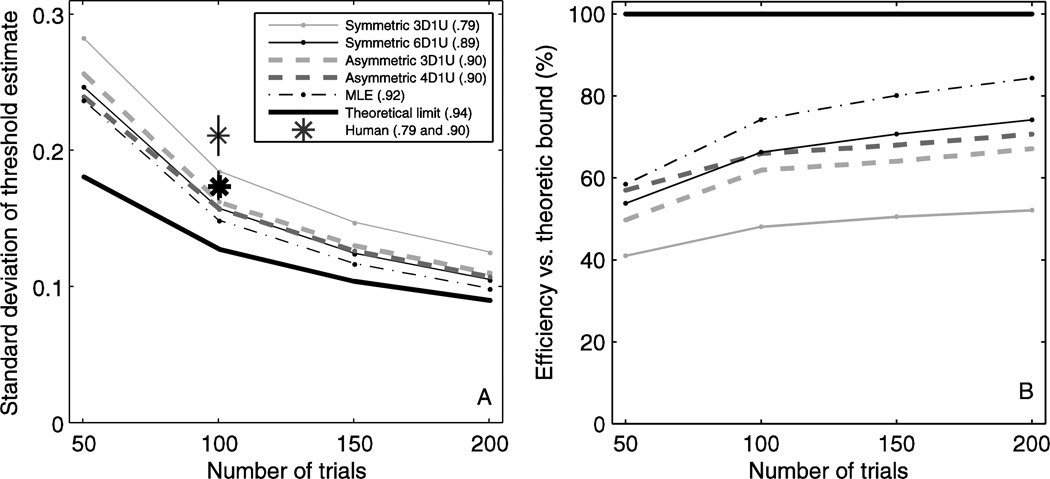
Figure 9A shows how the precision of the three adaptive sampling schemes and the theoretic bound improves with increasing numbers of trials. Each data point shows precision at the optimal target level for a given scheme and number of trials (the legend lists the target fraction correct for each scheme). As expected, standard deviation of the threshold estimate decreases as the number of responses increases for all approaches. The standard symmetric 3D1U staircase (thin solid dark line) produces estimates of threshold with much worse precision than other algorithms, while the 6D1U staircase (thin solid light line) performs better. The asymmetric 4D1U staircase (thick dashed line) and MLE procedure (thin dashed line) have precision similar to or better than the standard staircases. For 50 trials the two have similar precision, while for 100 trials and above, the MLE procedure slightly outperforms the asymmetric 4D1U staircase. Although the asymmetric 5D1U and 6D1U have minutely better precision (Table 1) compared to asymmetric 4D1U at the optimal target level, we believe that asymmetric 4D1U is a better choice because it is less disrupted by lapses, which is considered in Discussion. These results suggest that asymmetric 4D1U, symmetric 6D1U and the MLE procedures may be optimal for many experiments; other practical considerations are presented in Discussion.
Figure 9.
A: The improvement in precision of select adaptive sampling schemes as number of trials increases. Standard deviation is presented for each scheme at its optimal target level (Table 1, also shown in brackets in the legend). B: The efficiency of each scheme vs. the theoretic bound.
A practical use of Figure 9A is in determining the required number of responses in an experiment when the adaptive sampling scheme is changed and the same precision is desired. For example, if an experimenter is planning an experiment with 150 trials using 3D1U, they can trace horizontally to the left from that point and determine that to yield the same precision, the asymmetric 3D1U staircase would require roughly 124 trials, and the MLE procedure would require approximately 102 trials.
Figure 9B shows the psychometric test efficiency of selected adaptive sampling schemes using the theoretic bound as a benchmark of ideal precision. It is calculated using the ratio of the variance of the analytic approach for the ideal target level and the variance of the simulation. For example, the symmetric 3D1U staircase performed at 41% efficiency for 50 trials, growing to 52% for 200 trials. As expected, the asymmetric 3D1U staircase performed better, growing from 50% efficiency for 50 trials to 67% for 200 trials. The asymmetric 4D1U grew from 57% efficiency for 50 trials to 71% for 200 trials. The MLE procedure performed best, growing from 58% efficiency at 50 trials to 84% at 200 trials.
While the MLE method outperformed all other methods, for 50 trials, the asymmetric 4D1U and 6D1U also provided comparable performance. All methods became more efficient with additional trials, which is expected since the trials provided later in the sequence are usually closer to the optimal target level.
We also compared the precision of the threshold estimate for selected schemes to the commonly-used symmetric 3D1U staircase. For example the MLE procedure performed approximately 16% better for 50 trials and 21% better for 200 trials. The asymmetric 4D1U was consistently 14–15% better. The symmetric 6D1U was approximately 13% better for 50 trials and 16% better for 200 trials.
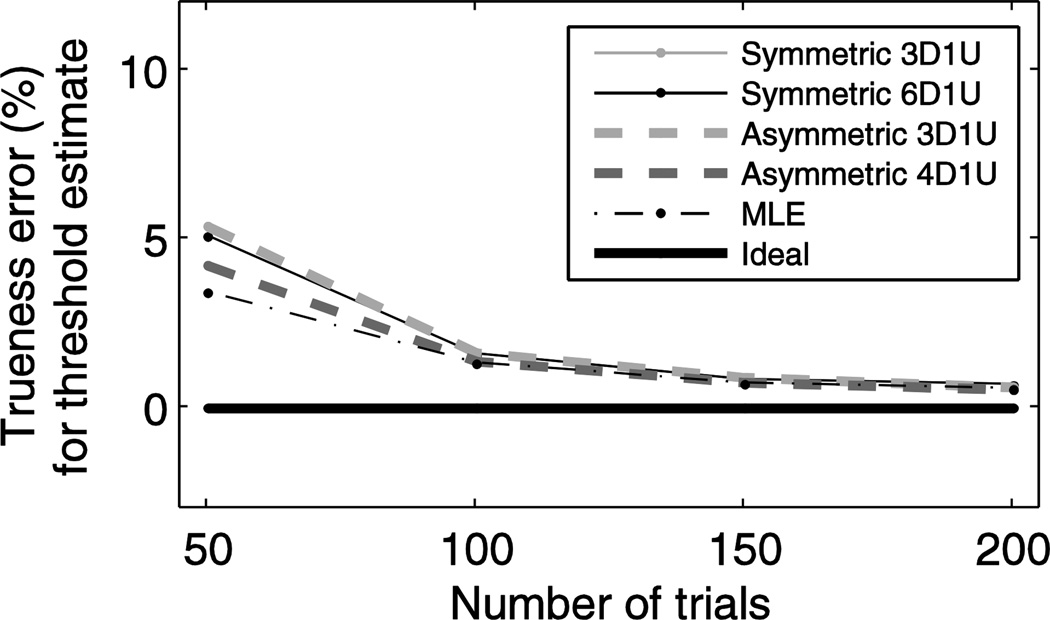
While our primary interest was determining the precision of the threshold estimate, we also used our simulations to see if there were inaccuracies (i.e. systematic deviations from the actual value) in these estimates. Figure 10 shows accuracy errors (biases) for the same optimal target levels used in Figure 9; these data show that there were small systematic overestimates (i.e., small parameter biases). For example, the inaccuracy is less that 2% for 100 trials or more, and less than 6% for 50 trials. When compared with standard deviations of 0.16 and 0.25, respectively, these biases are of little consequence (“as a rule of thumb, a bias of less than .25 standard errors can be ignored”, Efron and Tibshirani 1994). It is crucial to note that these fits accurately fit the data (i.e., parameter estimates were unbiased) because a bias-corrected fit was utilized (Chaudhuri and Merfeld 2013); this earlier publication presents in detail the accuracy of psychometric curve fits obtained with and without bias-corrected fits.
Figure 10.
Accuracy errors for threshold estimates are small for all adaptive sampling schemes.
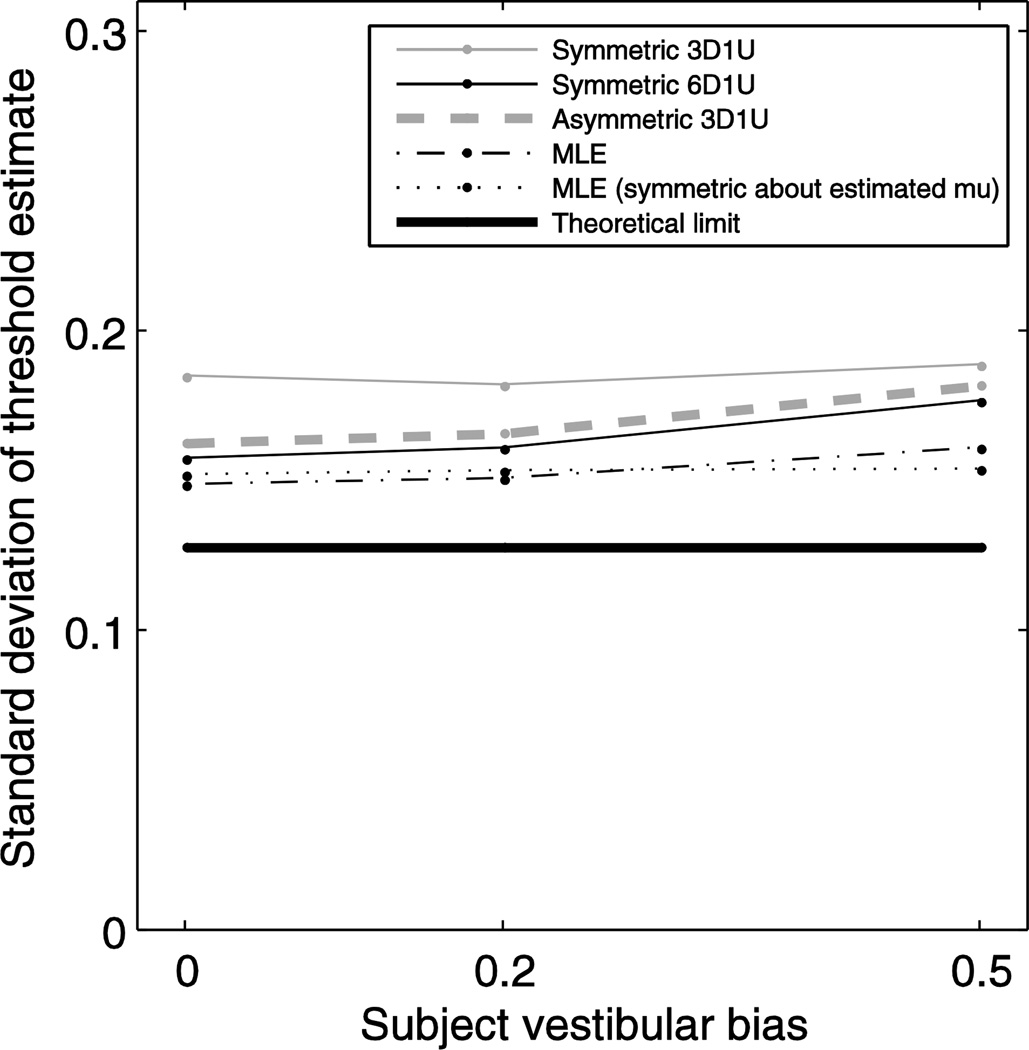
Effects of bias
Since all of the adaptive sampling schemes we analyzed place stimuli symmetrically around 0, a shift of the psychometric curve (i.e. a bias caused by non-zero mean noise) would cause stimuli intended to be placed at the target level to actually fall on a different part of the subject’s psychometric curve (Merfeld 2011). Figure 11 shows how threshold estimate precision is impacted by a bias in the same adaptive sampling schemes described above. Bias is shown as a fraction of threshold. In general, algorithms that sample at a higher target level, such as 6D1U (grey thin line) targeting 0.891, asymmetric 3D1U (thick dashed line) targeting 0.895 and the MLE procedure (black dotted line) targeting 0.92, worsen in performance as bias increases. Symmetric 3D1U (black thin line) targeting 0.794 has a much smaller decrement in performance as vestibular bias increases.
Figure 11.
The effects of vestibular bias on the precision of the threshold estimate. Based on simulation results with 100 responses each for different underlying μ. In addition to the adaptive sample schemes described above, results for a modification of the MLE procedure (dotted line) are shown in which stimuli are placed symmetrically around μ̂ instead of around 0.
One approach to overcome the effects of bias is to place stimuli symmetrically around the estimated bias (μ̂±kσ̂) instead of symmetrically around zero (0±kσ̂). A modified MLE procedure (Figure 11, grey dotted line) implementing this approach results in little worsening of threshold estimate precision as bias increases; Discussion describes disadvantages of this approach.
Discussion
Theoretical limits on precision
Our analytic approach determined the optimal target level for psychometric functions with underlying bidirectional Gaussian distribution. The overall results were similar to those for logistic distributions (Wetherill 1963), with small differences. For example, we found the target fraction correct level to optimize threshold for Gaussian distributions was 0.942, compared to 0.915 for logistic distributions. For both, the optimal target fraction correct to optimize bias was 0.5. If interested in both threshold and bias, we found the optimal target fraction correct was 0.873 for Gaussian distributions, compared to 0.824 for logistic distributions. Many studies now perform analysis using a Gaussian distribution and selection of appropriate target levels could improve efficiency.
While previous approaches have evaluated psychometric test efficiency by comparing simulation results for each adaptive sampling scheme with the results of omniscient experimenter simulations (Taylor and Creelman 1967), our approach uses a closed-loop analytic solution, providing robust support for the existing approach.
Comparison of analytic, simulation and experiment results
To our knowledge, this is the first time that analytic approaches have been compared with Monte Carlo simulations or human experiments, and also the first time the three have been directly compared, to evaluate efficiency of approaches to determine recognition thresholds. That the results broadly agree is important because each approach has untested assumptions. For example, analytic approaches do not account for the particulars of the adaptive algorithm used, and simulations do not say how close to the theoretic limit results are.
To our knowledge, this is also the first study to compare simulations and human experiments for an adaptive staircase recognition task, and the results suggests that human threshold forced-choice decision-making is modeled well by detection-theory models and that simulations incorporate acceptable models of human threshold decision making. It also suggests that human threshold decision-making functions near optimal levels. Previous studies (Kollmeier, Gilkey, and Sieben 1988;Garcia-Perez 2000;Garcia-Perez and Alcala-Quintana 2007;Garcia-Perez and Alcala-Quintana 2009), mostly using 2-alternative forced choice detection tasks and non-directional stimuli, found that experimental results are similar to simulations in some situations, but fundamental differences between detection (e.g. “did I move or not move?”) and recognition (e.g. “did I move left or right?”) tasks (Merfeld 2011) underline the importance of studying both recognition and detection. Figure 1 illustrates a few differences between recognition (Figure 1A) and detection (Figure 1B) that are noteworthy: 1) The stimulus amplitude for detection is always a positive scalar, and is typically depicted on a logarithmic axis to emphasize the plateau at small amplitudes, while recognition can be used for bidirectional measures. 2) Two-alternative forced-choice detection (with the exception of the yes-no staircase) has a plateau at the guessing level, which is expected on average to be 50% correct, but can vary with the subject’s decision boundary, and is typically more variable than the plateau at 0% positive for recognition. This is a fundamental difference, since recognition tasks do not need to sample extensively using stimuli that yield just 50% correct (“just guessing”). 3) While detection uses fraction correct as the ordinate axis, recognition uses fraction positive (with the exception of the yes-no staircase).
One simple message (Wetherill 1963;Taylor and Creelman 1967) highlighted by both the analytic (Figure 2 & Figure 3) and numeric (Figure 4) results is that the optimal strategy (on average) is to distribute the stimuli equally at just two levels located symmetrically on both sides of the point of subjective equality. For example, if interested only in σ, the stimuli should be placed at the two levels that yield 94% correct (μ ±1.575σ). This message differs from a common psychometric intuition that sampling at a range of stimulus amplitudes, including a few trials at the two extremes to “anchor” the fit, is desirable. The results (Figure 7, 8, 9) presented herein provide practical guidance that might help improve the efficiency of some experimental investigations. Given the limited time available for clinical and scientific testing, efficient data collection can make previously infeasible tests feasible. Since anchoring, especially to determine the lapse rate for the guessing level in detection tasks, requires tiny amplitude stimuli, further investigation is required to determine the most efficient approaches under these assumptions.
As a demonstration, we evaluated a few common adaptive algorithms, although the approach can and should be applied to other common sampling schemes that so far have been evaluated using simulations and experiments, such as “QUEST” (Watson and Pelli 1983) and “PSI” (Kontsevich and Tyler 1999). A few results stand out from the evaluation of common adaptive algorithms. First, symmetric 2D1U and 3D1U staircases perform quite close to the theoretic level for their target level, but they do not target the most efficient level if threshold is the parameter of interest. Across a broad range of target levels, the MLE procedure produces results close to the theoretic limit, especially for 200 trials. Asymmetric staircases exceed or match performance of symmetric staircases, suggesting that they can couple optimal efficiency with the ability to converge quickly towards the threshold level, and came close to matching the performance of the MLE procedure.
Most of our analyses focused on the efficient determination of threshold rather than bias. We do so because the origin of these biases is unclear, with some (Garcia-Perez and Alcala-Quintana 2013) suggesting that they could include both cognitive decision-making and perceptual biases. It would be straightforward to extend our analyses to other cases.
The similarity between the theoretic limit and simulations of the MLE procedure (Figure 8) and asymmetric staircases (Figure 7) lend support to the assumptions underlying both approaches. There are a few peculiarities that deserve explanation: optimal target level was slightly lower than that predicted by the theoretical limits, precision outperformed the theoretical limit at small target levels, and the precision for 50 trials of the MLE procedure was much worse than the theoretical limits, whereas for 200 trials it was comparable. These observations can be explained by recalling that actual stimuli are not all placed at the target level. We demonstrate this with an example that assumes the initial stimulus amplitude is higher than threshold, although analogous logic holds if the opposite is true. The initial staircase, which has 25 responses starting from the initial stimulus amplitude of 4 σ, places some trials above the target level. Indeed, it is necessary to have a range of stimulus amplitudes to roughly establish a psychometric curve, since, given that population thresholds vary more than an order of magnitude, there is little a priori information about threshold. Thus, especially for small n, some stimuli will be above target level, and the median stimulus amplitude may be somewhat higher than the target level. Likewise, when target level is lower than optimal, as the staircase traverses from the initial amplitude to the target level, it will provide some stimuli that are close to the optimal target level. This allowed the simulations to outperform theory. And when target level is at the optimal theoretic target level, some stimuli will be above the target level, reducing efficiency. This is why the most precise target level is slightly less than that predicted by theory, and why this gap diminishes as the number of trials increases. While it would be interesting to determine an “effective stimulus level” and compare it to the target level, from a practical perspective, the target level is the parameter set by the operator and thus is of direct interest. Furthermore, while target level is a single value, actual stimuli span a broad range, and calculating “effective stimulus level” would require additional assumptions.
Recommendations for adaptive sampling schemes
Three schemes had psychometric test efficiencies that approached the ideal predicted by theory: 1) a symmetric 6D1U standard staircase, which naturally targets a fraction correct of 0.89, 2) an MLE procedure targeting a fraction correct of 0.92, 3) an asymmetric 4D1U staircase targeting a fraction correct of 0.90. While they had similar precision at 50 trials, the MLE procedure outperformed at 100 trials and more (Figure 9). Accuracy errors were very small and similar for the three (Figure 10).
Overall, the results suggest that the MLE procedure would often be the best adaptive sampling scheme for most experiments, followed by the 4D1U asymmetric staircase, although an advantage of the 6D1U staircase is that it uses a simpler well-established approach. However, a few practical considerations not incorporated into the simulations presented in this paper are worthy of consideration.
First, these simulations do not include lapses, errors that are independent of stimulus amplitude (Wichmann and Hill 2001a). In particular, a lapse at high amplitudes during the initial staircase for the MLE procedure would cause a large overestimate of threshold, which would cause later stimuli to be placed at inefficient levels. In contrast, a 3D1U or 4D1U staircase would recover quickly from the lapse. Second, if the initial stimulus level is much larger than the target level, the 6D1U staircase can take a large number of high-amplitude, low-information trials to converge to the target level. Finally, while bias impacted precision similarly for MLE, symmetric 6D1U and asymmetric 4D1U (Figure 11), we also presented results for a modification of the MLE procedure that places stimuli symmetrically around μ̂ . While this improves the precision of the threshold estimate, it results in the physical stimulus amplitude differing for each of the two motion directions, which can sometimes provide unwanted cues to the subject. For example, many motion devices vibrate proportionally to motion speed, and subjects could learn to use vibration intensity as a cue to determine motion direction (Chaudhuri, Karmali, and Merfeld 2013). Anecdotally, one subject we have tested has a vestibular bias that is approximately half the measured threshold and has suggested the ability to do so.
Acknowledgements
We appreciate the participation of our anonymous subjects. Marcos Mattana assisted with data collection. We thank Bob Grimes and Wangsong Gong for technical support. Harvard Orchestra provided high-capacity computation for simulations. This research was supported by the National Institute on Deafness and Other Communication Disorders (NIDCD) grants R01-DC04158, R56-DC12038 and R03-DC013635. Some of this work was previous described in an academic report of a Harvard School of Engineering and Applied Sciences undergraduate senior design project: Chaudhuri SE (2011) Protocol Design for Characterizing Vestibular Thresholds.
Footnotes
The Cramér-Rao bound - named for Harold Cramér and C.R. Rao, two of the first to derive it - defines the theoretic lower bound for the variance of estimated parameters. More can be learned at http://en.wikipedia.org/wiki/Cramer-Rao_bound
Indeed, Wetherill (1963) stated that “ we need the asymptotic properties of various strategies.”
The authors declare no competing financial interests.
Contributor Information
Faisal Karmali, Jenks Vestibular Physiology Lab, Massachusetts Eye and Ear Infirmary, Boston, MA, Department of Otology and Laryngology, Harvard Medical School, Boston MA, USA
Shomesh E. Chaudhuri, Jenks Vestibular Physiology Lab, Massachusetts Eye and Ear Infirmary, Boston, MA, Department of Electrical Engineering and Computer Science, MIT, Cambridge, MA
Yongwoo Yi, Jenks Vestibular Physiology Lab, Massachusetts Eye and Ear Infirmary, Boston, MA, Department of Otology and Laryngology, Harvard Medical School, Boston MA, USA
Daniel M. Merfeld, Jenks Vestibular Physiology Lab, Massachusetts Eye and Ear Infirmary, Boston, MA, Department of Otology and Laryngology, Harvard Medical School, Boston, MA, USA
Reference List
- Agrawal Y, Bremova T, Kremmyda O, Strupp M, MacNeilage PR. Clinical testing of otolith function: perceptual thresholds and myogenic potentials. J.Assoc.Res.Otolaryngol. 2013;14:905–915. doi: 10.1007/s10162-013-0416-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson AJ, Hutt EC, Brown SF. Thresholds for the perception of whole body angular movement about a vertical axis. Aviat.Space Environ.Med. 1989;60:205–213. [PubMed] [Google Scholar]
- Benson AJ, Spencer MB, Stott JR. Thresholds for the detection of the direction of whole-body, linear movement in the horizontal plane. Aviat.Space Environ.Med. 1986;57:1088–1096. [PubMed] [Google Scholar]
- Butler JS, Smith ST, Campos JL, Bulthoff HH. Bayesian integration of visual and vestibular signals for heading. J.Vis. 2010;10:23. doi: 10.1167/10.11.23. [DOI] [PubMed] [Google Scholar]
- Chaudhuri SE, Karmali F, Merfeld DM. Whole-body motion-detection tasks can yield much lower thresholds than direction-recognition tasks: implications for the role of vibration. J.Neurophysiol. 2013;110:2764–2772. doi: 10.1152/jn.00091.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri SE, Merfeld DM. Signal detection theory and vestibular perception: III. Estimating unbiased fit parameters for psychometric functions. Exp.Brain Res. 2013;225:133–146. doi: 10.1007/s00221-012-3354-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornsweet T. The staircrase-method in psychophysics. Am.J.Psychol. 1962;75:485–491. [PubMed] [Google Scholar]
- Cramér H. Mathematical methods of statistics. Princeton: Princeton University Press; 1946. [Google Scholar]
- Crane BT. Fore-aft translation aftereffects. Exp.Brain. Res. 2012a;219:477–487. doi: 10.1007/s00221-012-3105-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane BT. Roll aftereffects: influence of tilt and inter-stimulus interval. Exp.Brain Res. 2012b;223:89–98. doi: 10.1007/s00221-012-3243-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixon WJ, Mood AM. A method for obtaining and analyzing sensitivity data. Journal of the American Statistical Association. 1948;43:109–126. [Google Scholar]
- Efron B, Tibshirani RJ. An introduction to the bootstrap. New York: CRC press; 1994. [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature. 2002;415:429–433. doi: 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
- Firth D. Bias reduction of maximum likelihood estimates. Biometrika. 1993;80:27–38. [Google Scholar]
- Fisher RA. On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society of London. Series. 1922:A309–A368. [Google Scholar]
- Fisher RA. Theory of statistical estimation. Proceedings of the Cambridge Philosophical Society. 1925;22:700–725. [Google Scholar]
- Fletcher H. Physical Measurements of Audition and Their Bearing on the Theory of Hearing*. Bell System Technical Journal. 1923;2:145–180. [Google Scholar]
- Garcia-Perez MA. Forced-choice staircases with fixed step sizes: asymptotic and small-sample properties. Vision Res. 1998;38:1861–1881. doi: 10.1016/s0042-6989(97)00340-4. [DOI] [PubMed] [Google Scholar]
- Garcia-Perez MA. Optimal setups for forced-choice staircases with fixed step sizes. Spat.Vis. 2000;13:431–448. doi: 10.1163/156856800741306. [DOI] [PubMed] [Google Scholar]
- Garcia-Perez MA, Alcala-Quintana R. Bayesian adaptive estimation of arbitrary points on a psychometric function. Br.J.Math.Stat.Psychol. 2007;60:147–174. doi: 10.1348/000711006X104596. [DOI] [PubMed] [Google Scholar]
- Garcia-Perez MA, Alcala-Quintana R. Empirical performance of optimal Bayesian adaptive estimation. Span.J.Psychol. 2009;12:3–11. doi: 10.1017/s1138741600001426. [DOI] [PubMed] [Google Scholar]
- Garcia-Perez MA, Alcala-Quintana R. Shifts of the psychometric function: distinguishing bias from perceptual effects. Q.J.Exp.Psychol.(Hove.) 2013;66:319–337. doi: 10.1080/17470218.2012.708761. [DOI] [PubMed] [Google Scholar]
- Grabherr L, Nicoucar K, Mast FW, Merfeld DM. Vestibular thresholds for yaw rotation about an earth-vertical axis as a function of frequency. Exp.Brain Res. 2008;186:677–681. doi: 10.1007/s00221-008-1350-8. [DOI] [PubMed] [Google Scholar]
- Green DM. Stimulus selection in adaptive psychophysical procedures. J.Acoust.Soc.Am. 1990;87:2662–2674. doi: 10.1121/1.399058. [DOI] [PubMed] [Google Scholar]
- Guedry FE, Collins WE, Sheffey PL. Perceptual and oculomotor reactions to interacting visual and vestibular stimulation. Percept.Mot.Skills. 1961;12:307–324. [Google Scholar]
- Haburcakova C, Lewis RF, Merfeld DM. Frequency dependence of vestibuloocular reflex thresholds. J.Neurophysiol. 2012;107:973–983. doi: 10.1152/jn.00451.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall JL. Maximum-Likelihood Sequential Procedure for Estimation. J.Acoust.Soc.Am. 1968;44:370. [Google Scholar]
- Hall JL. Hybrid adaptive procedure for estimation of psychometric functions. J.Acoust.Soc.Am. 1981;69:1763–1769. doi: 10.1121/1.385912. [DOI] [PubMed] [Google Scholar]
- Hartmann M, Haller K, Moser I, Hossner EJ, Mast FW. Direction detection thresholds of passive self-motion in artistic gymnasts. Exp.Brain Res. 2014;232:1249–1258. doi: 10.1007/s00221-014-3841-0. [DOI] [PubMed] [Google Scholar]
- Harvey LO. Efficient estimation of sensory thresholds. Behavior Research Methods, Instruments, & Computers. 1986;18:623–632. [Google Scholar]
- Kaernbach C. Simple adaptive testing with the weighted up-down method. Percept.Psychophys. 1991;49:227–229. doi: 10.3758/bf03214307. [DOI] [PubMed] [Google Scholar]
- Kaernbach C. Slope bias of psychometric functions derived from adaptive data. Percept.Psychophys. 2001;63:1389–1398. doi: 10.3758/bf03194550. [DOI] [PubMed] [Google Scholar]
- Karmali F, Lim K, Merfeld DM. Visual and vestibular perceptual thresholds each demonstrate better precision at specific frequencies and also exhibit optimal integration. J.Neurophysiol. 2014;111:2393–2403. doi: 10.1152/jn.00332.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolev O, Mergner T, Kimmig H, Becker W. Detection thresholds for object motion and self-motion during vestibular and visuo-oculomotor stimulation. Brain Res.Bull. 1996;40:451–457. doi: 10.1016/0361-9230(96)00141-4. [DOI] [PubMed] [Google Scholar]
- Kollmeier B, Gilkey RH, Sieben UK. Adaptive staircase techniques in psychoacoustics: a comparison of human data and a mathematical model. J.Acoust.Soc.Am. 1988;83:1852–1862. doi: 10.1121/1.396521. [DOI] [PubMed] [Google Scholar]
- Kontsevich LL, Tyler CW. Bayesian adaptive estimation of psychometric slope and threshold. Vision.Res. 1999;39:2729–2737. doi: 10.1016/s0042-6989(98)00285-5. [DOI] [PubMed] [Google Scholar]
- Leek MR. Adaptive procedures in psychophysical research. Percept.Psychophys. 2001;63:1279–1292. doi: 10.3758/bf03194543. [DOI] [PubMed] [Google Scholar]
- Leek MR, Hanna TE, Marshall L. Estimation of psychometric functions from adaptive tracking procedures. Percept.Psychophys. 1992;51:247–256. doi: 10.3758/bf03212251. [DOI] [PubMed] [Google Scholar]
- Levitt HCCH. Transformed up-down methods in psychoacoustics. The Journal of the Acoustical Society of America. 1971;49:467–477. [PubMed] [Google Scholar]
- Lewis RF, Priesol AJ, Nicoucar K, Lim K, Merfeld DM. Abnormal motion perception in vestibular migraine. Laryngoscope. 2011;121:1124–1125. doi: 10.1002/lary.21723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim K, Merfeld DM. Signal detection theory and vestibular perception: II. Fitting perceptual thresholds as a function of frequency. Exp.Brain Res. 2012;222:303–320. doi: 10.1007/s00221-012-3217-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacNeilage PR, Banks MS, DeAngelis GC, Angelaki DE. Vestibular heading discrimination and sensitivity to linear acceleration in head and world coordinates. J.Neurosci. 2010;30:9084–9094. doi: 10.1523/JNEUROSCI.1304-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullagh P, Nelder JA. Generalized linear models. London: Chapman and Hall; 1989. [Google Scholar]
- Merfeld DM. Signal detection theory and vestibular thresholds: I. Basic theory and practical considerations. Exp.Brain Res. 2011;210:389–405. doi: 10.1007/s00221-011-2557-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakayama K, Tyler CW. Psychophysical isolation of movement sensitivity by removal of familiar position cues. Vision Res. 1981;21:427–433. doi: 10.1016/0042-6989(81)90089-4. [DOI] [PubMed] [Google Scholar]
- Pentland A. Maximum likelihood estimation: the best PEST. Percept.Psychophys. 1980;28:377–379. doi: 10.3758/bf03204398. [DOI] [PubMed] [Google Scholar]
- Rao CR. Information and the accuracy attainable in the estimation of statistical parameters. Bulletin of the Calcutta Mathematical Society. 1945;37:81–89. [Google Scholar]
- Roditi RE, Crane BT. Directional asymmetries and age effects in human self-motion perception. J.Assoc.Res.Otolaryngol. 2012a;13:381–401. doi: 10.1007/s10162-012-0318-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roditi RE, Crane BT. Suprathreshold asymmetries in human motion perception. Exp.Brain Res. 2012b;219:369–379. doi: 10.1007/s00221-012-3099-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y, Dai W, Richards VM. A MATLAB toolbox for the efficient estimation of the psychometric function using the updated maximum-likelihood adaptive procedure. Behav.Res.Methods. 2015;47:13–26. doi: 10.3758/s13428-014-0450-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soyka F, Robuffo GP, Beykirch K, Bulthoff HH. Predicting direction detection thresholds for arbitrary translational acceleration profiles in the horizontal plane. Exp.Brain Res. 2011;209:95–107. doi: 10.1007/s00221-010-2523-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor MM. On the efficiency of psychophysical measurement. J.Acoust.Soc.Am. 1971;49(Suppl-8) doi: 10.1121/1.1912379. [DOI] [PubMed] [Google Scholar]
- Taylor MM, Creelman CD. PEST: Efficient estimates on probability functions. The Journal of the Acoustical Society of America. 1967;41:782–787. [Google Scholar]
- Treutwein B. Adaptive psychophysical procedures. Vision Res. 1995;35:2503–2522. [PubMed] [Google Scholar]
- Treutwein B, Strasburger H. Fitting the psychometric function. Percept.Psychophys. 1999;61:87–106. doi: 10.3758/bf03211951. [DOI] [PubMed] [Google Scholar]
- Valko Y, Priesol AJ, Lewis RF, Merfeld DM. Contributions of the Vestibular Labyrinth to Human }Whole-Body Motion Discrimination. J.Neurosci. 2012;32:13537–13542. doi: 10.1523/JNEUROSCI.2157-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Trees HL, Bell KL, Tian Z. Detection Estimation and Modulation Theory, Detection, Estimation, and Filtering Theory. New York: Wiley; 2013. [Google Scholar]
- Watson AB, Pelli DG. QUEST: a Bayesian adaptive psychometric method. Percept.Psychophys. 1983;33:113–120. doi: 10.3758/bf03202828. [DOI] [PubMed] [Google Scholar]
- Watt RJ, Andrews DP. APE: Adaptive probit estimation of psychometric functions. Current Psychological Reviews. 1981;1:205–213. [Google Scholar]
- Wetherill GB. Sequential Estimation of Quantal Response Curves. Journal of the Royal Statistics Society B. 1963;25:1–48. [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Percept.Psychophys. 2001a;63:1293–1313. doi: 10.3758/bf03194544. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: II. Bootstrap-based confidence intervals and sampling. Percept.Psychophys. 2001b;63:1314–1329. doi: 10.3758/bf03194545. [DOI] [PubMed] [Google Scholar]
- Zupan LH, Merfeld DM. Interaural self-motion linear velocity thresholds are shifted by roll vection. Exp.Brain Res. 2008;191:505–511. doi: 10.1007/s00221-008-1540-4. [DOI] [PMC free article] [PubMed] [Google Scholar]