Abstract
Purpose
A new approach to mapping the flip angle quickly and efficiently in 3D based on the Look-Locker technique is presented.
Methods
We modified the accelerated 3D Look-Locker T1 measurement technique to allow rapid measurement of flip angle. By removing the inversion pulses and interleaving two radio frequency pulses with different amplitude, it is possible to fit directly for the true flip angle using a reduced number of parameters. This technique, non-inverted Double Angle Look-Locker, allows quick and efficient mapping of the flip angle in 3D.
Results
non-inverted Double Angle Look-Locker is validated in vitro against the actual flip angle imaging technique for a range of flip angles and T1 values. Flip angle maps produced with non-inverted Double Angle Look-Locker can be acquired in approximately 1 min, and are accurate to within 10% of the actual flip angle imaging measurement. It is shown to accurately measure the excited slab profile of several different pulses. An application to correcting in vivo DESPOT T1 data is presented.
Conclusion
The presented technique is a rapid method for mapping flip angles across a 3D volume, capable of producing a flip angle map in approximately 1 min.
Keywords: B1+ mapping, flip angle, RF inhomogeneity, actual flip angle imaging (AFI)
At high magnetic fields (≥ 3.0 T), human-sized volume-transmit radio frequency (RF) coils no longer produce uniform excitation of tissue. As the magnetic field increases, the wavelength of the excitation pulse decreases, and as it approaches the scale of the object being imaged, it becomes impossible to avoid destructive interference of the field (1). This leads to non-uniform excitation of the desired imaging volume. The problem exists in a wide variety of other imaging applications, anywhere the transmit coil has non-uniform sensitivity.
In the least obtrusive cases, this non-uniform excitation manifests itself as an intensity variation across the sample; however, when steady-state or quantitative imaging is considered, the problem becomes more serious. For qualitative imaging, differences in excitation angle may lead to different tissue contrast in different parts of the imaging volume, and for quantitative imaging methods that rely on accurate knowledge of the flip angle, for example DESPOT1 and DESPOT2 (2), variations in flip angle will lead to errors in the quantitative measurements.
The effect of non-uniform excitation on quantitative imaging data can be corrected using a measured excitation profile. The excitation profile itself can also be flattened with tailored RF pulses (3), or using both coil profiles and spatially selective pulses as in transmit SENSE (4,5). What all these approaches require is a map of the transmit coil excitation profile , which is most often determined by mapping the flip angle. Once the flip angle is known, converting to is relatively straight forward, especially if a hard pulse is used, although some techniques, such as the Bloch–Siegert method, map directly. For transmit SENSE in particular, for which a profile of each coil in the array is required, the flip angle mapping technique must also be fast to avoid adding an inordinate amount of time to the exam.
Several methods of mapping the flip angle exist. A number of these are based on the double angle method (6,7). These either require a long repetition time or use saturation pulses (8) to avoid T1 bias. Both lead to inefficient use of the available magnetization. A more general approach is to fit the signal over a wider range of applied excitation angles (9). These methods assume linearity of the transmitter, and are susceptible to slab and slice profile variations at the required large applied excitation angles. There are alternative methods that do not rely on the RF transmitter linearity assumption. These include a fast interleaved repetition time (TR) method (10), dubbed actual flip angle imaging (AFI), and encoding the flip angle using image phase (11–13).
The AFI method has emerged as a popular technique. It is relatively simple to implement, and extraction of flip angle information from the intensity images is straightforward. It does, however, work best at moderate to large flip angles (60° and above) and short repetition times (10). These conditions pose a significant challenge in terms of spoiling the transverse magnetization to avoid a biased estimate of the flip angle (14–16), especially when the sequence is run rapidly.
The Look-Locker technique (17) was initially conceived as a technique to rapidly measure the longitudinal relaxation time, T1. Instead of waiting for the longitudinal magnetization to fully recover before the next inversion time sample is taken, the Look-Locker technique acquires multiple low flip angle spoiled, gradient recalled (SPGR) echoes during the longitudinal recovery. In this way, samples at multiple post inversion (TI) time points can be acquired far faster than conventionally possible.
The Look-Locker technique was modified first into a 2D imaging technique (18), by adding imaging gradients to each sampling segment, and repeating the inversion sampling scheme multiple times to encode all the necessary lines of k-space. The technique was then further developed into the accelerated 3D Look-Locker sequence (19). Rather than producing one TI image for each RF pulse in the sampling train, multiple contiguous RF pulses can be used to accelerate the filling of one k-space, and the k-space acquisition segmented so that NTI “effective TI” images could be reconstructed from N pulses sampling the recovery curve, with NTI < N, leading to an acceleration factor NETL = N/NTI. The inversion-α-train combination must then be repeated Nshots = NkyNkzNTI/N times to fully encode 3D k-space.
Parker et al. (20) proposed a method for determining the flip angle by measuring the relaxation constant at multiple nominal flip angles related by a known ratio, and then minimizing the variation in the resulting T1 values. In the special case where the ratio between the flip angles is 2:1, we have previously shown that using the trigonometric double angle formula, a closed form solution for the flip angle can be formed based on the two transients (21,22). Alternatively, rather than two different flip angles to untangle T1 and α in the measurement, we have also shown that two different values for the sampling repetition time, τ can also be used (21,23).
Whereas the above approaches to mapping the flip angle using a Look-Locker approach rely on fitting the two transients independently, here we will investigate a new technique that omits the inversion pulses completely, and gathers interleaved transient recovery curves having a 2:1 ratio of excitation angles. This eliminates the need to make assumptions of inversion efficiency and makes it possible to fit both recovery curves simultaneously. We term this new method the “non-inverted double angle Look-Locker” method, or in short form, niDALL.
THEORY
In the approach to steady state, the RF pulses of the Look-Locker technique not only sample the longitudinal relaxation, but in so doing, also perturb it, leading to a modified or driven longitudinal relaxation time (19):
| [1] |
where α is the tip angle of the sampling pulses, and τ is the repetition time of the α pulses. is measured by least squares fitting of an exponential recovery equation (19):
| [2] |
to the sampled points, and from this, assuming the flip angle is known, T1 can be extracted. This technique is desirable as it provides the ability to measure T1 very quickly while still retaining the signal-to-noise ratio (SNR) efficiency of the gold standard inversion recovery technique (24).
The signal, S(t), will relax toward the value A from the value, B, the latter being a complicated term that depends on the inversion pulse accuracy, as well as characteristics of the previously applied α pulse train, including the delays required for the inversion pulse, and the inversion pulse efficiency (18,19,25). A is more straightforward, as the transient relaxes toward the spoiled steady-state value (19).
Measuring the T1 value using the Look-Locker technique relies on accurate knowledge of the flip angle. The exponential fitting itself contains sufficient information to determine this directly. Instead of fitting for , A, and B in Eq. [2] above, it is possible to fit for α and T1 directly by combining Eq. [2], and the exact expression for A and B (18). This approach, however, assumes that the flip angle ratio of the sampling pulse to the preparation pulse is known. Alternatively, the flip angle can be derived from two or more measurements of based on two different values for the sampling angle, α. The special case where α = α1 = α2/2 is known as the double angle Look-Locker approach (DALL) (21,22). Nothing need be assumed about the efficiency of the inversion. Instead, it is left as a free parameter when fitting A1, B1, and to the transient based on one flip angle and A2, B2, and to the second transient, and the combination of and is all that is required to derive the flip angle.
If the inversion pulse is left out entirely and the two flip angles for sampling the transient are interleaved, as shown in Figure 1, there is no need to keep extra free parameters in the data fitting to account for the unknown inversion efficiency. The end of one α train would thus act as the seed for the next, removing the need for inversion pulses entirely. The flip angle can still be extracted from the and measurements made by fitting to each transient independently as in the DALL technique. Alternatively, the two transients, S1 and S2, can be fit simultaneously using the exact expressions for the recovery.
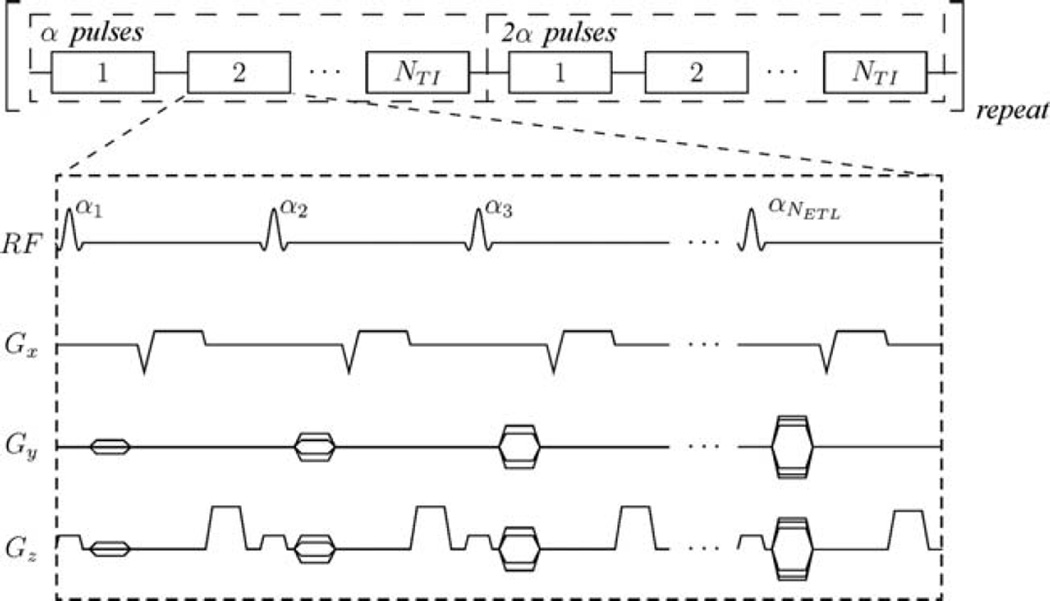
FIG. 1.
Timing diagram of the accelerated 3D niDALL sequence. N pulses along the recovery train are segmented into NTI effective TI volumes.
In the niDALL technique, the expressions for the two transients driven by α and 2α pulses are:
| [3] |
| [4] |
The two transients approach, but do not necessarily reach, the spoiled steady state values given by (19):
| [5] |
| [6] |
where Eτ = exp(−τ/T1). The starting value of each of the transients depends on the end state of the previous one. Once several repetitions of the α and 2α pulse trains are applied, a dynamic steady state will be reached, and each of the transients will start from B1 and B2 given by:
| [7] |
| [8] |
| [9] |
| [10] |
In this case, one train follows directly from the previous one, such that RF pulses are spaced by τ even at the boundary between the 1α and 2α trains. In the niDALL approach there is no need for inversion pulses, and thus assumptions of ideal inversion and negligible delays are removed. The expressions for B1 and B2 above become exact and no assumptions need to be made regarding the differing effectiveness of low tip angle and inversion pulses.
This makes it possible to directly fit three parameters: T1, α, and M0, to the combined theoretical transients S1 and S2. If Iα,i and I2α,i are the image intensities for the NTI image volumes based on the α and 2α sampling transients, the fitting of the two recovery curves means the minimization of the least squares parameter:
| [11] |
using the Levenberg–Marquardt algorithm.
Parameter Optimization
To find the optimum sequence timing and acquisition parameters, a Cramer–Rao analysis of noise propagation was performed. To achieve this, flip angle imaging efficiency was defined as the α to noise in the α map ratio (ANR) normalized by scan time:
| [12] |
Here Tseq = 2 · τ · NTI represents the effective sequence repetition time. The noise in the flip angle is found by computing the Fisher information matrix:
| [13] |
where the parameters are a1 = α, a2 = T1 and a3 = S0. The partial derivatives were solved using a symbolic math toolbox (MATLAB, The MathWorks, Natick, MA). The error matrix is then given by ε = β−1, and the noise in the flip angle would be given by:
| [14] |
It is then possible to vary the imaging parameters τ, α, N, and NTI to find the optimum choice in terms of flip angle mapping efficiency, Γ.
METHODS
All experiments were performed on a GE 3T human system using a transmit and receive quadrature head coil. In all niDALL experiments, eight dummy read-out trains were applied before imaging commenced to ensure the magnetization was in a dynamic steady-state. An RF spoiling scheme using a phase increment of 84° (26) was used to best approximate an ideally spoiled transient.
To produce the niDALL flip angle maps, the background was masked out using an intensity cut-off selected from the first post-inversion image. The two transients based on α and 2α sampling were then simultaneously fit by minimizing Eq. [11] to find the flip angle.
Spoiling Simulations
The error due to imperfect spoiling of the AFI method has already been significantly studied (15,16), and can largely be brought under control with an appropriate choice of RF and gradient spoiling. Imperfect spoiling in the case of niDALL will lead to non-exponential recovery curves (27), which will in turn propagate through the non-linear least squares fitting into the estimate of flip angle. This source of error was investigated by using Bloch simulations, implemented in Matlab (The Math-Works, Natick, MA), of the chosen spoiling scheme to track the magnetization in the approach to steady-state during the α and 2α trains. The flip angle was then fit to the simulated magnetization as discussed above for niDALL for the imaging and phantom parameters used.
Validation
A small cylindrical saline phantom (12 cm diameter) containing nine samples doped with NiCl to T1 values ranging from approximately 180 to 3000 ms was used to validate the proposed mapping techniques over a range of parameters. Such a small phantom is expected to show minimal artifact at 3 T.
T1 was measured using a 2D inversion prepared fast spin echo sequence, with a 128 × 128 imaging matrix over a field of view (FOV) of 12 cm, and acquired at TI = {50, 100, 150, 200, 300, 600, 1200, 2400, 4000} ms.
The imaging matrix for flip angle mapping was 42 × 42 in plane with 24 phase encodes in the slab selective direction, giving a resolution of approximately 3 mm × 3 mm in plane, with 10 mm thick slices. The accelerated 3D Look-Locker recovery was sampled with 192 RF pulses with repetition time minimized (τ = 3.7 ms) segmented into eight effective TI volumes. For DALL acquisitions, inversion was accomplished using a 16 ms, 2 kHz hyperbolic secant adiabatic inversion pulse (28), and the α pulses were 1 ms hard pulses. Inversion and α pulse amplitudes were initially set using the standard prescan for α = 6°, and then varied between 2° and 12° by modifying the transmit attenuation.
For comparison to the niDALL approach, an AFI map (10) based on the same imaging matrix and resolution as used for the niDALL experiments was acquired using the repetition times TR1/TR2 = 15/75 ms, and a nominal 36° flip angle. The accuracy of the techniques was investigated by repeating the niDALL approaches 10 times each to estimate the uncertainty in the measurements, and comparing the measured flip angle to the true flip angle. The true flip angle was calculated using a correction factor based on the AFI measurement:
| [15] |
for each of the sample sites.
Slab Selection
An important aspect of this technique is its inherent ability to map the flip angle in a fully 3D sense. Not only do wavelength effects produce a non-uniform field, leading to variations in flip angle, but coil geometries and RF pulse shapes also cause non-uniform excitation. Quantitative 3D techniques such as DESPOT or IDEAL are susceptible to all these sources of error, and as such, a technique capable of mapping the flip angle using exactly the same pulse as the method to be corrected would be useful. To investigate this property, a cylindrical, silicone oil phantom (29) (dielectric constant = 2.75) was chosen to minimize wavelength effects. It had a diameter of 16 cm and length of 27 cm with a T1 of 230 ms at 3 T. The imaging matrix was 40 × 40 in plane, with 40 phase encodes in the slab selective direction. The FOV in plane was 20 cm, and a 20 cm thick slab was acquired in the slab selective direction, giving 5 mm isotropic voxels.
Two different 800 ms, minimum phase pulses were investigated which included a 3 kHz bandwidth pulse and a 10 kHz bandwidth pulse, set to acquire an axial slab, with frequency encode perpendicular to the axis of the phantom. In addition to the shaped pulses, a 1 ms hard pulse was also used to excite the phantom, to give an RF profile independent measure of the flip angle. For this pulse, the frequency encode direction was set parallel to the axis of the phantom to prevent aliasing. The flip angle measured using the hard pulse could then be used to estimate the actual magnitude and act as a slab profile correction.
T1 Correction
The Look-Locker methods were tested as a flip angle correction technique for 3D variable flip angle T1 (DESPOT1) images in the head. Informed consent was obtained and the studies were done in accordance with the institutional research ethics board. The high resolution T1 images were acquired using 1 mm isotropic voxels (imaging matrix 220 × 220 × 160), TR = 9 ms, and αnom = 4° and 18° for a total scan time of approximately 11 min.
The flip angle mapping techniques investigated included niDALL and AFI. All were acquired with 5 mm isotropic voxels, and a matrix size of 44 × 44 × 32. In this way, the same volume, and the same RF pulse could be used to map the flip angle as used in the T1 mapping technique. The niDALL based method was acquired with αnom = 8°, τ = 3 ms with a total scan time of 1 min 10 sec using eight effective TI volumes. The AFI flip angle map was acquired with αnom = 40° using TR1/TR2 = 30/150 ms, with a scan time of approximately 4 min 30 s.
RESULTS
Parameter Optimization
The imaging sequence parameters were varied to find the set of parameters that would maximize the ANR efficiency for a range of flip angles using a Cramer–Rao lower bound analysis. These parameters were then inspected to find normalization factors that would allow general rules for optimum imaging parameters to be defined, and the results are presented in Figure 2. Provided that all the parameters are optimized, it was found that the ANR efficiency was independent of the nominal flip angle chosen.
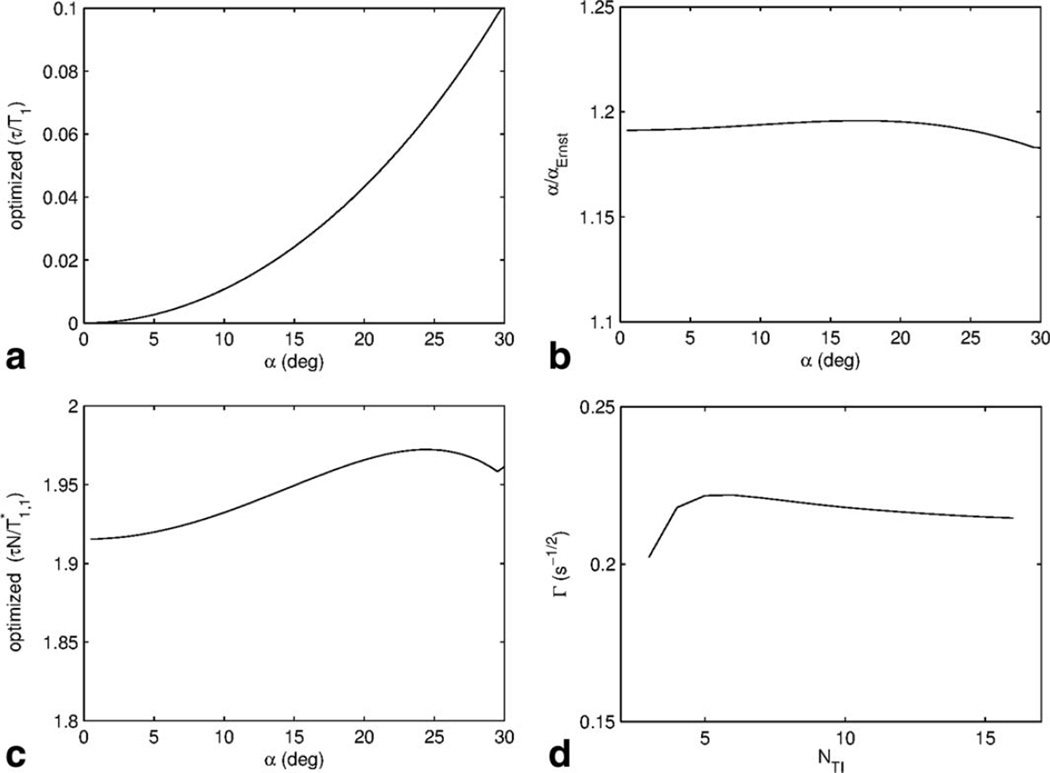
FIG. 2.
Parameters required to optimize the niDALL method. a: The optimum repetition time is lower with decreasing flip angle, which is related to the fact that the optimum ANR efficiency occurs for flip angles approximately 20% greater than the Ernst angle as indicated in (b). c: The number of α pulses used to sample the recovery is found by ensuring the duration of the sampling is approximately 1.9 times the driven T1. d: The number of effective TI times the recovery is divided into has little effect on the ANR efficiency.
Several interesting features can be observed from this analysis. The optimum repetition time increases with flip angle (Fig. 2a); however increasing the repetition time does not lead to an increase in ANR efficiency. Since a fast scan is generally desired, it is best to scan with the repetition time, τ, minimized, and then choose the optimum nominal flip angle based on Figure 2b, which indicates that it is best to operate with α near the Ernst angle. Once the minimum repetition time of the sequence is known, the best ANR will be achieved when α = 1.19 arccos(exp(−τ/T1)), or about 1.19 times the Ernst angle. While the goal is not to achieve steady state, the magnetization is constantly perturbed away from it. A value near the Ernst angle ensures a good amount of signal in the raw recovery images, but it is also important to ensure the transients are weighted by the flip angle. This occurs precisely when repetition times are kept short, or flip angles kept slightly elevated to ensure that the recovery constant, , is dominated by the term containing α.
NETL is chosen such that the duration of the transient is 1.93 times the driven T1, in other words, when (Fig. 2c). This value also corresponds to approximately . Typically when fitting transients for T1 it is best to sample out to 3–4.5 times T1 (24). In the case of niDALL, there are two transients involved, and , and a value of represents a compromise between the two. The total number of effective TI points (NTI) acquired has little impact on mapping efficiency (Fig. 2d). Below NTI = 5, the efficiency begins to fall off due to the number of degrees of freedom being too poor for a good estimate of α, but above this value, the additional effective TI volumes behave essentially like additional signal averages, and thus do not improve ANR efficiency. NTI = 8 generally provides sufficient SNR and dynamic range.
Phantom
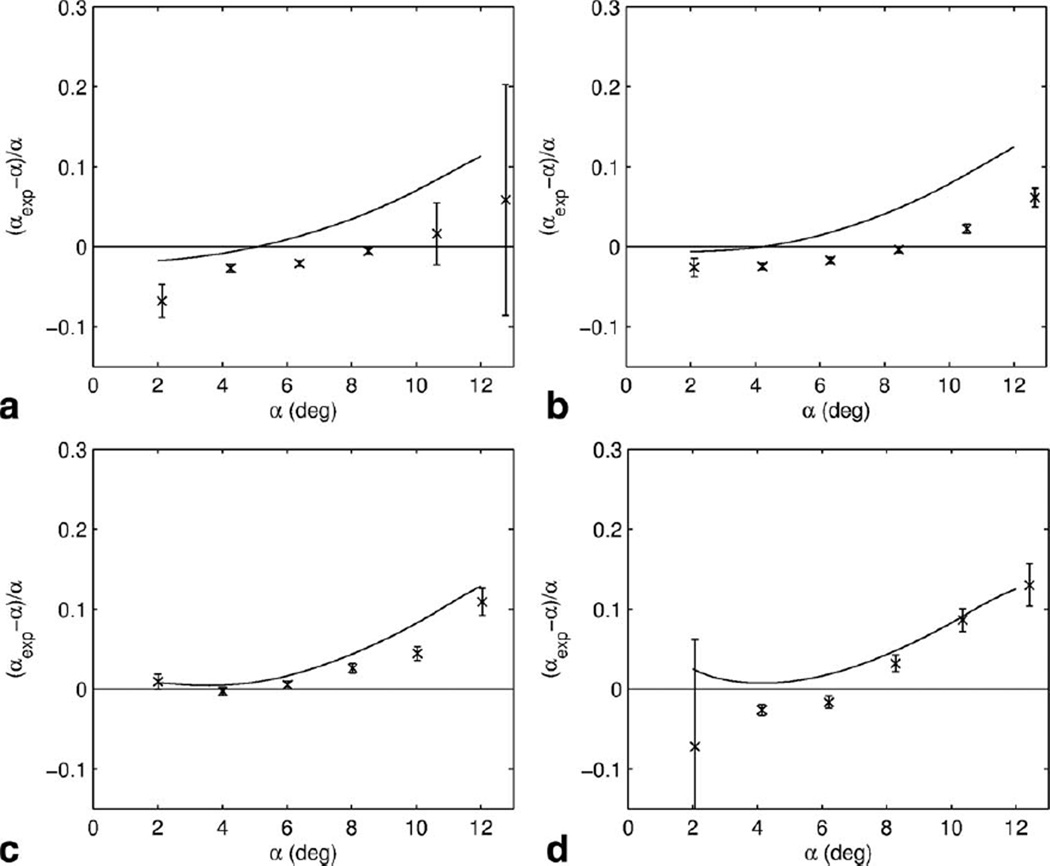
The precision and accuracy of the niDALL method was investigated in Figure 3 by plotting the relative flip angle error, based on multiple repeats of the image acquisition, against the true flip angle based on the AFI measurement. The flip angle as measured using the niDALL technique is within 10% of the AFI measurement for flip angles ranging from 2 to 10 degrees for the wide range of T1, values investigated in the phantom. The precision in the niDALL measurement is also worst at the extremes of the alpha range, as characterized by the error bars in Figure 3.
FIG. 3.
The accuracy of the non-inverted Look-Locker based flip angle mapping technique for T1/T2 values (a) 2953/61 ms, (b) 1283/58 ms, (c) 538/53 ms, and (d) 271/47 ms. The solid line represents the expected error due to imperfect spoiling as determined by Bloch simulations. The error bars are standard deviation based on multiple repeats.
The error due to imperfect spoiling of the transient investigated using Bloch simulations, and this predicted error is indicated by the solid lines in Figure 3. The measured bias of the niDALL measurement generally follows the same trend as that predicted by simulation, though there appears to be some vertical offset between simulation and experiment that is greater than that predicted by experimental uncertainty.
Slab Selection
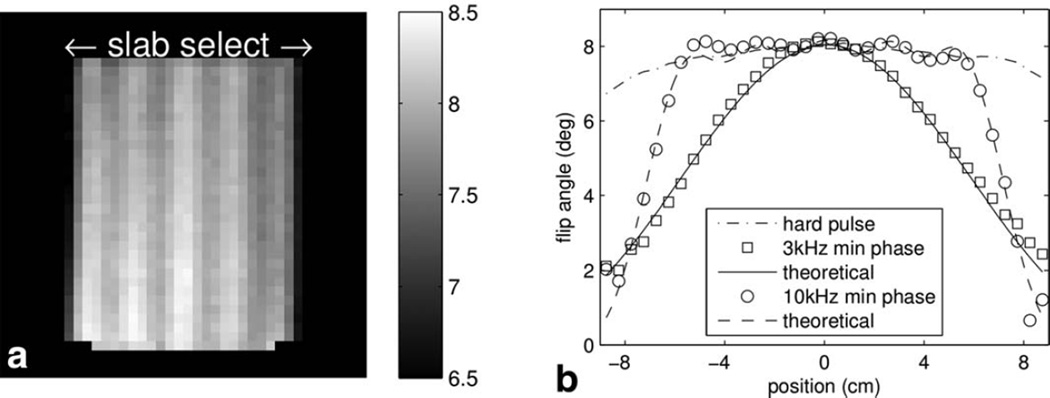
Full 3D maps of the flip angle were created of slabs excited using the three RF pulses described above. Theoretical slab profiles were calculated for the two shaped pulses using the prescribed slab thickness, the measured flip angle in the centre of the slab, and a smoothed version of the transmit coil profile as measured using the hard pulse as inputs to Bloch simulations. Figure 4a shows a flip angle image of the slab excited using the 10 kHz pulse. Despite the phantom extending outside the field of view in the horizontal direction, only the excited slab is visible in imaging, and here the contrast is set to highlight the ripple that is a result of the shaped pulse.
FIG. 4.
Sensitivity of niDALL method to slab selective pulses. a: Shows an image of the flip angle in degrees across the slab excited with the 10 kHz bandwidth pulse. Despite the phantom extending outside the imaged slab, only the excited slab is visible. (b) The experimentally measured slab profile matches the theoretical slab profile.
In Figure 4b, slab profiles are plotted based on a central voxel. The non-selective hard pulse profile remains relatively flat, only tailing off toward the ends of the coil. A second order polynomial was fit to the hard pulse profile for smoothing purposes. Bloch simulations were then used with the maximum observed flip angle, smoothed profile and prescribed slab thickness and overlaid with the experimentally measured slab profiles, showing very good agreement.
T1 Correction
Axial and sagittal slices through the 3D flip angle maps in the brain are shown in Figure 5. The data were collected assuming sagittal images using a slab selective pulse. Thus in the sagittal plane, there is approximately a 20% variation in flip angle due to wavelength effects. In the axial reformats, the profile of the slab selective pulse becomes apparent. This, combined with the wavelength effects, produces a nearly 50% variation in flip angle, primarily in the slab selective L/R direction.
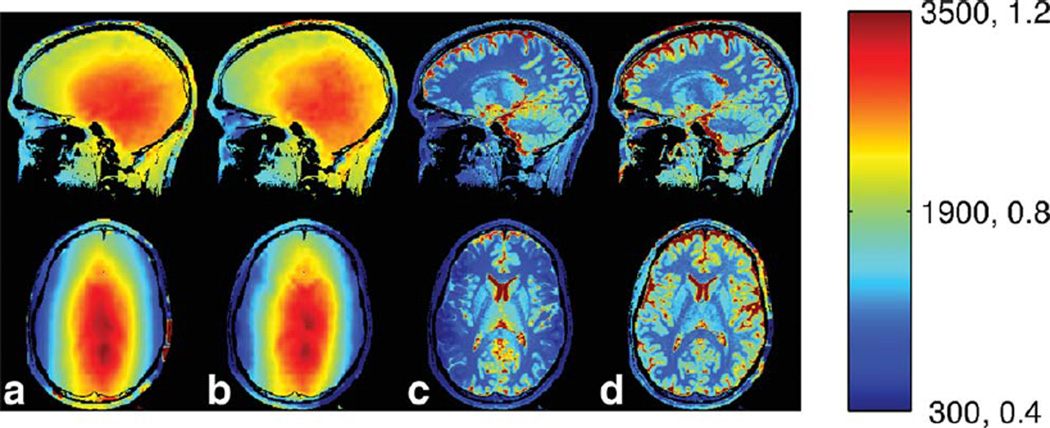
FIG. 5.
Flip angle and T1 maps for a sagittal acquisition (top row) and reformatted to axial (bottom row) in the head at 3 T. From left to right the methods of acquisition are (a) niDALL and (b) AFI. c: The T1 maps constructed from the DESPOT acquisition assuming the nominal flip angles throughout the head, and (d) the DESPOT T1 after being corrected with the niDALL flip angle. Units are in ms for T1 maps and α/αnom for flip angle.
In all these flip angle maps, the variation in flip angle is slow and smooth, as expected. In addition, there is only a slight indication of the cerebrospinal fluid in the ventricles, but otherwise there is no indication of the underlying anatomy, which is also expected. There is also good agreement between the different flip angle mapping techniques.
The T1 maps produced by the variable flip angle technique are presented in Figure 5c and d. The T1 map produced by assuming that the nominal 4° and 18° flip angles are achieved throughout is presented in Figure 5c. This produces an underestimation of T1 in the periphery of the brain due to the incorrect assumption of flip angle. This is most obvious in the axial image, but is also present in the sagittal image. If the flip angle is corrected using a map produced by the niDALL method in the middle column, the corrected T1 images in Figure 5d are produced. These have the slowly varying bias from the flip angle variation removed and correct T1 values throughout.
DISCUSSION
At the extremes of flip angle and/or T1 values, the inversion recovery curve will not be optimally sampled, and thus it will be difficult to derive a useful estimate of flip angle. niDALL recovery curves are optimally sampled with TI samples that extend to approximately 1.93 times (24). This source of error is apparent in Figure 3. At large flip angles and/or short T1 values, the becomes short and the recovery may be largely done by the acquisition of the second effective TI volume. For example, when imaged with a 12° RF pulse, the sample with T1 = 271 ms (Fig. 3d), has . The chosen imaging parameters have eight effective TI volumes that extend to 710 ms. As a result, the recovery is really only sampled by the first few TI volumes, and the precision suffers as a result. A smaller N and/or segmenting N into more TI volumes would be required to better sample the transient.
At the other extreme, low flip angles and/or long T1 values, too little of the inversion recovery curve will be sampled to derive a useful fit. For example, when imaged with a 2° RF pulse, the sample with T1 = 2952 ms, has , yet with the chosen imaging parameters, we are only sampling out to 710 ms, not enough to properly characterize this , and thus, the resulting niDALL flip angle measurement suffers as shown in Figure 3a. A larger N would be required to better sample the transient in this case.
The samples of the recovery curve, particularly at large flip angles, are not well described by an exponential function, and these deviations cannot be accounted for by system noise alone. These deviations are the result of the breakdown of spoiling, which leads to a non-exponential transient, and thus an inaccurate α derived from it (27). The Bloch simulations of the implemented spoiling scheme at the imaging parameters chosen for the phantom match the trends seen in the experimental results quite well in Figure 3, indicating that imperfect spoiling is the primary cause of the errors seen in the niDALL data. The spoiling seed value, 84°, was optimized for inversion recovery experiments, and a different value may be appropriate for niDALL.
The proposed method is based on a relatively low resolution acquisition and, as the flip angle varies slowly, a low resolution flip angle map is usually sufficient. The large voxels, however, may produce partial volume effects, and if multiple T1 species occupy the same voxel, multi-exponential curves might be expected. In the regime where niDALL is optimized (low repetition time and moderate flip angles) is dominated by the repetition time and flip angle, not T1, and as a result, even voxels with T1’s as different as 3 s and 100 ms can be shown through simulation to lead to at most a 3% underestimation of flip angle based on sampling with 6° pulses and τ = 3 ms.
The nominal flip angle for AFI (36°) was chosen because it was the largest value that could be obtained by adjusting transmit gain alone to achieve the smallest flip angles (2° for niDALL) and also the flip angle for AFI. Larger flip angles are generally more desirable for AFI, but this would necessitate using additional transmit gains.
As a result of the above, the niDALL approach has been shown to have good accuracy and precision. niDALL matches the flip angles measured using AFI (within 10%) across a large range of flip angles (2° – 10°) and T1 values (271–2952 ms). niDALL is also a rapid technique, capable of acquiring a 3D flip angle map in approximately 1 min, compared to 4 min for the AFI acquisition of the same resolution.
CONCLUSION
The accelerated 3D Look-Locker technique has been adapted to produce 3D flip angle maps. The 3D nature of the method allows it to map the flip angle variations arising from both wavelength effects and slab selective pulses, making it ideal for correcting quantitative 3D methods such as DESPOT at high main magnetic field values. Given the typically slow variation in flip angle, low resolution flip angle maps can be acquired over the whole brain volume in approximately 1 min, making this one of the faster mapping methods in existence.
REFERENCES
- 1.Van de Moortele P-F, Akgun C, Adriany G, Moeller S, Ritter J, Collins CM, Smith MB, Vaughan JT, Uğurbil K. B1 destructive interferences and spatial phase patterns at 7 T with a head transceiver array coil. Magn Reson Med. 2005;54:1503–1518. doi: 10.1002/mrm.20708. [DOI] [PubMed] [Google Scholar]
- 2.Deoni SCL, Peters TM, Rutt BK. High-resolution T1 and T2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magn Reson Med. 2005;53:237–241. doi: 10.1002/mrm.20314. [DOI] [PubMed] [Google Scholar]
- 3.Saekho S, Boada FE, Noll DC, Stenger VA. Small tip angle three-dimensional tailored radiofrequency slab-select pulse for reduced B1 inhomogeneity at 3 T. Magn Reson Med. 2005;53:479–484. doi: 10.1002/mrm.20358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Katscher U, Börnert P, Leussler C, van den Brink JS. Transmit SENSE. Magn Reson Med. 2003;49:144–150. doi: 10.1002/mrm.10353. [DOI] [PubMed] [Google Scholar]
- 5.Ullmann P, Junge S, Wick M, Seifert F, Ruhm W, Hennig J. Experimental analysis of parallel excitation using dedicated coil setups and simultaneous RF transmission on multiple channels. Magn Reson Med. 2005;54:994–1001. doi: 10.1002/mrm.20646. [DOI] [PubMed] [Google Scholar]
- 6.Insko EK, Bolinger L. Mapping of the radiofrequency field. J Magn Reson Ser A. 1993;103:82–85. [Google Scholar]
- 7.Stollberger R, Wach P. Imaging of the active B1 field in vivo. Magn Reson Med. 1996;35:246–251. doi: 10.1002/mrm.1910350217. [DOI] [PubMed] [Google Scholar]
- 8.Cunningham CH, Pauly JM, Nayak KS. Saturated double-angle method for rapid B1+ mapping. Magn Reson Med. 2006;55:1326–1333. doi: 10.1002/mrm.20896. [DOI] [PubMed] [Google Scholar]
- 9.Dowell NG, Tofts PS. Fast, accurate, and precise mapping of the RF field in vivo using the 180° signal null. Magn Reson Med. 2007;58:622–630. doi: 10.1002/mrm.21368. [DOI] [PubMed] [Google Scholar]
- 10.Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007;57:192–200. doi: 10.1002/mrm.21120. [DOI] [PubMed] [Google Scholar]
- 11.Oh CH, Hilal SK, Cho ZH, Mun IK. Radio frequency field intensity mapping using a composite spin-echo sequence. Magn Reson Imaging. 1990;8:21–25. doi: 10.1016/0730-725x(90)90207-i. [DOI] [PubMed] [Google Scholar]
- 12.Morrell GR. A phase-sensitive method of flip angle mapping. Magn Reson Med. 2008;60:889–894. doi: 10.1002/mrm.21729. [DOI] [PubMed] [Google Scholar]
- 13.Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. Magn Reson Med. 2010;63:1315–1322. doi: 10.1002/mrm.22357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin W, Song HK. Improved signal spoiling in fast radial gradient-echo imaging: applied to accurate T1 mapping and flip angle correction. Magn Reson Med. 2009;62:1185–1194. doi: 10.1002/mrm.22089. [DOI] [PubMed] [Google Scholar]
- 15.Nehrke K. On the steady-state properties of actual flip angle imaging (AFI) Magn Reson Med. 2009;61:84–92. doi: 10.1002/mrm.21592. [DOI] [PubMed] [Google Scholar]
- 16.Yarnykh VL. Optimal radiofrequency and gradient spoiling for improved accuracy of T1 and B1 measurements using fast steady-state techniques. Magn Reson Med. 2010;63:1610–1626. doi: 10.1002/mrm.22394. [DOI] [PubMed] [Google Scholar]
- 17.Look DC, Locker DR. Time saving in measurement of NMR and EPR relaxation times. Rev Sci Instrum. 1970;41:250–251. [Google Scholar]
- 18.Brix G, Schad LR, Deimling M, Lorenz WJ. Fast and precise T1 imaging using a TOMROP sequence. Magn Reson Imaging. 1990;8:351–356. doi: 10.1016/0730-725x(90)90041-y. [DOI] [PubMed] [Google Scholar]
- 19.Henderson E, McKinnon G, Lee T-Y, Rutt BK. A fast 3D Look-Locker method for volumetric T1 mapping. Magn Reson Imaging. 1999;17:1163–1171. doi: 10.1016/s0730-725x(99)00025-9. [DOI] [PubMed] [Google Scholar]
- 20.Parker DL, Christian BA, Goodrich KC, Alexander AL, Buswell HR, Yoon C. Improved accuracy in T1 measurements. Proceedings of the 6th Annual Meeting of ISMRM; Sydney, Australia. 1998. p. 2171. [Google Scholar]
- 21.Hsu J-J, Zaharchuk G, Glover GH. Rapid methods for concurrent measurement of the RF-pulse flip angle and the longitudinal relaxation time. Magn Reson Med. 2009;61:1319–1325. doi: 10.1002/mrm.21900. [DOI] [PubMed] [Google Scholar]
- 22.Wade T, Rutt BK. B1 correction using double angle Look-Locker (DALL). Proceedings of the 16th Annual Meeting of ISMRM; Toronto, Canada. 2008. p. 1246. [Google Scholar]
- 23.Wade T, Rutt BK. B1 correction using dual tau Look-Locker (DtLL). Proceedings of the 17th Annual Meeting of ISMRM; Honolulu, Hawaii, USA; 2009. p. 572. [Google Scholar]
- 24.Crawley AP, Henkelman RM. A comparison of one-shot and recovery methods in T1 imaging. Magn Reson Med. 1988;7:23–34. doi: 10.1002/mrm.1910070104. [DOI] [PubMed] [Google Scholar]
- 25.Nkongchu K, Santyr G. An improved 3-D Look–Locker imaging method for T1 parameter estimation. Magn Reson Imaging. 2005;23:801–807. doi: 10.1016/j.mri.2005.06.009. [DOI] [PubMed] [Google Scholar]
- 26.Epstein FH, Mugler JP, Brookeman JR. Spoiling of transverse magnetization in gradient-echo (GRE) imaging during the approach to steady state. Magn Reson Med. 1996;35:237–245. doi: 10.1002/mrm.1910350216. [DOI] [PubMed] [Google Scholar]
- 27.Wade T, McKenzie CM, Rutt BK. Transient RF spoiling for 3D Look-Locker acquisitions. Proceedings of the 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. p. 147. [Google Scholar]
- 28.Silver MS, Joseph RI, Hoult DI. Highly selective p/2 and p pulse generation. J Magn Reson. 1984;59:347–351. [Google Scholar]
- 29.Tofts PS, Barker GJ, Dean TL, Gallagher H, Gregory AP, Clarke RN. A low dielectric constant customized phantom design to measure RF coil nonuniformity. Magn Reson Imaging. 1997;15:69–75. doi: 10.1016/s0730-725x(96)00220-2. [DOI] [PubMed] [Google Scholar]