When physics takes over: BAR proteins and membrane curvature

Abstract

Cell membranes become highly curved during membrane trafficking, cytokinesis, infection, immune response or cell motion. Bin/amphiphysin/Rvs (BAR) domain proteins with their intrinsically curved and anisotropic shape are involved in many of these processes, but with a large spectrum of modes of action. In vitro experiments and multiscale computer simulations have contributed in identifying a minimal set of physical parameters, namely protein density on the membrane, membrane tension, and membrane shape, that control how bound BAR domain proteins behave on the membrane. In this review, we summarize the multifaceted coupling of BAR proteins to membrane mechanics and propose a simple phase diagram that recapitulates the effects of these parameters.

Physics of protein-membrane assemblies at large scales: beyond a structural description

Membranes are dynamic interfaces that separate a cell from its environment. They compartmentalize the cell’s contents, allowing for the coordination of biochemical reactions in space and time, which is essential for the life of a cell. They also take part in a host of dynamic cellular pathways, such as communication, division, infection, immune response, etc. [1]. From the structural point of view, the manifestation of membranes in biology is simply a consequence of partitioning water away from the hydrophobic lipid tails [2]. In other words, membranes are self-assembled, unlike enzymes whose DNA-programmed structure and the complex local stereochemistry a priori determines function. So, how do membranes acquire specific active roles in the cell? First, a lipid bilayer has remarkable material properties, setting it apart from other biomolecular assemblies. It resists bending and stretching deformations, much like a macroscopic elastic sheet (Box 1) [3]. At the same time, membranes are most often in a fluid phase, making their surface soft and permissive of the lateral diffusion of molecules. Another important aspect of a lipid bilayer is that the atomic-level interactions at the protein-lipid interface may have a profound effect on the large-scale behavior of the membrane [3].

BOX 1. Energy of the membrane with and without BAR proteins.

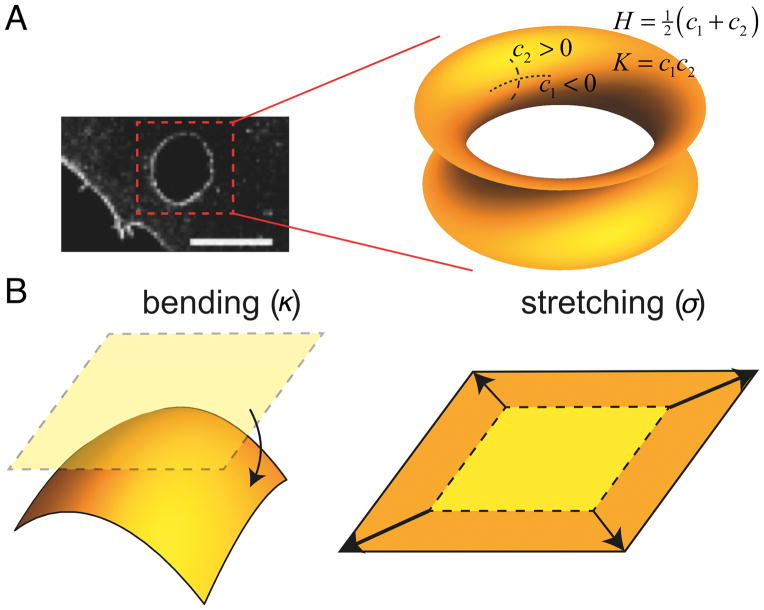
We highlight the physics of membranes decorated with BAR proteins. We focus on membrane tubules connected to a large, near-flat membrane/protein reservoir, relevant to the Golgi or endoplasmic reticulum, to ex/invaginations from the plasma membrane, or to controlled in vitro experiments on giant vesicles. Generally, the shape of the membrane can be described with two types of curvature: (1) mean curvature (H), defined by external observation and its sign arbitrarily assigned, and (2) Gaussian curvature (K), which is an intrinsic measure of curvature. Figure i, A illustrates these two types of curvatures on an example of a saddle-shaped membrane, such as found at the edges of a trans-cellular tunnel.

In the absence of proteins, a membrane is modeled as a thin elastic sheet, that undergoes bending and stretching deformations [59, 60]. Bending energy penalizes membrane curvature c = 1/R (R, radius of curvature) and is characterized by a bending stiffness κ. Membrane stretching energy penalizes in-plane stretching and is characterized by surface tension, σ (Fig. iB). In experiments on giant vesicles, σ is controlled by the aspiration pressure in the pipette holding the vesicle.

In the presence of BAR proteins, the membrane energy comprises two additional terms. First, there is an energy due to mismatch between the local membrane curvature and the intrinsic curvature of the protein, C̄. For very small protein surface densities (ϕ≪1%), this energy scales linearly with ϕ. Second, spatial inhomogeneities in a two-component system (lipids + proteins) cost mixing entropy. The total energy density of a tubule is therefore

$$\mathcal{F}=\frac{\kappa }{2R^2}+\sigma +\frac{{\kappa }_{\text{cm}}}{2}\varphi {\left(\frac{1}{R}-{\overline{C}}_p\right)}^2+f_{\mathrm{m}}(\varphi ),$$ (i)

where κ_cm is an elastic constant penalizing curvature mismatch and f_m is the mixing energy. Neglecting direct protein interactions (valid in dilute situations) f_m has the Flory-Huggins form:

$$f_{\mathrm{m}}(\varphi )=\frac{k_{\mathrm{B}}T}{a}[\varphi ln\varphi +(1-\varphi )ln(1-\varphi )],$$ (ii)

where k_B is Boltzmann’s constant and T is the temperature.

Without proteins, the R of a tubule with length L is found by minimizing 2πRLℱ (setting ϕ = 0) with respect to R, yielding $R=\sqrt{\kappa /(2\sigma )}$. Therefore, high κ favors wide and high σ favors small tubules. The force to hold the tubule, f, is found by minimization with respect to L, yielding $f=2\pi \sqrt{2\kappa \sigma }$. Thus, a linear dependence of f on σ^1/2 is a signature of lipid membrane-dominated behavior.

With proteins, the simplicity of Eq. i belies rich, nonlinear physics. The third term drives whereas the others oppose the coupling between protein density and membrane curvature. The dependence of ϕ on c, at equilibrium, is found by an expression similar to Eq. i for the near-flat reservoir (i.e., setting R=0), and balancing the protein chemical potentials between the vesicle (v) and the tubule (t), equivalent to ∂ℱ/∂ϕ_t = ∂ℱ/∂ϕ_v. Consequently, ϕ_t, R, and f are coupled, with R and f depending on κ, σ, and ϕ_v. The results depend strongly on ϕ_v:

• low densities: the sorting, S = ϕ_t/ϕ_v, is independent of ϕ_v, increases linearly with c for c ≪ C̄_p, and is maximum at c = C̄_p R and f, as a function of σ, are essentially given by the their protein-free values.

• high densities: S varies less quickly with c than at low densities. R is independent, and f varies linearly with σ, due to protein scaffolding on the tube.

Figure i.

Elasticity and curvature of the membrane. (A) An example of a highly curved membrane at the trans-cellular tunnel (scale bar: 5 μm, adapted from [43]), displaying a negative Gaussian or saddle-like curvature. (B) Basic elastic membrane deformations: bending (characterized by bending stiffness, κ) and stretching (characterized by membrane tension, σ)

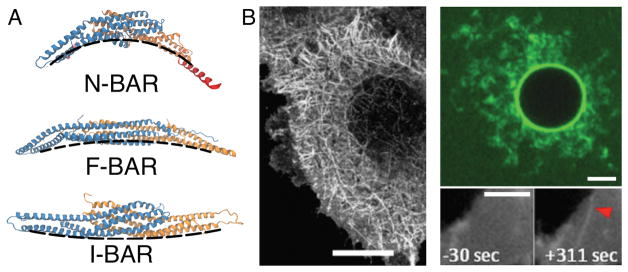
One of best-known regulators of cell membrane curvature is a family of proteins that contains a crescent-shaped Bin/amphiphysin/Rvs (BAR) domain (Fig. 1A) [4]. Numerous BAR proteins have been identified in the various parts of the cell (Fig. 2), however there are controversies surrounding their precise roles, often due to contradicting experimental evidence. Consider, for example, the N-BAR protein endophilin and its role in endocytosis, a process by which cells internalize extracellular material. Disrupting endophilin in some cases only results in minor quantitative effects on endocytosis [5], whereas in other cases, it detrimentally impacts the viability of the cell [6, 7]. These seemingly contradictory results, in part, can be attributed to the numerous endocytic pathways, typically involving different combinations of proteins. Thus, the internalization of cargos can be recovered by other BAR proteins or by using an entirely different route. For instance, it has been shown that endophilin can drive endocytosis used by several signaling proteins and by bacterial toxins [8, 9], different from the well-known clathrin-dependent pathway.

Figure 1. The structure and phenotype of BAR proteins.

(A) Representative members of the BAR protein family, each subunit differently colored. Shown are (top) endophilin A2 (red-colored N-terminal amphipathic helices were added by hand), (center) FCHo2, (bottom) IRSp53. Dashed lines are guides for the eyes showing the intrinsic curvature of the proteins. (B) Binding of BAR proteins induces membrane tubulation. (Left) overexpression of β2 centaurin (BAR), scale bar: 20 μm, adapted from [4], reprinted with permission from AAAS; (top right) incubation of giant unilamellar vesicles (composition DOPC:DOPS:DOPE = 1:1:1, molar ratio) with fluorescently labeled (green) 1 μM amphiphysin 1 (N-BAR), scale bar: 5 μm, adapted from [20]; (bottom right) recruitment of amphiphysin 1 (N-BAR) to the plasma membrane by a chemical trigger (initiated at time zero), scale bar: 2 μm, adapted by permission from Macmillan Publishers Ltd: Scientific Reports [19], copyright (2014).

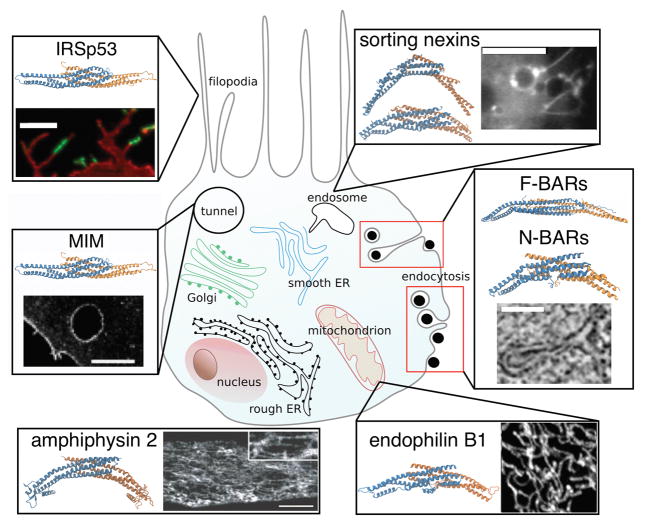
Figure 2. The biological role of BAR proteins.

Shown is a cartoon of a cell (not to scale) with a non-comprehensive list of BAR proteins found in various curvature-related phenomena. Counter-clockwise from top left: IRSp53 and other I-BAR proteins colocalize with filopodia. Fluorescence image shows an enrichment of fluorescently labeled (green) C. elegans I-BAR domain on filopodia, scale bar: 5 μm, adapted from [24], with permission from Elsevier, copyright (2009). MIM (I-BAR) is found enriched on the edges of trans-cellular tunnels formed by bacterial toxins. Image shows a tunnel with fluorescently labeled MIM, scale bar: 5 μm, adapted from [43], with permission from Elsevier, copyright (2011). Amphiphysin 2 (N-BAR) is crucial for the formation of T-tubules (tubular invaginations in the membrane of skeletal and cardiac muscles). Image shows the localization of fluorescently labeled endogenous amphiphysin 2 on differentiated myotubes, scale bar: 10 μm. Adapted from [11], reprinted with permission from AAAS. Endophilin B1 (N-BAR) is key for the formation of reticular membrane morphology of the mitochondrion. Shown is a mitochondrial network stained with anti-endophilin B1 antibody. Adapted from [53], copyright (2004) by The Journal of Cell Biology. A variety of BAR proteins colocalize with endocytosis, e.g. FCHo2, Syp1, Bzz1 (F-BARs) are found at early stages of endocytosis, syndapin (F-BAR), various amphiphysins, endophilins (N-BARs), and sorting nexin 9 (N-BAR-like protein) were found at later stages of endocytosis. Electron microscopy image shows an ultrastructure of a membrane invagination in the course of clathrin-mediated endocytosis in yeast. Scale bar: 100 nm. Adapted from [56], with permission from Elsevier, copyright (2012). Many sorting nexins (N-BARs) are found on endosomes. Shown are structures of sorting nexins 1 (top) and 9 (bottom). Image shows a membrane tubule budding from an endosome coated by fluorescently labeled sorting nexin 1. Scale bar: 10 μm. Republished with permission of the Company of Biologists Ltd., from [58], permission conveyed through Copyright Clearance Center, Inc.

Our main goal in this review is to bring attention to an aspect of complexity of protein-membrane interactions that is often overlooked in biology. The interaction between proteins and the membranes depends not only on their respective structures, but also on the physical state of the system, in particular the membrane shape, tension, and the protein density. The result of such interaction is that tuning just a few physical parameters can dramatically alter the way proteins interact with the membrane. For example, the surface density of the protein is one key parameter [10]: it has been shown in vivo that the density of the BAR protein amphiphysin 2, and consequently its membrane tubulation strength, strongly depend on a short sequence of charged residues [11]. These underlying dependencies on protein surface density and other physical parameters are often obscured by the complexity of the cell. Cell biology experiments use protein mutation or over-expression to elucidate their interactions with membrane, whereas in vitro experiments allow isolating the effect of changing a single parameter and measuring the corresponding protein-membrane response.

Before discussing the current understanding of the multifaceted action of BAR proteins on membranes, we first discuss mechanisms of generating cell membrane curvature and methods used to quantify this phenomenon.

Shaping biomembranes

Membrane curvature is essential for many aspects of cell’s viability [1]: (1), it permits forming the complex internal architecture, necessary for the operability of some organelles, (2), it enables dynamic tasks, and (3), it helps to control the spatial distribution of proteins and lipids [12]. In cells, there are multiple ways to generate curvature, usually by asymmetric lipid or protein composition. Consider a well-mixed lipid bilayer at equilibrium. If both layers have equal composition, it is expected to be as flat as possible. Enriching one layer with conically shaped lipids or transmembrane proteins expands the layer containing the bulkier moiety, hence generates curvature [1].

Some proteins bend the membrane by partly inserting an amphipathic motif into the bilayer [13, 14]. According to theoretical predictions, this mechanism is more complex than the stress exerted on the lipids by the conical inclusions, as the magnitude of spontaneous curvature non-monotonously depends on the insertion depth [15, 16].

Furthermore, biomembranes can be bent by the peripheral binding of some proteins. This mechanism can be explained in multiple ways: (a), each bound protein alters the underlying lipid organization, (b), proteins form a three-dimensional rigid network that imposes a shape as a mold, or (c), the membrane bends to maximize the distance between the crowded proteins [17].

Lastly, biomembranes can be reshaped by an energy-driven motion of molecular motors or by actin polymerization [1].

Structure of BAR proteins influences membrane shape

Each BAR protein contains one of many different BAR domains that usually vary in length, intrinsic curvature, and the binding affinity to the membrane (Fig. 1). BAR proteins also contain other variable domains, designed to target specific proteins and lipids, which makes each member functionally distinct and determines its localization in the cell [18].

Despite their high diversity, most BAR proteins cause a recognizable membrane phenotype, marked by large-scale tubulations of the cell membrane or that of synthetic liposomes (Fig. 1B) [4, 19, 20]. However, the direction of tubule growth and their radius relates to the structure of the BAR domain. Members of the classical BAR and N-BAR subfamily generate tubules, 20 to 60 nm wide, that grow toward the protein binding leaflet (defined as positive curvature) [18, 21]. Notable examples of classical BAR proteins are arfaptin and centaurin [4]. Most classical BAR proteins have an amphipathic helix, typically connected to the N-terminus—thus termed N-BAR proteins (Fig. 1A)—such as amphiphysin or endophilin, although in some members the amphipathic helix can be attached elsewhere in the structure, such as in sorting nexins [18, 22]. F-BAR proteins are characterized by having long and shallow BAR domains (Fig. 1A). They also couple with positive curvature, but induce wider tubules, with diameters from 60 to 100 nm [18, 23]. F-BARs do not contain amphipathic helices, although some members, like syndapin, display short loops that are thought to wedge into the bilayer. I-BAR proteins (Fig. 1A) couple with negative curvature, hence generate membrane protrusions. Some I-BARs contain amphipathic helices, like ABBA and MIM, although others, like IRSp53, do not [24].

In terms of the above-mentioned mechanisms, BAR proteins are thought to generate curvature by a combination of: (a), adhesion of the BAR domain, (b), shallow insertion of the amphipathic helices, and (c), under certain conditions, molding upon oligomerization.

Spectrum of BAR protein-membrane coupling

Regardless of the cellular processes in which BAR proteins participate (see Fig. 2), in vitro experiments and computer simulations, together provide a general framework for uncovering the physical principles that underlie how a collection of BAR proteins interact with membranes. Despite certain commonalities—BAR proteins all have a banana-shaped backbone—their distinctive marks (see previous section) require adapting the experimental technique. These methods probe the response of the system to changes in a few number of parameters, namely, (i) protein surface density, (ii) the mechanical properties of the membrane (e.g., surface tension or bending stiffness), and (iii) the geometry of the membrane (i.e., flat, spherical, or cylindrical curvature) (Box 1).

Studying the spectrum of curvature-coupled proteins demands a quantitative approach. Different from structure-focused and in vivo methods, reconstituting a minimal system in vitro allows us to systematically scan the effect on the membrane as a function of various physical parameters. This approach is usually complemented with analytical modeling and computational simulations to flesh out the underlying interactions responsible for the observed behavior. See Box 2 for an overview of quantitative approaches used to study membrane-reshaping phenomena. In the forthcoming sections, we discuss our current understanding of the mode of action of BAR proteins as a function of physical parameters.

BOX 2. Methods to study the coupling of proteins with membrane curvature.

To quantitatively study a cell phenomenon (e.g. endocytosis), we isolate a desired step (e.g. curvature sorting or membrane fission) and construct a controllable system, termed in vitro reconstitution. The disadvantage of this approach is that we neglect the important collective effect of numerous components, but the advantage is that we carefully control and measure the effect of many important parameters, such as protein concentration, lipid composition, surface tension, membrane geometry, etc.

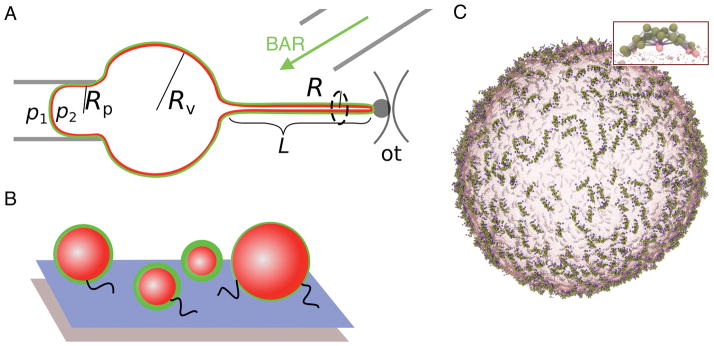
Giant unilamellar vesicles are commonly used as models of a quasi-flat membrane, as they are big enough (5–50 μm) to be observed by optical microscopy and they are amenable to micromanipulation (Fig. iiA). Protein surface density is measured from the fluorescence intensity [20, 61], while surface tension, σ, is set by the hydrostatic pressure inside the micropipette as [62]: $\sigma =(p_1-p_2)\frac{r_{\mathrm{p}}}{2(1-R_{\mathrm{p}}/R_{\mathrm{v}})}$, where p₁ and p₂ are pressures inside the pipette and vesicle, respectively and the radii are defined in Fig. ii, A. This method allows us to measure membrane’s elastic parameters and the correlation between protein’s surface density, membrane tension, and membrane reshaping from an initially flat topology.

Membrane tubules are extruded from giant vesicles by tethering a vesicle via streptavidin-biotin bonds to a micron-sized bead trapped with optical tweezers (Fig. iiA). The force to hold the tubule is calculated from bead displacement as f = k_OT(a − a₀), where k_OT is the stiffness of the trap and a and a₀ are, respectively, the current and the equilibrium bead displacement. The radius of the tubule can be measured from fluorescence intensity as $R~\frac{I_{\mathrm{l},\mathrm{t}}}{I_{\mathrm{l},\mathrm{v}}}$, where I_l,t and I_l,v are the lipid fluorescence intensities on the tubule and vesicle, respectively [20]. As shown in Box 1, the force and the radius of the tubule can be calculated independently, based on elastic theory, as $f=2\pi \sqrt{2\sigma \kappa }$ and $R=\sqrt{\kappa /2\sigma }$, where κ is the bending stiffness [63]. With another micropipette, fluorescently labeled proteins are injected near the system. Based on protein surface densities on the quasi-flat vesicle and on cylindrically curved tubule, the magnitude of protein sorting can be deduced as $S=\frac{I_{\mathrm{p},\mathrm{t}}/I_{\mathrm{p},\mathrm{v}}}{I_{\mathrm{l},\mathrm{t}}/I_{\mathrm{l},\mathrm{v}}}$, where I_p,t and I_p,v are protein fluorescence intensities on the tubule and vesicle, respectively. In the presence of the protein, many parameters may be changed, such as tubule radius or membrane-reshaping force.

Small vesicles report on the protein’s preference to spherical curvature. Vesicles (50–500 nm in diameter) are tethered via streptavidin-biotin bonds to a PEGylated surface, doped with a biotinylated polymer (Fig. ii, B). Surface density of the protein and the size of vesicles can be measured with fluorescence microscopy [37].

Coarse-grained simulations provide the finite-temperature dynamics of biomolecular systems by simulating the movement of each molecule, most often using Newton’s laws (the so-called molecular dynamics simulations). In these models, individual atoms are not resolved but are mapped into coarse-grained groupings that in turn interact through effective forces. Such simulations allow the study of much larger systems than with atomic-level simulations. Typically, we simulate μs timescales of near-μm systems (Fig. ii, C).

Figure ii.

Common methods to study curvature-coupled proteins. (A) Micropipette aspiration of giant vesicles and extrusion of membrane tubules by optical tweezers. (B) Tethered small vesicles. (C) Coarse-grained model of a lipid vesicle decorated with N-BAR proteins (magnified in inset).

Low-density behavior: assembly and curvature sensing

We first consider what happens when a low density of BAR proteins binds to an initially (near-)flat membrane such as a giant vesicle. Coarse-grained molecular dynamics simulations of N-BAR proteins bound to planar bilayers and large lipid vesicles (Box. 2, Fig. ii, C) have revealed the interesting result that N-BAR proteins assemble into string-like aggregates [25]. Due to the lack of explicit protein-protein attractions in the model, it appears that the effective interactions are solely mediated by the underlying membrane and, according to calculations, they have a very long range, comparable to the size of the protein [26].

It is difficult to isolate the precise physical force that drives the aggregation of BAR proteins. Prior numerical work has implicated the anisotropic interaction with the membrane [27] and the membrane-binding force [28] as key factors in generating the type of local curvature that can drive a one-dimensional assembly of membrane-embedded objects. Other factors could be at play, such as the Casimir effect, the hydrophobic mismatch, or the protein-membrane contact angle [29, 30]. Suppressing membrane fluctuations is therefore expected to inhibit the interactions among proteins. Indeed, simulations have shown that increasing surface tension decreases the effective inter-protein attraction strength and length scale, although interestingly it also determines the shape of aggregates (linear versus cluster-like). This observation is understood as a tradeoff between the cost of locally bending the membrane and the gain from protein-membrane binding force [26]. Therefore, in the cell, we expect the association of BAR proteins at low densities to depend on the presence of tension modulators, such as actin, and on the composition of the membrane. The most important biological implication is that BAR proteins can form long anisotropic aggregates even when very little protein is bound on the membrane (<10%), facilitating rapid protein recruitment to membrane-reshaping sites.

In many membrane-reshaping phenomena, curvature is induced by other factors, such as by cargo, by molecular motors or by other proteins in endocytosis [9, 31]. Hence, it is important to understand how BAR proteins interact with already curved membranes. An assay measuring the fluorescence intensity of proteins on membrane tubules connected to a giant vesicle (Box 2, Fig. ii, A) has shown that BAR proteins are sensors of membrane curvature. In particular, when the protein density on the quasi-flat surface of the vesicle is <5%, the density of BARs on the tubule can be ten to hundred-fold higher. Moreover, the magnitude of protein enrichment depends on the membrane curvature, known as curvature sorting of proteins [12, 32]. All tested BAR proteins so far have shown to be sorted on membrane tubules, namely amphiphysin [20], endophilin [33], BIN1 [34] (N-BARs), syndapin [35] (F-BAR), and IRSp53 [36] (I-BAR). The mechanical measurements have shown that BAR proteins in this concentration regime do not alter the natural dependence of membrane force on surface tension (see Boxes), although they nevertheless impose a spontaneous curvature in the membrane [20].

Surprisingly, there is evidence that the BAR domain itself, despite its curved shape, may not contribute to curvature sensing. Apparently, BAR proteins from different subfamilies are equally sorted on highly curved vesicles tethered to an inert surface (Box 2, Fig. ii, B), regardless of the sign and the magnitude of intrinsic curvature of the BAR domain. According to the experiment, their sorting only depends on the amphipathic helices [37]. One proposed explanation for this surprising result is that, unlike in the case of tubules connected to a vesicle, tethered vesicles do not have a lipid reservoir that would facilitate a rapid equilibration of protein density [38]. Another possibility is that the way proteins interact with the membrane depends on the geometry of the surface. Namely, it is conceivable that the anisotropic shape of a BAR domain prefers the anisotropic shape of a membrane cylinder on which it packs better. The amphipathic helices prefer spherical curvature, because this geometry promotes a high concentration of lipid packing defects (or in-plane stresses), sensed by amphipathic motifs [39–41]. Of note, amphipathic helices sense cylindrical curvature, as well [42].

The hypothesis that membrane geometry affects protein binding is a priori supported by the observed enrichment of an I-BAR protein MIM on the edge of a trans-cellular tunnel. The membrane on these tunnels has a saddle-shape topology, which displays both negative and positive curvature (Box 1, Fig. i, B), sensed by, respectively, the I-BAR domain and the amphipathic helix [43].

The underlying surface topology can even affect the atomic-level interactions with the proteins. An N-BAR protein endophilin penetrates deeper into the bilayer when bound to tubules, again possibly due to a preferred contact of the BAR domain with the cylindrical than the spherical membrane [44]. As a flat membrane primarily interacts with the amphipathic helices, a study has suggested that helices are responsible for curvature sensing at low protein concentrations, whereas the BAR domain takes over the role of controlling membrane curvature at high concentration [45]. Considering that the bound protein density was not measured in these studies and that there is experimental evidence that BAR proteins without amphipathic helices sense membrane curvature at low densities [35, 36], the role of helices versus the BAR domain in coupling with membrane curvature remains an unresolved issue.

Based on the large body of evidence from experiments on a membrane tubule connected to a lipid reservoir—a configuration characteristic of endocytosis—most, if not all, BAR proteins are sorted according to membrane curvature, regardless of the presence of amphipathic helices. The cell uses this mechanism to, under low surface densities, (a), rapidly enrich BAR proteins to membrane-reshaping sites and (b), control the spatial distribution of other biomolecules that bind to BAR proteins, such as dynamin [46], all without affecting the membrane mechanics.

High-density behavior: tubulation and scaffolding

At higher protein coverage on the membrane, long-range protein organization is strikingly altered, and the morphological changes to the membrane arise. Computational simulations on flat membranes have shown that at ~20% surface density, the proteins form a fully connected network. This assembly promotes the formation of membrane buds at the center of protein meshes [25] and it can lead to a tubulation of the membrane surface [47]. The important prerequisite for protein meshing is that the proteins couple with an anisotropic spontaneous curvature of the membrane [25, 47]. Interestingly, according to the simulations, if the spontaneous curvature imposed by bent objects has positive curvatures in both principal directions, linear aggregates can lead to tubular and disk-like instabilities, skipping the percolation step [47–49].

Experiments have shown that the onset of tubulation of a quasi-flat surface of a giant vesicle by endophilin (N-BAR) takes place above 5% protein density at vanishing tension. When tension is increased, the tubulation threshold requires a higher protein density and it is completely inhibited above 0.25 mN m⁻¹ [50]. Although this observation is a macroscopic effect of membrane mechanics, it could also be an effect of a tension-altered protein re-organization on a smaller scale [26]. The important biological implications are that (a), the local interactions of the protein with the membrane may significantly impact the global membrane morphology, and that (b), BAR proteins transition into tubulators at sufficient surface density and at low enough tension.

How do BAR proteins interact with already curved membranes? Under the same density regime, these proteins form an oligomer that coats a membrane tubule and alters its radius, independently of membrane tension [20]. Thus, when proteins coat a membrane tubule, they can either constrict or expand it. Due to the analogy to a framework at construction sites, we call this protein structure a scaffold. Another consequence of a scaffold is that it alters the natural dependence of the membrane force on surface tension (Box 1), which means that it affects the mechanical properties of the membrane [20]. The scaffold has been experimentally shown for amphiphysin [20] and endophilin [9] (N-BARs), whereas there is indirect evidence of scaffolding by syndapin (F-BAR) [35]. For amphiphysin it has been shown that the threshold density on the flat membrane above which it forms a scaffold on the connected tubule is ~5% [20]. Interestingly, the density on the vesicle (if above the scaffolding threshold) can be highly variable, however the density in the scaffold is always the same, measuring 25% for amphiphysin [20]. Importantly, this protein density is much lower than a near-complete coverage found in BAR domain coats resolved by electron microscopy [21, 23], and due to the configuration of the membrane it is likely relevant for endocytosis.

It seems that formation of a scaffold is a generic property of BAR proteins and only requires a sufficient density on the flat membrane connected to a tubule [20]. Likely, this threshold protein density can be shifted by the different intrinsic curvature presented by BAR domains and by the membrane tension. In cells, protein scaffolds serve to (a), constrict the neck of the endocytic bud; (b), help to elongate the neck such as in endophilin-mediated endocytosis [8, 9], and (c), prime the membrane for the last step in endocytosis, that is, fission [9].

Highest-density behavior or external pulling force: membrane fission

Incubating small vesicles (~200 nm) with a high concentration of BAR proteins usually results in the transformation of entire vesicles into tubules coated by proteins [21, 23]. Under the same conditions, a fraction of vesicles transform into an interconnected network of protein-coated tubules, as shown by a combined structural biology and multiscale computational study [51, 52]. These simulations have revealed that the mechanism of forming reticular membranes consists of first changing the membrane topology by strong in-plane stress variations, followed by folding of tubules into a reticular network by a high-density nematic protein assembly [51]. In these cases, membrane tubules are not directly connected to a protein-bound lipid reservoir, which likely permits a very high-density accumulation of proteins. Such mechanism is unlikely relevant for endocytosis, however its elements could help to explain the formation of reticular structures in the cell. For example, endophilin B1 (N-BAR) contributes to the formation of the tubular network in the mitochondrion [53], whereas amphiphysin 2 (N-BAR) helps to form the striated membranes in T-tubules [11] (Fig. 2). Importantly, based on these works, it appears that N-BAR proteins have fissiogenic capabilities at highest surface density.

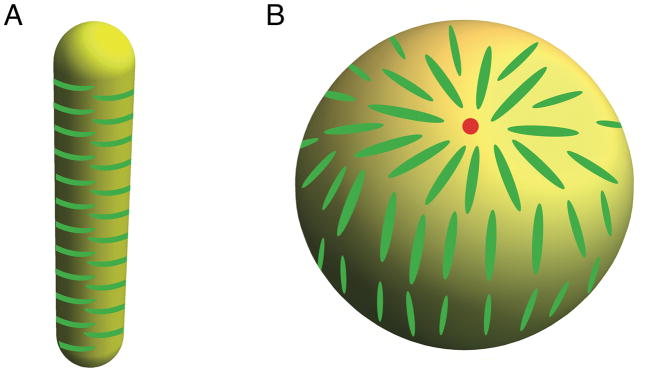
Incubating BAR proteins with small vesicles results in the fragmentation of the membrane, which is another important demonstration of fission by BARs. As the extent of membrane fragmentation directly correlates with the number of amphipathic helices per BAR domain, amphipathic helices are seen as a key factor driving fission [54]. By contrast, when BAR proteins are bound to preformed tubes, they either undergo sorting or form a scaffold, but they never induce fission [9]. This observation indicates that BAR proteins are unable to induce fission of membrane tubules in a static way. There are a few possible solutions to this paradox. As emphasized earlier, cylindrical geometry efficiently packs the rod-shaped BAR domain, thus stabilizing it; see Fig. 3, A. By contrast, high-density binding of BAR domains on small spherical vesicles would leave protein packing defects (Fig. 3, B), a mathematical result often known as the hairy ball theorem [55]. This issue may hypothetically have a destabilizing effect and contribute to fission. A complementary explanation is that the tubule geometry is a metastable state midway to fission and is stabilized by BAR proteins. As such, fission would eventually take place, but unlikely at the seconds time scales of endocytosis [8].

Figure 3. Influence of membrane geometry on BAR domain protein packing.

(A) Anisotropic, rod-shape proteins pack efficiently on a cylindrical membrane. (B) On a spherical vesicle, there are necessarily at least two aster-like packing defects (indicated by a red dot).

Fission of membrane tubules by N-BAR proteins may in fact be induced, but only after supplying an external pulling force that acts to elongate the scaffolded tubule [9]. It should be noted that this mechanism does not require a near-complete protein density; rather, the only prerequisite is that the proteins form a scaffold on membrane tubules. A simplified mechanism has been proposed so far. Due to a frictional force between the scaffold and the underlying lipids, continuous pulling of the tubule increases membrane tension, which would eventually lead to fission [9], for example by forming a hemifission state or by pore nucleation.

The dynamically observed fission provides a mechanism for the final step in endophilin-mediated endocytosis [9]. Furthermore, it implicates an unforeseen collaboration between BAR proteins and molecular motors, such as dyneins walking on microtubules, which supply the pulling force in endocytosis [31]. It could also help to explain the fission in the clathrin-mediated endocytosis in yeast that only relies on actin polymerization (the source of the pulling force) and BAR proteins; namely, two amphiphysin proteins, Rvs161 and Rvs167 (N-BARs) [56], and in one case an F-BAR protein Bzz1 [57].

Concluding Remarks

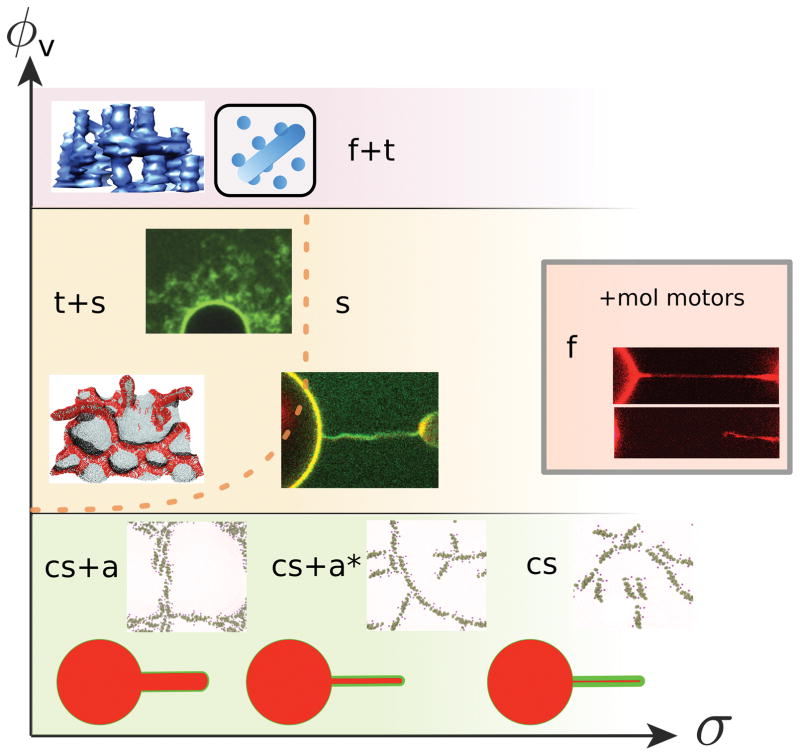
BAR domain proteins participate in multifaceted membrane-reshaping processes in cells. The results of current quantitative and in vitro approaches to this problem can be summarized by a schematic phase diagram, shown in Figure 4. There are two important parameters that can be controlled: the reservoir protein density, ϕ_v, and the membrane tension, σ (or equivalently for tubules, the curvature 1/R). The position in this diagram, defined by ϕ_v and σ, determines whether the same protein acts as a curvature sensor or as a generator (Fig. 4).

Figure 4. Phase diagram illustrating the coupling between BAR protein density and membrane mechanics.

Qualitatively different behaviors are found depending on position of the phase space spanned by the protein density, ϕ_v, on the membrane reservoir and the membrane tension, σ. The phase boundaries are schematic and their position will change depending on the intrinsic curvature of the protein, C̄_p. The different phases correspond to different behaviors protein-membrane system: cs = curvature sorting, a = linear assembly and netting, a* = disrupted linear assembly, t = tubulation, s = scaffolding, f = fission. The dashed line approximates the tension-inhibited onset of tubulation observed in [50]. The grey-framed inset represents high-density behavior of BAR proteins with added molecular-motor activity [9]. Image in f+t phase reprinted from [51], with permission from Elsevier, top image in t+s phase adapted from [20], bottom image in t+s kindly provided by Hiroshi Noguchi, image in s phase generated in our group, showing the stabilization of a membrane tubule by a BAR protein, as in [9, 20], method described in Box 2, image in f phase adapted from [9], images in the lowest-density part of the phase diagram, showing N-BAR protein assembly on a flat membrane, adapted from [26].

This diagram provides a roadmap for future work (see Outstanding Questions). Technical advances in experiments in vitro will focus on two areas: higher resolution in imaging, and high throughput analysis of curvature sensing for different membrane geometries. Biologically, one challenge will be to decipher how the cell controls the region of the phase diagram in which it operates, and how it moves between the different regions. Moreover, BAR domain proteins exist in vivo with a spectrum of intrinsic curvatures, comprising positive, negative, and zero values. It remains to be understood why the cell requires such a large variability in shape among proteins in the BAR domain family.