A generating function approach to HIV transmission with dynamic contact rates

Abstract

The basic reproduction number, R₀, is often defined as the average number of infections generated by a newly infected individual in a fully susceptible population. The interpretation, meaning, and derivation of R₀ are controversial. However, in the context of mean field models, R₀ demarcates the epidemic threshold below which the infected population approaches zero in the limit of time. In this manner, R₀ has been proposed as a method for understanding the relative impact of public health interventions with respect to disease eliminations from a theoretical perspective. The use of R₀ is made more complex by both the strong dependency of R₀ on the model form and the stochastic nature of transmission. A common assumption in models of HIV transmission that have closed form expressions for R₀ is that a single individual’s behavior is constant over time. In this paper we derive expressions for both R₀ and probability of an epidemic in a finite population under the assumption that people periodically change their sexual behavior over time. We illustrate the use of generating functions as a general framework to model the effects of potentially complex assumptions on the number of transmissions generated by a newly infected person in a susceptible population. We find that the relationship between the probability of an epidemic and R₀ is not straightforward, but, that as the rate of change in sexual behavior increases both R₀ and the probability of an epidemic also decrease.

1. Introduction

Human Immunodeficiency Virus (HIV) will elude control until we fully understand the theoretical conditions that allow it to persists in populations. Epidemiological models that assume mass-action dynamics have been informative for other sexually-transmitted infections (STI) [10]. However, those models are not well suited to understand the effects of variation in individual-level risk factors over time that drive the spread of HIV [28]. For example, prior models often assumed that high-risk people remain high-risk, forming a core of infected people that are the source of many new infections. While the assumption of stable behavior over the course of an infection might be reasonable for short-lived infections, an HIV infected individual under proper medical care can live for decades. Our theoretical models of HIV transmission need to be able to account for the real possibility of time-variable behavior at the individual-level over such long periods. In this paper we relax the assumption of constant behavioral patterns by introducing a simple model of HIV transmission that allows individuals to change their contact rate over time.

Contact rate heterogeneity (CRH), the variability in the distribution of sexual contact rates, has been recognized since Anderson’s 1988 paper as a key deviation from the homogeneous susceptible-infected (SI) models that typically describe STIs [1]. Empirical measurements of sexual contact rates by Halkitis et al. show more extreme values than homogeneous behavior assumptions would predict, because many people abstain from sex, while others are active to varying degrees [7]. Highly-active individuals comprise a large proportion of sexual contacts, skewing the contact rate distribution. Anderson and May calculated a closed form expression for the basic reproduction number in a susceptible-infected-removed (SIR) model with simple contact rate heterogeneity [2], showing that the basic reproduction number increases with increasing variance in the contact rate distribution. Contact rate heterogeneity makes elimination of the disease more challenging than would be expected in a homogeneous system with an equivalent average contact rate. Kretzschmar et al. showed how a small population of highly sexually-active individuals can define a core group within which transmission is maintained in the population [13].

Our model extends the formulation of CRH in Anderson and May by allowing individuals to re-sample their contact rate over time. We refer to this re-sampling of contact rates over time as contact rate volatility, CRV. In our formulation, the core group still exists, but it is populated by individuals experiencing brief episodes of high-risk behavior. Variation in individual-level contact rates could take many forms: slow-changing secular trends, faster periodic fluctuations that may correspond to partnership dynamics, and aperiodic random changes in sexual activity. We only deal with random fluctuations in contact rates here, characterized by a constant probability of resampling a new contact rate. This model is not indented to correspond to a particular population but rather illustrates the effects of contact rate volatility on the ability of HIV to establish and spread in a population.

In this paper we introduce CRV into the theory of stochastic branching processes to study the early epidemic behavior of an HIV epidemic. Probability generating functions (PGFs) were used to derive expressions for the random number of infections generated by newly-infected individuals in a susceptible population. We calculated the basic reproduction number, the variance in the number of transmission caused by a newly infected individual, and the probability of an epidemic given a singular introduction (as in Newman [20]).

2. Methods

2.1. Analytical approach

We approached this problem by deriving probability generating functions to express the probability that a newly infected individual generates a given number of infections, a random variable that we refer to as H_*. Generating functions have been successfully applied to a wide variety of infectious disease epidemiology problems, including configuration model contact networks [17, 26, 19]. This approach, although analytically tractable in many situations, cannot capture the complex non-linear infection dynamics over the course of the entire epidemic. We limit the scope of this paper to statistics that we can derive from the properties of the early epidemic. We find closed-form expressions for E(H_*), also known as the basic reproduction number, and Var(H_*), as well as a numerical solution for the probability of an epidemic given a singular introduction into the population.

2.2. Nomenclature

All of the random variables used in this paper and their generating functions are listed in table 1. Transmission model parameters are listed in table 2. H is defined as the number of transmissions made by a individual selected with uniform probability in a fully susceptible, large population. H_* is defined as the number of transmissions made by a individual selected with probability proportional to their contact rate in a fully susceptible, large population. The expectation of H_* gives the standard definition of the basic reproduction number as defined by Anderson and May [2], which we will refer to as R_*. Random variables are indicated with uppercase letters and generating functions of those variables use the corresponding lowercase letter with a dummy variable z. We will distinguish between contact rates of individuals selected at random from the population and individuals selected with probability proportional to contact rates. In the latter case, we will denote random variables with the symbol.

Table 1.

Random variables

Variable	Type	Description	Generating function
I1	Geometric	Total number of behavioral intervals in the first stage	$\frac{{\varphi }_1}{1-(1-{\varphi }_1)z}$
I2	Geometric	Total number of behavioral intervals in the second stage	$\frac{{\varphi }_2}{1-(1-{\varphi }_2)z}$
X̃	Gamma	Contact rate primary interval	$\frac{{(1-\theta \text{ log}(z))}^{-k}}{1-\theta \text{ log}(z)}$
X	Gamma	Contact rate secondary intervals	(1 − θ log(z))−k
T1	Exponential	Interval duration during acute stage	${(1-\frac{\text{log}(z)}{{\lambda }_1})}^{-1}$
T2	Exponential	Interval duration during chronic stage	${(1-\frac{\text{log}(z)}{{\lambda }_2})}^{-1}$
C̃1	Poisson	Number of transmissions in the primary interval in the acute stage
C̃s	Poisson	Number of transmissions in the primary interval in the spanning stage
C̃2	Poisson	Number of transmissions in the primary interval in the chronic stage
C1	Poisson	Number of transmissions in a non-primary interval in the acute stage
Cs	Poisson	Number of transmissions in a non-primary interval in the spanning stage
C2	Poisson	Number of transmissions in a non-primary interval in the chronic stage

Table 2.

Transmission parameters

Parameter	Description
θ	Gamma shape parameter for contact rate distribution
k	Gamma scale parameter for contact rate distribution
ρ	Contact rate volatility parameter
δ1	Rate of progression from acute to chronic stage
δ2	Rate of progression from chronic stage to death
ω	Natural removal rates
ε	Entry rate
β1	Transmissibility per acute contact
β2	Transmissibility per chronic contact
λ1 = ω + ρ + δ1	Rate that an acute interval terminates
λ2 = ω + ρ + δ2	Rate that an chronic interval terminates
ϕa = 1 − ρ/λ1	Probability that an acute interval ends in removal or progression
ϕc = 1 − ρ/λ2	Probability that a chronic interval ends in removal

2.3. Stochastic branching processes

The work in this paper is based on the theory of stochastic branching processes [12] developed by Harris [8] and Athreya and Ney [3]. A stochastic branching process is a Markov process that models the probability of observing a population of a given size, at generation n + 1, given the current number of individuals and a known probability distribution of offspring per generation for each individual. Branching processes can likewise describe the early dynamics of epidemics, as done by Ball [4], but this approximation becomes poor as the epidemic progresses due to the depletion of available susceptible hosts. However, branching processes are ideal for calculation of key quantities such as R_*, the initial growth rate, and the probability of observing an epidemic, which are properties of the early epidemic when the number of infected persons is very small.

Stochastic branching processes are analytically treated by the use of probability generating functions (PGFs). For a discrete random variable X with probability mass function Pr(x), the PGF of X is defined as

$$G_X(z)=E(z^X)=\sum _x^{\infty }\text{Pr}(x)z^x$$

and as ∫ Pr(x)z^xdx for a continuous random variable. The properties that we rely on for our derivations are listed below.

• G_X(1) = Pr(x₁)1^x₁ + Pr(x₂)1^x₂ + ⋯ + Pr(x_f)1^x_f = 1

• $G_X^{\prime }(1)=1\text{ Pr}(1)+\cdots +n\text{ Pr}(n)=\mathbf{E}(X)$

• The higher central moments can be calculated by further differentiation and algebraic manipulation. For example $\mathbf{\text{Var}}(X)=G_X^{″}(1)+G_X^{\prime }(1)-{[G_X^{\prime }(1)]}^2$

• The sum of a sequence of independent random variables, S = X₁ + X₂ + ⋯ + X_n can be represented as the product of n generating functions: $G_S(z)=\mathbf{E}(z^{{\sum }_i^n{X}_i})={\prod }_i^n{G}_{X_i}(z)$

• If n itself is a random variable, then the sum of random variables, S = X₁ + X₂ + ⋯ + X_n, is generated by G_Sn(z) = G_n(G_s(z))

2.4. Infection model

Both the viral titre [22] and the per act transmission probability [25, 27, 11, 23] are variable over the course of infection. We reflect this variability in the natural history of infection by splitting the course of an infection into two distinct stages. The acute stage immediately follows infection and is characterized by a short average duration, ${\delta }_1^{-1}$, and high contagiousness, β₁; the chronic stage follows the acute stage and is characterized by a long average duration, ${\delta }_2^{-1}$, and low contagiousness, β₂. The optimal number of infection stages to represent the natural history of infection remains under debate; Bezemer et al. and Longini et al. have argued that more than two infection stages are required to model the epidemic [5, 15]. Adding stages to our infection model is straightforward, but the algebra rapidly becomes cumbersome, obscuring the distinctiveness of CRV. Two stages enable us to capture the essence of the natural history of HIV and make it possible to represent the analysis in a concise way.

2.5. Contact rate heterogeneity and volatility model

Survey data reviewed by Anderon and by Liljeros et al. suggests that both sexual contact rates and partnership formation rates are heterogeneous between individuals [1, 14]. There exists growing evidence that contact rates too are heterogeneous within individuals over time (discussed in Romero-Severson et al. [24]). The contact rate heterogeneity model that we use in this paper attempts to integrate heterogeneity at both the population level between individuals and at the individual level over time.

We model the population distribution of contact rates at time t as X_t ~ Γ(k, θ) such that a randomly selected individual will have contact rate greater than or equal to x as $\text{Pr}(X\le x)=\gamma (k,\frac{x}{\theta })\mathrm{\Gamma }{(k)}^{-1}$. Our analysis is focused on the early epidemic period, so we assume that k and θ are constant over time, which is equivalent to a stationary secular trend in a large population. We modeled population-level heterogeneity as a Γ random variable for two primary reasons. First, the Γ distribution has a convergent closed form for its probability generating function, making it easier to find closed form expressions for the normalized moments of H_*. Second, the Gamma distribution phenomenologically captures several of the features of observed contact rate distributions such as long tails and a high degree of positive skew. Also, at certain parameterizations, this type of between individual heterogeneity can be easily simulated using the traditional compartmental models that are common in epidemiology.

Individuals experience periods of stable behavior (a behavioral interval), i.e., their contact rates are constant over the duration of a behavioral interval. At the beginning of a new interval, an individual re-draws a new contact rate from the population distribution. Figure 1 shows each possible type of behavioral interval based on in which infection state they occur. Termination of a behavioral interval occurs at the same rate for all individuals such that the length of behavioral intervals are exponentially distributed. The contact rate volatility model has a single parameter, ρ, that defines the rate that behavioral intervals terminate. The volatility model could be made more sophisticated by considering multiple types of behavioral intervals with different lengths, correlated contact rates, or periodicity in trend. However, more complex models not only get away from the fundamental effects of volatility on the statistics we are interested in, but they also make closed-form solutions less obtainable.

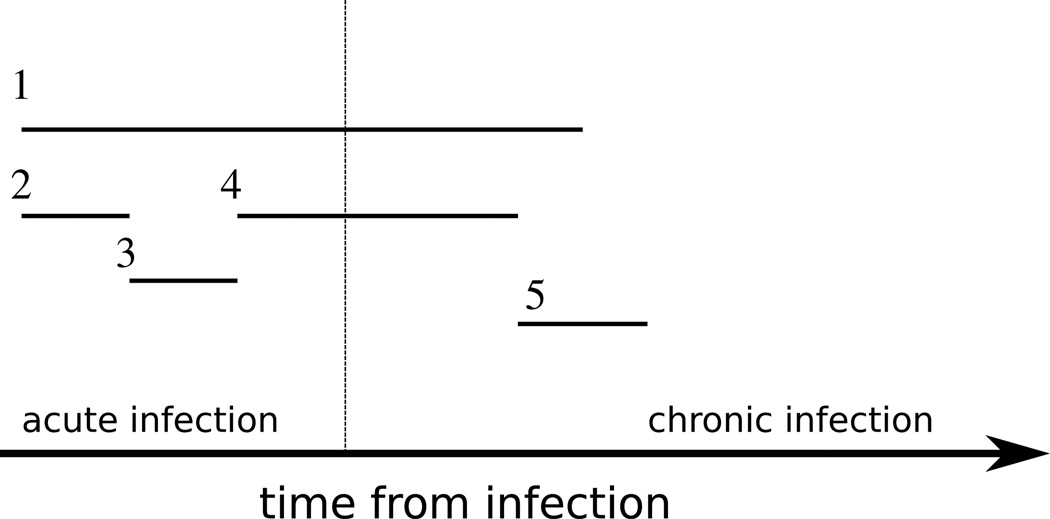
Figure 1.

Transmissions generated by various behavioral intervals. Interval type one begins after infection and terminates in chronic stage, the number of transmissions made in this interval is C̃_s; interval type two begins after infection and terminates in acute stage, the number of transmissions made in this interval is C̃₁; interval type three begins after re-sampling a new contact rate in the acute stage and terminates in the acute stage, the number of transmissions made in this interval is C₁; interval type four begins after re-sampling a new contact rate in the acute stage and terminates in the chronic stage, the number of transmissions made in this interval is C_s; interval type five begins after re-sampling a new contact rate in the chronic stage and terminates in the chronic stage, the number of transmissions made in this interval is C₂.

3. Results

3.1. Derivation of generating functions for the number of transmissions per behavioral interval

We must consider the first behavioral interval separately from the remaining intervals, because the contact rates in the first interval are generated by x̃(z), while in the remaining intervals contact rates are generated by x(z). We also need to consider if the interval occurs in the acute stage, spans the acute and chronic stages, or occurs in the chronic stage. These combinations define 5 possible types of intervals illustrated in figure 1.

Neither c(z)_1,2,s nor c̃(z)_1,2,s has a closed form. However, we are only interested in derivatives evaluated at z = 1, which do have closed forms. The following is a step-by-step derivation of $c_{1,2}^{\prime }(1)$ and $c_{1,2}^{″}(1)$. First we integrate over the probability of the interval length, T₁, and the contact rate, X, to get an expression for c₁(z):

$$c_1(z)=\int \text{Pr}(T_1)\int \text{Pr}(X){(e^{z-1})}^{X{\beta }_1{T}_1}dXd{T}_1,$$

which by the law of logarithms can be re-written as

$$c_1(z)=\int \text{Pr}(T_1)\int \text{Pr}(X){[e^{T_1{\beta }_1(z-1)}]}^{X}dXd{T}_1.$$ (3.1)

By the definition of PGFs, the expression ∫ Pr(X) [e^{T₁β₁(z−1)}]^X dX is formally equivalent to x(e^{T₁β₁(z−1)}) which upon substitution gives

$$c_1(z)=\int \text{Pr}(T_1){(1-\theta T_1{\beta }_1(z-1))}^{-k}d{T}_1.$$

Expanding Pr(T₁)

$$c_1(z)=\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}{(1-\theta T_1{\beta }_1(z-1))}^{-k}d{T}_1.$$

The value of that integral would have to be approximated if we wanted to work with that function directly. However we are only interested in the derivative of the function where z = 1

$$c_1^{\prime }(1)={[\frac{d}{dz}\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}{(1-\theta T_1{\beta }_1(z-1))}^{-k}d{T}_1]}_{z=1}.$$

The order of integration and differential can be reversed by Leibniz’s rule

$$c_1^{\prime }(1)=\int {\left[\frac{d}{dz}{\lambda }_1{e}^{-{\lambda }_1{T}_1}{(1-\theta T_1{\beta }_1(z-1))}^{-k}\right]}_{z=1}d{T}_1.$$

Rearranging gives

$$c_1^{\prime }(1)=\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}{\left[\frac{d}{dz}{(1-\theta T_1{\beta }_1(z-1))}^{-k}\right]}_{z=1}d{T}_1.$$ (3.2)

Evaluating the inner derivative

$$\frac{d}{dz}{[{(1-\theta T_1{\beta }_1(z-1))}^{-k}]}_{z=1}={[-k{(1-\theta T_1{\beta }_1(z-1))}^{-(k+1)}\frac{d}{dz}(1-\theta T_1{\beta }_1(z-1))]}_{z=1}={[-k{(1-\theta T_1{\beta }_1(z-1))}^{-(k+1)}(-\theta T_1{\beta }_1)]}_{z=1},=k\theta T_1{\beta }_1.$$

Substituting kθT₁β₁ in gives

$$c_1^{\prime }(1)=\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}k\theta T_1{\beta }_{1}d{T}_1.$$

The quantity ∫ T₁λ₁e^−λ₁T₁ dT₁ is the average interval duration in the acute stage which can be written in terms of the model parameters as $\frac{1}{{\lambda }_1}$. The final result is then

$$c_1^{\prime }(1)=\frac{\theta k{\beta }_1}{{\lambda }_1},$$

which in plain English is the mean effective contact rate, kθβ₁, multiplied by the mean interval duration, $\frac{1}{{\lambda }_1}$

The derivation of ${\tilde{c}}_1^{\prime }(1)$ follows the same steps as before. However, the substitution in 3.1 is with x̃(e^{T₁β₁(z−1)}) which changes the inner derivative in equation 3.2 to

$$\frac{d}{dz}\frac{{(1+T_1{\beta }_1\theta (1-z))}^{-k}}{1+T_1{\beta }_1\theta (1-z)}.$$

Differentiation by the quotient rule gives (k+1)θβ₁. Continuing the logic in the previous derivation gives a final result of

$${\tilde{c}}_1^{\prime }(1)=\frac{(k+1)\theta {\beta }_1}{{\lambda }_1}.$$

The second derivative of c₁(1) can be calculated by replacing equation 3.2 with the second derivative.

$$c_1^{″}(1)=\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}{\left[\frac{d^2}{d{z}^2}{(1-\theta T_1{\beta }_1(z-1))}^{-k}\right]}_{z=1}d{T}_1,=\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}{[(k+1)k{\theta }^2{T}_1^2{\beta }_1^2{(T_1{\beta }_1(\theta -z\theta )+1)}^{-(k+2)}]}_{z=1}d{T}_1,=\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}(k+1)k{\theta }^2{T}_1^2{\beta }_1^{2}d{T}_1,$$

which after rearranging becomes

$$c_1^{″}(1)=(k+1)k{\theta }^2{\beta }_1^2\int {\lambda }_1{T}_1^2{e}^{-{\lambda }_1{T}_1}d{T}_1.$$

The quantity $\int {\lambda }_1{T}_1^2{e}^{-{\lambda }_1{T}_1}d{T}_1$ is integrable by substituting ψ = λ₁T₁:

$$\int {\lambda }_1{T}_1^2{e}^{-{\lambda }_1{T}_1}d{T}_1=\int {\lambda }_1{\left(\frac{\psi }{{\lambda }_1}\right)}^2{e}^{-\psi }d{T}_1,=\int {\lambda }_1{\left(\frac{\psi }{{\lambda }_1}\right)}^2{e}^{-\psi }\frac{d\psi }{{\lambda }_1},=\frac{1}{{\lambda }_1^2}\int {\psi }^2{e}^{-\psi }d\psi .$$

∫ ψ²e^−ψdψ is the Gamma function Γ(z + 1) = ∫ ψ²e^−ψdψ = Γ(3) = 2, therefore $\int {\lambda }_1{T}_1^2{\beta }_1^2{e}^{-{\lambda }_1{T}_1}d{T}_1=\frac{2}{{\lambda }_1^2}$. Substituting in we get a final expression

$$c_1^{″}(1)=\frac{2(k+1)k{\theta }^2{\beta }_1^2}{{\lambda }^2}.$$

The second derivative of c̃₁(1) proceeds in the same fashion as above.

$${\tilde{c}}_1^{″}(1)=\int \lambda e^{-{\lambda }_1{T}_1}{\left[\frac{d^2}{d{z}^2}\frac{{(1+T_1{\beta }_1\theta (1-z))}^{-k}}{1+T_1{\beta }_1\theta (1-z)}\right]}_{z=1}d{T}_1,=\int \lambda e^{-\lambda T_1}{[(k+2)(k+1){\theta }^2{T}_1^2{\beta }_1^2{(T(\theta -z\theta )+1)}^{-(k+3)}]}_{z=1}d{T}_1,=\int {\lambda }_1{e}^{-{\lambda }_1{T}_1}(k+2)(k+1){\theta }^2{T}_1^2{\beta }_1^{2}dT,=\frac{2(k+2)(k+1){\theta }^2{\beta }_1^2}{{\lambda }_1^2}.$$

The derivations of c₂(z) and c̃₂(z) are identical to the above, albeit with subscripts corresponding to the chronic stage parameters.

In the interval that spans the transition from the acute to chronic stage, an individual’s contact rate is constant, but the probability of transmission per contact changes. To account for this correlation, we need to integrate over the lengths of the spanning interval on the acute side and on the chronic side respectively. The resulting integral is

$$c_s(z)=\int \text{Pr}(X)[\int \text{Pr}(T_1){(e^{z-1})}^{X{\beta }_1{T}_1}d{T}_1+\int \text{Pr}(T_2){(e^{z-1})}^{X{\beta }_2{T}_2}d{T}_2]dX,$$

The inner integrals can be rewritten as an exponential probability generating function ∫ Pr(T₂)e^{(z−1)(Xβ₂T₂)}dX = T₂(e^{(Xβ₂)(z−1)}) giving

$$c_s(z)=\int \text{Pr}(X)[\int \text{Pr}(T_1)e^{{(z-1)}^{(X{\beta }_1{T}_1)}}d{T}_1+\frac{{\lambda }_2}{{\lambda }_2+{\beta }_{2}X(1-z)}]dX.$$

The same can be done for the next integral giving

$$c_s(z)=\int \text{Pr}(X)\frac{{\lambda }_1}{{\lambda }_1+{\beta }_{1}X(1-z)}+\frac{{\lambda }_2}{{\lambda }_2+{\beta }_{2}X(1-z)}dX.$$ (3.3)

Equation 3.3 has no closed form but, as before, we only want to work with its derivatives. Reversing the order of integration and differentiation and setting z = 1 gives

$$c_s^{\prime }(1)=\int \text{Pr}(X)\frac{d}{dz}{[\frac{{\lambda }_1}{{\lambda }_1+{\beta }_{1}X(1-z)}+\frac{{\lambda }_2}{{\lambda }_2+{\beta }_{2}X(1-z)}]}_{z=1}dX=\int \text{Pr}(X)\frac{{\beta }_{1}X}{{\lambda }_1}+\frac{{\beta }_{2}X}{{\lambda }_2}dX.$$ (3.4)

∫ Pr(X)XdX is E(X) = kθ. Substituting in gives

$$c_s^{\prime }(1)=k\theta [\frac{{\beta }_1}{{\lambda }_1}+\frac{{\beta }_2}{{\lambda }_2}].$$

To get the $c_s^{″}$, we substitute the first for the second derivative in equation 3.4 giving

$$c_s^{″}(1)=\int \text{Pr}(X)\frac{d^2}{d{z}^2}{[\frac{{\lambda }_1}{{\lambda }_1{\beta }_{1}X(1-z)}+\frac{{\lambda }_2}{{\lambda }_2+{\beta }_{2}X(1-z)}]}_{z=1}dX,=\int \text{Pr}(X)[\frac{2{\beta }_1^2{X}^2}{{\lambda }_1^2}+\frac{2{\beta }_2^2{X}^2}{{\lambda }_2^2}]dX.$$

The quantity ∫ Pr(X)X² dX is the expectation of X² which is

$$\mathbf{E}(X^2)=\mathbf{\text{Var}}(X)+\mathbf{E}{(X)}^2,=k{\theta }^2+{(k\theta )}^2,=k\theta (k\theta +1).$$

Substituting in gives

$$c_s^{″}(1)=2k\theta (k\theta +1)[\frac{{\beta }_1^2}{{\lambda }_1^2}+\frac{{\beta }_2^2}{{\lambda }_2^2}].$$

${\tilde{c}}_s^{\prime }(1)$ is obtained by substituting X̃ for X in equation 3.4 and proceeding as before. The quantity ∫ Pr(X̃)X̃ dX̃ = E(X̃) = (k + 1)θ which gives

$${\tilde{c}}_s^{\prime }(1)=(k+1)\theta [\frac{{\beta }_1}{{\lambda }_1}+\frac{{\beta }_2}{{\lambda }_2}].$$

To get ${\tilde{c}}_s^{″}(1)$ we have to find ∫ Pr(X̃)X̃² dX̃ = E(X̃²).

$$\mathbf{E}({\tilde{X}}^2)=\mathbf{\text{Var}}(\tilde{X})+\mathbf{E}{(\tilde{X})}^2,=\tilde{x}″(1)+\tilde{x}\prime (1)-\tilde{x}\prime {(1)}^2+\tilde{x}\prime {(1)}^2,=\tilde{x}″(1)+\tilde{x}\prime (1),=2{\theta }^2(k+1)(k+2).$$

Substituting in gives

$${\tilde{c}}_s^{″}(1)=2{\theta }^2(k+1)(k+2)[\frac{{\beta }_1^2}{{\lambda }_1^2}+\frac{{\beta }_2^2}{{\lambda }_2^2}].$$

3.2. The expectation and standard deviation of H_* given heterogeneous and invariant contact rates

The basic reproduction number (R_* = E(H_*)) is commonly defined as the average number of infections generated by an average index case in a fully-susceptible population. In homogeneous systems, a randomly selected individual is, by definition, average, which simplifies the calculation of R_*. However, in systems with heterogeneous contact rates, we need to take additional care in what is meant by the notion of an average infector, specifically with respect to the hazard of transmission. The risk of an individual becoming infected is proportional to their contact rate; an individual that has higher sexual activity levels is at greater risk of infection. The index case is more likely to be have greater than average sexual activity levels [21].

The contact rate C of an individual selected at random in the population is generated by c(z). If we select an individual with probability proportional to contact rate, their contact rate C̃ is generated by c̃(z). If contact rates are stable over time, a newly infected individual maintains the same contact rate over the course of their infection such that the rate in the first and second stages are perfectly correlated. The number of transmissions produced by the index case is generated by c̃_s(z), which has no closed form for the Gamma distribution. However, the expectation and variance of C̃ do have closed form and can be calculated using the derivatives of c̃_s(z). The expectation is

$$\mathbf{E}({\tilde{C}}_s)={\tilde{c}}_s^{\prime }(1)=(k+1)\theta [\frac{{\beta }_1}{{\lambda }_1}+\frac{{\beta }_2}{{\lambda }_2}],$$

and the variance is

$$\mathbf{\text{Var}}({\tilde{C}}_s)={\tilde{c}}_s^{″}(1)+{\tilde{c}}_s^{\prime }(1)-{\tilde{c}}_s^{\prime }{(1)}^2=2{\theta }^2(k+1)(k+2)[\frac{{\beta }_1^2}{{\lambda }_1^2}+\frac{{\beta }_2^2}{{\lambda }_2^2}]+{\tilde{c}}_s^{\prime }(1)-{[{\tilde{c}}_s^{\prime }(1)]}^2.$$

Collapsing into one infection stage recovers the classic result by Anderson and May that

$$R_{*}=\frac{{\beta }_{1}k\theta +\frac{{\beta }_{1}k{\theta }^2}{{\beta }_{1}k\theta }}{{\lambda }_1},$$

where β₁kθ, β₁kθ², and ${\lambda }_1^{-1}$ are the mean and variance of the effective contact rate distribution and the mean duration of an infection respectively. Both the expectation and the variance in the number of infections generated by the index case are monotonically increasing with increasing variance in the contact rate distribution given a fixed mean value.

3.3. The basic reproduction number with heterogeneous and volatile contact rates

If the first interval terminates in the first stage then the number of transmissions is generated by

$$h_{*1}(z)={\tilde{c}}_1(z)i_1(c_1(z))c_s(z)i_2(c_2(z)).$$

If the first interval terminates in the second stage, then it must have spanned the entire first interval generating C̃_s transmissions. In the second stage the index case experiences I₂ behavioral intervals within each they generate C₂ transmissions. If the first interval terminates in the second stage, then the number of transmissions is generated by

$$h_{*2}(z)={\tilde{c}}_s(z)i_2(c_2(z)).$$

The total number of transmissions is generated by the sum of H_*1 and H_*2 weighted by their respective probabilities

$$h_{*}(z)=\frac{\rho }{{\lambda }_1}{h}_{*1}(z)+(1-\frac{\rho }{{\lambda }_1})h_{*2}(z).$$

Differentiating H_* and setting z = 1 gives the basic reproduction number

$$R_{*}=\frac{\rho }{{\lambda }_1}[{\tilde{c}}_1^{\prime }(1)+i_1^{\prime }(1)c_1^{\prime }(1)+c_s^{\prime }(1)+i_2^{\prime }(1)c_2^{\prime }(1)]+(1-\frac{\rho }{{\lambda }_1})[{\tilde{c}}_s^{\prime }(1)+i_2^{\prime }(1)c_2^{\prime }(1)],=\frac{\rho }{{\lambda }_1}[\frac{(k+1)\theta {\beta }_1}{{\lambda }_1}+\frac{1-{\varphi }_1}{{\varphi }_1}\frac{k\theta {\beta }_1}{{\lambda }_1}+k\theta [\frac{{\beta }_1}{{\lambda }_1}+\frac{{\beta }_2}{{\lambda }_2}]+\frac{1-{\varphi }_2}{{\varphi }_2}\frac{k\theta {\beta }_2}{{\lambda }_2}]+(1-\frac{\rho }{{\lambda }_1})[(k+1)\theta [\frac{{\beta }_1}{{\lambda }_1}+\frac{{\beta }_2}{{\lambda }_2}]+\frac{1-{\varphi }_2}{{\varphi }_2}\frac{k\theta {\beta }_2}{{\lambda }_2}].$$

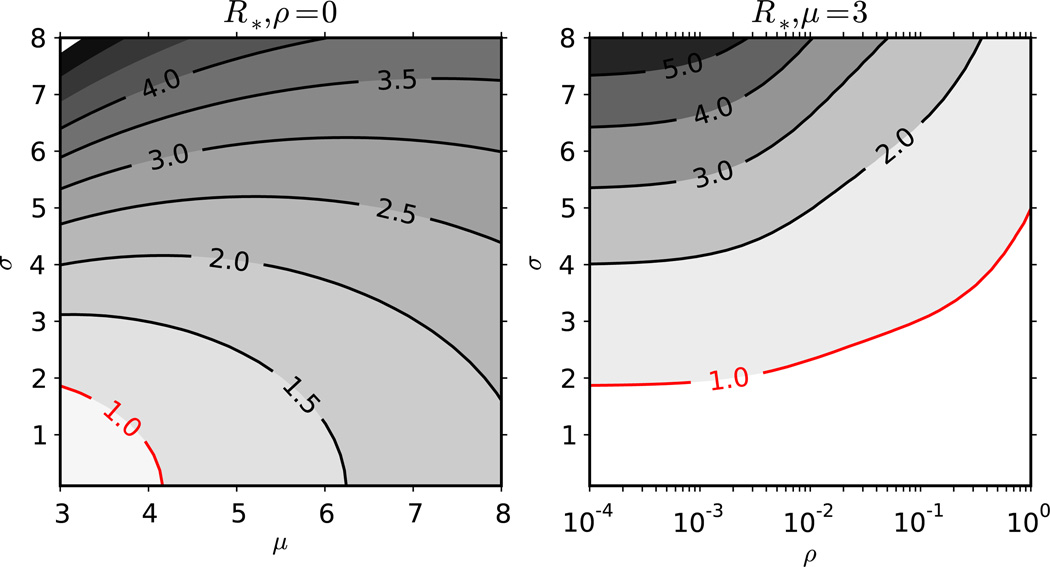
Figure 2 shows the effect of volatility on R_* at various levels of σ. The first stage is parameterized to be 50 times more contagious but much shorter than the second stage of infection. The transmission parameters were taken from a analysis by Pinkerton [23] of a longitudinal cohort of HIV serodiscordant couples. As expected from theory, R_* increases with increasingly heterogeneous contact rates (increasing σ). Volatility has an opposing effect, decreasing R_*. The reduction in R_* is monotonic in ρ and in the limit converges to the fully homogeneous model $R_{*}=\frac{k\theta {\beta }_1}{{\delta }_1+\omega }+\frac{k\theta {\beta }_2}{{\delta }_2+\omega }$. The reduction in R_* is caused by shorting of the first behavioral interval as volatility increases. By definition, the contact rates in the first interval are higher than in successive intervals, such that any process (e.g., increased volatility) that reduces the length of the first interval will reduce the average number of transmissions generated by the index case.

Figure 2.

Effect of contract rate volatility on R_*. We display (left panel) the effect of the mean (x-axis) and standard deviation (y-axis) of the contact rate distribution on the basic reproduction number without contact rate volatility. The panel on the right shows the effect of the standard deviation of contact rates (y-axis) and the degree of contact rate volatility (x-axis) on the basic reproduction number. The average duration of a behavioral interval is ρ⁻¹ such that low values of ρ signify essentially-static contact rates. The average duration of infection is 148 months with the first 2 months being the first stage and the remainder in the second. The probabilities of infection given contact are 0.05 and 0.001 in the first and second stages respectively.

The variance of H_* can be found by differentiating $h_{*}^{\prime }$. For example,

$$\mathbf{\text{Var}}(H_{*})=h_{*}^{″}(1)+h_{*}^{\prime }(1)-{[h_{*}^{\prime }(1)]}^2,=\frac{\rho }{{\lambda }_1}[{\tilde{c}}_1^{″}(1)+i_1^{″}(1)c_1^{\prime }{(1)}^2+i_1^{\prime }(1)c_1^{″}(1)+c_s^{″}(1)+i_2^{″}(1)c_2^{\prime }{(1)}^2+i_2^{\prime }(1)c_2^{″}(1)+2{\tilde{c}}_1^{\prime }(1)[i_1^{\prime }(1)c_1^{\prime }(1)+c_s^{\prime }(1)+i_2^{\prime }(1)c_2^{\prime }(1)]+2i_1^{\prime }(1)c_1^{\prime }(1)[c_s^{\prime }(1)+i_2^{\prime }(1)c_2^{\prime }(1)]+c_s^{\prime }(1)i_2^{\prime }(1)c_2^{\prime }(1)]+(1-\frac{\rho }{{\lambda }_1})[{\tilde{c}}_s^{″}(1)+i_2^{″}(1)c_2^{\prime }{(1)}^2+i_2^{\prime }(1)c_2^{″}(1)+2[{\tilde{c}}_s^{\prime }(1)+i_2^{\prime }(1)c_2^{\prime }(1)]]+R_{*}-R_{*}^2.$$

The variance of H_* can also be expressed in terms of the model parameters by substituting in the expressions for the generating functions in table 1.

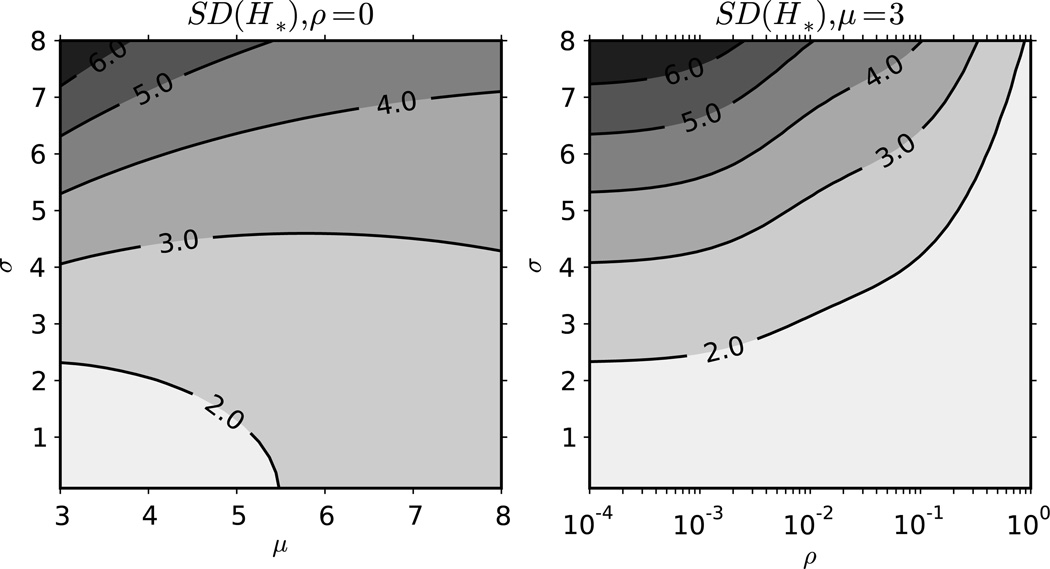
Figure 3 shows the effect of contact rate volatility on the standard deviation in the number of transmissions made by the index case, SD(H_*), at various levels of σ. Volatility has a similar effect on the standard deviation of H_* as it does on the expectation as seen in figure 2. The effect is due to both the reduction in contact rates by the shortening of the first behavioral interval and the reduction of the variance of average contact rates between individuals. Increasing ρ increases the number of behavioral intervals a single individual experiences, which reduces between-individual variance. In the limit of ρ, the between individual variance in the number of contacts converges to the expectation, which is consistent with a simple Poisson process.

Figure 3.

Effect of contract rate volatility on SD(H_*). This plot shows the effect of the mean (x-axis) and standard deviation (y-axis) of the contact rate distribution on the standard deviation of the number of transmissions generated by an index case, SD(H_*), without contact rate volatility (left panel). The panel on the right shows the effect of the standard deviation of contact rates (y-axis) and the degree of contact rate volatility (x-axis). The average duration of a behavioral interval is ρ⁻¹ such that low values of ρ mean essentially static contact rates. The average duration of infection is 148 months with the first 2 months being the first stage and the remainder in the second. The probabilities of infection given contact are 0.05 and 0.001 in the first and second stages respectively.

4. Probability of an epidemic

The probability of an epidemic is one minus the probability that an epidemic goes extinct if we infect a single individual with probability proportional to contact rate. The extinction probability of a branching process can be solved by a simple recurrence relation derived in Athreya et al. [3]. The variable u will denote the probability that an epidemic does not occur upon infecting a single individual with contact rate C̃. A necessary condition for a branching process to go extinct is that if a transmission occurs, the branching process initiated by the newly infected individual also goes extinct. Therefore, u must satisfy the self-consistent equation

$$u=h_{*}(u).$$

This equation can be solved by finding the equilibrium of a simple iterated map

$$u_{i+1}=h_{*}(u_i),$$

and starting from u₀ << 1.

The probability of an epidemic if we initially infect someone with probability proportional contact rate is 1 − h_*(u). If, on the other hand, the infected is selected uniformly at random, the probability of an epidemic is 1 − h(u).

5. Discussion

This study of CRV and R_* is the first, to our knowledge, that explicitly focuses on isolating the effects of volatility on R_* using methods that incorporate stochasticity. In Diekmann et al. the authors formalized a method for the calculation of R_* in a generalized heterogeneous transmission system as the dominant eigenvalue of the next generation operator. Their approach can be though of as formalizing an expression for the infectivity, A, as a function of time from infection, τ, and then integrating over τ to get an expression for R_*, ∫ A(τ)dτ = R_*. The next generation operator gives the value of the ∫ A_h(τ)dτ for each possible heterogeneity state; if we assume that transmission is dependent only on the heterogeneity state of the infector, then deriving the next generation matrix can be (in simple cases) straightforward. Their method nonetheless requires either the assumption of a deterministic system as noted in Heestereek and Dietz [9].

Explicit inclusion of the stochasticity inherent in transmission systems allows us to treat the quantity of interest realistically, not merely as a scalar, but as a random variable. R_* alone can give an idea how hard an infection is to eliminate. When the population of infected individuals is very small, such as during the early epidemic period, the system is dominated by stochastic effects, and R_* will not give a comprehensive picture of the rate of epidemic spread and the probability of the disease taking hold in the population [18]. Consider the result from Anderson and May [2] that $R_{*}\propto {\mu }_c+{\sigma }_c^2/{\mu }_c$ in a simple SI model with heterogeneous contact rates, where μ_c is the average contact rate and ${\sigma }_c^2$ is the variance of the contact rate distribution. This relation implies that while holding the average contact rate constant, increasing the variance of the contact rate distribution, increases R_* and, by the standard interpretation of R_*, makes controlling the epidemic more difficult. However, as we showed, that qualitative nature of the effect is unchanged, its magnitude is greatly reduced in the presence of contact rate volatility.

The functional form that the contact rate distribution takes is also important. Liljeros et al. [14] found that a cross-sectional distribution of the number of sexual partners from a large Swedish cohort followed a power law distribution with scaling exponent of 2.3 for males with more than 5 reported lifetime partners. Sexual networks with power-law distributed node distributions are referred to as scale-free networks. May and Lloyd [16] showed that, for infinite population sizes, scale-free networks do not show threshold behavior; for any non-zero transmission probability an epidemic can occur. The lack of threshold behavior emerges as a result of the underlying degree distribution having divergent variance (i.e. the variance goes to infinity as the number of nodes becomes large).

The concept of volatility would prove challenging to unify with work on scale-free networks. Networks are often thought of as static, or at least static over some period of time. The power law distribution found by Liljeros et al. aggregated the total number of lifetime partners, so it loses any measure of volatility in either the number of partnerships or the number of contacts. Even in a dynamic network, it is hard to imagine how volatility as we have implemented it here could be integrated into a network model. The problem arises because an individual’s actual contact rate is limited by the number of available contacts in the network at any point in time. Contact rates could be conceived as a preferred number of partners that would govern whether or not an individual would accept a new partner or terminate an existing partnership. Before branching into that line of research, we would conceptualize volatility in the broader context of stable and casual partners.

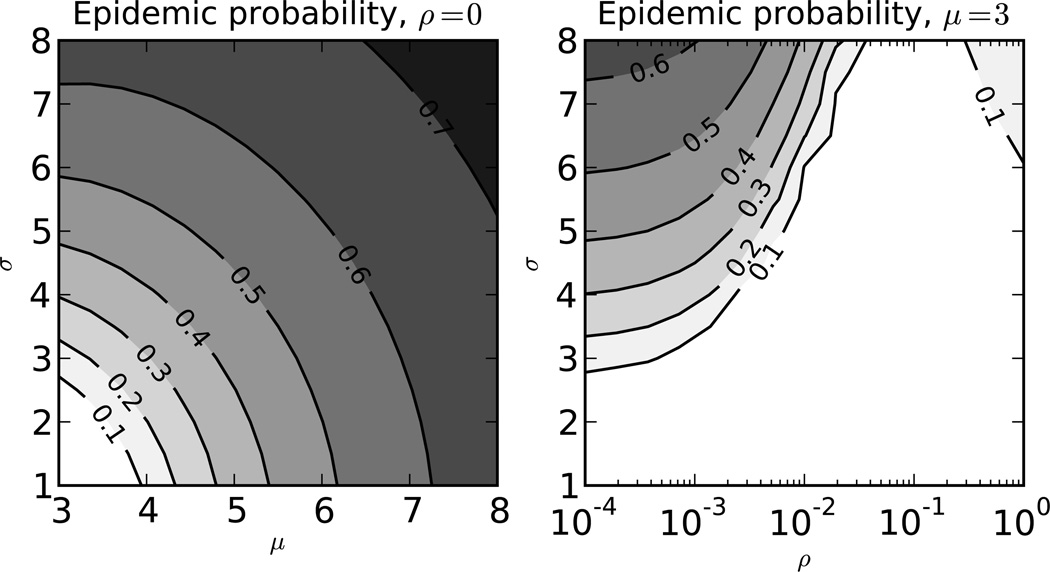
Figure 4.

Effect of contract rate volatility on the probability of an epidemic. This plot shows the effect of the mean (x-axis) and standard deviation (y-axis) of the contact rate distribution on the probability of an epidemic without contact rate volatility (left panel). The panel on the right shows the effect of the standard deviation of contact rates (y-axis) and the degree of contact rate volatility (x-axis). The average duration of a behavioral interval is ρ⁻¹ such that low values of ρ mean essentially static contact rates. The average duration of infection is 148 months with the first 2 months being the first stage and the remainder in the second. The probabilities of infection given contact are 0.05 and 0.001 in the first and second stages respectively.