Physiologically-Based Toxicokinetic Model for Cadmium Using Markov-Chain Monte Carlo Analysis of Concentrations in Blood, Urine, and Kidney Cortex from Living Kidney Donors

Abstract

The health effects of low-level chronic exposure to cadmium are increasingly recognized. To improve the risk assessment, it is essential to know the relation between cadmium intake, body burden, and biomarker levels of cadmium. We combined a physiologically-based toxicokinetic (PBTK) model for cadmium with a data set from healthy kidney donors to re-estimate the model parameters and to test the effects of gender and serum ferritin on systemic uptake. Cadmium levels in whole blood, blood plasma, kidney cortex, and urinary excretion from 82 men and women were used to calculate posterior distributions for model parameters using Markov-chain Monte Carlo analysis. For never- and ever-smokers combined, the daily systemic uptake was estimated at 0.0063 μg cadmium/kg body weight in men, with 35% increased uptake in women and a daily uptake of 1.2 μg for each pack-year per calendar year of smoking. The rate of urinary excretion from cadmium accumulated in the kidney was estimated at 0.000042 day⁻¹, corresponding to a half-life of 45 years in the kidneys. We have provided an improved model of cadmium kinetics. As the new parameter estimates derive from a single study with measurements in several compartments in each individual, these new estimates are likely to be more accurate than the previous ones where the data used originated from unrelated data sets. The estimated urinary excretion of cadmium accumulated in the kidneys was much lower than previous estimates, neglecting this finding may result in a marked under-prediction of the true kidney burden.

The health effects of low-level chronic exposure to cadmium (Cd) from dietary intake and smoking are increasingly recognized. To improve the risk assessment, it is essential to know the toxicokinetics, i.e., the relation between Cd intake, body burden, and biomarker levels of Cd. Several toxicokinetic models (Amzal et al., 2009; Kjellstrom and Nordberg, 1978; Sheng et al., 2000) have been developed to enable assessment of how Cd accumulates in and is eliminated from the human body. Of particular interest is the relation between Cd burden in the kidneys, the primary body compartment of Cd storage with an estimated biological half-life of 10–30 years, and urinary excretion, the main elimination route for absorbed Cd. Diet, being the main source of Cd exposure in the nonsmoking, nonoccupationally exposed population, has been estimated to result in an average Cd intake of 10–30 μg/day (WHO, 2011), with the absorbed fraction usually assumed to be ∼5% (Satarug et al., 2010). Besides uptake from diet, smokers are estimated to have an additional uptake of Cd of ∼1 μg/day for a smoking habit of 20 cigarettes per day (Jarup and Akesson, 2009).

Previous studies have also reported gender differences for urinary, blood, and kidney cortex Cd, with higher Cd burden in women (Barregard et al., 2010; Vahter et al., 2007). Because of the shared mechanisms of gastrointestinal uptake of iron and Cd, this difference has been partly explained by generally lower iron stores in women, indicated by low serum ferritin levels (Akesson et al., 2002; Barregard et al., 2010; Berglund et al., 1994; Julin et al., 2011).

Prediction of the body burden of Cd from low-level chronic exposure may be of increasing importance for changes in life-style, such as the benefits of quitting smoking or new dietary patterns. Orlich et al. (2013) have recently presented an evidence of decreased mortality among individuals on vegetarian diets using a large population cohort. However, a much smaller study by Krajcovicova-Kudladkova et al. (2006) showed that vegetarian diets are also associated with considerably higher Cd blood levels. To better understand the health effects of low-level chronic Cd exposure, a more accurate toxicokinetic model is needed. Such a model should preferably be developed using parallel measurements of Cd levels in multiple compartments for the same individual.

The first complex, physiologically-based toxicokinetic model for Cd was presented by Kjellström and Nordberg (K&N) (Kjellstrom and Nordberg, 1978; Nordberg and Kjellstrom, 1979). Their model comprises eight compartments, describing uptake from the lungs and the gastrointestinal tract followed by distribution to three different blood compartments, liver, kidney, and other tissue, and elimination by urinary and fecal excretion. The K&N model has since its original publications been further developed by Choudhury et al. (2001), and Diamond et al. (2003). Although the modifications to the original model were summarized in these publications, the equations of the model are not presented. The outlined modifications also mainly concern how descriptive data (e.g., lean body mass) and exposure data have been accounted for. To our understanding, the only new information regarding parameter values is the assumption that the gastrointestinal absorption of Cd fraction in general is twice as high in women. Hence, the model by Choudhury et al. (2001), Diamond et al. (2003), and subsequent work using this model, e.g., Ruiz et al. (2010), Satarug et al. (2013), mainly rely on the original estimates from the 36-year-old K&N model. Although such efforts may be valid, they imply a complete faith in the old parameter estimates, which are not accompanied by any standard errors, nor any information on residual errors (Kjellstrom and Nordberg, 1978; Nordberg and Kjellstrom, 1979). For the original model calibration, three separate studies were used: one comprising 292 autopsy cases where Cd levels in kidney cortex, liver, and pancreas were obtained (Elinder et al., 1976), another involving 132 individuals where urinary excretion of Cd was measured (Elinder et al., 1978), and a third comprising 80 individuals for whom Cd in fecal excretion was analyzed (Kjellstrom et al., 1978). For certain, no intraindividual correlation exists between Cd levels in kidney cortex and urinary excretion in the first two studies that can be used to inform the model. Also, none of the three studies make use of Cd levels in blood or plasma.

In this study, we re-estimated the most sensitive parameters in the K&N model using parallel measurements of Cd levels in blood, plasma, kidney cortex, and 24-h urinary excretion in 82 healthy individuals. We also tested the effect of gender and serum ferritin on systemic uptake.

MATERIALS AND METHODS

Study participants

Between 1999 and 2005, 152 healthy kidney donors were recruited as described previously (Barregard et al., 2010). In 109 of these (49 men and 60 women), a part of the kidney biopsy was available for analysis of Cd. Data were missing for 23 individuals on either height (N = 2), 24-h urine volume (N = 16), or Cd concentration in plasma (N = 5). Further, in four individuals 24-h urine volume was considered either too small (N = 3) or too large (N = 1) to give reliable information on the amount of Cd in 24-h urine. Thus, after exclusions, data on 82 individuals (38 men and 44 women) remained for modeling purposes. Their median age was 52 years (range 27–70), and 52 (62%; 24 men and 28 women) were current or former smokers (Akerstrom et al., 2013). Because Cd levels in whole blood and kidney cortex were still available in excluded individuals, these were used as a validation data set (N = 25), leaving out only the two individuals for which height was missing (height is needed to calculate compartmental volumes). The study was approved by the Ethics Committee of the University of Gothenburg.

Cd concentrations in whole blood ([Cd]_BLD), plasma ([Cd]_PLS), kidney cortex ([Cd]_KDC), and 24-h urine ([Cd]_U24) were determined at the Department of Occupational and Environmental Medicine, Lund University, by inductively coupled plasma mass spectrometry (ICP-MS; Thermo X7, Thermo Elemental, Winsford, UK). The procedure for analysis of Cd concentration in whole blood, plasma, kidney biopsies, and urine as well as acquisition of serum ferritin levels has been described elsewhere (Akerstrom et al., 2013; Barregard et al., 2010).

Data management

Four dependent variables (y₁, y₂, y₃, and y₄; see Fig. 1) were considered based on the measured concentrations [Cd]_BLD, [Cd]_PLS, [Cd]_KDC, and [Cd]_U24. The observed amount of Cd in whole blood (y₁) was formed by calculating the sum of the individually estimated volumes of red blood cells, V_RBC, and plasma, V_PLS, using body-surface area, gender, and age (Pearson et al., 1995), and multiplying by [Cd]_BLD:

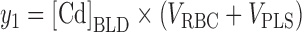(1)

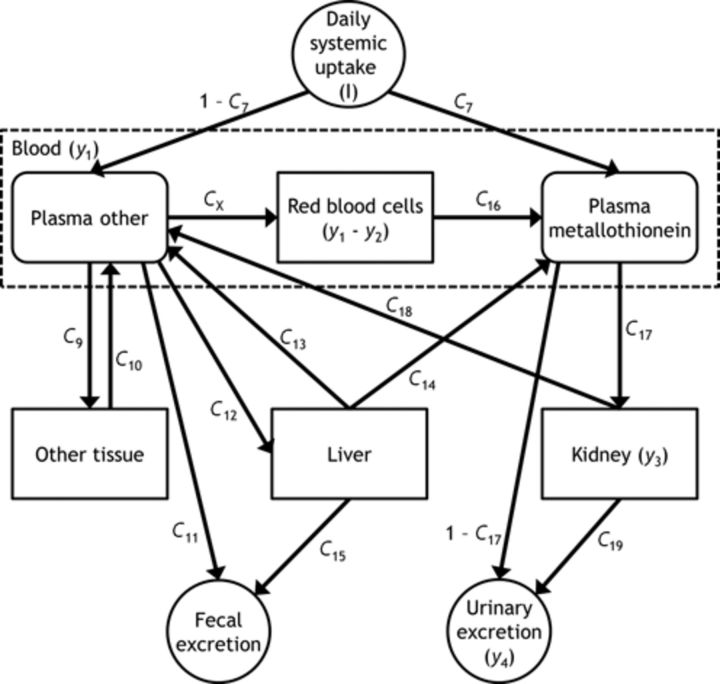
FIG. 1.

The second part of the K&N model, describing Cd kinetics from systemic uptake to excretion. The amount of Cd in total plasma (y₂) is calculated as C₂₀ × (Plasma other + Plasma metallothionein). Abbreviations: I, amount daily systemic uptake; y₁, amount in whole blood; y₂, amount in total plasma; y₃, amount in kidney; y₄, amount in 24-h urine; C₇, fraction from daily systemic uptake to plasma metallothionein; C₉, fraction from other plasma to other tissue; C₁₀, transfer rate from other tissue to other plasma; C₁₁, fraction from other plasma to fecal excretion; C₁₂, fraction from other plasma to liver; C₁₃, transfer rate from liver to other plasma; C₁₄, transfer rate from liver to plasma metallothionein; C₁₅, excretion rate from liver to feces; C₁₆, transfer rate from red blood cells to plasma metallothionein; C₁₇, tubular reabsorptive capacity; C₁₈, transfer rate from kidney to other plasma; C₁₉, excretion rate of Cd accumulated in kidney to 24-h urine; C_X, fraction from other plasma to red blood cells; C₂₀, fraction of Cd in the plasma compartments contributing to whole blood.

Hematocrit-corrected plasma volumes were calculated for each individual. In individuals with no information on hematocrit (N = 4), the originally estimated plasma volumes were used. The amount of Cd in total plasma (y₂) was then calculated by multiplying the plasma volume with [Cd]_PLS:

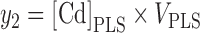(2)

The amount of Cd in the kidney (y₃) was formed by multiplying [Cd]_KDC by the estimated individual kidney weight, KDNW, using age, gender, weight, and height (He et al., 2009), and adjusting for the assumed higher concentration in the cortex by dividing by 1.5 (Nordberg and Kjellstrom, 1979):

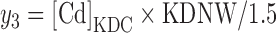(3)

Finally, the amount of Cd in 24-h urinary excretion (y₄) was formed by multiplying the measured 24-h Cd concentration by the urine volume over 24 h, V_U24:

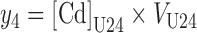(4)

Missing data on serum ferritin (N = 1) was imputed as the population median.

To further investigate differences in parameters, specifically the systemic uptake, Bayesian analysis was performed on three separate groups: never-smokers (N = 30), ever-smokers (N = 52), and all (N = 82).

Model development

Because no detailed information was available on Cd exposure, only the second part of the model as presented by Nordberg and Kjellstrom (1979) was considered for analysis (see Fig. 1 and Table 1). In addition, the following changes were made compared with the original K&N version: the model was implemented using differential equations instead of difference equations, a growth equation for body weight (BW) was used to model growth over a lifetime (O'Flaherty, 1993), and because only low levels of exposure were assumed, the maximum amount of 1 μg Cd/day for the plasma metallothionein compartment was not used, and hence the parameter C₈ was not included in the model. Further, the daily systemic uptake, I, was modeled as the sum of a BW-dependent term (I_BW), common to never- and ever-smokers, and a pack-year dependent term (I_SM) in the following way:

(5)

where PACKYR is the cumulative number of pack-years and STARTYR and STOPYR are the specific start and stop years of smoking for an ever-smoking individual. For currently smoking individuals, STOPYR was set to the current age of the individual.

TABLE 1. Model Parameters with Initial Ranges and Final Estimates as Presented by Nordberg and Kjellstrom (1979).

Name	Unit	Initially assumed range		Final estimate
		Minimum	Maximum
C7	unitlessa	0.2	0.4	0.25
C9	unitlessa	0.4	0.8	0.44
C10	day−1	0.00004	0.0002	0.00014
C11	unitlessa	0.05	0.5	0.27
C12	unitlessa	0.1	0.4	0.25
C13	day−1	0	0.0001	0.00003
C14	day−1	0.0001	0.0003	0.00016
C15	day−1	0	0.0001	0.00005
C16	day−1	0.004	0.015	0.012
C17	unitlessa	0.8	0.98	0.95b
C18	day−1	0	0.0001	0.00001
C19	day−1	0.00002	0.0002	0.00014c
CX	unitlessa	0.01	0.05	0.04
C20	unitlessa	0.05	0.5	0.1
C21	day−1	0	0.000002	0.0000011

Abbreviations: C₇, fraction from systemic uptake to plasma metallothionein; C₉, fraction from other plasma to other tissue; C₁₀, transfer rate from other tissue to other plasma; C₁₁, fraction from other plasma to fecal excretion; C₁₂, fraction from other plasma to liver; C₁₃, transfer rate from liver to other plasma; C₁₄, transfer rate from liver to plasma metallothionein; C₁₅, excretion rate from liver to feces; C₁₆, transfer rate from red blood cells to plasma metallothionein; C₁₇, tubular reabsorptive capacity; C₁₈, transfer rate from kidney to other plasma; C₁₉, excretion rate of Cd accumulated in kidney to 24-h urine; C_X, fraction from other plasma to red blood cells; C₂₀, fraction of Cd in the plasma compartments contributing to whole blood; C₂₁, decrease in C₁₉.

^aUnitless fraction, allowed range 0–1.

^bC₁₇ is assumed to decrease linearly from 0.95 at age 30 to 0.64 at age 80.

^cC₁₉ is assumed to increase by C₂₁ per year, starting at age 30.

Covariate modeling

Gender and serum ferritin were considered for covariate testing on the parameter describing BW-dependent daily uptake, I_BW. Gender (GEND) was categorized into either male (GEND = 0, N = 38) or female (GEND = 1, N = 44). For serum ferritin (SFER), a cut-off was used to form categories of ≥30 μg/l (SFER = 0, N = 62) and <30 μg/l (SFER = 1, N = 20) (Berglund et al., 1994; Julin et al., 2011). Both these effects were modeled exponentially as

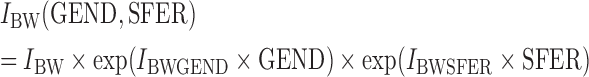(6)

where I_BWGEND and I_BWSFER are the estimated covariate effects due to gender and serum ferritin, respectively.

A covariate effect was considered significant if a zero effect was outside the 2.5 or 97.5 percentile of its posterior distribution.

Local sensitivity analysis

To determine which parameters should be estimated, a local sensitivity analysis was performed using the forward difference method implemented in acslX. The sensitivity coefficient (SC) was thus calculated as follows:

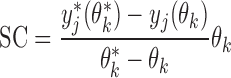(7)

for a dependent variable with nominal value y_j, perturbed by the change δ = θ_k* − θ_k, resulting in a perturbed value y_j*. Parameter normalization is obtained by multiplication of the nominal parameter value θ_k. Parameters C₇, C₉, C₁₀, C₁₁, C₁₂, C₁₃, C₁₄, C₁₅, C₁₆, C₁₇, C₁₈, C₁₉, C_X, C₂₀, and C₂₁ were tested separately using a δ corresponding to 1% change from the nominal parameter estimate according to Table 1. Also included in the analysis was the parameter describing the daily uptake of μg Cd/kg BW, I_BW, with a default of 0.01 μg Cd/day and kg BW, using the median BW for males among the never-smokers (N = 14) of 80.5 kg.

Time-averaged normalized sensitivity coefficients were calculated for each parameter with respect to each of the four dependent variables y₁, y₂, y₃, and y₄, in the time interval of 0–80 years of age. The parameter sensitivity in a dependent variable was then expressed as a percentage of the most sensitive parameter for that dependent variable. The average of the absolute values across the dependent variables was used to rank the overall parameter sensitivity.

Structural identifiability analysis

To understand if a set of parameters in a model is possible to estimate in theory from a set of dependent variables the structural (or a priori) identifiability of the parameters should be tested. A number of approaches exist to test structural identifiability (Chis et al., 2011), but the outcome can in general be classified as structurally globally identifiable (the parameter can be estimated at a unique value), structurally locally identifiable (the parameter can be estimated at a finite number of values), or structurally non-identifiable (the parameter can be estimated at an infinite number of values). Because the part of the K&N model under consideration comprises 16 parameters, including the external dose (I_BW), which was also being treated as a parameter, and because the MCMC analysis itself required significant computation time, we tested structural identifiability to find out if it was theoretically possible to estimate a specific set of parameters using the dependent variables y₁, y₂, y₃, and y₄.

Markov-chain Monte Carlo analysis

Markov-chain Monte Carlo (MCMC) analysis was used for parameter estimation. Preliminary analysis rendered the use of flat (uniform) priors insufficient. Hence, informative priors were created for the kinetic parameters Θ_C by assuming normal distribution with mean M equal to the estimate by K&N in Table 1, and a standard deviation S equal to twice the distance from the mean to the nearest minimum/maximum boundary, given by the “initially assumed ranges” (Table 1), so that Θ_C ∼ N(M, S²). Cut-offs for priors were defined as the interval [0, 1] for fractional parameters, and [0, ∞) for rate parameters.

A flat prior with a lower and upper boundary of 0.001 and 0.5 respectively was used for the uptake parameter I_BW ∼ U(0.001, 0.5). Given that only dietary exposure is present and using an absorbed fraction of 4.8% (Kjellstrom and Nordberg, 1978; Nordberg and Kjellstrom, 1979), the boundaries on I_BW correspond to a daily intake of 1.0–510 μg Cd/day for a 49 kg person and 2.3–1125 μg Cd/day for a 108 kg person, using the minimum and maximum BW in the data set. Further, flat priors were also used for the pack-year-dependent uptake parameter in (5), I_SM ∼ U(0, 10), and for the covariate parameters I_BWGEND and I_BWSFER, assumed ∼ U(−2, 2).

The log-transformation of an observation y_ij for individual i, dependent variable j was assumed to be normally distributed according to

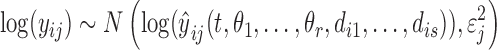(8)

where 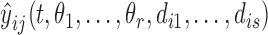is the corresponding model prediction with parameters 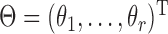and descriptive variables, 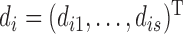and ε_j ∼ U(0, ε_j,max) is the error with assumed upper boundary ε_j,max = 10 for all dependent variables. Because of the log-transformation in (8) the residual error will describe the proportional (relative) error in the prediction. The residual errors for the four different dependent variables were assumed to be mutually independent. Taken together, the joint posterior distribution will then be proportional to the likelihood L of the data Y multiplied by the prior probabilities:

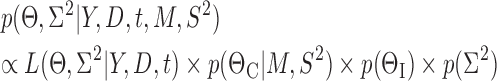(9)

where 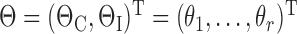, , 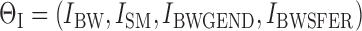with uniform probabilities according to above, 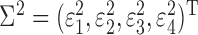, and 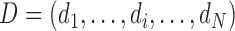for N individuals.

Component-wise random walk was used as the update method for proposing new samples to the chains. Convergence of chains was checked by visual inspection and by using the diagnostics proposed by Brooks, Gelman, and Rubin and the Heidelberger and Welch diagnostics (Smith, 2007).

In order to present the prior together with the corresponding posterior in the same graph, we produced smoothed probability density functions using the kernel density function in R with default settings.

Monte Carlo simulations and validation

The median, 2.5, and 97.5 percentiles from Monte Carlo simulations based on the MCMC posteriors and randomly selected individual records were used to assess the goodness-of-fit for the four dependent variables in the modeling data sets (N = 30, never-smokers; N = 82, all) as well as the validation data set (N = 25).

Software

Modeling, local sensitivity analysis, MCMC analysis, and Monte Carlo simulations were performed in acslX, version 3.0.2.1 (The AEgis Technologies Group, Inc., Huntsville, AL). Structural identifiability was tested using the GenSSI software (Chis et al., 2011) in combination with MATLAB, version 2007a (The MathWorks, Natick, MA). Convergence tests were conducted using R, version 3.0.1 (R Core Team 2013, Vienna, Austria), together with the Bayesian Output Analysis R-package (Smith, 2007).

RESULTS

Local Sensitivity Analysis

The results of the local sensitivity analyses are presented in Table 2. The parameter for the daily systemic uptake, I_BW, was the most sensitive parameter for almost all dependent variables, with a minor exception for the amount of Cd in kidney (y₃), for which C₁₇, describing the fraction of Cd reabsorbed in tubules, was more or equally sensitive. Parameters C₉, C₁₁, C₁₂, and C_X describe the fractional amounts of Cd leaving the nonmetallothionein plasma compartment. Because of the explicit dependence and condition of summing to one (and hence difficulties when specifying lower and upper boundaries for the prior distributions), these parameters were not used for estimation, but fixed according to their respective estimates in Table 1. Hence, in addition to I_BW, parameters C₇, C₁₇, C₂₀, C₁₆, and C₁₉ had the highest average sensitivity in decreasing order.

TABLE 2. Time-Averaged Normalized Sensitivity Coefficients of Model Parameters for Observed Amounts of Cd.

Parameter	y1 (%)	y2 (%)	y3 (%)	y4 (%)	Average (%)a
IBWb	100	100	99	100	100
C7b	−31	−11	45	43	32
C17b	2.2	1.8	100	−24	32
CX	91	−1.9	7.8	7.7	27
C11	−40	−34	−15	−17	26
C20b	4.0	100	0	0	26
C16b	−95	0.012	0.056	0.045	24
C12	−32	−18	18	20	22
C19b	−1.2	−1.0	−59	18	20
C9	−21	−18	−11	−11	15
C10	17	14	6.9	7.4	11
C14	−1.3	3.4	16	16	9.1
C15	−0.74	−2.2	−4.9	−5.6	3.3
C21	−0.14	−0.12	−7.5	4.8	3.1
C18	2.1	1.8	−3.5	−2.6	2.5
C13	3.2	1.8	−1.7	−1.9	2.1

Abbreviations: y₁, amount in whole blood; y₂, amount in total plasma; y₃, amount in kidney; y₄, amount in 24-h urine; I_BW, BW-dependent daily systemic uptake; C₇, fraction from daily systemic uptake to plasma metallothionein; C₉, fraction from other plasma to other tissue; C₁₀, transfer rate from other tissue to other plasma; C₁₁, fraction from other plasma to fecal excretion; C₁₂, fraction from other plasma to liver; C₁₃, transfer rate from liver to other plasma; C₁₄, transfer rate from liver to plasma metallothionein; C₁₅, excretion rate from liver to feces; C₁₆, transfer rate from red blood cells to plasma metallothionein; C₁₇, tubular reabsorptive capacity; C₁₈, transfer rate from kidney to other plasma; C₁₉, excretion rate of Cd accumulated in kidney to 24-h urine; C_X, fraction from other plasma to red blood cells; C₂₀, fraction of Cd in the plasma compartments contributing to whole blood; C₂₁, decrease in C₁₉.

^aAverage of the absolute values of the sensitivity coefficients.

^bParameter used in MCMC analysis.

Structural Identifiability Analysis

Parameters C₇, C₁₆, C₁₇, C₁₉, C₂₀, and I_BW were tested and shown to be structurally globally identifiable. Hence, it was possible in theory to estimate C₇, C₁₆, C₁₇, C₁₉, C₂₀, and I_BW from the dependent variables y₁, y₂, y₃, and y₄. This implies a unique solution of parameter estimates can be found provided that data are sufficient, for instance by the use of informative priors.

Markov-Chain Monte Carlo Analysis and Covariate Testing

Based on the results from the sensitivity analysis and the potential covariate effects, four different models were tested in the MCMC analysis. In the default model, only the five kinetic parameters C₇, C₁₆, C₁₇, C₁₉, and C₂₀ were included, together with the uptake parameters I_BW and, in the case of inclusion of ever-smoking individuals, I_SM. In addition, Model 1 included the parameter for a potential gender effect, I_BWGEND; Model 2 included both I_BWGEND and the parameter for a potential effect of serum ferritin, I_BWSFER, and Model 3 included I_BWSFER only.

Three chains with 5000 iterations each were used to obtain the posterior distributions. Removal of a burn-in period of 1500 iterations was considered sufficient using visual inspection of chains. This approach was supported by the Brooks, Gelman, and Rubin convergence diagnostics, which gave no indication of nonconvergence for iterations 1501–5001 in any case, and by the Heidelberger and Welch stationarity test, which only recommended removal of >1500 iterations in 11 cases out of the total of 420 tested combinations of data sets, chains, and parameters (Smith, 2007).

To reduce autocorrelation and decrease the amount of generated data, a thinning factor of 10 was used on the remaining iterations after burn-in removal, leaving 350 iterations per chain and parameter. After thinning, the three chains were combined for each parameter, resulting in 1050 iterations constituting the final posterior distributions. Posteriors for the uptake and covariate parameters are presented in Figure 2, and posteriors for the kinetic parameters, along with their respective priors, are presented in Figure 3.

FIG. 2.

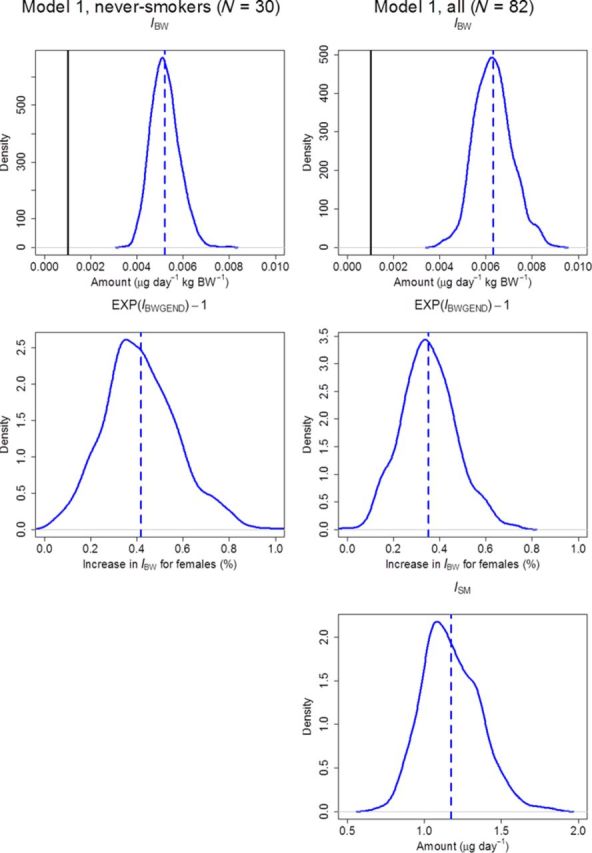
Kernel density estimators for posterior distributions (curves) of uptake and covariate effect parameters, with their respective median values (dashed lines). The lower limit of the uniform prior for I_BW is also shown (solid line). Abbreviations: I_BW, BW-dependent daily systemic uptake; I_BWGEND, exponential effect of gender on BW-dependent daily systemic uptake; I_SM, pack-year dependent daily systemic uptake.

FIG. 3.

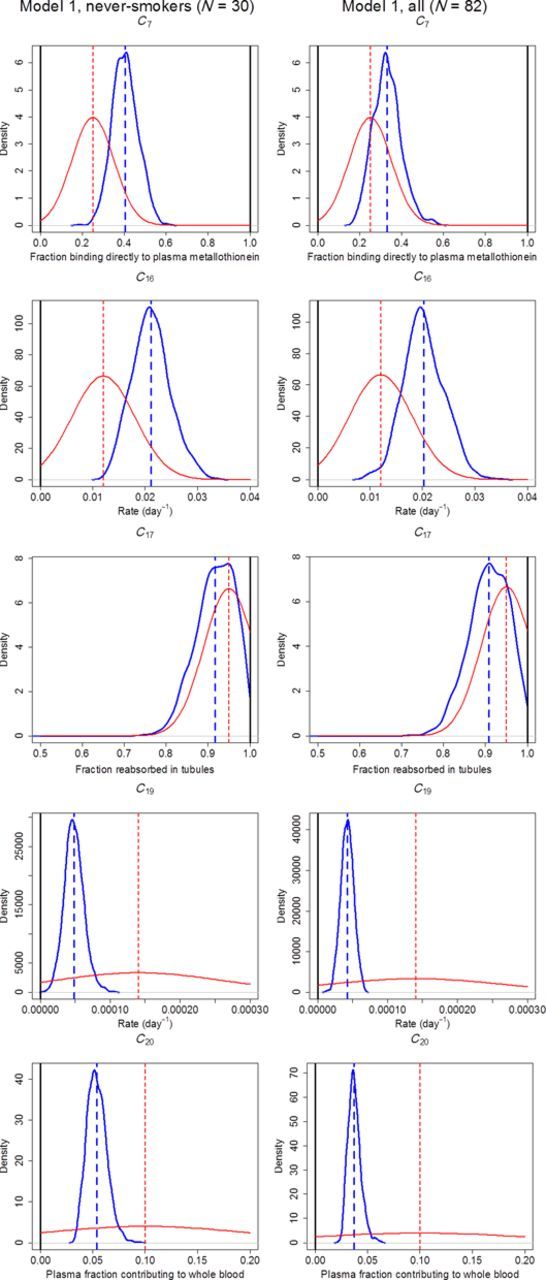
Kernel density estimators for posterior distributions (upper thick curves) of kinetic parameters, with their respective median values (thick dashed lines), and their respective prior distribution (lower thin curves), using the estimates from K&N (Table 1) as mean (thin dashed lines). The cut-off limits for the priors are also shown (thick solid lines). Abbreviations: C₇, fraction from daily systemic uptake to plasma metallothionein; C₁₆, transfer rate from red blood cells to plasma metallothionein; C₁₇, tubular reabsorptive capacity; C₁₉, excretion rate of Cd accumulated in kidney to 24-h urine; C₂₀, fraction of Cd in the plasma compartments contributing to whole blood.

The medians, 2.5, and 97.5 percentiles for the changes in the daily uptake, I_BW, caused by either or both covariate effect parameters I_BWGEND and I_BWSFER are presented numerically in Table 3. A significant effect (the zero effect was outside the 2.5–97.5 percentile interval) among never-smokers (N = 30), and all individuals (N = 82), was seen in I_BW for females, with a median increase of 40 and 35%, respectively. A similar, but weaker and nonsignificant effect was also seen among smokers (N = 52), with a 22% increase. No significant effect could be seen in I_BW for a serum ferritin level <30 μg/l in any of the data sets, although there was a trend toward an increased uptake for individuals having a serum ferritin level below the cut-off.

TABLE 3. Posterior Distributions of Covariate Effects on BW-Dependent Daily Systemic Uptake.

Percentile	Never-smokers (N = 30)		Ever-smokers (N = 52)		All (N = 82)
	Gendera	Serum ferritinb	Gendera	Serum ferritinb	Gendera	Serum ferritinb
Model 1
2.5	13%		−3%		13%
50.0	40%		22%		35%
97.5	77%		57%		61%
Model 2
2.5	7%	−11%	−9%	−19%	12%	−12%
50.0	37%	13%	18%	10%	33%	7%
97.5	73%	44%	53%	53%	57%	29%
Model 3
2.5		−5%		−9%		−2%
50.0		21%		20%		19%
97.5		56%		60%		43%

^aChange in I_BW caused by gender = EXP(I_BWGEND) − 1.

^bChange in I_BW caused by serum ferritin = EXP(I_BWSFER) − 1.

The medians, 2.5, and 97.5 percentiles for I_BW and the pack-year dependent daily uptake I_SM are presented in Table 4, together with the corresponding percentiles for the proportional residual errors.

TABLE 4. Posterior Distributions of Uptake Parameters and Residual Errors.

Percentile	IBW (μg/day kg per BW)	ISM (μg/day)	ε1 (%)	ε2 (%)	ε3 (%)	ε4 (%)
Model 1 based on never-smokers only (N = 30)
2.5	0.00410		46.3	54.3	44.8	47.7
50.0	0.00517		59.5	69.1	58.2	61.9
97.5	0.00644		79.9	93.4	79.3	84.2
Model 1 based on both never- and ever-smokers (N = 82)
2.5	0.00481	0.85	58.0	54.9	45.0	50.3
50.0	0.00629	1.15	67.4	65.2	52.5	57.9
97.5	0.00810	1.56	79.5	76.8	63.1	67.8

Abbreviations: I_BW, BW-dependent daily systemic uptake; I_SM, pack-year dependent daily systemic uptake; ε₁, proportional residual error for amount in whole blood; ε₂, proportional residual error for amount in total plasma; ε₃, proportional residual error for amount in kidney; ε₄, proportional residual error for amount in 24-h urine.

To compare with the original K&N model, additional MCMC analyses were performed for all individuals and for never-smokers only, with all parameters kept fixed to the estimates by K&N (Table 1) and only the daily systemic uptake, I_BW, and the daily uptake from smoking, I_SM, were estimated without covariate effects.

Model Fit and Monte Carlo Simulations

Observed amounts versus predicted amounts for the four dependent variables using Model 1 are presented in Figure 4 for never-smokers and in Figure 5 for all individuals.

FIG. 4.

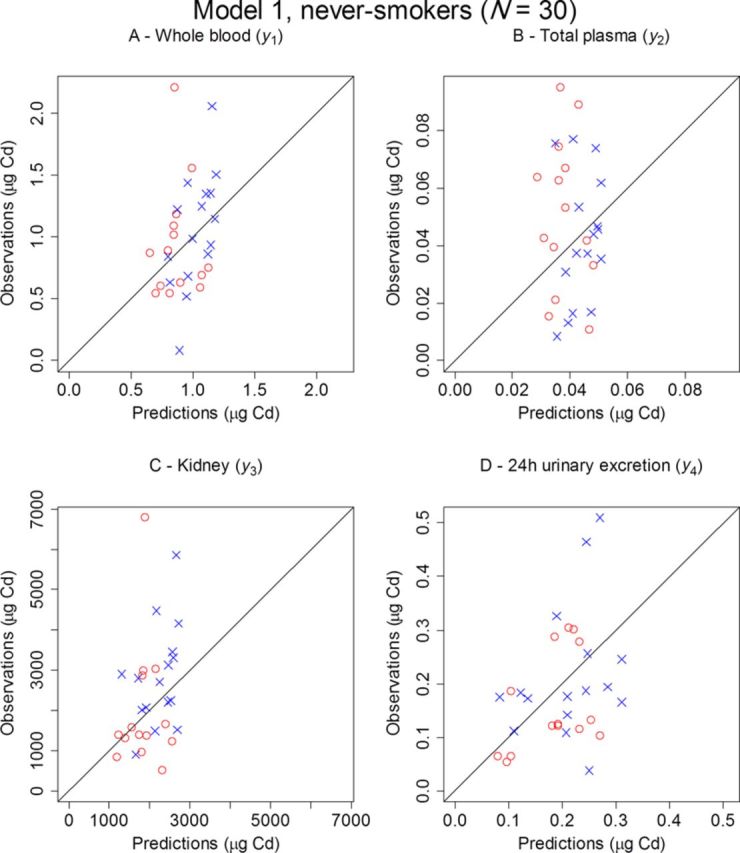
Observed versus predicted amounts of Cd for males (○) and females (×) in whole blood (A), total plasma (B), kidney (C), and 24-h urine (D) for the 30 never-smoking kidney donors using Model 1.

FIG. 5.

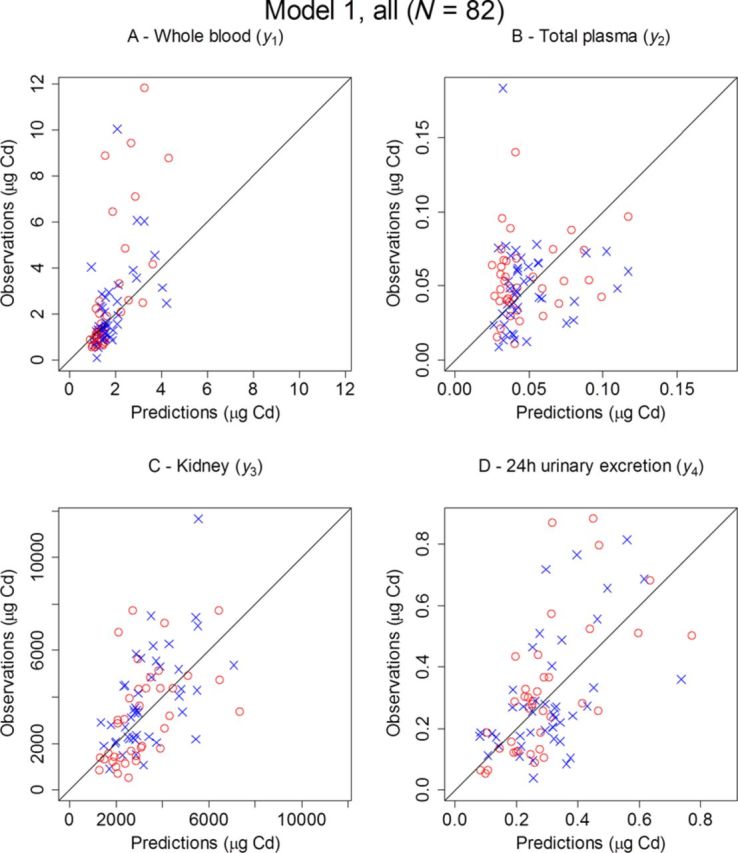
Observed versus predicted amounts of Cd for males (○) and females (×) in whole blood (A), total plasma (B), kidney (C), and 24-h urine (D), for all 82 kidney donors using Model 1.

Monte Carlo simulations were performed based on the 1050 iterations available for each parameter from the MCMC chains. Because the simulations also needed a value for each of the descriptive variables of gender, BW, current age, and smoking habits, information from a randomly selected individual record was used in each run. The simulation time was set to 80 years and the median, 2.5, and 97.5 percentiles for the dependent variables were then calculated for each time point with the results for never-smokers being shown in Figure 6, and for all individuals in Figure 7. The corresponding median for the original K&N model has also been included in all panels. The number of observations falling outside the 2.5–97.5 percentiles was noted for each of the data sets and for each dependent variable. For never-smokers, between 37 (Fig. 6, panel D, urinary excretion) and 60% (Fig. 6, panel A, whole blood) of the observations were covered by the 95% area. For all individuals, the predictive capability improved, with between 59 (Fig. 7, panel A, whole blood) and 73% (Fig. 7, panel B, total plasma) of the observations covered.

FIG. 6.

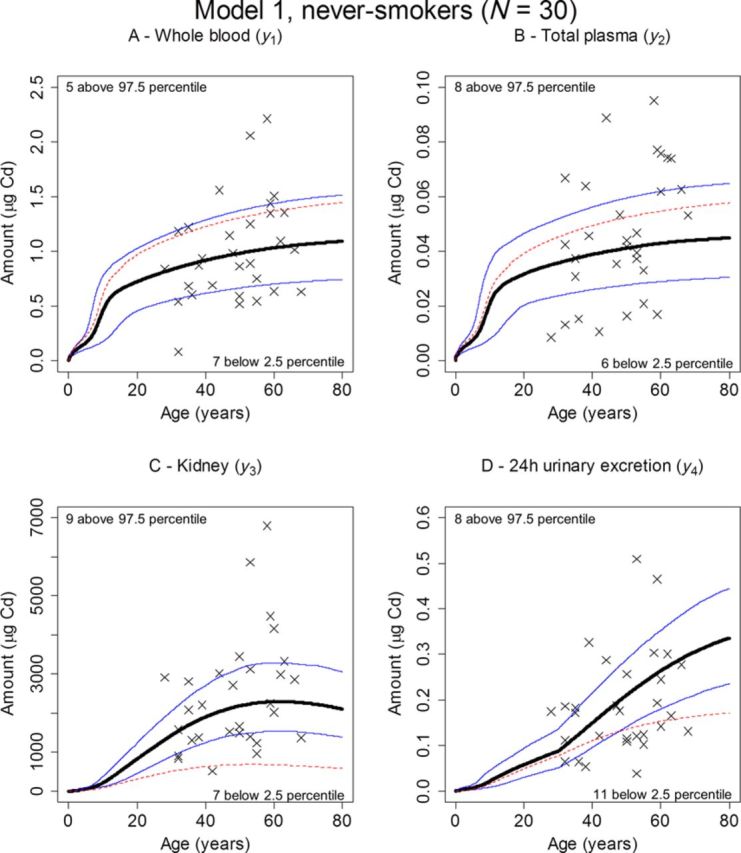
Predicted (median, thick, solid; 2.5 percentile, lower thin, solid; 97.5 percentile, upper thin, solid) versus observed amounts (×) of Cd in whole blood (A), total plasma (B), kidney (C), and 24-h urine (D). The percentiles were obtained by Monte Carlo simulation using randomly drawn demographic data from the 30 never-smoking kidney donors and posterior distributions obtained in the MCMC analysis with Model 1. Also shown are the corresponding predicted amounts (median, thin, dashed) when all parameters were kept fixed to their original K&N values in the MCMC analysis, and only the posterior for the daily systemic uptake, I_BW, was estimated. The number of observations falling above the 97.5 percentiles or below the 2.5 percentiles is also indicated.

FIG. 7.

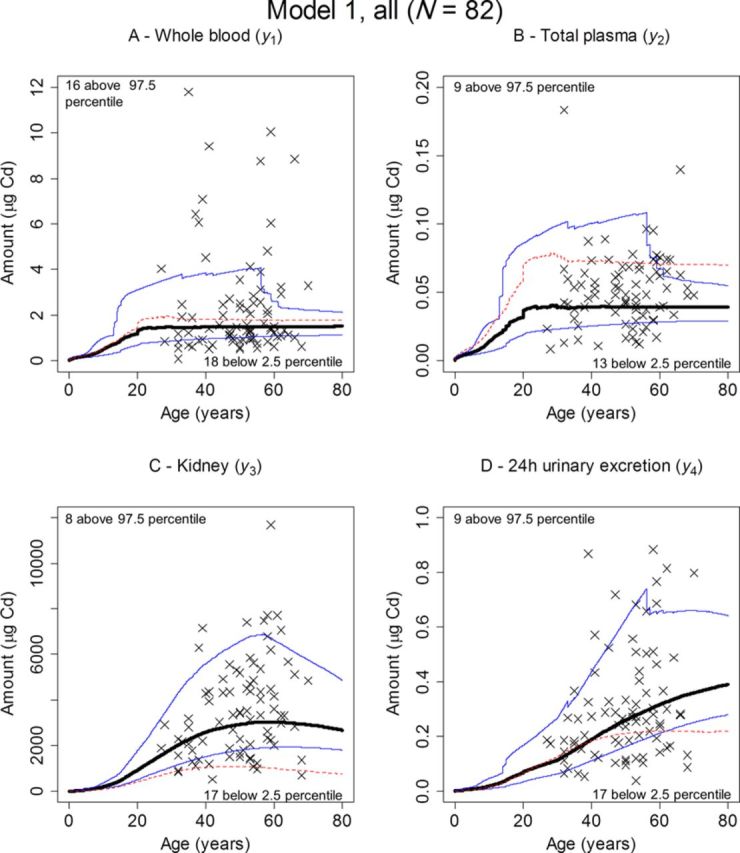
Predicted (median, thick, solid; 2.5 percentile, lower thin, solid; 97.5 percentile, upper thin, solid) versus observed amounts (×) of Cd in whole blood (A), total plasma (B), kidney (C), and 24-h urine (D). The percentiles were obtained by Monte Carlo simulation using randomly drawn records from all the 82 kidney donors and posterior distributions obtained in the MCMC analysis with Model 1. Also shown are the corresponding predicted amounts (median, thin, dashed) when all parameters were kept fixed to their original K&N values in the MCMC analysis and only the posteriors for the daily systemic uptake, I_BW, and the daily uptake from smoking, I_SM, were estimated. The number of observations falling above the 97.5 percentiles or below the 2.5 percentiles is also indicated.

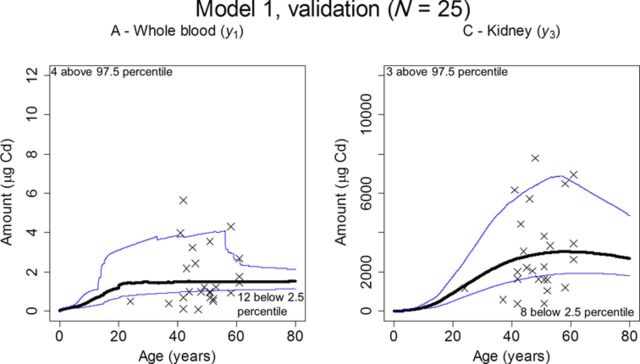
The Monte Carlo simulations based on posteriors using all individuals were also plotted against the validation data set (N = 25) in Figure 8. Thirty-six (panel A, whole blood) and 56% (panel B, kidney) of the observations were covered by the 2.5–97.5 percentiles.

FIG. 8.

Predicted (median, thick; 2.5 percentile, lower thin; 97.5 percentile, upper thin) versus the observed amounts (×) of Cd in whole blood (A) and kidney (B), for the 25 individuals in the validation data set. The percentiles were obtained by Monte Carlo simulation using randomly drawn records from all the 82 kidney donors and posterior distributions obtained in the MCMC analysis with Model 1. The number of observations falling above the 97.5 percentiles or below the 2.5 percentiles is also indicated.

DISCUSSION

In this study we present new estimates for the kinetic parameters in the K&N model, along with the effect of gender on systemic uptake based on data from 82 healthy individuals for which Cd levels have been measured in kidney cortex and plasma as well as in whole blood and urinary excretion. Because the new estimates come from a single study where the individual data sets will contain intraindividual information on correlations between observations in different compartments, the new estimates are likely to be more accurate than the ones given in the original publication where the data used originated from several studies. Also, in a previous report on kidney Cd levels a comparison between kidney Cd in the present study group and Swedish data from 1975 clearly shows that while the overall kidney Cd levels in the population have decreased, levels in never-smokers are similar to those found in the 1970s (Barregard et al., 2010). Therefore, the relative importance of dietary exposure has increased. The caveat in this context is of course the validity of the model structure itself, and whether it can be considered to have sufficient predictive capability.

As a first criterion of predictive capability the model should give reasonable estimates of the dietary intake of Cd, for which no data was available in this study. The mean of Cd exposure from dietary intake has previously been estimated at between 0.21 and 0.30 μg Cd/kg BW per day in the adult Swedish population, using a sample of 1210 individuals (European Food Safety Authority, 2012), i.e., between 16 and 22 μg Cd/day for a 74 kg adult (mean BW in our study group). Some recent studies using food frequency questionnaires have arrived at similar estimates: 15 μg Cd/day in women (Akesson et al., 2008) and 19 μg Cd/day in men (Julin et al., 2013). In the present study, a daily systemic uptake was estimated at 0.0052 μg Cd/kg BW in men and 0.0073 μg Cd/kg BW (40% higher) in women in the never-smoking population (N = 30), in Tables 3 and 4. Comparing the dietary intake with the predicted uptake will correspond to an absorbed fraction between 1.7 and 2.5% for men and 2.4 and 3.5% for women. These estimates are lower than the commonly used fraction of 5% (Satarug et al., 2010), but still within the reasonable range, considering uncertainty in the present estimates and dietary intake, and the variability in previous estimates of absorption (European Food Safety Authority, 2009). For all individuals (N = 82), the daily systemic uptake was estimated at 0.0063 μg Cd/kg BW in men and 0.0085 μg Cd/kg BW (35% higher) in women. The somewhat higher daily systemic uptake per kg BW for all individuals is likely a consequence of the additional gastrointestinal Cd intake from smoking, rather than smokers having a higher dietary intake of Cd. The median 1.2 μg/day of the daily uptake for each pack-year per calendar year of smoking is in accordance with previous estimates of an approximate daily uptake of 1 μg for a smoking habit of 20 cigarettes each day (Jarup and Akesson, 2009).

A comparison of the posteriors of the kinetic parameters with their respective priors in Figure 3 reveals that the new data have most impact on excretion rate of Cd accumulated in kidney to 24-h urine (C₁₉) and the fraction of Cd in the plasma compartments contributing to whole blood (C₂₀). A likely explanation is that the new data are most informative for these two parameters, since C₂₀ explicitly link observations in blood (y₁) with total plasma (y₂) while C₁₉ directly link observations in kidney (y₃) with urinary excretion (y₄). In addition, a value for C₂₀ would most likely be very difficult to verify experimentally, meaning that a lot of uncertainty may accompany the original estimate in the K&N model. The relatively large decrease in C₁₉ to a posterior mean of 0.000042 day⁻¹ (Table 5) corresponds to a half-life of Cd in kidney of 45 years. Although this number is higher than the usually assumed range of 10–30 years, it should not be confused with the half-life computed from a one-compartment model, where Cd in urine will be assumed to arrive from a single kidney compartment model without additional pathways. Instead, in the present model also the fraction of Cd arriving directly from plasma unabsorbed but via the kidney (1 – C₁₇) must be accounted for. Because the new estimate for parameter C₁₇ is only 91% (Table 5), compared with the prior mean of 95%, the lower contribution in urine from Cd accumulated in kidney, will be compensated by the higher fraction of Cd coming directly from plasma.

TABLE 5. Posterior Distributions of Kinetic Parameters.

Percentile	C7 (fraction)	C16 (day−1)	C17 (fraction)	C19 (day−1)	C20 (fraction)
Model 1 based on never-smokers only (N = 30)
2.5	0.288	0.0144	0.820	0.0000219	0.0381
50.0	0.404	0.0209	0.922	0.0000473	0.0530
97.5	0.527	0.0291	0.991	0.0000774	0.0736
Model 1 based on both never- and ever-smokers (N = 82)
2.5	0.209	0.0131	0.810	0.0000244	0.0275
50.0	0.327	0.0200	0.911	0.0000422	0.0366
97.5	0.471	0.0280	0.991	0.0000603	0.0509

Abbreviations: C₇, fraction from systemic uptake to plasma metallothionein; C₉, fraction from other plasma to other tissue; C₁₆, transfer rate from red blood cells to plasma metallothionein; C₁₇, tubular reabsorptive capacity; C₁₉, excretion rate of Cd accumulated in kidney to 24-h urine; C₂₀, fraction of Cd in the plasma compartments contributing to whole blood.

K&N used a correction factor of 1.5 to adjust the higher concentration of Cd in the kidney cortex to the lower average concentration in the kidney; however, this number has been questioned more recently. Svartengren et al. found that a correction factor of 1.25 was more representative between concentrations in cortex and average kidney in the left kidneys of 20 males (Svartengren et al., 1986). We chose to keep a correction factor of 1.5 to allow comparisons with the original K&N model, as a value of 1.25 would have caused a bias in the fixed parameters that were originally estimated using 1.5. However, we also reran the MCMC analysis with Model 1 and a factor of 1.25. The median estimates for I_BW, I_BWGEND, I_SM, C₇, C₁₆, C₁₇, and C₁₉ all shifted with <10%, indicating no major changes. The exception was the excretion rate of Cd accumulated in kidney to 24-h urine (C₁₉), which decreased by 25% to a new value corresponding to a half-life of 60 years.

Because only one observation per compartment and individual was available, no attempt was made to estimate the population variability in parameters. Hence, individual predictions could only be computed from fixed effects such as BW and gender. Consequently, the fit of observed versus predicted amounts in Figures 4 and 5 describe a reasonably good fit for a small-size population model, accounting only for demographic data and covariate effects.

The predictive capability of the model with the new estimates was also evaluated using the Monte Carlo simulations plotted against observations. Although this approach only gave a moderate fit for the never-smoking individuals (Fig. 6), a better coverage by the 95% interval band was obtained using all individuals (Fig. 7), indicating that an even larger population may be needed to fully evaluate the model using this approach. The small validation data set obtained a similar coverage as the modeling data sets (Fig. 8). There is a trend in both the full data set and the validation data set with more observations in general falling below the 2.5 percentile than above the 97.5 percentile, which may indicate over-prediction despite the use of a proportional error model.

The original parameter estimates in Table 1 resulted in a lower posterior mean of I_BW, both in all individuals (I_BW = 0.0046) and among never-smokers only (I_BW = 0.0040). Plotted against the new data with never-smokers, or the full data set, the original model showed a marked over-prediction of Cd levels in plasma (Figs. 6 and 7, panel B, dashed line) and a marked under-prediction of Cd levels in kidney (Figs. 6 and 7, panel C, dashed line). Interestingly, the original estimates still produce decent predictions of Cd levels in urine (Figs. 6 and 7, panel D, dashed line), and whole blood for all individuals (Fig. 7, panel A, dashed line). This may in fact be one reason that these estimates are still in use when modeling exposure assessment. Most studies rely on measurements in blood and/or urinary excretion and according to the present study these dependent variables are the ones that agree best with the original model.

Although the predictive capability of the updated model is only moderate, the poor agreement between the new data and the estimates using the old model should be considered before accepting estimates in the original model for use in exposure assessment.

In conclusion, we have improved the physiologically-based toxicokinetic model originally developed by K&N using data representative of a mixed healthy population subject to low-level chronic Cd exposure from diet and smoking. A gender effect on BW-dependent systemic uptake significantly improved the model and should be accounted for in future modeling efforts. A lower rate of urinary excretion from Cd accumulated in the kidney was estimated from the data at hand, in comparison to the original model parameter value. This should also be accounted for when using the K&N model to predict whole body and kidney Cd burden, since using the original excretion rate will tend to underestimate the amount in kidney for a specific amount of Cd in urine.

FUNDING

Sahlgrenska University Hospital (ALF 74580) ; Swedish Research Council for Health, Working Life, and Welfare (FORTE, ref. 2010-0216). Conflict of interest: Martin Fransson declares a potential competing financial interest since he is (as of January 2014) also hired as a consultant for PKxpert (www.pkxpert.com), a company that provides consultancy services in pharmacokinetics, drug metabolism, and preclincal research and development project management. No actual competing interests exist to date. Remaining authors declare they have no competing financial interests.