Abstract
Despite intense work, incorporating constraints on protein native structures into the mathematical models of molecular evolution remains difficult, because most models and programs assume that protein sites evolve independently, whereas protein stability is maintained by interactions between sites. Here, we address this problem by developing a new mean-field substitution model that generates independent site-specific amino acid distributions with constraints on the stability of the native state against both unfolding and misfolding. The model depends on a background distribution of amino acids and one selection parameter that we fix maximizing the likelihood of the observed protein sequence. The analytic solution of the model shows that the main determinant of the site-specific distributions is the number of native contacts of the site and that the most variable sites are those with an intermediate number of native contacts. The mean-field models obtained, taking into account misfolded conformations, yield larger likelihood than models that only consider the native state, because their average hydrophobicity is more realistic, and they produce on the average stable sequences for most proteins. We evaluated the mean-field model with respect to empirical substitution models on 12 test data sets of different protein families. In all cases, the observed site-specific sequence profiles presented smaller Kullback–Leibler divergence from the mean-field distributions than from the empirical substitution model. Next, we obtained substitution rates combining the mean-field frequencies with an empirical substitution model. The resulting mean-field substitution model assigns larger likelihood than the empirical model to all studied families when we consider sequences with identity larger than 0.35, plausibly a condition that enforces conservation of the native structure across the family. We found that the mean-field model performs better than other structurally constrained models with similar or higher complexity. With respect to the much more complex model recently developed by Bordner and Mittelmann, which takes into account pairwise terms in the amino acid distributions and also optimizes the exchangeability matrix, our model performed worse for data with small sequence divergence but better for data with larger sequence divergence. The mean-field model has been implemented into the computer program Prot_Evol that is freely available at http://ub.cbm.uam.es/software/Prot_Evol.php.
Keywords: structurally constrained substitution models, folding stability, misfolded state, maximum-likelihood estimate
Introduction
A variety of amino acid substitution models of evolution have been developed to perform phylogenetic analysis. The simplest models are based on the assumption that protein sites evolve independently and identically according to empirical substitution matrices such as JTT (Jones et al. 1992) or WAG (Whelan and Goldman 2001). Despite the great success of these simple models (Yang et al. 1998), in particular for evaluating phylogenetic trees and inferring evolutionary and population parameters with the maximum-likelihood (ML) method (Whelan et al. 2001; Felsenstein 2004), they present the important drawback that they ignore the information contained in protein structures (Robinson et al. 2003; Wilke 2012).
Selection on protein folding stability ultimately acts on interactions between sites, implying that sites do not evolve independently. Nevertheless, giving up the independence among sites generates huge complications in the computation of the likelihood. Because of this reason, several groups have tried to incorporate the effect of protein structure through site-specific substitution matrices. On one extreme, Koshi and Goldstein (1998, 2001) and Koshi et al. (1999) have developed substitution models that consider physicochemical properties of amino acids. On the other extreme, Halpern and Bruno (1998) proposed to adopt different amino acid frequencies for each position of a protein; despite improving over simpler models, this approach requires very large amount of data to fit all the needed parameters. Lartillot and Philippe (2004) interpolated between these two approaches letting the number of site classes to be a parameter of their model. Instead of fixing the number of classes and their parameters, which can result in overfitting, they integrate over all of these parameters through Monte Carlo sampling. This method is often used in simulations, but it is less established than nonmixture models for phylogenetic inference because of its computational burden.
On the other hand, progresses in statistical mechanical models of protein folding (Plotkin and Onuchic 2002; Shakhnovich 2006; Chan et al. 2011) have prompted since long time models of protein evolution that enforce selection on the stability of the native state (Gutin et al. 1995; Babajide et al. 1997; Bussemaker et al. 1997; Govindarajan and Goldstein 1997; Mirny et al. 1998; Tiana et al. 1998; Bastolla et al. 1999, 2003; Bornberg-Bauer and Chan 1999; Dokholyan and Shakhnovich 2001; Parisi and Echave 2001; Taverna and Goldstein 2002; Bloom et al. 2005; DePristo et al. 2005; Goldstein 2011; Grahnen et al. 2011; Huang et al. 2014), recently reviewed in Liberles et al. (2012). Although these models are not applicable to the important class of natively unfolded proteins (Uversky and Dunker 2010), it is clear that the stability of the native state is a very important determinant of protein evolution. Simple models of protein folding allow simulating protein evolution (see Arenas et al. 2013, for a recent implementation in the context of phylogenetic trees) and they produced important insights. Nevertheless, it has been difficult to apply them for phylogenetic inference. A pioneering contribution was made by Fornasari et al. (2002), who adopted simulations of their structurally constrained protein evolution model for computing site-specific substitution matrices still assuming independent sites. A few groups abandoned the independent sites approximation, proposing substitution models that take into account pairwise amino acid distributions, in particular Rodrigue et al. (2005) and, quite recently, Bordner and Mittelmann (2014). However, the computational implementation of pairwise-sites models is complicated and it cannot be combined with standard programs for phylogenetic inference.
New Approaches: The Mean-Field Model
Here, we build on previous work by one of us and coworkers, who noted that contact-based models of protein folding combined with the assumption of independent sites and other approximations allow to analytically compute site-specific amino acid frequencies. We call this a mean-field (MF) model, because each site evolves independently but taking into account in a self-consistent way the MF generated by the other sites. Approximating contact interaction energies with their hydrophobic component, the previous model established an explicit relationship between the average hydrophobicity of a site in a family of protein sequences and its connectivity at the structural level (Bastolla et al. 2005, 2008; Porto et al. 2005) and it was later extended to generate a substitution model (Bastolla et al. 2006). The MF model that we present here builds on that proposal, but is not explicitly based on hydrophobicity and it adopts an improved representation of the statistical mechanical model of the misfolded state (Minning et al. 2013). The model generates the site-specific amino acid distributions that are maximally close to a background amino acid distribution and fulfill a constraint on the average folding free energy that effectively maintains the stability of the native state. The only free parameters of the model are the Lagrange multiplier that imposes the selective constraint and the parameters that define the background distribution. They are determined imposing that the observed protein sequence has ML with respect to the site-specific amino acid distributions. For most proteins, the resulting amino acid distributions produce sequences in which the native state is on the average stable, as assessed through our folding model, despite this condition is not explicitly imposed. Importantly, we found that considering the misfolded state produces higher likelihood, larger stability, and more realistic hydrophobicity values than only considering the native and the unfolded state. In all cases, the amino acid distributions observed in natural protein families agreed better with the MF model than with the frequencies of empirical substitution models.
We then generated site-specific matrices of substitution rates by combining the MF site-specific stationary distributions with an exchangeability matrix obtained from an empirical substitution model. We applied the resulting rate matrices for phylogenetic inference, comparing their Akaike Information Criterion (AIC) scores (Akaike 1974) (likelihood penalized by the number of free parameters) with those of other structurally constrained models of protein evolution, finding that our model produces better results than a recent model with independent sites that takes into account solvent accessibility but disregards the misfolded state (Bordner and Mittelmann 2014), and even better than a pairwise model developed by Rodrigue et al (2005) as reported in Bordner and Mittelmann (2014), despite this model explicitly considers correlations between sites. With respect to the much more complex model recently developed by Bordner and Mittelmann (BM) (2014), that takes into account pairwise terms in the amino acid distributions and optimizes more parameters than our model, we obtained worse results for three protein families with very small sequence divergence but better results for one family with larger sequence divergence.
Finally, we examined eight highly divergent protein families obtained from the Pfam database (Punta et al. 2012). For most of them, the likelihood of our model was higher than one of the empirical model. For those cases in which the empirical model gave better performances, the MF model became superior if we eliminated proteins with sequence identity smaller than 35% with respect to the representative structure, consistent with the fact that proteins with low sequence identity may have divergent structures.
Overall, the MF model provides a structure-based modeling of protein evolution that considers the misfolded state, and it allows a fast computation of the evolutionary parameters per site that can be easily applied to phylogenetic inference. The MF model associates to a known protein structure a probability distribution in sequence space with the following properties:
- The global probability distribution of a protein family is modeled as the product of amino acid distributions of single sites, that is, sites are considered independent:
where i labels any of the L sites and ai labels the amino acid at site i. The assumption of site-independent evolution is necessary for computationally efficient algorithms, such as the most commonly used methods for phylogenetic inference (Felsenstein 2004).(1) - The single-site amino acid distributions are the product of the site-independent background distribution determined by the mutation process times site-specific selection factors ,
(2) The background distribution is modeled in two different ways: Either 1) the amino acid frequencies are treated as m = 19 free parameters (the 20th parameter is determined through the normalization condition) or 2) the amino acid frequencies are obtained from a codon-based substitution model that has m = 4 free parameters (three nucleotide frequencies and the transition–transversion ratio). This model is selectively neutral, except that stop codons are forbidden, and the amino acid frequencies are obtained as the sum of the stationary frequencies of their codons (see also Methods). In both cases, the free parameters are determined by maximizing the likelihood of the amino acid frequencies observed in the protein structure plus those present in a protein family, if they are available. In case (1), this simply means that we equate the background frequencies and the observed frequencies.
- The selection factors are determined imposing that the resulting global distribution presents minimum Kullback–Leibler (KL) divergence with respect to the background distribution , for given average folding free energy . If we impose this constraint through a Lagrange multiplier Λ, the 20L parameters are determined by minimizing the quantity
where zi is the Lagrange multiplier that imposes the normalization constraint is the contact matrix of the native structure, and is the folding free energy of the native state in the sequence . The sum is over all possible sequences of L amino acids. Although this is an astronomic number, the sum can be analytically computed exploiting the independence of each site. Note that the are not free parameters, because they are completely determined by the native structure, by the properties of the misfolded ensemble, and by Λ, the multiplier that imposes the constraint on the average folding free energy. Λ is treated as a free parameter that is fixed through the condition that the model maximizes the likelihood of the protein sequence in the Protein Data Bank (PDB), :(3) (4)
The minimum KL condition (eq. 3) is analogous to the condition that determines the Boltzmann distribution in statistical mechanics as the maximum entropy distribution with given average energy. Berg et al. (2004) and Sella and Hirsch (2005) showed that several models of evolutionary genetics are formally equivalent to statistical mechanics in the space of biological sequences, with minus fitness playing the role of energy and the inverse of population size playing the role of temperature. The minimum KL condition is equivalent to the maximum entropy condition if the background distribution due to mutation assigns equal probability to all amino acids, and it generalizes it for more realistic background distributions. In qualitative terms, minimum KL with respect to the mutational distribution means that selection produces the minimum possible deviation from what would be achieved by mutation alone, that is, that the selective pressure is minimal.
The evolutionary model requires to constrain the fitness, which is often modeled as the probability that the protein is in the native state, that is, (Goldstein 2011). Constraining the fitness represents the important saturation effect that evolution becomes more tolerant to deleterious mutations and effectively neutral if is very negative (Taverna and Goldstein 2002). However, the iterative procedure that we developed for computing the MF distribution has convergence problems if we constrain the fitness F exactly because of this reason: For large proteins, the fitness becomes almost a binary variable with values zero or one, and the iterative algorithm cycles between these two states. To avoid this problem, in equation (3) we resort to the better behaved approximation to constrain . Note that constraining fitness and constraining would be equivalent if the derivative of the fitness with respect to could be treated as a nonfluctuating variable.
Instead of determining the selection parameter Λ by imposing an experimentally determined value of the average folding free energy (the average is taken over the MF distribution), we determine it with the ML condition and from this we obtain the complete amino acid distribution and compute . It is remarkable that for most proteins the obtained is negative, that is, sequences described by the MF distribution are on the average stable, and its value is similar to the value computed for the native protein in the PDB. This is not trivial, because smaller values of Λ produce MF models with and larger values of Λ produce MF models with too negative .
In practice, it is very cumbersome to maximize the likelihood with respect to all parameters, and we resort to approximations that allow computing the MF distribution in a time that ranges from seconds to few minutes depending on the target protein. The steps of the algorithm are described in detail in the Methods section and in the Appendix.
To apply the site-dependent amino acid distributions to phylogenetic inference, we have to construct a substitution rate matrix that has these distributions as limit distributions. As most programs for phylogenetic inference do, we assume detailed balance and choose a symmetric exchangeability matrix that determines the site-specific substitution rates as
| (5) |
This ansatz automatically satisfies the detailed balance , which implies that is the limit distribution. The diagonal elements are determined through the normalization condition .
The symmetric exchangeability matrix has 190 free parameters. We did not attempt to determine an exchangeability matrix optimally suitable for our MF model, as it was made for instance in Bordner and Mittelmann (2014). This optimization may give room to large improvement of the results, because we observed that E strongly influences the resulting likelihood. Instead, the results presented in this work are based on an exchangeability matrix derived from an empirical substitution model such as WAG or JTT, with parameters and , according to one of the three following possible schemes:
The simplest choice (here denoted E) is to impose that the exchangeability matrix is the same as the empirical model, . However, we expect that this choice is not optimal because empirical substitution matrices represent both mutation and selection, whereas we need an exchangeability matrix that represents only mutation, because selection is modeled through the condition on .
- The second option, denoted as F, imposes that the site-averaged amino acid flux is the same as for the empirical model,
(6) - The third possibility, here denoted as Q, requires that the rate matrices Q = Ef of the MF model and the empirical model are as similar as possible. Because the rate matrix uniquely determines the stationary frequencies, it is not possible that the two matrices are equal, and we impose that they are most similar in the mean-square sense. This condition requires that the symmetric parts of the rate matrices are equal:
(7)
The MF model has been implemented into the computer program Prot_Evol that is freely available at http://ub.cbm.uam.es/software/Prot_Evol.php (last accessed April 13, 2015). This program can analyze any protein structure in the PDB with or without a protein sequence data set in a few seconds/minutes, producing as output the site-specific amino acid frequencies and the exchangeability matrix that define the substitution process together with information on the likelihood of the native sequence with respect to the model and the computed mean folding free energy of the MF model and the native protein.
We compute the likelihood of the substitution model in two steps. In the first step, we use a global average substitution matrix and we obtain optimal branch lengths for all sites with the PAML program (Yang 2007), conveniently modified (see Methods). In the second step, we run PAML for each site separately with the fixed branch lengths obtained in the first step. Note that this procedure only approximately achieves branch lengths that optimize the sum of the log likelihood of all sites.
Results
Assessment of the Mean-Field Model with Individual Proteins
In this section, we apply the MF model to a test set of 380 monomeric globular proteins in the PDB whose structure was determined through X-ray crystallography. The background distribution was obtained from the amino acid frequencies in the PDB sequence.
Site Specificity Is Determined by the Number of Contacts
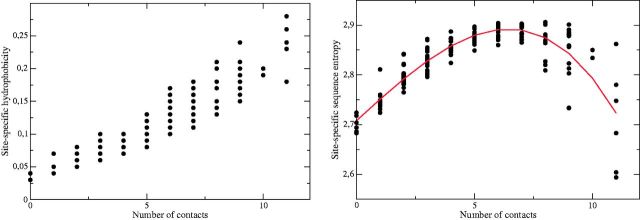
We found that the properties of the site-specific distributions strongly depend on the number of native contacts of each site. As predicted (see eq. 14 and Porto et al. 2005), the average hydrophobicity of the MF distributions is strongly negatively correlated with the number of contacts (fig. 1A). This is not surprising, because buried sites with more contacts tend to be more hydrophobic. However, this is not an assumption but a result of the model, and the strength of the correlation is remarkable (the correlation coefficient is r = 0.906 on the average).
Fig. 1.
Site-specific average hydrophobicity (left) and entropy (right) of the MF distributions as a function of the number of native contacts for the protein with PDB code 153l. As expected, there is a very strong correlation between hydrophobicity and number of contacts and the entropy reaches a maximum at an intermediate number of contacts.
Figure 1B shows that the entropy of the distributions has a maximum for an intermediate number of native contacts, consistent with our previous prediction (Porto et al. 2005). This property of our model contrasts with the common wisdom that more exposed sites are less conserved. However, it is compatible with the observation that buried sites evolve more slowly than exposed sites (Franzosa and Xia 2009). We indeed reproduced this observation using exchangeability matrices derived both from an empirical substitution process and from a mutation process (data not shown). The apparent contradiction is explained by the fact that in our model exposed sites are less variable than sites of intermediate exposure, but for proper choices of the exchangeability matrix they are characterized by a higher exchangeability rate although the number of allowed amino acids is smaller. We will discuss in detail this important aspect in a forthcoming publication.
Considering Misfolding Improves the Likelihood and Yields Stable Proteins with Realistic Hydrophobicity
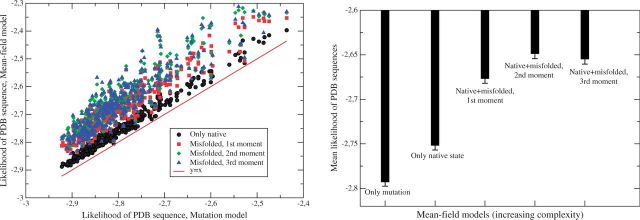
We plot in figure 2A the log likelihood per site of the PDB sequence with respect to different MF models that we denote here by , where k labels the MF model. Each point represents a protein. The likelihood of the mutation model , which is equal to minus the entropy of the PDB sequence, is used as a reference on the x-axis. The second type of model, k = 0, computes considering only the native and the unfolded state. The model with k = 1 considers the first moment of the contact energy of the misfolded state, . The model k = 2 also includes the second moment of the energy of the misfolded state, that is, the full equation (10), and the last one, k = 3, also includes the third moment of the misfolded energy.
Fig. 2.
Left: Log likelihood of various MF models as a function of the log likelihood of the purely mutation model. Each point represents a protein. Right: Mean log likelihood of the five types of MF models. The plotted statistical errors show that differences are significant except for the two rightmost bars.
We compare these different MF models in figure 2B, which shows the log likelihood per site averaged over all proteins for five different models. The number of parameters of the four models with selection is the same, just one more than for the purely mutational model, which corresponds to Λ = 0. Such an extra parameter yields a negligible correction to the AIC per site. One can see that the mean likelihood clearly improves going from the mutation model to the model that only takes into account the native state, and an even larger improvement is obtained considering the misfolding ensemble, which is not considered by other structurally constrained models for phylogenetic inference due to its computational complexity. The best results are obtained considering the second moment of the energy of the misfolded ensemble, while the third moment slightly worsens the results, probably due to the crude approximations needed to efficiently compute it. Therefore, in the following we adopt the model with the second moment.
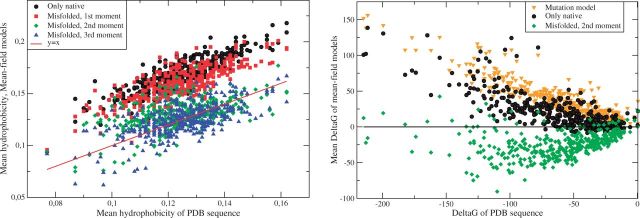
In figure 3A, we see that the models and have more realistic average hydrophobicities for all proteins, which contribute to their higher likelihood, whereas the models (only native) and tend to have hydrophobicity larger than that of the sequence in the PDB. As a result, the average folding free energy is positive for the model based only on the native state, in which the misfolded ensemble has lower free energy than the native ensemble, and for the mutation model that lacks site specificity, that is, the protein families described by these models are on the average unstable (fig. 3B). On the contrary, the models and (not shown) yield folding stability to most protein families. This is remarkable because the selection parameter Λ is fixed through the ML criterion, which does not require . We found that, for the proteins for which with the model , a value of Λ slightly larger than the ML produces a stable protein family. The same is not always true with the native-only model .
Fig. 3.
Left: Average hydrophobicity of the MF models versus the average hydrophobicity of the PDB sequence. Each point represents a protein. Right: Average folding free energy (native minus misfolded) of the MF models versus the average folding free energy of the PDB sequence. means that the MF model describes on the average stable proteins. Each point represents a protein.
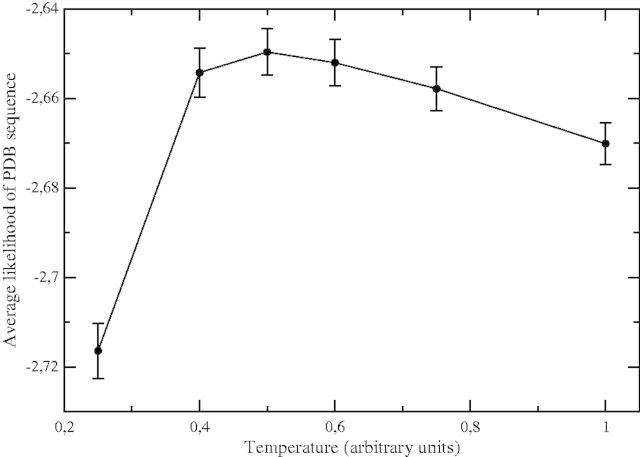
Finally, our results depend on the temperature at which the thermodynamic computations are performed. This temperature has arbitrary units, set by the units of the contact free energy function that we adopt. We can use the mean likelihood of the proteins in the test set with respect to the model to determine the temperature parameter that yields optimal results, and that we interpret as the room temperature expressed in units of contact interactions. This optimal temperature turns out to be T = 0.5 (fig. 4). For this value of the temperature, the model optimally describes protein sequences in the PDB. All reported computations are performed at this temperature.
Fig. 4.
Mean log-likelihood of the proteins in the test set with respect to the model versus the temperature in arbitrary units set by our contact interaction energy function.
Assessment of the Mean-Field Model with Protein Families
In this section, we compare the performances of the MF model with those of other substitution models by applying them to 12 different protein families (table 1). Four families had been previously studied by Bordner and Mittelmann (2014), so that we could directly compare the MF model with structurally constrained models presented therein, in particular the pairwise-sites substitution model based on factor graphs (hereafter BM), the independent sites model based on surface accessibility (hereafter, SA), and the pairwise model based on contact potentials that was developed by Rodrigue et al. (2005) (hereafter, RO). The remaining eight families were much more divergent than the four above (table 1), and they were randomly chosen from the seed alignments of the Pfam database (Punta et al. 2012) that possess at least ten sequences and one representative structure must be present in the PDB. In order to facilitate the comparison with the results of the RO model, we adopted an exchangeability matrix derived from the JTT model. We present results obtained with the condition F (eq. 6). Results obtained with the condition Q (eq. 7) are similar. We arbitrarily applied the WAG matrix for the other eight protein families (see below). We applied the default thermodynamic settings (i.e., temperature T = 0.5 and configurational entropy per residue ) described in Methods.
Table 1.
Protein Families Collected from the Pfam Database.
| Protein family | Pfam | Proteins | Uniprot | PDB | Length | |
|---|---|---|---|---|---|---|
| Glucokinase | PF02685 | 4 | GLK_ECO57 | 1SZ2 | 465 | 0.93 |
| Homogentisate 1,2-dioxygenase | PF04209 | 4 | HGD_HUMAN | 1EY2 | 319 | 0.92 |
| Cytochrome P450 | PF00067 | 4 | CP2A6_HUMAN | 1Z10 | 419 | 0.96 |
| Pancreatic ribonuclease | PF00074 | 4 | RNAS1_BOVIN | 1SRN | 113 | 0.74 |
| Triosephosphate isomerase | PF00121 | 56 | TPIS_TRYBB | 1TTI | 236 | 0.37 |
| Rubredoxis | PF00301 | 43 | RUBR2_PSEOL | 1R0F | 53 | 0.45 |
| Kinesin | PF00225 | 87 | KAR3_YEAST | 3KAR | 323 | 0.35 |
| Ferredoxin | PF05996 | 62 | PCYA_SYNY3 | 3NB8 | 242 | 0.33 |
| DNA ligase | PF13298 | 136 | B1L4V6_KORCO | 3P4H | 118 | 0.46 |
| Heat shock protein | PF00012 | 33 | DNAK_ECOLI | 2KHO | 600 | 0.53 |
| Oxysterol-binding protein | PF01237 | 153 | KES1_YEAST | 1ZHT | 436 | 0.25 |
| Retroviral aspartil protease | PF00077 | 50 | POL_FIVPE | 3OGQ | 112 | 0.25 |
Note.—For each family, the table indicates the Pfam code, sample size, UniProt entry for a protein sequence with a PDB structure, the PDB code, number of amino acids and average sequence identity with respect to the representative protein. Note that the first four entries were selected following the study by Bordner and Mittelmann (2013) and they present a very high sequence identity.
Amino Acid Distributions
In order to compare the amino acid distributions observed at each site of the multiple sequence alignment with the site-dependent distributions generated by the MF model on one hand, and with the site-independent distribution adopted by the empirical model on the other hand, we measured the KL divergence at each site i:
| (8) |
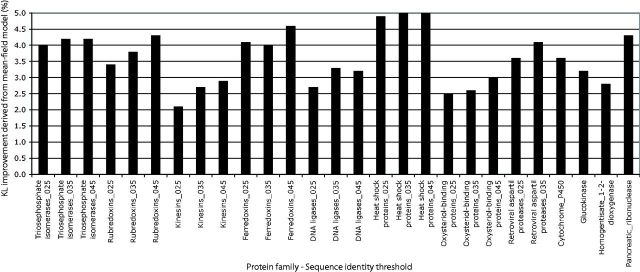
where a is any of the 20 amino acids. We compute the weighted sum , with weights wi proportional to the number of aligned residues (excluding gaps) in column i of the alignment. The smaller the , the closer the observed and model-provided distributions are. We found that the MF model presented lower than the empirical model for all protein families (fig. 5), which indicates that it better represents the amino acid distributions present in the real data. Furthermore, the difference between the MF model and the empirical model increases when sequences with less than 25% sequence identity with respect to the representative protein are eliminated from the test set.
Fig. 5.
Difference of KL divergence from the observed amino acid profile between the empirical model and the MF model (KLDobs_emp–KLDobs_mf) for the 12 studied protein families, under different conditions on the minimum sequence identity allowed. Positive differences mean that the observed profile agrees better with the MF model than with the empirical model.
Comparison with Other Substitution Models for Phylogenetic Inference
First, we examined the four protein families studied in the recent publication by Bordner and Mittelmann (2014) (table 1). We fitted the models and computed their ML with PAML, correcting for the number of degrees of freedom (dofs) with the AIC scores, both for the MF model (19 dofs) and for the reference model JTT +G, where +G indicates heterogeneous substitution rate across sites according to a gamma distribution (Yang 1993) (1 dof). The results derived from the models MF, BM, SA, and RO are reported in table 2. For all of the protein families, the MF model showed a better fitting than the RO model and it was also better than the SA model for three of the four protein families, whereas the BM model presented a better fitting than the MF model for three of the four protein families. Interestingly, the MF was the best model for the family with largest divergence (average sequence identity 0.74), whereas the BM model was the best model for the other three families that present an average sequence identity larger than 0.90.
Table 2.
Difference of AIC for the Structurally Constrained Substitution Models MF, BM, RO, and SA Relative to the Empirical Substitution Model JTT +G.
| Protein family | MF | RO | SA | BM |
|---|---|---|---|---|
| Glucokinases | −77.2 | −76.8 | −117.4 | −223.6 |
| Homogentisate 1,2-dioxygenases | −88.9 | −62.6 | −61.6 | −210.0 |
| Cytochrome P450 | −141.1 | −59.2 | −106.4 | −249.2 |
| Pancreatic ribonucleases | −29.5 | −13.1 | −23.4 | −26.2 |
Note.—The values for the latter models were collected from Bordner and Mittelmann (2013). More negative values indicate better models, and the best model is indicated in italics.
For the other eight protein families (entries 5–12 in table 1), we computed the AIC scores between MF and the WAG empirical substitution model, with 19 and 0 degrees of freedom, respectively. Here, we found a strong impact of data sets with low sequence identity on the fitting of the MF model (see sequence identities for these data sets in table 1). We explored this impact by filtering the data sets according to the sequence identity of all proteins with respect to the protein of the representative structure (too distant protein sequences are trimmed from the data set), in particular we analyzed these data sets adopting sequence identity thresholds of 0.25, 0.35, and 0.45. The AIC scores for all these data sets are presented in table 3. The results indicate that data sets with sequence identity with respect to the protein structure below 0.25 can be problematic for the MF model suggesting that distant protein sequences are poorly represented by the reference structure. All data sets with sequence identity levels higher than 0.35 presented a better fitting with the MF model than with the empirical model.
Table 3.
Difference of AIC, ΔAIC, for the Structurally Constrained Substitution Model MF Relative to the Empirical Substitution Model WAG for Protein Families Filtered at Different Levels of Sequence Identity with Respect to the Protein of the Reference Structure.
| Protein family | seq. id. >0.25 | seq. id. >0.35 | seq. id. >0.45 |
|---|---|---|---|
| Triosephosphate isomerases | −121.0 (53) | −57.8 (35) | −21.1 (4) |
| Rubredoxins | −54.7 (39) | −51.3 (33) | −51.9 (29) |
| Kinesins | 113.9 (85) | −37.4 (30) | −42.9 (6) |
| Ferredoxins | −99.5 (25) | −78.8 (24) | −114.8 (19) |
| DNA ligases | −414.6 (124) | −443.4 (113) | −367.0 (104) |
| Heat shock proteins | 114.1 (32) | −9.3 (30) | −41.4 (28) |
| Oxysterol-binding proteins | 118.9 (26) | −24.5 (22) | −60.1 (17) |
| Retroviral aspartil proteases | 30.1 (18) | −3.2 (3) | NA (2) |
Note.—Results for data sets where the empirical model better fits the data are shown in italics. In parenthesis, the sample size of such a data set is specified. Note that smaller sample sizes lead to lower absolute ML values and therefore could lead to higher (less negative) ΔAIC scores.
Discussion and Conclusions
It is known that the rate at which an amino acid site experiences change is altered by substitutions at neighboring sites due to structural constraints (Liberles et al. 2012; Wilke 2012). Models of evolution that incorporate structural constraints are therefore of increasing importance but, due to their intrinsic complexity, they have not yet been incorporated into the commonly used phylogenetic inference frameworks. This is because the common design of a likelihood function requires site-independent matrices of substitution (Felsenstein 1973, 2004).
Starting from a previous proposal from one of the authors and coworkers (Porto et al. 2005), in this article we have presented a new model for analytically computing site-specific amino acid profiles for proteins of known structure that take into account selection for the folding stability of the experimentally known native state. With respect to our previous work (Porto et al. 2005) based on the Principal Eigenvector (Bastolla et al. 2005) and on the Effective Connectivity (Bastolla et al. 2008) of the contact matrix, the present model implements two main improvements: 1) The algorithm constrains the difference in free energy between the native state and the misfolded state, represented through a simple statistical mechanical model (Minning et al. 2013) and 2) all the parameters are fixed through an ML criterion, with the aim that the model optimally represents observed protein structures.
Although some models of protein evolution consider the misfolded state, this is computationally cumbersome and it is made at the cost of approximations such as considering only maximally compact structures on the cubic lattice (Gutin et al. 1995) or generating misfolded conformations through threading (Bastolla et al. 2003; Goldstein 2011). Applying an analytic, although approximate, treatment of the misfolded state was crucial for its incorporation in the MF model. In addition, we do not know any other model of the substitution process for phylogenetic inference that considers the misfolded state.
Stability against misfolding is thought to be an important requirement in protein evolution. For instance, one of us and coworkers have shown through computational predictions of the stability of orthologous proteins (Bastolla et al. 2004) and through simulations (Mendez et al. 2010) that the interplay between the stability against unfolding and against misfolding is modulated by the mutation process and plays an important role in protein evolution. The results presented here show that considering the stability against misfolding improves the performances of the MF model with respect to a model in which only the native state is considered, because it provides larger likelihood to the observed protein sequences, it avoids that the hydrophobicity is overestimated, and it generates more stable protein sequences.
Besides representing misfolding, our model has another advantage with respect to other models of structural constrained protein evolution such as Rodrigue et al. (2005) and Bordner and Mittelmann (2014). These models approximate the amino acid distributions through pairwise terms, and therefore they cannot be implemented in standard programs of phylogenetic inference, whereas our model with independent sites is much simpler from a computational point of view and it can be combined with standard molecular evolution algorithms.
The method presented here has still a considerable room for improvement, in particular improving two key ingredients of our method that ultimately stem from the mutation model: The exchangeability matrix and the background distribution of amino acids.
The exchangeability matrix very strongly affects the values of the likelihood. We cannot adopt empirical exchangeability matrices such as JTT (Jones et al. 1992) and WAG (Whelan and Goldman 2001), because they represent both mutation and selection, whereas in our model selection is represented by the condition on . Consistently, if we adopt the exchangeability matrix of JTT or WAG together with our MF distributions, we get results that are worse than with the pure empirical models. We addressed this problem by adopting an exchangeability matrix that, together with the MF distributions, produces a flux of amino acids that is equivalent to the corresponding flux in the empirical model (we impose this condition because the parameters of the empirical models are obtained by estimating fluxes between amino acids). Nevertheless, the performances might improve considerably if we optimize the 190 parameters of the exchangeability matrix for the MF model using a large data set of aligned proteins, as BM did for their structurally constrained model.
An attractive possibility is to derive the exchangeability matrix from an underlying mutation model. We developed a mutation model at the codon level with the double goal to derive an exchangeability matrix devoid of the influence of the selection process that affects empirical exchangeability matrices, and to model a background distribution of amino acids with fewer than 19 free parameters. The model that we implemented considered a mutation process at the nucleotide level, the known enhancement of the mutation rate at CpG dinucleotides, and assumed that mutations to stop codons are strongly forbidden by natural selection (this was the only point at which selection entered the model). The parameters of the model were fixed through an ML procedure. Nevertheless, the AIC obtained with the background distributions derived from the mutation model was clearly worse than the one obtained with the frequencies derived from the alignments for all studied families, despite having 4 instead of 19 free parameters. Furthermore, the exchangeability matrix derived from the mutation model had poor performances in terms of likelihood. These results indicate that the mutation model that we applied was not sufficiently accurate with respect to empirical models with more parameters. However, we think that the difficult goal to obtain a better mutation model can be greatly rewarding. Because the requirements that this model has to fulfill to improve the likelihoods are highly demanding, their accomplishment may also yield interesting insight on protein evolution.
Although we only tested its performances for phylogenetic inference, the MF model may have as well applications in the context of protein sequence design, because sequences generated with the model are predicted to correspond to stable proteins, and of protein alignments, given its analogy with Hidden Markov Models.
It is remarkable that, despite the simplicity of the independent sites assumption, the MF model apparently performs better than the method of RO as reported in Bordner and Mittelmann (2014), which uses pairwise distributions. Note that the MF model and the RO model are quite similar under the point of view of parameters, because they both adopt the same empirical exchangeability matrix (JTT) and the same contact interaction energies (Bastolla et al. 2001). Therefore, their differences can be mainly attributed to three points: 1) Including (MF) or not (RO) stability against misfolding; 2) adapted exchangeability matrix (eq. 6) (MF) versus empirical exchangeability matrix (RO); and (3) independent sites (MF) versus pairwise (RO) approximation.
Furthermore, in three of the four cases the MF model performs better than the independent sites version of the method of BM that is based on the solvent accessibility of each site (SA) and in principle is similar to our method, despite the SA method optimizes a large number of parameters from databases of protein families. Then, in one over four cases, MF model performs better than the new pairwise model by Bordner and Mittelmann (2014) that is based on factor graphs and is computationally much more complex than the MF model and optimizes for phylogenetic inference parameters that are equivalent to a contact interaction matrix and an exchangeability matrix.
It is interesting that in all three cases in which the BM model outperforms the MF model, the sequence identity is larger than 90%, while the MF is the best one when the average sequence identity drops to the (still high) value of 74%. Based on few comparisons, we do not know whether this behavior is general; however, it suggests that the advantage of using pairwise distributions instead of independent sites does not increase for highly divergent sequences, as one might have expected, because the independent sites approximation is only accurate at small evolutionary distances.
Methods
Background Distribution
The first ingredient of our MF model is the site-independent background amino acids distribution that we attribute to the underlying mutation process. We obtained the best results when these frequencies are derived from the frequencies observed in the PDB sequence or in the multiple alignment. In this case, the background distribution has 19 free parameters. All results presented in the Results section were obtained with this choice. We also tried to reduce the number of free parameters defining a mutation process at the codon level. This attempt gave poor results, but it may be an important direction of future improvement. Another possible direction for improvement would be to weight the sequences in the multiple alignment in order to reduce the influence on the background distribution of unbalanced phylogenetic sampling.
Folding Free Energy
We adopt a model of protein folding stability based on contact interactions. We consider three thermodynamic states: The native state, which is assumed to consists of a folded structure with its attraction basin, a state consisting of misfolded compact conformation, and the unfolded state. The vibrational entropy (entropy of the protein confined to its local energy minimum, such that it can be computed through normal mode analysis of the native state or a particular misfolded state) of the folded native state is assumed to be compensated by the vibrational entropy of each misfolded state (Karplus et al. 1987), therefore it is not estimated. We estimate the native free energy as
| (9) |
where is the contact matrix of the native structure represented in the PDB ( if residues i and j are closer than 4.5 Å, 0 otherwise), Ai is the amino acid at position i, and U(a, b) is the 20 × 20 contact interaction matrix of Bastolla et al. (2001). The free energy of the unfolded state is estimated as , where T is the temperature in units in which kB = 1, L is the chain length, and SU is the conformational entropy per residue of an unfolded chain. The misfolded state consists of the ensemble of compact but wrongly folded conformations, which we model as an ensemble of contact matrices of length L and number of contacts in the range expected for compact protein structures, whose statistical properties are obtained analyzing the compact submatrices of L residues in the PDB, a technique designated as threading in the bioinformatics jargon. Its statistical mechanics is often described by the random energy model (Derrida 1981) that models the energy as a Gaussian random variable (Garel and Orland 1988; Shakhnovich and Gutin 1989; Bryngelson et al. 1995), so that the free energy is determined by the first and second moment of the energy. A more accurate computation also includes the third moment of the energy (Minning et al. 2013). We implemented this correction, but we found that it slightly worsens the likelihood, perhaps due to the approximations that we have to adopt for making the iterative computation feasible, and we do not consider it in our default algorithm, which is based on the following model of the free energy of the misfolded state:
| (10) |
where LSC is the logarithm of the number of compact contact matrices, represents the average over the set of compact contact matrices of L residues, and we assume for simplicity that the conformational entropy is approximately the same for all compact structures and it can be ignored for computing free energy differences.
Our computational problem is to compute the sequence average of equation (10) in a way that is fast enough for allowing several iterations of the MF algorithm. For this reason, we simplify the computation of the misfolding free energy as detailed in the next section.
Solution of the Mean-Field Model
By equating the derivatives of equation (3) to zero, we obtain the following implicit solution of the MF equation:
| (11) |
| (12) |
where a denotes one of the 20 amino acids, i is a protein site, zi is determined through the normalization condition , and is the MF average of the folding free energy. Starting from an initial guess or from the distribution previously obtained for a close value of Λ, these equations are iterated until convergence. However, because convergence is not guaranteed, after a large number of iterations our algorithm chooses the distribution closest to convergence. We observed that this criterion yields the largest final likelihood. The above equations are explicitated in the Appendix, where we describe all necessary computations.
ML Optimization of the Lagrange Multiplier
In order to numerically determine the value of Λ that maximizes the likelihood, we compute the MF distribution for values of Λ, starting from and incrementing it by 0.1 at each step. The solution relative to the previous value of Λ is used as the starting point of the iterative algorithm. After this coarse exploration, the value of Λ that maximizes the likelihood is obtained through iterative quadratic interpolations.
Methods for Phylogenetic Inference
In order to apply the MF model for phylogenetic inference, we input to our program Prot_Evol the representative protein structure and all the sequences of the protein family and we obtain as output the site-specific amino acid distributions and the global exchangeability matrix. We then align the sequences with the program MAFFT (Katoh and Standley 2013). This was done even for families that were aligned in the Pfam database (Punta et al. 2012), because we observed that realigning them improved the quality of the alignment and the values of the likelihood for all models. We discard columns of the alignment for which the representative protein or more than 50% of the proteins have a gap, and we compute a phylogenetic tree applying the Neighbor Joining algorithm of Saitou and Nei (1987).
The alignment, the tree, and the substitution models (either empirical substitution models or the model generated with the MF distributions) are then input to the program PAML (Yang 2007) for computing the likelihood of the data given in the model. For the site-specific MF models, we proceed in two steps. In the first step, we optimize the branch lengths for all sites using the complete alignment and the site-averaged amino acid frequencies, . In the second step, we compute the likelihood for each site using the corresponding column of the alignment, the site-specific frequencies, and the branch lengths optimized in the previous step. We use the same exchangeability matrix in both steps. The computation of branch lengths is required to modify the code of PAML, because this program internally normalizes the rate matrix in such a way that the average rate is always one. In this way, the time unit of the rate matrix is lost and the branch lengths are output in arbitrary units, which would prevent using them in the second step. To avoid this problem, we eliminated the internal normalization of the rates.
Supplementary Material
Acknowledgments
U.B. gratefully thanks Markus Porto for participating in many prior stages of this work. We would like to thank David Liberles for helpful comments and discussions. This work was supported by the Spanish Ministery of Economy through the grant BFU-40020 to U.B. M.A. was supported by the Spanish Government through the Juan de la Cierva fellowship JCI-2011-10452. Research at the CBMSO is facilitated by the Fundación Ramón Areces. We thank three anonymous reviewers for insightful comments.
Appendix: Numerical Solution of the Mean-Field Equations
We start by approximating the misfolding free energy through the average contact energy of the misfolding ensemble, so that it holds . This approximation was indicated as in the main text. In this case, equation (11) has the simple form
| (13) |
where is the interaction energy of amino acid a interacting with the ensemble of amino acids present at site j, in the spirit of the MF approximation. We can further simplify it by adopting the hydrophobic approximation , where the so-called hydrophobicity vector ha is determined as the main eigenvector of the contact interaction matrix U(a, b) [38]. In this case, we obtain
| (14) |
where the field can be interpreted as the MF hydrophobicity of site j. The self-consistent equation (14) can be solved iteratively and they rapidly converge. They can be used as a starting point for the more complicated MF models that include other terms of the misfolding free energy. In the following, we simplify the notation by omitting the superscript Λ, with the understanding that this parameter is fixed at the value determined by the ML condition (eq. 4).
If we set in the above equations, considering only the native free energy, we obtain the zeroth order MF model that is qualitatively similar to an earlier proposal by one of us and coworkers (Porto et al. 2005). The models and are obtained by adding the second and the third moment of the misfolding energy, respectively. We found the best results with , which we will denote as , omitting the superscript that specifies the order of the misfolding free energy.
When including the second moment of the energy, we have to consider the correlations between pairs of contacts, whose number grows as the fourth power of the number of sites L. There is not enough data to accurately compute such correlations, and storing this information in memory would cause computational problems. Therefore, we reduce the size of the data that have to be estimated and stored adopting the so-called homogeneous approximation (Minning et al. 2013). This approximation assumes that the probability of a contact between two sites only depends on their difference in the sequence but not on their absolute position, , so that the number of data increases only linearly with L. For estimating the contact correlations , we have to distinguish three cases: 1) ij = kl, that is, only two of the sites are different; we indicate the corresponding contact correlation as , where the numbers indicate that this is the contact correlation of order 2 with 2 different sites and 1 different contact; 2) i = k, , that is, three of the sites are different; we approximate neglecting the dependence on sites j and l; 3) all four sites are different, , and in this case we neglect the dependence on all four indices. These coefficients are estimated as
| (15) |
| (16) |
| (17) |
where mi is the number of contacts of site i, is its average over the misfolding ensemble, and is the total number of contacts. With this notation, we compute the second moment of the energy of the misfolded ensemble as
| (18) |
and the MF distribution can be computed as
| (19) |
| (20) |
with and .
Finally, we have to take into account that the analytic expression for computing the free energy of the misfolded state, equation (10), is only valid if the temperature is higher than the freezing temperature of the system, . For the MF model, we determine the freezing temperature using the average of the second moment of the energy over the MF distribution, . If the temperature T is smaller than the freezing temperature, we have to use Tf instead of T in equation (20).
References
- Akaike H. A new look at the statistical model identification. IEEE Trans Automatic Control. 1974;19:716–723. [Google Scholar]
- Arenas M, Dos Santos HG, Posada D, Bastolla U. Protein evolution along phylogenetic histories under structurally constrained substitution models. Bioinformatics. 2013;29:3020–3028. doi: 10.1093/bioinformatics/btt530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babajide A, Hofacker IL, Sippl MJ, Stadler PF. Neutral networks in protein space: a computational study based on knowledge-based potentials of mean force. Fold Des. 1997;2:261–269. doi: 10.1016/S1359-0278(97)00037-0. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Farwer J, Knapp EW, Vendruscolo M. How to guarantee optimal stability for most representative structures in the Protein Data Bank. Proteins. 2001;44:79–96. doi: 10.1002/prot.1075. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Moya A, Viguera E, van Ham RC. Genomic determinants of protein folding thermodynamics in prokaryotic organisms. J Mol Biol. 2004;343:1451–1466. doi: 10.1016/j.jmb.2004.08.086. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Ortiz AR, Porto M, Teichert F. Effective connectivity profile: a structural representation that evidences the relationship between protein structures and sequences. Proteins. 2008;73:872–888. doi: 10.1002/prot.22113. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Porto M, Roman HE, Vendruscolo M. Statistical properties of neutral evolution. J Mol Evol. 2003;57(Suppl 1):S103–S119. doi: 10.1007/s00239-003-0013-4. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Porto M, Roman HE, Vendruscolo M. Principal eigenvector of contact matrices and hydrophobicity profiles in proteins. Proteins. 2005;58:22–30. doi: 10.1002/prot.20240. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Porto M, Roman HE, Vendruscolo M. A protein evolution model with independent sites that reproduces site-specific amino acid distributions from the Protein Data Bank. BMC Evol Biol. 2006;6:43. doi: 10.1186/1471-2148-6-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastolla U, Roman HE, Vendruscolo M. Neutral evolution of model proteins: diffusion in sequence space and overdispersion. J Theor Biol. 1999;200:49–64. doi: 10.1006/jtbi.1999.0975. [DOI] [PubMed] [Google Scholar]
- Berg J, Willmann S, Lässig M. Adaptive evolution of transcription factor binding sites. BMC Evol Biol. 2004;4:42. doi: 10.1186/1471-2148-4-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom JD, Silberg JJ, Wilke CO, Drummond DA, Adami C, Arnold FH. Thermodynamic prediction of protein neutrality. Proc Natl Acad Sci U S A. 2005;102:606–611. doi: 10.1073/pnas.0406744102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bordner AJ, Mittelmann HD. A new formulation of protein evolutionary models that account for structural constraints. Mol Biol Evol. 2014;31:736–749. doi: 10.1093/molbev/mst240. [DOI] [PubMed] [Google Scholar]
- Bornberg-Bauer E, Chan HS. Modeling evolutionary landscapes: mutational stability, topology, and superfunnels in sequence space. Proc Natl Acad Sci U S A. 1999;96:10689–10694. doi: 10.1073/pnas.96.19.10689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- Bussemaker HJ, Thirumalai D, Bhattacharjee JK. Thermodynamic stability of folded proteins against mutations. Phys Rev Lett. 1997;79:3530–3533. [Google Scholar]
- Chan HS, Zhang Z, Wallin S, Liu Z. Cooperativity, local-nonlocal coupling, and nonnative interactions: principles of protein folding from coarse-grained models. Annu Rev Phys Chem. 2011;62:301–326. doi: 10.1146/annurev-physchem-032210-103405. [DOI] [PubMed] [Google Scholar]
- DePristo MA, Weinreich DM, Hartl DL. Missense meanderings in sequence space: a biophysical view of protein evolution. Nat Rev Genet. 2005;6:678–687. doi: 10.1038/nrg1672. [DOI] [PubMed] [Google Scholar]
- Derrida B. Random energy model: an exactly solvable model of disordered systems. Phys Rev B. 1981;24:2613–2626. [Google Scholar]
- Dokholyan NV, Shakhnovich EI. Understanding hierarchical protein evolution from first principles. J Mol Biol. 2001;312:289–307. doi: 10.1006/jmbi.2001.4949. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Maximum likelihood and minimum-steps methods for estimating evolutionary trees from data on discrete characters. Syst Zool. 1973;22:240–249. [Google Scholar]
- Felsenstein J. Sunderland (MA): Sinauer Associates; 2004. Inferring phylogenies. [Google Scholar]
- Fornasari MS, Parisi G, Echave J. Site-specific amino acid replacement matrices from structurally constrained protein evolution simulations. Mol Biol Evol. 2002;19:352–356. doi: 10.1093/oxfordjournals.molbev.a004089. [DOI] [PubMed] [Google Scholar]
- Franzosa EA, Xia Y. Structural determinants of protein evolution are context-sensitive at the residue level. Mol Biol Evol. 2009;26:2387–2395. doi: 10.1093/molbev/msp146. [DOI] [PubMed] [Google Scholar]
- Garel T, Orland H. Mean-field model for protein folding. Europhys Lett. 1988;6:307–310. [Google Scholar]
- Goldstein RA. The evolution and evolutionary consequences of marginal thermostability in proteins. Proteins. 2011;79:1396–1407. doi: 10.1002/prot.22964. [DOI] [PubMed] [Google Scholar]
- Govindarajan S, Goldstein RA. Evolution of model proteins on a foldability landscape. Proteins. 1997;29:461–466. doi: 10.1002/(sici)1097-0134(199712)29:4<461::aid-prot6>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- Grahnen JA, Nandakumar P, Kubelka J, Liberles DA. Biophysical and structural considerations for protein sequence evolution. BMC Evol Biol. 2011;11:361. doi: 10.1186/1471-2148-11-361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutin AM, Abkevich VI, Shakhnovich EI. Evolution-like selection of fast-folding model proteins. Proc Natl Acad Sci U S A. 1995;92:1282–1286. doi: 10.1073/pnas.92.5.1282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halpern AL, Bruno WJ. Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies. Mol Biol Evol. 1998;15:910–917. doi: 10.1093/oxfordjournals.molbev.a025995. [DOI] [PubMed] [Google Scholar]
- Huang TT, del Valle Marcos ML, Hwang JK, Echave J. A mechanistic stress model of protein evolution accounts for site-specific evolutionary rates and their relationship with packing density and flexibility. BMC Evol Biol. 2014;14:78. doi: 10.1186/1471-2148-14-78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Taylor WR, Thornton JM. The rapid generation of mutation data matrices from protein sequences. Comput Appl Biosci. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- Karplus M, Ichiye T, Pettitt BM. Configurational entropy of native proteins. Biophys J. 1987;52:1083–1085. doi: 10.1016/S0006-3495(87)83303-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katoh K, Standley DM. MAFFT multiple sequence alignment software version 7: improvements in performance and usability. Mol Biol Evol. 2013;30:772–780. doi: 10.1093/molbev/mst010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koshi JM, Goldstein RA. Models of natural mutations including site heterogeneity. Proteins. 1998;32:289–295. [PubMed] [Google Scholar]
- Koshi JM, Goldstein RA. Analyzing site heterogeneity during protein evolution. Pac Symp Biocomput. 2001:191–202. doi: 10.1142/9789814447362_0020. [DOI] [PubMed] [Google Scholar]
- Koshi JM, Mindell DP, Goldstein RA. Using physical-chemistry-based substitution models in phylogenetic analyses of HIV-1 subtypes. Mol Biol Evol. 1999;16:173–179. doi: 10.1093/oxfordjournals.molbev.a026100. [DOI] [PubMed] [Google Scholar]
- Lartillot N, Philippe H. A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process. Mol Biol Evol. 2004;21:1095–1109. doi: 10.1093/molbev/msh112. [DOI] [PubMed] [Google Scholar]
- Liberles DA, Teichmann SA, Bahar I, Bastolla U, Bloom J, Bornberg-Bauer E, Colwell LJ, de Koning AP, Dokholyan NV, Echave J, et al. The interface of protein structure, protein biophysics, and molecular evolution. Protein Sci. 2012;21:769–785. doi: 10.1002/pro.2071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendez R, Fritsche M, Porto M, Bastolla U. Mutation bias favors protein folding stability in the evolution of small populations. PLoS Comput Biol. 2010;6:e1000767. doi: 10.1371/journal.pcbi.1000767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minning J, Porto M, Bastolla U. Detecting selection for negative design in proteins through an improved model of the misfolded state. Proteins. 2013;81:1102–1112. doi: 10.1002/prot.24244. [DOI] [PubMed] [Google Scholar]
- Mirny LA, Abkevich VI, Shakhnovich EI. How evolution makes proteins fold quickly. Proc Natl Acad Sci U S A. 1998;95:4976–4981. doi: 10.1073/pnas.95.9.4976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisi G, Echave J. Structural constraints and emergence of sequence patterns in protein evolution. Mol Biol Evol. 2001;18:750–756. doi: 10.1093/oxfordjournals.molbev.a003857. [DOI] [PubMed] [Google Scholar]
- Plotkin SS, Onuchic JN. Understanding protein folding with energy landscape theory. Part II: quantitative aspects. Q Rev Biophys. 2002;35:205–286. doi: 10.1017/s0033583502003785. [DOI] [PubMed] [Google Scholar]
- Porto M, Roman HE, Vendruscolo M, Bastolla U. Prediction of site-specific amino acid distributions and limits of divergent evolutionary changes in protein sequences. Mol Biol Evol. 2005;22:630–638. doi: 10.1093/molbev/msi048. [DOI] [PubMed] [Google Scholar]
- Punta M, Coggill PC, Eberhardt RY, Mistry J, Tate J, Boursnell C, Pang N, Forslund K, Ceric G, Clements J, et al. The Pfam protein families database. Nucleic Acids Res. 2012;40:D290–D301. doi: 10.1093/nar/gkr1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson DM, Jones DT, Kishino H, Goldman N, Thorne JL. Protein evolution with dependence among codons due to tertiary structure. Mol Biol Evol. 2003;20:1692–1704. doi: 10.1093/molbev/msg184. [DOI] [PubMed] [Google Scholar]
- Rodrigue N, Lartillot N, Bryant D, Philippe H. Site interdependence attributed to tertiary structure in amino acid sequence evolution. Gene. 2005;347:207–217. doi: 10.1016/j.gene.2004.12.011. [DOI] [PubMed] [Google Scholar]
- Saitou N, Nei M. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol Biol Evol. 1987;4:406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
- Sella G, Hirsh AE. The application of statistical physics to evolutionary biology. Proc Natl Acad Sci U S A. 2005;102:9541–9546. doi: 10.1073/pnas.0501865102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakhnovich E. Protein folding thermodynamics and dynamics: where physics, chemistry, and biology meet. Chem Rev. 2006;106:1559–1588. doi: 10.1021/cr040425u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakhnovich EI, Gutin AM. Formation of unique structure in polypeptide chains. Biophys Chem. 1989;34:187–199. doi: 10.1016/0301-4622(89)80058-4. [DOI] [PubMed] [Google Scholar]
- Taverna DM, Goldstein RA. Why are proteins marginally stable? Proteins. 2002;46:105–109. doi: 10.1002/prot.10016. [DOI] [PubMed] [Google Scholar]
- Tiana G, Broglia RA, Roman HE, Vigezzi E, Shakhnovich EI. Folding and misfolding of designed proteinlike chains with mutations. J Chem Phys. 1998;108:757–761. [Google Scholar]
- Uversky VN, Dunker AK. Understanding protein non-folding. Biochim Biophys Acta. 2010;1804:1231–1264. doi: 10.1016/j.bbapap.2010.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whelan S, Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol Biol Evol. 2001;18:691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
- Whelan S, Liò P, Goldman N. Molecular phylogenetics: state-of-the-art methods for looking into the past. Trends Genet. 2001;17:262–272. doi: 10.1016/s0168-9525(01)02272-7. [DOI] [PubMed] [Google Scholar]
- Wilke CO. Bringing molecules back into molecular evolution. PLoS Comput Biol. 2012;8:e1002572. doi: 10.1371/journal.pcbi.1002572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. Maximum likelihood estimation of phylogeny from DNA sequences when substitution rates differ over sites. Mol Biol Evol. 1993;10:1396–1401. doi: 10.1093/oxfordjournals.molbev.a040082. [DOI] [PubMed] [Google Scholar]
- Yang Z. PAML 4: phylogenetic analysis by maximum likelihood. Mol Biol Evol. 2007;24:1586–1591. doi: 10.1093/molbev/msm088. [DOI] [PubMed] [Google Scholar]
- Yang Z, Nielsen R, Masami H. Models of amino acid substitution and applications to mitochondrial protein evolution. Mol Biol Evol. 1998;15:1600–1611. doi: 10.1093/oxfordjournals.molbev.a025888. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.