Are Convergent and Parallel Amino Acid Substitutions in Protein Evolution More Prevalent Than Neutral Expectations?

Abstract

Convergent and parallel amino acid substitutions in protein evolution, collectively referred to as molecular convergence here, have small probabilities under neutral evolution. For this reason, molecular convergence is commonly viewed as evidence for similar adaptations of different species. The surge in the number of reports of molecular convergence in the last decade raises the intriguing question of whether molecular convergence occurs substantially more frequently than expected under neutral evolution. We here address this question using all one-to-one orthologous proteins encoded by the genomes of 12 fruit fly species and those encoded by 17 mammals. We found that the expected amount of molecular convergence varies greatly depending on the specific neutral substitution model assumed at each amino acid site and that the observed amount of molecular convergence is explainable by neutral models incorporating site-specific information of acceptable amino acids. Interestingly, the total number of convergent and parallel substitutions between two lineages, relative to the neutral expectation, decreases with the genetic distance between the two lineages, regardless of the model used in computing the neutral expectation. We hypothesize that this trend results from differences in the amino acids acceptable at a given site among different clades of a phylogeny, due to prevalent epistasis, and provide simulation as well as empirical evidence for this hypothesis. Together, our study finds no genomic evidence for higher-than-neutral levels of molecular convergence, but suggests the presence of abundant epistasis that decreases the likelihood of molecular convergence between distantly related lineages.

Introduction

Convergence refers to the evolutionary phenomenon that identical or similar traits emerge independently in two or more lineages such as the origins of wings in birds and bats (Stern 2013). Phenotypic convergence is widespread and has long been viewed as evidence for independent adaptations of different species to a common environmental challenge, because the probability of multiple independent origins of the same complex trait by genetic drift alone is likely to be extremely low (McGhee 2011). Convergence can also occur at the protein sequence level, and such molecular convergences are often separated into two types: convergent and parallel amino acid substitutions (Zhang and Kumar 1997). Convergent substitutions at an amino acid position of a protein refer to changes from different ancestral amino acids to the same descendant amino acid along independent evolutionary lineages. They are distinguished from parallel substitutions where the independent changes have occurred from the same ancestral amino acid. For simplicity, we refer to both types as molecular convergence in this article, unless otherwise noted. Similar to phenotypic convergence, molecular convergence is widely believed to reflect common adaptations of different organisms. But, because of the limited number of amino acids acceptable at any position, molecular convergence may occur by chance without the involvement of positive selection (Zhang and Kumar 1997).

The last decade has seen a surge in the number of reports of molecular convergence, virtually all of which were interpreted as results of positive selection (Zhang 2006; Christin et al. 2008, 2010; Jost et al. 2008; Castoe et al. 2009; Li et al. 2010; Liu et al. 2010, 2011, 2012; Davies et al. 2012; Feldman et al. 2012; Shen et al. 2012; Zhen et al. 2012; Stern 2013), although rigorous demonstrations of the involvement of adaptive selection are not easy and thus have been rare (Zhang 2006). For example, seven hearing-related proteins are known to exhibit various degrees of molecular convergence among two groups of bats and toothed whales that independently acquired echolocation (Li et al. 2008, 2010; Liu et al. 2010, 2011, 2012; Davies et al. 2012; Shen et al. 2012). But, only in prestin, the motor protein of the outer hair cells of the inner ear of the mammalian cochlea, is there evidence that the number of observed parallel amino acid substitutions in echolocators significantly exceeds the chance expectation (Li et al. 2010) and that these parallel substitutions are responsible for parallel functional changes of the protein (Liu et al. 2014). Despite these caveats, the growing number of molecular convergences discovered raises the intriguing question of whether adaptive molecular convergence is a common phenomenon in protein evolution.

Rokas and Carroll (2008) addressed the above question by examining eight genome-scale gene sets, each including four species. They showed that, in each gene set, the observed number of parallel amino acid substitutions significantly exceeds the random expectation under a neutral model of amino acid substitution. They suggested that this excess arose from common positive selection in two lineages and/or purifying selection constraining the number of amino acids acceptable at a site that was not incorporated into their neutral model. A similar conclusion was reached by Bazykin et al. (2007). Castoe et al. (2009) also reported a larger amount of molecular convergence as well as divergence in vertebrate mitochondrial genes than expected from a neutral model. However, none of the studies investigated whether the observed amount of molecular convergence can be fully explained without invoking positive selection. As such, the prevalence of adaptive molecular convergence remains unclear.

In this study, we address the above question using genome-wide data sets of protein sequence alignments of fruit flies and mammals, respectively. We compare the inferred numbers of molecular convergences between a pair of lineages with the neutral expectations derived from several different substitution models, including those incorporating site-specific amino acid compositions. We found that the neutral expectations vary substantially depending on the model used and that some neutral models are capable of explaining the large numbers of molecular convergences observed. Interestingly, the observed number of molecular convergences relative to the neutral expectation decreases with the genetic distance between the two evolutionary lineages concerned, regardless of the specific neutral model assumed. We propose and provide evidence that this phenomenon is a result of prevalent epistasis in protein evolution, which renders the amino acids acceptable at a position different in different species.

Results

Observed and Expected Numbers of Molecular Convergences

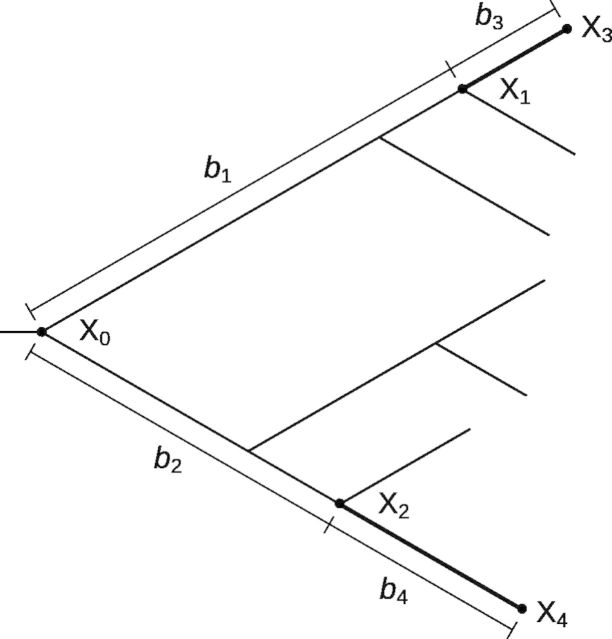
Let us use an alignment of seven orthologous protein sequences, whose phylogenetic relationships are depicted by the tree in figure 1, as an example to illustrate our analysis. Suppose we are interested in molecular convergence along the two thick branches (fig. 1). We first infer the ancestral amino acids at all interior nodes of the tree for each site of the protein (see Materials and Methods). Let X_i be the amino acid at node i for a given site. By definition, convergent substitutions on the thick branches occur at those sites where X₁ ≠ X₂, X₃ = X₄, X₃ ≠ X₁, and X₄ ≠ X₂. Similarly, parallel substitutions on the thick branches occur at those sites where X₁ = X₂, X₃ = X₄, X₃ ≠ X₁, and X₄ ≠ X₂. This way, the numbers of sites that have experienced convergent and parallel substitutions in the thick branches are respectively counted and referred to as the “observed” numbers of convergent and parallel substitutions.

Fig. 1.

A tree illustrating the counting of the numbers of observed and expected molecular convergences between two thick branches. For a given position, the amino acids at nodes 0–4 are indicated by X₀–X₄, respectively. The relevant branch lengths are indicated by the b values.

Under the assumption that amino acid substitutions at a site follow a Markov process, we can compute the probability that a site experiences convergent (or parallel) substitutions along the thick branches, given the amino acid substitution rate matrix, the substitution rate at the site relative to the average rate of the protein considered, amino acid equilibrium frequencies, and all branch lengths measured by the expected numbers of substitutions per site for the protein considered (see Materials and Methods). For a protein, the expected number of sites with convergent (or parallel) substitutions is the sum of these probabilities across all sites of the protein.

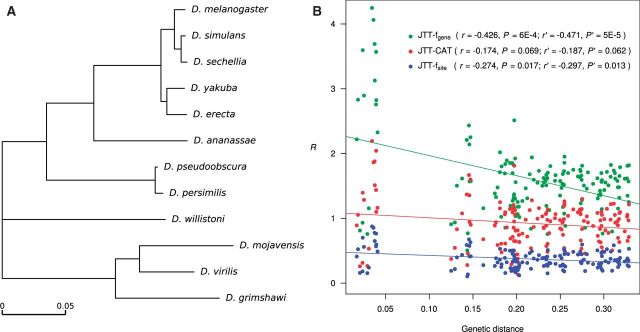
Using this framework, we compared the observed and expected numbers of convergent and parallel substitutions, respectively, in 5,935 orthologous protein alignments of 12 Drosophila species, totaling 2,028,428 amino acid sites after the removal of gaps and ambiguous sites. For each alignment, we used PAML (Yang 2007) to infer the branch lengths, substitution rate of each site relative to the average rate of the entire protein, and ancestral sequences under the known topology of the species tree (fig. 2A). We first focused on the two exterior branches that respectively lead to Drosophila yakuba and D. mojavensis. In computing the expected numbers of convergent and parallel substitutions in a protein, we used the Jones, Taylor, and Thorton (JTT)-f_gene model of amino acid substitution. This model is based on the average substitution patterns of many proteins known as the JTT model (Jones et al. 1992), with the equilibrium frequencies of the 20 amino acids replaced by the observed amino acid frequencies in the protein concerned.

Fig. 2.

The observed numbers of molecular convergences, relative to the expected numbers, in Drosophila proteins. (A) Phylogeny of the 12 Drosophila species. The topology follows Drosophila 12 Genomes Consortium et al. (2007), and the branch lengths are inferred using the concatenated sequences of all 5,935 proteins, under the JTT-f model, where f refers to the overall amino acid frequencies from all 5,935 proteins. (B) Negative correlation between the observed number of molecular convergences relative to the expected number (R) and the genetic distance between the two branches concerned. Each dot represents one branch pair, and different colors show the results under different substitution models. The R values under JTT-f_gene and JTT-f_site are based on all 5,935 proteins, whereas those under JTT-CAT are based on a subset of 1,081 proteins. Genetic distance is the number of amino acid substitutions per site between the two younger ends of the two branches considered. Lines show linear regressions. The r values are Pearson’s correlation coefficients. Both r and P values are from Mantel tests, and r′ and P′ are from partial Mantel tests controlling the between-node amino acid content difference.

The total number of observed convergent sites in the 5,935 fly proteins is 292 for the pair of branches considered, whereas the expected number is only 194.2 (table 1); the difference is statistically significant (P < 10⁻¹⁰, Poisson test). The total number of observed parallel sites is 650, also significantly greater than the expected number of 388.6 (P < 10⁻¹²²). The ratio (R) between the observed and expected numbers of sites is 1.50 for convergent substitutions and 1.67 for parallel substitutions (table 1). Rokas and Carroll (2008) were unable to study convergent substitutions due to their use of four-taxon trees. For parallel substitutions, our result is similar to what Rokas and Carroll reported.

Table 1.

Observed Numbers of Convergent and Parallel Sites and the Corresponding Numbers Expected under Various Neutral Models of Amino Acid Substitution.

Type of Sites	Number of Sites Examined	Observed Number of Sites	Expected Number of Sites		Ra	P Valueb
			Substitution Model	Number of Sites
Convergent sites
	2,028,428	292	JTT-fgene	194.2	1.50	3.8E-11
	2,028,428	292	JTT-fsite	475.2	0.61	9.4E-20
	780,615	93	JTT-CAT	118.0	0.79	1.0E-3
Parallel sites
	2,028,428	650	JTT-fgene	388.6	1.67	3.2E-34
	2,028,428	650	JTT-fsite	2125.7	0.31	8.8E-309
	780,615	218	JTT-CAT	184.8	1.18	9.4E-3

Note.—Results presented are for the two exterior branches leading to Drosophila yakuba and D. mojavensis, respectively, in figure 2A.

^aRatio between the observed number and expected number.

^bA statistical test is conducted under the assumption that the number of convergent (or parallel) sites follows a Poisson distribution with the mean equal to the expected number. When the observed number is smaller than the expected, the lower tail probability is given; when the observed number is larger than the expected, the upper tail probability is given.

Considering that the amino acids acceptable at a site likely differ from those acceptable at another site because of differences in structural and functional roles of different sites, we used a second model termed JTT-f_site to compute the expected numbers of convergent and parallel sites, respectively. That is, for each site, the equilibrium amino acid frequencies in the JTT model are replaced with the observed amino acid frequencies at the site across all sequences in the alignment. We found that the number of observed amino acids at a site averages 1.56 across all sites and 2.74 across all variable sites. Obviously, considering this small number of acceptable amino acids at a site should increase the expected number of molecular convergence. Indeed, the expected numbers of convergent (475.2) and parallel (2125.7) sites both increase substantially, compared with those under the JTT-f_gene model (table 1). As a result, R reduces to 0.61 for convergent sites and 0.31 for parallel sites, respectively (table 1). Thus, if the amino acid frequencies observed at a site across the 12 Drosophila species truly reflect the equilibrium frequencies at the site, molecular convergence has occurred not more but less frequently than what the neutral model predicts. One caveat in the above analysis is that, because the number of taxa used is smaller than 20 and because the total branch length (0.796 substitutions per site) of the Drosophila tree is also much smaller than 20, the observation of a limited number of different amino acids at a site may not mean that only the observed amino acids are acceptable but could be due to insufficient evolutionary time and taxon sampling for all acceptable amino acids to appear.

For the above reason, we tried the third model, JTT-CAT (Lartillot and Philippe 2004), in estimating the expected numbers of convergent and parallel sites. Instead of having one set of equilibrium amino acid frequencies for all sites of a protein (JTT-f_gene) or one set per site (JTT-f_site), CAT uses a Bayesian mixture model for among-site heterogeneities in amino acid frequencies. It estimates the total number of classes of sites and their respective amino acid frequencies, as well as the affiliation of each site to a given class. We expect that the JTT-CAT model will produce results that are between those from JTT-f_gene and JTT-f_site. However, because JTT-CAT is highly computationally intensive, we analyzed 1,081 relatively long proteins from the entire set of 5,935 proteins in an attempt to acquire the most information with the least amount of time. The expected numbers of convergent and parallel sites under JTT-CAT (table 1), after being extrapolated to all 5,935 proteins, are 306.6 and 480.2, respectively. As predicted, these numbers are between the corresponding values under JTT-f_gene and JTT-f_site. Consequently, R values under JTT-CAT (0.79 for convergent sites and 1.18 for parallel sites) are between those under JTT-f_gene and JTT-f_site (table 1).

To examine if the above patterns are specific to the pair of branches considered, we also analyzed molecular convergence for the two exterior branches respectively leading to D. melanogaster and D. yakuba. Similar patterns were found, although both observed and expected numbers of molecular convergences are much lower for this branch pair (supplementary table S1, Supplementary Material online), likely due to the much shorter D. melanogaster branch compared with the D. mojavensis branch (fig. 2A). Together, these results show that the observed numbers of convergent and parallel substitutions are no longer greater than their respective neutral expectations when among-site heterogeneities in equilibrium amino acid frequencies are considered.

Lower Rates of Molecular Convergence in More Distantly Related Lineages

In addition to the two pairs of exterior branches in the Drosophila tree, we analyzed all other pairs of branches in the tree that are unconnected and do not belong to the same evolutionary path. We excluded connected branch pairs because of the difficulty in inferring molecular convergence in these branch pairs. For example, parallel substitutions in the exterior branches respectively leading to D. yakuba and D. erecta will almost always be inferred as a substitution in the interior branch leading to the common ancestor of these two species (fig. 2A). Pairs of branches in the same evolutionary path were excluded, because in such cases the node at the beginning of one branch is a descendant of the node at the end of the other branch, violating the requirement for independent evolution in the definition of convergence. Note that although the tree in figure 2A is unrooted, we treated the deepest node as the root when deciding the evolutionary direction, which should not affect our analysis under the Markov process of amino acid substitution assumed here. For each pair of branches considered, we calculated the aforementioned ratio (R) between the number of molecular convergences (i.e., the total number of convergent and parallel sites) observed and that expected under a neutral substitution model. Under the same substitution model, we compared R of different branch pairs. Interestingly, R declines with the increase of the genetic distance between the two branches compared, where the genetic distance is measured by the total length of the branches connecting the younger ends of the two branches concerned (fig. 2B). Because the same branch is used in multiple branch pairs, branch pairs are not independent from one another. We thus tested the statistical significance of Pearson’s correlation between R and genetic distance using a Mantel test that controls such nonindependence (Mantel 1967). We found the correlation significant when the neutral expectations were computed under the JTT-f_gene model (Pearson’s correlation coefficient r = −0.426, P = 0.0006) or JTT-f_site model (r = −0.274, P = 0.017). When the neutral expectations were computed under JTT-CAT (based on the subset of 1,081 genes analyzed), the correlation was marginally significant (r = −0.174, P = 0.069).

To examine the generality of the above observation, we repeated the analysis in a set of 17 mammals, including 14 placental mammals, 2 marsupials, and the monotreme platypus (fig. 3A). The data set consists of 2,759 one-to-one orthologous proteins, with a total length of 1,079,696 amino acid sites after the removal of gaps and ambiguous sites. We used either the JTT-f_gene model or JTT-f_site model to compute the expected numbers of molecular convergences, but did not use the JTT-CAT model due to its high demand for computing time. The results obtained from the mammalian proteins are highly similar to those from the Drosophila proteins. First, R generally exceeds 1 under JTT-f_gene but is lower than 1 under JTT-f_site (fig. 3B). Second, regardless of the substitution model used in computing the expected numbers of molecular convergences, R declines with the increase of the genetic distance between the pair of evolutionary lineages compared (fig. 3B). Mantel test of the negative correlation between genetic distance and R showed statistical significance under each model applied (r = −0.747, P = 0.0002 under JTT-f_gene; r = −0.618, P = 0.0004 under JTT-f_site).

Fig. 3.

The observed numbers of molecular convergences, relative to the expected numbers, in mammalian proteins. (A) Phylogeny of the 17 mammalian species. The topology follows Romiguier et al. (2013), and the branch lengths are inferred using the concatenated sequences of all 2,759 proteins, under the JTT-f model, where f refers to the overall amino acid frequencies from all 2,759 proteins. (B) Negative correlation between the observed number of molecular convergences relative to the expected number (R) and the genetic distance between the two branches concerned. Each dot represents one branch pair, and different colors show the results under different substitution models. Genetic distance is the number of amino acid substitutions per site between the two younger ends of the two branches considered. Lines show linear regressions. The r values are Pearson’s correlation coefficients. Both r and P values are from Mantel tests, and r′ and P′ are from partial Mantel tests controlling the between-node amino acid content difference.

Epistasis Reduces the Probability of Molecular Convergence between Divergent Lineages

What makes the observed number of molecular convergences relative to the neutral expectation decrease as the two lineages compared diverge? One likely scenario is that, at a given site, amino acids that are acceptable in one clade of a phylogeny become unacceptable in another clade, resulting in a decrease in the probability of convergence. In other words, if equilibrium amino acid frequencies at a site gradually change in evolution, branch pairs with higher genetic distances should show lower probabilities of molecular convergence, which is not considered in the current computation of the neutral expectation and hence results in lower R values.

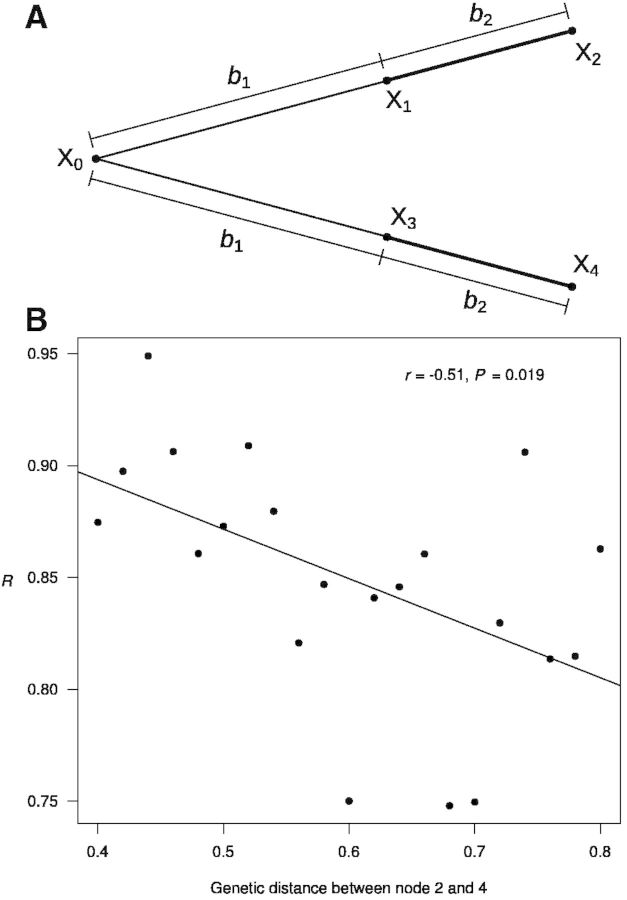
To test the hypothesis that changing site-specific equilibrium amino acid compositions in evolution could generate a negative correlation between R and the genetic distance between the branches under study, we first conducted a computer simulation using a simple tree of four taxa (fig. 4A), in which the two thick branches being investigated for molecular convergence have the same length of b₂, whereas the two interior branches have the same length of b₁. Thus, the genetic distance between nodes 2 and 4 is B = 2(b₁ + b₂). We simulated the evolution of 500,000 sites using a modified JTT-f_site model, where the equilibrium amino acid frequencies at each site gradually change in a random-walk fashion from the initial values taken from the original JTT model (Jones et al. 1992). For the two thick branches, we counted the number of molecular convergences that occurred and computed the expected number of molecular convergences assuming that the equilibrium amino acid frequencies were constant during evolution and equaled the average equilibrium frequencies in nodes 2 and 4. As predicted, the simulation showed that the number of observed molecular convergences relative to the expected number decreases with the rise in B (r = −0.51, P = 0.019), demonstrating that our hypothesis of changing site-specific equilibrium amino acid frequencies in evolution can in principle explain the reduction in the probability of molecular convergence between distantly related lineages. As a negative control, we repeated the above simulation with constant equilibrium amino acid frequencies in evolution. As expected, the number of observed molecular convergences relative to the expected number is no longer correlated with B (r = −0.13, P = 0.57).

Fig. 4.

Simulation of protein sequence evolution with changing equilibrium amino acid frequencies at each site. (A) The tree used in the simulation. Molecular convergence is examined for the two thick branches. Amino acids at nodes 0–4 are indicated by X₀–X₄, respectively. The branch lengths are indicated by the b values. (B) The number of observed molecular convergences relative to the expected (R) decreases with the genetic distance between nodes 2 and 4. Each dot represents a simulation of 500,000 sites. For different dots, b₁ varies but b₂ is the same.

To examine if acceptable amino acids at a site indeed differ between clades of organisms, we analyzed 16 proteins that have orthologous sequences from hundreds to thousands of species (Breen et al. 2012). They include 13 mitochondrial genome-encoded proteins, 1 chloroplast genome-encoded protein (Rubisco), and 2 nuclear genome-encoded proteins (elongation factor and histone). For each protein alignment, two mutually exclusive monophyletic clades were chosen, and the presence/absence of each of the 20 amino acids at each site in each clade was recorded. Because the number of taxa within each clade is large and the total branch length within each clade is ≫20 for most of the 16 proteins (fig. 5A), the amino acids allowed at a particular site can be approximated by the observed amino acids. For each site, we used the number of amino acids present in one clade but absent in the other clade (i.e., Hamming distance) as a measure of their amino acid compositional distance. For comparison, we computed the compositional distances after 1,000 random separations of all sequences from the two clades into two groups that are of the same sizes as the original clades. We calculated the P value as the proportion of times in which the randomized compositional distance equals or exceeds the observed distance. Because one test was conducted for each site in a protein, we corrected for multiple testing by converting the P values to corresponding Q values using the Benjamini–Hochberg method (Benjamini and Hochberg 1995). For all but one protein, the observed compositional distance is significantly (i.e., Q value <0.05) greater than the random expectation for a considerable number of sites (fig. 5A). The exception is the highly conserved histone H3.2, for which none of the 120 sites show significant between-clade differences in acceptable amino acids.

Fig. 5.

Site-specific differences in acceptable amino acids between different clades of organisms. (A) Frequency distribution of −log₁₀(Q value) measuring the significance of difference in acceptable amino acids at a site between two distantly related large clades. Arrows correspond to Q value = 0.05. For each plot, the name, total branch lengths (L), and number of species (N) of each of the two clades compared are indicated. The number of sites with Q value < 0.05 is indicated, followed by the total number of sites examined. (B) Frequency distribution of −log₁₀(Q value) measuring the significance of difference in acceptable amino acids at a site between two closely related clades.

In the above analysis, the two clades defined in the analysis of each protein tend to be old (e.g., ray-fined fishes and tetrapods) such that the two clades are relatively distantly related. Between such distantly related clades, it may not be surprising that acceptable amino acids are significantly different. To examine if the same phenomenon exists between relatively closely related clades, we examined COX2 and CYTB, for which sufficient numbers of sequences are available for this analysis. We found that between the Drosophila and Sophophora subgenera, 4 of 229 sites in COX2 show significant amino acid compositional differences (fig. 5B). Similarly, between the sister families of Muridae and Cricetidae, 50 of 381 sites in CYTB show significant compositional differences (fig. 5B).

These results demonstrate that acceptable amino acids at a site change significantly between sister families of mammals or even within an insect genus during evolution. It is likely that epistasis, or interactions between amino acid residues within or between proteins, is the cause of this change. In the presence of epistasis, the amino acids acceptable at a site depend on the amino acids at its interacting sites. Consequently, when the amino acids at the interacting sites change in evolution, the amino acids acceptable at the focal site also change, resulting in an alteration of site-specific equilibrium amino acid frequencies. In essence, the microenvironment of the focal site changes in evolution, rendering the same amino acid different in functional effect, which reduces the probability of molecular convergence.

An alternative explanation of a decreasing R with an increasing genetic distance is a genome-wide change in amino acid content during evolution. To evaluate this possibility, for a pair of branches in the Drosophila or mammalian data set, we computed the amino acid frequency vector for each younger end of the two branches for sites that differ between the two younger ends, and then calculated the Euclidian distance between the two vectors. We conducted a partial Mantel test of the correlation between R and genetic distance among branch pairs, after the control of the above Euclidian distance. We found that the negative correlation between R and genetic distance remains largely unchanged even after the control (Drosophila: r = −0.471, P = 5 × 10⁻⁵ under JTT-f_gene; r = −0.297, P = 0.013 under JTT-f_site; r = −0.187, P = 0.062 under JTT-CAT. Mammals: r = −0.752, P = 5 × 10⁻⁵ under JTT-f_gene; r = −0.622, P = 1.5 × 10⁻⁴ under JTT-f_site). Hence, potential genome-wide changes in amino acid content cannot explain the negative correlation.

Discussion

To examine the prevalence of adaptive molecular convergence in protein sequence evolution, we calculated the ratio (R) between the number of observed molecular convergences in a pair of branches and the expected number under various neutral substitution models. We found that R generally exceeds 1 when all sites in a protein are assumed to have the same equilibrium amino acid frequencies (figs. 2 and 3). But when the among-site heterogeneity in equilibrium amino acid frequencies is considered by either the CAT model or the observed amino acid frequencies at each site, R is generally close to or smaller than 1 (figs. 2 and 3). As shown previously, models considering the among-site heterogeneity in equilibrium amino acid frequencies almost always fit actual protein sequence data better than comparable models assuming among-site homogeneity (Lartillot and Philippe 2004, 2006). Because the amount of molecular convergence observed in both fruit flies and mammals can be largely explained by chance under a reasonable neutral substitution model, we conclude that there is no evidence for prevalent adaptive molecular convergence at the genomic scale. In this context, it is worth mentioning a recent study that claimed the detection of genomic signatures of adaptive molecular convergence in echolocating mammals (Parker et al. 2013). Two subsequently analyses, however, found no evidence supporting this claim (Thomas and Hahn 2015; Zou and Zhang 2015).

The lack of genome-wide excess of molecular convergence relative to the neutral expectation is not incompatible with adaptive molecular convergence in a small number of proteins. But, what is notable is the relatively large number of molecular convergences at the proteome level that are expected under realistic neutral models. For instance, between the exterior branches respectively leading to D. yakuba and D. mojavensis (fig. 2A), 2,601 molecular convergences are expected among approximately 2.03 million sites under the JTT-f_site model (table 1). This frequency means that 1.28 molecular convergences are expected for a protein of 1,000 amino acids. The chance probability of observing three or more molecular convergences in this protein would be 0.138. It is thus almost guaranteed to find a protein with this amount of molecular convergence from a sizeable set of proteins surveyed. In other words, observations of molecular convergence, especially through a search in multiple proteins, should not be automatically interpreted as evidence for adaptation. Zhang and Kumar previously proposed a statistical test for adaptive molecular convergence in a protein (Zhang and Kumar 1997), but the substitution model they used was JTT-f_gene. We suggest that JTT-f_site or JTT-CAT be used in Zhang and Kumar’s test to guard against false positives caused by the use of neutral models with inadequate among-site heterogeneity in equilibrium amino acid frequencies. When multiple proteins are searched, a correction for multiple testing should also be applied. Castoe et al. (2009) previously showed that the number of sites experiencing convergence substitutions relative to the number of sites experiencing divergent substitutions (C/D) is approximately constant across different branch pairs in a tree. They suggested that adaptive convergence can be detected for a branch pair if its C/D substantially exceeds those of other branch pairs. Unfortunately, this signal simply indicates a variation in C/D among branch pairs; it does not prove or disprove adaptive convergence. For instance, a uniform C/D among branch pairs could mean widespread adaptive molecular convergence throughout the tree. Conversely, variation in C/D among branch pairs could arise from nonadaptive processes (Goldstein et al. 2015).

We found in both Drosophila proteins and mammalian proteins that R decreases with the increase of the genetic distance between the two lineages where molecular convergence is examined. Notably, a related phenomenon was reported by Rogozin et al. (2008) in the analysis of highly conserved (but not invariable) amino acid sites that they used for reconstructing the metazoan phylogeny (Rogozin et al. 2008). These authors noted that when parallel substitutions were observed at such sites, the substitutions were more likely to occur in interior branches of the tree rather than exterior branches. Because exterior branches tend to be relatively distant from one another compared with interior branches, their observation is broadly consistent with ours, although these authors did not explicitly consider the expected number of parallel sites. While our paper was under review, Goldstein et al. (2015) published a similar finding in mitochondrial genes. They showed that C/D decreases when the genetic distance between the branch pair under investigation increases. However, because this trend of C/D is expected even under simple neutral models without epistasis (Goldstein et al. 2015), the biological meaning of their finding is less clear than that of our R-based result.

We hypothesize that the negative correlation between R and the genetic distance of the two lineages considered is caused by changes in acceptable amino acids at individual sites of a protein during evolution. Indeed, the negative correlation could be recapitulated by a simulation of protein sequence evolution with gradual, random changes in site-specific equilibrium amino acid frequencies. Furthermore, the sequences of 16 proteins with hundreds to thousands of orthologs revealed widespread among-clade differences in amino acid compositions at individual sites. Our hypothesis is also consistent with previous case studies where the same amino acid substitutions show similar functional effects in relatively closely related homologs, but show different and even opposite functional effects in relatively distantly related homologs (Zhang 2003).

If the equilibrium amino acid frequencies at a site change in evolution, the equilibrium frequencies for a Drosophila species or lineage would differ from the average equilibrium frequencies calculated from all sequences in the Drosophila tree. Consequently, the number of acceptable amino acids at the site for the species is likely smaller than predicted from the average equilibrium frequencies. This bias causes an underestimation of the expected number of molecular convergences and hence an overestimation of R. Hence, positive selection need not be invoked even when R exceeds 1 under JTT-CAT or JTT-f_site, as observed in some closely related lineages (figs. 2B and 3B). Note that this bias does not affect the comparison of R among different branch pairs in figures 2B and 3B, because the bias applies to all branch pairs similarly.

Given the exclusion of impacts from a potential genome-wide change in amino acid content (figs. 2B and 3B), we believe that epistasis is the best explanation of why the equilibrium amino acid frequencies at a site change during evolution. Because of epistasis, what amino acids are acceptable at a site depends on what amino acids are present at its interacting sites. Thus, amino acid replacements in evolution at these interacting sites alter the equilibrium amino acid frequencies at the focal site. Our results are consistent with the covarion model of protein evolution (Fitch and Markowitz 1970) and many studies that reveal or suggest the prevalence of epistasis in protein evolution (Zhang and Rosenberg 2002; Breen et al. 2012; Harms and Thornton 2013; Parera and Martinez 2014; Xu and Zhang 2014). Notably, Breen et al. (2012) reported that the observed ratio between the nonsynonymous (d_N) and synonymous (d_S) substitution rates for a gene is substantially lower than predicted based on the mean number of observed amino acids per site in a large phylogeny across all sites of the protein. They explained this phenomenon by a difference in the amino acids acceptable in different parts of the phylogeny as a result of epistasis. McCandlish et al. (2013) pointed out that not all amino acids at a site are equally fit and a nearly neutral model can explain Breen et al.’s observation without invoking epistasis, because, if most amino acids are acceptable but suboptimal, d_N/d_S would be lower than predicted from the number of acceptable amino acids. However, the nearly neutral hypothesis cannot explain the negative correlation between R and the genetic distance between two lineages. In other words, our observation provides additional evidence for the prevalence of epistasis in protein evolution. It is worth noting that changes in the equilibrium amino acid frequencies at a site could also be caused by differential adaptations of different species to their respective environments. However, because the genetic distance between two species is not expected to correlate with their environmental difference at the phylogenetic scale examined in the present study, the adaption hypothesis cannot explain why R declines with the genetic distance.

That the equilibrium amino acid frequencies at a site change in evolution makes it difficult to quantify these frequencies, rendering the expected amount of molecular convergence hard to estimate. Ideally, the equilibrium frequencies at a site should be estimated from an alignment of many sequences such that all acceptable amino acids are observed multiple times. But the changing equilibrium frequencies also require that only closely related sequences be used in the estimation. In the study of molecular convergence between two closely related lineages, the use of a few closely related sequences in the estimation of equilibrium amino acid frequencies may upward bias the neutral expectation of the number of molecular convergences under neutrality, which will lead to a more conservative test of adaptive convergence. To guard against false positives, we advocate this strategy as opposed to the use of many distantly related sequences in estimating equilibrium amino acid frequencies, until the advent of a better test. The study of molecular convergence between two distantly related lineages is more complex due to potential changes in equilibrium frequencies. Using average equilibrium frequencies from multiple distantly related sequences will already lead to an overestimation of the neutral expectation of the number of molecular convergences. Until further research for a better strategy, we suggest that this strategy be used so that the test of adaptive convergence will also be conservative. Although molecular convergence is the exclusive subject of this study, the finding of among-site and among-clade heterogeneities in protein sequence evolution has implications for other evolutionary analyses of protein sequences (Blanquart and Lartillot 2008; Jayaswal et al. 2014). Further investigations of this subject are thus highly recommended.

Materials and Methods

Protein Sequence Data

The protein sequence alignments of 12 species in the genus Drosophila were downloaded from the FlyBase FTP (St Pierre et al. 2014), whereas those of 17 species in the class Mammalia were downloaded from OrthoMaM (Douzery et al. 2014). Protein isoforms corresponding to the same gene and translated from alternatively spliced transcripts were identified and only one was randomly chosen and retained in the Drosophila data set. No such problem existed for the mammalian data. In each alignment, any site with gap or ambiguous amino acid in any taxon was removed. Alignments with only one remaining site after the removals were excluded from further analysis. Amino acid frequencies at each site and the average amino acid frequencies across all sites were computed.

Parameter Estimation

Each protein alignment was analyzed using the codeml program in PAML v4.7 (Yang 2007). The Empirical+F model coupled with the JTT matrix implemented in the software was used. A discrete gamma model with eight rate categories was used to account for among-site rate variation. For the Drosophila data, we used the tree topology (fig. 2A) provided in a previous study (Drosophila 12 Genomes Consortium et al. 2007). For the mammalian data, the 17 taxa were chosen such that ambiguous nodes in Romiguier et al. (2013) could be avoided; the unambiguous phylogeny resulted (fig. 3A) was then used. Potential discordances between gene trees and species trees were ignored due to low probabilities (P < 3 × 10⁻⁵ based on parameters pertaining to the species used; Nei and Kumar 2000). From the PAML output, all branch lengths of the tree, relative substitution rate of each site, and inferred ancestral sequences were obtained. In addition, we concatenated all alignments and analyzed it by codeml with the same setting. The output branch lengths were used in the trees of figures 2A and 3A and were used to calculate the genetic distances presented in figures 2B and 3B. The genetic distance between a pair of branches is the sum of the lengths of all branches connecting the two younger ends of the two branches.

All 1,100 alignments with over 500 residues were chosen from the Drosophila data set and were subject to analysis by PhyloBayes 3.3f (Lartillot et al. 2009). The JTT-CAT model with the discrete gamma distribution of among-site rate variation (with eight rate categories) was used. The tree topology was fixed as in the PAML analysis. The Markov chain Monte Carlo process was set to run for 6,000 steps. After 1,000 burn-in steps, the remaining steps were sampled once every five steps to estimate parameters, following a recent analysis (Parker et al. 2013) of data sets comparable in size to ours. Results were obtained for 1,081 alignments, because PhyloBayes was not able to analyze the other 19 alignments. Branch lengths, site-specific substitution rates, class-specific amino acid frequencies, and the class affiliations of all sites were obtained and used in downstream analysis.

Expected Number of Molecular Convergences

Let us use figure 1 as an example to explain how we computed the expected number of molecular convergences. For a site, let the probabilities for the 20 amino acids to occupy node i be $P(X_i)$, a vector of length 20. We use $I^{(j)}$ to denote a vector with the jth element equal to 1 and all other 19 elements equal to 0. The inferred most likely amino acid for the common ancestor (X₀) at the site concerned was extracted from the PAML output. If the most likely amino acid is k, $P\left(X_0\right)=I^{(k)}$. The equilibrium amino acid frequency vector π for a site was estimated from the observed amino acid frequencies among all taxa at the site for JTT-f_site and across all sites of the protein for JTT-f_gene, respectively. The substitution matrix was then derived from the JTT matrix M₀ provided in PAML. Given the original equilibrium frequency vector π₀ determined by the JTT matrix, the new substitution matrix was derived as $M=\left(M_{ij}\right)=(M_{0ij}\text{·}{\pi }_j/{\pi }_{0j})$. We then calculated the amino acids at node 1 and node 2 by $P\left(X_1\right)=P\left(X_0\right)\text{·}{M}^{r{b}_1}$ and $P\left(X_2\right)=P\left(X_0\right)\text{·}{M}^{r{b}_2}$, respectively, where b₁ and b₂ are branch lengths measured by the expected numbers of substitutions per site for the protein concerned for the relevant sets of branches, respectively (fig. 1), and r is the substitution rate of the site considered, relative to the average for the protein. Conditional on the amino acid appearing at node 1, $P\left(X_3|X_1=j\right)=I^{(j)}\text{·}{M}^{r{b}_3}$. Similarly, $P\left(X_4|X_2=j\right)=I^{(j)}\text{·}{M}^{r{b}_4}$. Thus, the joint probability of having amino acids A, B, C, and D at nodes 1–4 can be calculated as $P\left(A,B,C,D\right)=P(X_1=A)\text{·}P(X_3=C|X_1=A)\text{·}P(X_2=B)\text{·}P(X_4=D|X_2=B)$. For a given site, the probability of occurrence of convergent substitutions in the thick branches equals $P_{\text{convergent}}={\displaystyle \sum }_{A\ne C,B\ne D,C=D,A\ne B}P(A,B,C,D)$, whereas the probability of occurrence of parallel substitutions equals $P_{\text{parallel}}={\displaystyle \sum }_{A\ne C,B\ne D,C=D,A=B}P(A,B,C,D)$. The total probability of molecular convergence at the site is P = P_convergent + P_parallel. The expected number of molecular convergence for all proteins is the sum of P over all sites of all alignments.

Mantel Tests

Mantel tests and partial Mantel tests were conducted using the R package “ncf”. In the matrix containing pairwise R values, entries were set as “NA” if R values do not exist. The partial Mantel test used method 1 of permutation, which permutes the entire matrix of R values (Legendre 2000).

Simulation of Sequence Evolution When the Equilibrium Amino Acid Frequencies Change

Simulation of sequence evolution followed the tree in figure 4A. For a site, $P(X_0)$ was set to be the equilibrium amino acid frequencies specified in the JTT model (π₀), and the initial state was chosen randomly according to π₀. The equilibrium frequencies change as in a random walk. At each step of frequency changes, two entries in the frequency vector were randomly chosen, with one subtracted by 0.01 and the other added by 0.01. When a frequency is 0 (or 1), it can only increase (or decrease). The frequency vector changes for five steps before each step of sequence evolution. The changed frequency vector is then used to derive a new JTT-f substitution matrix as described above. The site with the initial probability vector $I^{(j)}$ then evolves by a Markov process for one step to $I^{(j)}\text{·}M$, corresponding to 0.01 substitutions per site, or 1 PAM (point accepted mutation). The new state k is chosen multinomially according to the evolved probability vector, and the simulation continues. The rate of change in amino acid frequencies assumed in the simulation approximates the observed values in the fly data. The branch lengths (b₁ and b₂), in the unit of 1 PAM, were set as shown in figure 4A. We kept b₂ constant as 10 PAM and varied b₁ between 10 and 30 PAM. The observed number of molecular convergences was counted in 500,000 simulations for each b₁ value. For each parameter set, the expected number of molecular convergences was calculated as mentioned above, with the average of the equilibrium amino acid frequency vectors at nodes 2 and 4 used as equilibrium frequencies.

Amino Acid Compositions in 16 Proteins with Huge Numbers of Sequences

We obtained the 16 protein alignments from a previous study (Breen et al. 2012). For each protein, two taxonomic units representing two mutually exclusive monophyletic clades (e.g., ray-finned fishes vs. tetrapods; arthropods vs. chordates) were chosen. For each site in the protein alignment, the presences/absences (1 for presence and 0 for absence) of the 20 amino acids were recorded as a vector of length 20 for each of the two clades. Sites with gaps in all species of a clade were excluded. The compositional distance between the two clades was measured by the Hamming distance between the two presence vectors of the site. To test if the observed compositional distance is significantly larger than the random expectation, for each protein, we mixed the sequences from the two clades, randomly divided them into two groups with the actual sizes of the two original clades, and calculated the Hamming distance. This process was repeated 1,000 times to obtain the null distribution of the Hamming distance for each site. A site-wise P value was computed by the proportion of times in which the randomized distance from the null distribution equals or exceeds the observed distance for the site. Q value was then derived for each site within a protein using the Benjamini–Hochberg method (Benjamini and Hochberg 1995). Note that we compared the observed amino acids between two clades rather than the frequencies of observed amino acids, because of the possibility that the latter differ from the equilibrium frequencies. Comparing only the observed amino acids made our results more conservative.

Supplementary Material

Supplementary table S1 is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).