Abstract
Non-invasive ultrafast imaging for human cardiac applications is a big challenge to image intrinsic waves such as electromechanical waves or remotely induced shear waves in elastography imaging techniques. In this paper we propose to perform ultrafast imaging of the heart with adapted sector size by using diverging waves emitted from a classical transthoracic cardiac phased array probe. As in ultrafast imaging with plane wave coherent compounding, diverging waves can be summed coherently to obtain high-quality images of the entire heart at high frame rate in a full field-of-view. To image shear waves propagation at high SNR, the field-of-view can be adapted by changing the angular aperture of the transmitted wave. Backscattered echoes from successive circular wave acquisitions are coherently summed at every location in the image to improve the image quality while maintaining very high frame rates. The transmitted diverging waves, angular apertures and subapertures size are tested in simulation and ultrafast coherent compounding is implemented on a commercial scanner. The improvement of the imaging quality is quantified in phantom and in vivo on human heart. Imaging shear wave propagation at 2500 frame/s using 5 diverging waves provides a strong increase of the Signal to noise ratio of the tissue velocity estimates while maintaining a high frame rate. Finally, ultrafast imaging with a 1 to 5 diverging waves is used to image the human heart at a frame rate of 900 frames/s over an entire cardiac cycle. Thanks to spatial coherent compounding, a strong improvement of imaging quality is obtained with a small number of transmitted diverging waves and a high frame rate, which allows imaging the propagation of electromechanical and shear waves with good image quality.
Keywords: Ultrafast Imaging, Diverging waves, Spatial coherent compounding, Shear wave imaging, Cardiac Imaging, Cardiac phased array
I. Introduction
Echocardiography is the most common modality used to image the human heart in real time. Typical frame rates in two-dimensional echocardiography are 30-100 frames/s, which allows visualizing the heart motion and quantifying myocardial velocities and strains during the cardiac cycle [1],[2]. However, such frame rates are insufficient to track mechanical waves such as remotely induced shear waves [3],[4],[5] intrinsic shear waves [6] or electromechanical waves [7],[8] because of their high propagation speed in the myocardium (between 1 and 10 m/s).
In ultrasound imaging, the frame rate is limited by the number of transmitted ultrasound beams needed to construct an image. Many approaches have been developed to reduce the number of transmits, often at the cost of a lower spatial resolution or a reduced field-of-view. In 1977, an original approach based on an optical processing system to treat the ultrasonics signals [9] was proposed by Bruneel et al. They obtained the first images of the cardiac muscle acquired at 5000 frames per second. However, such acousto-optics system was too complex and this concept was abandoned. In 1984, Shattuck et al [10] introduced a parallel beamforming system driving conventional imaging probes. Up to date, in the conventional transmit focusing mode, the increase of the frame rate is achieved through the reduction of the number of beamformed lines in transmit, which either reduces the sector size or the line density of the image. Successive ECG-gated focused acquisitions at high frame rate have been also proposed to maintain a large line density and sector [7],[8] but this approach cannot be used for real-time imaging of single heartbeats or shear wave imaging. The concept of ultrafast imaging using non-focused transmit waves [11],[12],[13],[14] has been proposed to drastically reduce the number of transmits keeping the number of scan lines and the image size. Plane waves transmitted by linear transducer arrays have been successfully implemented on commercial scanners to image the propagation of remotely induced shear waves at frame rates up to 10,000 images/seconds in many organs of human patients including the breast [15], the liver [16], the carotid artery [17], the cornea [18] and in the heart [3],[19], where it provides a non-invasive way to access the myocardial contractility [5]. Moreover, successive plane waves acquisitions performed with tilted plane waves can be combined either incoherently to improve transverse motion estimates [20] or coherently to increase the poor image quality obtained by using only one plane wave in terms of contrast and resolution. This technique known as plane wave spatial compounding [21] has been shown to improve rapidly the image quality with the number of transmits without sacrificing the frame rate. With only 2 to 20 transmits, coherent spatial compound imaging can thus recreate a synthetic focus in transmit everywhere in the image as it is done in synthetic aperture imaging techniques (STA) [22] but with high frame rate and large apertures for high signal to noise ratio (SNR). STA was originally introduced in the field of ultrasonic imaging as a way to improve contrast and resolution of ultrasonic images by achieving dynamic focusing both in transmit and in receive. Driven by the need for increasing the frame rate, in particular for real-time 3D imaging, sparse STA imaging techniques have then been proposed [22],[23],[24],[25] and by reducing the number of STA transmits, at the cost of lower resolution and higher side lobes but also lower signal to noise ratio (SNR).
Ultrafast imaging with plane wave coherent compounding as well as sparse STA enables very high frame rate imaging (>1000 image/s) using only one to five transmits. In practical situations, the two techniques mainly differ in the diffraction of the transmitted beams, the amplitude of the plane wave being almost unaffected during wave propagation, which provides higher SNR at large depths. The geometry of the field of view differs also in the two techniques. For applications that require large field of view such as in transthoracic cardiac imaging, the plane wave approach remains too limited. Transthoracic phased array probes have small apertures that generate narrow plane waves, which cannot cover the entire heart with a large sector.
Moreover, the coherent compound technique becomes rapidly inefficient at large imaging depths with small apertures, because the plane waves transmitted at different angles do not overlap in the region of interest. On the other hand, sparse STA allows imaging a large sector but at the cost of the SNR loss. In applications of ultrafast imaging such as shear wave imaging, very small tissue displacements are generated and high SNR is crucial to ensure the quality of the displacement estimation. Moreover, in many cases, such as shear wave imaging or ultrafast Doppler imaging there is not necessary the need to image the full sector. In these situations, a reduced field of view could be used to increase the SNR and improve the tissue and blood velocity estimation within the region of interest.
Based on our previous development of coherent compound plane waves, we propose to adapt this approach to ultrafast imaging with diverging waves in order to track the propagation of remotely induced and natural mechanical waves in the heart. The approach is similar to the method proposed by [24],[25],[26],[27] in the framework of STA, by placing several virtual sources behind the probes in order to achieve real-time 3D imaging. Hasegawa, Kanai and other groups [28] have also proposed a similar approach using diverging beams transmitted along several direction to cover the entire sector (15 transmits in [29]). Contrary to this approach, we propose here to transmit at very high frame rate, one or more diverging waves that illuminates the entire field of view in order to achieve ultrafast imaging of the heart. In this paper, we focus on the practical implementation of this technique for 2D ultrafast imaging of mechanical waves in the heart using a transthoracic phased array. First, we investigated numerically the positions of the virtual point sources in different situations to ensure the imaging quality and SNR. Experiments are then performed in phantoms using a cardiac phased array to quantify the image quality increase in B-mode and shear waves velocity images, and finally in vivo experiments are performed in human hearts.”
II. Simulation
A. Principles
In this part, the coherent summation of multiple diverging waves was performed analytically in order to investigate the synthetic focus achieved in transmit. In two dimensions, each transmitted circular wave was defined by the position of a virtual source located behind the probe.
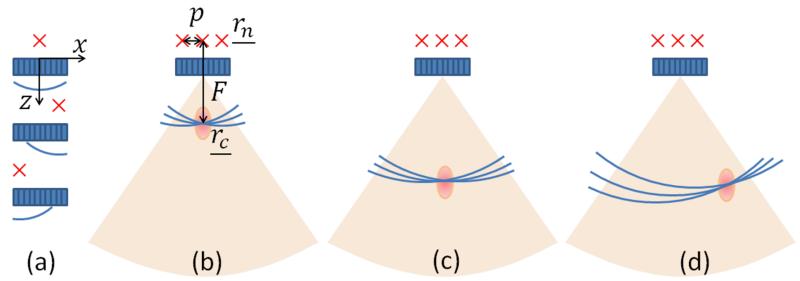
The principle of coherent compounding with diverging waves is illustrated in Fig. 1. The choice of the position of virtual sources is crucial and can lead to very different results. For example, in synthetic aperture imaging techniques, the virtual sources usually coincide with the transducer elements and the diverging waves are successively generated by each elements to restore a high quality synthetic image [22]. However, at high frame rate, only a small number of diverging waves can be transmitted. In this case, if the virtual sources are superimposed onto probe elements, the total energy emitted is reduced and the large distance between sources will induce side-lobes in the synthetic transmit field. To overcome this situation, the use of virtual sources placed behind the transducer was proposed [24].
Fig. 1.
Principle of Coherent Compounding with diverging waves. Three Diverging Waves defined by their virtual source (Red Cross at rn) spaced by a virtual pitch p, are sent independently with a phased array probe directly in contact with the region of interest. Each Diverging wave is backscattered by heterogeneities and the array receives the corresponding echo. Beamforming is processed by making interfere coherently these diverging waves at the focal point rc with the adequate delays Fig. 1(b). By changing the delay applied to each backscattered echoes from (a), the resulting waves can interfere and virtually focus at different depth as in Fig. 1(c) and laterally as in Fig. 1(d).
Then, the main question is where the virtual sources should be placed in order to maximize the image quality keeping a very high frame rate?
Let’s consider a virtual array of N punctual sources (from −m to m) located behind the probe at positions , zn is kept constant for the different sources and xn = n p where p is the pitch of the virtual array. If we apply the coherent summation of the acoustic fields generated by each diverging wave at a point of space over the bandwidth (k1, k2), we can write the field Φ(r) as:
| (1) |
where e−jk|rc-rn| is the phase correction needed to achieve the coherent summation at rc, A(k) is the amplitude. In order to obtain a simple representation of the pressure field, equation 1 can be simplified. Considering the far-field approximation, at a certain focal distance F, near the central line x = 0, a simple expression is obtained for the acoustic field at a point rc in the monochromatic case.
| (2) |
where N = (2n + 1) is the number of virtual sources (the complete derivation is given in appendix).
From this expression, we can derive the dimension of the main lobe and the positions of the side lobes in the monochromatic case at the center frequency.
With X = (x − xc) Zeros occur when:
| (3) |
With the wave length
| (4) |
We see in (4) that the width of the principal lobe decreases with the total aperture of the virtual array, which results in an improvement of the lateral resolution as the number of transmits or the virtual pitch increases.
Maxima of the pressure field occur when:
| (5) |
| (6) |
For l′ ≠ 0, Xmax is the position of grating lobes. Equation (6) shows that, as the pitch p between virtual sources decreases, the grating lobes are rejected far from the focus (Xmax becomes large).
To be strictly accurate, the elements width and the subapertures size should be considered in this derivation. Furthermore, it is only true for compounding on the central line in the far field. However, the derivation gives an idea of how synthetic pressure field varies in terms of maxima and zeros with respect to the number of virtual sources and their position, which shows that the total aperture should be maximized to increase the lateral resolution and the distance between sources should be minimized to decrease the grating lobes.
B. Numerical simulations
A standard phased-array probe of 64 elements with 0.28-mm pitch, 13-mm height, a center frequency of 2.7-MHz (100% bandwidth), and a 60-mm elevation focus was implemented in Field II [30],[31]. The coordinates of the elements were set as . The sampling frequency of acoustic pulses was 200-MHz. The acoustic field transmitted from each virtual source placed behind the probe was calculated using Field II. For more than one transmit, spatial coherent compound was performed as shown in figure 1. More specifically, the transmit delays associated with the virtual source coordinates were calculated as:
| (7) |
Where c the speed of sound in soft tissues (1540 m.s−1). Simulations of the synthetic acoustic field were performed to investigate the dependence with the position of the virtual sources, the size of the transmit apertures (subapertures), and the number of virtual sources.
C. Angular aperture and transmit subapertures
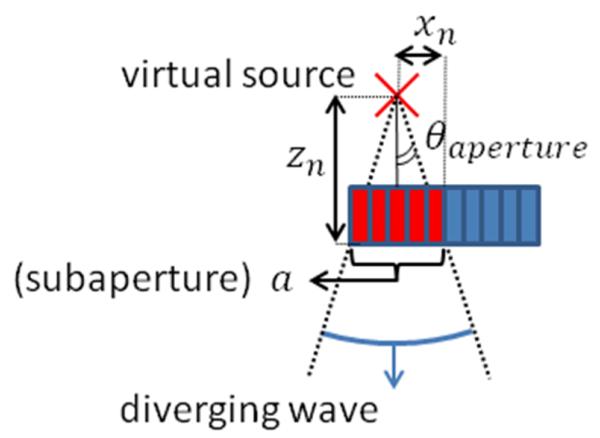
The angular aperture of the transmitted beam is important to define the field of view achieved in the final image. In this study we assume that the transmitted wave must be symmetrical and homogeneous over the entire sector image. Therefore, the virtual point source must be placed at the center of the transmit subaperture (e.g. figure 2). Angular aperture for each transmits is defined geometrically by:
| (8) |
where a is the size of the subaperture (number of elements which participate to the diverging wave transmission as shown in figure 2) and zn is the virtual source position on the z-axis relative to the ultrasound probe.
Fig. 2.
The virtual source is placed at a probe distance distance zn. It is placed at the center of the subaperture. The diverging wave is transmitted over the entire field of view.
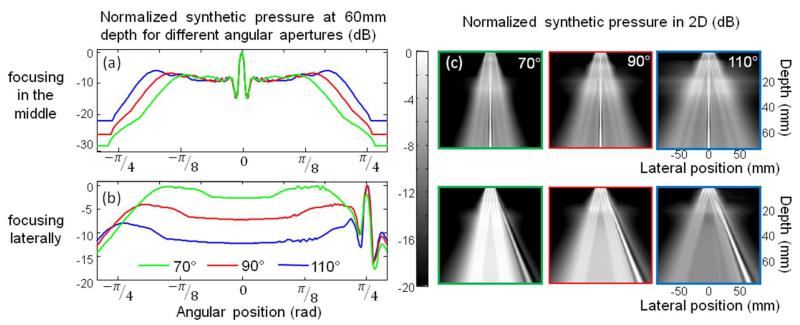
Figure 3 shows the synthetic pressure field from three diverging waves. Coherent summation was performed at a depth of 60-mm at two extreme lateral positions of the field of view: on the central line (top of fig.2) and on the edge of a 90° sector (bottom of fig.2). Three different transmitted angular apertures are shown (70°, 90°, 110°). The angular aperture variation was obtained by varying, with subapertures of 21 elements. Lateral positions of the virtual sources were placed in the middle of the 21 elements subapertures respectively at a position xn = [-5.9;0;5.9]-mm. The left hand size of figure 3, shows the synthetic pressure distribution on an arc of circle at a 60 mm depth where coherent summation is made. The right hand size of figure 3, shows this pressure distribution in all space.
Fig. 3.
Normalized transmitted pressure field for three angular apertures (70°, 90°, 110°). Three virtual sources placed at (xn = [−5.9;0;5.9]-mm) were used. Coherent summation was made at a depth of 60 mm a) on the central axis and b) on the side at 60 mm. c) 2D normalized synthetic pressure distribution obtained for the different configuration.
A quasi-identical focusing is obtained on the central axis with the three angular apertures, whereas off-axis focusing capacity varies with the angular aperture. The steering capability depends strongly on the angular transmit aperture. Figure 3 shows that an angular aperture of more than 90° is required to lower the grating lobes generated on the central axis and to achieve a good focusing on the off axis position at (which is a large imaging sector configuration).
The other important dimension of the transmit aperture is its physical extent on the transducer array. This parameter was already investigated by Lokwood et al [24] who showed that the signal to noise ratio improved with the number of transducer as ~N1/2.
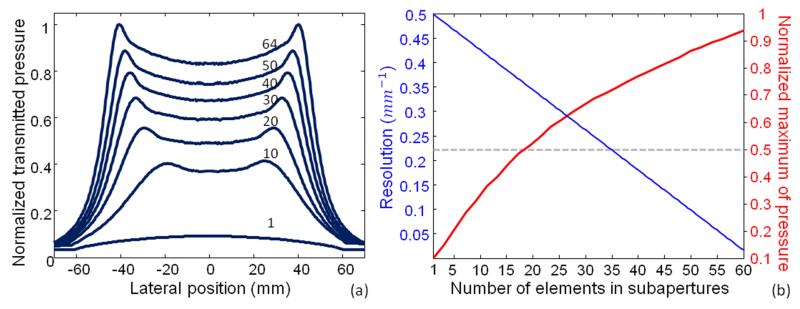
Figure 4 shows the pressure field 60 mm away from the transducer as a function of the size of the transmit subaperture. The subapertures were defined in terms of number of element. One virtual source was placed at their center. As shown in figure 4, the transmitted pressure increases with the number of elements. With only one transmit element, such as in synthetic aperture imaging, less than 10% of the pressure transmitted by the entire array is obtained. On the other hand, large subapertures do not allow large virtual pitch p (as virtual sources are placed at the center of subapertures) which is required to improve the lateral resolution e.g. equation 4. Therefore, to maximize resolution the transmit subaperture must be as small as possible. A transmit subaperture of approximately 20 elements is a good tradeoff to obtain a high pressure (more than half of the pressure transmitted with the entire probe e.g. dashed line on figure 4 (b)) and a wide variety of possible virtual source positions (figure 4 (b)).
Fig. 4.
(a) Simulation of Normalized Pressure field of one diverging wave for an angular sector of 90° at a depth of R=6 cm for increasing number of transmit elements (1 to 64). (b) shows the simulated maximum synthetic pressure when three sources were used as a function of subaperture size (red plot). The associated resolution (inverse of the main lobe −6dB width) when virtual sources were placed at the center of subaperture is plotted in blue.
D. Lateral positions of the virtual sources
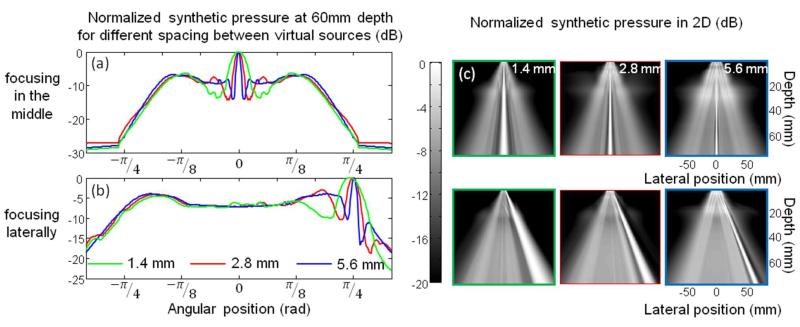
Figure 5 represents the synthetic transmitted pressure field obtained for three different virtual sources spacing. Three diverging waves were used and coherent summation was made at a depth of 60-mm at two positions of the field of view: on the central line (top of figure 5) and on the edge of a 90° sector (bottom of figure 5). The angular aperture (100°) and the subaperture (21 elements) were kept constant. A virtual source was placed on the central axis and the two others are placed symmetrically at a varying distance (1.4, 2.8, and 5.6 mm). In agreement with equation 4, we find that the lateral resolution is increased with the virtual source spacing. The widths of the main lobe at −6 dB are 11 mm, 5.5 mm, and 2.8 mm, respectively. On the other hand, the grating lobes move closer to the focus when the spacing is enlarged. It is in good agreement with the grating lobe position derived from equation (6).
Fig. 5.
Normalized transmitted pressure field for different virtual sources lateral position. Three different distances between virtual sources (1.4, 2.8, 5.6 mm) are compared. Coherent summation was made at a depth of 60 mm a) on the central axis and b) on the side at 60 mm are compared. c) 2D normalized synthetic pressure distribution obtained for the different configuration.
E. Number of diverging waves
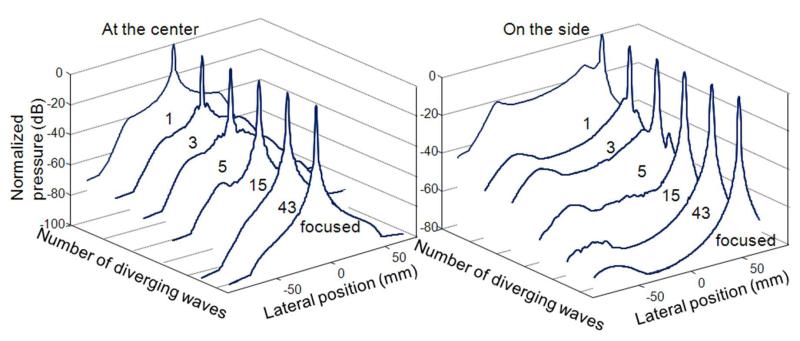
Because the number of transmitted waves determines the maximum frame rate achievable, it is important to determine how fast the image quality improves with the number of diverging waves in ultrafast imaging applications. The virtual sources were placed behind the probe at a distance zn = 2.94 mm. Each virtual source was positioned in the center of a 21 elements subaperture (e.g. figure 2(a)). These parameters were set to get a 90° angular aperture according to equation (8). The first virtual source was placed at xn = 0 (center of transducer array). The number of diverging waves was then increased by adding virtual sources around the first virtual source placed at the center. For three transmits, we added two virtual sources on the edge of the transducer array (xn = [−5.9;0;5.9]-mm). This way, the distance between the two extreme sources was maximized to get a good resolution and allowed to place the sources in the middle of a 21 elements subaperture. Then two virtual sources were added between the previous three to obtain five transmits (lateral source positions [−5.9;−2.95;0;2.95;5.9]-mm) and so on. Additionally, conventional focusing in reception was performed at the transmit focus location to investigate the final image quality.
Figure 6 shows the focusing quality improvement with the number of transmits (on pressure amplitude and PSF). A big improvement is achieved with only 3 transmits, particularly off axis where the mean pressure level is reduced by 18.4-dB. Focusing is then progressively improved with the number of transmits, and with 43 transmits, the focus becomes comparable to conventional focusing. The normalized Point Spread Functions (PSF) for 1, 3 diverging waves and focused are imaged to illustrate the improvement. It shows that with coherent compound imaging a small number of transmits enables a major improvement of the focusing quality while maintaining a high frame rate.
Fig. 6.
Normalized synthetic pressure field at two points of space (center, side) for a 90° sector at 60 mm depth against lateral position. The synthetic fields induced by 1 diverging wave, 3,5,15,43 diverging waves are presented and compared to the focused emission. Focus in reception was added to the transmission. Side lobes and Mean level decreases when the number of diverging waves increases leading to classical focusing. Normalized PSF for 1, 3 diverging waves and focused at the center were also imaged.
III. Experiments
A. Diverging waves spatial coherent compounding in a heart phantom
The imaging quality was assessed experimentally in a heart phantom (CIRS, model 067). A standard phased array probe (64 elements, 2.7-MHz central frequency, Vermon, France) with the same characteristics as the one used in simulations, was used to image the phantom. The technique of coherent diverging waves compounding was implemented in real-time on an ultrafast scanner (Aixplorer, SuperSonic Imaging, France). The imaging depth was set to 12 cm. The number of emitted diverging waves was varied from 1 to 20 diverging waves, providing a frame rate between 4600 and 250 frames/s, respectively. A sequence with conventional focusing in transmit (160 focused transmits at 60 mm) was also used for comparison. In reception, conventional dynamic focusing beamforming with the full aperture was used for all the acquisitions. The magnitude of the beamformed IQ data was normalized. Each depth was normalized by the maximum magnitude at this depth. It was then scan-converted and log-compressed to obtain the final B-mode image with a 50-dB dynamic range. This normalization gives how the contrast varies as a function of depth.
The angular aperture was set to 90°, the subapertures were composed of 21 elements, and virtual source positions (xn) were the same as in part II.5.
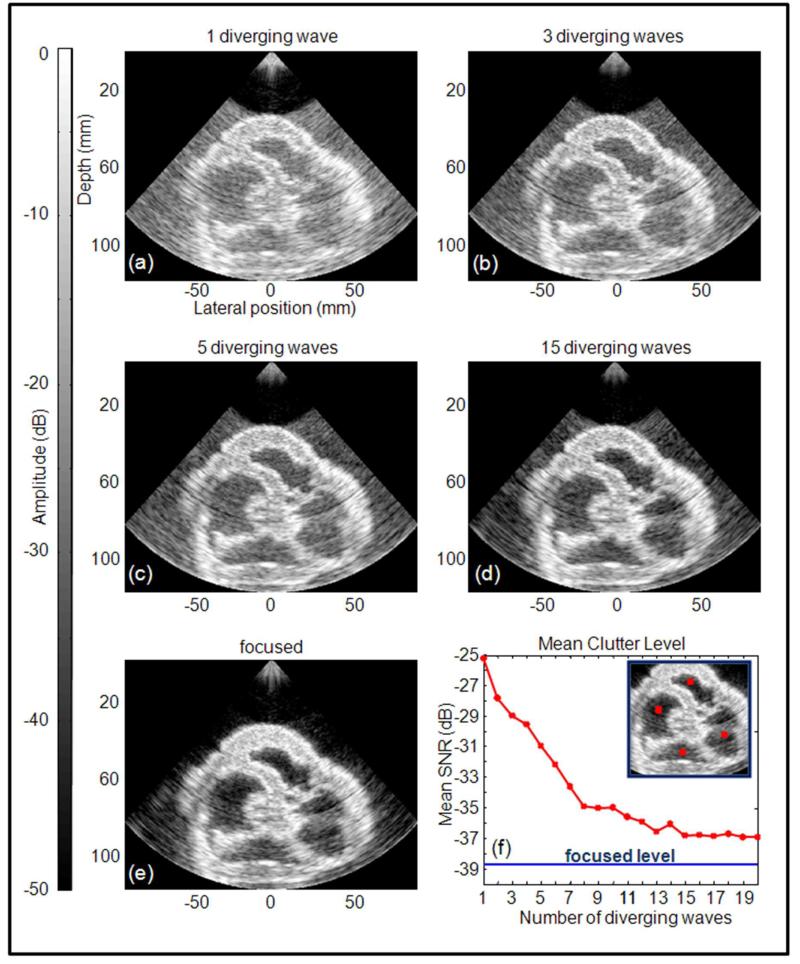
Figure 7 shows the improvement of the imaging quality with the number of transmits. One can notice the improvement of both the lateral resolution and the SNR (Signal to noise ratio) between a single diverging wave transmitted (e.g. figure 7 (a)) and the image made of a several transmits (e.g. figure 7 (b), (c), (d)). A strong improvement is found for a small number of transmits, e.g., 3 or 5. With only 15 diverging waves (e.g. figure 7 (d)) the image quality is qualitatively comparable with the one obtained with conventional focusing (e.g. figure 7 (e)). SNR of clutter signal level was assessed by averaging in the four cardiac cavities, (red squares in figure 7 (f)), the absolute level of normalized images. Figure 7 (f) shows an important improvement of SNR (−25dB to −36.5dB) when the number of waves is first increased from 1 to 15 diverging waves, after which the improvement becomes smaller (−36.5dB to −37dB from 15 diverging waves to 20 diverging waves respectively). The clutter level of conventional focusing was also assessed (38.5dB). With only 15 diverging waves the SNR is only 2dB lower than the SNR of focused mode. Nevertheless, to achieve very high frame rate (~ 1000 images/sec) at such depth (12 cm) the number of transmits cannot exceed 5 transmits, the important result here is the improvement of clutter level in the ultrafast imaging range: 1 to 10 diverging waves.
Fig. 7.
Comparison between 4 configurations using a different number of diverging waves and conventional focusing on a heart phantom. The average clutter signal level was evaluated at several positions shown by the boxes (f).
B. Ultrafast imaging of shear wave propagation
Coherent compounding with diverging waves was then evaluated for imaging the propagation of shear waves at very high frame rate. Two different sequences were made. The first one shows the improvement of coherent compounding. The second one, shows the importance of the angular aperture.
a) Number of transmit
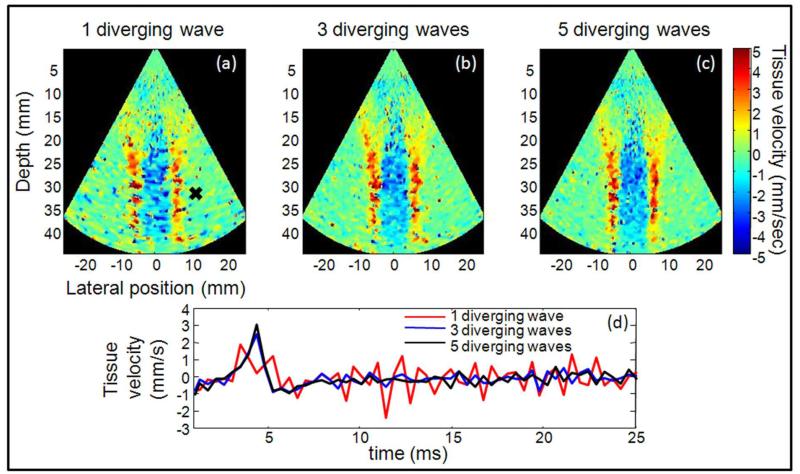
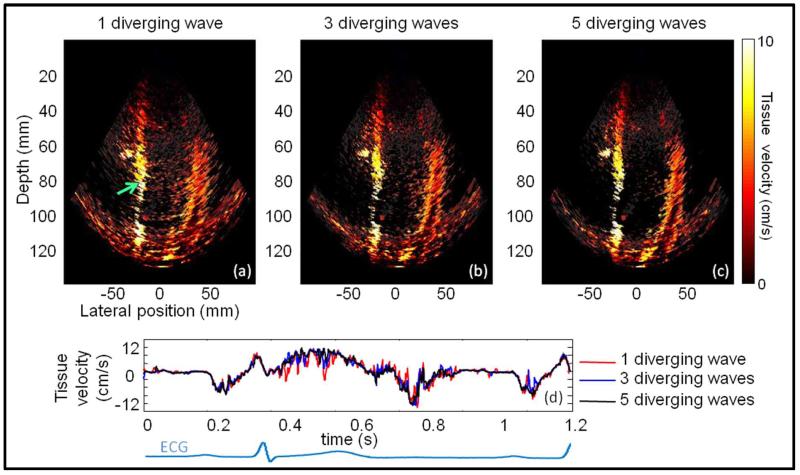
The phased array probe described in part III.1was used to image a breast phantom (CIRS, model 059) in which shear wave velocity is about 2.3 m/s, and two phantoms made of Agar-gelatin (2%-2% and 2%-10%) in which shear waves propagate at 1.3 m/s and 5.5 m/s respectively. A sequence was designed to remotely generate shear waves based on the radiation force induced by a focused ultrasonic burst [32],[33]. The pushing depth was set at 30 mm, and push duration was set to 300 μs. To image the shear wave propagation, 100 frames were acquired at the frame rate of 2500 frames/s. It was repeated three times for each phantom. The imaging depth was set to 45 mm and the pulse repetition frequency (PRF) was the same for all the acquisitions (12500 Hz). Different transmits schemes were used to compare the performances of 1, 3 and 5 virtual sources and keep the same number of acquisitions. For one virtual source, transmit was repeated at the PRF and five successive acquisitions were averaged to make one image. With three virtual sources placed laterally at [−5.9;0;5.9]-mm the three different transmits were performed successively followed by another two lateral transmits, and the five acquisitions were used to make one compound image. Finally, the five virtual sources located at [−6.7;3.35;0;3.35;6.7]-mm laterally and at a distance of 3 mm behind the probe were transmitted and used to make one image. Shear waves propagate on a small distance therefore the imaging sector size was reduced and a small angular aperture was set to 70°. Tissue velocities were then obtained using a per pixel frame to frame 1D cross-correlation on demodulated IQ images with an axial kernel size of 3 pixels (1.5 mm) to obtain images of tissue frame-to-frame axial displacements. Figure 8 shows the tissue velocity generated by the shear wave during its propagation. It shows a clear increase of the SNR of the velocity estimation and of the lateral resolution with the number of virtual sources.
Fig. 8.
Tissue velocity images of shear wave propagation at 1.6-ms after the push. Imaging with one diverging wave (a), three (b) and five (c) diverging waves with the spatial coherent compound method. The tissue velocity at one point of space (black cross) is plotted against time for the three configurations (d).
The SNR improvement can be seen on figure (d). Fluctuations are more important when only one diverging wave is used.
In order to quantify the improvement of tissue velocity estimations in the entire image the SNR was calculated as follows for each set of acquisition and for the three different phantoms:
| (9) |
| (10) |
S is the tissue velocity due to the shear wave and the amplitude of fluctuations is given by:
| (11) |
Where t + dt is the time after the shear wave propagation. From this we get a mean SNR presented in table 1. It shows a significant improvement of the SNR. This increase is slightly reduced when the gel gets stiffer due to the higher tissue velocities and the competition between frame rate and tissue estimation e.g. figure 12 in discussion.
Table 1.
| Number of diverging | 1 | 3 | 5 | |
|---|---|---|---|---|
| Gel speed | waves | |||
| 1.3 m/s | 26.4 dB | 28.1 dB | 30 dB | |
| 2.3 m/s | 16.1 dB | 17.1 dB | 19.1 dB | |
| 5.5 m/s | 16.5 dB | 17.6 dB | 18.5 dB | |
Fig 12.
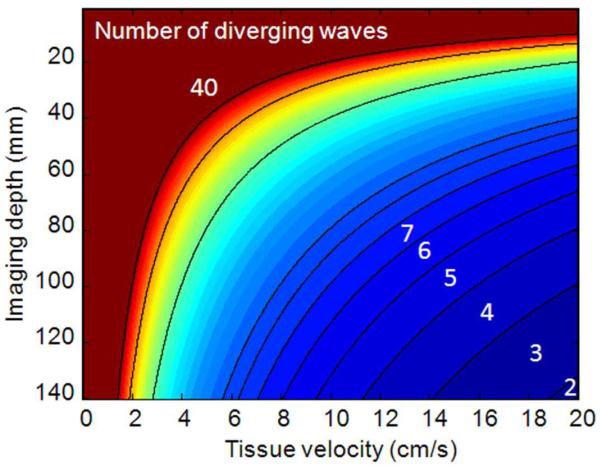
Maximum number of diverging waves insuring a motion artifact smaller than δ = λ/6 between the first and last plane wave transmission as a function of imaging depth and local tissue velocity. The normal and physiological ranges for longitudinal myocardial velocities are in the range 2-15 cm/s.
b) Angular aperture and SNR
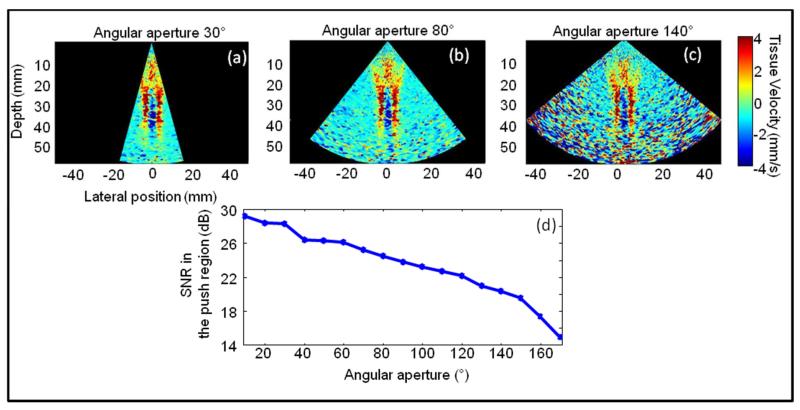
The dependence of the SNR with the transmitted angular aperture was investigated. With the same phased array, the pushing depth was set to 30 mm, and the push duration to 300 μs. To image the shear wave propagation, 100 frames were acquired at the frame rate of 2000 frames/s. It was repeated three times. The imaging depth was 55 mm and the pulse repetition frequency (PRF) was kept the same for all the acquisitions (10000 Hz). Laterally, five virtual sources were placed at the same location as previously in the part a). Different transmits schemes were used to compare the performances of angular apertures. Angular aperture was varied from 10° to 170°. Figure 9 (a),(b),(c) shows the strong difference in terms of SNR between the different angular apertures. Figure 9 (d) quantifies the SNR in the push region as a function of angular aperture. High SNR is obtained by reducing the angular aperture.
Fig. 9.
Three acquisitions with different angular apertures 30° (a), 80° (b) and 140°(c) are imaged. The SNR within the push region is quantified for angular apertures from 10° to 140°.
C. In vivo ultrafast imaging in a large sector view of the human heart
Finally, we investigated experimentally the performance of ultrafast imaging of the human heart in vivo. The transthoracic phased array probe described in III.1 is placed to visualize the entire left ventricle in an apical two chamber view. A classical focusing B-mode running in real time at 30 frames/s permitted to place the probe in the apical view. An ultrafast sequence was computed on the Aixplorer with 5 diverging waves with the same virtual sources positions than in III.1. The PRF was set to 4500 Hz allowing us to reach a frame rate of 900 frames/s. The acquisition was triggered on the ECG. We recombined the backscattered signals off-line by three different ways. The first set of images was obtained by using only the central transmit acquisition (one virtual source laterally placed at the middle of the probe). Then, the second set was obtained by spatial coherent compounding of three virtual sources. Finally, the third set was obtained by applying the spatial coherent compounding method on the five diverging waves.
For each set, a classical frame to frame correlation technique was used to derive the tissue velocities in the myocardium during time [33]. Figure 10 shows the velocity field combined linearly to the B-mode, a cineloop is attached to the figure. The improvement of the image quality is clear when the number of waves is increased. Both contrast and resolution are strongly improved and the clutter signal level is reduced. Noise fluctuations are also decreased when the number of waves is increased (d). This shows the possibility to improve the image quality over a large field of view and to keep at the same time a high frame rate over one cardiac cycle which is important for imaging applications such as electromechanical and mechanical wave imaging (e.g. figure 11).
Fig. 10.
Tissue velocity map in an in vivo human volunteer heart superimposed on the B-mode image for three configurations 1, 3, 5 diverging waves during the Q wave (a),(b),(c). The tissue velocity at one point of space (green arrow) is plotted against time for the three configurations (d).
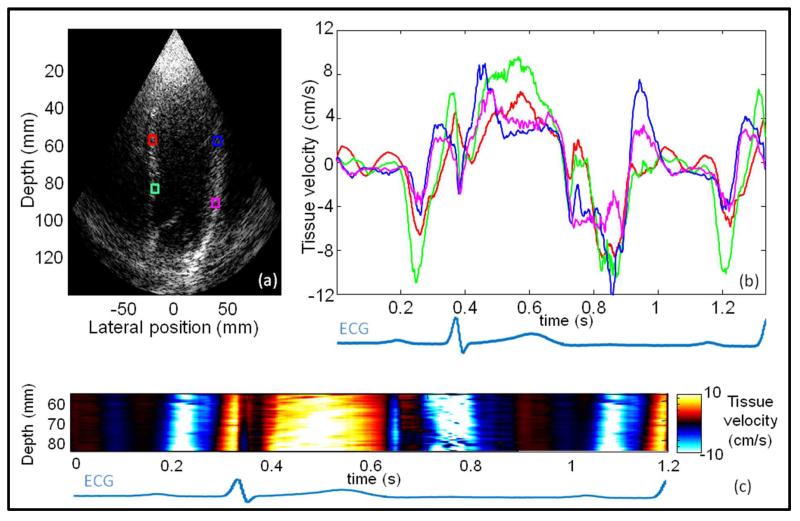
Fig. 11.
Four different locations in the the heart (a) and their associated tissue velocities are plotted (b). Spatial and temporal tissue velocities along the septum over one cardiac cycle is imaged (c).
Figure 11 demonstrates the feasibility to obtain good tissue velocity estimation at every location of the heart in the same acquisition.
IV. Discussion
In this paper, ultrafast imaging was performed using diverging waves transmitted by a conventional phased array over a large imaging sector. The image quality was found to improve rapidly with the number of transmits, which allows maintaining a high frame rate, a large imaging sector, and a large SNR simultaneously.
The focusing quality was investigated as a function of the virtual source positions and the technique was implemented on a commercial scanner.
The feasibility of improving the imaging quality at high enough frame rate to image the propagation of shear waves in the myocardium was shown in this study. Shear waves remotely induced by the phased array probe were imaged in a phantom at a depth of 45 mm at 2500 frames/s using 5 diverging waves. At such imaging depth, the anterior wall of the left ventricle for example should be reached in most of the patients in a parasternal long-axis view to make the shear waves propagate along the septum of inferior wall. For imaging at higher depth, the number of compounded waves needs to be reduced to two or three in order to maintain the frame rate. As the quality of tissue velocity estimation is crucial to image correctly the shear wave propagation, these results are promising and should help for the non-invasive real time elasticity mapping of the human anterior wall of the left ventricle.
We have also shown that spatial coherent compounding permits to image with better quality the propagation of mechanical waves in tissues due to valve closure and electromechanical waves (typical speed in the range of 1-5 m/s). The electromechanical activation has been imaged at typical frame rates of 800-2000 images/s using single diverging waves [35],[36]. Using 5 waves, we have shown in vivo in the human heart a strong improvement of both the B-mode and the velocity estimation quality compared to one diverging wave imaging.
One important issue to deal with is the influence of motion artifacts on the coherent summation of backscattered echoes from successive virtual sources as pointed out by different groups [37],[38],[39]. Because fast tissue motion can occur during the cardiac cycle, the degradation of coherent summation should be taken into account. Whereas a small number of diverging waves should not be influenced by motion as the acquisition of the successive set of backscattered echoes is performed before significant tissue motion, this problem could become critical for a large number of transmit diverging waves. One way to estimate the maximum number of compounded diverging waves that can be used without affecting the image quality of the compounded image is to consider that the coherent summation of images corresponding to different transmit angles is done for motion artifacts smaller than δ = λ/6 (from −λ/12 to λ/12) between the first and last compounded diverging wave transmission. In the field of adaptive focusing, this λ/6 value is a well accepted value for a limited influence of medium aberrations or time delay discrete sampling of transmit signals on the focus beam profile [40]. In that case, it is known from diffraction theory that the loss of wave amplitude at focus due to δ = λ/6 aberrations is equal to which can be considered in our case as very moderate [41]. We can use here the same value for a limited influence of motion on the coherent summation of several diverging waves. In that case, it becomes possible to estimate the maximum number of compounded diverging waves that can be used for a desired imaging depth and a maximum velocity while satisfying this criterion (one should notice that such a criterion on the compounded image quality is much more severe than a criterion on the quality of the tissue velocity estimate). Figure 12 presents the number of diverging waves that can be used with respect to imaging depth (and consequently pulse repetition frequency) and maximum velocity estimation. One can notice that a N=5 number of diverging waves permits an estimation of 15 cm/s maximum tissue velocities for a 10 cm imaging depth while preserving any significant effect on the compounded ultrasonic image quality and consequently tissue velocity estimation.
Doppler imaging of cardiac blood flows could also highly benefit from this technique. Blood flow mapping in the heart is a very demanding application that requires a large field of view, a high frame rate and an excellent imaging quality simultaneously to lower the clutter signal originating from the heart walls. Coherent compound with diverging waves at high frame rate could be used to map the flow pattern in the ventricles and obtain Doppler spectrum for each point of the map. Another advantage of such a compounded high frame rate acquisition would be to provide both tissue and blood velocities simultaneously [42]. This particular implementation of the technique will be presented in a future work.
Finally, the concept of compounded diverging waves could be also extended to other types of arrays. For example, plane wave coherent compounding with linear arrays has the disadvantage to reduce the field of view on the side of the images because the different plane wave transmits don’t overlap. Diverging waves with small angular apertures would enable to regain the entire field of view of the image.
V. Conclusion
We have investigated the use of spatial coherent compounding with diverging waves to obtain very high frame rate acquisition of the heart while maintaining high tissue velocity estimation quality over a large field-of-view. Simulations revealed that by optimizing the location of virtual sources, the image quality can be improved strongly with a few transmits. The technique has been implemented on an ultrasound scanner for cardiac applications and experiments were performed in phantoms with a cardiac phased array probe to quantify and validate the improvement predicted by simulations. Motion and elasticity maps obtained using spatial coherent compounding with diverging waves in phantoms during Shear Wave Imaging resulted in higher SNR and resolution than with single source acquisitions. Finally, the method was used in the human heart non-invasively over a large field of view during entire cardiac cycles at ultrafast frame rate (900 frames/s). Improvements in image quality were consistent with simulations and phantom studies. This technique has a strong potential to significantly improve the imaging of natural waves such as Electromechanical waves and remotely-induced shear waves for elasticity mapping in the human heart in real-time.
APPENDIX
Expression of acoustic field Φ(r) when coherent summation of the acoustic fields generated by each diverging wave at a point of space over the bandwidth (k1, k2) is made:
| (A1) |
In the far-field approximation, at a certain distance of the probe, near the central linex = 0, we can assume that: |zc − zn| >> |x − zn|. Let’s consider the central line at a distance zc − zn = F.
Approximation can be made on the amplitude:
Approximation can also be made on the phase:
Therefore:
| (A2) |
We can develop the expression:
| (A3) |
Rearranging this expression:
| (A4) |
For our periodic virtual sources array xn = n p:
| (A5) |
is a geometrical series that can be added explicitly, we end up with:
| (A6) |
Finally it leads to equation 1:
References
- [1].D’hooge J, Heimdal A, Jamal F, Kukulski T, Bijnens B, Rademakers F, Hatle L, Suetens P, Sutherland GR. Regional Strain and Strain Rate Measurements by Cardiac Ultrasound: Principles, Implementation and Limitations. Eur J Echocardiogr. 2000 Janv;1(3):154–170. doi: 10.1053/euje.2000.0031. et. [DOI] [PubMed] [Google Scholar]
- [2].Sutherland GR, Bijnens B, McDicken WN. Tissue Doppler Echocardiography: Historical Perspective and Technological Considerations. Echocardiography. 1999 Juill;16(5):445–453. doi: 10.1111/j.1540-8175.1999.tb00091.x. et. [DOI] [PubMed] [Google Scholar]
- [3].Couade M, Pernot M, Messas E, Bel A, Ba M, Hagege A, Fink M, Tanter M. In vivo quantitative mapping of myocardial stiffening and transmural anisotropy during the cardiac cycle. IEEE Trans Med Imaging. 2011 Févr;30(2):295–305. doi: 10.1109/TMI.2010.2076829. et. [DOI] [PubMed] [Google Scholar]
- [4].Bouchard RR, Hsu SJ, Palmeri ML, Rouze NC, Nightingale KR, Trahey GE. Acoustic Radiation Force-Driven Assessment of Myocardial Elasticity Using the Displacement Ratio Rate (DRR) Method. Ultrasound in Medicine & Biology. 2011 Juill;37(7):1087–1100. doi: 10.1016/j.ultrasmedbio.2011.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Pernot M, Couade M, Mateo P, Crozatier B, Fischmeister R, Tanter M. Real-time assessment of myocardial contractility using shear wave imaging. J. Am. Coll. Cardiol. 2011 Juin;58(1):65–72. doi: 10.1016/j.jacc.2011.02.042. [DOI] [PubMed] [Google Scholar]
- [6].Kanai H. Propagation of spontaneously actuated pulsive vibration in human heart wall and in vivo viscoelasticity estimation. IEEE Trans Ultrason Ferroelectr Freq Control. 2005 Nov;52(11):1931–1942. doi: 10.1109/tuffc.2005.1561662. [DOI] [PubMed] [Google Scholar]
- [7].Pernot M, Fujikura K, Fung-Kee-Fung SD, Konofagou EE. ECG-gated, mechanical and electromechanical wave imaging of cardiovascular tissues in vivo. Ultrasound Med Biol. 2007 Juill;33(7):1075–1085. doi: 10.1016/j.ultrasmedbio.2007.02.003. [DOI] [PubMed] [Google Scholar]
- [8].Provost J, Lee W-N, Fujikura K, Konofagou EE. Electromechanical Wave Imaging of Normal and Ischemic Hearts In Vivo. IEEE Trans Med Imaging. 2010 Mars;29(3):625–635. doi: 10.1109/TMI.2009.2030186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Bruneel C, Torguet R, Rouvaen KM, Bridoux E, Nongaillard B. Ultrafast echotomographic system using optical processing of ultrasonic signals. Applied Physics Letters. 1977 Avr;30(8):371–373. [Google Scholar]
- [10].Shattuck DP, Weinshenker MD, Smith SW, von Ramm OT. Explososcan: a parallel processing technique for high speed ultrasound imaging with linear phased arrays. J. Acoust. Soc. Am. 1984 Avr;75(4):1273–1282. doi: 10.1121/1.390734. [DOI] [PubMed] [Google Scholar]
- [11].Lu J-Y, Greenleaf JF. Pulse-echo imaging using a nondiffracting beam transducer. Ultrasound in Medicine & Biology. 1991 Janv;17(3):265–281. doi: 10.1016/0301-5629(91)90048-2. [DOI] [PubMed] [Google Scholar]
- [12].Sandrin L, Catheline S, Tanter M, Hennequin X, Fink M. Time-resolved pulsed elastography with ultrafast ultrasonic imaging. Ultrason Imaging. 1999 Oct;21(4):259–272. doi: 10.1177/016173469902100402. [DOI] [PubMed] [Google Scholar]
- [13].Lu J-Y, Cheng J, Wang J. High frame rate imaging system for limited diffraction array beam imaging with square-wave aperture weightings. IEEE Trans Ultrason Ferroelectr Freq Control. 2006 Oct;53(10):1796–1812. doi: 10.1109/tuffc.2006.112. [DOI] [PubMed] [Google Scholar]
- [14].Provost J, Nguyen VT-H, Legrand D, Okrasinski S, Costet A, Gambhir A, Garan H, Konofagou EE. Electromechanical wave imaging for arrhythmias. Phys Med Biol. 2011 Nov;56(22):L1–11. doi: 10.1088/0031-9155/56/22/F01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Tanter M, Bercoff J, Athanasiou A, Deffieux T, Gennisson J-L, Montaldo G, Muller M, Tardivon A, Fink M. Quantitative assessment of breast lesion viscoelasticity: initial clinical results using supersonic shear imaging. Ultrasound Med Biol. 2008 Sep;34(9):1373–1386. doi: 10.1016/j.ultrasmedbio.2008.02.002. et. [DOI] [PubMed] [Google Scholar]
- [16].Muller M, Gennisson J-L, Deffieux T, Tanter M, Fink M. Quantitative viscoelasticity mapping of human liver using supersonic shear imaging: preliminary in vivo feasibility study. Ultrasound Med Biol. 2009 Févr;35(2):219–229. doi: 10.1016/j.ultrasmedbio.2008.08.018. et. [DOI] [PubMed] [Google Scholar]
- [17].Couade M, Pernot M, Prada C, Messas E, Emmerich J, Bruneval P, Criton A, Fink M, Tanter M. Quantitative assessment of arterial wall biomechanical properties using shear wave imaging. Ultrasound Med Biol. 2010 Oct;36(10):1662–1676. doi: 10.1016/j.ultrasmedbio.2010.07.004. et. [DOI] [PubMed] [Google Scholar]
- [18].Nguyen T-M, Aubry J-F, Touboul D, Fink M, Gennisson J-L, Bercoff J, Tanter M. Monitoring of cornea elastic properties changes during UV-A/riboflavin-induced corneal collagen cross-linking using supersonic shear wave imaging: a pilot study. Invest. Ophthalmol. Vis. Sci. 2012 Août;53(9):5948–5954. doi: 10.1167/iovs.11-9142. et. [DOI] [PubMed] [Google Scholar]
- [19].Bouchard RR, Hsu SJ, Wolf PD, Trahey GE. In Vivo Cardiac, Acoustic-Radiation-Force-Driven, Shear Wave Velocimetry. Ultrason Imaging. 2009 Juill;31(3):201–213. doi: 10.1177/016173460903100305. et. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Tanter M, Bercoff J, Sandrin L, Fink M. Ultrafast compound imaging for 2-D motion vector estimation: application to transient elastography. IEEE Trans Ultrason Ferroelectr Freq Control. 2002 Oct;49(10):1363–1374. doi: 10.1109/tuffc.2002.1041078. et. [DOI] [PubMed] [Google Scholar]
- [21].Montaldo G, Tanter M, Bercoff J, Benech N, Fink M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans Ultrason Ferroelectr Freq Control. 2009 Mars;56(3):489–506. doi: 10.1109/TUFFC.2009.1067. et. [DOI] [PubMed] [Google Scholar]
- [22].Jensen JA, Nikolov SI, Gammelmark KL, Pedersen MH. Synthetic aperture ultrasound imaging. Ultrasonics. 2006;44:e5–e15. doi: 10.1016/j.ultras.2006.07.017. et. [DOI] [PubMed] [Google Scholar]
- [23].Cooley CR, Robinson BS. Synthetic focus imaging using partial datasets. 1994 IEEE Ultrasonics Symposium, 1994. Proceedings; 1994; pp. 1539–1542. et. vol.3. [Google Scholar]
- [24].Lockwood GR, Talman JR, Brunke SS. Real-time 3-D ultrasound imaging using sparse synthetic aperture beamforming. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 1998;45(4):980–988. doi: 10.1109/58.710573. et. [DOI] [PubMed] [Google Scholar]
- [25].Hazard GRLCR. Theoretical assessment of a synthetic aperture beamformer for real-time 3-D imaging. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on. 1999;(4):972–980. doi: 10.1109/58.775664. [DOI] [PubMed] [Google Scholar]
- [26].Nikolov SI, Kortbek J, Jensen JA. Practical applications of synthetic aperture imaging. 2010 IEEE International Ultrasonics Symposium (UIS), 2010; San Diego, California. 2010; et. [Google Scholar]
- [27].Nikolov SI. Synthetic aperture tissue and flow ultrasound imaging. Technical University of Denmark, 2800; Lyngby, Denmark: 2001. Ph.d. dissertation, Orsted-DTU. [Google Scholar]
- [28].Tong L, Gao H, Choi HF, D’hooge J. Comparison of conventional parallel beamforming with plane wave and diverging wave imaging for cardiac applications: a simulation study. IEEE Trans Ultrason Ferroelectr Freq Control. 2012 Août;59(8):1654–1663. doi: 10.1109/TUFFC.2012.2371. et. [DOI] [PubMed] [Google Scholar]
- [29].Hasegawa H, Kanai H. High-frame-rate echocardiography using diverging transmit beams and parallel receive beamforming. Journal of medical ultrasonics. 38(3):129–140. doi: 10.1007/s10396-011-0304-0. et. [DOI] [PubMed] [Google Scholar]
- [30].Jensen JA. Field: A Program for Simulating Ultrasound Systems. 10th Nordic-Baltic Conference on Biomedical Imaging Published in Medical & Biological Engineering & Computing. 1996;34(Supplement 1) 351-353. [Google Scholar]
- [31].Jensen JA, Svendsen NB. Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 1992;39(2):262–267. doi: 10.1109/58.139123. et. [DOI] [PubMed] [Google Scholar]
- [32].Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Trans Ultrason Ferroelectr Freq Control. 2004 Avr;51(4):396–409. doi: 10.1109/tuffc.2004.1295425. et. [DOI] [PubMed] [Google Scholar]
- [33].Papadacci C, Pernot M, Couade M, Fink M, Tanter M. Shear Wave Imaging of the heart using a cardiac phased array with coherent spatial compound; Ultrasonics Symposium (IUS), IEEE; 07-oct-2012; et. [Google Scholar]
- [34].Bonnefous O, Pesqué P. Time domain formulation of pulse-Doppler ultrasound and blood velocity estimation by cross correlation. Ultrason Imaging. 1986 Avr;8(2):73–85. doi: 10.1177/016173468600800201. et. [DOI] [PubMed] [Google Scholar]
- [35].Provost J, Thiébaut S, Luo J, Konofagou EE. Single-heartbeat electromechanical wave imaging with optimal strain estimation using temporally unequispaced acquisition sequences. Phys Med Biol. 2012 Févr;57(4):1095–1112. doi: 10.1088/0031-9155/57/4/1095. et. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Provost J, Gambhir A, Vest J, Garan H, Konofagou EE. A clinical feasibility study of atrial and ventricular electromechanical wave imaging. Heart Rhythm. 2013 Juin;10(6):856–862. doi: 10.1016/j.hrthm.2013.02.028. et. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Kim KS, Hwang JS, Jeong JS, Song TK. An efficient motion estimation and compensation method for ultrasound synthetic aperture imaging. Ultrason Imaging. 2002 Avr.24(2):81–99. doi: 10.1177/016173460202400202. et. [DOI] [PubMed] [Google Scholar]
- [38].Wang J, Lu J. Motion artifacts of extended high frame rate imaging. IEEE Trans Ultrason Ferroelectr Freq Control. 2007 Juill;54(7):1303–1315. doi: 10.1109/tuffc.2007.391. et. [DOI] [PubMed] [Google Scholar]
- [39].Oddershede N, Jensen JA. Effects influencing focusing in synthetic aperture vector flow imaging. IEEE Trans Ultrason Ferroelectr Freq Control. 2007 Sep;54(9):1811–1825. doi: 10.1109/tuffc.2007.465. et. [DOI] [PubMed] [Google Scholar]
- [40].Goodman JW. Introduction to Fourier Optics. Second Edition McGraw-Hill International Editions; 1996. [Google Scholar]
- [41].Born M, Wolf E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. 7eéd. Cambridge University Press; 1999. et. [Google Scholar]
- [42].Luo J, Konofagou EE. Imaging of wall motion coupled with blood flow velocity in the heart and vessels in vivo: a feasibility study. Ultrasound Med Biol. 2011 Juin;37(6):980–995. doi: 10.1016/j.ultrasmedbio.2011.03.004. et. [DOI] [PMC free article] [PubMed] [Google Scholar]