Behavioral contagion during learning about another agent’s risk-preferences acts on the neural representation of decision-risk

Significance

Why do we on some occasions engage in risky behavior but not on other occasions? Here, we explore the neural mechanisms of one possible account: a contagion effect. Using neuroimaging combined with computational modeling, we show that if we observe others behaving in a risk-seeking/risk-averse fashion, we become in turn more/less prone to risky behavior, and the behavioral shift is specifically implemented via neural processing of risk in a brain region, caudate nucleus. We further show that functional connectivity between the caudate and the dorsolateral prefrontal cortex, a region implicated in learning about others’ risk-attitude, is associated with susceptibility to the contagion effect, providing an account for how our own behavior can be influenced through observing other agents.

Abstract

Our attitude toward risk plays a crucial role in influencing our everyday decision-making. Despite its importance, little is known about how human risk-preference can be modulated by observing risky behavior in other agents at either the behavioral or the neural level. Using fMRI combined with computational modeling of behavioral data, we show that human risk-preference can be systematically altered by the act of observing and learning from others’ risk-related decisions. The contagion is driven specifically by brain regions involved in the assessment of risk: the behavioral shift is implemented via a neural representation of risk in the caudate nucleus, whereas the representations of other decision-related variables such as expected value are not affected. Furthermore, we uncover neural computations underlying learning about others’ risk-preferences and describe how these signals interact with the neural representation of risk in the caudate. Updating of the belief about others’ preferences is associated with neural activity in the dorsolateral prefrontal cortex (dlPFC). Functional coupling between the dlPFC and the caudate correlates with the degree of susceptibility to the contagion effect, suggesting that a frontal–subcortical loop, the so-called dorsolateral prefrontal–striatal circuit, underlies the modulation of risk-preference. Taken together, these findings provide a mechanistic account for how observation of others’ risky behavior can modulate an individual’s own risk-preference.

An individual’s attitude toward risk can exert a profound influence on his/her life in a wide array of contexts (1, 2). For example, risk-attitude governs an individual’s decision to purchase a safe asset or to invest in a risky stock (3). Moreover, a risk-seeking attitude can lead to an increased tendency toward behaviors leading to adverse outcomes such as drug-taking, unsafe sexual behavior, pathological gambling, and other potentially life-threatening pursuits; on the other hand, a risk-averse tendency can result in a reduced prospect of attaining the potentially high gains associated with the pursuit of risky options (4, 5). Given the importance of risk-attitudes in influencing everyday behavior, considerable research has been conducted on the factors influencing risky decision-making. For instance, there is substantial evidence that a number of extraneous variables such as the framing of a decision context in terms of losses or gains (6, 7), exposure to stressful life events (8, 9), and experiences of losses and gains (10) can modulate risk-preferences.

Less studied however is the role of a contagion effect (11) in modulating risk-seeking/averse behavior. That is, it remains elusive how one’s risk-related behavior is influenced by observing the behavior of others. The role of contagion may be especially important for understanding how and why risky behavior can become manifest in a number of critical situations. For example, observing a peer’s risk-seeking behaviors might exert a profound influence on conspecifics (12), resulting in an increased tendency toward risk-seeking behavior, especially during adolescence. Furthermore, the tendency of financial markets to collectively veer from bull to bear markets and back again (13) could arise in part because of the contagion of observing the risk-seeking or risk-averse investment behaviors of other market participants.

There is considerable evidence that contagion or conformity can affect an individual’s belief and behavior (11, 14, 15). For instance, an individual’s decision-making, including risk-related choice, can be changed by observing other peoples’ behavior (14–18), and the behavioral shift is reflected in value-related neural activity (16, 17, 19). However, little is known about the computational mechanisms underlying the contagion effect.

Here, we aimed to provide a mechanistic account of how contagion from observing or learning from other agents modulates an individual’s own risk-related behavior by testing the following three hypotheses. First, the act of observing and learning from other agents will alter an individual’s own risk-preferences. Second, the behavioral change will be associated specifically with modulation of the neural processing of risk. That is, the neural representation of risk per se, will be modulated, resulting in an increased or reduced perception of risk for gambles. Third, an interaction between neural systems implicated in representing risk and learning about others’ risk-preference will capture individual differences in susceptibility to the contagion effect.

Results

Experimental Task.

To test these hypotheses, we scanned 24 human participants using functional magnetic resonance imaging (fMRI), while they repeatedly chose between a risky gamble and a guaranteed $10 (Self trials) (Fig. 1A), observed decisions of confederates (Observe trials), and predicted the confederates’ decisions (Predict trials). The set of gambles presented (Fig. S1 A and B) was designed to decorrelate the risk (variance of reward) from the expected value of reward across trials (1).

Fig. 1.

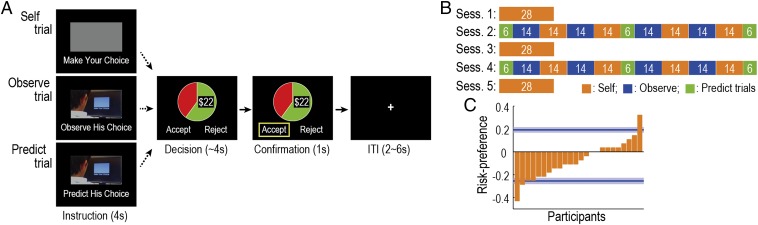
Experimental task and basic behaviors. (A) Timeline of each trial. On Self trials, participants decide whether to accept or reject a gamble within 4 s (response time range, 0.29–3.88 s; mean $\pm$ SD, 1.62 $\pm$ 0.51; data from all of the participants are collapsed). If participants accept, they can gamble for a specific amount of money; otherwise, they can take a guaranteed $10. The reward probability and magnitude of the gambles are varied on every trial and are represented by a pie chart (size of the green area indicates the probability; and the digits denote the magnitude). On Observe trials, participants are asked to observe a choice of another person, the “observee.” On Predict trials, participants predict the choice that the observee would make (response time range, 0.78–3.90 s; mean $\pm$ SD, 1.79 $\pm$ 0.56). Note that instruction phases were presented only during the first trial in each block. (B) Overall schedule. Sessions 1, 3, and 5 include only Self trials, whereas sessions 2 and 4 contain all of the three trial types in a block-wise manner. Orange, blocks of Self trials; blue, blocks of Observe trials; green, blocks of Predict trials. White digits denote the number of trials in each block. (C) Participants’ risk-preference in Session 1 (orange) and the two observees’ preferences (blue, mean $\pm$ SD). Positive and negative values indicate risk-seeking and -averse, respectively.

Fig. S1.

Experimental task. (A) Set of gambles presented in Self trials. Each point denotes one gamble characterized by the probability and the magnitude of reward. The 28 gambles are presented in a random order in Sessions 1, 3, and 5 (Fig. 1B). In Sessions 2 and 4, we show the 28 gambles in a random order for the first and second blocks of the Self trials and again for the third and forth blocks. The solid line indicates the indifference curve, on which the utility of the gamble is equal to that of sure $10, under the risk-neutral preference. Note that we do not use small probabilities (P < 0.3), so that distortion of the subjective probability proposed in Prospect Theory (7) does not play a crucial role and that the actual reward magnitude presented in each trial was jittered by adding a small noise randomly drawn from {−1, 0, 1}. (B) Set of the gambles presented in Observe trials and the observees’ choice pattern. The format is the same for A except for the color code. Graded color of each point represents the probability that the observee choose to accept the gamble (1 for the rich blue; 0 for the white). (B, Left) Session with the risk-averse observee. (B, Right) session with the risk-seeking observee. (C) Set of the gambles presented in Predict trials. The format is the same for A. The three gambles are presented twice in a random order for each block of the Predict trials. Here, to efficiently examine the participants’ learning performance about the observees’ risk-preference, the gambles were located on the indifference curve. (D) Images for the two observees used in the experiment. To minimize potential effects of their appearance, the images were taken from the back, and the association between the images and the observees was randomized across participants. (E) Cross-correlations of the three measures of risk-preference for each session (r > 0.94 for all of the cases): ρ is based on exponential utility function, α is based on mean-variance utility function, and P(gamble) is based on the proportion of gambles accepted (see SI Methods for details). (F) Participants’ risk-preference in Session 1 (orange) and the two observees’ preferences (blue) (mean $\pm$ SD) on the three measures of risk-preference. (F, Left) ρ based on exponential utility function. (F, Center) α based on mean-variance utility function. (F, Right) P(gamble) based on the proportion of gambles accepted. The format is the same for Fig. 1C.

The experiment consisted of five sessions, in which the three types of trials were presented in a block-wise manner (Fig. 1B): Sessions 2 and 4 involved all three types, whereas Sessions 1, 3, and 5 included only Self trials. The confederate (“observee”) for Observe/Predict trials was different between Session 2 and 4: one for Session 2 was risk-averse and the other for Session 4 was risk-seeking, or vice versa (Fig. S1B). We instructed participants that the choices they observed were made by a real person recorded from a previous experiment. In actuality, however, the observees’ choices were generated by computer algorithms, as in previous studies (14, 15, 17, 19, 20).

Basic Behavioral Results.

Consistent with previous findings (21), before observing the others’ decisions, the majority of participants exhibited risk-averse behavior, although there were considerable individual differences (Fig. 1C). Here, we defined each participant’s risk-preference as the proportion of gambles accepted relative to the proportion accepted by the risk-neutral agent (i.e., positive/negative values indicate risk-seeking/averse, respectively), unless specifically mentioned otherwise. This simple model-free measurement was highly consistent with other prevalent model-based measurements based on utility functions (Fig. S1 E and F).

Behavioral Evidence for Contagion of Risk-Preference.

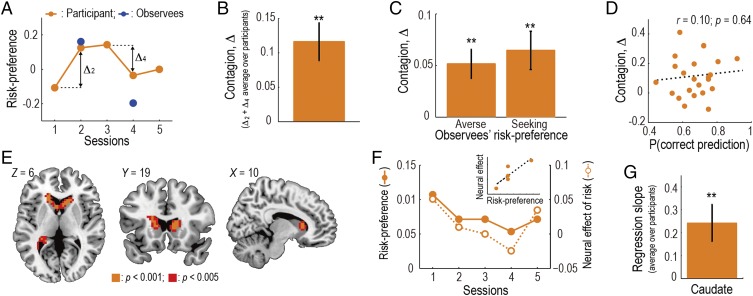
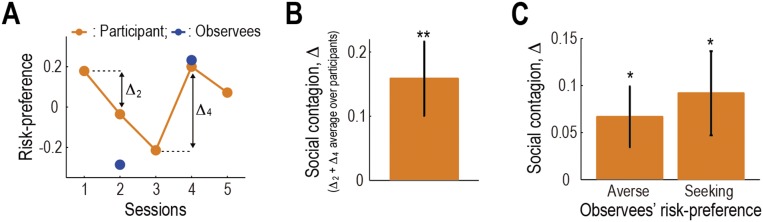
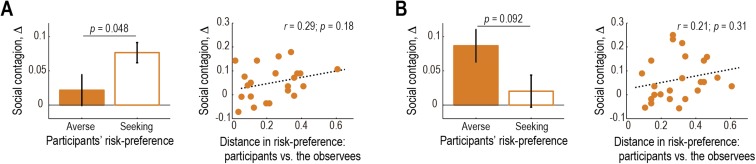
Participants’ behavior showed an effect of contagion. That is, the participants’ risk-preference was shifted toward the observees’ (see Fig. 2A for an example participant who exhibited a clear effect). The degree of contagion, defined as positive when the participant conformed to the observee (see Fig. 2A and the legend for details), was significantly positive (P < 0.01; Fig. 2B). This effect was also confirmed to be significant for both the risk-seeking and -averse observees (P < 0.01 for both; Fig. 2C) and replicated in an independent behavioral experiment (Fig. S2). A closer examination revealed a trend that the effect was more prominent when participants’ own risk-preference was incongruent with the observee’s, but the distance between participants’ and the observees’ preferences did not parametrically covary with the degree of contagion (Fig. S3). Furthermore, the degree of contagion was not significantly correlated with the proportion of correct predictions in Prediction trials (P > 0.05; Fig. 2D), implying that the contagion was not primarily triggered by predicting the observees’ choices.

Fig. 2.

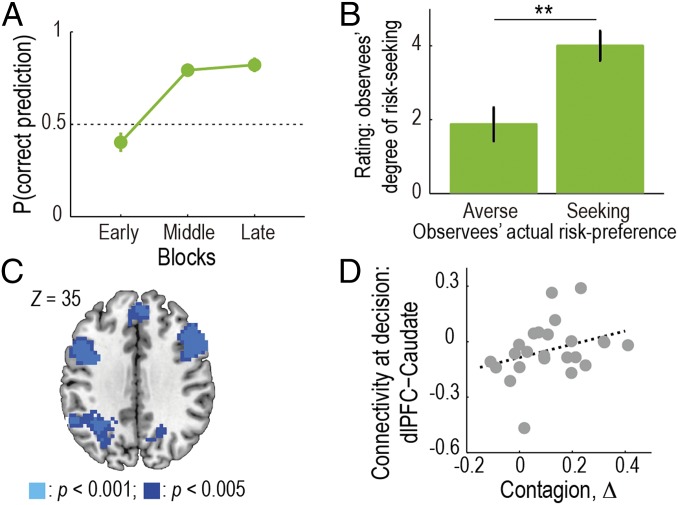
Contagion of risk-preference. (A) Change of an example participant’s risk-preference toward the observees’. Orange indicates the participant’s risk-preference in each session, and blue indicates the observees’ preference. The degree of contagion is defined as Δ: the change of the risk-preference (i.e., proportion of gambles accepted) from the last session. Δ is positive when the participant conformed to the observee; negative when she/he anticonformed. (B) Degree of contagion (mean $\pm$ SEM across participants, n = 24). The degree, Δ, is defined as the sum of Δ₂ and Δ₄. **P < 0.01. (C) Degree of contagion plotted separately for the risk-averse and -seeking observees (mean $\pm$ SEM across participants). (D) Degree of contagion in each participant plotted as a function of the proportion of the correct predictions made on Predict trials. (E) Neural representation of risk. Activity in the caudate significantly correlated with risk of the gamble at the time of decision in Self trials [P < 0.05 FWE corrected at cluster-level; GLM I (SI Methods)]. (F) Relation between the behavioral risk-preference and the neural effect of risk in the caudate in an example participant. Filled points indicate the participant’s behavioral risk-preference in each session; open points indicate the neural effect of risk (i.e., β value for the risk regressor in GLM I) in each session. (Inset) Scatter plot of the same data. (G) Relation between the behavioral risk-preference and the neural effect of risk (mean $\pm$ SEM across participants). We regressed the neural effect in the caudate against the behavioral risk-preference across sessions and plot the average regression coefficient over the participants.

Fig. S2.

Social contagion of risk-preference in an independent behavioral experiment. (A) Change of an example participant’s risk-preference toward the observees’. The format is the same for Fig. 2A. Twelve healthy participants (six female participants; age range, 18–43 y; mean $\pm$ SD, 27.42 $\pm$ 7.48) took part in the behavioral experiment. The experimental procedure was the same as the main experiment, but the participants were not scanned. (B) Degree of social contagion (mean $\pm$ SEM across participants; n = 12). The format is the same for Fig. 2B. **P < 0.01. (C) Degree of social contagion plotted separately for the risk-averse and -seeking observees (mean $\pm$ SEM across participants). The format is the same for Fig. 2C. *P < 0.05.

Fig. S3.

Effect of participants’ own and the observees’ risk-preferences on the degree of social contagion. (A) Session with the risk-averse observee. (A, Left) Degree of social contagion plotted separately for participants’ own risk-preference. (A, Right) Degree of social contagion plotted as a function of the distance between the participants’ own and the observees’ risk-preferences. (B) Session with the risk-seeking observee. The format is the same for A.

To exclude other accounts for the behavioral shift, we conducted additional analyses. First, we examined whether participants became more “rational” by observing the observees’ choices and found no significant evidence of a change in their rationality across sessions (Fig. S4 A and B and SI Text 1). Second, we confirmed that the behavioral shift cannot be explained by “regression to the baseline” (Fig. S4C and SI Text 1).

Fig. S4.

Additional behavioral results. (A) Change of the proportion of choices for the risk-free gambles as a function of time (mean $\pm$ SEM across participants; n = 24). See SI Text 1 for details. n.s., nonsignificant as P > 0.05 in ANOVA. (B) Change of risk-neutrality as a function of time (mean $\pm$ SEM across participants). See SI Text 1 for details. Risk-neutrality is defined as absolute value of risk-preference (smaller values close to zero indicate the more risk-neutral; see SI Methods for details). (C) Change of the distance between participants’ risk-preference and the baseline as a function of time (mean $\pm$ SEM across participants). See SI Text 1 for details. (C, Left) The baseline is defined as each participant’s preference in Session 1. (C, Right) The baseline is defined as the mean preference over the participants in Session 1.

Next, we aimed to show that the shift in participants’ choices across sessions was better captured by a change in their risk-preferences rather than a change in their subjective judgments about the probabilities (7, 22, 23). To this end, we constructed two computational models, one with varying risk-preference across sessions and the other with varying probability-weighting, and compared their goodness-of-fit (SI Text 2). The analysis revealed that the first model provided the better fit, indicating that the behavioral shift was better explained by a change in risk-preference. Similar analyses also revealed that it is unlikely that participants simply biased utility (16) or choice probability (24) of gambling options, possibly by copying the observee’s tendency to take a gamble, without changing their own risk-preference (SI Text 3 and SI Text 4). These behavioral results together suggest that decision-making under risk can be altered by observing others’ decisions through the change of one’s own risk-preference.

Finally, to examine the extent to which the contagion effect depends on observing the behavior of another human vs. a nonhuman computer agent, we conducted an additional behavioral experiment in which participants observed/predicted choices of another human and a computer agent on different sessions (see SI Methods for details). The result indicates that the contagion effect is present for both the human and computer observees (P < 0.01 for both of the sessions, with no significant difference between the sessions; P = 0.20). These results suggest that the extent to which the observed agent is human or artificial does not affect the extent to which the contagion effect is manifest.

Neural Encoding of Risk.

At the neural level, risk was represented in a dorsal part of striatum: the caudate nucleus (Fig. 2E and Table S1). Blood-oxygen-level dependent (BOLD) signal in the caudate significantly correlated with the trial-by-trial risk of the gambling option at the time of decision in Self trials [P < 0.05 whole-brain familywise error (FWE) corrected at cluster level; general linear model (GLM) I (SI Methods)]. The right caudate activity was also significant (P < 0.05) under the whole-brain FWE correction at voxel level. As a robustness check, we included the following variables into our regression model as regressors of no-interest (GLM I-2; SI Methods): the response time, the decision-related response, and the motor-related response. Running this revised model with the motor covariates on the anatomically defined caudate region of interest (25), we confirmed a significant effect of risk on the neural activity after adjusting for the effects of motor activity (P < 0.05). The risk effect also continued to survive a whole-brain voxel-wise analysis with these motor covariates included, albeit at a reduced threshold (P < 0.005 uncorrected; cluster size, k > 45). Taken together, these results indicate that the caudate represents risk during decision-making, over and above effects of motor-responses and response-time.

Table S1.

Areas exhibiting significant changes in BOLD associated with the risk and the expected value

Region	Hemi	BA	x	y	z	t static	P value	Voxels
Risk
Caudate (head)	Bi		9	20	7	6.26	0.000	189
Caudate (tail)	L		−27	−37	4	4.21	0.000	94
Expected value
Visual cortex	Bi	17/18/19	−6	−70	16	7.25	0.000	4,151
PCC/TPJ/IPL	Bi	23/39/40	9	−40	37	6.93	0.000	1,487
mPFC	Bi	8/910/32	−12	41	40	5.27	0.000	1,491
Insula	L	13	−33	11	−8	4.78	0.000	73
Precentral gyrus	R	4	51	−19	46	4.45	0.000	154
IFG	R	47	27	29	−11	4.40	0.000	63
IPL	L	40	−30	−43	40	4.12	0.000	67

Activated clusters observed in the whole-brain analysis (P < 0.05, FWE corrected at cluster level) for risk and expected value of the gamble at the time of self-decision. The stereotaxic coordinates are in accordance with MNI space. t statistics and uncorrected P values at the peak of each locus are shown. In the far right column, the number of voxels in each cluster is shown. BA, Brodmann area; Bi, bilateral; Hemi, hemisphere; IFG, inferior frontal gyrus; L, left; PCC, posterior cingulate cortex; R, right; TPJ, temporoparietal junction.

Neural Encoding of Risk Associated with the Behavioral Shift in Risk-Preference.

We then found that the neural effect of risk in the caudate covaried with the behavioral shift in risk-preference across sessions (see Fig. 2F for an example participant showing a clear effect). Here, the neural effect of risk in each session is expressed as a β value (i.e., regression coefficient) of the risk regressor from GLM I. To quantify this finding, we regressed the neural effect of risk in the caudate against the behavioral risk-preference across sessions and confirmed that the regression slope was significantly positive (P < 0.01; Fig. 2G). The result does not change if we use the data from sessions including only Self trials (i.e., Sessions 1, 3, and 5) (P < 0.01). We also conducted a whole-brain analysis to search for brain regions in which the neural effect of risk covaried with the behavioral preference across sessions and found only one region: caudate nucleus (P < 0.05 whole-brain FWE corrected at cluster level).

On the other hand, the expected value of the gambling option was correlated with activity in frontoparietal network brain regions including medial prefrontal cortex (mPFC) (P < 0.05 whole-brain FWE corrected at cluster level; Table S1 and Fig. S5A). However, the neural effects of expected value were not correlated with the behavioral shift in risk-preference across sessions (P > 0.05 for all of the activated clusters; see Fig. S5B and the legend for details). Moreover, we found that, consistent with a previous study (16), mPFC and other regions tracked the utility signal incorporating the change in risk-preference across trials, but the neural effects were not associated with the behavioral shift across sessions (P > 0.05 for all of the activated clusters; Fig. S5C). We also confirmed that the behavioral change of risk-preference did not covary with the neural effects of other decision-related variables: reward probability, magnitude, or squared magnitude of the gambling option (P > 0.05 for all of the activated clusters; Fig. S5 D–F). These neural findings together support our hypothesis that contagion modulates the neural representation of risk per se, not the representations of other factors such as expected value or integrated utility.

Fig. S5.

Neural representations of expected value, utility, reward probability, reward magnitude, and squared reward magnitude. (A) Neural representation of expected value. Activity in a network of brain regions including mPFC was significantly correlated with expected value of the gamble at the time of decision in Self trials (P < 0.05 FWE corrected at cluster-level; GLM I). (B) Relationship between neural effects of expected value and behavioral risk-preference. For each brain region whose activity correlated with expected reward, we regressed the neural effect (β value of the expected value regressor in GLM I) against the behavioral risk-preference across sessions and then plotted the regression slope (mean $\pm$ SEM across participants). The format is the same for Fig. 2G. IFG, inferior frontal gyrus; n.s., nonsignificant as P > 0.05 (Bonferroni corrected based on the number of activated clusters); PCC, posterior cingulate cortex; TPJ, temporoparietal junction. (C) Relationship between neural effects of utility (GLM III) and behavioral risk-preference. The format is the same for B. pSTS, posterior superior temporal sulcus. (D) Relationship between neural effects of reward probability (GLM II) and behavioral risk-preference. The format is the same for B. (E) Relations between neural effects of reward magnitude (GLM II) and behavioral risk-preference. The format is the same for B. (F) Relations between neural effects of squared reward magnitude (GLM IV) and behavioral risk-preference. The format is the same for B.

Learning About Others’ Risk-Preference.

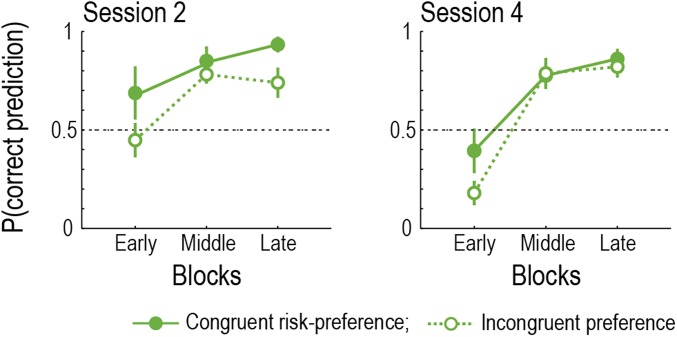
To exhibit contagion in this task, participants first needed to learn observees’ risk-preference from their choices. The proportion of correct predictions in Predict trials and postexperiment ratings about the observees’ risk-preference showed that participants indeed succeeded in learning about their risk-preference (Fig. 3 A and B). Furthermore, a closer examination of the prediction performance revealed that the learning was faster when the participants’ preference was congruent with the observee’s (Fig. S6), suggesting that the participants used their own preference as a starting point.

Fig. 3.

Learning about others’ risk-preferences. (A) Participants’ learning curve of the observees’ risk-preferences. The proportion of correct predictions in Predict trials is plotted as a function of time (mean $\pm$ SEM across participants; n = 24). Data from Sessions 2 and 4 are collapsed. (B) Postexperiment ratings about the observees’ risk-preferences. We plot participants’ ratings (six-point scale) about how likely the observee would accept a gamble, separately for risk-averse and -seeking observees (mean $\pm$ SEM across participants). **P < 0.01. (C) Neural representation of belief-updating during learning about others’ risk-preferences. Activity in the dlPFC, the dmPFC, and the IPL significantly correlated with the update signal, D_KL, which is measure of the difference between the posterior and the prior, at the time of confirmation in Observe trials [P < 0.05 FWE corrected at cluster-level; GLM V (SI Methods)]. (D) Functional connectivity between dlPFC and caudate at the time of decision on Self trials reflected the degree of behavioral contagion across participants (ρ = 0.38; P = 0.035).

Fig. S6.

Learning about the observees’ risk-preference. Proportions of the correct predictions on Predict trials are plotted as a function of time. (Left) Session 2. (Right) Session 4. Filled points denote the case where participants’ own risk-preference was congruent with the observee’s preference. Open points represent the case where participants’ risk-preference was incongruent with the observee’s.

This suggestion is also supported by a formal model-based analysis. We constructed a family of computational models and fit those models to the participants’ prediction behavior (SI Text 5 and Table S2). The model comparison revealed that a Bayesian learning model using each individual’s own risk-preference as a prior belief provided a better fit to the participants’ actual predictions than alternative models did.

Table S2.

Behavioral model fits to the participants’ prediction data

Model	-LL	#prms	BIC
Session 2
Random	297	0	595
Fixed Probability	296	1	599
Bayesian	232	4	488
Bayesian (self-projection)	229	3	477
Session 4
Random	295	0	591
Fixed Probability	295	1	597
Bayesian	206	4	437
Bayesian (self-projection)	214	3	446
Bayesian (carry-over)	206	3	429
Bayesian (self-projection + carry-over)	191	4	407

Comparison of each model’s goodness-of-fit to the participants’ prediction behaviors. For BIC, smaller values indicate better fit. -LL, negative log likelihood (smaller values indicate better fit); #prms, no. of free parameters. The best model in each session is shown in bold.

Neural Correlates of Learning About Others’ Risk-Preference.

To examine the neural substrates of learning about others’ risk-preferences, we searched for brain regions associated with updating the belief about others’ risk-preference, which is captured by the Kullback–Leibler divergence (D_KL) between the posterior and the prior (26). The belief-updating signal, D_KL, was found to correlate with activity in dorsolateral prefrontal cortex (dlPFC) as well as other regions including dorsomedial prefrontal cortex (dmPFC) and inferior parietal lobule (IPL) at the time of confirmation in Observe trials (Fig. 3C and Table S3; P < 0.05 whole-brain FWE corrected at cluster level). Notably, the right dlPFC activity was also significant (P < 0.05) under the whole-brain FWE correction at voxel level. Furthermore, we confirmed these activations survived even when potential confounds, such as the observee’s response time, decision, motor responses, were included into the regression analysis [GLM V-2 (SI Methods)]. These results suggest that updating of the belief in learning about others’ risk-preference may occur in the dlPFC, dmPFC, and IPL—regions previously implicated in learning about others’ reward structure and mental states (19, 27–30).

Table S3.

Areas exhibiting significant changes in BOLD associated with the belief-updating signal (D_KL) between the posterior and the prior

Region	Hemi	BA	x	y	z	t static	P value	Voxels
dlPFC	R	9	54	17	34	6.70	0.000	568
	L	9	−45	8	34	5.16	0.000	481
IPL	L	40	−36	−52	40	5.94	0.000	686
	R	40	42	−49	43	4.18	0.000	233
dmPFC	R	8	−3	35	49	5.38	0.000	804
Insula	L	13	−30	20	−5	5.27	0.000	117
V1	L	17	−12	−76	13	4.31	0.000	121

Activated clusters observed in the whole-brain analysis (P < 0.05, FWE corrected at cluster level) for belief-updating at the time of confirmation in Observe trials. The format is the same for Table S1. BA, Brodmann area; Hemi, hemisphere; L, left; R, right; V1, primary visual cortex.

Functional Connectivity Between the dlPFC and the Caudate.

Given the above results together with previous findings of the anatomical and functional connectivity between dlPFC and caudate (31, 32), we further reasoned that functional connectivity between the two regions would account for individual differences in the degree of behavioral contagion. To test this, we conducted a psychophysiological interaction (PPI) analysis on the caudate with a psychological factor, the timing of self-decision, and a physiological factor, the dlPFC activity (see SI Methods for details). This analysis revealed that functional coupling between the two regions at the time of self-decision (i.e., effect of the PPI term) was significantly correlated with the degree of behavioral contagion across participants (Fig. 3D; P < 0.05; see SI Text 6 for robustness check). More specifically, the PPI effect was negative and around 0 for those participants with lower and higher behavioral contagion effect, respectively (Fig. 3D), and the main effect of the dlPFC activity was significantly positive (P < 0.01). A possible interpretation of these findings is that, for those individuals who are less susceptible to the contagion effect, the default connectivity between dlPFC and caudate is suppressed at the time of decision-making for the self.

SI Text 1

To test whether participants became “rational” by observing the others’ choices, we conducted two behavioral analyses based on different notions of rationality. The set of gambles used in this experiment involved two risk-free gambles (i.e., reward probability is one, and the magnitude is $20 and $30; Fig. S1A). Rational participants should prefer the risk-free gambles to the sure $10, regardless of their risk-preference (called “monotonicity” in economics). One definition of rationality is therefore the act of choosing the risk-free gambles (sure $20 and $30) over the sure $10. Given this, we examined whether the proportion of choosing the risk-free gambles was changed across sessions and found no significant effect (ANOVA, P = 0.59; Fig. S4A). Another possible definition of rationality is to make decisions based on a risk-neutral preference (i.e., relying only on expected value but not on risk). Note that we here define rationality in the sense it maximizes expected monetary reward, apart from the conventional definition (i.e., maximization of expected utility) used in economics. We checked whether participants became risk-neutral as the experiment proceeded and found no significant effect (ANOVA, P = 0.18; Fig. S4B). In sum, we conclude that there is no significant evidence that participants became more “rational” through observation of others’ behavior.

One might argue that the shift in participants’ risk-preference can be explained by “regression to the baseline” (e.g., each participant’s preference in Session 1 or the mean over the participants). Additional behavioral analyses, however, provided no significant evidence that participants’ risk-preference approached the baseline as the experiment proceeded (ANOVA: P = 0.30 for the regression to each participant’s baseline; and P = 0.47 for the mean preference; Fig. S4C).

SI Text 2

Here, we aimed to show that the shift in participants’ behavior is better captured by the change in their risk-preference rather than the change in their subjective judgment about probabilities. To this end, we constructed two computational models, one with varying risk-preference across sessions and the other with varying probability-weighting across sessions and compared their goodness-of-fits to the participants’ actual choices.

In both models, participants are assumed to convert the instructed objective probability to the subjective probability as suggested in the previous study (22):

$$\pi \left(p\right)=1/exp\left\{{\left[log\left(1/p\right)\right]}^{\gamma }\right\},$$

where γ governs the probability-weighting. If γ = 1, the subjective probability is identical to the objective probability. Then, given the subjective probability, the participants compute the utility of each option based on mean-variance utility function (SI Methods, Behavioral Data Analyses).

In the first model, we assign different risk-preference parameters into the five sessions and a single common probability-weighting parameter into the sessions. In contrast, in the second model, different probability-weighting parameters are assigned into the five sessions and one common risk-preference parameter is assigned. Fitting these models to each participant’s behavior separately, we found the first model provided the better fit than the second model did [(Exceedance probability in Bayesian Model Selection (61) is 0.94]. Here, it is worth noting that each model’s goodness of fit was assessed using the log model evidence, approximated by the Bayesian information criterion (BIC) (62), which penalizes models with more free parameters compared with those with fewer free parameters.

The same result was obtained when we used an exponential utility function (SI Methods, Behavioral Data Analyses) instead of a mean-variance utility. That is, the model with varying risk-preference provided a better fit than the model with varying probability-weighting (Exceedance probability favoring the first model is 0.99). These findings suggest that, regardless of the specific forms of utility function, the session-by-session behavioral shift we observed reflects a change in the participants’ risk-preference rather than probability-weighting.

SI Text 3

We aimed to confirm that the shift in participants’ behavior was better captured by the change in their risk-preference rather than the change in the simple bias for/against utility of gambling options (16). For this purpose, as in SI Text 2, we constructed two computational models and compare their goodness-of-fits. In both of the two models, a bias for/against utility of gambling options is incorporated. That is, under mean-variance utility function (SI Methods, Behavioral Data Analyses), the utility of a gambling option is computed by

$$U\left(X\right)=E\left(X\right)+\alpha V\left(X\right)+\delta ,$$

where $\delta$ denotes the bias. The bias term can be similarly introduced into exponential utility function (SI Methods, Behavioral Data Analyses): $U\left(X\right)=p\hspace{0.17em}{r}^{\rho }+\delta ,$ which is equivalent to the other-conferred utility (OCU) model introduced by ref. 16.

As in SI Text 2, the first model has different risk-preference parameters for the five sessions and a single common bias parameter, δ, whereas the second model has different bias parameters and a single risk-preference parameter. The model comparison revealed that the first model provided the better fit than the second model. Exceedance probability (61) favoring the first model is 0.99 in the case with mean-variance utility function and 1.00 in the case with exponential utility function. These results support our claim that the shift in participants’ behavior was driven by the change in their risk-preference.

SI Text 4

Here, we aimed to demonstrate that the shift in participants’ behavior is better captured by a change in risk-preference rather than a change in a simple bias for/against the choice probability of gambling options (24). Following the procedure in SI Text 2, we constructed two computational models and compared their goodness-of-fits. In both of the two models, a bias for/against choice probability of gambling options is incorporated. That is, after computing the utility of the gambling and sure options (based on either mean-variance or exponential utility function; SI Methods, Behavioral Data Analyses), participants make a choice based on the choice probability:

$$q\left(\text{gamble}\right)=\delta +\left(1-\delta \right)/[1+\text{exp}\{-\beta (U\left(\text{gamble}\right)-U\left(\text{sure}\right))\}]\hspace{0.17em}\text{if}\hspace{0.17em}\delta \ge 0,$$

$$q\left(\text{gamble}\right)=\left(1+\delta \right)/[1+\text{exp}\{-\beta (U\left(\text{gamble}\right)-U\left(\text{sure}\right))\}]\text{if}\hspace{0.17em}\delta <0,$$

where $\delta \in \left[-\mathrm{1,1}\right]$ denotes the bias to the choice probability. If $\delta =1,$ the participant always choose the gambling option independent of the utility; if $\delta =-1,$ she/he always choose the sure $10; and if $\delta =0$, she/he makes decisions based only on the utility. Note that the model with the biased choice probability is referred to as parametric approach–avoidance decision model in the previous study (24).

As in SI Text 2, the first model has different risk-preference parameters for the five sessions and a single bias parameter, δ, whereas the second model has different bias parameters and a single risk-preference parameter. The model comparison revealed that the first model was better fit than the second model. Exceedance probability (61) favoring the first model is 0.98 in the case with the mean-variance utility function and 1.00 in the case with the exponential utility function. These results suggest that the shift in participants’ behavior is captured by a change in risk-preference rather than a change in the bias to choice probability.

SI Text 5

To capture the computational process of participants’ learning about the observees’ risk-preference, we constructed a family of computational models and fit those models to the participants’ actual prediction behaviors.

Bayesian Learning Models.

In this family of models, an observee’s risk-preference is inferred by a simple Bayesian learning algorithm. The Bayesian learner updates the estimation of an observee’s risk-preference, when she/he observes the observee’s choice (at the time of confirmation in Observe trials). Using the estimated risk-preference, she/he predicts the observee’s choice in Predict trials.

Given the mean-variance utility function, the learner estimates and updates an observee’s risk-preference, α_O, as follows:

$$p\prime \left({\alpha }_O\right)\propto \hspace{0.17em}p\left({\alpha }_O\right)\hspace{0.17em}\hspace{0.17em}{p}_O\left(C_O|{\alpha }_O\right),$$

where C_O and p_O denote the observee’s choice and the choice probability, respectively. Here, the observee’s choice probability can be derived by

$$\begin{array}{l}{p}_O\left(C_O=\text{gamble|}{\alpha }_O\right)=1/\left\{1+exp\left[-{\beta }_O\left(U\left(\text{gamble}\right)-U\left(\text{sure}\right)\right)\right]\right\}\\ =1/\left\{1+exp\left[-{\beta }_O\left(E\left(X\right)+{\alpha }_{O}V\left(X\right)-10\right)\right]\right\},\end{array}$$

where U denotes utility of each option, E(X) and V(X) represent expected value and risk of the gamble, and β_O controls the degree of stochasticity in the observee’s choice (treated as a free parameter in the model fitting).

Based on the estimated risk-preference, the learner computes the observee’s choice probability as follows:

$$p_O\left(C_O\right)={{\displaystyle \int }}^{}{p}_O\left(C_O|{\alpha }_O\right)p\left({\alpha }_O\right)d{\alpha }_O;$$

and finally predicts the observee’s choice:

$$p_S\left(C_O=\text{gamble}\right)=1/\left\{1+exp\left[-{\beta }_S\left(p_O\left(C_O=\text{gamble}\right)-p_O\left(C_O=\text{sure}\right)\right)\right]\right\},$$

where $p_S$ represents the probability that the learner predicts the observee’s choice of the gamble or sure option, and β_S controls the degree of stochasticity in the prediction (a free parameter).

At the beginning of each session, we assume that the Bayesian learner has a normally distributed prior belief about the observee’s risk-preference, α_O.

Each model included in this family is different with respect to shape of the prior belief. In the Bayesian (simple) model, both mean and variance of the normal prior belief are free parameters, in addition to β_O and β_S. On the other hand, in the Bayesian (self-projection) model, the mean of the prior is extracted from the participant’s own risk-preference in the last session (i.e., Session 1 for Session 2; and Session 3 for Session 4), whereas the variance is a free parameter. For Session 4, we constructed additional two models: a Bayesian (carry-over) and a Bayesian (carry-over + self-projection) model. In the Bayesian (carry-over) model, the mean of the prior is equal to the mean of the posterior in Session 2 (the variance is a free parameter). That is, learning in Session 2 carries over to Session 4, which would capture the fact that the participants’ prediction performance at the beginning of Session 4 was below the chance-level (Fig. S6, Right). In the Bayesian (carry-over + self-projection) model, the mean prior is a weighted sum of the participant’s own risk-preference and the mean of the posterior in Session 2, where the weight is a free parameter.

Null Models.

In addition to the Bayesian learning models, we constructed two null models. One is a Random Prediction model that predicts observees’ choice randomly. The other is a Fixed Probability model that predicts that observees accept a gambling option with a fixed probability (independently of the reward probability and magnitude).

Model Comparison.

We fit each model to the aggregated data from all of the participants together because of the small number of Predict trials (i.e., we used a fixed-effects analysis). Each model’s goodness of fit was then assessed using the BIC, which penalizes models with more free parameters compared with those with fewer free parameters. The model comparison process revealed that, for Session 2, the Bayesian (self-projection) model provided the best fit to the participants’ actual prediction behaviors and that, for Session 4, the Bayesian (carry-over + self-projection) model best fit the data (Table S2). These results together suggest that the participants learned the observees’ risk-preference in a manner consistent with a Bayesian learning algorithm featuring the use of their own risk-preference as a prior.

SI Text 6

We confirmed that the correlation (Fig. 3D) remained significant (P < 0.05), even when (i) controlling for individual differences in the strength of the neural representation of a belief-updating signal in the dlPFC (i.e., using partial correlation); (ii) removing outliers based on a Jackknife procedure (63); or (iii) analyzing the data separately for the left and the right dlPFC (P < 0.05 for both regions).

Discussion

The present study uncovers the computational process by which contagion effects arising from observing the behavior of another agent can influence one’s own decision-making under risk.

Contagion Modulates Human Risk-Preference.

Behaviorally, we demonstrate that human risk-preference can be altered by a contagion effect and rule out alternative possibilities such as changes in subjective judgment about the probabilities (22, 23) or simple bias for/against gambling options (16, 24). In economics and finance, the idea that risk-preferences can be changed is still controversial, and it is difficult to exclude the possibility that the observed shift in behaviors merely reflects the change of something else such as beliefs in expected value, reward probability, or integrated utility (33). Our behavioral analyses provide evidence for the view that risk-preferences can indeed be altered.

Why did the participants change their risk-preference toward the others? In our experiment, the participants were monetarily incentivized to learn others’ risk-preference and predict their future choices. One possibility is that the learning with an explicit incentive for correct prediction leaked over to influence the participants’ own choices. However, we found no association between the degree of contagion and the prediction performance in our data. Furthermore, previous studies have demonstrated that in various contexts, contagion can occur by merely observing/learning others’ without any explicit incentive for prediction (14–17, 19). When taken together, the evidence suggests that the contagion effect is not contingent on the provision of an explicit incentive for prediction. An important direction for future studies will be to identify the specific contextual elements that gives rise to the emergence of a contagion effect on risk-preference (see SI Text 7 for further discussion).

We also found that contagion occurs with both human and artificial agents. In a behavioral experiment, we found that participants changed their risk-preference after observing not only human but also computer observees. This finding has an implication for finance. In modern financial markets, the use of algorithmic trading (trades generated by artificial intelligence) has become increasingly popular (34). Our finding implies that contagion of risk-preference can work in such markets and potentially play a critical role in financial bubble formation and collapse.

Risk-Preference Is Altered Through the Modulation of the Neural Processing of Decision-Risk.

The neural representation of decision-risk in the caudate nucleus was found to be specifically modulated, in line with the behavioral shift in risk-preferences. On the other hand, representations of other decision-related variables such as expected value, reward probability, reward magnitude, and integrated utility signals, were unaffected by the behavioral shift. These results indicate that the neural representation of decision-risk per se is directly modulated by the contagion effect, consistent with the view that risk-preferences are altered through changes in risk perception.

Our finding that risk signals that can be used as an input to the decision process are encoded in the caudate nucleus stands in contrast to some other studies that have reported risk representations in ventral striatum as well as insular cortex (1, 35, 36). A key difference between those previous studies and the present study is that those previous studies probed the neural representation of “anticipation risk,” in that they measured activity during an anticipatory phase in which an outcome was imminent, without a choice being rendered or after a choice was made. In the present study, we designed our experimental task to capture neural processing of risk at the time of decision-making without the contribution of other risk-related effects such as anticipation risk and the effects of learning from reward feedback. The outcome of each choice was not revealed (37), ensuring that an outcome was not immediately anticipated and that valuations were not influenced by the history of previous outcomes (see (38, 39) for the discrimination of instructed and learned value information). According to our literature survey (Table S4), only a few studies used such a design, and they reported neural activity related to decision-risk in diverse regions including caudate and insula (37, 40–43). The present study provides additional evidence that caudate tracks decision-risk.

Table S4.

Literature survey about the neural correlates of decision-risk

Study	Contrast	Activated regions
Instructed-risk without feedback
Hsu et al. (2005) (40)	Decision with risk > ambiguity	Caudate, culmen, lingual gyrus, cuneus, precuneus, precentral gyrus, precuneus, angular gyrus
Labudda et al. (2008) (43)	Decision with risk > without information incentive	Anterior cingulate gyrus, middle frontal gyrus, inferior parietal lobe, lingual gyrus, precuneus
Weber and Huettel (2008) (41)	Decision with risk > delayed reward	Lingual gyrus, middle occipital gyrus, superior parietal lobule, precuneus, middle frontal gyrus, inferior frontal gyrus, anterior cingulate cortex, orbitofrontal cortex, hippocampus, superior frontal sulcus, anterior insula, inferior temporal gyrus
	Choice of riskier option > safer option	Insula, posterior cingulate, anterior cingulate, medial frontal gyrus, caudate, postcentral gyrus, superior temporal gyrus, inferior frontal gyrus
Christopoulos et al. (2009) (37)	Decision with high risk > low risk	Dorsal anterior cingulate cortex
Symmonds et al. (2011) (42)	Variance of reward (parametric)	Posterior parietal cortex
Instructed-risk with feedback
Paulus et al. (2003) (68)
Huettel et al. (2006) (69)
van Leijenhorst et al. (2006) (70)
Lee et al. (2008) (71)
Engelman and Tamir (2009) (72)
Smith et al. (2009) (73)
Xue et al. (2009) (74)
Learned risk
Paulus et al. (2001) (75)
Volz et al. (2003) (76)
Matthews et al. (2004) (77)
Volz et al. (2004) (78)
Cohen et al. (2005) (79)
Huettel et al. (2005) (80)
Huettel (2006) (81)
Mohr et al. (2010) (82)
Bach et al. (2011) (83)
Payzan-LeNestour et al. (2013) (84)

The top set of studies are those controlling for effects of learning from reward feedback: as in the present study, information about risk was provided by instruction, and the outcome of each choice was not revealed. See refs. 38 and 39 for the discrimination of instructed and learned value information. The middle set of studies are those not controlling for effects of learning: information about risk was provided by instruction, but the outcome of each choice was revealed to the participants (i.e., valuations can be influenced by the history of previous outcomes). Activated regions and the contrast were omitted. The bottom set of studies are those not controlling for effects of learning: information about risk was acquired through learning (i.e., the information was not instructed explicitly). Activated regions and the contrast were omitted. A region of interest discussed in the main text, caudate, is shown in bold.

The contribution of the caudate to decision-risk is broadly consistent with the view that dorsal striatum is implicated in motivational and reward-related processes that involve decisions about action (44, 45). Combining this view with our finding that risk-related caudate activity remains even after controlling for motor-related responses, we suggest that the caudate is involved in risk-processing during decision-making, above and beyond any contribution of this structure in motor responding per se. Moreover, a number of clinical studies have demonstrated that individuals with anxiety disorders show reduced reward-related neural responses in caudate (46), while being more risk-averse than other clinical patients and normal control groups (47, 48). These findings broadly support our claims about a role for the caudate in risk representation and modulation of risk-preference. However, it is important to note that the present findings do not exclude the possibility that insular cortex and/or other structures could also play a role in encoding risk signals at the time of decision-making, above and beyond a role in anticipation risk, particularly under conditions where an outcome is imminent.

Biological and social sciences have accumulated evidence that human valuations can be altered by a contagion effect (14, 15, 17, 19, 49, 50). However, we know little about which components of the value computation is affected. Does human valuation work at the level of specific decision-related attributes or at the level of an integrated utility signal that combines across multiple types of attribute? Our findings in the context of decision-making under risk imply, in a broad sense, that human valuation can be modulated through a change in the neural processing of a particular decision-related attribute (in this case, the risk representation), rather than necessarily acting on an integrated utility signal.

Modulation of Risk-Preference Is Mediated by an Interaction Between Neural Systems Implicated in Representing Risk and Learning About Others.

By using model-based analyses on the behavioral and fMRI data, we showed that the process of learning about others’ risk-preferences is well-captured by a Bayesian learning algorithm with the use of one’s own preference as a prior belief and that the belief-updating in the learning is associated with dlPFC. The behavioral finding suggests that an individual uses his/her own preference as a starting point for learning and making inferences about other people, compatible with the concepts of “anchoring-and-adjustment” (51) and “self-projection” (52, 53).

We also demonstrated via a connectivity analysis that functional coupling between the dlPFC and the caudate nucleus reflects individual differences in susceptibility to contagion. These results suggest that the contagion effect modulates the neural representation of risk in caudate through functional connectivity with the dlPFC. The role of a dorsolateral prefrontal–striatal circuit (31) in contagion of risk-preferences can be interpreted within a broader literature implicating this circuit in cognitive functions more generally such as in response-selection, planning, and set-shifting (32). The dlPFC and caudate have also been specifically implicated in goal-directed learning and model-based reinforcement-learning (54–56). Taken together, the present findings suggest that the contagion effect may act on neural circuits underpinning a model-based “cognitive” decision-making system.

The conclusions of the present study differ from previous findings by Chung et al. (16), who argued that contagion works by means of a constant bias to an integrated utility but not via risk-preference per se. Whereas the present study involved repeated opportunities to observe the risky behavior of another specific agent, in the Chung et al. study, participants interacted with multiple (six in total) anonymous agents throughout and thus did not have as much opportunity to learn about the specific risk-preferences of individual agents. Such task differences could potentially account for the difference in the overall findings between the studies. Our present findings indicate that when an individual has the opportunity to consistently observe the risky behavior of another agent, one’s own risk-preference can be directly influenced.

In conclusion, our results provide a computational account of how human risk-preferences are altered by the contagion effect. This finding has implications for economic and clinical studies. Although previous studies in economics and finance have linked financial bubbles to herd behaviors based on social learning (57, 58), our findings provide evidence for the existence of a novel and parsimonious effect that could potentially contribute to financial bubble formation and collapse: contagion of risk-preference through changes in the perception of risk. Furthermore, given that adolescent behavior can be strongly influenced by peers (12), contagion of risk-preference could play a significant role in leading to increases in adolescent risk-taking resulting in maladaptive behavioral outcomes.

SI Text 7

The shift in risk-preference we observed here is unlikely to be explained by a simple imitation of the others’ choices (i.e., by merely copying a stimulus-response association). In our experiment, on each trial, two options, accept and reject, were randomly positioned left or right of the screen, and the actual reward magnitude presented was jittered (Fig. S1A), thereby minimizing the potential effects of simple imitation. Furthermore, social learning (49)—learning from others’ choices based on the belief that the others have expertise or information superiority—is unlikely to account for the behavioral shift, because we explicitly instructed participants that the observees did not have any further information about the task such as knowing the outcome of the gambles. Finally, our experimental task is fundamentally different from others used in previous studies, in that there is no effect of learning from reward feedback (10), emotion regulation (64), task contexts (6, 65), explicit incentive (66), or priming with a financial boom/bust (67) on the changes of risk-preferences.

Methods

This study was approved by the Institutional Review Board of the California Institute of Technology, and all participants gave their informed written consent. We provide a comprehensive description of the experimental procedures in SI Methods.

In Self trials, participants chose whether to “accept” or “reject” a gamble for themselves. If they chose accept, they gambled for some amount of money; otherwise, they took a guaranteed $10. Reward probability and magnitude of the gamble were varied in every trial (Fig. S1A), so that risk of the gamble (mathematical variance of reward) was decorrelated with the expected value of reward. In Observe trials, participants observed a choice made by the observee. The trials were designed to minimize differences from the Self trials, and so the timeline of a trial and the set of gambles presented were the same between the two types of trials (Fig. 1A and Fig. S1 A and B). Furthermore, in the participant instructions, we emphasized that the observees did not have any further information about the task such as knowledge of the outcome of the gambles. Predict trials were introduced to confirm that the participants learned the observee’s behavioral tendency (i.e., risk-preference) through the observation of his choices in Observe trials, and therefore the number of trials was less than the other two trial types (Fig. 1B and Fig. S1 A–C).

SI Methods

Participants.

We recruited 26 healthy participants (11 female participants; age range, 22–38 y; mean $\pm$ SD, 29.35 $\pm$ 4.71) from the general population. All participants were preassessed to exclude those with any previous history of neurological/psychiatric illness, and they gave their informed written consent. Two participants were excluded from the subsequent behavioral and neuroimaging analyses because in the postexperiment questionnaire, they doubted that the other persons’ choices were real. We therefore used the data from the remaining 24 participants (10 female participants; age range, 22–38 y; mean $\pm$ SD, 29.50 $\pm$ 4.85).

Experimental Task.

Our task contained three types of trials (Fig. 1A). In Self trials, participants made decisions under risk (see below for details); in Observe trials, participants observed decisions of another person (“observee”) who had performed the Self trials; and in Predict trials, participants were asked to predict the observee’s decisions.

The whole experiment consisted of five sessions, in which the three types of trials were presented to the participants in a block-wise manner (Fig. 1B). Sessions 2 and 4 involved all three trial types; and Sessions 1, 3, and 5 included only Self trials. Notably, each block began with the presentation of text and a picture indicating the trial type (Instruction phase; Fig. 1A). Because these instruction phases were presented only at the first trial in each block, the neural responses to this phase were unlikely to contaminate the decision-related responses of interest.

The observee for Observe/Predict trials was different between Sessions 2 and 4, and the two observees were distinguished by the images of two males presented in the instruction phase (see Fig. 1A and Fig. S1D). To minimize potential effects of their appearance, the images were taken from the back, and association between the images and the observees was randomized across participants. We instructed participants that the choices they observed in each session were made by a real person recorded from a previous experiment. In actuality, as in previous studies (14, 15, 17, 19, 20), the observees’ choices were generated by computer algorithms. The two simulated observees had different risk-preferences (Fig. S1 B and F): one for Session 2 was risk-averse (α = −0.013 and β = 5 in mean-variance utility function; see SI Methods, Behavioral Data Analyses), and the other for Session 4 was risk-seeking (α = 0.03 and β = 5) or vice versa (counterbalanced across participants). Furthermore, in the participant instructions, we emphasized that the observees did not have any further information about the task such as knowledge of the outcome of the gambles.

In Self trials, participants chose whether to accept or reject a gamble for themselves. If participants chose accept, they gambled for some amount of money; otherwise, they took a guaranteed $10. Reward probability and magnitude of the gamble were varied in every trial (Fig. S1A), so that risk of the gamble (mathematical variance of reward) was decorrelated with the expected value of reward. At the beginning of each trial, participants were asked to make a choice between a gamble and the sure option by pressing a button with their right hand (index finger for the left option; and middle finger for the right option) within 4 s (Decision phase; Fig. 1A). Here, two options, accept and reject, were randomly positioned to the left or right of the screen in every trials, and information about the gamble was indicated by a pie chart (size of the green area indicates the probability and the digits denote the magnitude of reward). After making a response, the chosen option was highlighted by a yellow frame (Confirmation phase, 1 s), followed by the uniformly jittered intertrial interval (ITI) (2–6 s). Notably, the outcome of the gamble was not revealed to the participants in each trial (one choice was randomly selected and actually implemented at the end of the experiment; see SI Methods, Reward Payment for details), to exclude potential effects of learning from reward feedback.

In Observe trials, participants observed a choice made by the observee. The trials were designed to minimize differences from the Self trials, and so the timeline of a trial and the set of gambles presented were the same between the two types of trials (Fig. 1A and Fig. S1 A and B). Specifically, information about the gamble the observee would accept or reject was shown in the decision phase by a pie chart, and then the observee’s actual choice was revealed to the participants in the confirmation phase (the observee’s response time was 3–4 s), so that the participants could learn the observee’s risk-preference. Furthermore, participants were also asked to press the third key after observing the observee’s choice, to make motor-related neural responses in Observe trials comparable with those in the other types of trials.

Predict trials were introduced just to confirm that the participants learned the observee’s behavioral tendency (i.e., risk-preference) through the observation of his choices in Observe trials, and therefore the number of trials was smaller relative to the other two trial types (Fig. 1B and Fig. S1 A–C). Each trial began with the decision phase in which participants predicted whether the observee would accept or reject the gamble presented by a pie chart (Fig. 1A). The prediction was immediately highlighted by a yellow frame, initiating the confirmation phase. Here, the observee’s actual choice was not revealed to the participants in each trial to prevent them from further learning (if the prediction was correct, the participant earned $10 at the end of the experiment; see SI Methods, Reward Payment for details).

Postexperiment Questionnaire.

After the experimental task, participants were asked to rate “How much do you think the first/second person is likely to accept a risky gamble?” (data shown in Fig. 3B), “How similar are you and the first/second person in terms of your preference for risky gambles?,” and “How likely are you to accept a risky gamble?” in a six-point scale (from “not at all” to “very much”). We also asked another yes/no question, “Do you strongly doubt that the other persons’ choices presented during the task were real?” (used for the exclusion of participants; SI Methods, Participants).

Reward Payment.

Participants received a show-up fee of $30. In addition, at the end of the experiment, the computer randomly selected one of the participant’s choices from the Self trials, and the selected choice was actually implemented. The computer also selected one of the participant’s predictions from the Predict trials at random. If the selected prediction was correct, the participant obtained $10. The total earnings were on average $52 $\pm$ $14 (mean $\pm$ SD across participants). Importantly, because participants did not know which trial would be selected, they should have treated every trial as if it were the only one.

Additional Behavioral Experiment.

Eleven healthy participants (five female participants; age range, 19–48 y; mean $\pm$ SD, 29.36 $\pm$ 8.08) took part in the experiment. The experimental procedure was almost the same as the main experiment, but the participants observed/predicted choices of another person for one session and a computer agent for another session. In a session with the computer agent, we instructed participants to observe/predict the computer’s outputs.

The combination of the observees’ type (human or computer) and their risk-preference (risk-averse or -seeking) was counterbalanced across participants. That is, there were four cases: (i) participants observed/predicted a risk-averse human in Session 2 and a risk-seeking computer in Session 4 (n = 3); (ii) a risk-seeking human in Session 2 and a risk-averse computer in Session 4 (n = 3); (iii) a risk-averse computer in Session 2 and a risk-seeking human in Session 4 (n = 3); and (iv) a risk-seeking computer in Session 2 and a risk-averse human in Session 4 (n = 2). Here, choices (outputs) of the risk-seeking and the -averse human/computer observees were generated by the same algorithms as the human observees in the main experiment (see SI Methods, Experimental Task).

Behavioral Data Analyses.

We used three approaches to estimate participants’ risk-preference for each session. Notably, the three approaches were found to provide highly consistent estimates at least in our task (Fig. S1 E and F).

One is a simple model-free approach based on the proportion of accepting gambles. That is, risk-preference is measured by $P\left(\text{gamble}\right)-\hspace{0.17em}{P}^{\ast }\left(\text{gamble}\right),$ where $P\left(\text{gamble}\right)$ denotes the participant’s proportion of accepting gambles and $P^{\ast }\left(\text{gamble}\right)$ indicates the proportion given the risk-neutral preference. That is, positive and negative values indicate risk-seeking and -averse preferences, respectively. In this approach, risk-neutrality can be defined by the absolute value of risk-preference (smaller values close to 0 indicate the more risk-neutral).

Another model is based on mean-variance utility function; the utility of each option is constructed by

$$U\left(X\right)=E\left(X\right)+\alpha V\left(X\right),$$

where $E\left(X\right)$ indicates expected value, whereas $V\left(X\right)$ denotes risk of the option. Let p be the reward probability and r be the reward magnitude of the option. Then, $E\left(X\right)=pr$ and $V\left(X\right)=r^{2}p(1-p).$ Here, risk-preference is characterized by α (negative values for risk-averse and positive for risk-seeking preference). The utility governs the participant’s probability of accepting the gamble as follows:

$$q\left(\text{gamble}\right)=1/[1+\text{exp}\{-\beta (U\left(\text{gamble}\right)-U\left(\text{sure}\right))\}],$$

where β is a parameter controlling the degree of stochasticity in the choice. We estimated the risk-preference α, as well as the parameter β, by fitting this model to the participant’s choice data (i.e., estimating the parameter values that maximize the likelihood function).

In the other approach based on an exponential utility function, the utility of each option is constructed by

$$U\left(X\right)=p\hspace{0.17em}{r}^{\rho },$$

where ρ represents the participant’s risk-preference. ρ is less and greater than 1 if she/he is risk-averse and risk-seeking, respectively. The value of ρ can be estimated by model fitting, as well as the case with the mean-variance utility function.

fMRI Data Acquisition.

The fMRI images were collected using a 3T Siemens (Erlangen) Tim Trio scanner located at the Caltech Brain Imaging Center with a 32-channel radio frequency coil. The BOLD signal was measured using a one-shot T2*-weighted echo planar imaging sequence [volume repetition time (TR): 2,780 ms; echo time (TE): 30 ms; flip angle (FA): 80°]. Forty-four oblique slices (thickness, 3.0 mm; gap, 0 mm; field of view, 192 × 192 mm; matrix, 64 × 64) were acquired per volume. The slices were aligned 30° to the anterior–posterior commissure (AC–PC) plane to reduce signal dropout in the orbitofrontal area (59). After the five functional sessions, high-resolution (1-mm³) anatomical images were acquired using a standard Magnetization Prepared Rapid Gradient Echo (MPRAGE) pulse sequence (TR: 1,500 ms; TE: 2.63 ms; FA: 10°).

fMRI Data Analyses.

Preprocessing.

We used the Statistical Parametric Mapping 8 (SPM8) software (Wellcome Department of Imaging Neuroscience, Institute of Neurology) for image processing and statistical analysis. fMRI images for each participant were preprocessed using the standard procedure in SPM8: after slice timing correction, the images were realigned to the first volume to correct for participants’ motion, spatially normalized, and spatially smoothed using an 8-mm full width at half maximum Gaussian kernel. High-pass temporal filtering (using a filter width of 128 s) was also applied to the data.

GLM I.

A separate GLM was defined for each participant. The GLM contained parametric regressors representing risk (standard deviation of reward) and expected value (expected value of reward) of the gamble at the time of decision (Fig. 1A). Specifically, the participant-specific design matrices contained the following regressors: boxcar functions in the period of the decision phase (i.e., the duration is equal to the response time; see Fig. 1A) for Self, Observe, and Predict trials (regressors for Observe and Predict trials were included only in Sessions 2 and 4); boxcar functions in the period of the confirm phase (duration, 1 s) for Self, Observe, and Predict trials (regressors for Observe and Predict trials were included only in Sessions 2 and 4); a boxcar function in the period of the instruction phase (duration, 4 s); and a stick function at the timing of motor response (i.e., button press). Furthermore, trials on which participants failed to respond were modeled as a separate regressor. We also included parametric modulators at the period of the decision phase for Self, Observe, and Predict trials separately, representing the risk and the expected value of the gamble. All of the regressors were convolved with a canonical hemodynamic response function. In addition, six motion-correction parameters were included as regressors of no-interest to account for motion-related artifacts. In the model specification procedure, serial orthogonalization of parametric modulators was turned off. For each participant, the contrasts were estimated at every voxel of the whole brain and entered into a random-effects analysis.

GLM I-2.

The GLM contained parametric regressors representing response time, decision-related response (1 for accept the gamble; 0 for reject), and motor-related response (1 for choosing the left option, 0 for the right; note that accept and reject were randomly positioned left or right in every trial) at the time of decision, in addition to the other regressors included in GLM I.

GLM II.

The GLM contained parametric regressors representing reward probability and reward magnitude of the gamble at the time of decision, instead of the risk and the expected value, in addition to the other regressors included in GLM I.

GLM III.

The GLM contained a parametric regressor representing utility of the gamble, estimated based on mean-variance utility function, at the time of decision, instead of the risk and the expected value, in addition to the other regressors included in GLM I.

GLM IV.

The GLM contained parametric regressors representing squared reward magnitude and reward uncertainty, defined as p (1 − p), where p denotes the reward probability, at the time of decision, instead of the risk and the expected value, in addition to the other regressors included in GLM I.

GLM V.

The GLM contained a parametric regressor representing “update of the belief about others’ risk-preference” at the confirm phase in Observe trials, in addition to the regressors included in GLM I. Here, the update of the belief was defined as the D_KL between the posterior and the prior (26), derived from the best-fitting Bayesian learning model (SI Text 4 and Table S2). Notably, in the model specification procedure, we concatenated five sessions to capture the long-term learning process across sessions (note: constant regressors coding for each session were included).

GLM V-2.

The GLM contained parametric regressors representing the observee’s response time, decision-related response (1 for accept the gamble; 0 for reject), and motor-related response (1 for choosing the left option; 0 for the right) at the confirm phase in Observe trials, in addition to the regressors included in GLM V.

PPI analysis.

The PPI analysis was performed by using the standard procedure in SPM8. We first extracted a BOLD signal from the dlPFC identified as tracking update of the belief about others’ risk-preference (Fig. 3C; 8-mm sphere centered at the peak voxel) and then created a PPI regressor by forming an interaction of the BOLD signal (physiological factor) and the boxcar function regressor in the period of the decision phase for Self trials over the course of the five sessions (psychological factor). The GLM for the PPI analysis therefore contained the following regressors: (i) a physiological factor, the BOLD signal in the bilateral dlPFC; (ii) a psychological factor, the boxcar function regressor in the period of the decision phase for Self trials; and (iii) a PPI factor, the interaction term of the psychological and physiological factors, as well as the other regressors included in GLM V.

Whole-brain analysis.

We set our significance threshold at P < 0.05 whole-brain FWE corrected for multiple comparisons at cluster level. The minimum spatial extent, k = 63, for the threshold was estimated based on the underlying voxel-wise P value, P < 0.005 uncorrected, by using the AlphaSim program in Analysis of Functional NeuroImages (AFNI) (60).