Matching on the Disease Risk Score in Comparative Effectiveness Research of New Treatments

Abstract

Purpose

We use simulations and an empirical example to evaluate the performance of disease risk score (DRS) matching compared with propensity score (PS) matching when controlling large numbers of covariates in settings involving newly introduced treatments.

Methods

We simulated a dichotomous treatment, a dichotomous outcome, and 100 baseline covariates that included both continuous and dichotomous random variables. For the empirical example, we evaluated the comparative effectiveness of dabigatran versus warfarin in preventing combined ischemic stroke and all-cause mortality. We matched treatment groups on a historically estimated DRS and again on the PS. We controlled for a high-dimensional set of covariates using 20% and 1% samples of Medicare claims data from October 2010 through December 2012.

Results

In simulations, matching on the DRS versus the PS generally yielded matches for more treated individuals and improved precision of the effect estimate. For the empirical example, PS and DRS matching in the 20% sample resulted in similar hazard ratios (0.88 and 0.87) and standard errors (0.04 for both methods). In the 1% sample, PS matching resulted in matches for only 92.0% of the treated population and a hazard ratio and standard error of 0.89 and 0.19, respectively, while DRS matching resulted in matches for 98.5% and a hazard ratio and standard error of 0.85 and 0.16, respectively.

Conclusions

When PS distributions are separated, DRS matching can improve the precision of effect estimates and allow researchers to evaluate the treatment effect in a larger proportion of the treated population. However, accurately modeling the DRS can be challenging compared with the PS.

INTRODUCTION

Evaluating the comparative effectiveness of newly introduced treatments presents unique challenges in pharmacoepidemiologic research. The propensity score, defined as the conditional probability of treatment given a set of observed covariates, has become a standard tool for controlling large numbers of confounding variables.^{1, 2} However, accurately modeling the PS for a new treatment can be difficult if the treated population is small or factors affecting treatment assignment change rapidly.^{3, 4}

In a recent paper, Glynn et al.³ proposed using an alternative covariate summary score, the disease risk score (DRS), to control for confounding in settings involving new treatments. Glynn et al. argued that factors affecting disease risk are more likely to be stable over time than are factors affecting treatment, potentially simplifying the estimation of the DRS compared with a time-varying PS. While the DRS can be more stable over time, modeling the DRS in practice also presents unique challenges that are not shared by the PS. Unlike the PS which models covariate associations with treatment, the DRS models covariate associations with the potential outcome under the control or comparator treatment.⁵ In practice, however, this potential outcome is not observed for all individuals in the study population, but only for those receiving the comparator treatment. Consequently, the DRS must be modeled indirectly for treated individuals.

The DRS has typically been estimated in one of two ways. The first is to fit a regression model within the cohort of individuals receiving the comparator treatment and then extrapolate this model to predict disease risk for the full cohort. The second is to fit a regression model within the full cohort as a function of baseline covariates and treatment and then estimate the disease risk for each individual after setting treatment status to zero. ^{3, 5–8} Hansen discussed limitations to both of these strategies, which have been termed “same-sample” estimation.⁵

Fitting the DRS to the full cohort benefits from increased sample size, but introduces additional complexity as it requires accurately modeling the relation between treatment and outcome. Small misspecifications in the full-cohort DRS model can introduce bias by resulting in estimated scores that are non-ancillary or carry information about the treatment effect.^{5, 9} Consequently, Hansen⁵ recommends using only the control population when fitting the DRS model. Leacy and Stuart⁹ explained that using only the control population when modeling the DRS tends to result in estimated scores that are more robust to model misspecification. Fitting the DRS only among individuals receiving the comparator treatment, however, can lead to overfitting, which results in overestimating disease risk for high-risk comparator patients and underestimating disease risk for low-risk comparator patients.^{3, 5} Such overfitting can lead to apparent treatment effect heterogeneity over the distribution of disease risk and potentially bias overall effect estimates.^{3, 5}

To circumvent the problems of same-sample estimation, both Hansen⁵ and Glynn et al.³ have proposed using controls from a period prior to the current study to fit the DRS model. Glynn et al. suggested that estimating the DRS with historical data can be particularly advantageous in pharmacoepidemiologic studies using large administrative healthcare databases to evaluate newly introduced treatments or evolving drug therapies. Modeling the DRS with historical data can avoid the problems associated with “same-sample” estimation, but can also result in fitted risk models that are not generalizable to the study population. This strategy assumes that the effects of risk factors on the outcome, surveillance of individuals, and coding practices do not change over time. Violation of these assumptions could result in misspecified estimates of disease risk when applied to the study cohort.

Little evidence exists to confirm the theoretical advantages of a historically estimated DRS over a traditional PS when evaluating new treatments. A number of studies have shown that simply fitting time-specific PS models can perform well when the indication for treatment changes rapidly over time.^{4, 10} Further, the limitations of the PS when the number of exposed individuals is small are not well understood. Previous studies have also shown that overfitting the PS model does not necessarily compromise confounding control.¹¹ There remain few examples demonstrating the application of a historically estimated DRS when evaluating new treatments. Potential advantages and challenges of using DRSs in these settings remain unclear.

In this paper, we use both simulations and an empirical example to compare the performance of DRS matching with that of PS matching when controlling large numbers of covariates in settings involving newly introduced treatments. We discuss both challenges and potential advantages of using the DRS for confounding control as well as required assumptions for using historical data to model the DRS. We then evaluate the performance of DRS matching with PS matching in an empirical example where we compare the new oral anticoagulant dabigatran with warfarin in preventing ischemic stroke and all-cause mortality in patients diagnosed with atrial fibrillation in the Medicare population.

METHODS

Simulation Study

We simulated a causal scenario that was motivated by an empirical example (described later) comparing dabigatran with warfarin in preventing ischemic stroke and all-cause mortality among new users. We simulated 100 baseline covariates. As in most pharmacoepidemiologic settings, the majority of these baseline covariates were dichotomous (simulated as binomial random variables). We simulated a dichotomous treatment and a dichotomous outcome according to equations 1 and 2.

$$\mathit{logit}(E[T\mid X_i])={\alpha }_0+{\alpha }_1{X}_1+\dots +{\alpha }_{100}{X}_{100}$$ [1]

$$\mathit{logit}(E[Y\mid X_i,T])={\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_{100}{X}_{100}+{\beta }_{T}T+{\beta }_{\mathit{int}}{X}_{1}T$$ [2]

We considered scenarios where we varied the sample size and the strength of covariate-treatment and covariate-outcome associations. We also considered a scenario involving treatment effect heterogeneity since, in the presence of heterogeneity, incomplete matching can result in an estimand that is different from the average treatment effect in the full treated population.^{12, 13} For all scenarios, values for α₀ and β₀ in Equations 1 and 2 were selected so that the baseline prevalence for both treatment and outcome was 30%.

In scenario 1, we considered a constant treatment effect (β_T = 0 and β_int = 0) and selected values for the coefficients α₁ through α₁₀₀ and β₁ through β₁₀₀ so that the effects of covariates on both the treatment and outcome were mild (coefficients values ranging from −0.182 to 0.182). In Scenarios 2 and 3, we again considered a constant treatment effect, but selected values for the coefficients α₁ through α₁₀₀ and β₁ through β₁₀₀ to allow for moderate and strong effects, respectively, on the treatment and outcome (coefficient values ranging from −0.405 to 0.405 for moderate effects, and from −0.693 to 0.693 for strong effects). In Scenario 4 we selected values for the coefficients to allow for moderate effects on both the treatment and outcome, but also included treatment effect heterogeneity by setting β_int= 0.693.

We allowed coefficients to be both positive and negative to reflect practical settings where baseline covariates induce confounding in both directions. For each scenario, we considered sample sizes of 10,000 and 1,000 for a total of eight scenarios. A full description of the simulated structure is provided in the Supporting Information.

We modeled the DRS within a simulated historical population of controls and the PS within the original simulated cohort. For each scenario, the historical population of controls consisted of 10,000 individuals and was simulated to be similar to the original cohort, but with no treatment introduced. We estimated both the PS and DRS using logistic regression that included main effects for each of the baseline covariates X₁ through X₁₀₀. Because the true PS model (Equation 1) and true DRS model (i.e., outcome model in Equation 2 with treatment set to 0) were simulated as a function of only the main effects of X₁ through X₁₀₀, this simulation compared the PS and DRS in a situation where both the fitted models were correctly specified.

We implemented the estimated PSs and DRSs using 1-1 nearest neighbor matching within a specified caliper distance. Matching was carried out without replacement. We considered two caliper distances. We first followed the recommendation of Rosenbaum and Rubin and used a caliper distance of 0.25 standard deviations of the respective PS or DRS distribution on the logit scale.¹⁴ We then repeated the analysis using a ten-fold decrease in the caliper distance of 0.025 standard deviations of the logit of the respective PS or DRS distribution. We chose to include a very small caliper distance to observe the sensitivity in the number of individuals being matched on the PS versus the DRS as the caliper size is reduced by a considerable amount.

We measured the performance of DRS and PS matching by calculating the bias, mean squared error (MSE), and precision of the effect estimates. The bias, defined as the expected value of the difference between the effect estimate and the true effect, was calculated by taking the mean of this difference over all simulation runs. For scenarios involving treatment effect heterogeneity, the true value for the average treatment effect in the treated was calculated by simulating the predicted response under both treatment and control for each individual in the treated population (i.e., potential outcomes). These potential responses were then used to calculate the true value for the average treatment effect in the treated population. Details are provided in the Supporting Information. The MSE was calculated by taking the mean of the squared bias over all simulation runs. To evaluate precision, we estimated the standard error (SE) using the empirical standard deviation of the distribution of the treatment-effect estimates across all simulation runs.

Empirical Study: Dabigatran vs. Warfarin in Patients with Atrial Fibrillation

We compared the performance of dabigatran versus warfarin in an elderly population using linked Medicare Parts A (hospital), B (outpatient), and D (pharmacy) data. We identified eligible individuals from a 20% random sample of Medicare beneficiaries with fee-for-service enrollment in all three plans for at least one month from October 19, 2010 (when dabigatran was introduced) through December 31, 2012. New users were defined as individuals who initiated dabigatran or warfarin after a 1-year washout period with no prescription for any oral anti-coagulant.¹⁵ We required continuous enrollment in Medicare for at least 12 months prior to drug initiation. All demographic and clinical covariates (described later) were defined during the 12 months prior to drug initiation. Individuals were censored only if they lost Medicare enrollment during follow-up (intent-to-treat analysis).

We restricted our study cohort to individuals who were 65 years of age or older and had an inpatient or outpatient diagnosis code for atrial fibrillation or atrial flutter (ICD-9 427.31, 427.32) prior to initiation of dabigatran or warfarin. We excluded individuals with a known heart valve replacement because this is a contraindication for dabigatran use. We also excluded individuals at a skilled nursing facility at drug initiation.

We modeled the one-year risk of combined ischemic stroke and all-cause mortality within a population of new warfarin users with an index date prior to the introduction of dabigatran (between January 1, 2008 and October 18, 2010). This model was then used to predict the disease risk for all individuals within the study cohort. We also estimated the PS within the study cohort for comparison. The PS and DRS models included main effects for 37 covariates (described later), which were selected a priori using expert knowledge. We added 200 empirically selected covariates based on Medicare medication claims, inpatient and outpatient diagnostic codes, and procedural codes. We identified the 200 most prevalent codes within each data dimension using both the historical population of new warfarin users and original study cohort of new-users of warfarin and dabigatran (codes with a prevalence greater than 0.5 were subtracted from 1). Of the 600 covariates identified in this way, we selected the 200 with the strongest univariate associations (odds ratios) with the outcome after restricting to individuals receiving the comparator treatment (all new-users of warfarin). The estimated PSs and DRSs were implemented using 1-1 nearest neighbor caliper matching without replacement. We used the same caliper distances described in the simulation study (0.25 and 0.025 standard deviations of the logit of the respective PS or DRS distribution). Similar to the simulation study, we repeated the analyses using two different calipers distances to observe the sensitivity in the number of individuals matched on the PS versus the DRS as the caliper size is reduced. We estimated the hazard ratio (HR) within the matched populations using Cox proportional hazards models.

We conducted analyses using 20 and 1 percent samples of the Medicare data to observe the sensitivity of the results as the sample size is reduced. Previous studies have shown that confounding can be stronger shortly after a treatment’s introduction.^16–18 To observe the sensitivity of the results to the duration of follow-up, we repeated the analysis using data only for the first year of dabigatran use (index date between October 19, 2010 through October 18, 2011).

RESULTS

Simulation results

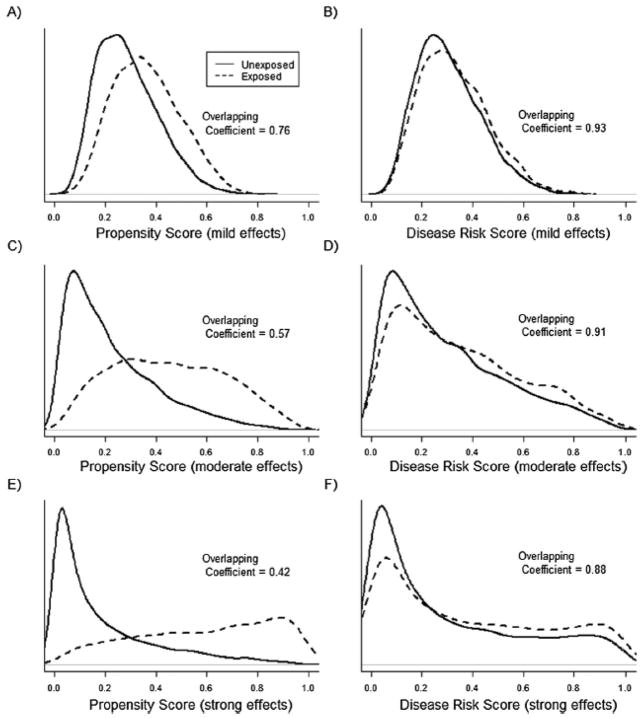
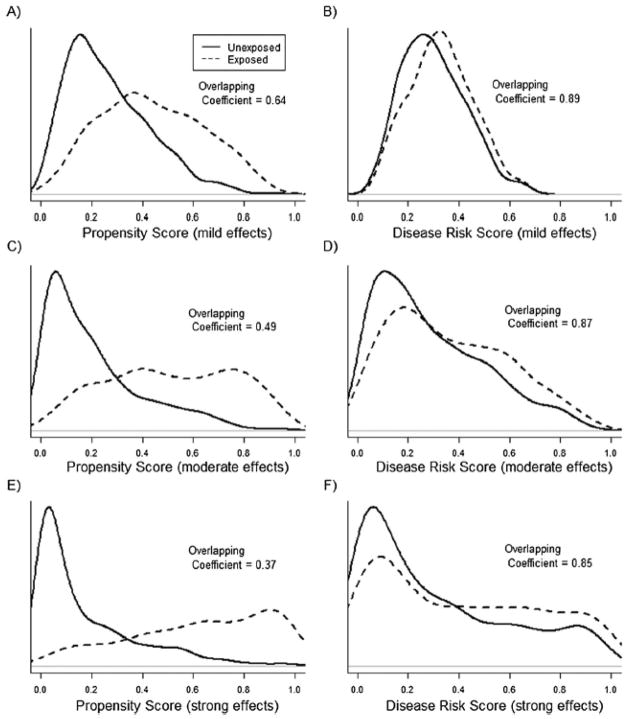
For simulation scenarios not involving treatment-effect heterogeneity, Figures 1 and 2 show the PS and DRS distributions by treatment group for one simulation run with a sample size of 10,000 (Figure 1) or 1,000 (Figure 2). The degree of overlap (i.e., area of overlapping region) between the DRS distributions was always larger than the degree of overlap between the PS distributions. Varying the sample size and the strengths of covariate-treatment and covariate-outcome associations affected the overlap in PS distributions more strongly than it affected the overlap in DRS distributions (Figures 1 and 2).

Figure 1.

Propensity score (PS) and disease risk score (DRS) distributions across treatment groups for one run of the simulation study with a sample size of 10,000 subjects and 100 covariates included in the PS and DRS models. In plots A and B the effects of covariates on both treatment and the outcome were mild, in plots C and D covariate effects were moderate, and in plots E and F the covariate effects were strong. The overlapping coefficient is an estimate of the percentage of overlapping area between the two density functions.

Figure 2.

Propensity score (PS) and disease risk score (DRS) distributions across treatment groups for one run of the simulation study with a sample size of 1,000 subjects and 100 covariates included in the PS and DRS models. In plots A and B the effects of covariates on both treatment and the outcome were mild, in plots C and D covariate effects were moderate, and in plots E and F the covariate effects were strong. The overlapping coefficient is an estimate of the percentage of overlapping area between the two density functions.

Table 1 shows results when matching on the smaller caliper distance of 0.025 standard deviations of the logit of the PS or DRS distribution. For every scenario, a larger percentage of the treated population could be matched on the DRS versus the PS because of the greater overlap in DRS distributions (percent matched was approximately 100 for DRS matching and ranged from 96.5 to 54.5 for PS matching). The DRS-matched estimate generally had greater precision and lower MSE compared to the PS-matched estimate, with MSE ranging from 0.02 to 0.30 for DRS matching and 0.03 to 0.39 for PS matching (Table 1). Both DRS and PS matching resulted in approximately unbiased estimates for scenarios where there was no treatment effect heterogeneity. In the presence of treatment effect heterogeneity, matching on the DRS resulted in a more accurate evaluation of the treatment effect within the entire treated population (Table 1). When using a larger caliper distance of 0.25 standard deviations of the logit of the PS or DRS distribution, differences in the percent matched and standard errors were smaller, but the overall patterns were similar (not shown).

Table 1.

Simulation results

Scenarioa,b	Sample Size	Method	Bias	St. Error	MSE x 10	% matched
A
	10,000
		Unadjusted	0.11	0.05	0.15	---
		PS match	0.00	0.05	0.03	96.5
		DRS match	0.01	0.06	0.03	99.9
	1,000
		Unadjusted	0.12	0.15	0.36	---
		PS match	0.01	0.19	0.34	86.1
		DRS match	0.01	0.17	0.30	99.4
B
	10,000
		Unadjusted	0.26	0.05	0.69	---
		PS match	0.00	0.06	0.03	82.1
		DRS match	0.01	0.05	0.03	99.9
	1,000
		Unadjusted	0.25	0.15	0.86	---
		PS match	0.00	0.19	0.38	72.2
		DRS match	0.00	0.16	0.25	99.4
C
	10,000
		Unadjusted	0.33	0.05	1.14	---
		PS match	0.00	0.06	0.04	63.0
		DRS match	0.01	0.05	0.02	99.8
	1,000
		Unadjusted	0.33	0.14	1.27	---
		PS match	0.00	0.20	0.39	54.5
		DRS match	0.00	0.13	0.18	99.3
D
	10,000
		Unadjusted	0.27	0.04	0.74	---
		PS match	0.03	0.05	0.03	72.0
		DRS match	0.01	0.04	0.02	99.6
	1,000
		Unadjusted	0.25	0.13	0.84	---
		PS match	0.05	0.18	0.35	63.1
		DRS match	0.01	0.13	0.18	98.6

^aScenario A: mild covariate effects on treatment and outcome; Scenario B: moderate covariate effects on treatment and outcome; Scenario C: strong covariate effects on treatment and outcome; Scenario D: treatment effect heterogeneity with strong covariate effects on treatment and outcome

^bThe mean overall incidence of the outcome in the full population across all simulation runs ranged from 31% to 34% for both sample sizes. The mean overall prevalence of treatment in the full population ranged from 29% to 36% for both sample sizes.

Empirical results

We present results for the empirical study in Figures 3 and 4 as well as Tables 2 and 3. Table 2 shows the distribution of the 37 a priori selected covariates by treatment group. New users of dabigatran were generally healthier, with fewer comorbidities and greater use of the healthcare system than new users of warfarin (Table 2). Similar patterns of initiation have been found in other studies.^{19, 20}

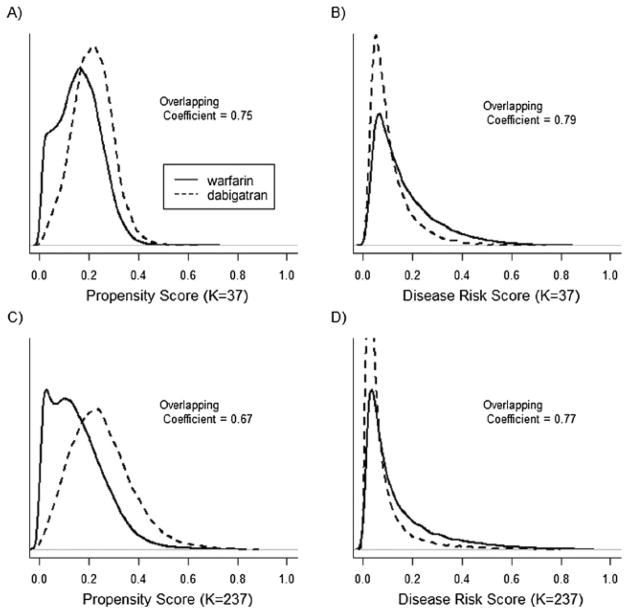
Figure 3.

propensity score (PS) and disease risk score (DRS) distributions across dabigatran and warfarin treatment groups for a 20% sample of the Medicare data and individuals with an index date between October 2010 and December 2012. In plots A and B the PS and DRS models included 37 a priori selected covariates, in plots C and D the PS and DRS models included 37 a priori selected covariates and 200 empirically selected covariates. The overlapping coefficient is an estimate of the percentage of overlapping area between the two density functions.

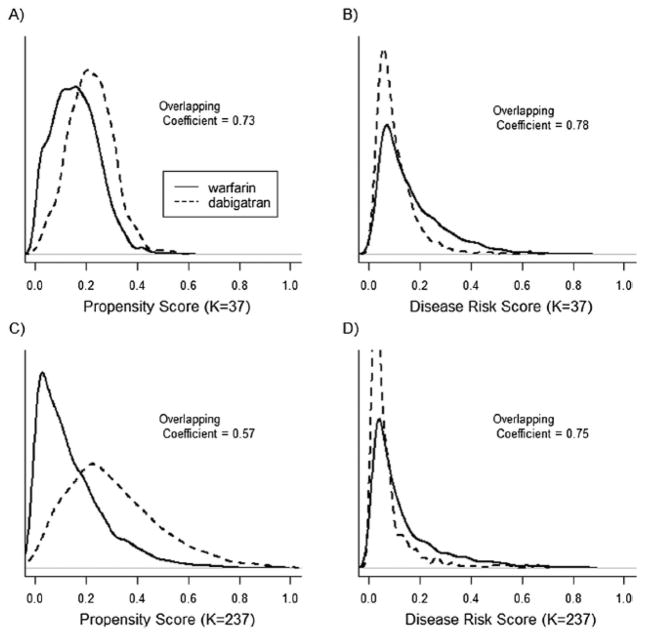
Figure 4.

propensity score (PS) and disease risk score (DRS) distributions across dabigatran and warfarin treatment groups for a 1% sample of the Medicare data and individuals with an index date between October 2010 and December 2012. In plots A and B the PS and DRS models included 37 a priori selected covariates, in plots C and D the PS and DRS models included 37 a priori selected covariates and 200 empirically selected covariates. The overlapping coefficient is an estimate of the percentage of overlapping area between the two density functions.

Table 2.

Baseline covariates measured during 1-year washout period

	Warfarin (N=56,260)	Dabigatran 150mg (N=11,407)
Demographics:
Age	78.91	76.76
Race (1 white, 0 other) (%)	89.2	91.72
Sex (% female)	42.17	48.95
Diagnoses: (%)
Cardiovascular:
Chest pain	38.41	35.05
Heart disease	74.56	66.62
Heart failure	30.74	19.23
Hypertension	65.08	63.30
Hyperlipidemia	35.21	41.09
Myocardial Infarction	3.49	1.89
Cerebrovascular disease	21.29	17.38
Stroke
Ischemic	6.09	4.31
Hemorrhagic	0.34	0.16
TIA	6.9	6.34
VTE	10.36	1.67
Diabetes	35.09	30.02
Kidney disease	12.58	4.74
Renal failure	16.09	5.75
Bleeding	1.88	0.68
Anemia	15.63	9.95
Baseline Meds: (%)
Anti-depressants	28.27	22.89
Antihypertensives:
ACE/ARB	52.22	50.23
Loop diuretics	40.91	28.70
Nonloop diuretics	52.55	41.97
Hypolipidemic drugs:
Statins	49.40	52.45
Fibrate	5.02	4.98
Rate Control Therapy:
Beta blockers	70.83	71.99
CCB	43.97	41.80
Glycoside	18.49	17.10
Rhythm Control Therapy	19.10	23.21
Healthcare Use (average #):
# ECG claims	3.74	3.80
# PSA claims	0.36	0.49
# of fecal occult blood tests	0.12	0.13
# colonoscopies	0.14	0.14
# flu shot claims	0.76	0.79
# of lipid assessments	1.52	1.72
# of mammography claims	0.25	0.29
# of PapSmear claims	0.05	0.07

TIA, transient ischemic attack; VTE, venous thromboembolism; ACE/ARB, angiotensin-converting enzyme/angiotensin II receptor blocker; CCB, calcium channel blockers; ECG, electrocardiography; PSA, prostate-specific antigen.

Table 3.

Empirical results comparing new users of dabigatran with new users of warfarin in preventing combined ischemic stroke and all-cause mortality in the Medicare population between October 19, 2010 and December 31, 2012.

Sample Sizea	# covsb	Method	Hazard Ratioc	St. Errord	95% CI	% matched	Model Fite
							c-stat	p-value	ASAMDf
20% Sample
		Unadjusted	0.48	0.02	(0.46, 0.50)	----	----	----	0.14
	37
		PS match	0.75	0.03	(0.70, 0.80)	99.9	0.68	0.16	<0.01
		DRS match	0.73	0.03	(0.69, 0.77)	100	0.73	<0.01	----
	237
		PS match	0.88	0.04	(0.81, 0.95)	99.2	0.73	0.18	<0.01
		DRS match	0.87	0.04	(0.81, 0.94)	99.7	0.78	<0.01	----
1% Sample
		Unadjusted							0.17
	37
		PS match	0.75	0.14	(0.57, 0.99)	98.5	0.71	0.49	0.01
		DRS match	0.74	0.14	(0.57, 0.98)	99.1	0.73	0.18	----
	237
		PS match	0.89	0.19	(0.61, 1.29)	92.0	0.79	0.47	0.01
		DRS match	0.85	0.16	(0.62, 1.16)	98.5	0.78	<0.01	----

^a20% (N=67,667) and 1% (N=3,383) samples of the Medicare data. The 20% sample consisted of 11,407 dabigatran new-users. The 1% sample consisted of 576 dabigatran new-users.

^bNumber of covariates in PS and DRS model

^cRELY trial relative risk for 150mg dabigatran vs warfarin: 0.76 (0.60, 0.98) for ischemic stroke; 0.88 (0.77, 1.00) for death from any cause. In the current study, >90% of the outcomes were death from any cause.

^dBootstrapped standard errors. Hazard ratio estimates are the mean of the bootstrapped sampling distribution

^ec-statistic and p-value for each PS and DRS model.

^fThe average standardized absolute difference (ASAMD) of covariates across PS matched treatment groups. Because the DRS does not balance covariates across treatment, the ASAMD was only calculated for PS models. The unadjusted ASAMD was calculated for all 237 covariates.

Figures 3 and 4 show the PS and DRS distributions by treatment group for the 20% (Figure 3) and 1% (Figure 4) samples of the Medicare data, with follow-up through 2012. In both analyses, controlling for the larger set of empirically selected covariates resulted in greater separation in PS distributions while having little impact on the separation in DRS distributions.

For the 20% sample (Table 3), approximately 100% of the treated population was matched on the PS and the DRS, regardless of the caliper distance or number of covariates included in the models. In this case, both PS and DRS matching resulted in similar hazard ratios and standard errors, both when controlling for the covariates selected a priori (HRs 0.75 and 0.73 respectively; SEs both 0.03) and after adding the empirically selected covariates (HRs 0.88 and 0.87 respectively; SEs both 0.04).

When using the 1% sample of the Medicare data and controlling for the covariates selected a priori (Table 3), PS and DRS matching yielded similar results, with approximately 100% of the treated population being matched for both methods and caliper distances (HR and SE of 0.75 and 0.14 for PS matching and 0.74 and 0.14 for DRS matching). However, when controlling for the expanded covariate set in this sample and matching on the smaller caliper distance, only 92% of the treated patients were matched on the PS, compared to approximately 99% on the DRS (Table 3). The reduction in the percentage matched resulted in reduced precision for the PS-matched estimate (SE 0.19 versus 0.16) (Table 3). When matching on the larger caliper distance (not shown), the overall patterns were similar except the differences in the percent matched on the PS versus the DRS were smaller (e.g., 95.3% and 99.9% were matched on the PS and DRS, respectively, when controlling the expanded set of covariates with the 1% Medicare sample). In the analyses evaluating treatment effects in the first year of dabigatran use (not shown), the pattern of results was similar to that shown in Table 3, except that unadjusted and adjusted estimates were further from the null and standard errors were larger.

Each of the PS models resulted in good model fit in terms of calibration and discrimination for all scenarios (Hosmer-Lemeshow p-value ranging from 0.16 to 0.49; c-statistic ranging from 0.68 to 0.79). The PS models also performed well in terms of balancing covariates across treatment groups with an average standardized absolute mean difference (ASAMD) of 0.01 or less for all scenarios. In terms of predictive performance, the DRS models had good discrimination (c-statistic ranging from 0.73 to 0.78), but performed poorly in terms of calibration (Hosmer-Lemeshow p-value <0.01 for three out of four scenarios).

DISCUSSION

In this study, we used both simulations and an empirical example to explore potential benefits of using a historically estimated DRS when controlling large numbers of covariates in settings with newly introduced treatments. With few exposed individuals and smaller sample sizes, fitting a high-dimensional PS model can increase separation between the PS distributions of the treatment groups, reducing the number of treated individuals who can be matched on the PS. In theory, the overlap in DRS distributions across treatment groups should always be at least as great as the overlap in PS distributions when the PS and DRS models include the same covariates. Therefore, matching on the DRS may allow researchers to evaluate the treatment effect within a larger proportion of the treated population, compared to matching on the PS.

This potential for greater overlap in the distribution of disease risk across treatment groups is because conditioning on the PS (e.g., matching or stratifying) is more restrictive than conditioning on the DRS. PS methods require that there be no combination of covariate values that result in individuals receiving treatment or control with certainty (i.e., positivity assumption).^{5, 21, 22} Hansen formally shows that adjustment on the DRS requires a weaker condition that there be no levels of disease risk at which treatment or control is received with certainty.⁵ Consequently, adjustment using the DRS can allow researchers to include individuals who would otherwise be excluded with PS adjustment. Even when positivity is satisfied, conditioning on the PS can still be more restrictive than conditioning on the DRS. Balance on the PS will result in covariates being independent of treatment assignment. This implies that any function of baseline covariates, including the DRS, will also be independent of treatment. Therefore, PS balance across treatment groups implies balance on the DRS in expectation. The reverse is not true. Because the DRS does not balance covariates across treatment, but only with respect to the potential outcome under control, balance on the DRS across treatment does not imply balance on the PS.⁵ DRS matched treatment groups can include the same population of individuals who are balanced on the PS as well as individuals who may have differing PS distributions but similar overall risk for the outcome.⁵

In the simulations, we demonstrated that when there was strong separation in the PS distributions across treatment groups, matching on the DRS can result in a larger proportion of the treated population being matched, improving the precision of the effect estimate and, in the presence of treatment effect heterogeneity, provide more accurate estimates of the treatment effect in the full treated population. As with any simulation, results are specific to the scenarios considered. In this simulation study, we did not consider unmeasured confounding or instrumental variables (i.e., variables that do not affect the outcome except through treatment). The inclusion of instruments would have created larger differences in the degree of overlap in PS versus DRS distributions and, in the presence of unmeasured confounding, resulted in greater bias amplification when matching on the PS versus a historically estimated DRS.²³

For the empirical example, we found that when there was moderate separation in the PS distributions across treatment groups, DRS and PS matching gave similar estimates of the effect of the new oral anticoagulant dabigatran versus warfarin in reducing combined ischemic stroke and all-cause mortality within the Medicare population. However, when controlling for large numbers of covariates with reduced sample size, the separation in the PS distribution across treatment groups increased and matching on a historically estimated DRS improved the precision of the effect estimate by allowing a larger proportion of the treated population to be matched. For both PS and DRS matching, when we added a large set of empirically selected covariates, effect estimates became more consistent with the results of clinical trials and other studies comparing these treatments within the Medicare population.^{24, 25} When we restricted the analysis to the first year of dabigatran use, estimates moved further from the null (becoming less consistent with trial results), likely reflecting the strong channeling that occurs shortly after a treatment’s introduction.^16–18

With greater overlap in the distribution of disease risk across treatment groups, it is likely that for any given study, the optimal caliper distance for matching on the DRS will be smaller than the optimal caliper distance for matching on the PS. For both the simulations and empirical example, we found that reducing the caliper distance resulted in fewer individuals being matched on the PS while having less of an impact on the number of individuals being matched on the DRS. While many studies have discussed the importance of choosing an appropriate caliper distance when matching on the PS, more research is needed in determining appropriate caliper distances when matching on the DRS.^{13, 26}

While matching on the DRS can allow for a larger portion of individuals to be compared across treatment when there is separation in the PS distributions, it is important to consider why the PS distributions are separated. If the separation is due to strong differences in confounding variables rather than overfitting the PS model, researchers should proceed cautiously. Strong differences in measured confounders can indicate strong differences in unmeasured confounders, which could be addressed best in the study design phase rather than the analysis phase. We stress the importance of reducing differences in the distribution of baseline covariates across treatment groups through proper study design (e.g., new-user design and other restriction criteria).^{16, 27}

While we have focused on potential benefits of matching on the DRS, the DRS also has some theoretical disadvantages compared to the PS. Because the DRS is formally defined in terms of a potential outcome, estimating the DRS in practice can be challenging and requires additional assumptions. Further, unlike the PS, the DRS cannot be evaluated using measures of covariate balance within the full study population. In this study, the estimated PS models resulted in good model fit and PS matching balanced covariates across treatment groups. When modeling the DRS using historical data, we found it difficult to obtain good model fit in terms of the Hosmer-Lemeshow test, particularly when controlling for larger numbers of covariates. Other studies have reported similar findings when estimating high-dimensional DRSs and have proposed implementing shrinkage methods to reduce the dimensionality of covariates to improve model fit.²⁸ For this study, however, poor fit in terms of the Hosmer-Lemeshow test did not appear to have a strong impact on the performance of the DRS compared with the PS. More research is needed to determine how best to estimate and evaluate the validity of DRS models.

We conclude that under certain assumptions, using historical data to model the DRS is a valid method to control for confounding when evaluating newly marketed drugs. Further, when there is strong separation in the distribution of the PS across treatment groups, matching on a historically estimated DRS versus a PS can allow researchers to evaluate the treatment effect within a larger proportion of the treated population. We further conclude, however, that accurately modeling the DRS can be more challenging as compared with modeling the PS, even in settings involving newly introduced treatments. When using summary scores for confounding control, we recommend conducting and reporting results from PS analyses in addition to analyses using a historically estimated DRS.

KEY POINTS.

• In theory, the degree of overlap in the distribution of disease risk across treatment groups will always be at least as large as the overlap in the propensity score across treatment groups.

• Controlling for a high-dimensional set of covariates can improve confounding control, but increases separation between the PS distributions of the treatment groups while having less impact on the separation between the disease risk distributions of the treatment groups.

• Matching on the DRS can allow researchers to evaluate the treatment effect within a larger proportion of treated individuals, compared to matching on the PS. However, accurately modeling the DRS can be challenging compared to the PS, even in settings involving newly introduced treatments.