Subcellular Dynamics and Protein Conformation Fluctuations Measured by Fourier Imaging Correlation Spectroscopy

Abstract

Novel high signal-to-noise spectroscopic experiments that probe the dynamics of microscopic objects have the potential to reveal complex intracellular biochemical mechanisms, or the slow relaxations of soft matter systems. This article reviews the implementation of Fourier imaging correlation spectroscopy (FICS), a phase-selective approach to fluorescence fluctuation spectroscopy that employs a unique route to elevate signal levels while acquiring detailed information about molecular coordinate trajectories. The review demonstrates the broad applicability of FICS by discussing two recent studies. The dynamics of S. cerevisiae yeast mitochondria are characterized with FICS and provide detailed information about the influence of specific cytoskeletal elements on the movement of this organelle. In another set of experiments, polarization-modulated FICS (PM-FICS) captures conformational dynamics and molecular translational dynamics of the fluorescent protein DsRed, and analyses by four-point correlation and joint distribution functions of the corresponding data reveal statistically meaningful pathways of DsRed switching between different optical conformations.

1. INTRODUCTION

Achieving a detailed understanding of many biophysical phenomena rests on the ability to quantify microscopic behavior in biological systems. As aspirations to look deeper into microscopic realms lead to the extension of new technologies, methods in fluorescence imaging and spectroscopy remain a focal point where techniques evolve and develop in response to the demands of shorter time-scales, smaller signals and higher information content.

Among recent technological developments are improved optical detectors and multi-array cameras to increase the signal collected in fluorescence experiments. In addition to improved fluorophore labels, these advances contribute towards the goal of resolving dynamics at the level of individual particles. For example, the advantage of tracking a single object as it moves through the compartment of a living cell is that one may ascribe a distribution to the object’s displacements, which is an informative characterization of its dynamical behavior [1, 2].

There are, however, numerous obstacles to observing the dynamics of a single fluorescent object using a CCD camera. First, any non-resonant background or auto-fluorescence contribution to the collected signal diminishes the signal-to-noise (S/N) level considerably. Second, the mean fluorescence intensity collected over the course of the experiment decreases due to photo-degradation of the chromophore labels. The number of frames (i) captured by a CCD camera may be approximated by iCCD ∝ Ω / ε, where Ω represents the average number of photons a fluorescent object emits before its fluorophores are degraded, and ε is the threshold number of photons that a set of pixels in the CCD must detect in order to distinguish the object from the background [3]. Thus, the success of fluorescence microscopy tracking experiments often relies on the performance of high sensitivity cameras and fluorophore robustness. In addition to the technical limitations of CCD fluorescence microscopy, there is the potential for cell damage due to the oftentimes necessary high photon flux, or the reactive oxygen species generated by the fluorophore [4, 5]. This is especially true when short time scale dynamics are investigated using high intensity excitation.

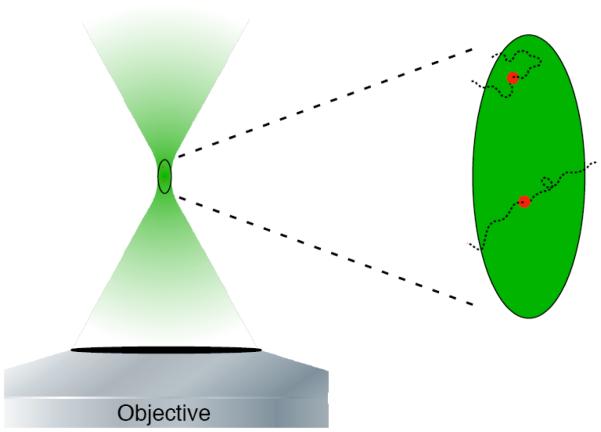
Since the development of fluorescence correlation spectroscopy (FCS) over 30 years ago, fluorescence fluctuation measurements have been implemented to study dynamics of molecular systems on time scales longer than the excited state lifetime. Such kinetic phenomena include translational diffusion, molecular aggregation and chemical rate kinetics in living cells [6, 7]. FCS monitors the variation in the number of fluorescent particles occupying a small, micron scale volume illuminated by a focused laser beam (Figure 1). The fluctuations of the fluorescence emission collected on a single element detector are then proportional to the diffusion of the fluorescent molecules as they move into and out of resonance with the exciting laser field.

Figure 1.

Rendering of an FCS experiment. Two particles travel into the excitation volume at the focal point in the sample and cause a fluctuation in the emitted fluorescence. The zoomed-in portion to the right depicts the random path of each fluorescent particle as it travels through the excitation volume.

An important advantage of FCS over CCD microscopy is that the efficiency of signal acquisition is enhanced by a factor proportional to the number of molecules within the laser illumination volume: iFCS ∝ NΩ / # , where N denotes the number of optically excited molecules. Although this represents an improvement over the efficiency of CCD fluorescence microscopy, interpretation of the data derived from FCS must rely heavily on the availability of an accurate model for the particular experimental situation under consideration. The illuminated volume through which the fluorescent molecules diffuse must be carefully calibrated before any assessment of translational dynamics is made. Furthermore, only a small number of fluorescent molecules may occupy the excitation volume at any one time, since too large a number of molecules will decrease the measurement’s sensitivity to a molecular fluctuation. As with direct imaging experiments, one may increase the signal level from the sample using higher laser intensity, so as to gain improved temporal resolution. However, this can also have the undesirable effect of driving the optical behavior of the chromophore into a non-linear regime, and further complicate the interpretation of the data. Such non-linear effects have been observed in the spectral properties of several fluorescent proteins commonly used in FCS [8, 9].

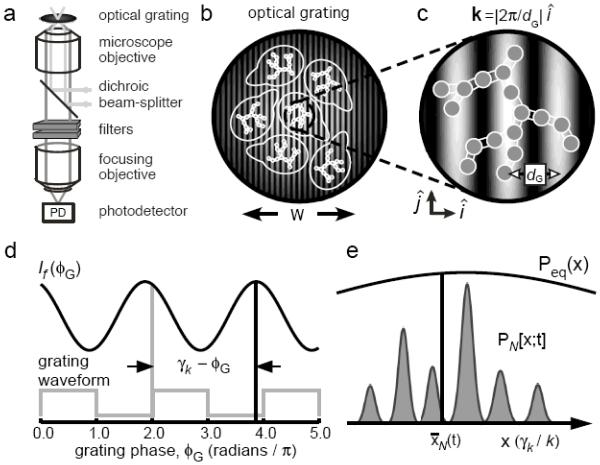
The constraints imposed by limited CCD efficiency and the complications imposed by model dependent interpretations of FCS data led to the development of Fourier imaging correlation spectroscopy (FICS). This method expands on the concepts of fluorescence fluctuation experiments as is done in FCS. However, by incorporating a means to account for a spatial scale in the form of an optical signal phase, FICS is able to relax the dependence of the data analysis on the details of phenomenological models. By using a fringed excitation pattern (i.e. an optical grating) to excite a relatively large number of fluorescent particles (N ≈ 1 million), FICS experiments also represent a strategy to greatly enhance signal levels. As is the case with FCS, the signal strength in FICS is proportional to NΩ / ε. However, the signal is acquired over a much larger region than the small excitation volume of the FCS experiment. In FICS experiments, a fluctuation in the microscopic coordinates of the labeled system of particles is proportional to a fluctuation in the fluorescence signal due to the overlap of the particle distribution and the fringed laser excitation profile (see Figure 2a-c), i.e.

Figure 2.

Schematic diagram of the optical layout for FICS experiments, performed on fluorescently labeled yeast mitochondria. (a) The sample is placed at the focal plane of a fluorescence microscope. The excitation beams (light gray lines) are sent to a focusing objective using a dichroic beam-splitter, and create a spatially modulated intensity grating at the sample. The spatially integrated fluorescence (dark gray lines) is collected by the same objective and focused onto a photo-detector. (b) Condensed view of the focused laser spot with beam waist ~ 50 µm. (c) Fluorescently labeled mitochondrial filaments, represented as N interconnected gray disks, are excited by the optical grating with fringe spacing d_G. Signal fluctuations occur as mitochondrial filaments move relative to one another. (d) Schematic of the total fluorescence intensity I _f as a function of the grating phase ϕ_G. The modulated component of the signal has phase γ_k. (e) The signal phase is proportional to the mean position ${\stackrel{‒}{x}}_N\left(t\right)$ of the sampled particle distribution P_N [x;t]. The sampled distribution is a time-dependent subset of the equilibrium distribution P_eq (x). Figure adapted from Reference 12.

$$I_f({\varphi }_G,t)={\int }_{-\infty }^{\infty }{I}_L(\mathbf{r},{\varphi }_G)c(\mathbf{r},t)d\mathbf{r}$$ 1.

In Equation 1, $I_f({\varphi }_G,t)$ is the integrated intensity at the detector, c(r,t) is the spatial configuration of particles, and $I_L(\mathbf{r},{\varphi }_G)$ is the laser optical grating at the sample. The laser beam is weakly focused at the sample, so that the optical grating is well approximated as an infinite plane wave, $I_L(\mathbf{r},{\varphi }_G)=I_0[1+\cos (\mathbf{k}\cdot \mathbf{r}+{\varphi }_G)]$, where I₀ is a constant intensity level, k is the grating wave vector, and ϕ_G is the grating phase. The variables r and t denote the position in the sample and the time that an observation is recorded, respectively. Since the laser profile extends over a wide field of view (~ 50 µm beam waist), the fluorescence intensity is collected from a large number of labeled particles. The concentration of particles is chosen so that the average inter-particle spacing roughly matches the spatial length scale imposed by the optical grating. The signal intensity given by Equation 1 is then dependent on the grating phase. As we discuss below, phase-selective measurements of the fluctuating fluorescence signal allows us to extract useful information about time-dependent molecular coordinate distributions. The large sample volumes probed by FICS permits the use of relatively low excitation laser power and reduces the risk of inducing non-linear optical behavior, photo bleaching of the fluorescent particles, and the exposure of living cells to photo-reactive molecules.

This review describes the development and evolution of FICS experimentation, from analog methods to photon counting instrumentation used for low-signal detection techniques. Our first examples discuss the methodology employed in experiments with fluorescently labeled Mitochondria. The observables in these experiments are interpreted in terms of center-of-mass particle behavior. We next discuss low-signal studies of the fluorescent protein DsRed using polarization-modulation FICS (PM-FICS), and a four-point correlation analysis of the resultant anisotropy data to obtain insight about the optical conformational fluctuations of this molecule.

2. FICS EXPERIMENTS ON FLUORESCENTLY LABELED MITOCHONDRIA IN LIVE CELLS

Here we show how the FICS observable contains information about partially averaged time-dependent distributions of the spatial coordinates of fluorescent particles. The FICS signal is generated by overlapping a resonant optical excitation grating, created by interfering two laser beams (Figure 2a), with a finite population of fluorescent particles (e. g, mitochondria in yeast cells) as described by Equation 1. The microscopic particle density, $c(\mathbf{r},t)=\frac{1}{V}{\sum }_{i=1}^N{A}_i\delta [\mathbf{r}-{\mathbf{r}}_i\left(t\right)]$, characterizes the coordinate configuration sampled by the measurement. Here V is the illuminated volume, A_i is the absorption and emission efficiency of the ith fluorescent particle, and δ(x) is the Dirac delta function. The particle density is non-zero only in the local vicinity of a fluorescent particle. Upon carrying out the integration of Equation 1, the resulting expression for the fluorescence is given by [3, 10]

$$I_f({\varphi }_G,t)=I_0\langle c\rangle +I_0\mid {\widehat{c}}_k\left(t\right)\mid \cos [{\gamma }_k\left(t\right)+{\varphi }_G],$$ 2.

where $\langle c\rangle$ is the average particle concentration, $\mid {\widehat{c}}_k\left(t\right)\mid$ is the amplitude, and γ_k(t) is the phase of the Fourier transform of the microscopic density defined at the wave vector of the grating: ${\widehat{c}}_k\left(t\right)={\left(\frac{1}{2\pi }\right)}^{3∕2}\int c(\mathbf{r},t)e^{-i\mathbf{k}\cdot \mathbf{r}}d\mathbf{r}$. Operationally, the grating phase ϕ_G is swept at a frequency $({\omega }_G∕2\pi \simeq 50\mathrm{kHz})$ much higher than those of the particle coordinate fluctuations we wish to study, so that on the time scale of the phase modulation, the detected signal has both stationary and oscillatory components. By applying lock-in detection, the signal is amplified, filtered from 1/f noise, and the complex observable ${\widehat{c}}_k\left(t\right)$ is retrieved in terms of its sine and cosine projections [3, 10]. Figure 2d illustrates how the phase of the modulated fluorescence intensity is shifted by an amount γ_k (t) relative to the phase of the optical grating. It is important to emphasize that the phase of each successive data point is referenced (or “locked”) to that of the exciting laser ϕ_G.

The time-dependence of ${\widehat{c}}_k\left(t\right)$ arises due to the center-of-mass particle coordinate displacements as they project onto the fringes of the optical grating. Since the grating wave vector k_G points in the $\widehat{i}$ -direction, only the x-components of the coordinate displacements contribute to the signal. The N coordinates {x₁ (t), x₂ (t),…, x_N (t)} fluctuate continuously about their mean values according to $x_i\left(t\right)=\delta x_i\left(t\right)+\langle x_i\rangle$. In Figure 2e, we schematically represent a hypothetical continuous distribution Peq (x) that describes the equilibrium probability of observing a randomly selected particle with coordinate x, mean ${\langle x\rangle }_{eq}={\int }_{-\infty }^{\infty }x{\mathit{P}}_{eq}\left(x\right)dx=0$ and variance ${\sigma }_{eq}^2={\int }_{-\infty }^{\infty }{x}^2{P}_{eq}\left(x\right)dx$. At a given instant, the FICS observable samples the Fourier transform ${\widehat{c}}_{k_G}\left(t\right)$ of a subset ${\mathit{P}}_N[x;t]=c(x,t)=\frac{1}{N}{\sum }_{i=1}^N{A}_i\delta [x-x_i\left(t\right)]$ of the equilibrium distribution. The FICS signal can be Taylor expanded in terms of the raw moments of P_N :

$${\widehat{c}}_k\left(t\right)=\sum _{m=0}^{\infty }\frac{{\left(ik\right)}^m}{m!}{\mu }_m^{\prime },\text{where}{\mu }_m^{\prime }\left(t\right)={\int }_{-\infty }^{\infty }{x}^m\left(t\right){\mathit{P}}_N[x;t]dx\left(t\right).$$ 3.

Alternatively, ${\widehat{c}}_k\left(t\right)$ is approximated by a cumulant expansion, truncated at m = 2 [11].

$${\widehat{c}}_k\left(t\right)\simeq \text{exp}\left\{ik{\stackrel{‒}{x}}_N\left(t\right)-\frac{1}{2}{k}^2{\left[\delta {\stackrel{‒}{x}}_N\left(t\right)\right]}^2\right\}.$$ 4.

Equation 4 shows that the measured phase and the amplitude of ${\widehat{c}}_k\left(t\right)$ can be assigned the following physical significance. The signal phase ${\gamma }_k\left(t\right)=k{\stackrel{‒}{x}}_N\left(t\right)$ is related to the mean sampled center-of-mass coordinate, and the amplitude $\mid {\widehat{c}}_k\left(t\right)\mid =\exp \{-\frac{1}{2}{k}^2{\left[\delta {\stackrel{‒}{x}}_N\left(t\right)\right]}^2\}$ is related to the size N of the sampled distribution {through the relationship ${\left[\delta {\stackrel{‒}{x}}_N\left(t\right)\right]}^2\propto N^{-1}$ (illustrated in Figure 2e) [12].

It is useful to characterize translational dynamics by performing a time autocorrelation of the fluctuating Fourier space density

$$F(k,\tau )=\langle {\widehat{c}}_k\left(0\right){\widehat{c}}_k^{\ast }\left(\tau \right)\rangle ,$$ 5.

where τ is the time interval over which successive data points are correlated, and the angled brackets indicate an average over initial times. The time correlation function (TCF) F (k, τ) is a statistically averaged distribution function related to the van Hove space-time correlation function by its Fourier transform [13],

$$F(k,\tau )=\int d^{3}R{G}_s(\mathbf{R},\tau )e^{i\mathbf{k}\cdot \mathbf{R}}.$$ 6.

The van Hove function is the conditional probability that a particle can be found at position R at time τ, given that it was previously at position R = 0 at time t = 0. The Gaussian model for single particle motion assumes that self-displacements can be accurately modeled as a Gaussian random variable. In the Gaussian model, the van Hove correlation function takes the form

$$G_s(\mathbf{R},\tau )={\left[\frac{2\pi }{3}\langle \Delta R^2\left(\tau \right)\rangle \right]}^{-3∕2}\exp \left[\frac{-3R^2}{2\langle \Delta R^2\left(\tau \right)\rangle }\right],$$ 7.

where the mean-square-displacement (MSD) is given by $\langle \Delta R^2\left(\tau \right)\rangle$. For particles undergoing simple Brownian motion, the MSD scales linearly in time, i. e. $\langle \Delta R^2\left(\tau \right)\rangle =6\Delta \tau$, where D is the diffusion constant. Should the underlying mechanism of particle motion be affected by interactions with the local environment, the temporal scaling of the MSD is subject to the power law relation MSD ∝ Dτ^α, where α is a temporal scaling exponent. Under circumstances where the particle can travel along an uninterrupted path for extended periods, α = 2 [13]. This type of motion would appear to be ballistic, but if it were observed in the cell, a possible underlying mechanism would be the active transport of a particle to a target location. The exponent α may range from 2 to 1 and, in the sub-diffusive case, less than 1. The temporal scaling of the MSD is thus a useful characterization of the dynamic environment of a fluctuating particle.

In the Gaussian model of particle diffusion, the TCF F (k, τ) takes the form

$$F(k,\tau )=\exp (-k^2\langle \Delta R^2\left(\tau \right)\rangle ∕6)$$ 8.

Equation 8 can be solved for the MSD, and its temporal scaling can be directly examined.

In the biological context, we anticipate labeled particles to exhibit more complicated behavior than simple Brownian motion. While the motions of small proteins in bacteria appear to be diffusive [14-16], observations on larger mRNA-protein clusters in E. coli as well as motions of yolk granules in yeast both appear to be sub-diffusive [17, 18]. The cell is also host to self-assembling cytoskeletal proteins, such as actin, which can produce physical forces as the protein polymers grow [19]. The assembly of branched actin networks, for example, are an underlying molecular mechanism of cell motility [20]. Should a sub-cellular object directly experience the fluctuating forces of actin network assembly and disassembly, one might expect it to exhibit anomalous, intermittent motions that are best characterized as sub-diffusive. Thus, an undetermined combination of thermal diffusion, macromolecular crowding, and actin network dynamics can potentially mediate the transport of intracellular species.

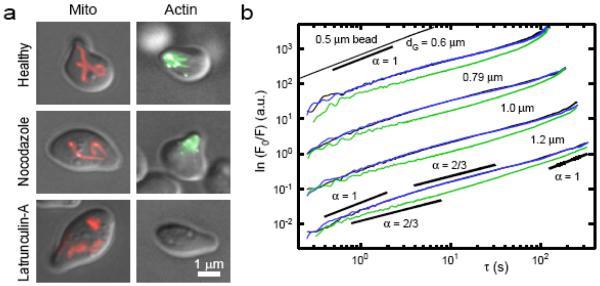
Mitochondria are well known for their role in intracellular ATP production, heme and fatty-acid biosynthesis, and programmed cell death [21-23]. They are also known to exhibit complex intracellular motions [24]. Using in vivo fluorescent labeling methods and FICS, it is possible to study which factors influence the motions of mitochondria in mating S. cerevisiae. Previous FICS research on mitochondria of osteosarcoma cells identified a strong dependence on actin microfilaments and microtubules for the normal dynamics of the organelle [25]. To quantify the anomalous movements of mitochondria in yeast under conditions of varied cytoskeletal integrity, TCFs of mitochondria in healthy cells were compared to cells treated with microtubule (MT) destabilizing Nocodazole, and to cells treated with actin microfilament (MF) destabilizing Latrunculin-A (Figure 3a). From the measured TCFs, $F(k,\tau )=F_0\exp [-k^2\langle \Delta {\mathit{R}}^2\left(\tau \right)\rangle ∕6]$, we determined the MSDs $[\langle \Delta R^2\left(\tau \right)\rangle =6D{\tau }^{\alpha }]$ according to $\ln [F_0∕F(k,\tau )]\propto 2\ln k+\ln \langle \Delta R^2\left(\tau \right)\rangle$. These functions, presented on a log-log plot, are proportional to 2 ln k + ln D + α lnτ. Each curve is the sum of two contributions; a term that is linear with respect to lnτ with slope α, and an offset 2 ln k + ln D. In Figure 3b, we show four sets of curves (displaced vertically by factors of 10), with each set corresponding to one of the experimentally adjustable length scales d_G = 0.6, 0.79, 1.03 and 1.19 µm. These data span three orders of magnitude in time, allowing us to distinguish transitions in the temporal scaling behavior. On sub-second time scales, the curves appear to scale diffusively as α = 1, followed by a sub-diffusive regime with α = 2/3, which persists over many tens-of-seconds. At very long times (> 50 s), the curves crossover to α = 1, indicating a return to diffusive behavior. For MT inhibited cells (blue), the behavior is indistinguishable from healthy cells (black), indicating that the dynamics of the local environment in the absence of MTs are unaltered. For cells in which MFs are destabilized (green), the three regimes of temporal scaling remain. However, the time window corresponding to the sub-diffusive regime is shifted to shorter times. For the MF destabilized cells, the magnitude of the MSD is smaller than healthy cells for all four of the length scales we investigated, indicating that the magnitude of forces experienced by mitochondria under f-actin depleted conditions is significantly diminished. These data show that mitochondrial dynamics in mating yeast exhibit diffusive behavior at short and long times, and sub-diffusive behavior at intermediate times. The interactions between mitochondria and the local microenvironment that lead to sub-diffusive motion are sensitive to the integrity of the actin MFs, but not to MTs.

Figure 3.

(a) Micrographs of fluorescently labeled yeast mitochondria (left column, red) and MFs (right column, green), under different cytoskeletal conditions. (b) MSD of mitochondrial fluctuations in healthy cells (black), cells treated with the f-actin inhibitor Latrunculin-A (green), and cells treated with the microtubule inhibitor Nocodazole (blue). Each set of curves represents measurements performed at a different length scale d_G = 0.6 µm, 0.79 µm, 1.03 µm and 1.19 µm. For all of the length scales investigated, cells treated with Latrunculin-A show a pronounced decrease in mitochondrial mobility. A control measurement of a 0.5 µm colloid sample in viscous, concentrated sorbitol solution is presented at the top of the figure. Various lines with slopes representing the temporal scaling parameter α are also provided to guide the eye.

3. MACROMOLECULAR CONFORMATIONAL FLUCTUATIONS OBSERVED WITH POLARIZATION-MODULATED FICS

The aforementioned relationship between the FICS obervable ${\widehat{c}}_{k_G}\left(t\right)$ and the mean-square-displacement establishes the effectiveness of the method for studying translational dynamics. An important advantage of the phase-selectivity in FICS emerges from experiments carried out on populations of molecules labeled with two resonantly coupled chromophores. This variation of FICS, termed polarization-modulation FICS (PM-FICS), is able to separate the signal component imparted through translational dynamics from that which arises due to variations in optical coupling caused by conformational fluctuations.

In the above discussion, the number of fluorescent molecules that decorate each particle site is large (≥ 10³), so that the system is optically isotropic. When the individual sites correspond to isolated fluorescent molecules, then the system has a continuously fluctuating steady-state anisotropy. In addition to center-of-mass motions, a PM-FICS signal can contain information about molecular anisotropy fluctuations if a polarization grating is implemented in the excitation field. As discussed further below, the anisotropy fluctuations can reflect conformational transitions of appropriately labeled macromolecules.

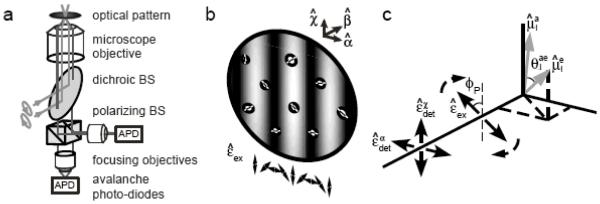
In polarization-modulated FICS (PM-FICS), two orthogonal elliptically polarized beams cross in the sample plane to simultaneously generate a linear polarization grating and an intensity interference pattern at the sample (Figure 4a, b). The signal fluctuations arise from combined projections of the molecular center-of-mass coordinates onto the intensity grating, and the transition dipole orientational coordinates onto the polarization grating. A polarizing beam splitter separates the polarized fluorescence into laboratory frame orthogonal directions, and both signals are phase-synchronously detected (Figure 4c).

Figure 4.

(a) Schematic diagram of the optical layout for polarization-modulated (PM-) FICS experiments, performed on DsRed fluorescent proteins in dilute viscous solution. Two orthogonal, elliptically polarized laser beams are crossed at the sample plane of a fluorescence microscope. The spatially and temporally integrated fluorescence is split using a polarizing beam-splitter (BS), and detected in parallel using two synchronized photon-counting detectors. (b) At the sample, the superposition of the two laser beams creates (simultaneously) a spatially modulated intensity interference pattern and a plane polarization grating. Molecular chromophores are depicted as white circles bisected by line segments, indicating the orientations of transition dipoles. (c) Each optical chromophore is characterized by its absorption and emission dipole moments (${\widehat{\mu }}_i^a$ and ${\widehat{\mu }}_i^e$, respectively), and its depolarization angle ${\theta }_i^{ae}$. The two polarized emission signals are each projected onto orthogonal laboratory frame axes (labeled $\widehat{\alpha }$ and $\widehat{\chi }$). Figure adapted from Reference 12.

The plane-polarized fluorescence intensity from the ith molecule $A_i^{\alpha ,\chi }\left({\theta }_i^{ae},{\varphi }_P\right)$ is proportional to $\langle {\mid {\widehat{\epsilon }}_{ex}\left({\varphi }_P\right)\cdot {\widehat{\mu }}_i^a\mid }^2{\mid {\widehat{\epsilon }}_{det}^{\alpha ,\chi }\cdot {\widehat{\mu }}_i^e\mid }^2\rangle$, where ${\widehat{\mu }}_i^a$ and ${\widehat{\mu }}_i^e$ are the absorption and emission transition dipole moments, respectively, ${\theta }_i^{ae}$ is the fixed angle that subtends them, and the brackets $\langle \cdots \rangle$ indicate an orientational average over the distribution of absorption dipoles [26]. In Figure 4c, the laboratory frame detection electric field directions are given by ${\widehat{\epsilon }}_{det}^{\alpha }$ and ${\widehat{\epsilon }}_{det}^{\chi }$, and the rotating excitation field direction is given by ${\widehat{\epsilon }}_{ex}\left({\varphi }_P\right)={\sin }_P\widehat{\alpha }+\cos {\varphi }_P\widehat{\chi }$. In this case, the local concentration of excited molecules is polarization-dependent, i.e. $c^{\alpha ,\chi }\left(\mathbf{r},{\theta }^{ae}\right)=\frac{1}{V}{\sum }_{i=1}^N{A}_i^{\alpha ,\chi }\left({\theta }_i^{ae},{\varphi }_G\right)\delta \left({\theta }^{ae}-{\theta }_i^{ae}\right)\delta (\mathbf{r}-{\mathbf{r}}_i)$, and the total fluorescence, as determined by the spatial integration of Equation 3, is given by [27]

$$I_f^{\alpha ,\chi }(k,{\varphi }_G,t)=\frac{I_0}{V}\sum _{i=1}^N{A}_i^{\alpha ,\chi }[{\theta }_i^{ae}\left(t\right),{\varphi }_G]\{1+\cos [k{x}_i\left(t\right)+{\varphi }_G]\}.$$ 9.

The phase ${\varphi }_G\left(t^{\prime }\right)=\Omega t^{\prime }+{\varphi }_{G0}$ is swept at the carrier frequency Ω/2π = 10 MHz. Since the period of modulation is much shorter than the time scales for the center-of-mass displacements and any conformational fluctuations, the PM-FICS method has the necessary dynamic range to observe molecular fluctuations. From the demodulated polarization components of the signal, $Z_k^{\chi }$ and $Z_k^{\alpha }$, are constructed linear combinations. The number density $Z_k^{ND}=Z_k^{\chi }+2Z_k^{\alpha }={\widehat{c}}_k\left(t\right)\propto \langle e^{ikx}\rangle$ isolates the effects of translational motion, while the anisotropy density $Z_k^{AD}=Z_k^{\chi }-2Z_k^{\alpha }\propto \langle e^{ikx-i2{\theta }^{ae}}\rangle$ includes the effects of internal fluctuations of the resonant dipolar coupling [28].

Using the theory of cumulants, a good approximation of ${\widehat{c}}_k\left(t\right)$ is given by its cumulant expansion truncated to second order, as described by Equation 4. A similar treatment of the anisotropy density leads to the approximation

$$Z_k^{AD}\left(t\right)\simeq \exp \left\{i[k{\stackrel{‒}{x}}_N\left(t\right)+2{\stackrel{‒}{\theta }}_N^{ae}\left(t\right)]-\frac{1}{2}{[k\delta {\stackrel{‒}{x}}_N\left(t\right)+2\delta {\stackrel{‒}{\theta }}_N^{ae}\left(t\right)]}^2\right\},$$ 10.

where the mean depolarization angle of the sampled distribution is given by ${\stackrel{‒}{\theta }}_N^{ae}\left(t\right)={\sum }_{i=1}^N{\theta }_i^{ae}\left(t\right)P_N\left[{\theta }_i^{ae}\left(t\right)\right]$, and the variance is ${\left[\delta {\stackrel{‒}{\theta }}_N^{ae}\left(t\right)\right]}^2={\sum }_{i=1}^N{\left[{\theta }_i^{ae}\left(t\right)\right]}^2{P}_N\left[{\theta }_i^{ae}\left(t\right)\right]$.

Having already established that polarization-modulated FICS (PM-FICS) is a method able to separate a signal due to internal conformational changes from the part that stems from translational dynamics[28], here we explore the topography of 2D spectra defined by the fluctuations in DsRed depolarization [29]. This tetrameric protein has the overall effect of depolarizing light as energy transfer processes occur between the four chromophores residing in DsRed, and as the four chromophores switch between different spectral states, there are consequent changes to the degree of depolarization.

In an analogy to 2D NMR and optical coherence spectroscopy, we generate 2D FICS spectra using phase-selective signals derived from PM-FICS measurements on DsRed. By moving to higher four point correlation functions, the PM-FICS optical anisotropy signal due to Forster energy transfer between two chromophores can lead us to putative models of molecular inter-conversion between different DsRed conformational states. Our work on DsRed exemplifies the power of PM-FICS as a new, optical method to study intra-molecular dynamics with applications ranging from live cell biology to microscopic dynamics occurring at the glass transition.

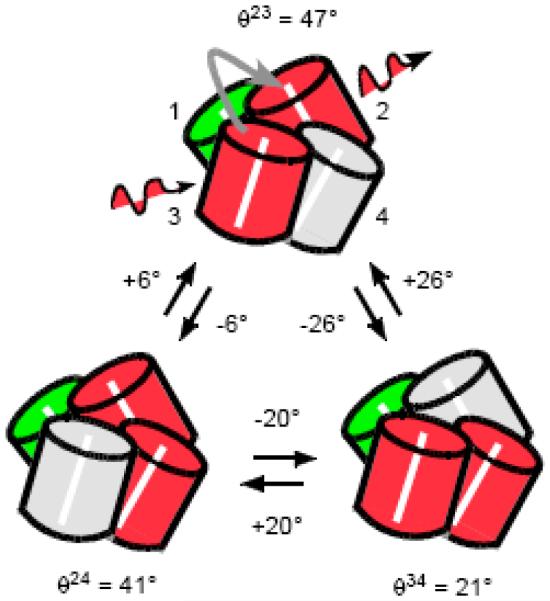
Most DsRed tetramers contain at least one immature green chromophore, which matures to red over time periods much longer than the course of a PM-FICS measurement (~ 10 minutes) [30-33]. The sites that have matured to red (with absorption maximum λ_max ~ 563 nm) undergo reversible inter-conversion to the far-red conformation (λ_max ~ 577 nm), or to a weakly fluorescent green conformation (λ_max ~ 484 nm), on time scales of tens-of-milliseconds and longer [34-37]. Figure 5 depicts a DsRed molecule with a single static (immature) green site and three dynamically interconverting red sites. Both red and far-red conformations are considered bright states (shaded red in Figure 5) since these are selectively excited with green light, while green states of the mature chromophore are dark (shaded gray). When two sites in the DsRed complex are optically coupled through an energy transfer mechanism, the emission polarization rotates by the angle θ^ae, which subtends the absorption dipole moment of the initially excited chromophore and the emission dipole moment of the emitting chromophore [34, 37]. Figure 5 illustrates three possible pair-wise couplings between bright chromophore sites (for molecules with one site in the immature state). Similar pair-wise couplings and transitions are possible for a molecule with a different combination of sites in mature red, shifted-red or weakly green fluorescent states. However, for a molecule with two or more sites in the immature green state, transitions between distinct pair-wise coupled conformations are not possible, and such species are not expected to contribute to the fluctuating emission signals.

Figure 5.

Optical conformational transitions of the ‘mature’ red chromophores in DsRed. DsRed is a tetrameric complex of cylindrically shaped fluorescent protein subunits, with relative orientations approximated in the figure. Each subunit has at its center an optical chromophore that can occupy one of two chemical states, corresponding to green or red emission. The green chromophores (shaded green) do not undergo chemical conversion to the red state on the time scales of our measurements. Red chromophores can interconvert on millisecond time scales between two highly luminescent “bright” states (shaded red), and one “dark” state (shaded gray). From the crystallographic structure of DsRed, the relative angles θ^ae between adjacent absorption and emission transition dipole moments are known, and identified according to the numbering system shown on the top species. Polarization- and spectrally-selective excitation of the red chromophore subunits, mediated by electronic excitation transfer between coupled chromophores occupying adjacent sites, results in discrete transitions in the fluorescence depolarization angle Δθ^ae. Figure adapted from Reference 29.

Four-point time correlation functions (TCF) for the number density and anisotropy density fluctuations were constructed from products of four sequential data points:

$$C_{ND}^{\left(4\right)}(t_{43},t_{32},t_{21})\equiv \langle Z_k^{ND\ast }\left(0\right)Z_k^{ND}\left(t_{21}\right)Z_k^{ND}(t_{32}+t_{21})Z_k^{ND\ast }(t_{43}+t_{32}+t_{21})\rangle$$ 11.

and

$$C_{AD}^{\left(4\right)}(t_{43},t_{32},t_{21})\equiv \langle Z_k^{AD\ast }\left(0\right)Z_k^{AD}\left(t_{21}\right)Z_k^{AD}(t_{32}+t_{21})Z_k^{AD\ast }(t_{43}+t_{32}+t_{21})\rangle .$$ 12.

Equations 11 and 12 define the time intervals t₄₃ (= t4 − t3), t₃₂, and t₂₁ with t₄ ≥ t₃ ≥ t₂ ≥ t₁ ≥ 0. These four-point TCFs have a mathematical form similar to those obtained by magnetic resonance and optical techniques, and can provide information about the rates of chemical processes [38]. Four-point TCFs contain information about the correlations between sequential events during the periods t₄₃ and t₂₁, separated by the intervening interval t₃₂. The magnitudes of the TCFs decay on time scales for which the phase displacements during t₄₃ and t₂₁ exceed ~ π/4. Such correlations diminish with increasing waiting period t₃₂, so that they appear indistinguishable from the products of functionally independent two-point TCFs. It is therefore useful to focus on the t₃₂-dependence of the difference correlation functions, $C^{\left(4\right)}(t_{43},t_{32},t_{21})-C^{\left(2\right)}\left(t_{43}\right)C^{\left(2\right)}\left(t_{21}\right)$. The four-point TCF is commonly represented in the frequency domain through its partial Fourier transform, with respect to t₄₃ and t₂₁

$$S^{\left(4\right)}(V_{43},t_{32},V_{21})={\int }_0^{\infty }d{t}_{43}{\int }_0^{\infty }d{t}_{21}[C^{\left(4\right)}(t_{43},t_{32},t_{21})-C^{\left(2\right)}\left(t_{43}\right)C^{\left(2\right)}\left(t_{21}\right)]e^{i{V}_{21}{t}_{21}+i{V}_{43}{t}_{43}}.$$ 13.

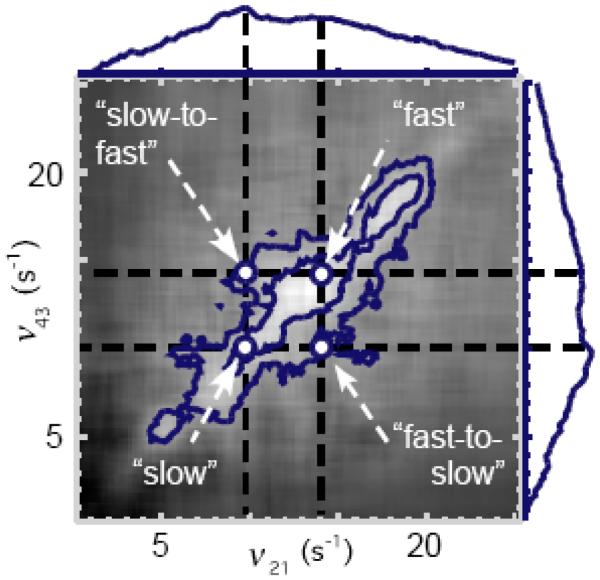
The 2D spectral density $\mid S^{\left(4\right)}(V_{43},t_{32},V_{21})\mid$ is related to the joint probability that the system undergoes two successive coordinate displacements at the transition rates ν₂₁ and ν₄₃, separated in time by the interval t₃₂. In Figure 6 is shown the logarithm of the 2D spectral density of the anisotropy fluctuations of the DsRed system, $\mid S_A^{\left(4\right)}(V_{21},t_{32},V_{43})\mid$, as a contour diagram in the ν₂₁ − ν₄₃ plane, with t₃₂ = 20 ms. Features along the diagonal of the spectrum (ν₂₁ = ν₄₃) indicate sampled populations that maintain their rate of conformational transitions over the duration of the waiting period. Features that lie off the diagonal line, i.e. ν₂₁ ≠ ν₄₃, represent populations that undergo changes in their rates of conformational transitions during the waiting period. In Figure 6, the sampled populations are broadly distributed among transition rates ranging from 0 – 25 Hz, and are roughly partitioned into two peaks centered at ~ 10 and 14 Hz and indicated by “slow” and “fast”. Off-diagonal features in Figure 6 are labeled “slow-to-fast” and “fast-to-slow,” to indicate molecular sub-populations that make transitions between the two spectral regions. The narrow shape of the 2D spectrum in the direction of the anti-diagonal (ν₂₁ = −ν₄₃) suggests that the sampled populations do not readily exchange between fast and slow spectral regions on the time scale of ~ 20 ms.

Figure 6.

Logarithm of the two-dimensional spectral density of the mean depolarization angles $\mid S_A^{\left(4\right)}(V_{21},t_{32},V_{43})\mid$, for waiting period t₃₂ = 20 ms. Features along the diagonal line (labeled “fast” and “slow”) indicate the distribution of conformational transition rates, while off-diagonal features indicate molecular populations that “exchange” between conformational transition rates. Along the horizontal and vertical axes is projected the magnitude of the spectrum, evaluated at the diagonal ν₂₁ = ν₄₃. Contours are shown at 0.5 and 0.25 times the peak height. Figure adapted from Reference 29.

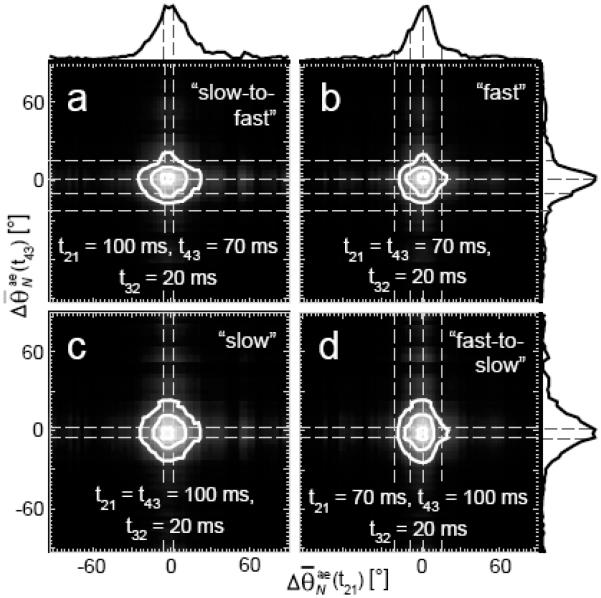
Four-point distribution functions (DFs) of the PM-FICS measurement can establish the existence of “pathways” between adjacent conformational transitions. In Figure 7 are shown contour diagrams of the joint DFs, $\mathit{P}\left(4\right)[\Delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{43}\right);\Delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{21}\right)]$ corresponding to each of the four labeled points in the 2D spectrum of Figure 6. The magnitudes of the DF, are projected along the horizontal and vertical axes of Figure 9. For the DF representing “slow” displacements (Figure 7c), there are peaks centered at the coordinates $[\Delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{21}\right),\Delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{43}\right)=(-6°,-6°),(+2°,-6°)]$ and $(-6°,+2°)$. For the distribution representing “fast” displacements (Figure 7b), there are peaks at the coordinates $(+2°,+2°),(+16°,+16°),(+2°,+16°),(+2°,-22°),(+16°,+2°)$ and $(-22°,+2°)$. These peaks indicate temporally correlated events, in which a change in molecular conformation of a given magnitude is connected to that of another. The diagonal symmetry of the “fast” and “slow” DFs suggests that for the relatively short waiting period of t₃₂ = 20 ms, there is no temporal ordering of the two correlated events.

Figure 7.

(a – d) Joint distributions of the sampled mean displacements of depolarization angles ${\mathit{P}}^{\left(4\right)}[\Delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{43}\right);\Delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{21}\right)]$, where the waiting period t₃₂ = 20 ms, and t₂₁, $t_{43}\in \{70\mathrm{ms},100\text{ms}\}$, as shown. Selected features in the joint distributions (indicated by horizontal and vertical dashed gray lines) reflect temporally correlated transitions that participate in “fast” (~ 70 ms) and “slow” (~ 100 ms) conformational transition pathways. The magnitudes of the distributions are projected onto horizontal and vertical axes. Contours are shown at 0.9, 0.5, and 0.25 times the peak height. Figure adapted from Reference 29.

Figure 9.

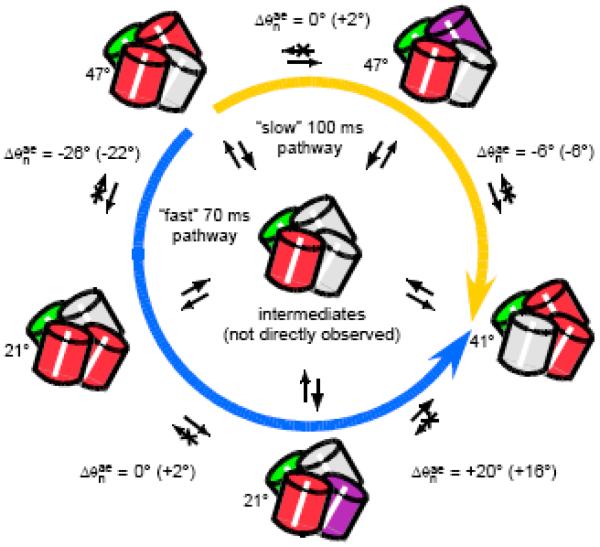
Possible model for the conformational transition pathways observed in DsRed. The structural and color conventions are the same as adopted in Fig. 1, except that the “far-red” chromophore state is indicated by purple shading. The measured displacements in the depolarization angle are shown in parentheses next to the expected values from the crystallographic data. The molecule undergoes temporally correlated (cooperative) transitions between different optically coupled conformations. There are distinct “fast” and “slow” transition pathways, operating on the 70 and 100 ms time scales, respectively (indicated by the blue and gold arrows). Intermediates lacking dipolar coupling, such as the one generically depicted at the center of the diagram, connects adjacent species. Exchange processes involve correlations between transitions that occur on separate pathways, and occur on the mean time scale of 8 s. Figure adapted from Reference 29.

The results of Figure 7 suggest that there are two significant optical conformation pathways in DsRed; (i) a “slow” pathway connecting at least two sequential steps, which involve the angular displacements $\Delta {\stackrel{‒}{\theta }}_N^{ae}=+2°\mathrm{and}-6°$; and (ii) a “fast” pathway connecting at least three sequential steps, which involve the displacements $\Delta {\stackrel{‒}{\theta }}_N^{ae}=+2°,+16°$, and $-22°\cdot (-22°,+16°)$. The distributions representing off-diagonal features in the spectral density (Figures 7a and 7d) contain information about exchange processes between the fast and slow pathways. Features present in the exchange distributions indicate bridging steps between “fast” and “slow” kinetic pathways.

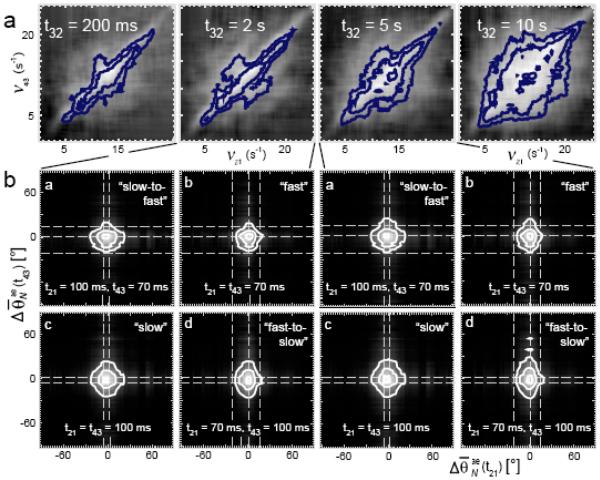
The time for an exchange between “fast” and “slow” kinetic pathways is obtained from the t-dependence of the 2D spectrum. The logarithm of $\mid S_A^{\left(4\right)}(V_{21},t_{32},V_{43})\mid$ for sequentially increasing values of the waiting period(t₃₂ = 200 ms, 2 s, 5 s and 10 s) is shown in Figure 8a. The spectral density broadens in the transverse (off-diagonal) direction on the time scale of a few seconds as the value of t₃₂ is increased. This transverse broadening indicates that sub-populations of molecules in the “fast” pathway undergo exchange with molecular populations in the “slow” pathway. Two sets of the joint distributions, corresponding to t₃₂ = 2 s and 5 s are shown in Figure 8b. These DFs exhibit features at the same coordinates as those observed for the t₃₂ = 20 ms DFs (indicated by dashed lines); however, as the waiting period is increased, there is a gradual loss of diagonal symmetry for “fast” and “slow” DFs (sub-panels B and C, respectively), such that they broaden in the direction of the vertical axis. This loss of diagonal symmetry corresponds to the introduction of a temporal bias that indicates which of the two correlated transitions precedes the other.

Figure 8.

(a) Logarithm of the two-dimensional spectral density of the sampled mean depolarization angles $\mid S_A^{\left(4\right)}(V_{21},t_{32},V_{43})\mid$, for t₃₂ = 200 ms, 2 s, 5 s, and 10s. The transverse broadening indicates that the average exchange time scale of the anisotropy fluctuations is approximately the same as the mean relaxation time τ_A = 8 s. (b) Joint distributions ${\mathit{P}}^{\left(4\right)}[\Delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{43}\right);\delta {\stackrel{‒}{\theta }}_N^{ae}\left(t_{21}\right)]$, with t₃₂ = 2 s and 5 s. Figure adapted from Reference 29.

An analysis of the resulting DFs can be combined with the model presented in Figure 5 in order to establish possible depolarization angle of DsRed optical conformations. We propose the mechanism illustrated in Figure 9 to partially account for our observations of the conformational transition pathways. Based on the crystal structure of DsRed [39], three conformations are possible for which the coupled dipoles have relative orientations ${\theta }_n^{ae}=47°,41°,\mathrm{and}21°$ (see Figure 5). The “fast” pathway, indicated by the blue arrow, consists of three temporally correlated steps: $-22°\to +2°\to +16°$. The “slow” pathway, indicated by the gold arrow, consists of two temporally correlated steps: $+2°\to -6°$. The observed (in parentheses) and the expected angular displacements accompanying the conversion between species is indicated for each step, and the observations of the angular displacement $\Delta {\stackrel{‒}{\theta }}^{ae}=+2°$ are assigned to conformational transitions in which a red site is converted into a far-red site (purple). Intermediates lacking dipolar coupling, such as the one generically depicted at the center of the diagram, are also hypothesized to connect adjacent species. Any upstream conformational transition in the pathway is correlated to an adjacent downstream transition. Nevertheless, for t₃₂ xxx 8 seconds, the time ordering of events is not established. That is, an upstream transition is as likely to occur before a downstream transition, as it is likely to occur after one.

For t₃₂ ≥ 8 seconds, according to the loss of diagonal symmetry of the “fast” and “slow” joint distributions (Figure 8b), downstream transitions tend to occur with greater probability after the waiting period. Corresponding inverse processes, in which downstream events occur prior to upstream events, receive less weight.

4. CONCLUDING REMARKS

FICS experiments on mitochondria of mating yeast cells show that the organelle undergoes anomalous sub-diffusive movements similar to those of dividing yeast cells [40]. We have extended our study of mitochondrial dynamics to this stage of the cell cycle to expand on the underlying mechanism behind the motion of the organelle. Our method of recording and analyzing the dynamics of mitochondria using FICS is sensitive to very small displacements across many decades in time, and is therefore useful to address the question of which sub-cellular components play a role in the cytoskeleton-related movements of mitochondria [25].

PM-FICS was applied to simultaneously monitor molecular center-of-mass and anisotropy fluctuations. When applied to the system of DsRed molecules undergoing free diffusion, the approach allowed us to isolate the effects of optical switching conformational transitions. The PM-FICS method shares common attributes with 2D optical spectroscopy, single-molecule spectroscopy, and fluorescence fluctuation spectroscopy. The detailed information provided by PM-FICS measurements should be useful to address broad ranging problems in the fields of polymer and glass transition dynamics, as well as other areas in complex systems. The ability to perform such measurements on proteins and nucleic acids, in solution and in cell compartments, could enable future studies of in vivo enzymatic function.

Terms/Definitions list.

• o Joint distribution function: A function of two independent variables that characterizes the probability that the values obtained for both variables are simultaneously realized.

• o 2D spectral density: A two-dimensional correlation plot of the frequencies of microscopic coordinate fluctuations probed during an initial time interval, and the frequencies of coordinate fluctuations during a subsequent time interval.

• o Subdiffusion: Characterization of hindered translational motion effected by a particle’s interactions with its local environment.

• o Electronic energy transfer: The process by which an electronically excited chromophore transfers its excited state amplitude to a nearby acceptor chromophore through a resonant dipole-dipole interaction.

Summary Points.

• o In FICS experiments, a spatially modulated optical grating excites a dilute solution of fluorescently labeled particles. Phase-synchronous detection of the fluorescence, with respect to the phase of the exciting optical grating, measures the collective spatial and conformational fluctuations of the labeled species.

• o FICS is a phase-selective fluorescence technique, which achieves a high signal-to-noise ratio by monitoring fluctuations of partially averaged molecular coordinates.

• o In analogy to magnetic resonance and optical coherence spectroscopy, the phase-selectivity of FICS allows for determination of multi-point time correlation functions, and by extension multi-dimensional spectral densities.

• o Because FICS experiments directly monitor coordinate fluctuations, it is possible to construct joint distributions to identify temporal correlations between successive coordinate displacements, thus providing detailed information about transition pathways.

• o The influence of cytoskeletal proteins on the motions of mitochondria in mating S. cerevisiae was studied using FICS. These measurements provide length scale dependent information about the dynamic behavior of mitochondria and support a model of actin polymerization involvement in mitochondrial dynamics.

• o The optical switching pathways of DsRed, a tetrameric complex of fluorescent protein subunits, were examined using PM-FICS. An analysis of PM-FICS coordinate trajectories, in terms of 2D spectra and joint probability distributions, provides detailed information about the transition pathways between distinct dipole-coupled DsRed conformations.

• o Potential applications of FICS extend from studying the motile behavior of cellular organelles to in vitro and in vivo conformational fluctuations of biological molecules, as well as the decoupling of rotational and translational diffusion in polymers near the glass transition.

Acronyms list

CCD

Charge-coupled device

FCS

Fluorescence correlation spectroscopy

FICS

Fourier imaging correlation spectroscopy

PM-FICS

Polarization-modulated Fourier imaging correlation spectroscopy

TCF

Time correlation function

DF

Distribution function