Evaluation of a Two-Stage Approach in Trans-ethnic Meta-Analysis in Genome-Wide Association Studies

Abstract

Meta-analysis of Genome-Wide Association Studies (GWAS) has achieved great success in detecting loci underlying human diseases. Incorporating GWAS results from diverse ethnic populations for meta-analysis, however, remains challenging because of the possible heterogeneity across studies. Conventional fixed- (FE) or random-effects (RE) methods may not be most suitable to aggregate multi-ethnic GWAS results because of violation of the homogeneous effect assumption across studies (FE) or low power to detect signals (RE). Three recently proposed methods, modified RE (RE-HE) model, binary-effects (BE) model and a Bayesian approach (MANTRA), show increased power over FE and RE methods while incorporating heterogeneity of effects when meta-analyzing trans-ethnic GWAS results. We propose a two-stage approach to account for heterogeneity in trans-ethnic meta-analysis in which we clustered studies with cohort-specific ancestry information prior to meta-analysis. We compare this to a no-prior-clustering (crude) approach, evaluating type I error and power of these two strategies, in an extensive simulation study to investigate whether the two-stage approach offers any improvements over the crude approach. We find that the two-stage approach and the crude approach for all five methods (FE, RE, RE-HE, BE, MANTRA) provide well-controlled type I error. However, the two-stage approach shows increased power for BE and RE-HE, and similar power for MANTRA and FE compared to their corresponding crude approach, especially when there is heterogeneity across the multi-ethnic GWAS results. These results suggest that prior clustering in the two-stage approach can be an effective and efficient intermediate step in meta-analysis to account for the multi-ethnic heterogeneity.

Introduction

Genome-wide association studies (GWAS) have identified many genetic loci contributing to the variation of complex human diseases [Hindorff, et al. ; Hindorff, et al. 2009; Mahajan, et al. 2014; Morris, et al. 2012; Welter, et al. 2014]. Despite this success, the effect sizes of these loci are usually modest so that a large number of samples are needed and the analysis in any single study is likely under powered [Manolio, et al. 2009; McCarthy, et al. 2008]. Moreover, the identified genetic variants from GWAS may not be the true causal variants but are more likely to be in linkage disequilibrium (LD) with nearby causal variants [Morris 2011].

Meta-analysis is an effective approach to combine multiple GWAS and increase power by boosting sample sizes. Such meta-analysis has typically been conducted under a fixed-effects model among studies with similar ancestry to avoid violation of the assumption of between-study effect homogeneity [Cantor, et al. 2010; de Bakker, et al. 2008; Zeggini and Ioannidis 2009]. Because meta-analysis has become more popular and feasible through the use of comprehensive reference panels such as the International HapMap Project [Altshuler, et al. 2010] and the 1000 Genome Project [Abecasis, et al. 2010] permitting calculation of good quality genotype imputations, the number of GWAS meta-analyses, restricted to a single ancestry group and across multiple different populations, has increased. However, it remains unclear how to better leverage the allelic heterogeneity and different LD structure across populations of different ancestries since the differences in the LD structure can cause effect heterogeneity. Properly analyzing association results from different ancestry samples can increase the sample size and hence may lead to higher power to identify novel loci [Li and Keating 2014]. In addition, meta-analyses including populations of different genetic backgrounds may enhance the ability to fine-map causal signals by leveraging the differences in LD across ancestral groups [Boerwinkle and Heckbert 2014; Franceschini, et al. 2012; Li and Keating 2014; Liu, et al. 2014; Liu, et al. 2012]. Therefore, while challenging, it is worth exploring approaches for meta-analysis of multiple GWAS across different ethnic ancestral populations.

Conventional meta-analysis methods such as inverse-variance weighted fixed-effects (FE) and random-effects (RE) models have been used in GWAS. These methods were developed in the clinical trial setting [Fleiss 1993; Hedges and Olkin 1985]. The FE model assumes that the effect sizes are consistent across individual studies. If the underlying effects are inconsistent, the FE model does not properly incorporate heterogeneity among studies and underestimates the standard error of the combined effect estimates. RE models account for heterogeneity, correctly estimate the standard errors, and provide more appropriate confidence intervals for the effect estimates when heterogeneity is present. Although these two conventional methods are useful, they may not always be suitable for GWAS. The FE model depends on a rather strong assumption of consistent effect sizes across contributing studies and hence it is not appropriate when meta-analyzing GWAS over populations of different ancestry. The RE model is designed to handle heterogeneity; however, it relies on a conservative assumption that effect sizes are different even under the null hypothesis of no association, thereby making the procedure more conservative in detecting genetic association.

In addition to the two conventional methods, there are three methods recently proposed specifically for meta-analysis of GWAS in the presence of heterogeneity of effect sizes among independent studies. To cope with low power and the conservativeness of the conventional RE model, Han and Eskin developed an alternative random-effects (RE-HE) model that assumes no heterogeneity under the null hypothesis of no association [Han and Eskin 2011]. Han and Eskin proposed a second method called the binary-effects (BE) model [Han and Eskin 2012]. This method is based on a new statistic called the m-value, which is the posterior probability of the non-zero effect size of a study. The m-values are calculated using all studies assuming the effect sizes are similar among studies if their effects are non-zero. The third method, Meta-analysis of Transethnic Association studies (MANTRA), uses a Bayesian framework to account for heterogeneity [Morris 2011].

In this paper, we propose a two-stage clustering strategy in the context of multi-ethnic meta-analysis of GWAS. This approach utilizes prior knowledge of genetic dissimilarity among studies in terms of their mean allele frequency. Our goal is to explore the performance of the two-stage clustering approach in various simulation scenarios using the five methods (RE, FE, RE-HE, BE and MANTRA), to suggest the best strategy in the meta-analysis of potentially heterogeneous studies, and to examine whether the two-stage approach offers any advantages over a crude approach.

Methods

Two Clustering Approaches

We apply the five existing meta-analytic methods to trans-ethnic meta-analysis in a two-stage clustering approach and compare to a crude approach. We assume that there are N independent studies. In the crude approach, we simply use the existing methods to meta-analyze over the N independent GWAS. In the two-stage approach, we utilize known study-specific information and group them into N* subgroups (N* ≤ N) according to the (dis)similarity of genetic characteristics; for example, ethnically closely-related studies are grouped into the same cluster and distantly-related studies are separated into different clusters.

Any measure can be applied to evaluate the dissimilarity of the participating cohorts. We specifically evaluate the dissimilarity between the participating cohorts by calculating pairwise Euclidean distance of their average allele frequencies. The dissimilarity between samples from two cohorts is evaluated by the square root of the sum of squares of the average allele frequency differences of variants available in both cohorts. We assume that the studies within each cluster have homogeneous effect sizes and we use a FE model among studies within a cluster. We implement the methods discussed below to combine FE-derived meta-analysis results across the different clusters in the two-stage approach. In practice, it is more reasonable to use ethnic clustering such that studies from the same ethnic ancestry are allocated to the same cluster.

Fixed-effects (FE) model

The FE model assumes a common true association effect parameter β across N independent studies and provides a test statistic, testing H₀: β = 0 vs. H₁: β ≠ 0, using an inverse-variance-weighted pooled effect estimator and its standard error. Let b_i be the effect estimate for the i^th study test assumed to follow a normal distribution with the true effect size β and variance $s_i^2$. Suppose the variance $s_i^2$ of each study is estimated and treated as the true variance for the study i. The inverse-variance-weighted pooled effect estimator is

$$\widehat{\beta }=\frac{\sum _{i=1}^N{w}_i{b}_i}{\sum _{i=1}^N{w}_i},$$

where the weight $w_i=\frac{1}{s_i^2}$. The standard error of $\widehat{\beta }$ is $\text{SE}\left(\widehat{\beta }\right)=\frac{1}{\sqrt{{\sum }_{i=1}^N{w}_i}}$. Hence the test statistic of FE model is

$$Z_{FE}=\frac{\widehat{\beta }}{\text{SE}\left(\widehat{\beta }\right)}=\frac{\sum _{i=1}^N{w}_i{b}_i}{\sqrt{\sum _{i=1}^N{w}_i}}.$$

Under the null hypothesis of no association, the test statistic follows a standard normal distribution [Fleiss 1993; Hedges and Olkin 1985].

Random-effects (RE) model

The RE model assumes the true effect parameter β_i for each study follows a normal distribution with population effect parameter β as mean and between-study variance τ². The null and alternative hypotheses are H₀: β = 0, τ² > 0 vs. H₁: β ≠ 0, τ² > 0. The between-study variance τ² can be estimated by the method of moments using the DerSimonian and Laird approach [DerSimonian and Laird 1986]. Given the estimated between-study variance ${\widehat{\tau }}^2$, the inverse-variance-weighted pooled effect estimator ${\widehat{\beta }}^{\ast }$ and its standard error can be estimated in a similar way to that of the FE model except that the denominator of its weight includes the between-study variance. The inverse-variance-weighted pooled effect estimator is

$${\widehat{\beta }}^{\ast }=\frac{\sum _{i=1}^N{w}_i^{\ast }{b}_i}{\sum _{i=1}^N{w}_i^{\ast }},$$

where the weight $w_i^{\ast }=\frac{1}{s_i^2+{\widehat{\tau }}^2}$. The standard error of ${\widehat{\beta }}^{\ast }$ is $\text{SE}\left({\widehat{\beta }}^{\ast }\right)=\frac{1}{\sqrt{{\sum }_{i=1}^N{w}_i^{\ast }}}$. Hence the test statistic of RE model is

$$Z_{RE}=\frac{{\widehat{\beta }}^{\ast }}{\text{SE}\left({\widehat{\beta }}^{\ast }\right)}=\frac{\sum _{i=1}^N{w}_i^{\ast }{b}_i}{\sqrt{\sum _{i=1}^N{w}_i^{\ast }}}.$$

Under the null hypothesis of no association (H₀: β = 0, τ² > 0), the test statistic follows a standard normal distribution [Fleiss 1993; Hedges and Olkin 1985].

Likelihood approach to RE model by Han and Eskin (RE-HE)

Han and Eskin propose a likelihood based method that assumes no heterogeneity under the null hypothesis of no association; hence the mean and between-study variance are equal to zero, while allowing for heterogeneity under the alternative. By relaxing the conservative assumption of heterogeneity under the null hypothesis of RE, the power of the RE-HE model is increased substantially compared to the conventional RE model. The likelihoods under the null (H₀: β = 0 and τ² = 0) and the alternative (H₁: β ≠ 0 and τ² ≠ 0) are

$$L_0=\prod \frac{1}{\sqrt{2\pi s_i^2}}exp(-\frac{b_i^2}{2s_i^2}),$$

$$L_1=\prod \frac{1}{\sqrt{2\pi (s_i^2+{\tau }^2)}}exp(-\frac{{(b_i-\beta )}^2}{2(s_i^2+{\tau }^2)}).$$

The notation is the same as the notation used in the description of the FE and RE models. The maximum likelihood estimates (MLE) for β and τ² can be obtained by an iterative procedure suggested by Hardy and Thompson [Hardy and Thompson 1996]. Given the estimated $\widehat{\beta }$ and ${\widehat{\tau }}^2$, the likelihood ratio test (LRT) statistic is constructed as follows

$$T_{REHE}=-2\text{log}\left(\frac{\text{sup}{L}_0}{\text{sup}{L}_1}\right)=\sum log\left(\frac{s_i^2}{s_i^2+{\widehat{\tau }}^2}\right)+\sum \frac{b_i^2}{s_i^2}-\sum \frac{{(b_i-\widehat{\beta })}^2}{s_i^2+{\widehat{\tau }}^2}.$$

The test statistic T_REHE asymptotically follows an equal mixture of ${\chi }_1^2$ and ${\chi }_2^2$ distributions when the number of studies is large. The asymptotic p-value is overly conservative when the number of studies is small due to the heavier tail of the asymptotic distribution compared to the true distribution at genome-wide significance level. Hence tabulated values provided by Han and Eskin are used for determining the statistical significance [Han and Eskin 2011].

Binary Effects (BE) model

The binary effects model is a new type of RE model. It uses the newly proposed statistic called m-value and weighted z-score. The z-score (Z_i) is defined by observed effect size (b_i) divided by its standard error (s_i) for study i. The m-value, ranging from 0 to 1, can be interpreted as the posterior probability that the effect is non-zero in each study in a meta-analysis. The test statistic of the BE model (T_BE) is a weighted sum of z-scores, where greater weight is assigned to studies that are expected to have a non-zero effect (by incorporating the m-values). The test statistic is

$$T_{BE}=\frac{\sum m_i\sqrt{w_i}{Z}_i}{\sqrt{\sum m_i^2{w}_i}},$$

where m-value is computed by $m_i=P(T_i=1\mid b)=\frac{p(b\mid T_i=1)P(T_i=1)}{p(b\mid T_i=0)P(T_i=0)+p(b\mid T_i=1)P(T_i=1)}$, T_i is a random variable that has a value 1 if study i has an effect and 0 otherwise. The prior probability of each study having an effect, P(T_i = 1), assumes a beta prior and the observed effect size, b_i assumes a $N(\beta ,s_i^2)$. A simple Markov Chain Monte Carlo (MCMC) method is proposed to estimate the m-value [Han and Eskin 2012]. z_i = b_i/s_i is the z-score and the weight can be approximated by $\sqrt{w_i}\approx \sqrt{n_i{p}_i(1-p_i)}$ where n_i is the sample size and p_i is the minor allele frequency (MAF) for the i^th study [Zaitlen and Eskin 2010]. If the MAFs are similar among studies the weight $\sqrt{w_i}$ approximates $\sqrt{n_i}$ [de Bakker, et al. 2008].

Meta-analysis of Transethnic Association studies (MANTRA)

This method is developed in a Bayesian framework and implemented in the MANTRA software [Morris 2011]. It takes into account the estimated similarity among studies with respect to genetic relatedness using a Bayesian partition model [Denison and Holmes 2001; Knorr-Held and Rasser 2000] and takes genetic distance between studies into account. This approach exploits the notion that similar studies are more likely to have similar effect sizes, while dissimilar studies should, in principle, have more variable effect estimates. The statistical evidence of association is evaluated by the Bayes’ factor (BF) [Kass and Raftery 1995]; that is,

$$\Lambda =\frac{f(\mathit{b},\mathit{s}\mid M_1)}{f(\mathit{b},\mathit{s}\mid M_0)},$$

where b and s are the observed allelic effects and respective standard errors under the null (M₀) and alternative (M₁) models. Under the null model (M₀), there is no association of a variant with a trait in any population, β = 0, while the alternative model (M₁) corresponds to β ≠ 0. The marginal likelihood of the observed allelic effects under model M

$$f(\mathit{b},\mathit{s}\mid M)\propto {\int }_{\theta }f(\mathit{b},\mathit{s}\mid \theta )f(\theta \mid M)\partial \theta$$

is given by the integration over the unknown parameters, θ, including study-specific true allelic effect β_i and additional hyper-parameters relating to their prior distribution, where the likelihood

$$f(\mathit{b},\mathit{s}\mid \theta )=f(\mathit{b},\mathit{s}\mid \beta )=\sum _{i=1}^{N}f(b_i,s_i\mid {\beta }_i)$$

and

$$f(b_i,s_i\mid {\beta }_i)\propto \frac{1}{s_i}\text{exp}\left[-\frac{{(b_i-{\beta }_i)}^2}{2s_i^2}\right]$$

The marginal likelihood f(b,s|M) cannot be directly evaluated; however, the joint posterior density can be approximated by a Metropolis-Hastings MCMC algorithm.

Simulation Study

We performed a simulation study to compare the type I error and power of both clustering approaches using the five methods, with the goal of identifying more efficient meta-analysis strategies for multi-ethnic studies.

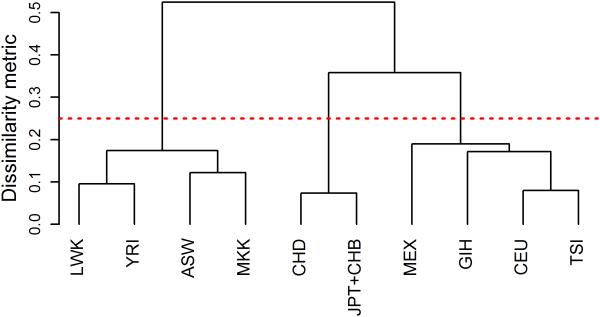
We used the International HapMap Project Phase 3 (HapMap3) [Altshuler, et al. 2010] haplotype data to simulate genotypes for 10 populations. In the HapMap3 data, there were four African-ancestry (AfA) cohorts (African ancestry in Southwest USA (ASW), Luhya in Webuye, Kenya (LWK), Maasai in Kinyawa, Kenya (MKK), Yoruba in Ibadan, Nigeria (YRI)) and two Asian-ancestry (AsA) cohorts (Chinese in Metropolitan Denver (CHD), Japanese in Tokyo and Han Chinese in Beijing (JPT+ CHB)), two European-ancestry (EuA) cohorts (Utah residents with North and Western European ancestry (CEU), Toscani in Italy (TSI)), one Mexican (Mexican ancestry in Los Angeles (MEX)) and one Gujarati Indian (Gujarati Indians in Houston (GIH)). We grouped two EuA cohorts, MEX and GIH cohorts together as GEM (GIH+EuA+MEX) studies since they are clustered together as shown below. The pairwise dissimilarity metric among all ten populations was presented in the Supplemental Table I. A shorter distance between two studies indicated closer genetic relatedness. We graphically showed the two-stage clustering approach using a dendrogram (Figure 1). In Figure 1, a threshold at 0.25 of the dissimilarity metric would leave three clusters, and studies within a cluster are relatively close to each other as measured by genetic distance, while studies in different clusters are further apart.

Figure 1.

Dendrogram showing the dissimilarity among ten populations from the International HapMap Project Phase 3 data. The distance between populations represents a Euclidean distance calculated using allele frequencies. A shorter distance between populations indicates closer genetic relatedness. The red dotted line indicates an arbitrary but clear fixed threshold at 0.25 in distance that leaves three clusters where studies within a cluster are relatively close to each other in their genetic relatedness. Population samples are from: African ancestry in Southwest USA (ASW); Utah residents with North and Western European ancestry (CEU); Chinese in Metropolitan Denver (CHD); Gujarati Indians in Houston (GIH); Japanese in Tokyo and Han Chinese in Beijing (JPT+ CHB); Luhya in Webuye, Kenya (LWK); Mexican ancestry in Los Angeles (MEX); Maasai in Kinyawa, Kenya (MKK); Toscani in Italy (TSI); and Yoruba in Ibadan, Nigeria (YRI).

We simulated genotypes of variants on chromosome 21 using HAPGEN2 software [Su, et al. 2011] which simulated haplotypes based on a reference set of haplotypes and an estimate of the recombination rate across a region. Therefore, the simulated data shared LD patterns similar to the HapMap3 reference data. For each simulation replicate, we generated a continuous trait Y from a normal distribution with mean β and standard deviation 1 where the value of β depends on each scenario. Once the genotypes and the phenotype were simulated, we performed association analysis using SNPTEST v2 [Marchini and Howie 2010] on common variants (MAF>3%, 11,575 single nucleotide polymorphisms (SNPs)) and then ran the trans-ethnic meta-analysis using METASOFT and MANTRA software. For the equal sample size scenario, each study contained a sample size of 3,000 and hence 30,000 samples in total were available for meta-analysis. For the unequal sample size scenario, we increased sample size in the AfA studies by 1.5 times (4,500) and decreased the sample size in the other ancestry studies by 2/3 (2,000) so that the total sample size (30,000) was the same as the equal sample size situation.

Under the null hypothesis of no association, we simulated 1,000 replicates (11,575,000 null SNPs) to evaluate Type I error for the crude and two-stage approaches for the FE, RE, RE-HE, BE and MANTRA methods at varying asymptotic thresholds (for α = 0.05 through 0.00001). A continuous trait Y was generated from a normal distribution with mean 0 and standard deviation 1. We pooled all the variants from the 1,000 replicates and assess type I error by calculating the proportion of SNPs whose meta-analytic p-value is less than pre-specified asymptotic thresholds. For the Bayesian method MANTRA, we only presented the proportion of SNPs with BF greater than preselected thresholds because there was no metric to convert BFs to p-values [Wang, et al. 2013].

For power analyses, we considered four heterogeneity scenarios: (1) Effect-size homogeneity, (2) Ancestry-specific effects, (3) Effect-size heterogeneity, and (4) Western exposure effects. In the Effect-size homogeneity scenario (scenario 1), all 10 studies have the same effects and therefore there is no heterogeneity among the studies. In the Ancestry-specific scenario (scenario 2), we considered only studies in one ancestry cluster to have non-zero effects. Specifically, we assumed only four AfA studies have non-zero allelic effects in this scenario and we named it as African-specific effects scenario. In the Effect-size heterogeneity scenario (scenario 3), we considered that a SNP has an effect in multiple studies, assuming the same effect size among studies in the same ethnic group but allowing the effect size to vary across different ethnic groups (effect sizes: 0.05 for four AfA studies, 0.025 for two AsA studies and 0.0125 for four GEM studies). In the Western exposure effects scenario (scenario 4), we assumed that shared environments such as life style would result in similar genetic effects and hence we assigned equal, non-zero effect size to the causal variants only in the samples living in Europe or North America (ASW, CHD, CEU and TSI) regardless of their ethnicity. For scenarios 1, 2 and 4, we assessed power varying effect sizes from 0.05 to 0.2, which is roughly equivalent to 0.045% to 0.72% of the trait variation explained by a SNP with MAF 0.1.

We picked six causal SNPs based on their allele frequency as follows. Four SNPs had comparable effect allele frequency (EAF) (0.05, 0.1, 0.2, and 0.4, respectively) across the 10 studies. The remaining two causal SNPs had varying allele frequencies for a selected allele across studies: one SNP with EAF in a range of 0.2 to 0.5 and the other with frequency between 0.2 and 0.8. Because there was no unified threshold to compare Frequentist and Bayesian methods, we assessed empirical thresholds for all five methods for two clustering approaches under the null hypothesis of no association by pooling the null p-values or BFs and determining the desired quantile as the empirical thresholds (Supplemental Table II). We calculated the power for a single variant analysis by the proportion of simulation replicates with a causal SNP association p-value less than or BF greater than the empirical thresholds for each meta-analysis method and clustering approach.

We also calculated region-wise power. In most genetic studies, the causal variants are often not available for analysis. In many cases, identified associated genetic variants are not the causal variants but in LD with those variants. Therefore, it is worthwhile to explore the surrounding region of a causal variant, including or excluding the causal variant, and to evaluate the performance of the two-stage clustering approach. We defined the regions of the six causal SNPs by start and end positions including all SNPs with r²>0.2 with the causal SNPs, totaling up to 652 SNPs for the six causal SNPs, and assessed power in those regions with and without the causal SNPs. We defined the regions by r² because we knew the causal SNPs and were interested in examining how LD with the causal variants would influence on power. However, in practice, we may not know causal variants and selecting a region based on location (e.g., a gene location) would be more practical. We defined statistical significance in the region-wise analysis by comparing p-value or BF of all SNPs in a region to an empirical threshold after adjusting for multiple testing. Similarly, we used empirical thresholds to evaluate power. To correct for multiple comparisons, we used a minimum p-value or a maximum BF of a region from each replicate to construct the empirical distribution. We then select the empirical threshold at a desired significance level based on this empirical distribution. The empirical thresholds are presented in the Supplemental Tables III and IV.

Results

Type I error

Table I shows that the four Frequentist methods of both one- and two-stage approaches had well-controlled type I error except that the crude BE model had slightly inflated type I error. The RE model was consistently conservative. We could not evaluate type I error of MANTRA against the asymptotic thresholds because it uses BFs. Instead, we present the proportion of SNPs whose BF was greater than some preselected thresholds for MANTRA. In the unequal sample size scenario, the type I error rates (Supplemental Tables V) and the empirical thresholds (Supplemental Tables VI) were similar to the equal sample size situation.

Table I.

Type I error rates of both one- and two-stage clustering approaches for FE, RE, RE-HE, BE and MANTRA methods when sample size was equal. The thresholds for the Frequentist and Bayesian methods (^a and ^b) are not interchangeable. The P-values and the Bayes’ factors are assessed under the null hypothesis of no association using 11,575,000 null SNPs.

		Crude clustering approach					Two-stage clustering approach
Thresholda for FE, RE, RE-HE, BE	Thresholdb for MANTRA logBF > 0	FE	RE	RE-HE	BE	MANTRAc	FE 2-stage	RE 2-stage	RE-HE 2-stage	BE 2-stage	MANTRA 2-stage
5e-2	logBF > 0	5.01E-02	3.88E-02	4.97E-02	5.04E-02	1.36E-01	5.01E-02	3.70E-02	4.94E-02	5.04E-02	1.34E-01
1e-2	>1	1.00E-02	7.22E-03	9.95E-03	1.01E-02	9.18E-03	1.00E-02	7.06E-03	9.89E-03	1.01E-02	9.00E-03
1e-3	>2	1.01E-03	6.75E-04	9.95E-04	1.03E-03	7.71E-04	1.01E-03	6.81E-04	9.92E-04	1.02E-03	7.44E-04
1e-4	>3	9.97E-05	6.51E-05	9.66E-05	9.84E-05	6.74E-05	9.97E-05	6.53E-05	9.59E-05	9.60E-05	6.61E-05

^aAsymptotic thresholds for the type I error of the crude and the two-stage clustering approaches for the Frequentist’s methods (Fixed-Effects (FE), Random-Effects (RE), Random-Effects model by Han and Eskin (RE-HE) and Binary Effects (BE) model)

^bThresholds for the crude and the two-stage clustering approaches for the Bayesian method (Meta-analysis of Transethnic Association studies (MANTRA) method).

^cWe presented proportions that SNPs had BF greater than preselected thresholds.

Power

To evaluate power, we considered four scenarios as described above. In all of the power scenarios, we compared 1) the two-stage approach to the crude approach in the aforementioned five methods, 2) the recent methods (RE-HE, BE and MANTRA) to the conventional FE and RE methods in both two-stage and crude approaches, and 3) all of the ten combinations (five methods by two clustering approaches) to see which one is the most powerful in each scenario. We used the empirical thresholds for power analysis because there was no unified threshold to compare Frequentist and Bayesian methods. The statistical significance for comparison among the approaches and methods was assessed by comparing 95% confidence intervals.

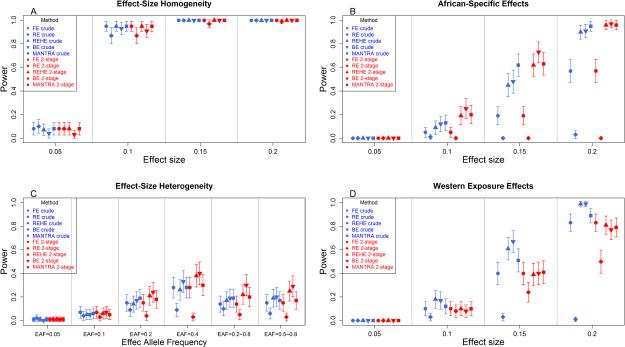
For scenario 1, where there was no heterogeneity in effect sizes among the studies, all meta-analysis methods in both clustering approaches showed similar power. The differences between the two-stage and the crude approaches among the methods were trivial except in the two-stage conventional RE model (Figure 2A). The RE model showed slightly higher power in the crude analysis than the 2-stage approach.

Figure 2.

Power comparisons for ten models (two approaches of five meta-analytic methods) for the four simulated scenarios when the sample size is equal (sample size=3,000 for each study and 30,000 in total, EAF=5% and α=1e-4). The four scenarios of heterogeneity of allelic effects: (A) Scenario1: Effect-size Homogeneity scenario – equal, non-zero allelic effects on the causal variant across the ten studies; (B) scenario 2: African-Specific Effects scenario – equal, non-zero allelic effects on the causal variant only in four AfA studies (AWS, LWK, MKK and YRI); (C) scenario 3: Effect-size Heterogeneity scenario – non-zero allelic effects in multiple studies, equal effect size among studies in the same ethnic group and the different effect size across the different ethnic groups (effect sizes: 0.05 for four AfA studies, 0.025 for two AsA studies and 0.0125 for four GEM studies); and (D) Western Exposure Effects scenario – equal, non-zero allelic effects on the causal variant only in the study samples living in Europe or USA (AWS, CHD, CEU and TSI).

In the Ancestry-specific effect size (scenario 2) and the Effect-size heterogeneity (scenario 3) scenarios, we introduced heterogeneity in the effect sizes according to the population ancestry. In the Ancestry-specific effect size scenario (Figure 2B), we set the African-ancestry studies to have equal, non-zero effect sizes. We observed a significant power increase in the 2-stage BE models when β=0.15 compared to its crude counterpart as their 95% confidence intervals did not overlap. In general, the 2-stage approach of all the other models had either higher or similar power numerically compared to their crude counterparts but their 95% confidence intervals overlapped. In both clustering approaches, the recent meta-analytic methods (RE-HE, BE and MANTRA) performed significantly better than the conventional methods (FE and RE). Among all of the recent methods, the two-stage BE model was significantly more powerful than the crude RE-HE and crude BE models and marginally better than the two-stage RE-HE and MANTRA in the one- and two-stage approaches.

In the Effects-size heterogeneity scenario (scenario 3), we varied the size of the effect for the populations in the different ethnic clusters while the effect sizes were equal across studies within a cluster. Therefore, the heterogeneity arose from different magnitude of positive effect sizes across the clusters. In Figure 2C, we show power over six allele frequency scenarios. The two-stage approaches showed a slightly higher or similar power compared to the same methods in the crude approach except for the conventional RE model (Figure 2C). The two-stage BE model repeatedly appeared numerically more powerful than the other models but it was only significantly different from both crude and 2-stage RE models. Interestingly, a variant with EAF of 0.4 (observed average EAF over 10 studies was 0.394, observed EAF=0.358~0.427) was more powerful than a variant with EAF=0.2~0.5 (observed average EAF was 0.366, observed EAF=0.206~0.494) in both two-stage and crude approaches. Although the variant with EAF=0.4 had slightly higher observed average EAF, a variant that was consistently present across different ethnicities in terms of allele frequency seemed to be better aggregated in a meta-analysis stage compared to a variant with somewhat diverse EAFs across different populations.

In the Western exposure effects scenario (scenario 4), among the recent methods (RE-HE, BE and MANTRA), the two-stage approach was significantly (RE-HE and BE) or nominally (MANTRA) less powerful compared to the crude approach (Figure 2D). This result was because we clustered the studies according to the dissimilarity of mean allele frequency and therefore the true source of heterogeneity in the effect size was not correctly taken into consideration. As a result, studies in each cluster remained heterogeneous and therefore using the FE model over the heterogeneous studies (the two-stage approach) reduced power. In this situation, the crude approach was more powerful. Interestingly, we observed the opposite phenomenon in the RE model. The two-stage RE model was more powerful than the crude RE model. This contrast suggests that, despite its power loss over heterogeneous studies, the prior use of the FE in the 2-stage RE model was more beneficial than the crude RE model.

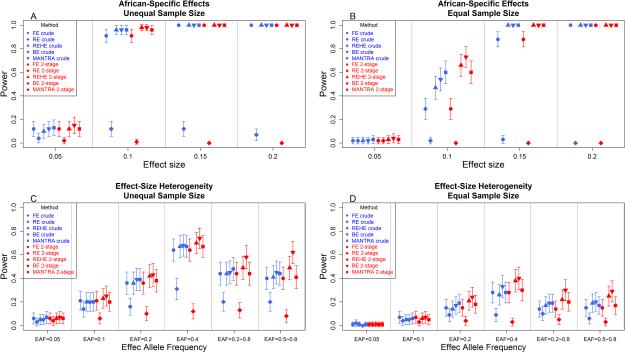
We also considered unequal sample size scenarios since that is typical of real genetic study meta-analyses. In the unequal sample size situation, we increased the sample size (as described in the simulation study) in the AfA studies while decreased in the other studies to keep the total sample size the same. We observed improved power as expected due to the increased sample size in the AfA studies because the simulation model included a true effect in the AfA samples only, while there were no simulated effects in samples from other ancestries. We show the unequal size simulation results in the scenarios 2 and 3 in comparison to the equal sample size results (Figure 3A and 3C).

Figure 3.

Power comparisons for ten models (two approaches of five meta-analytic methods) for the African-Specific Effects and Effect-size Heterogeneity scenarios for unequal vs. equal sample sizes (EAF=10% and α=1e-4). For equal sample size simulation, the sample size=3,000 for each study and 30,000 in total. For unequal sample size simulation, the sample size in the AfA studies is increased by 1.5 times (4,500) and the sample sizes in the other ancestry studies are decreased by 2/3 (2,000) but the total sample size (30,000) remains the same. (A) African-Specific Effects scenario using unequal sample size; (B) African-Specific Effects scenario using equal sample size; (C) Effect-size Heterogeneity scenario using unequal sample size; (D) Effect-size Heterogeneity scenario using equal sample size.

We also examined the sensitivity of our two-stage clustering approach in additional simulations by varying the threshold to a different value of the dissimilarity metric in Figure 1, resulting in a different number of clusters. If we move the threshold up from 0.25 to 0.4 it would result in two clusters; four AfA studies in one cluster and the rest of the studies belonging to the other cluster (2 Clusters). We can also move the threshold down such that we may have five clusters from Figure 1 where each cluster includes: the first two AfA studies; the other two AfA studies; two AsA studies; MEX and GIH; and two EuA studies (5 Clusters). Supplemental Figure 1 showed one Crude and three 2-stage clustering approaches (2 Clusters, 3 Clusters and 5 Clusters). The results suggested that our 2-stage approach is quite robust to the different dissimilarity thresholds where, in fact, the three clustering scenarios yielded the same power. We performed this additional simulation study only with Effect-Heterogeneity (Scenario 3).

Region-wise analysis with causal variants included vs. excluded

Because, in most genetic studies, identified associated genetic variants were not causal variants but in LD with those variants, we explored the surrounding region of a causal variant, including or excluding the causal variant, and evaluated the performance of the two-stage clustering approach. The overall pattern of the results was similar to what we had observed except in the Effect-size Heterogeneity scenario (Scenario 3). It was evident that the inclusion of a causal variant in the analysis suggested higher power than when it was excluded (Supplemental Figures 2 and 3). Although less deviation in power appeared among the models in the African-specific scenario, the two-stage RE-HE and BE models were slightly more powerful compared to their counterpart crude approaches (Supplemental Figures 2B, 2C, 3B and 3C). As we previously observed, the two-stage approach had no benefits over the crude analysis when the heterogeneity in effect size was due to an environmental factor rather than genetic dissimilarity.

Discussion

Meta-analysis has been predominantly performed among European-ancestry population studies. However, with the use of comprehensive reference panels, the number of genome-wide association studies in other ethnic populations has increased. While meta-analyzing over multiple GWAS across genetically different populations may provide an opportunity to enhance power by increasing sample size and to explore genetic variants that are either transferable among populations or unique to a certain ethnicity [Liu, et al. 2013; Liu, et al. 2012], this approach also presents challenges such as potential heterogeneity due to the linkage disequilibrium, the different spectra of causal variants and their allele frequencies from diverse genetic architecture, different genotype platforms, imputation accuracy and possible environmental influence on genetic impacts.

With these opportunities and challenges of trans-ethnic meta-analysis, we proposed a two-stage clustering approach instead of the crude approach and assessed the performance of five meta-analytic methods that are currently available and widely being used. Our two-stage approach was applied to account for between-cluster heterogeneity as well as to bolster within-cluster homogeneity. We showed in a simulation study that our two-stage approach can improve power in RE-HE and BE models in the presence of heterogeneity among multiple GWAS due to the genetic dissimilarity and can also reduce the computational intensity by reducing the number of studies entering the meta-analysis in MANTRA while maintaining similar power. We showed a comparative computation time analysis results in Supplemental Table VII. The average computational time was 5.9 minutes to analyze 652 variants when the number of studies included in the meta-analysis in MANTRA was three in the two-stage approach while it took 10.9 minutes for the same number of variants when the number of studies was ten in the crude approach.

We have examined the power and type I error of our approach in five meta-analytic methods. The type I error rates of all of the Frequentist methods are well controlled in both one- and two-stage approaches; we lack the ability to evaluate the type I error in the Bayesian method MANTRA. For a fair power comparison, we have calculated empirical thresholds for all five methods in the two approaches and used empirical thresholds for the power computation. For the region-wise simulation studies, the empirical thresholds are computed using minimum p-value or maximum BF. The results show that our two-stage approach has noticeable improvement in power especially for BE and RE-HE models and in computational efficiency for MANTRA compared to the crude approach when we assume that the heterogeneity arises from the different genetic structure across diverse populations. Thus, the results suggest the two-stage approach may be an effective intermediate step in a multi-ethnic meta-analysis of GWAS that would improve power.

Note that MANTRA already takes into account the estimated similarity among studies with respect to genetic relatedness using a Bayesian partition model. In comparison, our two-stage approach showed no discernable loss in power but reduced the computational burden by reducing the total number of studies entering MANTRA analysis. Therefore, the two-stage clustering approach using the prior knowledge of genetic relatedness in terms of mean allele frequency improves power when the difference between studies is due to genetic dissimilarity, and enhances the computational efficiency by diminishing the computation burden for the Bayesian method MANTRA.

We acknowledge that there may be limitations in our two-stage approach. Because we use the genetic distance as prior information to cluster, the cluster classification is pre-fixed and is not updated using other information such as allelic effect estimates as in MANTRA. Further, the fixed threshold applied to the genetic distance in the dendrogram for clustering is rather subjective and arbitrary, and may be prone to mis-clustering of genetically heterogeneous studies. However, as shown in Supplemental Figure 1, the two-stage approach is robust to mis-clustering by taking a sub-optimal dissimilarity value for the threshold. In practice, clustering using the prior knowledge of ancestry of study samples is recommended. Alternatively, a data-driven approach can be used to find an optimal threshold for clustering. Assessing the power in the region-wise analysis using the empirical threshold computed by minimum p-value or maximum BF in a region would be more precise if a number of replicates were evaluated. Lastly, when the heterogeneity arises from environmental factors rather than genetic dissimilarity, our two-stage approach tends to lose power due to incorrect clustering. In such a case, further refinement of current approaches need to be developed, such as introducing another layer of clustering or treating those environmental factors as random effects, to properly account for the multiple sources of the heterogeneity and to retain good power.

In conclusion, with the growing interest and availability of GWAS results from diverse populations, the use of appropriate strategies and analytic tools in multi-ethnic meta-analysis will be crucial. In such meta-analyses, our two-stage approach accounts for potential heterogeneity due to genetic dissimilarity and therefore boosts power to detect genetic signals. In addition, our simulation study shows that the conventional FE and RE models may not be suitable for the trans-ethnic meta-analysis in GWAS because the assumption of the FE model may be violated and that of the RE model may be too conservative. In that case, the three recently developed methods have great advantages over the conventional methods. They are robust and more powerful especially when the studies in the meta-analysis are potentially heterogeneous. However, inappropriate and incorrect clustering of studies could result in power loss. Therefore the use of the three robust recent meta-analytic methods in the appropriate two-stage clustering strategy may enhance the ability to uncover and understand genetic signals contributing to human complex disease.