1. Introduction
Electroencephalogram (EEG) and electromyogram (EMG) combination recordings are often used to study sleep and circadian rhythms in both humans and animals. Using such EEG/EMG recordings, researchers can determine what sleep/wake state the animal is in at each time point during the recording period. This allows researchers to quantify an animal's sleep architecture, i.e. the timing and duration of different sleep stages, as well as to study the brain's electrophysiological activity during sleep. The recordings obtained this way are usually divided into short time segments, called epochs, which are manually scored to label what sleep/wake stage the animal is in.
However, sleep scoring is a very time-consuming, subjective, and monotonous process. Because of the high labor cost of scoring, sleep researchers have rarely done long-term EEG recordings. Circadian biologists, in contrast, commonly record activity continuously for a month or longer, and this disparity may be one reason why sleep science and circadian biology developed so separately in the past several decades (Dement, 2011). In addition to recording length, scoring limitations also restrict sample size. Modern genomics (and other “-omics”) studies typically require sample sizes of several hundred (e.g. Winrow et al., 2009), which quickly become burdensome to score.
Methods to automate sleep-scoring have been proposed to solve this problem. Early techniques were mainly based on logic-based threshold rules, with amplitude and frequency-derived features as inputs (Van Gelder et al., 1991; Itil et al., 1969; Neuhaus and Borbely, 1978). More recently, machine-learning classification algorithms have been applied to the task (Sunagawa et al., 2013 contains a good summary). These classifier algorithms are usually supervised learners, meaning that an algorithm is first “trained” on manually-scored example epochs, from which parameters for classification are derived; the rest of the recording is then scored based on these parameters. The supervised learning process works well for sleep scoring because it allows the algorithms enough flexibility to adapt to the unique characteristics of each animal. Supervised classifier algorithms such as support vector machine (Crisler et al., 2008), linear discriminant analysis, decision tree (Brankačk et al., 2010), neural nets (Robert et al., 1997), and Naive Bayes (Rytkönen et al., 2011) have previously been applied to sleep-scoring in rodents. Machine learning classification has also been used for other types of EEG analyses, such as for brain-computer interfaces (Müller et al., 2008) and epilepsy diagnosis (Subasi, 2007).
A very effective way to improve classification accuracy is to employ a multiple classifier system (MCS). Specifically, in the classifier fusion method, a collection of algorithms each classify the set of inputs individually, and then the classifications outputted from the individual algorithms are combined to form a composite best-guess. An MCS may be composed of many repeats of a single type of base algorithm, in which case it is referred as an ensemble classifier, or it may be composed of several different types of base algorithms. The MCS's success can be intuitively explained by the fact that each classifier algorithm is subject to different biases and weaknesses, i.e. they are diverse, and combining diverse classifiers prevents a single classifier's misclassifications from strongly affecting the results. Multiple classifier systems have been applied with success to EEG classification in a non-sleep context (Sun et al., 2007), and also to many machine-learning tasks such as handwriting recognition (Günter and Bunke, 2005), face recognition (Czyz et al., 2004), and medical diagnosis (Sboner et al., 2003).
Here, we demonstrate a multiple classifier algorithm for sleep scoring. We show that using the MCS improves accuracy over using a single classifier, and the MCS's accuracy was on par with a second human rescoring the same recording. We also show that scoring with a modest number of rejections greatly improves accuracy at the cost of only a small amount of additional human effort.
2. Methods
2.1 Animals and Recordings
We used EEG/EMG recordings from mice to test the autoscoring method (n=16). The mice were a mixture of A/J (n=4), C57BL/6 (n=2), (A/J × C57BL/6) F1 (n=7) and (A/J × C57BL/6) F2 (n=3). All recordings were 24 hours long and were recorded under normal, baseline conditions on a 12L:12D light-dark cycle.
To collect the recordings, we implanted mice with EEG and EMG electrodes for sleep recording while under ketamine and xylazine anesthesia. The EEG electrodes were four stainless steel screws inserted through the skull over the cerebral cortex, and the EMG electrodes were two iridium/silver alloy wires inserted bilaterally into the nuchal muscles. The electrodes were part of a pre-fabricated head mount (Part #8201, Pinnacle Technologies, Lawrence, KS), which was fixed in place with glue and dental acrylic. Two channels of EEG were collected: one from prefrontal cortex (EEG2) and the other from more posterior cortex near the hippocampus (EEG1). We used PAL 8200 Acquisition software (Pinnacle Technologies, Lawrence, KS) to obtain recordings, which were then exported to European Data Format (EDF) files. Signals were recorded at 1000 Hz, but to speed up computation time, only every fifth sample in the signal was used, which effectively reduced sampling rate to 200 Hz. Recordings were divided into 10-second epochs for scoring, and each 24 h recording consisted of 8640 epochs. We used Pinnacle PAL 8200 Acquisition and Sleep Score software for data collection and manual scoring. Protocols were approved by the Northwestern University Animal Care and Use Committee.
2.2 Human Scoring
Each recording was scored by two human experts: the primary scorer was used to train the classifiers and compare computer-human agreement, while the secondary scorer was used to compare human-human agreement. Using PAL 8200 Sleep Score software (Pinnacle Technologies, Lawrence, KS), the scorer viewed each 10-second epoch and labeled it as either Wake, rapid eye movement sleep (REM), or non-rapid eye movement sleep (NREM), or excluded it from analysis if the signal contained a major artifact. Each recording was scored to completion this way. EEG2 was considered primary while EEG1 was considered supplementary when making scoring decisions. Generally speaking, Wake epochs have low-amplitude, high-frequency EEG and high-amplitude EMG; NREM epochs have high-amplitude, low-frequency EEG and low-amplitude EMG; REM epochs have low-amplitude, high-frequency EEG and low-amplitude EMG. In addition, some characteristic EEG waveshape differences between the different sleep-wake stages also aid in scoring. Some epochs with artifacts were excluded from the analysis. These mostly consisted of “spikes” in the EEG signal, which must last 2 s or more for that epoch to be excluded. An average of 38 epochs were excluded per recording; the most had 499 artifacts, and 7 recordings had no artifacts at all. An experienced scorer requires about 4 h of time to score 24 h of recording.
2.3 Computer Scoring
2.3.1 Feature selection
For feature selection, we used a procedure similar to Rytkönen et al., 2011. Only EEG2 was used; using both channels of EEG reduced the accuracy of classification, perhaps because of a surplus of non-useful features. The EEG power spectral density of each epoch was obtained by short-time Fourier transform, using a Hamming window of length equal to the length of the epoch; this was done using the “spectrogram” function in MATLAB. The power spectral density was binned into 20 logarithmically-distributed power bands between 0.5 Hz and 100 Hz, such that the lower, more biologically-relevant frequencies had more fine-grain bins. EMG power between 4 and 40 Hz was also used as a feature. The 20 EEG and 1 EMG features formed a feature vector of 21 elements in total.
2.3.2 Training epochs
We wanted our training epoch selection process to mimic how one would score training epochs in actual use, so training epochs were selected in continuous blocks rather than at random. In addition, a challenging aspect of sleep EEG classification is that REM comprises only a small minority of epochs, about 3%, so we wanted to ensure that enough REM epochs were selected as training. To select our training set, a random REM epoch was selected, and the preceding 90 epochs (15 minutes) and following 90 epochs were selected as training scores. This process was repeated until a total of 720 epochs (2 h) of training were selected. The remaining 7920 epochs (22 h) of the recording was designated as the test set. If at least 40 epochs of each category were not selected as training, then the whole process was repeated and a new set of training scores were selected.
2.3.3 Single classifiers
Based on the features in the training epochs, each of the six single classifier algorithms individually classified the entire recording's epochs. The six single classifiers used were naïve Bayes, linear discriminant analysis, support-vector machine, k-nearest neighbors, decision tree, and a neural network.
k-nearest neighbors (kNN), with k=1 and simple Euclidian distance, labels an epoch the same as the training epoch which is nearest to it in feature space. We used the MATLAB function fitcknn.
Linear discriminant analysis (LDA) searches for a linear combination of features which statistically best distinguishes objects in different classes from each other. We used the MATLAB function fitcdiscr.
Support vector machine (SVM) is a binary classifier. For all epochs in 21-dimensional feature space, SVM searches for a 20-dimensional hyperplane that best divides epochs from two different classes. SVM is a binary classifier, and thus we broke the problem down into three binary comparisons: Wake vs. not-Wake, NREM vs. not-NREM, and REM vs. not-REM. We used the MATLAB function fitcsvm with a soft boundary.
Naive Bayes (NB) creates a probability distribution of each feature from the training epochs. When classifying a new epoch, that epoch's feature values are compared with the probability distribution, and the likelihood of its membership in each class can be calculated. The algorithm is “naive” in that it assumes independence of features, i.e. that features do not covary with each other. We used the MATLAB function fitcnb.
Decision tree (DT) creates a series of binary decisions on the features which best distinguishes classes. We used the MATLAB function classification fitctree. Several specific decision tree algorithms exist; we believe MATLAB uses CART (Breiman et al., 1984) and/or PC (Coppersmith et al., 1999).
A neural network (NN) consists of interconnected “neurons” with weighted connections. The value of each neuron is a linear combination of the values of neurons which are connected towards it. We used a feedforward pattern-recognition network, in which an input feature layer of neurons are connected towards a hidden layer consisting of ten neurons, which are then connected towards three classification output neurons. The overall two-hour set of training epochs was subdivided into a one-hour NN-training set and one-hour NN-validation set. The NN is trained on the NN-training set and its accuracy compared to the NN-validation set. Connection weights were updated using the scaled conjugate gradient method, and the cycle of training, validating and updating was iterated until the validation error was minimized. We used the MATLAB function patternnet and the associated functions in the Neural Network Toolbox.
2.3.4 Ensemble classifiers
In an ensemble classifier, many instances of a single type of algorithm each classify the target epoch based on slightly different criteria, which generates diversity; the collection of classifiers then votes on the final classification. We used two common ensemble methods for generating diversity: bootstrap aggregating (“bagging”) (Breiman, 1996) and random subspace (Ho, 1998). In the bagging method, each of an ensemble of 100 base classifiers is trained on a different subset of training epochs. The subset of training epochs are chosen by selecting 720 epochs with replacement from the pool of 720 training epochs; selection with replacement causes an average of 1/e = 37% of total training epochs to be excluded from each subset. The consensus score for the ensemble is determined by majority vote. In the random subspace method, diversity is generated by using a random subset of 10 of the 20 EEG features; EMG was always included, for a total of 11 features. As with bagging, an ensemble of 100 base classifiers performs a majority vote to determine the final score.
Bagging only produced improvements when using DT (Fig. 3A) and random subspace only produced improvements with DT and kNN (Fig. 3B). This is not surprising, since DT and kNN are the most sensitive to local variations. NB and LDA, on the other hand, rely on statistical distributions, and SVM sets the decision boundary based on the positions of all known data points, so their decision structures do not change much when given different training inputs. For the multiple classifier system, DT was replaced with its ensembles DT-Bag and DT-RS, and kNN was replaced with its ensemble kNN-RS (Fig.1).
Figure 3.
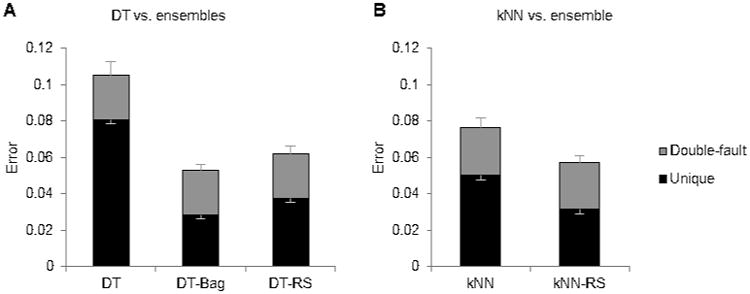
Ensemble classifiers. A) Base classifier DT compared with ensemble classifiers DT-Bag and DT-RS. B) Base classifier kNN compared with ensemble classifier kNN-RS. The portion in grey designates errors which the second human also made (“double-fault” errors), and the portion in black designates errors which the algorithm made but the second human did not (“unique” errors). The lower set of error bars display the SE of unique errors, while the higher set of error bars display the SE of all errors.
Figure 1.
Overall organization of the multiple classifier system. 21 features are extracted from the EEG/EMG signal in each epoch, which are fed to the six base classifiers. Three ensemble classifiers are created from DT and kNN using the random subspace and bagging methods. Each classifier classifies the epoch as either Wake, NREM, or REM, and outputs confidence scores for each class indicating how strongly it believes the epoch to be from that class. The confidence scores from the classifiers are averaged to form a consensus confidence score. The class with the greatest consensus confidence score is chosen as the final classification, unless the confidence score is below the rejection threshold, in which case it is left unscored.
2.3.5. Multiple classifier consensus
A consensus classification for the MCS is decided based on results from LDA, SVM, NB, NN, DT-Bag, DT-RS, and kNN-RS. (Although ensemble classifiers are a type of multiple classifier system, we will refer to the overall consensus algorithm as the MCS). In addition to outputting a classification label for each epoch, each classifier also outputs a confidence score for each class ranging from 0 to 1 (Fig.1). For LDA, SVM, NB, and NN, the confidence scores are posterior probabilities. For the ensemble classifiers kNN-RS, DT-RS, and DT-Bag, the confidence score is the proportion of component classifiers which labeled the target epoch as a certain class. The consensus confidence score of MCS for a particular class was the average of the confidence scores for that class from the 7 component classifiers. The class which had the highest confidence score was chosen as the label for that epoch.
2.3.6 Scoring with rejections
Autoscoring with rejections is effective at reducing classification errors. The epochs which are most difficult to score are left unclassified for a human to manually score later. Rejections were based on a cutoff of the MCS confidence score for the winning class. For example, if we wished to reject 2% of epochs, then the 2% of epochs which had the lowest confidence scores were rejected. (In actual use, one may prefer to use a constant cutoff value rather than rejecting a set proportion of epochs.) From beginning to end, the algorithm requires roughly four minutes to score a 24 h recording on a standard personal computer.
2.4 Transitional epochs
REM epochs are more likely to be misclassified. Since REM typically occurs in very short bouts (∼1 min), and the transitions between sleep/wake states are often ambiguous to categorize even for a human, we suspected that the higher error rate for REM sleep was simply due to there being a greater proportion of transitional REM epochs relative to the total number of REM epochs. To examine this, we counted the number of “boundary” epochs, which are located at the front or end of bouts, where a bout is a sequence of epochs of the same sleep/wake state. Therefore, each bout of two epochs or longer had two boundary epochs, and each bout of one epoch consists of a single boundary epoch. Not all boundary epochs are ambiguous, and not all ambiguous epochs are located at boundaries, but this metric should be approximately proportional to the number of ambiguous transitional epochs.
2.5 Statistics
When evaluating the classifiers, we compared epochs in the 22-hour test set. An autoscored epoch is considered to be in error if the algorithm's classification for the epoch disagreed with human's classification. Error rate is equal to the number of incorrect epochs divided by the total number of epochs. We used paired t-tests on error rate values to compare methods. Sensitivity for class A is equal to the number of epochs labeled A by both human and computer divided by the number of epochs labeled A by the human. Specificity for class A is equal to the number of epochs labeled A by both human and computer divided by the number of epochs labeled A by the computer. Sensitivity error is equal to 1 minus sensitivity.
3. Results
3.1 No rejections
A second human scorer disagreed with the original scorer at an average error rate of 0.046 (Fig.2). Among the single classifiers, SVM is the most accurate, with an error rate of 0.054, though it was not significantly different from NN and LDA, the next most accurate single classifiers (p>0.05). The ensemble classifiers DT-Bag and DT-RS had much fewer errors than DT (p<0.001) (Fig.3A), reducing errors by 50% and 58% respectively compared to the base classifier. KNN-RS was also more accurate than KNN (p<0.001) (Fig.3B), reducing errors by 25%. The multiple classifier system (MCS) had an error rate of 0.049, a reduction of 9.4% from SVM (p<0.001) (Fig.4). While SVM had significantly more errors than a second human scorer (p=0.007), MCS did not significantly differ from a second human scorer (p=0.19). A confusion matrix of MCS is presented in Table 1.
Figure 2.
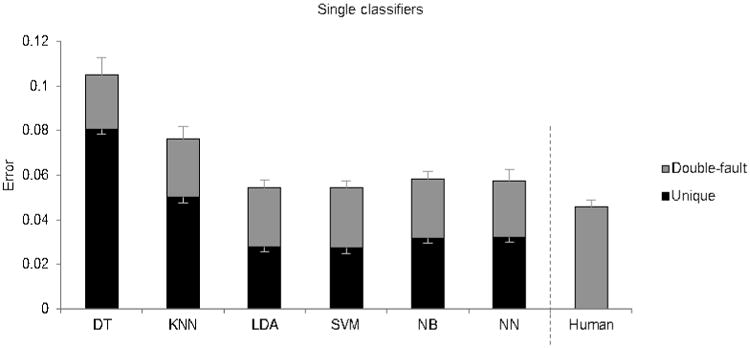
Mean error rates of the base classifiers, as well as a second human scorer. The height of the entire bar indicates the error rate of the classifier. The portion in grey designates errors which the second human also made (“double-fault” errors), and the portion in black designates errors which the algorithm made but the second human did not (“unique” errors). The lower set of error bars display the SE of unique errors, while the higher set of error bars display the SE of all errors.
Figure 4.
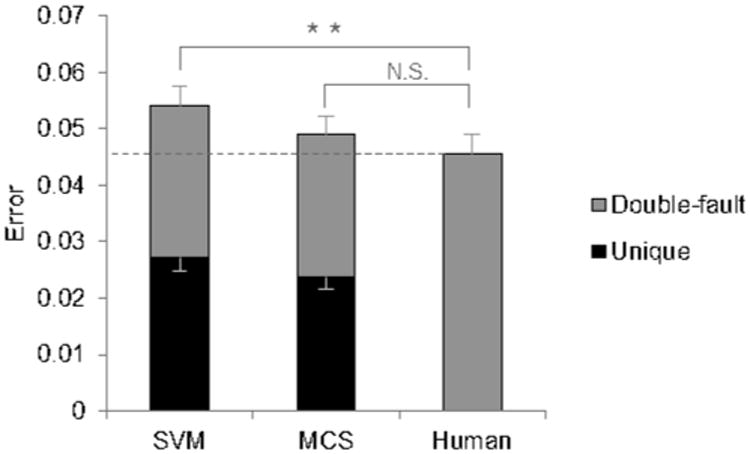
Error rate of MCS compared with SVM, the most accurate single classifier, and a second human scorer. SVM made significantly more errors than the second human scorer (p=0.007), but MCS did not. The portion in grey designates errors which the second human also made (“double-fault” errors), and the portion in black designates errors which the algorithm made but the second human did not (“unique” errors). The lower set of error bars display the SE of unique errors, while the higher set of error bars display the SE of all errors.
Table 1.
Confusion matrix comparing human scoring against MCS with no rejections. The numbers displayed in the main table are percentages of epochs in a recording. For example, on average 1.10% of epochs in a recording were labeled as NREM by the human but as Wake by MCS. Precision is presented below the main table, and sensitivity is presented to the right of the main table. Overall accuracy is displayed in the bottom-right cell.
| MCS – No rejections | ||||||
|---|---|---|---|---|---|---|
| Wake | NREM | REM | Rejections | Sensitivity | ||
| Human | Wake | 53.61 | 1.95 | 0.54 | 0 | 0.96 |
| NREM | 1.10 | 37.96 | 0.54 | 0 | 0.96 | |
| REM | 0.48 | 0.31 | 3.52 | 0 | 0.82 | |
|
| ||||||
| Precision | 0.97 | 0.94 | 0.77 | - | 0.95 | |
Epochs which both the algorithm and the second human scored incorrectly were called double-faults. Epochs which the algorithm scored incorrectly but the human scored correctly were called unique errors. Presumably, epochs which two human scorers disagree over are inherently more ambiguous, making double-fault errors more “excusable” than unique errors. More than half of the errors of MCS were double-faults (Fig.4). Consistently across all classifiers, about 0.025 of epochs consisted of double-faults (Fig. 2, 3, 4).
3.2 With rejections
There is a tradeoff between reducing the number of rejected epochs and improving the accuracy of accepted epochs, as can be seen by the rejection-error curve (Fig. 5A). To match the error rate of a second human scorer, MCS needed a rejection rate of only 0.007 (0.7%), while SVM needed to a rejection rate of 0.019 to reach the same accuracy. Fig. 5B takes a closer look at MCS and SVM at two rejection rates. At 0.02 rejection rate, the error rate of MCS was lower than a second human scorer (p<0.001). The difference between MCS and SVM is magnified after rejections, with MCS having 12% fewer errors than SVM. At a 0.10 rejection rate, MCS had 22% fewer errors than SVM, and only 31% of MCS's errors were unique errors, suggesting that most the epochs which MCS disagreed with were inherently more ambiguous. Table 2 presents a confusion matrix of MCS at 0.10 rejection rate.
Figure 5.
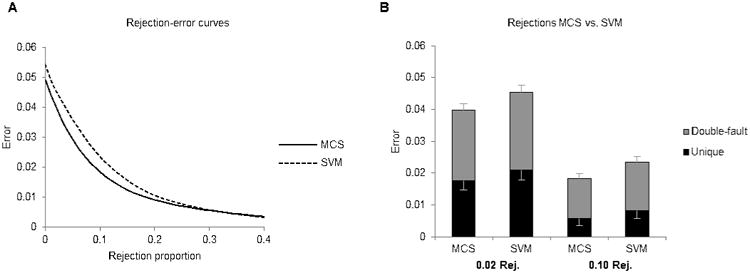
Rejections. A) Rejection-error curve displaying the trade-off between the proportion of epochs rejected and the error rate of the remaining epochs. B) Comparing MCS and SVM at two rejection rates, 0.02 and 0.10. The portion in grey designates errors which the second human also made (“double-fault” errors), and the portion in black designates errors which the algorithm made but the second human did not (“unique” errors). The lower set of error bars display the SE of unique errors, while the higher set of error bars display the SE of all errors.
Table 2.
Confusion matrix comparing human scoring against MCS at 0.10 rejection rate. The numbers displayed in the main table are percentages of epochs in a recording. For example, on average 3.81% of epochs in a recording were labeled as NREM by the human but rejected by MCS. Precision of non-rejected epochs is presented below the main table, and sensitivity is presented to the right of the main table. Overall accuracy of non-rejected epochs is displayed in the bottom-right cell.
| MCS – 0.10 rejection rate | ||||||
|---|---|---|---|---|---|---|
| Wake | NREM | REM | Rejections | Sensitivity | ||
| Human | Wake | 50.80 | 0.94 | 0.11 | 4.24 | 0.98 |
| NREM | 0.30 | 35.38 | 0.11 | 3.81 | 0.99 | |
| REM | 0.09 | 0.10 | 2.19 | 1.93 | 0.91 | |
|
| ||||||
| Precision | 0.99 | 0.97 | 0.91 | - | 0.98 | |
3.3 Boundary Epochs
Classifying REM has a higher error rate than classifying Wake or NREM. The proportion of REM epochs which had a sensitivity error was 0.19, which is higher than that of the other classes (Fig. 6A). Of those error epochs, 61% were also boundary epochs. Meanwhile, 79% of Wake error epochs and 66% of NREM error epochs were also boundary epochs. Fig. 6B shows that 0.34 of REM epochs are boundary epochs, which is a much higher proportion than Wake or NREM. This reflects the fact that REM typically occurs in very short bouts. Of those boundary REM epochs, 32% are errors. In total, these data suggest that the higher misclassification rate for REM is mostly, but not entirely, explained by a higher proportion of boundary epochs, which are more likely to be inherently ambiguous.
Figure 6.
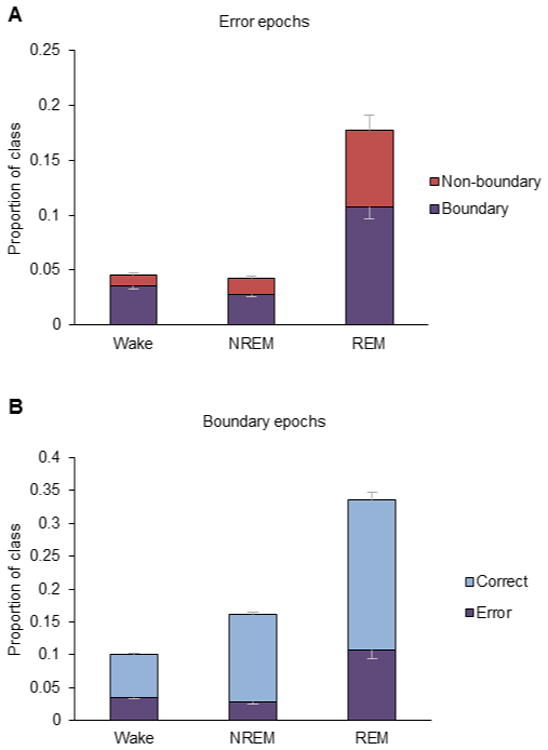
Transitional epochs and error rate. (A) The error rate is represented by the entire bar, and the fraction of those errors which were transitional epochs is represented by the purple bars. Only sensitivity errors are considered. (B) The percentage of epochs which are transitional is represented by the entire bar, and the fraction of those epochs which were errors is represented by the purple bars. Error bars are 1 SE.
4. Discussion
Using a multiple classifier system improved the accuracy of automatic sleep scoring. First, we compared the performance of six single classifiers to human scorers, and we found that SVM was the most accurate. Then we showed that accuracy of DT and kNN can be improved by using ensemble methods such as bagging and random subspace. Accuracy can be further improved by aggregating the predictions of several single and ensemble classifiers into a consensus. Errors can be reduced by rejecting epochs which are difficult to classify and leaving them for a human scorer to review. We also investigated the cause of the high REM error rate, and determined that it was largely due to the higher proportion of REM epochs which are located at the boundaries between different sleep/wake states.
Typically in our laboratory, recordings will be autoscored by this algorithm at a rejection threshold such that about 5% of epochs will be rejected. To improve accuracy, a tightened rejection stringency for REM is used so that more REM epochs are rejected. Training scores take precedence over autoscores when they disagree. We also use criteria to reject potential artifacts (e.g. if EEG power greater than 4× mean) and improbable patterns which are often due to misclassification (e.g. if Wake is followed by REM, or if REM is followed by NREM). Afterwards, a human scorer reviews the autoscored recording and fills in the unscored rejected epochs, which can be quickly located using the scoring software's “jump to next unscored” function. A second pass is made to review and correct REM epochs; because of this, it is preferable to have high REM sensitivity at the cost of low REM precision. In total, the process requires about twenty minutes to manually score 2 h of training epochs, four minutes for the algorithm to run, and one hour to fill in unscored epochs at a 5% rejection rate. This is compared to the approximately 4 h of manual scoring required for the same 24 h recording.
Some users may wish to make changes to the algorithm to suit their needs. Potential modifications include using alternate features, adding artifact detection criteria, or using additional information to fine-tune confidence scores. Some researchers prefer to identify additional sleep stages, such as quiet wake (e.g. Takahashi et al., 2008) or transitional states; this algorithm likely could be developed to classify additional sleep-wake stages, either by directly introducing a fourth class or by using the confidence scores to mark transitional states.
We tried several methods for combining classifiers into a consensus, including using hard classifications instead of confidence scores, weighting scores by estimated accuracies, weighting by diversity, model selection based on estimated accuracies, behavior-knowledge space (Huang and Suen, 1993), an evolutionary feature space-splitting algorithm (Jackowski and Wozniak, 2009), stacking (Wolpert, 1992) using a naive Bayes combiner, decision tree, or neural net, as well as various other configurations of different classifiers and hyper-parameters. Surprisingly, none of these classifier fusion methods was better than a simple average of confidence scores. Many of these other methods require a set of validation epochs in addition to a set of training epochs in order to estimate hyper-parameters of how to optimally combine classifiers, so given a large enough validation set, these other methods may surpass majority vote in accuracy. However, having a large set of training and validation epochs would require lots of pre-scoring by a human, and increasing the amount of human scoring decreases the practical usefulness of automatic scoring. For features, we also tried using ratios of frequency bins, zero crossings counts, peak-to-peak distances, and the classes of the previous and following epochs, but none of these improved accuracy.
Although we use 10 s epoch lengths, the method should work just as well with shorter or longer epoch lengths. Naive Bayes has been used with 4-5 s epochs (Rytkönen et al., 2011), SVM has been used with 20 s epochs (Crisler et al., 2008), and Brankačk et al. (2010) has shown that there is very little difference in accuracy between 4 s and 10 s epoch lengths when using LDA and DT. This method should work equally well with rats, since SVM (Crisler et al., 2008) and Naive Bayes (Rytkönen et al., 2011) have already been applied in rats successfully. Human EEG records are scored into more sleep stages than rodents and thus may pose a greater challenge; nevertheless, much research has been done in improving human EEG classification as well (Becq et al., 2005; Güneş et al., 2010), though accuracies tend to be lower. A much larger body of research dealing with human EEG classification exists in the field of brain-machine interfaces (Lebedev and Nicolelis, 2006), where multiple classifiers are an active area of research as well (Ahangi et al., 2013; Sun et al., 2007). Therefore, improvements to human sleep scoring could likely be made by applying multiple classifier systems and other brain-machine interface techniques to the task.
In conclusion, multiple classifier systems are an effective and efficient way to improve accuracy of automated sleep scoring, and semi-automated scoring can increase scoring speed dramatically while maintaining high accuracy. Development of effective and accurate automatic scoring would make it easier to perform long-term recordings on large sample sizes, greatly lowering the barrier to investigation of sleep on the scale of genomes, transcriptomes, and proteomes.
The MATLAB code for this is available upon request by emailing v-gao@u.northwestern.edu.
Highlights.
Six machine-learning classifiers were combined into a multiple classifier system.
Using multiple classifiers improves accuracy of automatic sleep scoring.
At 1% rejection rate, the algorithm matches the accuracy of a human scorer.
Acknowledgments
This work was supported by The Defense Advanced Research Projects Agency (government contract/grant number W911NF1010066). The views, opinions, and/or findings contained in this article are those of the author and should not be interpreted as representing the official views or policies, either expressed or implied, of the Defense Advanced Research Projects Agency or the Department of Defense. Vance Gao is also grateful to NIH T32 HL007909 for support.
Footnotes
Ethical Standards: I have read and have abided by the statement of ethical standards for manuscripts submitted to the Journal of Neuroscience Methods.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahangi A, Karamnejad M, Mohammadi N, Ebrahimpour R, Bagheri N. Multiple classifier system for EEG signal classification with application to brain–computer interfaces. Neural Comput Appl. 2013;23:1319–1327. [Google Scholar]
- Becq G, Charbonnier S, Chapotot F, Buguet A, Bourdon L, Baconnier P. Comparison Between Five Classifiers for Automatic Scoring of Human Sleep Recordings. In: Halgamuge SK, Wang L, editors. Classification and Clustering for Knowledge Discovery. 2005. [Google Scholar]
- Brankačk J, Kukushka VI, Vyssotski AL, Draguhn A. EEG gamma frequency and sleep-wake scoring in mice: Comparing two types of supervised classifiers. Brain Res. 2010;1322:59–71. doi: 10.1016/j.brainres.2010.01.069. [DOI] [PubMed] [Google Scholar]
- Breiman L. Bagging Predictors. Mach Learn. 1996;24:123–140. [Google Scholar]
- Breiman L, Friedman J, Stone CJ, Olshen RA. Classification and regression trees. Wadsworth International Group; 1984. [Google Scholar]
- Coppersmith D, Hong S, Hosking JM. Partitioning Nominal Attributes in Decision Trees. Data Min Knowl Discov. 1999;3:197–217. [Google Scholar]
- Crisler S, Morrissey MJ, Anch aM, Barnett DW. Sleep stage scoring in the rat using a support vector machine. J Neurosci Methods. 2008;168:524–34. doi: 10.1016/j.jneumeth.2007.10.027. [DOI] [PubMed] [Google Scholar]
- Czyz J, Kittler J, Vandendorpe L. Multiple classifier combination for face-based identity verification. Pattern Recognit. 2004;37:1459–1469. [Google Scholar]
- Dement Principles and Practice of Sleep Medicine. Principles and Practice of Sleep Medicine. Elsevier; 2011. [Google Scholar]
- Van Gelder RN, Edgar DM, Dement WC. Real-time automated sleep scoring: validation of a microcomputer-based system for mice. Sleep. 1991;14:48–55. doi: 10.1093/sleep/14.1.48. [DOI] [PubMed] [Google Scholar]
- Güneş S, Polat K, Yosunkaya Ş. Efficient sleep stage recognition system based on EEG signal using k-means clustering based feature weighting. Expert Syst Appl. 2010;37:7922–7928. [Google Scholar]
- Günter S, Bunke H. Off-line cursive handwriting recognition using multiple classifier systems—on the influence of vocabulary, ensemble, and training set size. Opt Lasers Eng. 2005;43:437–454. [Google Scholar]
- Ho TK. The random subspace method for constructing decision forests. IEEE Trans Pattern Anal Mach Intell. 1998;20:832–844. [Google Scholar]
- Huang Y, Suen C. The behavior-knowledge space method for combination of multiple classifiers. Proc IEEE Conf Comput Vis Pattern Recognit. 1993:347–352. [Google Scholar]
- Itil T, Shapiro D, Fink M, Kassebaum D. Digital computer classifications of EEG sleep stages. Electroencephalogr Clin Neurophysiol. 1969;27:76–83. doi: 10.1016/0013-4694(69)90112-6. [DOI] [PubMed] [Google Scholar]
- Jackowski K, Wozniak M. Algorithm of designing compound recognition system on the basis of combining classifiers with simultaneous splitting feature space into competence areas. Pattern Anal Appl. 2009;12:415–425. [Google Scholar]
- Lebedev MA, Nicolelis MAL. Brain-machine interfaces: past, present and future. Trends Neurosci. 2006;29:536–46. doi: 10.1016/j.tins.2006.07.004. [DOI] [PubMed] [Google Scholar]
- Müller KR, Tangermann M, Dornhege G, Krauledat M, Curio G, Blankertz B. Machine learning for realtime single-trial EEG-analysis: from brain-computer interfacing to mental state monitoring. J Neurosci Methods. 2008;167:82–90. doi: 10.1016/j.jneumeth.2007.09.022. [DOI] [PubMed] [Google Scholar]
- Neuhaus H, Borbely A. Sleep telemetry in the rat. II. Automatic identification and recording of vigilance states. Electroencephalogr Clin Neurophysiol. 1978;44:115–119. doi: 10.1016/0013-4694(78)90112-8. [DOI] [PubMed] [Google Scholar]
- Robert C, Guilpin C, Limoge A. Comparison between Conventional and Neural Network Classifiers for Rat Sleep-Wake Stage Discrimination. Neuropsychobiology. 1997;35:221–225. doi: 10.1159/000119348. [DOI] [PubMed] [Google Scholar]
- Rytkönen KM, Zitting J, Porkka-Heiskanen T. Automated sleep scoring in rats and mice using the naive Bayes classifier. J Neurosci Methods. 2011;202:60–4. doi: 10.1016/j.jneumeth.2011.08.023. [DOI] [PubMed] [Google Scholar]
- Sboner A, Eccher C, Blanzieri E, Bauer P, Cristofolini M, Zumiani G, Forti S. A multiple classifier system for early melanoma diagnosis. Artif Intell Med. 2003;27:29–44. doi: 10.1016/s0933-3657(02)00087-8. [DOI] [PubMed] [Google Scholar]
- Subasi A. EEG signal classification using wavelet feature extraction and a mixture of expert model. Expert Syst Appl. 2007;32:1084–1093. [Google Scholar]
- Sun S, Zhang C, Zhang D. An experimental evaluation of ensemble methods for EEG signal classification. Pattern Recognit Lett. 2007;28:2157–2163. [Google Scholar]
- Sunagawa Ga, Séi H, Shimba S, Urade Y, Ueda HR. FASTER: an unsupervised fully automated sleep staging method for mice. Genes to Cells. 2013;18:502–518. doi: 10.1111/gtc.12053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K, Lin JS, Sakai K. Neuronal activity of orexin and non-orexin waking-active neurons during wake-sleep states in the mouse. Neuroscience. 2008;153:860–70. doi: 10.1016/j.neuroscience.2008.02.058. [DOI] [PubMed] [Google Scholar]
- Winrow CJ, Williams DL, Kasarskis A, Millstein J, Laposky AD, Yang HS, Mrazek K, Zhou L, Owens JR, Radzicki D, Preuss F, Schadt EE, Shimomura K, Vitaterna MH, Zhang C, Koblan KS, Renger JJ, Turek FW. Uncovering the genetic landscape for multiple sleep-wake traits. PLoS One. 2009;4:e5161. doi: 10.1371/journal.pone.0005161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert DH. Stacked generalization. Neural Networks. 1992;5:241–259. [Google Scholar]



