Potential Role of the Glycolytic Oscillator in Acute Hypoxia in Tumors

Abstract

Tumor acute hypoxia has a dynamic component that is also, at least partially, coherent. Using blood oxygen level dependent (BOLD) magnetic resonance imaging (MRI), we observed coherent oscillations in hemoglobin saturation dynamics in cell line xenograft models of head and neck squamous cell carcinoma. We posit a well-established biochemical nonlinear oscillatory mechanism called the glycolytic oscillator as a potential cause of the coherent oscillations in tumors. These data suggest that metabolic changes within individual tumor cells may affect the local tumor microenvironment including oxygen availability and therefore radiosensitivity. These individual cells can synchronize the oscillations in patches of similar intermediate glucose levels. These alterations have potentially important implications for radiation therapy and are a potential target for optimizing the cancer response to radiation.

Introduction

Solid tumors are typically poorly vascularized, with highly irregular, tortuous and shunt microvessels that sometimes lack endothelial lining and basement membrane (Brown and Giaccia, 1998). This would result to sluggish and highly irregular blood flow and hence red cell flux, leading to different kinds of nutrients and oxygen (hypoxia) depletion in different regions (Vaupel, 2004). Hypoxia can be chronic or acute (Dewhirst et al., 1996). Chronic hypoxia, also often called diffusion limited hypoxia is a permanent form of hypoxia that results from a wide distance between cells and blood vessels, making it hard for any oxygen to be still available for distant cells (Harris, 2002). The other form of hypoxia, acute hypoxia, also sometimes referred to as transient, intermittent or cycling hypoxia because of its spatial and temporal variation, is not well understood. Temporal variations have been observed to be on the order of seconds, minutes, hours and even days (Dewhirst, 2009, Dewhirst et al., 1996, Cairns et al., 2001, Baudelet and Gallez, 2003). Temporal perturbations in red blood cell flux have been found to correlate with perivascular oxygen partial pressures changes (Kimura et al., 1996, Dewhirst et al., 1996). One may also attribute the diffusion of oxygen to cells to be an important cause of acute hypoxia with a time scale greater than a minute. This is however not very likely as oxygen takes far less than a minute to equilibrate across tissue as it diffuses (Vaupel et al., 1991), and we see periodic dynamics that exceed such time scales. We think that an alternative or additional mechanism for the cause of the type of cyclic hypoxia that we observe is metabolic, caused by the glycolytic oscillator. Some of the periods observed in cyclic hypoxia are very similar to those observed in the glycolytic oscillator in a variety of other cells (Hess and Boiteux, 1971).

To date, there have not been any links described between acute hypoxia and metabolic causes in the literature. Cancer cells have been known to undergo glycolysis even in the presence of oxygen, a condition known as the Warburg Effect (López-Lázaro, 2008, Dang, 2012, Warburg, 1956). The amount of glucose present has a direct correlation with the amount of oxygen present if tissue is too far from a microvessel (Vaupel, 2004). The glycolytic oscillator was first described nearly 50 years ago by Sel'Kov and colleagues (Sel'Kov, 1968). Under certain ranges of substrate depletion, the entire metabolic chain of glycolysis spontaneously oscillates over time (Hess, 1979). This response has been best studied in yeast cells and extracts of yeast. Studies of the glycolytic oscillator with continuous (von Klitzing and Betz, 1970) and random (Boiteux et al., 1975) flow of substrate have shown continuous sustained oscillations proving that it is a nonlinear system, with the period being a function of the average input substrate flow rate. The beta cells of the pancreas use this oscillatory mechanism for the pulsatile release of insulin in the blood stream in order to maintain homeostatic blood glucose levels (Ristow et al., 1999).

A better understanding of the glycolytic oscillator's role in cyclic hypoxia could open doors for novel therapeutic agents, and could guide and personalize treatment. It could also help in prognosis as intermittent hypoxia promotes metastasis through promotion of epithelial to mesenchymal transition (Dewhirst et al., 2008). Many tumors must adapt to relatively low levels of oxygen (McKeown, 2014, Brown, 2007), a state that can increase resistance to radiotherapy (Gray et al., 1953, Hodgkiss et al., 1987). In fact, cells at intermediate oxygen states are of the most concern as they are the most important to therapy resistance dynamics (Wouters and Brown, 1997). It is also these intermediate states of oxygen that would coincide with intermediate states of glucose availability where the glycolytic oscillator is expected to occur locally.

In this work, we used the relative intensities of BOLD-MRI signals to monitor changes in tumor blood oxygen on the hind flanks of anesthetized mice over a period of one hour. Our approach to data acquisition and analysis is similar to Baudelet and Gallez (2003) whose technique we closely followed.

Material and Methods

Mice

Five NOD-SCID gamma (NSG, NOD.Cg-Prkdc^scid Il2rg^tm1Wjl/SzJ) mice (Jackson Laboratories) were inoculated onto bilateral hind flanks with 0.1ml of suspension (1:1 tumor:matrigel) containing the UM-SCC-22B cell line xenografts (Brenner et al., 2010, Kimple et al., 2013). All mice were kept in the Association for Assessment and Accreditation of Laboratory Animal Care-approved Wisconsin Institute for Medical Research (WIMR) Animal Care Facility. Food and water were provided ad libitum. Animals were housed in specific pathogen free rooms, in autoclaved, aseptic, microisolator cages with a maximum of four animals per cage. All studies involving the mice were carried out under an approved animal use protocol. Mice were monitored twice weekly until palpable tumors developed.

Data Acquisition

Mice were placed in an anesthesia induction chamber with an oxygen flow rate of 1 L/min and anesthetized with 3% isoflurane. Each anesthetized mouse was then transferred to a tray fitted to the radiofrequency (RF) imaging coil, and immobilized with adhesive tape. Anesthesia was maintained via a nose cone through the continuous delivery of 1-2% isoflurane at an oxygen flow rate of 1 L/min. A respiratory pad was placed on the tray below the mouse to monitor the respiratory rate throughout imaging. The mouse's internal temperature was monitored with a fiber optic probe inserted into the rectum and the mouse maintained at a target temperature of 37 °C by delivery of warm air. The mouse secured within the RF coil was then positioned within the 20 cm diameter bore of a 4.7 T small animal scanner (Agilent, Palo Alto, CA, USA) for imaging.

Axial, T₂-weighted, fast-spin-echo (FSE) images (TR/TE_eff = 3500/66 ms, 90° flip angle, 0.25 × 0.25 × 2 mm³ voxels) were first acquired for anatomical reference and localization of the tumors. A multi-slice, multi-gradient-echo sequence (TR/TE₁ = 350/1.4 ms with an echo spacing of 1.5 ms, 30° flip angle, 0.5 × 0.5 × 2 mm³ voxels, 32 echoes, 2 axial slices) was then acquired to obtain BOLD data. This sequence was acquired every 70 s for 1 hour (except for Mouse 1, where data was only acquired for 42 minutes) to generate a dynamic data set. After completion of imaging studies, mice were euthanized according to standard protocol.

Data Analysis

Data were analyzed by closely following the approach of Baudelet and Gallez (2003). Unlike Baudelet and Gallez (2003) where T₂*-weighted images were analyzed, R2* maps were generated from the first 16 echoes for a voxel by voxel analysis. To generate the R2* maps, BOLD images from the shortest TE were first normalized and a threshold was then defined to segment the images into two regions: background and mouse body. All voxels with signal magnitude below 5 times the standard deviation of the background noise were then excluded from the analysis, across all 16 echo times. Voxels with signal greater than this noise threshold for more than 2 echo times were fit to a linearized signal model of R2* decay using a linear regression function in MATLAB (2012b, MathWorks, Inc., Natick, MA, USA) to determine their R2* values.

An operator-selected region of interest (ROI) was separated into voxels with fluctuating time series BOLD MRI signal and non-fluctuating signals with a statistical test assuming white noise. We started by applying a baseline subtraction correction through a linear regression process to eliminate linear drift of signal over time. A windowed autocovariance function was computed for each time series using a triangular window. The power spectrum density (PSD) function for each autocovariance function was calculated. After using a rectangular moving average window to smooth the PSD, each PSD coefficient at each frequency was tested for significance using a chi-square (χ²) test at a 99.9% significance level. A PSD coefficient was considered significant if it was greater than the product of the variance of the corrected time series and χ² value divided by the number of degrees of freedom associated (d.f. = 6) with the smoothing window. A voxel was considered oscillating if its PSD had at least 3 coefficients that were statistically significant. Otherwise, the voxel was considered non-fluctuating. Note that we are not attempting to set the robust absolute value for the blood oxygen level, but instead, we focus on the dynamics.

Using the Welch's estimator and a Hamming window in the computer software MATLAB, the power spectrum of the time series function of each fluctuating voxel was computed and all power spectra averaged and plotted against 1/f noise (Figure 2). The same math was done to the time series functions of the non-fluctuating voxels and plotted on the same graphs for comparison. The autocorrelation function of each function was also computed and plotted. The significance of the autocorrelation function was tested for randomness using a Ljung-Box test (Ljung and Box, 1978). In the test, Q was computed for each function and compared to χ² value at a 95% significance level.

$$Q=n(n+2){\sum }_{l=1}^m{(n-l)}^{-1}{r}_l^2.$$ (1)

where n is the number of time point, l is the lag time, m is the number of lag times tested, and $r_l^2$ is the sample's autocorrelation at lag time l. At significance level α, the rejection of the hypothesis for randomness occurs when $Q>{\chi }_{(1-\alpha ,m)}^2$. The quantity $Q>{\chi }_{(1-\alpha ,m)}^2$ for all voxels that were considered fluctuating, and $Q\le {\chi }_{(1-\alpha ,m)}^2$ for all non-fluctuating functions are listed below (Table 1).

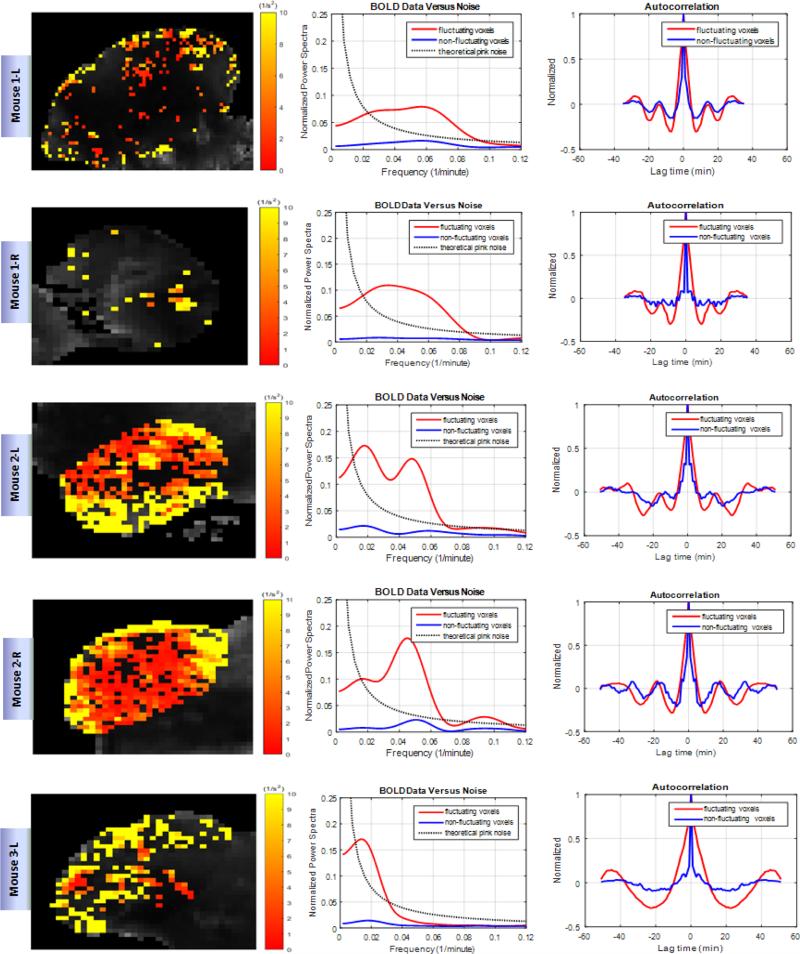
Figure 2. Fluctuation in oxygenation in HNC xenografts.

Shown are representative tumors. Each row represents data for one individual tumor. Left column shows the variance of R2* signal of voxels spatially distributed over the tumor. The dark voxels are considered non-fluctuating. Center column demonstrates the averaged power spectra of fluctuating and non-fluctuating voxels compared to pink noise. Right column shows the averaged autocorrelation functions of the time series functions of fluctuating and non-fluctuating voxels.

Table 1.

Calculated Q values for the averaged autocorrelation function of the time series functions of fluctuating and non-fluctuating voxels using Eqn 1: see text for details.

		Mouse 1		Mouse 2		Mouse 3		Mouse 4		Mouse 5
		Left tumor	Right tumor	Left tumor	Right tumor	Left tumor	Right tumor	Left tumor	Right tumor	Left tumor	Right tumor
Q	fluctuating	127	138	231	208	364	433	243	207	205	169
	Non-fluctuating	56	44	95	101	73	78	59	58	72	66
${\chi }_{(1-0.05,m)}^2$		92	92	128	128	128	128	128	128	128	128

Results

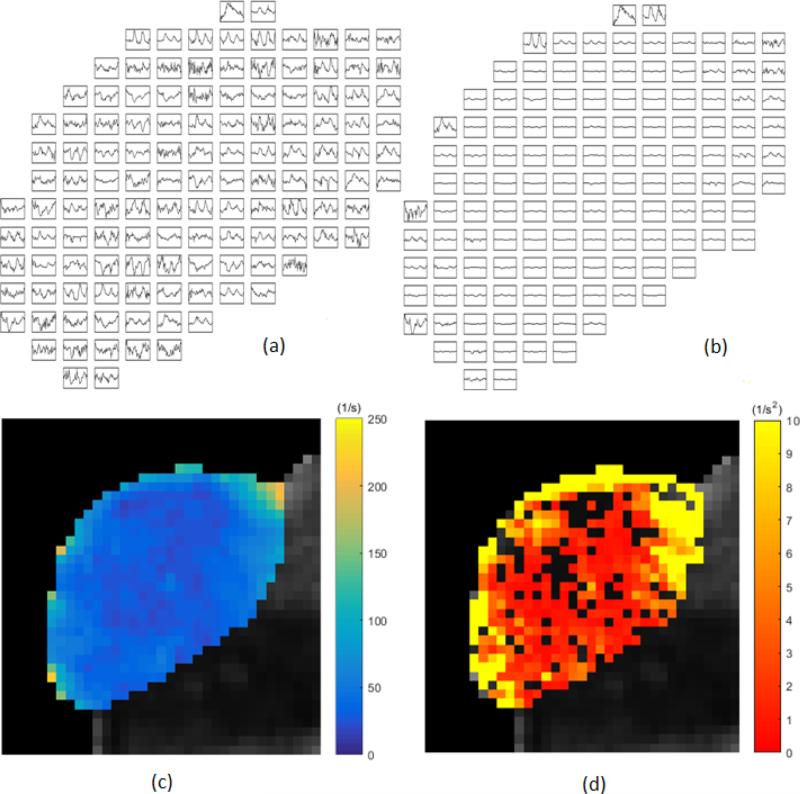
We observe oscillations and fluctuations that are both coherent and incoherent. Coherent is used here to describe the fluctuations as not just random, but definite oscillations in which some synchronization of many cells must be taking place. With the use of autocorrelation analysis and power spectral analysis, a coherent character of some of the oscillations is confirmed. As an example of the raw temporal data, sampled about every 70 seconds for an hour, see Figure 1(a) & (b) for the time behavior in every other voxel in a slice of one of the xenografts. Figure 1(c) is the mean R2* map through time, and 1(d), the variance of R2* map for the same slice. Note that the oscillations occur in particular locations, and even some voxels that have less than significant fluctuations still appear to coherently oscillate. Note also in Figure 1 that there is a sense of intermittency of the oscillations in the data from voxel to voxel. See Figure 2 for a representative 5 of the 10 xenografts in this study. Note that upon averaging successive xenograft power spectra together for fluctuating voxels, beyond 8 xenografts, the averaged spectrum is unchanged. The xenograft is labeled with mouse number (1-5) and right flank (R) or left flank (L) in Figure 2. Figure 1 shows data for the second mouse, right side flank. Note the time scales observed in the oscillations are minutes to tens of minutes. Since the autocorrelation functions taper, there is randomness in addition to the coherence. These data are windowed with a Hamming filter, but even a rectangular filter did not significantly change the power spectra, except very near the ordinate. The oscillations near 10-25 minutes are robust in the analysis.

Figure 1.

Individual voxel intensity from tumor 2R (right side of mouse #2). (a) Sample spatial and temporal distribution of BOLD MRI signal intensity. Each voxel was scaled to itself (every other voxel shown). Data was sampled every 70 seconds for one hour. (b) All voxels shown with the same scale (every other voxel shown). (c) Parametric map of the mean R2* through time. (d) Colored heat map demonstrates the variance of R2* signal of voxels spatially distributed over the same slice through the tumor. Black voxels are non-fluctuating according to the test outlined in the text.

Discussion

We set out to measure relative changes in blood oxygen levels in xenografts of head and neck squamous cell carcinoma using BOLD-MRI techniques. The voxel by voxel depiction of Figure 1 shows that these changes can be spontaneous, intermittent or cyclic, and are heterogeneously distributed throughout the tumor. From the figure, we see that most of these fluctuations occur at the periphery of the tumor. Presumably, this is the part of the tumor with more functional vascular supply and away from the potentially deeply hypoxic, deeply hypoglycemic and often necrotic center. Figure 1 (c) shows a parametric map of the mean R2* signal through time. This quells the concern that simple susceptibility weighting and/or motion drift is driving the variance observed at the periphery of the tumors. The power spectra calculated by averaging all fluctuating voxels gives us information about the range of periods of oscillation going from 14 minutes to 25 minutes. These periods we observe could be read out as peaks in the autocorrelation plots. On the one hand, we see peaks above noise on the power spectrum plot, suggesting synchronization of voxels. Peaks below noise may suggest dephasing oscillations when averaged.

These oscillations match the dominant time scales of what others have been observing in acute hypoxia for decades. For example: “... few cycles per hour to many hours or days.” (Dewhirst, 2009); “... cycle times ranging from 20-60 min.” (Dewhirst et al., 1996); “... kinetics on the scale of minutes,” (Cairns et al., 2001); also see figure 6 of Baudelet et al. (2004), ~ 20 min period with MRI-BOLD is shown. These are also the very same time scales for the glycolytic oscillator: minutes to tens of minutes (Sel'Kov, 1968, Boiteux et al., 1975, Bier et al., 2000, Goldbeter and Lefever, 1972).

Given that the periphery of the tumors used in these experiments has more functional vascular supply compared to its core, it is expected that vasomotion would contribute to the fluctuations that are observed in the results presented in this paper. There has been considerable research on vasomotion oscillation showing that cytoplasmic Ca²⁺ flux producing these vasomotions have periods much lower (seconds to minutes) compared to the metabolic cycles of the glycolytic oscillator (1 minute to 20 minutes)(Aalkjaer and Nilsson, 2005, Goldbeter, 1996). Also, Dewhirst et al. (1996) showed that oscillations in vasomotion had frequencies similar to those that were observed in cyclic hypoxia, which are frequencies similar to our observations. Considering these ranges in frequencies, it is quite likely that the glycolytic oscillator may be working in conjunction with vasomotion.

As a result of the data being sampled nearly every minute, each point is more than an oxygen equilibration time from the last. Photodynamic therapy studies, for example, have seen equilibration at less than 30 sec (Geel et al., 1996). The oxygen level dynamics would therefore be due to changes in the source: the red blood cell flux (Kimura et al., 1996) or vasomotion, or due to changes in the uniquely glycolytic metabolism of cancer cells (Warburg, 1956). A power spectrum of the hemoglobin saturation would come from both the changes in the red cell flux or changes in the metabolism, and the two may have distinct patterns in Fourier space. The data indicates oscillations that come and go, and the power spectra from the data (Figure 2) indicate features in the range of oscillations that others see.

Presented here are qualitative simulations of the condition where the glucose source flow is dominated by randomness and the metabolic dynamics are dominated by the glycolytic oscillator that gets triggered on and off by the random source flow. The glycolytic oscillator, at its heart, is due to the allosteric positive feedback behavior of autocatalytic phosphofructokinase (PFK) with adenosine diphosphate (ADP) that oscillates spontaneously in hypoglycemic conditions. ADP is produced from adenosine triphosphate (ATP) as fructose-6-phosphate (F6P) is converted to fructose-1,6-biphosphate (FBP) (Wiley). An equation schematically representing this autocatalytic reaction is as follows:

$$\text{glucose}\underset{\mathrm{b}}{\to }y\underset{\mathrm{a}}{\to }\underset{↵PFK}{x}\to \text{products}.$$ (2)

Here the rate b can be thought of as a flow rate of glucose into the metabolic chain of reactions, and a is a constant reaction rate, but it will increase as x is produced via the PFK autocatalytic behavior. The metabolic quantity x can be thought of as either ADP or FBP, and y as either ATP or F6P: either way would be consistent. This model was successfully developed by E.E. Sel’kov in 1968 for self-oscillations in yeast under hypoglycemic conditions (Sel'Kov, 1968). Sel’kov then modeled the feedback with a quadratic term, but a variety of exponents greater than unity will work as well. The simplest possible model is then a two dimensional set of coupled, nonlinear differential rate equations as follows which we implemented with MATLAB:

$$\begin{array}{cc}\hfill \frac{dx}{dt}=& -x+(a+x^2)y\hfill \\ \hfill \frac{dy}{dt}=& b-(a+x^2)y,\hfill \end{array}$$ (3)

and these equations produce limit cycles with the right combinations of a and b. A limit cycle is a stationary state of a nonlinear system that is not a single point in the phase space of x versus y, but a locus of points that is repeated in a cyclical manner. There are many other equations that will couple into these equations, and such studies are in the published literature (Goldbeter and Lefever, 1972), but the fundamental Fourier modes can be captured with the approximation of Eqn. 3. The oscillations come from a temporary and local depletion of substrate after the reaction rate increases as ADP attaches to PFK. When the reaction temporarily crashes, the substrate builds up again with a lower reaction rate until the ADP again continues to reattach and speeds up the reaction again, and the process repeats. The Eqns. 3 capture this dynamic.

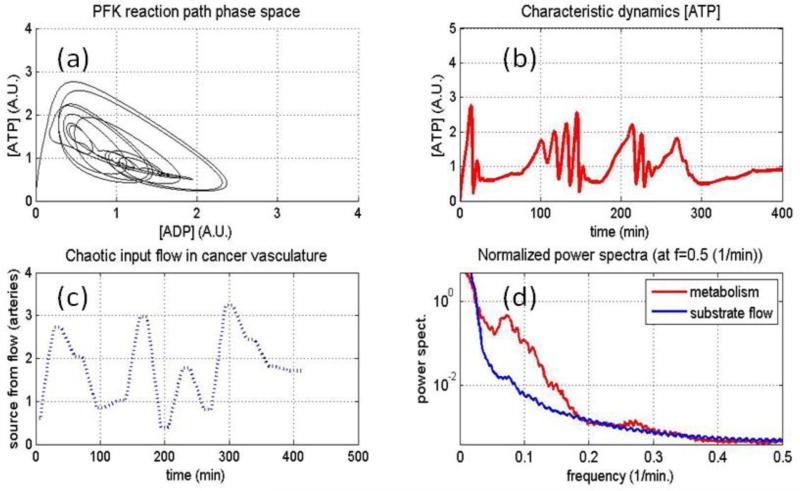
We would then expect threshold behavior for the oscillations based on the flow rate, b and the reaction rate a, and that threshold could be triggered on and off by glucose flow dynamics. The following simulation produces power spectra for the glucose flow rate and one of the metabolic quantities, ATP normalized to each other to emphasize any differences in shape (see Figure 3(d)). Different shapes would imply that one is not simply following the other. The simulated glycolytic oscillator (phase space path, Figure 3(a)) responds to the random changes in glucose flow (Figure 3(c)), and also to the oscillations randomly triggered by changes in ‘b’ but once started are of a purely metabolic nature. The simulation is therefore attempting to capture the basic character of the data's power spectra in as reduced a manner as possible to help separate what could be metabolic causes versus source flow causes in the hemoglobin saturation and blood volume dynamics seen with our experiments.

Figure 3.

Using an original and reduced model of the glycolytic oscillator (see text for details), limit cycles and changes in limit cycles are simulated (a). A plot of either metabolic quantity would show glucose flow induced changes with oscillations spontaneously starting or stopping (b). These changes in the oscillations are modulated by randomness in the flow of glucose (c), the normalized power spectra for the glucose flow and one of the metabolic quantities are shown overlaid in (d) to observe what is similar or what is different between them. All coupled metabolic quantities would likewise show these oscillations but at various phase and shape differences from each other as dictated by the path in phase space shown in (a).

The cells would likely synchronize their oscillations as has been reported in yeast (Bier et al., 2000) so that whole patches of the interstitium would oscillate together. Of particular concern for radiation therapy is that these oscillations would be present at intermediate hypoxic zones, shown to be more important for radiosensitivity (Wouters and Brown, 1997). It has also been demonstrated that cyclical hypoxia stabilized (hypoxia inducible factor) HIF-1α to a much larger degree than either normoxia or chronic hypoxia (Martinive et al., 2009). It is well established that HIF-1α is a prognosticator for therapy success (Harris, 2002). These oscillations are seen in yeast originally as well as other tissues such as pancreatic cells (Merrins et al., 2013), and most recently in hypoglycemic breast cancer cells (Hung, 2012). It is therefore possible that the mechanism most responsible for radiation therapy success, adaptation, and potential to be patient-specific, may require high time scale resolution measurements.

Conclusion

We have demonstrated that regular (coherent) oscillations exist in tumors along with more random (incoherent) components. The time scale of these oscillations matches perfectly with the ranges of what one would expect from basic theory and observation for the glycolytic oscillator, sometimes called the substrate-depleted oscillator. From a voxel-by-voxel analysis with MRI BOLD data on 10 xenografts, and following an established technique to separate significant fluctuations, these observations are robust. It is suggested that along with red cell flux and vasomotion dynamics, the glycolytic oscillator also provides a plausible mechanism for the coherent part of acute hypoxia.