Abstract
The ability to monitor tumor motion without implanted markers is clinically advantageous for lung image-guided radiotherapy (IGRT). Existing markerless tracking methods often suffer from overlapping structures and low visibility of tumors on kV projection images. We introduce the short arc tumor tracking (SATT) method to overcome these issues. The proposed method utilizes multiple kV projection images selected from a nine-degree imaging arc to improve tumor localization, and respiratory-correlated 4D cone-beam CT (CBCT) prior knowledge to minimize the effects of overlapping anatomies. The 3D tumor position is solved as an optimization problem with prior knowledge incorporated via regularization. We retrospectively validated SATT on 11 clinical scans from four patients with central tumors. These patients represent challenging scenarios for markerless tumor tracking due to the inferior adjacent contrast. The 3D trajectories of implanted fiducial markers were used as the ground truth for tracking accuracy evaluation. In all cases, the tumors were successfully tracked at all gantry angles. Compared to standard pre-treatment CBCT guidance alone, trajectory errors were significantly smaller with tracking in all cases, and the improvements were the most prominent in the superior-inferior (SI) direction. The mean 3D tracking error ranged from 2.2–9.9 mm, which was 0.4–2.6 mm smaller compared to pre-treatment CBCT. In conclusion, we were able to directly track tumors with inferior visibility on kV projection images using SATT. Tumor localization accuracies are significantly better with tracking compared to the current standard of care of lung IGRT. Future work involves the prospective evaluation and clinical implementation of SATT.
1. Introduction
Lung tumors often exhibit large respiratory motion ranges (Barnes et al, 2001; Stevens et al, 2001; Keall et al, 2006). The current standard of care of lung image-guided radiotherapy (IGRT) accounts for respiratory motion by adding margins to the target volumes based on the respiratory-correlated 4-dimensional (4D) planning CT, and delivering the dose with a static beam position based on a daily kV cone-beam CT (CBCT) scan. Consequently, changes in respiratory patterns and intrafraction deviations from mean CBCT tumor positions can degrade the delivered dose. Dosimetric differences on the order of 3–5% have been observed for large disparities in respiratory pattern between 4D CT and daily CBCT (Seco et al, 2008). Intrafraction deviations in mean target position exceeding 5 mm have also been reported in >7% of treatments (Guckenberger et al, 2007; Sonke et al, 2009; Shah et al, 2012). To ensure optimal radiation delivery, real-time guidance is required.
Current real-time tumor tracking technologies rely on radiopaque fiducial markers (Seiler et al, 2000; Sharp et al, 2004; Tang et al, 2007) or electromagnetic transponder beacons (Willoughby et al, 2006; Kupelian et al, 2007). However, marker or beacon implantation is an invasive, expensive, and time consuming procedure, and is not available at every radiotherapy clinic. Marker induced toxicity (Kothary et al, 2009) and marker migrations (Imura et al, 2005; van der Voort van Zyp et al, 2011; Hong et al, 2013) are also common problems. Markerless tumor tracking is thus arguably the holy-grail of modern IGRT.
Several markerless lung tumor tracking methods have been proposed using MV electronic portal imaging devices (EPID) (Richter et al, 2010; Rottmann et al, 2013; Bryant et al, 2014; Serpa et al, 2014) or kV imaging systems (Hugo et al, 2010; Lewis et al, 2010; Gendrin et al, 2012; Yang et al, 2012; van Sornsen de Koste et al, 2015). MV EPID based methods are limited by the treatment field size and poor contrast. Richter et al (2010) reported that tumor visibility was insufficient for tracking in 53% of EPID images. On the other hand, kV imaging based methods benefit from a larger view and better image quality. Hugo et al (2010) have reported a mean tracking error of 2 mm using a 4D CT based template matching method on CBCT projection images. Also using a 4D CT template matching based method, Lewis et al (2010) have reported a maximum 95th percentile error of 3.3 mm. Both methods were tested on phantom studies and two patient scans with relatively high tumor visibility, i.e. isolated or peripheral tumors. Gendrin et al (2012) proposed a fast GPU-based 2D/3D registration method that monitors both 2D translational motion 3D rotational motion of the tumor with an update rate of 2 Hz. The method was further improved to include tracking along the kV beam direction by utilizing perpendicular MV EPID images (Furtado et al, 2013). Phantom and patient cases were included in both studies, but no ground truth trajectory was available for evaluating tracking accuracies of the patient cases.
Existing markerless tracking methods rely on the tumors to be consistently visible on kV projection images (van Sornsen de Koste et al, 2015). This raises challenges when the tumors are small, attached to nearby structures (e.g. central tumors), obstructed by high-density objects (e.g. bony anatomy), or when the radiological depth varies due to gantry rotation. In a study by Teske et al (2015), tumor visibility was insufficient for tracking in 6 out of 14 patients in the anterior-posterior (AP) view. More patients are expected to be ineligible for markerless tracking during gantry rotation. Yang et al (2012) used the average 4D CT image to subtract overlapping anatomies on the CBCT projection images by generating “tumor-removed” digitally reconstructed radiographs (DRRs). The method was tested on one phantom and four patient scans, but no ground truth comparison was available for the patient cases. van Sornsen de Koste et al (2015) used a band-pass spatial filter to enhance tumor visibility on CBCT projections. The method was validated on five patients with a mean absolute tracking error of 0.5–1.4 mm. The fraction of kV images with insufficient tumor visibility for tracking was found to range from 2–64%.
Several studies have exploited the potential of digital tomosynthesis (DTS) for 3D tumor localization (Godfrey et al, 2006; Descovich et al, 2008; Maurer et al, 2008; Ren et al, 2008; van der Reijden et al, 2013; van Sornsen de Koste et al, 2013; Zhang et al, 2013; Ren et al, 2014). By using spatially distributed kV projection images (typically 30–90 degree span), a 3D image with much improved tumor visibility can be reconstructed. Currently DTS is only used for pre-treatment imaging, and has not yet been implemented for real-time guidance.
In this paper we present a 3D markerless lung tumor tracking method based on kV imaging under gantry rotation that is robust to inferior tumor visibility. Our method, referred as the short arc tumor tracking (SATT) method, differs from other markerless tracking approaches in that we utilize a nine-degree imaging arc and incorporate respiratory-correlated 4D CBCT prior knowledge. The key steps of the method and the datasets used for validation are described in section 2. The tracking results and discussions are given in section 3 and section 4.
2. Methods
2.1. Short arc tumor tracking (SATT)
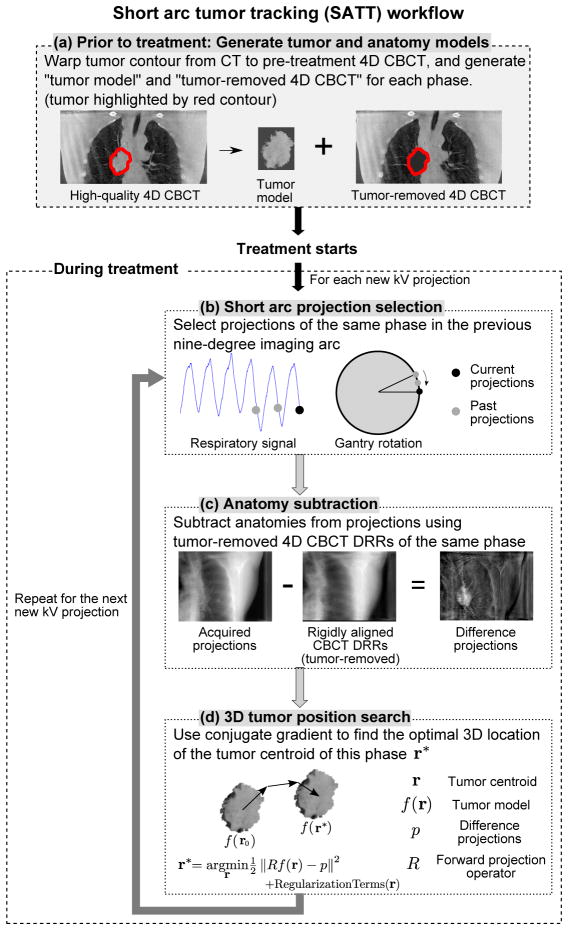
The workflow of the SATT method is outlined in figure 1. It is assumed that the tumor has been contoured on the planning CT, and a respiratory-correlated 4D CBCT scan prior to the treatment is available. The method was developed using the Insight Toolkit (ITK) (Johnson et al, 2015) and Reconstruction Toolkit (RTK) (Rit et al, 2014). The four major steps are described in detail in the following sections.
Figure 1.
The workflow of the proposed SATT method.
2.1.1. Generate tumor and anatomy models
Prior to the treatment, 4D models of the tumor and the surrounding anatomy are generated from pre-treatment 4D CBCT images. This is done by warping the tumor contour on the planning CT onto the 4D CBCT using deformable image registration (DIR). For each phase of the 4D CBCT, a tumor model and a “tumor-removed” 4D CBCT image are generated (cf. figure 1a). The former is a direct extraction of the 4D CBCT image pixels within the warped contour, while the latter is the 4D CBCT image with pixel values within the warped contour set to zero attenuation. The tumor models represent the targets to be tracked, and the tumor-removed 4D CBCT images are anatomy models that estimate the contribution of surrounding anatomies to the integral attenuation on kV projection images. The qualities of both models are highly dependent on the quality of the 4D CBCT images. In this work, the 4D CBCT images were reconstructed using our previously developed anatomical-adaptive image regularization (AAIR) technique to reduce noise and streaking artifacts while preserving image sharpness (Shieh et al, 2015), combined with the prior-image-constrained-compressed-sensing (PICCS) algorithm (Chen et al,2008) to improve the contrast of the bony anatomy.
2.1.2. Short imaging arc projection selection
During the treatment, tracking is performed at every kV projection acquisition time stamp. For each new kV projection, the respiratory phase is first determined by the projection intensity analysis method (Kavanagh et al, 2009). In this work, retrospective respiratory phase was used. In practice, real-time phase can be calculated using the method proposed by Ruan et al (2009). Projections of the same phase in the previous nine-degree imaging arc are then selected (cf. figure 1b). The arc size of nine degrees was chosen as it was found to be the smallest arc that rendered successful tracking in all cases included in this study (cf. section 2.2 and Appendix A). Compared to using a single projection, a nine-degree arc exploits the 3D information of the tumor in multiple views, making it possible to track cases that would otherwise be challenging, e.g. tumors attached to neighboring structures. In addition, a nine-degree imaging arc can be acquired within 1.5–9 seconds with a typical gantry speed of 1–6 degrees/s, which is in general a sufficiently short time interval for the time resolution required for treatment guidance. A larger arc of thirty degrees was tested and found to slightly improve tumor localization, but at the same time further degrade the time resolution, leading to overall similar tracking performance (cf. Appendix A). In practice, the optimal arc size may depend on multiple factors such as the visibility, size, and location of the tumor, and gantry speed.
2.1.3. Anatomy subtraction
Before the projections selected in the previous step are used for tumor position matching, the contribution of all the anatomies except for the tumor to the integral attenuation values is first estimated and subtracted from the projections. This is done by first forward projecting the tumor-removed 4D CBCT image of the same phase to generate tumor-removed DRRs at the gantry angles of the selected projections. Each DRR is then rigidly registered to and subtracted from the corresponding projection, resulting in a set of “difference projections” (cf. figure 1c). The difference projections, denoted as p, are assumed to contain only attenuation contributed from the tumor, therefore the exact tumor position can be found by matching the tumor model with p. In practice, however, exact subtraction of anatomies from the projections is not possible due to the change in patient anatomy during treatment and the approximation errors from the reconstructed 4D CBCT images and DRRs.
2.1.4. 3D tumor position search
The tumor position can be found by rigidly moving the tumor model f in the 3D space until the optimal match between the forward projections of the tumor model Rf and the difference projections p is reached, where R is the forward projection operator. Assuming no rotation and deformation of the tumor within the same respiratory phase, the tumor model can be considered a function of its centroid position f(r), where r = [x, y, z]T (in mm) is the tumor centroid expressed in the IEC 61217 geometry standard, i.e. x is left-right (LR), y is superior-inferior (SI), and z is anterior-posterior (AP) (IEC 61217: Radiotherapy Equipment - Coordinates, Movements and Scales, 2011). The problem of searching for the optimal tumor centroid position r* can then be described as the following optimization problem:
| (1) |
The first term of the objective function represents the L2-norm of the disparity between Rf(r) and p. The other three terms are regularization terms that prevent erroneous tracking results which can potentially be caused by inferior anatomy subtraction as mentioned in section 2.1.3, e.g. residual highly attenuated structures in the difference projections. The regularization terms penalize tracking results that deviate considerably from an a priori tumor position rPrior based on the squared distances in the kV short arc in-depth (ID), lateral (Lat), and SI directions, respectively. The in-depth directional vector ûID = [− sin θ̄, 0, cos θ̄]T is defined to be in the direction of the middle angular value θ̄ of the selected projections, while the lateral directional vector ûLat = [cos θ̄, 0, sin θ̄]T is defined to be perpendicular to both ûID and the SI directional vector ûSI = [0, 1, 0]T. The γ’s are introduced as parameters to adjust the powers of the squared distances, as higher power terms are more forgiving to small deviations while more intolerant to large deviations. In other words, with larger γ values, the regularization terms have smaller effects on the tracking results when r is reasonably close to rPrior, and larger effects when r deviates significantly from rPrior. In this work, all the γ’s were set to 2. The λ’s control the regularization strengths in the in-depth, lateral, and SI directions. In general, λID is larger than λLat and λSI as the selected projections contain much less information in the in-depth direction than in the lateral and SI directions. In this work the λ values were selected based on a heuristic scheme such that the regularization terms have minimal influences on tracking when ||r − rPrior|| is small, and start to have noticeable impacts only when ||r − rPrior|| is larger than a certain threshold (cf. Appendix B).
The local minima of (1) were solved by the nonlinear conjugate gradient method (cf. Appendix C for mathematical details). It is important to point out that the objective function in (1) is generally not convex and has multiple minima, because the anatomy subtraction is often imperfect and can cause residual highly attenuated structures in p that may mislead the tracking. Nevertheless, with appropriate regularization and initialization of r, the algorithm can mostly be guided towards the minimum of interest, i.e. the solution that closely represents the true tumor centroid. The nonlinear conjugate gradient method often converges to the closest minimum, and tumors generally have minimal motion between consecutive kV projection acquisitions provided the typical acquisition rate is ~5 Hz. Thus, in this work the initial r0 was set to the tumor centroid position tracked in the previous kV acquisition time stamp. In addition, the tumor centroid position in the 4D CBCT image of the same phase was used as rPrior for regularization to stabilize the tracking.
2.2. Patient data
We retrospectively validated SATT on kV imaging datasets from an NCI-sponsored lung cancer trial with seven locally advanced non-small-cell lung cancer patients treated with definitive radiochemotherapy with 3D conformal radiotherapy (cf. Roman et al (2012) for detailed descriptions of the datasets). These patient cases represent challenging scenarios for markerless tumor tracking, as the tumors were attached to the mediastinum and cannot be visually identified in most of the kV projection images due to inferior adjacent contrast. Each patient was implanted with 2–4 fiducial gold coil markers within and/or around the tumor, the trajectory of which was used in this work as the ground truth for computing tracking accuracy (cf. section 2.3). Three out of the seven patients were excluded for this work as their sizes exceed the field-of-view (FOV) of half-fan CBCT, causing truncation artifacts that hinder the iterative reconstruction step necessary for SATT (cf. section 2.1.1). Although no kV images were acquired during the treatment, on some treatment days two half-fan 4D CBCT scans were acquired before and after/both before the treatment. For the purpose of this work, only these “scan pairs” were selected. Among the remaining four patients, a total of 11 scan pairs were available. The first 4D CBCT scan was used as the pre-treatment 4D CBCT scan as mentioned in section 2.1.1, and projection images from the second 4D CBCT scan were used as the kV imaging sequence for tumor tracking. Henceforth, the second 4D CBCT scan is referred to as the “tracking scan”, assuming that there was an earlier pre-treatment 4D CBCT within the same day. At some gantry angles the tumors may be partially or completely outside the projection view due to half-fan acquisition. Only the largest continuous set of projection images that capture the entire view of the tumor were used, which constitutes at least half of the total projection images and 180 degree span in each tracking scan.
Planning CT scans were obtained using respiratory-correlated 4D fan-beam CT (FBCT) with 10 respiratory phases (Brilliance Big Bore, Philips Medical Systems, Andover, MA). 4D CBCT scans were obtained with slow gantry rotation (1.5 deg/s or 0.75 deg/s) and a half-fan bowtie filter on the Varian on-board kV imaging device (Varian Medical Systems, Palo Alto, CA). The exposure parameters were 125 kVp, 20 mA and 20 ms per projection. The imaging frequency was approximately 5 Hz, and scan duration was either 4 minutes or 8 minutes, resulting in a total of approximately 1200 or 2400 projection images each scan. The size of the projection image is 1024 × 768 pixels with a pixel spacing of 0.388 mm in both directions. Audiovisual biofeedback was performed for both the CT and CBCT acquisitions. The 4D CBCT scans were reconstructed into 10 respiratory phases using projection intensity based phase binning. The reconstruction voxel size was 1 mm in all directions.
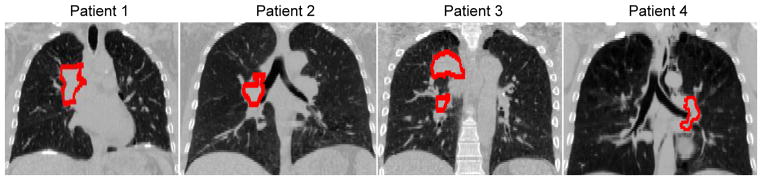
The details of the scans are summarized in table 1. The average 4D planning CT image and the gross tumor volume (GTV) contour of each patient are shown in figure 2. The time interval required for a nine-degree arc acquisition in these tracking scans was either 6 s or 12 s depending on the gantry speed.
Table 1.
Summary of the number of fiducial markers, tumor location, and gross tumor volume (GTV) (as contoured on the planning CT) for each patient. The gantry speed, time interval required for a nine-degree arc acquisition of each scan are also shown.
| Patient No. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Number of scans | 3 | 2 | 3 | 3 |
| Number of fiducial markers | 2 | 4 | 2 | 1a |
| Tumor locationb | RUL | Right hilum | Right hilum/RLL | LLL |
| GTV volume (cm3) | 88.9 | 30.3 | 58.3c | 42.7 |
| Gantry speed (deg/s) | 1.5 | 1.5 or 0.75d | 0.75 | 0.75 |
| Short arc time interval (s) | 6 | 6 or 12e | 12 | 12 |
Two markers implanted within close proximity and segmented as one.
RUL=right upper lobe; RLL=right lower lobe; LLL=left lower lobe.
Sum of two isolated volumes.
Scan 1 of patient 2: 1.5 deg/s. Scan 2 of patient 2: 0.75 deg/s.
Scan 1 of patient 2: 6 s. Scan 2 of patient 2: 12 s.
Figure 2.
The average 4D planning CT of each patient, with the GTV highlighted as the red contour. (C/W=−250/1500 HU)
2.3. Tracking accuracy evaluation
Fiducial markers in both the pre-treatment 4D CBCT and tracking scan projection images were segmented using a robust template-based segmentation method (Poulsen et al, 2011) which has been shown to be successful in more than 99.9% of the cases. The 2D segmented positions were converted to 3D trajectories using a probability-density-function based method (Poulsen et al, 2008) with submillimeter accuracy. The 3D centroid trajectory of the markers in the tracking scan was used as the ground truth to evaluate the tracking accuracy of SATT. The markers were then removed from the projection images by interpolating across surrounding pixels with Poisson noise added, so that the high contrast of the markers does not bias the tracking performance. Poisson noise was modeled using the mean photon counts of surrounding pixels.
To compare SATT with the marker ground truth, the tracked tumor centroid positions were converted to expected marker centroid positions by the relative position between tumor and marker centroid in the pre-treatment 4D CBCT image for each respiratory phase. The “trajectory error” of SATT was then calculated as the displacement between the ground truth marker centroid position and that inferred from SATT. SATT was also compared with the current standard of care, i.e. a fixed tumor position at all tracking time stamps inferred from the pre-treatment (3D) CBCT scan. The trajectory error of CBCT was thus calculated as the displacement between the ground truth and the time-averaged marker centroid position, i.e. averaged over all the pre-treatment CBCT projections. The trajectory error was analyzed in terms of its 3D magnitude as well as the SI and MV lateral component, i.e. the direction on the MV beam’s eye view (BEV) plane that is perpendicular to the SI direction. The latter two components span the MV BEV plane and are the most relevant to dose delivery. The trajectory error in the MV lateral direction is expected to be larger than that in the SI direction, as the MV lateral direction is almost parallel to the in-depth direction of SATT, while the SI direction always lies on the kV imaging plane.
The marker ground truth itself contains uncertainties due to marker migration between the pre-treatment 4D CBCT scan and the tracking scan, and also differential motion between markers. These uncertainties were quantified by the differences in the relative positions of markers to their centroid between the pre-treatment 4D CBCT scan and the tracking scan. The “ground truth uncertainty” for each tracking time stamp was defined to be the largest absolute difference among all implanted markers in each direction.
3. Results
3.1. Ground truth uncertainty
The mean ground truth uncertainty calculated over each tracking scan ranged from 0.5–1.6 mm. The 95th percentile value of the uncertainty calculated over all 11 scans was 1.8 mm.
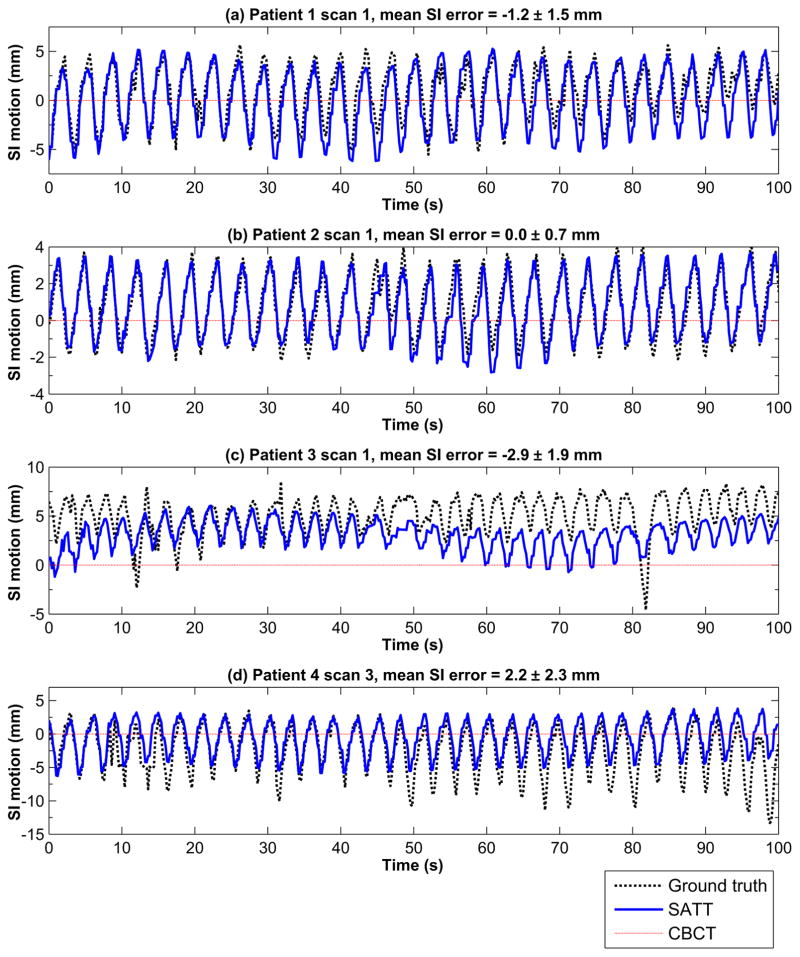
3.2. Tracking trajectory
We were able to track the tumors in all 11 scans at all gantry angles. Figure 3 shows 100 seconds of four example tracking trajectories in SI (one from each patient). The best tracking accuracy was observed for scan 1 of patient 2 (cf. figure 3b) with a mean SI error of 0.0 ± 0.7 mm (mean±standard deviation). Similar tracking performance was observed for scan 1 of patient 1 (cf. figure 3a), with a slightly larger mean SI error of −1.2 ± 1.5 mm. Scan 1 of patient 3 (cf. figure 3c) represents the most challenging scenario for SATT. In this scan the tumor has deviated considerably from the mean CBCT position. With such large deviations, it is likely that the overall anatomies have also varied, which can degrade the accuracy of the pre-treatment 4D CBCT anatomy models. Nevertheless, the tracking trajectory was still considerably more accurate than the pre-treatment CBCT position. After approximately t = 60 s the kV imaging plane was aligned near the LR view, in which case finding a good match between Rf and p is difficult due to the larger radiological depth. Consequently, the regularization terms started to have noticeable impacts on the tracking results, constraining the tracked tumor positions closer to the 4D CBCT locations. Scan 3 of patient 4 (cf. figure 3d) suffered from similar issues of degraded 4D CBCT anatomy model accuracy, but the tracking error was smaller as the deviation from the pre-treatment CBCT position was less severe.
Figure 3.
A hundred seconds of four example tracking trajectories in SI (one from each patient). The time-averaged marker centroid position in the pre-treatment CBCT imaging session is represented by the red dotted horizontal line. The SI motion was plotted with the pre-treatment CBCT position shifted to 0 mm.
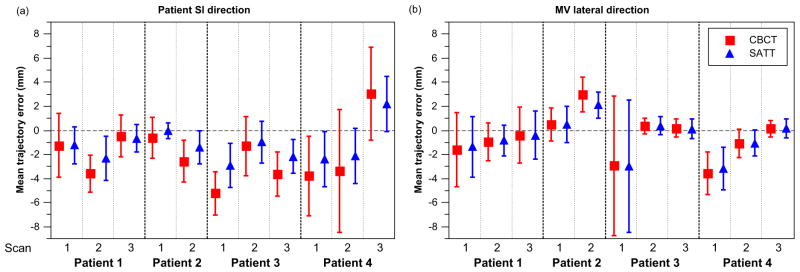
3.3. Quantification of trajectory error
Table 2 shows the mean and 95th percentile values of the 3D trajectory errors. Compared to CBCT, the mean 3D trajectory error was significantly smaller with tracking in all cases, with the reduction ranging from 0.4–2.6 mm. The mean 3D tracking error ranged from 2.2–9.9 mm, and the 95th percentile 3D tracking error ranged from 3.2–11.8 mm. Figure 4 shows the mean±standard deviation (SD) values of trajectory error in the SI and MV lateral directions. It can be seen that improvements in trajectory errors determined by SATT compared to CBCT were more prominent in the SI direction and for tumors with larger absolute mean CBCT trajectory errors, i.e. larger tumor excursion from mean CBCT positions. The reduction in MV lateral error was small (mostly below 1 mm) but statistically significant (p-value< 10−3) except for two scans (scan 1 of patient 3 and scan 2 of patient 4).
Table 2.
The mean and 95th percentile values of the 3D trajectory error.
| Patient No. | 1 | 2 | 3 | 4 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Scan No. | 1 | 2 | 3 | 1 | 2 | 1 | 2 | 3 | 1 | 2 | 3 |
| Mean 3D trajectory error (mm) | |||||||||||
|
| |||||||||||
| CBCT | 5.7 | 4.6 | 3.8 | 2.6 | 5.1 | 11.3 | 2.7 | 3.9 | 7.1 | 6.1 | 4.0 |
| SATT | 4.3 | 3.3 | 3.0 | 2.2 | 3.8 | 9.9 | 2.2 | 2.8 | 5.8 | 3.5 | 2.8 |
|
| |||||||||||
| 95th percentile 3D trajectory error (mm) | |||||||||||
|
| |||||||||||
| CBCT | 8.9 | 6.1 | 5.0 | 4.2 | 7.1 | 12.2 | 4.8 | 6.5 | 10.0 | 10.0 | 10.1 |
| SATT | 6.2 | 6.1 | 4.6 | 3.2 | 5.8 | 11.8 | 4.0 | 4.9 | 8.7 | 6.5 | 6.9 |
Figure 4.
The mean trajectory error of CBCT and SATT in the (a) patient SI and (b) MV lateral directions. The standard deviations of the trajectory errors were plotted as the error bars to indicate the spread of the trajectory errors.
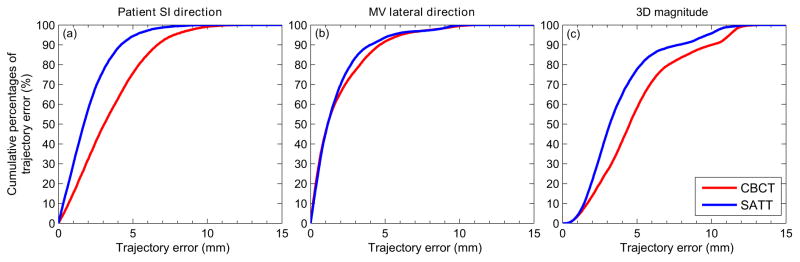
Figure 5 shows the cumulative percentages of trajectory errors that were below certain values in terms of the SI, MV lateral components, and 3D magnitude, calculated over all 11 scans. Similar to that observed from figure 4, improvements are the most evident in the SI direction, with 77% of the trajectory errors smaller than 3 mm with tracking, compared to 49% for CBCT. In the MV lateral direction, 83% of the trajectory error was below 3 mm, compared to 77% for CBCT.
Figure 5.
Cumulative percentages of trajectory errors (y–axis) that are below certain values (x–axis) for the (a) patient SI component, (b) MV lateral component, and (c) magnitudes of the 3D trajectory error vectors.
4. Discussion
To the best of our knowledge, SATT is the first markerless lung tumor tracking method that employs extremely short imaging arc projection matching (nine degrees) and 4D CBCT prior knowledge. These two components enable tumors with inferior visibility on the kV projection images to be directly tracked. This is also the first study that includes an extensive set of central tumor cases (4 patients, 11 scans) for validation.
SATT requires a pre-treatment 4D CBCT scan and continuous kV image acquisition during treatment delivery, which are both readily compatible with the workflow of modern radiotherapy. The tumor tracking procedure does not interfere with the treatment procedures as it is performed independently of treatment delivery. The short-arc nature of SATT assumes delivery techniques that involve continuous gantry rotation, e.g. Volumetric Modulated Arc Therapy. Nevertheless, the methodology of SATT can also be applied to treatments with static gantry such as step-and-shoot Intensity-Modulated Radiation Therapy and conformal radiotherapy. In these treatment scenarios, the short arc selection step reduces to using one single projection. In addition, stronger in-depth regularization (higher λID) is needed to compensate for the loss in in-depth resolution.
4.1. Comparisons with the standard of care
We were able to track the tumors at all gantry angles in all 11 scans. This suggests that most patients would be eligible for markerless tracking using SATT, as central tumors are generally more difficult to track due to the lack of adjacent contrast. More importantly, trajectory errors were significantly smaller with tracking as compared to CBCT for all scans, and the improvements were most significant for tumors with large deviations from the mean CBCT locations. This highlights the usefulness of SATT in IGRT, as it always provides more accurate position information than the standard of care, and especially when large tumor excursions are present.
4.2. Tracking accuracy
Tracking accuracy was found to vary from case to case. Larger trajectory errors were observed for cases with large deviations from the mean CBCT locations. This is most likely because large tumor excursions often accompany changes in surrounding anatomies especially for tumors attached to nearby structures, thereby degrading the accuracy of the 4D CBCT anatomy models. Nevertheless, the use of 4D CBCT prior knowledge is still expected to be more accurate than methods based on 4D CT prior models (Hugo et al, 2010; Lewis et al, 2010). The improvements relative to CBCT were found to be larger in the SI direction and smaller in the MV lateral direction. This is because tracking in the MV lateral direction, which is almost parallel to the kV short arc in-depth direction, is ill-posed, thus increasing the impacts of the 4D CBCT based regularization terms. Tracking in the MV lateral direction is a common challenge to kV imaging based approaches on most commercial linacs with perpendicular kV-MV orientation. Techniques that utilize both kV and MV images can be used to improve MV lateral tracking accuracies (Furtado et al, 2013; Ren et al, 2014). Alternatively, we expect better MV lateral tracking accuracies if SATT is implemented on linacs with non-perpendicular kV-MV orientation, such as the Vero SBRT system (BrainLab AG, Feldkirchen, Germany) (Depuydt et al, 2014).
The tracking scans in this work were acquired with relatively slow gantry rotation of 1.5 deg/s or 0.75 deg/s, which corresponds to a 6 s or 12 s time interval for a nine-degree arc acquisition. The tracking performance is expected to improve for a typical gantry rotation of 3–6 deg/s (short arc time interval of 1.5–3 s).
4.3. Comparisons with other studies
Several kV imaging based markerless tracking methods have been proposed and tested on clinical cases. Hugo et al (2010) reported a mean tracking error of 2 mm. Lewis et al (2010) reported a maximum 95th percentile error of 3.3 mm. van Sornsen de Koste et al (2015) found the mean tracking error on the projection domain to be 0.5–1.1 mm. These studies investigated mainly isolated tumors, which have relatively high visibility on kV projection images. The results are similar to that observed in this work for the good case scenarios, e.g. patient 1 scan 3, patient 2 scan 1. In addition, the results reported by Hugo et al (2010) and Lewis et al (2010) were obtained for only two clinical scans. van Sornsen de Koste et al (2015) investigated a total of 22 scans, and found that the fraction of kV images with insufficient tumor visibility for tracking ranges from 2–64%. Teske et al (2015) also reported in their study that tumor visibility was insufficient for tracking in 6 out of 14 patients in the AP view. In contrast, our method is able to track the tumors at all gantry angles regardless of the inferior tumor visibility. Compared to single projection based template matching methods, our method allows more patients to be eligible for and benefit from markerless guidance.
The drawback of SATT is the trade-off in time resolution (1.5–9 s depending on gantry speed) due to the short-arc nature, and the computation time needed to process multiple projections and anatomy subtraction (cf. section 4.4). In scenarios with a strict requirement for time resolution, e.g. a short SBRT fraction, a fast single projection/projection pair method is preferred (Gendrin et al, 2012; Furtado et al, 2013). On the other hand, SATT is useful when tumor visibility is insufficient for single projection based and template matching based tracking methods.
4.4. Future work
Our goal is to clinically implement SATT for real-time guidance. In terms of the clinical aspect, further investigations and developments are needed. Firstly, the tracking performance on various types of tumors (e.g. small tumors) needs to be investigated. Secondly, only patients within the FOV of half-fan CBCT acquisition were eligible for this work, as truncation artifacts hinder the pre-treatment iterative reconstruction step (cf. section 2.2). This excludes larger patients, which are generally challenging for markerless tumor tracking due to the larger radiological depths, and represent potential future area of development and investigation. Thirdly, the regularization parameters were determined based on a heuristic scheme (cf. Appendix B). The size of the short imaging arcs (nine degrees) was determined as the smallest arc that was found to render successful tracking in all cases studied (cf. Appendix A). Both parameters can potentially be further optimized on a case-by-case basis depending on properties such as the motion range, visibility, shapes, and sizes of the tumor, and gantry speed, etc. Finally, tracking accuracies were found to vary between and within cases. A confidence measure of the tracking results needs to be developed for making clinical decisions.
A few improvements have to be made to enable real-time implementation. Firstly, retrospective phase calculation needs to be replaced with real-time respiratory phase (Ruan et al, 2009). Secondly, the trade-off in time resolution due to short arc acquisitions (1.5–9 s depending on gantry speed) needs to be compensated. Potential options include implementing SATT as a moving average tracking approach (George et al, 2008), or compensating for the latency by prediction algorithms (Trofimov et al, 2008). Finally, the computation time of SATT was found to be 1–30 s for each tracking time stamp depending on the number of projections selected for tracking, and needs to be further reduced for real-time guidance. Currently 90% of the computation time is attributed to the rigid registration of tumor-removed DRRs, which was implemented on CPUs. Preliminary investigations suggested that this can be reduced by more than a factor of thirty with GPU implementation. In addition, the projection image size used in this work (approximately 40 by 30 cm) was much larger than necessary for lung tumor tracking. By full GPU implementation and using smaller projection images (e.g. 15 by 15 cm), the computation time can likely be reduced to <1 s.
5. Conclusion
We have developed the SATT method, a markerless lung tumor tracking method based on short kV imaging arcs and 4D CBCT prior knowledge, to address the challenge of inferior tumor visibility in markerless tracking. We retrospectively validated SATT on patients with central tumors, which are difficult to track due to the lack of adjacent contrast. In all of the cases investigated, the tumors were successfully tracked, and the mean trajectory errors were significantly smaller with tracking compared to standard pre-treatment CBCT guidance alone, with the reduction ranging from 0.4–2.6 mm. Our results show that SATT is robust to low tumor visibility, and can potentially allow more patients to be eligible for markerless real-time guidance. The tumor localization accuracies are also significantly improved with SATT compared to the current standard of care of lung IGRT. We are now focused on the prospective evaluation and clinical implementation of SATT.
Acknowledgments
We thank Assistant Professor Geoffrey Hugo from the Virginia Commonwealth University for providing the clinical datasets. We thank the anonymous reviewers for their valuable comments which helped improve the paper. This project is supported by an NHMRC Australia Fellowship, NHMRC project grant 1034060, US NCI P01CA116602, and an International Postgraduate Research Scholarship.
Appendix A. Tracking results using different arc sizes
Table A1 summarizes the mean 3D trajectory errors of tumor tracking using different arc sizes. The short arc acquisition time intervals for these arc sizes are listed in Table A2. In this study, the largest trajectory error of the conventional CBCT case was found to be 15 mm. Tracking cases with maximum trajectory errors of >15 mm are thus considered unsuccessful and highlighted in Table A1. Single projection tracking was found to perform worse than a nine-degree arc in all cases. Furthermore, single projection tracking was unsuccessful in 7 cases. We expect that this is because a single projection image does not contain sufficient information to correctly identify a tumor with inferior visibility at every gantry angle. A six-degree arc was found to perform better than single projection tracking, but also led to unsuccessful tracking in three cases. Compared to a nine-degree arc, a six-degree arc resulted in slightly smaller mean trajectory errors in three cases, possibly due to the shorter short arc time interval. A nine-degree arc was the smallest arc that was found to achieve successful tracking in all cases. A larger arc size of thirty degrees resulted in overall similar tracking performance. We expect that this is due to the trade-off between time resolution and tumor localization.
Table A1.
The mean 3D trajectory errors of tracking using different arc sizes.
| Patient No. | 1 | 2 | 3 | 4 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Scan No. | 1 | 2 | 3 | 1 | 2 | 1 | 2 | 3 | 1 | 2 | 3 |
| Single projection | 6.3 | 11.7* | 5.4 | 4.1 | 7.0* | 20.8* | 16.0* | 13.9* | 12.2* | 9.4* | 7.2 |
| 6 degrees | 4.3 | 4.4 | 2.7 | 2.2 | 3.6 | 17.4* | 14.0* | 7.6 | 11.8* | 5.4 | 2.7 |
| 9 degrees | 4.3 | 3.3 | 3.0 | 2.2 | 3.8 | 9.9 | 2.2 | 2.8 | 5.8 | 3.5 | 2.8 |
| 30 degrees | 4.1 | 3.2 | 3.2 | 2.4 | 4.0 | 9.0 | 2.5 | 3.0 | 4.9 | 3.9 | 3.5 |
Tracking cases with maximum 3D trajectory errors of >15 mm and considered unsuccessful. The largest trajectory error of conventional CBCT was found to be 15 mm in this study.
Table A2.
The short arc acquisition time intervals of different arc sizes in seconds.
| Patient No. | 1 | 2a | 3 | 4 |
|---|---|---|---|---|
| Single projectionb | 0.2 | 0.2 | 0.2 | 0.2 |
| 6 degrees | 4 | 4 or 8 | 8 | 8 |
| 9 degrees | 6 | 6 or 12 | 12 | 12 |
| 30 degrees | 20 | 20 or 40 | 40 | 40 |
Gantry rotation speed was 1.5 deg/s for scan 1 and 0.75 deg/s for scan 2 of patient 2. The short arc time intervals for scan 1 are therefore shorter than that for scan 2.
Projection acquisition rate was ~5 Hz.
Appendix B. Estimating the regularization parameters
The selection of regularization parameters is a common challenge for optimization algorithms. Ideally the regularization terms should only have noticeable impacts on the results when the algorithm struggles to find a good match between Rf and p. In this work the λ values were heuristically selected based on balancing the scales of ||Rf(r) − p||2/2 and regularization terms. The idea is that the range of ||Rf(r) − p||2/2 between a good and bad matches of Rf and p, i.e. from 0 (perfect match) to ||Rf||2/2 (worst match), is made comparable to the magnitude of the regularization terms when each component of r − rPrior is equal to a threshold that is considered “too large”. The thresholds in the SI and kV short arc lateral directions, DSI and DLat, were set to 200 mm, while the threshold in the kV short arc in-depth direction, DID, was set to 100 mm since tracking in the in-depth direction is ill-posed and requires stronger regularization. The heuristic formulas used to determine the λ values were thus:
| (B.1) |
| (B.2) |
| (B.3) |
Note that ||Rf|| does not depend on r as long as f is within the projection view, and thus can precomputed before tracking.
Appendix C. Solving for the 3D tumor centroid position
The local minima of (1) were solved by the nonlinear conjugate gradient method together with the Newton-Raphson method to initialize the step size before the line search. Firstly, the gradient g and the Hessian matrix H (for initializing the line search) of the objective function can be written as:
| (C.1) |
| (C.2) |
The partial derivatives of f can be approximated using finite difference methods. It is noteworthy that f and its partial derivatives only need to be shifted in (x, y, z) but not re-calculated for every new r, since f is assumed to have only translational motion.
Then, the algorithm can be outlined in the pseudo code below.
| 1: | NMaxIterations ← 100 | ▷ Maximum number of iterations |
| 2: | Δrmin ← 0.01 | ▷ Stopping criterion in Δr in mm |
| 3: | r ← r0 | ▷ Initialize r with the tracking result in the previous time stamp |
| 4: | C1 ← 10−4; C2 ← 0.5 | ▷ Parameters for the line search |
| 5: | for n = 1 : NMaxIterations do | |
| 6: | gn ← Calculate g according to (C.1) with r | |
| 7: | if n = 1 then | ▷ Update the conjugate direction |
| 8: | dn ← −gn | |
| 9: | else | |
| 10: | ▷ The Fletcher-Reeves method | |
| 11: | dn ← −gn + βndn−1 | |
| 12: | end if | |
| 13: | H ← Calculate H according to (C.2) with r | |
| 14: | ▷ Step size initialization by the Newton-Raphson method | |
| 15: | O0 ← Calculate objective function according to (1) with r | |
| 16: | rnew ← r + ηdn | |
| 17: | OLHS ← Calculate objective function according to (1) with rnew | |
| 18: | ||
| 19: | while OLHS > ORHS do | ▷ Line search |
| 20: | η ← C2η | ▷ Reduce η |
| 21: | rnew ← r + ηdn | |
| 22: | OLHS ← Calculate objective function according to (1) with rnew | |
| 23: | ||
| 24: | end while | |
| 25: | r ← rnew | |
| 26: | if ||ηdn|| < rmin then | ▷ Stopping criterion |
| 27: | break | |
| 28: | end if | |
| 29: | end for | |
| 30: | return r |
References
- Barnes E, Murray B, Robinson D, Underwood L, Hanson J, Roa W. Dosimetric evaluation of lung tumor immobilization using breath hold at deep inspiration. Int J Radiat Oncol. 2001;50(4):1091–1098. doi: 10.1016/s0360-3016(01)01592-9. [DOI] [PubMed] [Google Scholar]
- Bryant JH, Rottmann J, Lewis JH, Mishra P, Keall PJ, Berbeco RI. Registration of clinical volumes to beams-eye-view images for real-time tracking. Med Phys. 2014;41(12) doi: 10.1118/1.4900603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen GH, Tang J, Leng S. Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med Phys. 2008;35(2):660–663. doi: 10.1118/1.2836423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Depuydt T, Poels K, Verellen D, Engels B, Collen C, Buleteanu M, Van den Begin R, Boussaer M, Duchateau M, Gevaert T, Storme G, De Ridder M. Treating patients with real-time tumor tracking using the Vero gimbaled linac system: Implementation and first review. Radiother Oncol. 2014;112(3):343–351. doi: 10.1016/j.radonc.2014.05.017. [DOI] [PubMed] [Google Scholar]
- Descovich M, Morin O, Aubry JF, Aubin M, Chen J, Bani-Hashemi A, Pouliot J. Characteristics of megavoltage cone-beam digital tomosynthesis. Med Phys. 2008;35(4):1310–1316. doi: 10.1118/1.2868763. [DOI] [PubMed] [Google Scholar]
- Furtado H, Steiner E, Stock M, Georg D, Birkfellner W. Real-time 2D/3D registration using kV-MV image pairs for tumor motion tracking in image guided radiotherapy. Acta Oncol. 2013;52(7):1464–1471. doi: 10.3109/0284186X.2013.814152. [DOI] [PubMed] [Google Scholar]
- Gendrin C, Furtado H, Weber C, Bloch C, Figl M, Pawiro SA, Bergmann H, Stock M, Fichtinger G, Georg D, Birkfellner W. Monitoring tumor motion by real time 2D/3D registration during radiotherapy. Radiother Oncol. 2012;102(2):274–280. doi: 10.1016/j.radonc.2011.07.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George R, Suh Y, Murphy M, Williamson J, Weiss E, Keall P. On the accuracy of a moving average algorithm for target tracking during radiation therapy treatment delivery. Med Phys. 2008;35(6):2356–2365. doi: 10.1118/1.2921131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godfrey D, Yin F, Oldham M, Yoo S, Willett C. Digital tomosynthesis with an on-board kilovoltage imaging device. Int J Radiat Oncol Biol Phys. 2006;65(1):8–15. doi: 10.1016/j.ijrobp.2006.01.025. [DOI] [PubMed] [Google Scholar]
- Guckenberger M, Meyer J, Wilbert J, Richter A, Baier K, Mueller G, Flentje M. Intra-fractional uncertainties in cone-beam CT based image-guided radiotherapy (IGRT) of pulmonary tumors. Radiother Oncol. 2007;83(1):57–64. doi: 10.1016/j.radonc.2007.01.012. [DOI] [PubMed] [Google Scholar]
- Hong JC, Eclov NCW, Yu Y, Rao AK, Dieterich S, Le QT, Diehn M, Sze DY, Loo BW, Jr, Kothary N, Maxim PG. Migration of implanted markers for image-guided lung tumor stereotactic ablative radiotherapy. J Appl Clin Med Phys. 2013;14(2):77–89. doi: 10.1120/jacmp.v14i2.4046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hugo GD, Liang J, Yan D. Marker-free lung tumor trajectory estimation from a cone beam CT sinogram. Phys Med Biol. 2010;55(9):2637–2650. doi: 10.1088/0031-9155/55/9/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Technical report. International Electrotechnical Commission; 2011. IEC 61217: Radiotherapy Equipment - Coordinates, Movements and Scales. [Google Scholar]
- Imura M, Yamazaki K, Shirato H, Onimaru R, Fujino M, Shimizu S, Harada T, Ogura S, Dosaka-Akita H, Miyasaka K, Nishimura M. Insertion and fixation of fiducial markers for setup and tracking of lung tumors in radiotherapy. Int J Radiat Oncol. 2005;63(5):1442–1447. doi: 10.1016/j.ijrobp.2005.04.024. [DOI] [PubMed] [Google Scholar]
- Johnson HJ, McCormick M, Ibáñez L Consortium TIS. The ITK Software Guide. Kitware, Inc; 2015. [Google Scholar]
- Kavanagh A, Evans PM, Hansen VN, Webb S. Obtaining breathing patterns from any sequential thoracic x-ray image set. Phys Med Biol. 2009;54(16):4879. doi: 10.1088/0031-9155/54/16/003. [DOI] [PubMed] [Google Scholar]
- Keall PJ, Mageras GS, Balter JM, Emery RS, Forster KM, Jiang SB, Kapatoes JM, Low DA, Murphy MJ, Murray, Brad R, Ramsey CR, Van Herk MB, Vedam SS, Wong JW, Yorke E. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med Phys. 2006;33(10):3874–3900. doi: 10.1118/1.2349696. [DOI] [PubMed] [Google Scholar]
- Kothary N, Heit JJ, Louie JD, Kuo WT, Loo BW, Jr, Koong A, Chang DT, Hovsepian D, Sze DY, Hofmann LV. Safety and efficacy of percutaneous fiducial marker implantation for image-guided radiation therapy. J Vasc Interv Radiol. 2009;20(2):235–239. doi: 10.1016/j.jvir.2008.09.026. [DOI] [PubMed] [Google Scholar]
- Kupelian P, Willoughby T, Mahadevan A, Djemil T, Weinstein G, Jani S, Enke C, Solberg T, Flores N, Liu D, Beyer D, Levine L. Multi-institutional clinical experience with the Calypso System in localization and continuous, real-time monitoring of the prostate gland during external radiotherapy. Int J Radiat Oncol. 2007;67(4):1088–1098. doi: 10.1016/j.ijrobp.2006.10.026. [DOI] [PubMed] [Google Scholar]
- Lewis JH, Li R, Watkins WT, Lawson JD, Segars WP, Cervino LI, Song WY, Jiang SB. Markerless lung tumor tracking and trajectory reconstruction using rotational cone-beam projections: a feasibility study. Phys Med Biol. 2010;55(9):2505–2522. doi: 10.1088/0031-9155/55/9/006. [DOI] [PubMed] [Google Scholar]
- Maurer J, Godfrey D, Wang Z, Yin FF. On-board four-dimensional digital tomosynthesis: First experimental results. Med Phys. 2008;35(8):3574–3583. doi: 10.1118/1.2953561. [DOI] [PubMed] [Google Scholar]
- Poulsen PR, Cho B, Keall PJ. A method to estimate mean position, motion magnitude, motion correlation, and trajectory of a tumor from cone-beam CT projections for image-guided radiotherapy. Int J Radiat Oncol. 2008;72(5):1587–1596. doi: 10.1016/j.ijrobp.2008.07.037. [DOI] [PubMed] [Google Scholar]
- Poulsen PR, Fledelius W, Keall PJ, Weiss E, Lu J, Brackbill E, Hugo GD. A method for robust segmentation of arbitrarily shaped radiopaque structures in cone-beam CT projections. Med Phys. 2011;38(4):2151–2156. doi: 10.1118/1.3555295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren L, Zhang J, Thongphiew D, Godfrey DJ, Wu QJ, Zhou SM, Yin FF. A novel digital tomosynthesis (DTS) reconstruction method using a deformation field map. Med Phys. 2008;35(7):3110–3115. doi: 10.1118/1.2940725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren L, Zhang Y, Yin FF. A limited-angle intrafraction verification (LIVE) system for radiation therapy. Med Phys. 2014;41(2) doi: 10.1118/1.4861820. [DOI] [PubMed] [Google Scholar]
- Richter A, Wilbert J, Baier K, Flentje M, Guckenberger M. Feasibility study for markerless tracking of lung tumors in stereotactic body radiotherapy. Int J Radiat Oncol. 2010;78(2):618–627. doi: 10.1016/j.ijrobp.2009.11.028. [DOI] [PubMed] [Google Scholar]
- Rit S, Oliva MV, Brousmiche S, Labarbe R, Sarrut D, Sharp GC. The Reconstruction Toolkit (RTK), an open-source cone-beam CT reconstruction toolkit based on the Insight Toolkit (ITK) J Phys : Conf Ser. 2014;489(1):012079–012079. [Google Scholar]
- Roman NO, Shepherd W, Mukhopadhyay N, Hugo GD, Weiss E. Interfractional positional variability of fiducial markers and primary tumors in locally advanced non-small-cell lung cancer during audiovisual biofeedback radiotherapy. Int J Radiat Oncol. 2012;83(5):1566–1572. doi: 10.1016/j.ijrobp.2011.10.051. [DOI] [PubMed] [Google Scholar]
- Rottmann J, Keall P, Berbeco R. Markerless EPID image guided dynamic multi-leaf collimator tracking for lung tumors. Phys Med Biol. 2013;58(12):4195–4204. doi: 10.1088/0031-9155/58/12/4195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruan D, Fessler JA, Balter JM, Keall PJ. Real-time profiling of respiratory motion: baseline drift, frequency variation and fundamental pattern change. Phys Med Biol. 2009;54(15):4777–4792. doi: 10.1088/0031-9155/54/15/009. [DOI] [PubMed] [Google Scholar]
- Seco J, Sharp GC, Wu Z, Gierga D, Buettner F, Paganetti H. Dosimetric impact of motion in free-breathing and gated lung radiotherapy: A 4D Monte Carlo study of intrafraction and interfraction effects. Med Phys. 2008;35(1):356–366. doi: 10.1118/1.2821704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seiler PG, Blattmann H, Kirsch S, Muench RK, Schilling C. A novel tracking technique for the continuous precise measurement of tumour positions in conformal radiotherapy. Phys Med Biol. 2000;45(9):N103. doi: 10.1088/0031-9155/45/9/402. [DOI] [PubMed] [Google Scholar]
- Serpa M, Baier K, Cremers F, Guckenberger M, Meyer J. Suitability of markerless EPID tracking for tumor position verification in gated radiotherapy. Med Phys. 2014;41(3) doi: 10.1118/1.4863597. [DOI] [PubMed] [Google Scholar]
- Shah C, Grills IS, Kestin LL, McGrath S, Ye H, Martin SK, Yan D. Intrafraction variation of mean tumor position during image-guided hypogractionated stereotactic body radiotherapy for lung cancer. Int J Radiat Oncol. 2012;82(5):1636–1641. doi: 10.1016/j.ijrobp.2011.02.011. [DOI] [PubMed] [Google Scholar]
- Sharp GC, Jiang SB, Shimizu S, Shirato H. Tracking errors in a prototype real-time tumour tracking system. Phys Med Biol. 2004;49(23):5347. doi: 10.1088/0031-9155/49/23/011. [DOI] [PubMed] [Google Scholar]
- Shieh CC, Kipritidis J, O’Brien RT, Cooper BJ, Kuncic Z, Keall PJ. Improving thoracic four-dimensional cone-beam CT reconstruction with anatomical-adaptive image regularization (AAIR) Phys Med Biol. 2015;60(2):841. doi: 10.1088/0031-9155/60/2/841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonke JJ, Rossi M, Wolthaus J, van Herk M, Damen E, Belderbos J. Frameless stereotactic body radiotherapy for lung cancer using four-dimensional cone beam CT guidance. Int J Radiat Oncol. 2009;74(2):567–574. doi: 10.1016/j.ijrobp.2008.08.004. [DOI] [PubMed] [Google Scholar]
- Stevens C, Munden R, Forster K, Kelly J, Liao Z, Starkschall G, Tucker S, Komaki R. Respiratory-driven lung tumor motion is independent of tumor size, tumor location, and pulmonary function. Int J Radiat Oncol. 2001;51(1):62–68. doi: 10.1016/s0360-3016(01)01621-2. [DOI] [PubMed] [Google Scholar]
- Tang X, Sharp GC, Jiang SB. Fluoroscopic tracking of multiple implanted fiducial markers using multiple object tracking. Phys Med Biol. 2007;52(14):4081. doi: 10.1088/0031-9155/52/14/005. [DOI] [PubMed] [Google Scholar]
- Teske H, Mercea P, Schwarz M, Nicolay NH, Sterzing F, Bendl R. Real-time markerless lung tumor tracking in fluoroscopic video: Handling overlapping of projected structures. Med Phys. 2015;42(5):2540–2549. doi: 10.1118/1.4917480. [DOI] [PubMed] [Google Scholar]
- Trofimov A, Vrancic C, Chan TCY, Sharp GC, Bortfeld T. Tumor trailing strategy for intensity-modulated radiation therapy of moving targets. Med Phys. 2008;35(5):1718–1733. doi: 10.1118/1.2900108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Reijden A, van Herk M, Sonke JJ. Motion compensated digital tomosynthesis. Radiother Oncol. 2013;109(3):398–403. doi: 10.1016/j.radonc.2013.09.002. [DOI] [PubMed] [Google Scholar]
- van der Voort van Zyp NC, Hoogeman MS, van de Water S, Levendag PC, van der Holt B, Heijmen BJ, Nuyttens JJ. Stability of markers used for real-time tumor tracking after percutaneous intrapulmonary placement. Int J Radiat Oncol. 2011;81(3):e75–e81. doi: 10.1016/j.ijrobp.2010.12.026. [DOI] [PubMed] [Google Scholar]
- van Sornsen de Koste JR, Dahele M, Mostafavi H, Senan S, van der Weide L, Slotman BJ, Verbakel WFAR. Digital tomosynthesis (DTS) for verification of target position in early stage lung cancer patients. Med Phys. 2013;40(9) doi: 10.1118/1.4817245. [DOI] [PubMed] [Google Scholar]
- van Sornsen de Koste JR, Dahele M, Mostafavi H, Sloutsky A, Senan S, Slotman BJ, Verbakel WFAR. Markerless tracking of small lung tumors for stereotactic radiotherapy. Med Phys. 2015;42(4):1640–1652. doi: 10.1118/1.4914401. [DOI] [PubMed] [Google Scholar]
- Willoughby T, Kupelian P, Pouliot J, Shinohara K, Aubin M, Roach M, Skrumeda L, Balter J, Litzenberg D, Hadley S, Wei J, Sandler H. Target localization and real-time tracking using the calypso 4D localization system in patients with localized prostate cancer. Int J Radiat Oncol. 2006;65(2):528–534. doi: 10.1016/j.ijrobp.2006.01.050. [DOI] [PubMed] [Google Scholar]
- Yang Y, Zhong Z, Guo X, Wang J, Anderson J, Solberg T, Mao W. A novel markerless technique to evaluate daily lung tumor motion based on conventionalcone-beam CT projection data. Int J Radiat Oncol. 2012;82(5):E749–E756. doi: 10.1016/j.ijrobp.2011.11.035. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Yin FF, Segars WP, Ren L. A technique for estimating 4D-CBCT using prior knowledge and limited-angle projections. Med Phys. 2013;40(12) doi: 10.1118/1.4825097. [DOI] [PubMed] [Google Scholar]