Collaborative Regression-based Anatomical Landmark Detection

Abstract

Anatomical landmark detection plays an important role in medical image analysis, e.g., for registration, segmentation and quantitative analysis. Among various existing methods for landmark detection, regression-based methods recently have drawn much attention due to robustness and efficiency. In such methods, landmarks are localized through voting from all image voxels, which is completely different from classification-based methods that use voxel-wise classification to detect landmarks. Despite robustness, the accuracy of regression-based landmark detection methods is often limited due to 1) inclusion of uninformative image voxels in the voting procedure, and 2) lack of effective ways to incorporate inter-landmark spatial dependency into the detection step. In this paper, we propose a collaborative landmark detection framework to address these limitations. The concept of collaboration is reflected in two aspects. 1) Multi-resolution collaboration. A multi-resolution strategy is proposed to hierarchically localize landmarks by gradually excluding uninformative votes from faraway voxels. Moreover, for the informative voxels near the landmark, a spherical sampling strategy is also designed in the training stage to improve their prediction accuracy. 2) Inter-landmark collaboration. A confidence-based landmark detection strategy is proposed to improve the detection accuracy of “difficult-to-detect” landmarks by using spatial guidance from “easy-to-detect” landmarks. To evaluate our method, we conducted experiments extensively on three datasets for detecting prostate landmarks and head & neck landmarks in computed tomography (CT) images, and also dental landmarks in cone beam computed tomography (CBCT) images. The results show the effectiveness of our collaborative landmark detection framework in improving landmark detection accuracy, compared to other state-of-the-art methods.

I. INTRODUCTION

Anatomical landmark detection aims to automatically localize specific points of interest in human anatomy. These points are named landmarks, which often lie on the organ/structure boundary. These landmarks are important in registration, segmentation and quantitative analysis, e.g., for landmark-guided deformable registration [1], model initialization in deformable segmentation [2, 3], and dental deformity quantization [4]. Despite its importance, anatomical landmark detection still remains a challenging problem due to many reasons: 1) poor image contrast, 2) image artifacts, and 3) large appearance variations of landmark.

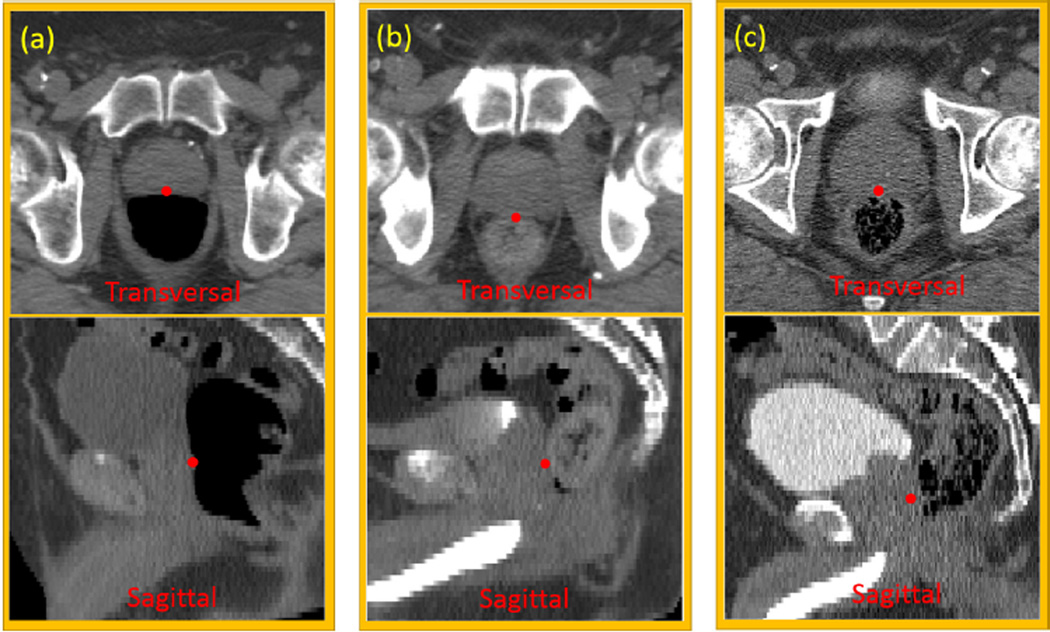
Fig. 1 gives an example of one prostate landmark, which lies on the boundary between the prostate and rectum. Its local appearance could dramatically change due to the uncertainty of bowel gas in the rectum. Besides, CT scans may be acquired after the injection of contrast agent, which changes the surrounding appearance of the landmark, and makes automatic landmark detection even more challenging.

FIG. 1.

Illustration of one prostate landmark (red point) in transversal and sagittal views of three patients. This landmark locates at the most posterior point of the prostate on the prostate central slice. Three column panels show three patients with different amounts of injected contrast agent in the bladder, and with different amounts of bowel gas in the rectum. (a) no contrast agent, and large bowel gas; (b) partial contrast agent, and almost no bowel gas; (c) full contrast agent, and some bowel gas.

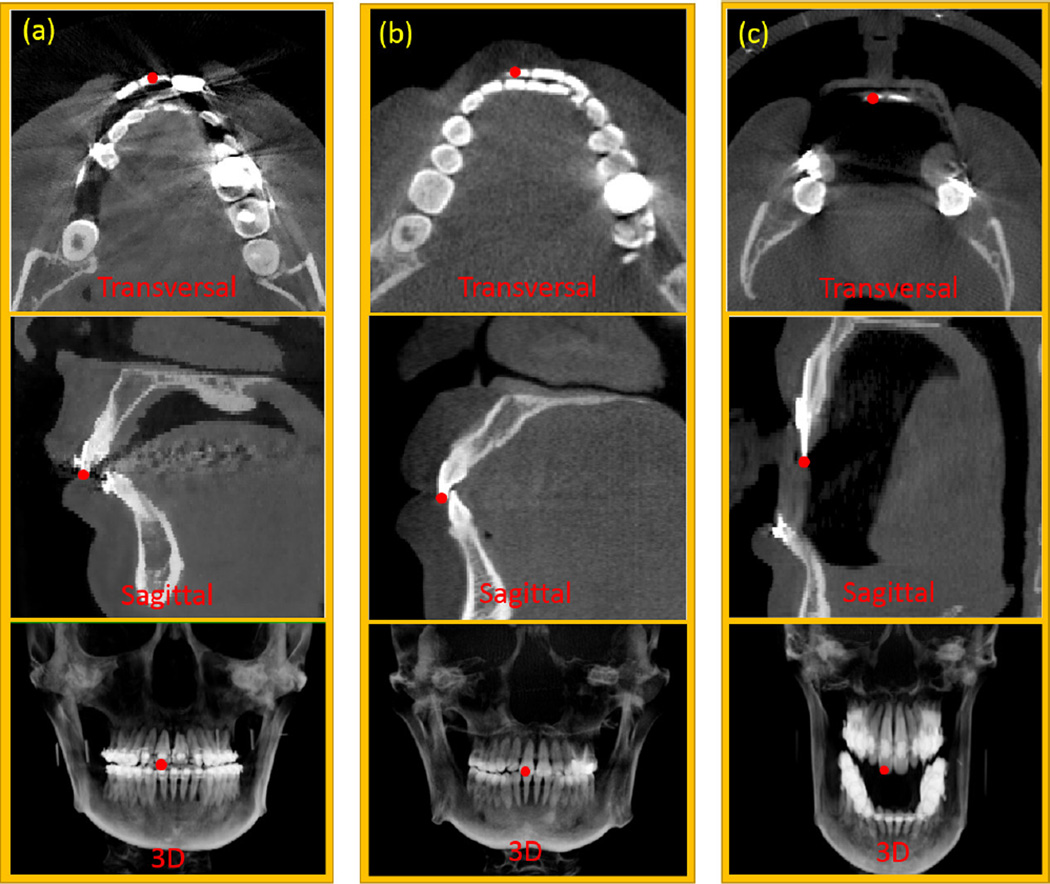
Fig. 2 gives an example of one tooth landmark in cone beam computed tomography (CBCT) images. As shown in the transversal view of Fig. 2(a), metal dental braces can cause severe streaking artifacts, which makes the landmark difficult to be recognized. Besides, the challenges of teeth landmark detection also come from various deformities of patients. Fig. 2 (c) shows a patient with anterior open-bite. This deformity leads to dramatic appearance changes of the same landmark across different patients, which increases the difficulty of landmark detection.

FIG. 2.

Illustration of one upper tooth landmark (red point) in different views of three patients. This landmark indicates a right central incisor on the maxilla. Column panels (a) and (b) show two patients with and without dental braces, respectively. Panel (c) shows a patient who cannot closely bite his teeth due to maxillary hypoplasia and mandibular hyperplasia. Red points indicate the positions of the same landmark in different views of various CBCT scans.

Due to the aforementioned challenges, it is difficult to empirically handcraft all rules to address the landmark detection problem. In the literature, researchers often rely on machine learning based approaches to tackle this problem. The mainstream landmark detection methods can be categorized into two types: classification-based and regression-based landmark detections.

In the classification-based methods, strong classifiers are usually learned to distinguish the correct position of anatomical landmark from the wrong ones. For example, Zhan et al. [5] used cascade Adaboost classifiers to classify each image voxel for detecting anatomical landmarks on MR knee images. Zheng et al. [6] proposed marginal spacing learning, which used probabilistic boosting trees [7] as classifiers, to detect the positions of heart chambers for deformable model fitting. Gao et al. [3] proposed an online updating scheme named “incremental learning with selective memory” to update the population-learned cascade classifiers with the online collected patient-specific data for improving the accuracy of landmark detection on daily treatment CT images.

In contrast to the classification-based approaches, which often require voxel-wise classification to determine the correct landmark position, the regression-based approaches predict the landmark position from each image voxel. In the training stage, a regression model is often learned to predict the 3D displacement from any image voxel to the target landmark. In the application/testing stage, the learned regression model can be used to predict the 3D displacement for every voxel in the image. Then, based on the estimated 3D displacement, each image voxel casts one vote to a potential landmark location. Finally, all votes from different image voxels are aggregated to localize the target landmark, such as at the voxel with the maximum vote. For example, Criminisi et al. [8] proposed to use regression forest with context-rich visual features for detecting bounding boxes of organs in CT images. Instead of determining the bounding box by checking the local image features within the box, they showed that the context appearance information is also important in the bounding box detection. Recently, researchers [9, 10] have shown that the bounding box detection method [8] can also be easily extended to anatomical landmark detection. Besides the aforementioned methods, there are methods that combine both classification and regression for landmark detection. Lay et al. [2] first used regression forest to detect candidate positions for each landmark, and then applied probabilistic boosting trees as classifiers to accurately identify the landmark location within all candidates.

Compared to classification-based methods, regression-based methods integrate context appearance information to localize landmarks, which makes it less sensitive to the anatomical structures with similar local appearances to the target landmark but with completely different anatomical positions in the image. Recently, Cootes et al.[11] have also shown that random forest regression method is significantly faster and more accurate than the equivalent classification-based methods in driving the deformable segmentation of different datasets. Despite the success of recent regression-based landmark detection methods, they still suffer several limitations:

1. Inclusion of faraway image voxels in the voting procedure. In the conventional regression-based method [8], all image voxels are involved in voting the landmark location. As many voxels are not near the target landmark, they are not informative to local anatomical variations of the landmark. Thus, inclusion of these voxels in the voting procedure would limit the detection accuracy.

2. Neglect of landmark dependency in the detection step. Many anatomical landmarks are spatially dependent. Independent detection of them may cause inconsistent detection results. In the literature, most works [5, 12, 13] exploited the landmark spatial dependency in the post-processing step that is separated from the detection step. For example, Zhan et al. [5] exploited a linear spatial relationship between landmarks for correcting wrongly localized landmarks on MR knee images. Donner et al. [12] adopted Markov random field to find the optimal landmark configuration, given a set of landmark candidates. Because the spatial dependency is exploited after the detection step, it only helps filter out wrongly detected landmarks, not improve the accuracy of individual landmark detections.

In this paper, we propose a collaborative regression-based framework for solving the above limitations. Specifically, our framework consists of two components:

1. Multi-resolution collaboration. We propose a multi-resolution strategy named “multi-resolution regression voting” to detect a landmark hierarchically. In the coarsest resolution, all image voxels are allowed to vote the landmark position for rough localization. Once the rough position is known, the landmark position can be refined by voting from nearby voxels. The training of our multi-resolution framework also takes into account the idea that nearby voxels are more useful for localizing the landmark than faraway voxels. Particularly, we propose a spherical sampling strategy, which associates the sampling probability of a voxel with its distance to the target landmark. In this way, spherical sampling strategy tends to draw more training samples towards the target landmark, thus improving the prediction accuracy for voxels near the target landmark.

2. Inter-landmark collaboration. We exploit the detection reliability of each landmark and then propose a confidence-based landmark detection strategy, which uses ”easy-to-detect” (reliable) landmarks to guide the detection of ”difficult-to-detect” (challenging) landmarks. Particularly, we introduce context distance features, which measure the displacements of an image voxel to the reliable landmarks. Context distance features can be used to guide the detection of challenging landmarks, because the displacements of an image voxel to the reliable and challenging landmarks are often highly correlated. If this correlation is exploited, the reliable landmarks can be used to improve the detection accuracy of challenging landmarks.

In the experiments, we extensively evaluate our method on 127 images, including 73 CT prostate images each with 6 landmarks, 14 CBCT dental images each with 15 landmarks, and 40 CT head & neck images each with 5 landmarks. Experimental results show that, with the proposed strategies, our method outperforms the conventional regression-based method, and a classification-based method in landmark detection. Moreover, our method is able to localize a landmark in 1 second with accuracy comparable to the inter-observer variability.

The preliminary version of this work was published in [1], where we used landmark detection for initializing deformable registration. The method described in this work extends our previous work in the following three aspects.

• We propose a spherical sampling strategy in the multi-resolution framework. As validated on three datasets, the spherical sampling strategy improves the accuracy of landmark detection, compared to the conventional uniform sampling strategy.

• We propose a collaborative landmark detection strategy, by using easy-to-detect land-marks to guide and improve the detection accuracy of difficult-to-detect landmarks. This strategy is important for detecting those challenging landmarks with large variation of landmark appearance.

• Compared to our previous work [1], which was applied only to MRI brain images, we have now extensively evaluated our method on three different datasets. The results show that our method works not only for the landmarks with clear appearances, but also for the landmarks with indistinct appearances, such as prostate landmarks in CT images.

The rest of paper is organized as follows. Section II presents the conventional regression-based landmark detection to familiarize readers with the overall flowchart. Section III elaborates the proposed multi-resolution strategy. Section IV provides the details of confidence-based landmark detection. Experimental results of different strategies on three applications are given in Section V. Finally, Section VI and Section VII present the conclusion and discussion of the paper, respectively.

II. REGRESSION-BASED LANDMARK DETECTION

In this section, we will first introduce the basics of regression forest, which is often used as a regression model in the conventional regression-based landmark detection. Then, we will describe the conventional regression-based landmark detection method in details.

A. Regression Random Forest

Regression random forest is one type of random forests specialized for non-linear regression tasks. It consists of multiple independently-trained binary decision trees. Each binary decision tree is composed of two types of nodes, namely leaf node and split node. Each leaf node records the statistics that summarizes target values of all training samples falling into it. In our implementation, mean d̄∈ℝ^M and variance v∈ℝ^M are recorded in each leaf node, where M is the dimension of target vector we want to predict/regress, such as M = 3 in our case of detecting the location of landmark in the 3D images. Each split node is a split function, which often uses a decision stump with one feature f and a threshold t, i.e., Split(Ω|f, t) = H(Ω_f < t), where Ω represents an input sample, Ω_f is the value of feature f at sample Ω, and H is the Heaviside step function. If Split(Ω|f, t) = 0, sample Ω is split to the left child of this split node. Otherwise, it is split to the right child node.

Each binary decision tree in regression random forest is independently trained with boot-strapping on both samples and features. Given a random subset of training samples and features, a binary decision tree is trained recursively, starting from the first split node (root). A good split function should separate training samples into two subsets with consistent target vectors. This could be achieved by maximizing variance reduction. Thus, the optimal parameters {f*, t*} of a split function can be found by maximizing the following objective function:

$$\{f^{*},t^{*}\}=\underset{f,t}{\text{max}}\sum _{i=1}^M({\mathbf{v}}_i^{\text{spilt}}-\sum _{j\in \{L,R\}}\frac{N^j}{N}{\mathbf{v}}_i^j)$$ (1)

where ${\mathbf{v}}_i^{\text{spilt}}$ is the variance of the i-th target of all training samples arriving at the split node. N^j, j ∈ {L, R}, is the number of training samples split into the left/right child, given a pair of {f, t}. ${\mathbf{v}}_i^j$ is the variance of the i-th target of training samples split into the left/right child node, i.e., j = L or j = R. To maximize Eq. 1, exhaustive search over a random subset of features and thresholds is often conducted in the random forest optimization [14]. Specifically, a set of thresholds is randomly sampled for each feature in the bootstrapped feature set. Every combination of feature and threshold is evaluated on Eq. 1 to find out the optimal pair that achieves the maximum objective value. Once the split function is determined, it is used to split the training samples into two subsets: left subset with training samples satisfying Split(Ω|f, t) = 0, and right subset with training samples satisfying Split(Ω|f, t) = 1. For each subset, a split function can be similarly trained to further separate training samples into subsets with more consistent target vectors. The splitting functions is thus recursively trained until one of stopping criteria is met: 1) the number of training samples is too few to split; 2) the maximum tree depth is reached. In such cases, the current node becomes a leaf node and the statistics (i.e., mean d̄ and variance v) of training samples falling into this node is stored for future prediction.

In the testing stage, a testing sample is pushed to each binary decision tree, starting at the root node. Based on the split nodes learned in the training stage, the testing sample is guided towards leaf nodes. When it arrives a leaf node, the mean d̄ stored in the leaf node is retrieved to serve as the prediction result of this tree. Finally, the results from all different trees are fused to obtain the prediction result of the entire forest. Conventionally, averaging is often used to fuse prediction results from different trees due to its simplicity and efficiency.

$${\hat{\mathbf{d}}}_i=\frac{{\sum }_{k=1}^K{\overline{\mathbf{d}}}_i^{(k)}}{K}$$ (2)

where K is the number of trees in the forest, and d̂_i is the i-th predicted target for this testing sample. d̄_i^(k) is the mean of the i-th target stored in the leaf node reached in the k-th tree. Since variance of each leaf indicates the prediction uncertainty (i.e., large variance indicates high uncertainty, while small variance indicates low uncertainty), it is better to also exploit this piece of information when fusing results from different trees. Therefore, in this paper we use the variance-weighted averaging to fuse prediction results from different trees:

$${\hat{\mathbf{d}}}_i=\frac{{\sum }_{k=1}^K{\mathbf{w}}_i^{(k)}{\overline{\mathbf{d}}}_i^{(k)}}{{\sum }_{k=1}^K{\mathbf{w}}_i^{(k)}},{\mathbf{w}}_i^{(k)}=\frac{1}{{\mathbf{v}}_i^{(k)}+\epsilon }$$ (3)

where ${\mathbf{v}}_i^{(k)}$ is the variance of the i-th target stored in the leaf node reached in the k-th tree. ${\mathbf{w}}_i^{(k)}$ is the weight to measure the prediction confidence of the i-th target by the k-th tree, which is defined as the inverse of ${\mathbf{v}}_i^{(k)}$. The smaller the variance is, the larger the confidence is. ε is a very small number (1.0×10⁻⁶) to deal with the case when variance of leaf node is zero.

B. Regression-based Anatomical Landmark Detection

Regression-based landmark detection utilizes context appearances to localize the target landmark. This characteristic differentiates it from the classification-based landmark detection, which localizes a landmark via voxel-wise classification according to the local appearance of each voxel. As a machine-learning-based approach, regression-based landmark detection has two stages, the training stage and the testing stage. In the training stage, the goal is to learn a regression model (i.e., regression forest) that predicts the 3D displacement from any image voxel to the target landmark according to the local image appearance of the voxel. In the testing stage, the learned regression model is used to predict the 3D displacement for each image voxel in the new testing image. Based on the estimated 3D displacement to the target landmark, each image voxel casts one vote to a potential landmark position. Finally, by collecting votes from all image voxels, the position that receives the maximum votes is taken as the detected landmark position. In the following paragraphs, the details of respective training and testing stages are provided in the context of single-landmark detection for the sake of concision. However, they can also be used in the multi-landmark setting by assuming the independence among landmarks.

Training stage

The input of the training stage is a number of training images, each with its interested landmark annotated. To train a regression forest, training samples need to be extracted from these training images. In this paper, each training sample is a voxel from one training image, thus also referred as training voxel in the rest of the paper. A training voxel is represented by a feature vector and associated with a target vector, which is the 3D displacement from this voxel to the target landmark in the same image.

The training stage consists of three successive steps: 1) sampling training voxels, 2) extracting feature and target vectors, and 3) training regression forest. Since Step 3) is straightforward, we detail only Step 1) and Step 2) in the following paragraphs.

1. Sampling training voxels: Theoretically all image voxels in all training images can be used as training voxels to train a regression forest. However, as each training voxel is often represented by a long feature vector, it is practically impossible to use all image voxels for training due to the limit of memory and training time. Therefore, sampling is often used to draw a limited number of representative training voxels from each training image for training. In the conventional regression-based landmark detection, uniform sampling is commonly adopted, where each voxel in the training images has the same probability to be sampled. For each training image, a fixed number τ of training voxels is uniformly and randomly sampled. After sampling, we have τ × Z training voxels, where Z is the number of training images.

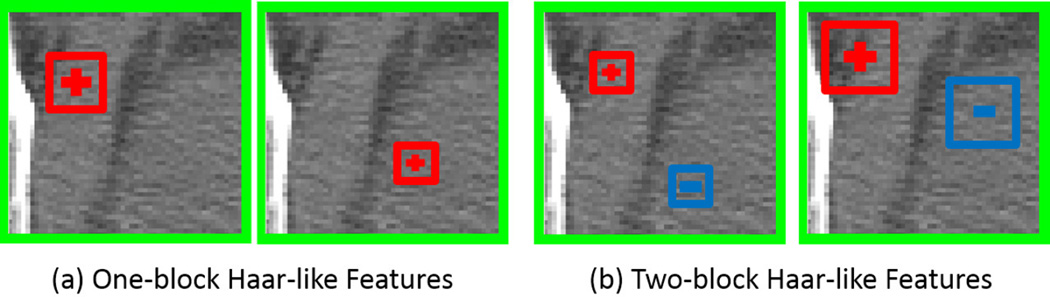
2. Extracting features and target vectors: As the interested landmark is manually annotated on each training image, we can easily compute the target vector d of each sampled training voxel, i.e., d = x^LM − x, where x and x^LM are the positions of a training voxel and the landmark, respectively. The features of each training voxel are often calculated as 3D Haar-like features, which measure the average intensity of an arbitrary position, and also the average intensity difference of two arbitrary positions within the local patch of this voxel (see Fig. 3). Mathematically, the 3D Haar-like features used in our paper are formulated as:

   $$f(I_{\mathbf{x}}|{\mathbf{c}}_1,s_1,{\mathbf{c}}_2,s_2,\delta )=\frac{1}{{(2s_1+1)}^3}\sum _{\Vert \mathbf{y}-{\mathbf{c}}_1\Vert \le s_1}{I}_{\mathbf{x}}(\mathbf{y})-\frac{\delta }{{(2s_2+1)}^3}\sum _{\Vert \mathbf{y}-{\mathbf{c}}_2\Vert \le s_2}{I}_{\mathbf{x}}(\mathbf{y})$$ (4)

   where I_x denotes a local patch centered at voxel x. f(I_x|c₁, s₁, c₂, s₂, δ) denotes one Haar-like feature with parameters {c₁, s₁, c₂, s₂, δ}, where c₁ ∈ ℝ³ and s₁ are the center and size of the first positive block, respectively, and c₂ ∈ ℝ³ and s₂ are the center and size of the second negative block, respectively. Note that c₁ and c₂ refer to the center of the blocks relative to the patch rather than the overall image. δ ∈ {0, 1} switches between two types of Haar-like features (Fig. 3), with δ = 0 indicating one-block Haar-like features (Fig. 3(a)) and δ = 1 indicating two-block Haar-like features (Fig. 3(b)).

FIG. 3.

Illustration of 3D Haar-like features. Red and blue boxes denote positive and negative blocks. Green boxes denote local patches. One-block Haar-like features (a) compute the average intensity of an arbitrary position within the local patch, and two-block Haar-like features (b) compute the average intensity difference of two arbitrary positions within the local patch.

By changing the parameters {c₁, s₁, c₂, s₂, δ} in Eq. 4, we can compute various Haar-like features that capture the average intensities and intensity differences at different locations in the patch. Following the idea of feature bootstrapping in the random forest, only a subset of Haar-like features is sampled to represent each training voxel by randomizing the four parameters {c₁, s₁, c₂, s₂, δ}.

Once the feature vector (i.e., Haar-like features) and target vector (i.e., 3D displacement) of each training voxel are computed as described above, all training voxels/samples are used to train the regression forest in a tree-by-tree manner. As mentioned above, each binary decision tree is trained independently. Each tree uses different random subsets of training voxels and Haar-like features in order to increase the diversity among trained trees, thus potentially being able to improve the performance of the ensemble model.

Testing stage

The input of the testing stage is a new image, for which the method will localize the position of the target landmark. The testing stage consists of two sucessive steps: 1) 3D displacement prediction, and 2) landmark voting and localization.

1. 3D displacement prediction: In the first step, the 3D displacement of each voxel in the new image (also referred as testing voxel) is predicted using the regression random forest learned in the training stage.

2. Landmark voting and localization: After the 3D displacement of each testing voxel is predicted, it is used to vote for the potential landmark position. Specifically, for each testing voxel x ∈ ℝ³ with the predicted 3D displacement d̂, one vote is cast onto the voxel at ROUND(x + d̂), where function ROUND(.) rounds each dimension of the input vector to the nearest integer. After collecting votes from all image voxels, we obtain a landmark voting map, where the value of each voxel in the voting map denotes the number of votes it receives from all locations in the image. The landmark position is the voxel that receives the maximum vote.

III. MULTI-RESOLUTION COLLABORATION: MULTI-RESOLUTION REGRES-SION VOTING

As briefly mentioned in the introduction, the limitation of conventional regression-based landmark detection is the inclusion of faraway voxels in both training and testing stages. Because local appearances of faraway voxels are insensitive to deformations happened around landmark, faraway voxels are not informative to precise landmark position, although they are useful for rough localization.

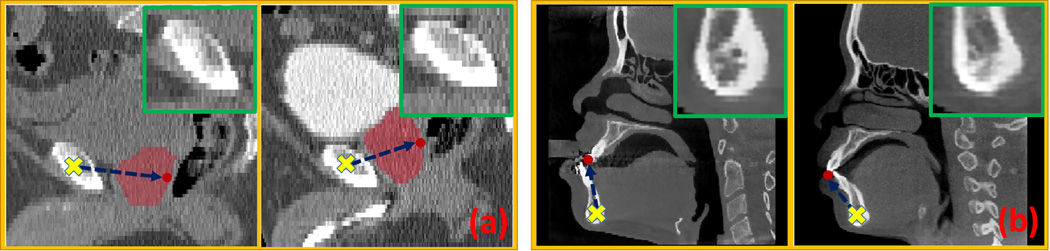
Fig. 4 provides two scenarios for illustration. In the CT prostate case (Fig. 4(a)), the relative position of the prostate landmark to the pelvic bone could change due to the inflation of bladder or rectum. Hence, voxels of the pelvic bone in different images may have distinct displacements to the same prostate landmark even though their local image appearances are quite similar. The same situation applies to the CBCT dental landmark detection (Fig. 4(b)). Due to the deformities of patients and also the individual shape differences of the mandible, the 3D displacement from mandible bottom to the upper frontal tooth landmark could change significantly across patients, even though the image appearances of mandible-bottom voxels look similar across patients. These facts cause the ambiguity of 3D displacements associated with faraway voxels, thus bringing problems to both training and testing of regression-based landmark detection.

FIG. 4.

Voxels (yellow crosses) with similar local appearances (green boxes) may have quite different 3D displacements (blue arrows) to the same landmark (red points) in different patient mages. (a) shows two cases for a prostate CT landmark, and (b) shows two cases for a dental CBCT landmark. The right-top corner of each image shows the zoomed-in local patch centered at he voxel marked by the yellow cross in each image. In the prostate cases, due to the indistinct rostate boundary, we overlap the manually labeled prostate region as red mask onto the original CT image for better visualization.

The above examples illustrate that faraway voxels are not informative for precise landmark detection. However, in the testing stage, without pre-knowing the landmark position, it is impossible to distinguish nearby voxels from faraway voxels. Actually, this dilemma can be well addressed by the multi-resolution strategy. In this paper, we propose a multi-resolution strategy named “multi-resolution regression voting” to address this issue.

Specifically, in the testing stage, a landmark is detected in a hierarchical way. In the coarsest resolution, the landmark position is roughly localized by landmark voting from the entire image domain. Once the rough landmark position is detected, voxels within distance ρ mm from it (also referred as ρ-neighborhood) are identified as nearby voxels and used to refine the landmark position in the finer resolution. With the increase of resolution, ρ is gradually decreased to exclude faraway and also less informative voxels in the landmark voting step. Alg. 1 gives the algorithm for our multi-resolution landmark detection.

The training of our multi-resolution strategy follows the same idea of hierarchical land-mark detection as described above. Specifically, a regression forest is independently trained at each resolution. The regression forest in the coarsest resolution is trained with training voxels sampled from the entire image domain, while the regression forest in the finer resolution is trained with training voxels sampled only from the ρ-neighborhood of the annotated landmark position in each training image. To take into account that nearby voxels are more informative than faraway voxels, a spherical sampling strategy is further proposed, which draws training voxels based on the distance of a voxel to the landmark. In this spherical sampling strategy, given a ρ-neighborhood of an annotated landmark x^LM and the number of training voxels N_sample to draw, the algorithm aims to distribute all training voxels evenly on each concentric sphere, which makes the concentric spheres with different radiuses have roughly the same number of training voxels (see illustration in Fig. 5). Mathematically, the sampling probability of each voxel can be computed as:

$$P_{\text{sample}}(\mathbf{x})=\{\begin{array}{cc}\frac{1}{\rho }\times \frac{1}{4\pi {\Vert \mathbf{x}-{\mathbf{x}}^{\mathrm{L}\mathrm{M}}\Vert }^2},\hfill & \text{if}{\Vert \mathbf{x}-{\mathbf{x}}^{\mathrm{L}\mathrm{M}}\Vert }_2\le \rho \hfill \\ 0,\hfill & \text{if}{\Vert \mathbf{x}-{\mathbf{x}}^{\mathrm{L}\mathrm{M}}\Vert }_2>\rho \hfill \end{array}$$ (5)

It is clear to see that the sampling probability is inversely proportional to the square distance of voxel x to the target landmark x^LM. Therefore, more training voxels would be drawn near the landmark than far away from the landmark, thus potentially improving the displacement

ALGORITHM 1.

Multi-resolution Regression Voting Algorithm

Input: Itest - a testing image with an unknown landmark position

ℛi, i = {Coarsest, ⋯, Finest} − ℛi is the regression forest trained in the i-th resolution

ρ0 - the voting neighborhood size for the 2nd coarsest resolution

Output: p - detected landmark position

Notations: 𝒩(x, ρ) - ρ-neighborhood of voxel x; 𝒩(Itest) - entire image domain of Itest

Initialization: ρ = ρ0

for i = Coarsest To Finest do

Re-sample image Itest to resolution i

/* Set the voting area Φ */

Φ = 𝒩(Itest)

if i ≠ Coarsest then

Φ = 𝒩(p, ρ)

ρ = ρ=2   /* Reduce the voting area by 23 in the next finer resolution */

end if

/* 3D displacement prediction */

for every voxel x in region Φ do

Predict the 3D displacement d̂(x) by regression forest ℛi

end for

/* Landmark voting */

Initialize voting map V to be zero and of the same size with Itest

for every voxel x in region Φ do

V (ROUND(x + d̂(x)) + = 1

end for

/* Landmark localization */

p = maxx V (x)

end for

Return p

prediction accuracy for nearby voxels. Algorithm 2 gives the detail implementation of our spherical sampling strategy.

FIG. 5.

(a) Illustration of the spherical sampling strategy. Yellow cross denotes a target landmark x^LM. Red circles denote concentric spheres. (b) An example of the distribution of training voxels with ρ = 60 mm

IV. INTER-LANDMARK COLLABORATION: CONFIDENCE-BASED LAND-MARK DETECTION

As will be shown in the experimental section, much more accurate landmark detection can be achieved with the proposed multi-resolution strategy than the conventional regression-based landmark detection. However, for certain challenging landmarks, where appearance variations are large, it is still difficult to accurately detect them independently from other landmarks. To improve their detection accuracies, it is necessary to exploit the spatial dependency between these challenging landmarks and other reliable landmarks.

Joint landmark detection [8] is a simple way to consider inter-landmark spatial relationship in the landmark detection step. It jointly predicts the 3D displacements of a voxel to multiple landmarks using a common regression forest, instead of using separate regression forests as in individual landmark detection. Sharing a common regression forest increases the prediction efficiency. However, it also brings a limitation. As detections of different landmarks may prefer different features and splitting functions in the random forest, land-mark detection accuracy could be compromised by sharing a common forest. Besides, all landmarks are equally treated in the joint detection without considering the detection confidence of each landmark. The detection accuracy of reliable landmarks may decrease due to the negative influence from challenging landmarks.

ALGORITHM 2.

Spherical Sampling Strategy

Input: xLM		- an annotated landmark position
	ρ	- the neighborhood size for sampling
	Nsample	- the number of training voxels requested
Output: sampled training voxel set 𝕊
Initialization: 𝕊 = ∅
for i = 1 to Nsample do
/* Randomly choose a concentric sphere based on the uniform distribution */
r = Random(0, ρ)
/* Randomly sample a point on the unit sphere based on the uniform distribution */
α = Random(0, 2π)
z = Random(−1, 1); x = sqrt(1 − z2)cosα; y = sqrt(1 − z2)sinα
/* Shift and scale it onto the selected concentric sphere */
xi = xLM + r[x y z]T
/* Push it into the sampled training voxel set 𝕊 */
𝕊 = 𝕊 ∪ {xi}
end for

To effectively exploit the spatial dependency among landmarks, we propose a confidence-based landmark detection strategy, which uses reliable landmarks (with high detection confidence) to guide the detection of challenging landmarks (with low detection confidence). There are generally two ways to determine reliable and challenging landmarks. In applications where the spatial dependency is explicitly known, such as one landmark is annotated according to other landmarks, the dependents are challenging landmarks, and those which they depend on are reliable landmarks. In other applications where no such dependency is provided, we first compute the variance of Euclidean distances between any pair of land-marks across subjects. Landmark pairs with small variances are considered spatially highly correlated. Next, we use cross validation to determine the detection accuracy of each land-mark. If two landmarks are spatially correlated and their validated detection accuracies are statistically different (p < 0.05), we use the landmark with higher detection accuracy as the reliable landmark to guide the detection of the one with lower detection accuracy. It should be noted that the above cross validation is performed on the training data, without using the testing data.

Suppose that LM_a is a challenging landmark and {LM₁, ⋯ LM_b, ⋯ LM_B} is a set of reliable landmarks, the following paragraphs introduce how the reliable landmarks can be used to guide the detection of challenging landmark in the confidence-based landmark detection.

• Training Stage: The regression forest training for B reliable landmarks is the same as described in Section III. To train regression forest for challenging landmark LM_a, the learned regression forests for the B reliable landmarks are first applied to detect their positions $\{{\mathbf{p}}_j^{\mathrm{L}{\mathrm{M}}_1},\cdots {\mathbf{p}}_j^{\mathrm{L}{\mathrm{M}}_b},\cdots {\mathbf{p}}_j^{\mathrm{L}{\mathrm{M}}_B}\}$ on each (j-th) training image $I_j^{\text{train}}$. Then, the 3D displacements between each training voxel x and detected reliable landmarks of the same training image are measured, i.e., $\{{\mathbf{p}}_j^{\mathrm{L}{\mathrm{M}}_1}-\mathbf{x},\cdots {\mathbf{p}}_j^{\mathrm{L}{\mathrm{M}}_b}-\mathbf{x},\cdots {\mathbf{p}}_j^{\mathrm{L}{\mathrm{M}}_B}-\mathbf{x}\}$. These displacements are named “context distance features”, which are used as additional geometric features for each training voxel and further combined with 3D Haar-like features to train the regression forests ${ℛ}_i^{\mathrm{L}{\mathrm{M}}_a}$, i = {Coarsest, ⋯, Finest}.

• Testing Stage: The testing stage follows a similar procedure as the training stage. First, the positions of B reliable landmarks $\{{\mathbf{p}}_{\text{test}}^{\mathrm{L}{\mathrm{M}}_1},\cdots {\mathbf{p}}_{\text{test}}^{\mathrm{L}{\mathrm{M}}_b},\cdots {\mathbf{p}}_{\text{test}}^{\mathrm{L}{\mathrm{M}}_B}\}$ are detected in the testing image using the multi-resolution strategy as described in Alg. 1. Then, to predict the 3D displacement of each testing voxel x to landmark LM_a, the context distance features $\{{\mathbf{p}}_{\text{test}}^{\mathrm{L}{\mathrm{M}}_1}-\mathbf{x},\cdots {\mathbf{p}}_{\text{test}}^{\mathrm{L}{\mathrm{M}}_b}-\mathbf{x},\cdots {\mathbf{p}}_{\text{test}}^{\mathrm{L}{\mathrm{M}}_B}-\mathbf{x}\}$ are calculated and combined with 3D Haar-like features as input to the trained regression forest ${ℛ}_i^{\mathrm{L}{\mathrm{M}}_a}$. Once the displacements of all testing voxels are estimated, the landmark voting and localization steps are the same as described in Section II.

It can be seen from the above descriptions that the only difference between confidence-based landmark detection and regular regression-based landmark detection is the introduction of “context distance features”, which bridges reliable and challenging landmarks. As the selected reliable landmarks are spatially highly correlated with the challenging landmarks, for any voxel, its displacements to the reliable landmarks must be also highly correlated with those to the challenging landmarks. Therefore, a voxel’s displacements to the reliable landmarks (context distance features) are very informative to regress its displacements to the challenging landmarks. With the help of these 3D displacements, the 3D displacement prediction accuracy for the challenging landmarks could be improved, eventually leading to better landmark detection accuracy.

V. EXPERIMENTAL RESULTS

In this section, we extensively evaluate our collaborative landmark detection framework for detecting landmarks on three datasets: 1) CT prostate images, 2) CBCT dental images, and 3) CT head & neck images. The organization of this section is as follows: the parameter setting of our method is first presented in Section VA. In all three datasets, the same parameter setting is used if not explicitly mentioned. Next, Section VB reports both training and testing time of our method. Finally, Sections VC to VE present the experimental results of our method on three datasets, respectively.

A. Parameter Setting

Multi-resolution Setting

Our multi-resolution landmark detection consists of 3 resolutions. The detailed parameters of each resolution are shown in Table I. The original spacings of CT and CBCT images in our dataset are about 1 × 1 × 3 mm³ and 0.4 × 0.4 × 0.8 mm³, respectively. To ease image processing, CT and CBCT images are linearly resampled to the isotropic volumes with spacings 1 × 1 × 1 mm³ and 0.4 × 0.4 × 0.4 mm³, respectively. These spacings denote the spacings used in the finest resolution.

TABLE I.

Parameter setting for each resolution.

	R3 (Coarsest)	R2 (Medium)	R1 (Finest)
Spacing (mm)	4×	2×	1×
Patch Size (voxel)	15	30	30 (dental, HN), 50 (prostate)

4× and 2× means that the spacing is four times and two times larger than that of the finest resolution, respectively. HN denotes head & neck.

Regression Forest Setting

The training parameters for regression random forest is provided in Table II. Similar as in [15], the maximum tree depth is large, which makes the trained trees as deep as possible. To prevent overfitting, a “Minimum Leaf Sample Number” is set to stop splitting if the number of samples falled into the node is less or equal than the specified value (i.e., 8). Empirically, we found the detection accuracy increases with the increase of 1) tree number K, 2) the number of bootstrapped thresholds, and 3) the number of bootstrapped features. However, the increase of “tree number K” will linearly increase the runtime for landmark detection. Similarly, the increase of “number of bootstrapped thresholds” and “number of bootstrapped features” will linearly increase the time and memory cost in the training stage. As a compromise, we adopt the parameters shown in Table II, which gives good results on all three datasets. Thus, we believe it should also work for other applications.

TABLE II.

Training parameter setting for regression random forest

Tree Number K	10	Maximum Tree Depth 𝒟	100
Number of Bootstrapped Thresholds	100	Number of Bootstrapped Features	2000
Minimum Leaf Sample Number	8

Other Parameters

The number of training voxels τ sampled from each training image is 10000. The local voting neighborhood size ρ₀ is 30 voxels. The block sizes {s₁, s₂} are limited to {3, 5}. For each one-block Haar-like feature, we randomly sample a value from {3, 5} for s₁. For each two-block Haar-like feature, we random sample one value with replacement from {3, 5} for s₁ and s₂, respectively. Both one-block and two-block features are used in the training.

B. Training and Testing Timing

Our experiments are conducted on a laptop with Intel i7-2720QM CPU (2.2 GHz) and 16 GB memory. All algorithms are implemented with C++. OpenMP is used to parallelize the code by multi-threading. The typical runtime to detect a landmark on a 512 × 512 × 61 image volume is about 1 second. The training time is 27 mins for one tree with 54 training images and the parameter setting described in Section VA. This training time is linearly proportional to the number of training images, the number of bootstrapped thresholds, and the number of bootstrapped features.

C. CT Prostate Dataset

Data Description

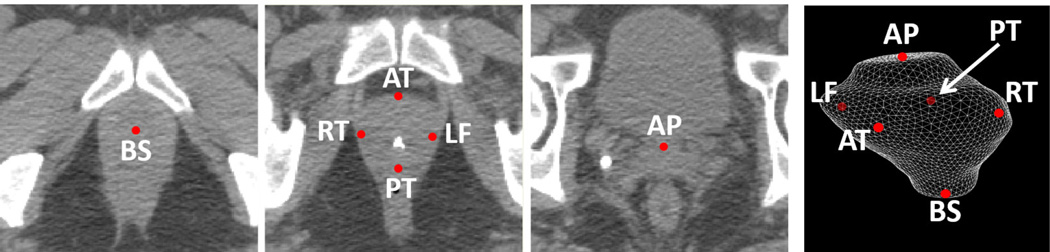
Our CT Prostate dataset consists of 73 CT images from 73 different prostate cancer patients acquired from North Carolina Cancer Hospital. A radiation oncologist has manually delineated the prostate in each CT image. Based on the delineation, six prostate landmarks are defined as shown in Fig. 6, where BS and AP are defined as the prostate centers in the most inferior and superior slices of the prostate volume, respectively. RT, LF, AT and PT are defined on the same central slice of the prostate volumn. They correspond to the rightmost, the leftmost, the most anterior, and the most posterior points of the prostate on the central slice, respectively.

FIG. 6.

Illustration of six prostate landmarks (transversal view along with 3D rendering).

Applications

These landmarks can be used to align the mean prostate shape onto the testing image for fast prostate localization [3]. The mean prostate shape is represented as a 3D mesh. To construct it, the marching cube algorithm [16] is first used to extract a 3D mesh from the manual prostate segmentation of each training image. Then, the coherent point drift algorithm [17] is used to build the vertex-to-vertex correspondence for all prostate meshes. Finally, all correspondent meshes are affinely registered into a common space, where the mean prostate shape is obtained by vertex-wisely averaging the aligned meshes. In the testing stage, once the prostate landmarks are detected in the new image, an affine transformation is estimated between the detected landmarks and their correspondent vertices on the mean prostate mesh. Then, the prostate in the new image can be quickly localized by applying the estimated transformation onto the mean prostate mesh. For details, readers might be interested in [3].

Evaluations

Four-fold cross validation is used to evaluate each component of our method. Specifically, the entire dataset is evenly divided into four folds. To test the detection accuracy of one fold, other three folds are used as training data to learn regression forests and construct mean prostate shape. Two metrics are used to evaluate the performance:

• Landmark Detection Error: Euclidean distance between the ground truth landmark position and the automatically detected landmark position.

• Prostate Overlap Ratio: Dice Similarity Coefficient (DSC) between manually annotated prostate and automatically localized prostate using six detected landmarks:

  $$\mathrm{D}\mathrm{S}\mathrm{C}=\frac{2|{\text{Vol}}_{\mathrm{g}\mathrm{t}}\cap {\text{Vol}}_{\text{auto}}|}{|{\text{Vol}}_{\mathrm{g}\mathrm{t}}|+|{\text{Vol}}_{\text{auto}}|}$$ (6)

  where Vol_gt is the voxel set of the manually annotated prostate, Vol_auto is the voxel set of the automatically localized prostate using the six landmarks, and |.| denotes the cardinality of a set.

• Single-resolution versus multi-resolution: Table III quantitatively compares the average landmark detection error between single-resolution and multi-resolution landmark detections. Both methods use uniform sampling and the same parameters to train regression random forest. We can clearly see that single-resolution landmark detection always leads to poor detection performance (i.e., mean error ~ 9mm). In contrast, by using three resolutions, our multi-resolution landmark detection significantly improves the detection accuracy by reducing the mean landmark detection errors by half. In terms of the prostate overlap ratio, compared with the best performance of single-resolution methods, which obtains the mean DSC 67.0 ± 11.6% on 73 cases, our multi-resolution method significantly improves the mean DSC to 81.0 ± 4.49%, which is comparable to the inter-operator variability of manual prostate delineation 81.0 ± 6.00% reported in [18].

• Uniform sampling versus spherical sampling: To justify the use of spherical sampling strategy, we quantitatively compare uniform and spherical sampling in both single-resolution and multi-resolution. Table IV presents the comparison results. We can see that the spherical sampling strategy significantly (p < 0.05) improves the detection accuracy in both single-resolution and multi-resolution. In terms of the prostate overlap ratio, the mean DSC obtained by multi-resolution landmark detection with spherical sampling is 81.0 ± 4.49%, which is also statistically (p = 4.9 × 10⁻⁴) better than the mean DSC 80.3 ± 5.05% obtained by multi-resolution landmark detection with uniform sampling.

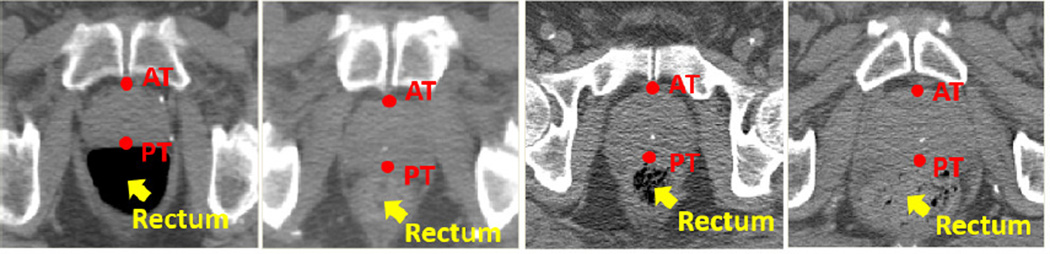
• Joint landmark detection versus confidence-based landmark detection: With the multi-resolution and spherical sampling strategies, we obtain detection errors 4.4 ± 3.0 mm for landmark PT and 3.8±2.1 mm for landmark AT. The inferior detection accuracy of landmark PT owes to the fact that its local appearance is much more complex than that of landmark AT (Fig. 7). As landmarks AT and PT are spatially highly correlated, we use landmark AT as reliable landmark to guide the detection of landmark PT.

TABLE III.

Quantitative comparison between single-resolution and multi-resolution landmark detections on the CT prostate dataset.

Method	Single-resolution			Multi-resolution
	Finest (R1)	Medium (R2)	Coarsest (R3)
Error (mm)	9.3 ± 5.1	8.7 ± 4.6	8.6 ± 4.6	4.4 ± 2.5
p-value	1.3 × 10−71	1.2 × 10−69	2.6 × 10−68	N/A

p-values are computed with paired t-test between single-resolution methods and our multi-resolution method. The Bold number indicates the best performance.

TABLE IV.

Quantitative comparison between uniform sampling and spherical sampling on CT prostate dataset.

Method	Single-resolution						Multi-resolution
	Finest (R1)		Medium (R2)		Coarsest (R3)
Sampling	Uniform	Spherical	Uniform	Spherical	Uniform	Spherical	Uniform	Spherical
Error (mm)	9.3 ±5.1	7.8 ±4.6	8.7 ±4.6	7.8 ±4.4	8.6 ±4.6	8.3 ±4.3	4.4 ±2.5	4.2 ±2.5
p-value	4.0 ×10−24	N/A	3.6 ×10−17	N/A	3.1 ×10−7	N/A	0.01	N/A

p-values are computed with paired t-test between every two methods. Bold number indicates the best performance.

FIG. 7.

Appearance variations of prostate landmarks AT and PT across patients (transversal view).

Table V shows the detection accuracy of the six landmarks by the confidence-based landmark detection (“Confidence”), and compares it with the detection accuracies of joint and individual landmark detections. All three methods use the same multi-resolution strategy proposed in this paper. We can see that joint landmark detection performs worse than individual landmark detection, which justifies our previous statement that sharing a common regression model among different landmarks would compromise the landmark detection accuracy.

TABLE V.

Quantitative comparison between joint landmark detection (Joint), individual landmark detection (Individual), and confidence-based landmark detection (Confidence).

Error (mm)	RT	LF	PT	AT	BS	AP	Average	p-value
Joint	4.7 ±2.7	4.4 ±2.7	5.2 ±3.4	3.9 ±2.1	4.9 ±2.7	6.3 ±4.5	4.9 ±3.2	1.8 ±10−13
Individual	4.1 ±2.1	3.9 ±2.4	4.4 ±3.0	3.8 ±2.1	4.7 ±2.5	4.5 ±2.9	4.2 ±2.5	0.01
Confidence	4.0 ±2.2	3.8 ±2.0	4.0 ±2.7	3.7 ±1.9	4.7 ±2.4	4.6 ±2.6	4.1 ±2.4	N/A

p-values are computed between confidence-based landmark detection and other methods.

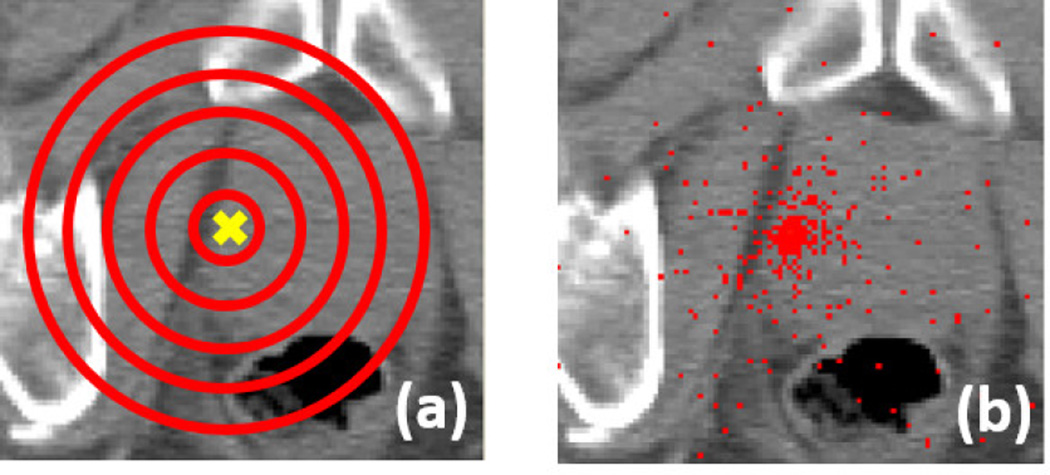
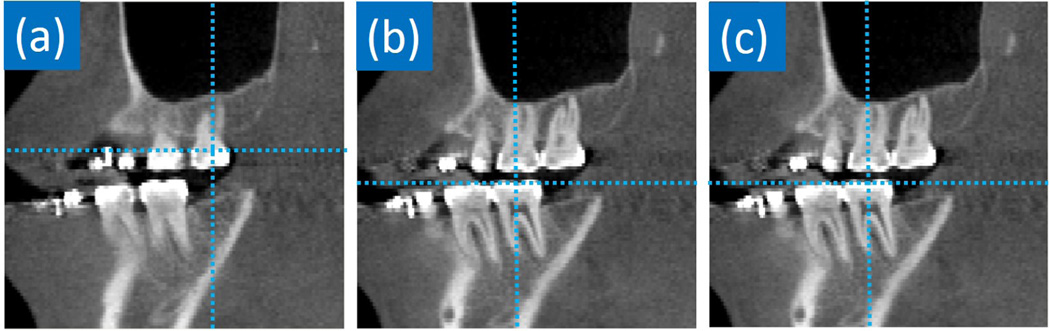
On the other hand, by comparing confidence-based landmark detection with individual landmark detection, we observe significant improvement (p-value=0.01) on detection accuracy of landmark PT, which improves from 4.4±3.0mm to 4.0±2.7mm (with 9% reduction in mean detection error) due to the guidance from landmark AT. Besides, it is surprising to see that the detection accuracies of most other landmarks also get slight improvements by using the context guidance from landmark AT. This may be explained by the weak spatial correlations associated with these prostate landmarks and landmark AT. Additionally, we also notice that the context guidance from landmark A T improves its own detection accuracy as well. This is because the sagittal plane of landmark AT can be localized very accurately and reliablely using our multi-resolution strategy (i.e., with mean and max errors 0.8±0.6 mm and 2.6 mm, respectively). With the guidance of such reliably localized sagittal plane, the 3D displacement along the lateral dimension could be more accurately predicted, compared with solely relying on the local image appearance. Consequently, votes are more clustered towards the correct sagittal plane (Fig. 8(d)), compared to the case without self-guidance (Fig. 8(c)). This difference finally leads to the improved detection accuracy of landmark AT.

FIG. 8.

(a) a transversal CT prostate slice. (b) the zoomed-in view of red rectangle in (a), where the red point indicates the position of landmark AT. (c) and (d) are the voting maps of landmark AT in the fine resolution (R1) without and with self-guidance, respectively.

In terms of prostate overlap ratio (DSC), joint landmark detection obtains 77.6±7.14%, which is worse than 81.0 ± 4.49% achieved by individual landmark detection. With confidence-based landmark detection, the DSC for prostate localization gets slightly improved to 81.1 ± 4.32%.

• Comparison with a multi-resolution classification-based method: Finally, we compare our method with a multi-resolution classification-based method [3] in Table VI. Both methods use the same number of resolutions and the same parameter setting for each resolution. Besides, the same type of Haar features are also used in both methods to encourage a fair comparison. We can see from Table VI that our method is significantly better than [3] in CT prostate landmark detection. For CT prostate landmarks, whose local appearances are indistinct, it is very likely to encounter local patches with similar appearances to the target landmark. In such situation, classification-based methods may suffer. In contrast, with the help from context image patches, regression-based methods are more robust, which explains why the regression-based method achieves higher detection accuracy in this task. In terms of prostate overlap ratio, our proposed method is also significantly higher than the classification-based method [3], which obtains DSC 73.3 ± 11.6% on this dataset.

TABLE VI.

Quantitative comparison between the multi-resolution classification-based landmark detection method [3] and our method.

Error (mm)	RT	LF	PT	AT	BS	AP	Average	p-value
Classification	6.5 ±3.7	6.5 ±4.8	7.4 ±5.3	4.9 ±2.7	6.2 ±3.5	8.8 ±6.7	6.7 ±4.8	1.0 ±10−29
Proposed	4.0 ±2.2	3.8 ±2.0	4.0 ±2.7	3.7 ±1.9	4.7 ±2.4	4.6 ±2.6	4.1 ±2.4	N/A

Bold numbers indicate the best performance.

D. CBCT Dental Dataset

Data descriptions

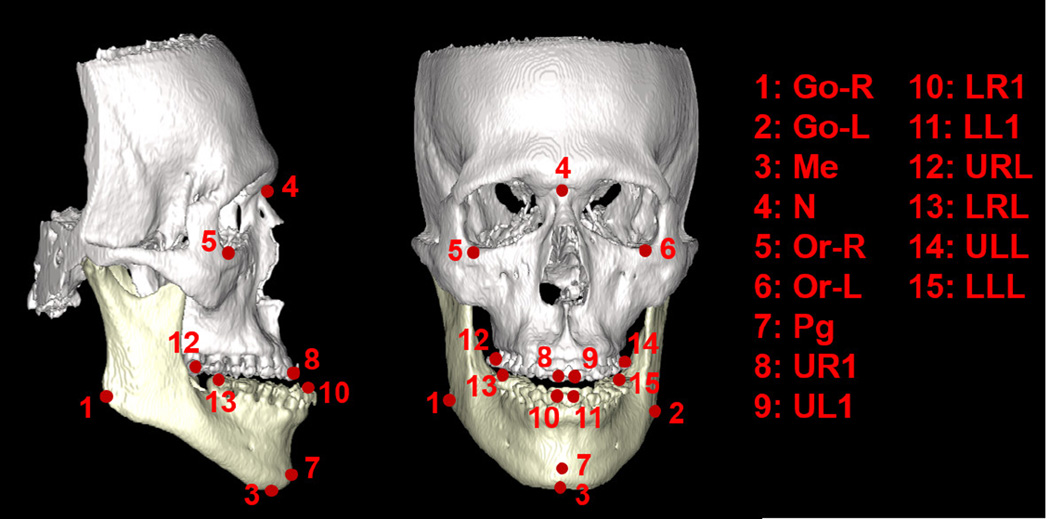
Our CBCT dataset consists 14 patients, each with one CBCT scan. These patients suffer from either one or two of the following deformities: 1) maxillary hypoplasia, 2) mandibular hyperplasia, 3) mandibular hypoplasia, 4) bimaxillary protrusion, and 5) condylar hyperplasia. In each CBCT image, 15 landmarks are manually annotated by a physician based on the CBCT segmentation (i.e., segmentation of maxilla and mandible), as shown in Fig. 9.

FIG. 9.

Illustration of 15 dental landmarks on a 3D rendering skull, where white and yellow parts of the skull indicate maxilla and mandible, respectively.

Motivations

These dental landmarks are important in deformity diagnosis and treatment planning. For example, they provide important symmetry measurements that could be used in the analysis of maxillofacial deformities [19]. They can also be used to estimate the patient-specific normal craniomaxillofacial shape for guiding the surgery planning [4]. Besides, by superposing dental landmarks of the same patient acquired from different time points, physicians can monitor temporal changes associated with orthodontic treatment and growth. Despite the clinical importance of dental landmarks, it is very time-consuming and labor-intensive to manually annotate these landmarks. Specifically, physician needs to first manually segment bony structures from CBCT and separate maxilla from mandible. This procedure often takes 5 hours. The purpose of segmentation is to separate different anatomical structures (e.g., maxilla and mandible) and remove metal artifacts. After that, 3D models are generated from the segmented CBCT image. Then, it takes another 30 mins for landmark annotation on 3D models. Therefore, it is clinically desirable to develop an automatic method that can efficiently and accurately localize dental landmarks directly from CBCT image without relying on the segmentation, which is often time-consuming to get.

Evaluations

Two-fold cross validation is used to evaluate our method on this dataset. Specifically, the entire dataset is divided into two folds, with 7 CBCT scans in each fold. To test the detection accuracy of one fold, CBCT images in the other fold are used to learn the regression forest for each landmark. To enrich the training dataset, we also add 30 CT images, considering the similar appearances of dental landmarks in CT and CBCT images (Fig. 10).

• Evaluation of the proposed strategies: Similarly as conducted in the previous dataset, Table VII to Table IX show the quantitative comparisons 1) between single-resolution and multi-resolution landmark detections, 2) between uniform and spherical sampling, and 3) between joint and individual landmark detections. These results indicate the effectiveness of our proposed strategies in improving landmark detection accuracy. It should be noted that confidence-based landmark detection is not used in this dataset because 1) the detection accuracies of all dental landmarks are already high with our multi-resolution strategy; 2) for landmarks with spatial dependency (i.e., two upper teeth landmarks UR1 and UL1, and two lower teeth landmarks LR1 and LL1), their detection accuracies are almost same, which makes it unlikely to get further improvement by using one landmark to guide the other.

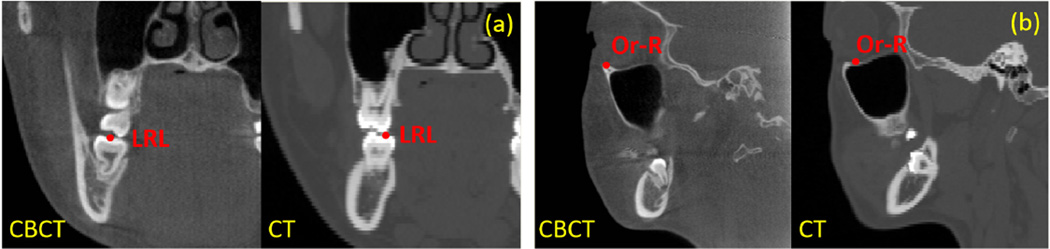
• Comparison with the multi-resolution classification-based method: Similarly, Table IX quantitatively compares our method with the multi-resolution classification based method [3]. We can see that our method significantly outperforms the conventional multi-resolution classification based method in almost all landmarks. By carefully analyzing the results, we notice that the improvement of our method over [3] is bigger in teeth landmarks than non-teeth landmarks. This is due to the metal artifacts mentioned in the introduction. For patients with dental braces, their CBCT images suffer severe streaking artifacts (Fig. 2), which make appearances of upper and lower teeth similar and hard to distinguish. As a result, the classification-based method may detect the lower tooth landmark on the upper teeth (Fig. 11(a)) because it checks only the local appearance. In contrast, with the help of context appearances, our regression-based method can easily overcome this limitation and produce a good detection result (Fig. 11(b)).

FIG. 10.

Qualitative comparison between the landmark appearances in CBCT and CT images.

TABLE VII.

Quantitative comparison between single-resolution and multi-resolution landmark detections on CBCT dental dataset.

Method	Single-resolution			Multi-resolution
	Finest (R1)	Medium (R2)	Coarsest (R3)
Error (mm)	12 ±8.6	10 ±7.5	9.3 ±7.0	2.8 ±4.2
p-value	8.8 × 10−48	4.1 × 10−46	7.2 × 10−52	N/A

p-values are computed with paired t-test between single-resolution methods and our multi-resolution method. Bold number indicates the best performance.

TABLE IX.

Quantitative comparisons between joint and individual landmark detections, and between the multi-resolution classification based method [3] and the proposed method on CBCT dental dataset.

Error (mm)	Go-R	Go-L	Me	N	Or-R	Or-L	Pg	UR1
Joint	3.8 ±2.0	2.5 ±2.0	2.2 ±1.1	2.2 ±1.5	3.7 ±3.0	3.0 ±1.2	1.9 ±1.3	5.6 ±4.3
Classification [3]	2.5 ±2.4	2.5 ±1.4	1.6 ±1.3	1.4 ±1.8	1.6 ±0.9	1.3 ±1.2	1.5 ±0.7	1.4 ±1.4
Proposed (Individual)	1.6 ±1.0	1.7 ±1.0	1.1 ±0.4	1.2 ±0.7	1.3 ±0.9	1.5 ±0.9	1.2 ±0.7	0.9 ±0.7
Error (mm)	UL1	LR1	LL1	URL	LRL	ULL	LLL	Average
Joint	5.5 ±4.5	6.0 ±4.4	6.8 ±3.3	6.8 ±3.6	3.8 ±3.6	4.5 ±2.9	4.9 ±4.2	4.2 ±3.5
Classification [3]	1.7 ±2.1	2.6 ±1.9	2.2 ±1.6	3.6 ±4.3	1.8 ±1.4	2.7 ±3.7	4.7 ±4.4	2.2 ±2.5
Proposed (Individual)	0.9 ±0.4	1.9 ±1.1	1.9 ±1.5	2.0 ±0.7	1.5 ±0.9	1.8 ±0.9	1.8 ±0.8	1.5 ±0.9

Bold numbers indicate the best performance.

FIG. 11.

Visual comparison between the classification-based method [3] and our regression-based method in detecting landmark LLL on a CBCT scan. (a) Landmark position detected by the classification-based method. (b) Landmark position detected by our method. (c) Ground-truth landmark position.

E. CT Head & Neck Dataset

Data descriptions

Our CT head & neck dataset is acquired from PDDCA (http://www.imagenglab.com//pddca_18.html). PDDCA version 1.1 comprises 40 patient CT images from the Radiation Therapy Oncology Group (RTOG) 0522 Study (a multi-institutional clinical trial led by Dr. Kian Ang). Each CT image has five bony landmarks manually annotated: chin (chine), right condyloid process (mand r), left condyloid process (mand l), odontoid process (odont proc), and occopital bone (occ bone). Fig. 12 shows the positions of these landmarks on one subject.

FIG. 12.

Illustration of the positions of five bony landmarks in CT head and neck dataset.

These bony landmarks are used to align CT images of different patients for correcting orientation and translation incurred by different patient setups. The accuracy of alignment could largely influence the later processing steps, e.g., multi-atlas based tissue segmentation. Therefore, it is important to accurately detect these landmarks.

This dataset is interesting because it provides explicit spatial dependency between land-marks, which could be used to evaluate our confidence-based landmark detection strategy. Specifically, landmark “occ bone” is manually annotated on the same sagittal slice of land-mark “chin”.

Evaluation

Four-fold cross validation is used to evaluate our method on this dataset. To test the detection accuracy of one fold, CT images in other folds are used to learn the regression forest for each landmark.

• Evaluation of the proposed strategies: Similarly as done in the previous datasets, Table X to Table XI provide quantitative comparisons 1) between single-resolution and multi-resolution landmark detections, and 2) between uniform and spherical sampling, respectively. The results indicate the effectiveness of the proposed multi-resolution and spherical sampling in improving landmark detection accuracy.

• Joint landmark detection versus confidence-based landmark detection: Since landmark “occ bone” is annotated according to landmark “chin”, we exploit this dependency in our confidence-based landmark detection. Specifically, landmark “chin” is used as reliable landmark to help detect landmark “occ_bone”. Table XII quantitatively compares joint landmark detection (Joint), individual landmark detection (Individual), with the confidence-based landmark detection (Confidence). Similar to the previous datasets, individual landmark detection outperforms joint landmark detection. However, compared to “Confidence”, its detection accuracy is still limited. By incorporating context distance features, “Confidence” achieves the best detection accuracy for “occ bone”, by reducing the landmark detection error more than half, compared to “Individual”.

• Comparison with the multi-resolution classification-based method [3] : Table XII quantitatively compares our method with the multi-resolution classification based method [3] on this dataset. We can clearly observe the better detection accuracy obtained by our method. Particularly, the detection error of landmark “occ bone” is reduced by almost two thirds with our method, compared to [3], which indicates the effectiveness of our collaborative landmark detection framework over the conventional classification-based method.

TABLE X.

Quantitative comparison between single-resolution and multi-resolution landmark detections on CT head & neck dataset.

Method	Single-resolution			Multi-resolution
	Finest (R1)	Medium (R2)	Coarsest (R3)
Error (mm)	12 ±6.9	9.2 ±5.7	8.9 ±5.6	2.6 ±2.1
p-value	3.0 × 10−42	7.2 × 10−36	1.5 × 10−35	N/A

p-values are computed with paired t-test between single-resolution methods and our multi-resolution method. The bold number indicates the best performance.

TABLE XI.

Quantitative comparison between uniform sampling and spherical sampling on CT head & neck dataset.

Method	Single-resolution						Multi-resolution
	Finest (R1)		Medium (R2)		Coarsest (R3)
Sampling	Uniform	Uniform	Uniform	Spherical	Uniform	Spherical	Uniform	Spherical
Error (mm)	12 ±6.9	12 ±6.9	9.2 ±5.7	7.8 ±5.3	8.9 ±5.6	7.9 ±5.3	2.6 ±2.1	2.5 ±2.0
p-value	1.1 ×10−19	1.1 ×10−19	1.8 ×10−19	N/A	1.2 ×10−13	N/A	8.2 ×10−4	N/A

p-values are computed between every two methods. The bold number indicates the best performance.

TABLE XII.

Quantitative comparison between the multi-resolution classification based method [3], joint landmark detection (Joint), individual landmark detection (Individual), and confidence-based landmark detection (Confidence) in the CT head & neck dataset.

Error (mm)	chin	mand_r	mand_l	odont_proc	occ_bone	Average	p-value
Classification [3]	2.1±1.0	3.6±2.4	3.7±2.3	2.3±1.3	6.5±4.2	3.6±2.9	1.2 × 10−14
Joint	2.2±1.0	2.8±1.9	2.9±1.7	2.1±1.3	6.5±4.0	3.3±2.7	3.6 × 10−7
Individual	1.6±0.7	2.2±1.2	2.4±1.1	1.7±1.1	5.1±3.6	2.6±2.2	1.9 × 10−5
Confidence	1.6±0.7	2.2±1.2	2.4±1.1	1.7±1.1	2.3±1.4	2.0±1.2	N/A

p-values are computed between “Confidence” and the other methods. Bold numbers indicate the best performance.

VI. CONCLUSION

In this paper, we propose a collaborative landmark detection framework to improve the detection accuracy of conventional regression-based method. Specifically, two strategies are respectively proposed. The first multi-resolution strategy detects a landmark location from the coarsest resolution to the finest resolution. It improves detection accuracy by gradually filtering out faraway voxels during the landmark voting step. The second confidence-based landmark detection strategy utilizes reliable landmarks to guide the detection of challenging landmarks. It improves detection accuracy by exploiting inter-landmark spatial relationship. Validated on 127 CT/CBCT scans from three applications, our method obtains accurate detection results with the speed of 1 second per landmark. Besides, it also shows better performance than the conventional classification-based and regression-based approaches.

VII. DISCUSSION

Ground-truth Annotations

In the prostate application, the landmark positions were annotated by a radiation oncologist and then reviewed by another radiation oncologist, in order to minimize the potential bias. In CBCT dental application, both maxilla and mandible are first segmented and separated by physician from CBCT image. Then, the segmentation is utilized to construct a 3D surface model. Finally, landmarks are manually annotated on the constructed 3D model. Compared to the manual annotation on CBCT, our manual annotation on the constructed 3D surface model is much more reliable, suffers less inter-patient variation, and also potentially reduces the bias in manual annotation. As for the head-neck dataset, we acquired it from the public site. Thus, we have limited information regarding how the manual annotation was performed. But our visual inspection shows that all land- marks are annotated on the distinctive anatomical structures. Thus, we believe that the quality of manual annotation in this dataset is sufficiently good to serve as the ground-truth for evaluation.

Assessment of Landmark Detection Accuracy

To assess landmark detection accuracy of our method, we can compare it with intra-operator or inter-operator variation of manual landmark annotation. Specifically, the inter-operator variation of CT prostate landmark annotation is about 5 mm as shown in [3]. In comparison, our method yields detection error 4.2 ± 2.5 mm, which is clinically acceptable. In the CBCT-based dental application, less than 2 mm detection error is clinically acceptable. Based on the references [20, 21], the intra-operator and inter-operator variations of dental landmark detection from 3D CT and CBCT are mostly from 1:5 mm to 2 mm. In comparison, our method yields detection error 1.5 ± 0.9 mm, which is thus acceptable. In the head-neck application, we didn’t find any reference standard. But, considering the slice thickness 3 mm and our method obtained detection error 2.0 ± 1.2 mm, we believe the accuracy of our method is sufficient for many applications, such as for global alignment.

Appearance Features

In our method, Haar-like features are used as the only appearance features, which have shown to be effective in CT/CBCT images. However, if we want to extend our method to landmark detection on MR images, which have more complex textures than CT images, it may be necessary to add other sophisticated features. Recently, deep learning attracts much attention in machine learning and computer vision. Its main idea is to automatically learn useful appearance features from data, instead of handcrafting features as often done in previous researches. We are planning to borrow deep learning techniques, such as convolution neural network, to learn high-level discriminant features to further boost the detection accuracy of our method, and also extends it to detect landmarks on other modalities, such as MRI.

Large-scale Landmark Detection

We are also targeting the large-scale landmark detection problem, where hundreds of landmarks need to be detected on a single image. In such case, the efficiency may be a concern if using the current framework, as the detection time of our method is linear to the number of landmarks. To address this issue, we are considering to split landmarks into spatially coherent groups, and use joint landmark detection for detecting landmarks within the same group. Similarly, the confidence-based landmark detection can be also applied by first detecting landmarks in reliable groups, and then using them to guide the detection of landmarks in challenging groups.

Transfer Learning

Another interesting direction, which may be worth exploring, is the transfer learning for landmark detection, as we have slightly touched in the CBCT dental dataset. Specially, due to the limited number of CBCT images, we added 30 CT dental images and mixed them with CBCT images for enriching the training dataset. Experimental results showed that the average detection accuracy is significantly (p < 0.05) improved from 2.0 ± 2.1 mm to 1.5 ± 0.9 mm, which justifies the benefit of using additional CT images for training. The same situation may happen in many cases. More validations are still required to answer the question whether high-quality images are indeed helpful in improving the accuracy of landmark detection in low-quality images.

TABLE VIII.

Quantitative comparison between uniform sampling and spherical sampling on CBCT dental dataset.

Method	Single-resolution						Multi-resolution
	Finest (R1)		Medium (R2)		Coarsest (R3)
Sampling	Uniform	Spherical	Uniform	Spherical	Uniform	Spherical	Uniform	Spherical
Error (mm)	12 ±8.6	3.9 ±4.1	10 ±7.5	4.4 ±3.9	9.3 ±7.0	5.2 ±3.8	2.8 ±4.2	1.5 ±0.9
p-value	7.3 ×10−35	N/A	3.7 ×10−25	N/A	2.3 ×10−19	N/A	2.0 ×10−6	N/A

p-values are computed with paired t-test between every two methods. Bold number indicates the best performance.