Comparing Postural Stability Entropy Analyses to Differentiate Fallers and Non-Fallers

Abstract

The health and financial cost of falls has spurred research to differentiate the characteristics of fallers and non-fallers. Postural stability has received much of the attention with recent studies exploring various measures of entropy. This study compared the discriminatory ability of several entropy methods at differentiating two paradigms in the center-of-pressure (COP) of elderly individuals: 1.) eyes open (EO) versus eyes closed (EC) and 2.) fallers (F) versus non-fallers (NF). Methods were compared using the area under the curve (AUC) of the receiver-operating characteristic (ROC) curves developed from logistic regression models. Overall, multiscale entropy (MSE) and composite multiscale entropy (CompMSE) performed the best with AUCs of 0.71 for EO/EC and 0.77 for F/NF. When methods were combined together to maximize the AUC, the entropy classifier had an AUC of for 0.91 the F/NF comparison. These results suggest researchers and clinicians attempting to create clinical tests to identify fallers should consider a combination of every entropy method when creating a classifying test. Additionally, MSE and CompMSE classifiers using polar coordinate data outperformed rectangular coordinate data, encouraging more research into the most appropriate time series for postural stability entropy analysis.

3.0 Introduction

Numerous studies examining the issue of fall risk have been conducted recently as attention has been placed on both the health and financial costs of falls in the elderly and other at-risk groups. Postural stability and stabilometric measures from quiet standing are able to identify differences in individuals with a history of falls (i.e., fallers) from individuals with no history of falls (i.e., non-fallers) ^1–6. However, the conclusions about postural sway as a clinical predictor of falls are remain unclear ⁷. Recently, various dynamical system analyses have been applied to the center-of-pressure (COP) time-series to help further clarify the associations between quiet standing and fall history. Within these tools, entropy measures, which quantify the amount of information contained within the signal (Shannon entropy, Renyi entropy) and the complexity and regularity of the signal (approximate entropy, sample entropy), have shown utility ^8–11.

The two forms of entropy currently used to analyze biomechanical data are those that quantify the amount of information contained within the signal (state entropy) and those that examine the repetition of patterns within a signal (sequence entropy). The first type of entropy is derived from Shannon’s information theory ¹² and evaluates the repetition of certain states within a signal. Shannon (ShanEn) and Renyi (RenyEn) entropies are this form and are measures of the probability of the signal occupying discrete states. Within COP time-series data, Shannon and Renyi entropies examine the frequency that a COP position (an x, y vector) is visited throughout the signal without regarding the path to or from that position ¹⁰. In comparison, the second type, which includes approximate entropy (ApEn) and its derivatives (sample entropy, multiscale entropy, composite multiscale entropy), examines the frequency of series of values rather than single values. These sequence entropies evaluate the probability that particular values occur within a signal given that the sequence preceding that value is similar to a template sequence. Thus, while Shannon and Renyi entropies consider the repetition of instantaneous states, the sequence entropies consider the repetition of paths.

Using sample entropy (SaEn), Borg & Laxåback ⁸ found that the anterior-posterior (AP) COP data was more complex, as indicated by higher entropy values representing fewer instances of pattern repetition within the AP COP data, in fallers compared to non-fallers during eyes closed quiet standing. Costa et al. ⁹ used a multiscale version of sample entropy known as multiscale entropy (MSE) and found opposite results; the complexity (i.e. irregularity of patterns within the data) of the anterior-posterior (AP) COP data was significantly higher for non-fallers. Ramdani et al. ¹³ used recurrence quantification analysis entropy (RQAEn) to differentiate fallers from non-fallers using the mediolateral (ML) COP signals. In a different application of these methods, Gao et al. ¹⁰, observed a recovery in postural stability over time in athletes who sustained a concussion, which often causes short- to long-term balance impairments ^{14, 15}, using the Shannon and Renyi entropies of the COP time-series. Though the COP entropy analyses have shown usefulness, the number of similar entropy algorithms and sometimes contradictory results can be confusing to researchers who wish to perform these analyses.

While the difference between state and sequence entropies is important in selecting the correct algorithm for a particular analysis, multiple sequence entropy algorithms exist which can further complicate the decision. ApEn was introduced by Pincus ¹⁶ as a practical application of the Kolmogorov-Sinai (K-S) entropy. Nearly all other forms of sequence entropy follow from ApEn. Unlike K-S entropy, which requires an infinite (or near-infinite) time-series and zero signal noise, ApEn can be used with relatively short data lengths and with signals containing noise. ApEn utilizes three parameters: the sample length, N, the tolerance for similitude, r, and the length of the template vector, m. ApEn is the sum of natural logs of a conditional probability that a data point v_i will be similar to the template point u_i given that the m-dimensional preceding vector [v_i−m,…, v_i−1] is similar to the template vector [u_i−m,…,u_i−1], where similarity is defined as within ± r for each entry of the m-dimensional vector. Because ApEn involves taking the natural log of a conditional probability, the algorithm includes self-matches, v=u. This introduces a bias towards low ApEn values for shorter time series ¹⁷ caused by the decrease in the number of vectors throughout the signal that match the reference vector, thereby increasing the weight of the self-match. Therefore, not only does the selection of m and r affect the outcome, but the data length N carries significant weight as well.

Sample entropy (SaEn) was developed to reduce the effects of sample length seen in ApEn by eliminating self-matches ¹⁸. The process is identical to that used by ApEn, except that the constraint v ≠ u is imposed. Complexity values obtained from SaEn and ApEn are limited to the time scale used in the sampling frequency of the data acquisition in the experimental set up. Multiscale entropy (MSE) offers another variation on ApEn and SaEn, calculating either value at a variety of time scales by averaging the points along the time series at various scales using a coarse-graining technique ¹⁹. In the MSE method with time scale τ, the length of the coarse-grained time series is reduced by the factor of τ which partially insulates MSE from the record length sensitivities of SaEn and ApEn in shorter time series ²⁰. Furthermore, composite multiscale entropy (CompMSE) uses a moving average procedure to compute MSE in the time scale τ. CompMSE then takes the mean value of MSE over the time series to reduce the effect of shortening the time series due to the scale factor ²¹.

Similar to the previously described entropies, RQAEn has also been applied to biomechanical and COP data. Unlike the state and sequence entropies discussed above, RQAEn is an entropy algorithm applied to the recurrence plot rather than to the time-series directly. RQAEn uses ShanEn to determine the probability of line segment lengths from the recurrence plot ^{22, 23}. Even though ShanEn is used in the analysis, the recurrence plot is formulated from a reconstructed state-space often involving time-delayed embedding ¹³. RQAEn quantifies the probability that nearby state-space trajectories remain nearby as the signal moves forward in time. RQAEn is thus similar to the sequence entropies described above in that it measures the repetition of patterns; yet unique in that it measures the length of time similar patterns persist.

Though all these techniques are called entropy, the calculations and the interpretation of results are quite different from method to method. Previous studies have compared one or more measures against each other to assess their sensitivity to data length ¹⁷ and noise ²⁴ but no study has examined all measures side by side to look at the sensitivity to changes in a large population. Specifically, no study has examined which measures may be most sensitive to the COP changes between fallers and non-fallers. Such a comparison, across many different forms and types of COP entropy analyses may be useful to researchers and heath care professionals in generating an effective fall risk assessment tool. Additionally, a comparison of two common sensory feedback conditions (eyes open, eyes closed) across a wide range of entropy measures can serve as a guide to future researchers on any COP analysis. To address this need, this study sought to compare the ShanEn, RenyEn, ApEn, SaEn, MSE, CompMSE, and RQAEn calculated from the COP data during eyes open and eyes closed quiet standing in both fallers and non-fallers. The goals of this study were to compare the discriminatory ability of different entropy methods to two paradigms 1.) eyes open versus eyes closed postural stability which are known to elicit different postural responses ²⁵ and 2.) fallers and non-fallers postural stability.

4.0 Materials and Methods

4.1 Participants

Seventy-six elderly individuals, mean age (SD) = 74.4 (9.0) years, were recruited from the northern Virginia area for this study as part of the Northern Virginia Fall Prevention Coalition. One subject’s data were not analyzed because it was missing the eyes closed postural stability measurement. Participant demographics for the remaining 75 participants is shown in Table 1. The data was collected as part of a free Community Fall Risk Screening Event that involved meetings with medical personnel and pharmacists, and a series of mobility tasks for the elderly at local community centers. Participants were required to be generally healthy with no history of musculoskeletal disorders. Exclusion criteria included cardiovascular problems (e.g. chronic heart failure, enlarged heart, weakened heart, foot pain associated with chronic diabetes, etc.), respiratory problems (e.g. difficulty breathing during normal walking), neurological problems (e.g. stroke resulting in weakness in one of both legs, Parkinson’s disease), and musculoskeletal problems (e.g. persistent muscle weakness, recent ankle injury, routine back/neck pain, etc.). All participants signed an informed consent form and the procedure was reviewed and approved by the Virginia Tech Institutional Review Board.

Table 1.

Mean (SD) demographic data for all participants, stratified into fallers and non-fallers.

	Fallers	Non-Fallers
N	7M/23F	9M/36F
Height (cm)	167 (9)	167 (10)
Mass (kg)	76.8 (18.0)	73.9 (15.2)
Falls in past 12 months	2.4 (1.8)	0 (0)

4.2 Experimental Procedure

Participants were asked to stand quietly with the arms at their sides for one minute while standing on a force plate (AMTI, Model # BP400600-2K, Advanced Mechanical Technology, Inc., Watertown, MA, USA) with their eyes open (EO). The participants were then given a short break to sit down before repeating the procedure with their eyes closed (EC). Other tasks, which were recorded but not presented here, included a timed get-up and go task, a ten-meter walk task, and a sit-to-stand task. During the postural stability tasks, the participants’ stance width was standardized to 6 inches between the inside of their feet to be consistent with the recommended standardized foot placement for balance testing ²⁶ and to control for the effect of stance width variation on postural stability ^{27, 28}. The postural stability data COP data were collected through the force plate at 1000 Hz for both the eyes closed and eyes open conditions for the complete sixty-second duration.

4.3 Data Analysis

COP data were calculated using the force plate data and were down-sampled to 100 Hz to reflect the upper limit for sampling postural stability data ²⁹. Traditional COP measures of 95% ellipsoidal area, COP velocity, ML standard deviation (x SD) and AP standard deviation (y SD) were calculated and compared to the entropy methods. For all entropies except RenyEn and ShanEn, non-stationarities in the data were removed using bivariate empirical mode decomposition ³⁰, removing intrinsic mode functions (IMFs) with frequencies below 1 Hz ⁹. The full 60 seconds of data were analyzed using each of the entropies discussed below. All analyses were performed in MATLAB (MATLAB and Statistics Toolbox Release 2014a, The MathWorks, Inc., Natick, Massachusetts, United States).

4.3.1 Renyi and Shannon Entropy

RenyEn is defined as the sum of the probabilities that a data point will fall within one of the pre-specified discrete areas within the overall signal ¹⁰. Following the procedure described by Gao et al. ¹⁰, RenyEn was calculated using a box size of 5 mm × 5 mm. The Renyi order α can be adjusted to increase or decrease the influence of outliers within the data. In this study, α was set at 2 to match previous studies which calculated RenyEn for COP data ¹⁰.

For data with limited outliers, RenyEn can be modified to take the form of Shannon entropy. For calculating ShanEn, the generalized equation for RenyEn is calculated for an order of α → 1 ³¹. Although higher order RenyEn can eliminate skew from the less visited areas, ShanEn can provide information on the characteristics of the data. For our analysis of ShanEn, the same window size as that of the RenyEn (5 mm × 5 mm) was chosen for consistency. Both RenyEn and ShanEn represent the amount of information within a signal. Thus, higher RenyEn and ShanEn values indicate the COP exists more equally across the various states (boxes). Lower RenyEn and ShanEn values indicate the COP tends to reside within some discrete areas more often than others.

4.3.2 Approximate and Sample Entropy

Approximate entropy (ApEn) analyzes the predictability and regularity of changes in a time-series. A full description of the procedure was presented by Pincus ¹⁶. Succinctly, ApEn is a conditional probability measure of the system’s regularity described by 

$$\mathit{ApEn}(m,r,N)=\text{average}\text{over}i\text{of}log\left[\begin{array}{c}\text{conditional}\text{probability}\text{that}\mid u(j+m)-u(i+m)\mid \le r\\ \text{given}\text{that}\mid u(j+k)-u(i+k)\mid \le r\text{for}k=0,1,\dots ,m-1\end{array}\right],$$ (1)

where u is a time series of data, m defines the length of the compared vectors, r defines the tolerance of the comparison, and N defines the length of the time series. Our analysis used N = 6000 (60 seconds at 100 Hz), m = 3, and r = 20% of the standard deviation of the COP values, based on the original values used by Pincus ¹⁶.

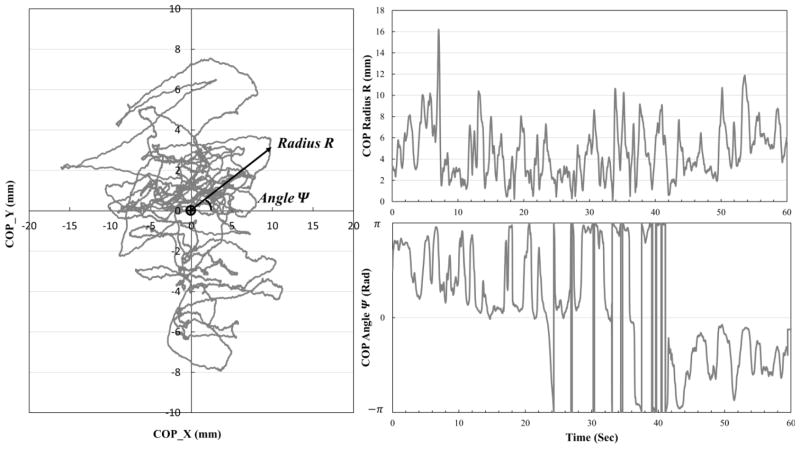
In contrast to previous studies, the COP position radius, R = √(x²+y²), with the origin R = 0 at the centroid of the data, and the position angle, Ψ = tan⁻¹(y/x), (Figure 1) were used instead of values for the separate x and y COP coordinates ^{8, 9, 13}. While using the x and y coordinates independently can yield information about the AP (forward-backward) and ML (side to side) control, the position vector represents the overall displacement from mean. If the COP trace lies within an individual’s basin of stability ^32–34, the radius R represents the deviation from the center of that basin towards the unstable edges. Furthermore, changes in Ψ represent the tendency of the individual at returning back to the mean COP position (e.g. no change in Ψ shows a straight path towards or away from the origin, while changes in Ψ demonstrates a circuitous route away from or back to the origin). However, the use of Ψ did introduce a discontinuity in the data when the bounds of +π or −π were crossed, as seen in the right half of Figure 1. To address this, an additional condition was applied to the matching criteria in Equation 1 for all Ψ time-series to adjust the tolerance r to reflect this discontinuity:

$$\text{Additional}\text{Matching}\text{Criteria}\text{for}\mathit{\Psi }\mid u(j+m)-u(i+m)\mid \le r\mathit{OR}\mid u(j+m)-u(i+m)\mid \ge (2\pi -r).$$ (2)

Figure 1.

(Left) Diagram of the two time-series (radius R and angle Ψ) used in the analysis. The radius R is calculated for each point in time as the distance from the mean of the entire COP trace to that point. Similarly, the angle Ψ was calculated for each point in time using the mean of the time series as the origin. (Right) The one dimensional time-series R (upper right) and Ψ (bottom right) for one individual during eye’s open quiet standing.

Sample entropy (SaEn) is a slight modification to ApEn which eliminates self-matches. Presented in detail by Richman & Moorman ¹⁷, SaEn provides a measure that is less sensitive to the data length N. In this analysis, SaEn was calculated using the same parameters m = 3, r = 20% standard deviation that were used in the ApEn calculation.

Higher ApEn and SaEn values represent more complex signals with less regularity ¹⁶. Thus, low entropy signals have patterns that are more likely to repeat and repeat for longer durations. Because ApEn and SaEn are nearly identical calculations, they tend to follow the same direction; signals with high ApEn will likely have high SaEn, and vice versa. However, directionality differences can occur in signals with low ApEn values. At low ApEn, self-matches of v=u account for a larger proportion of pattern matches. Removing those self-matches can result in greater SaEn compared to ApEn. For identical signals, different trends between SaEn and ApEn likely represent a large proportion of self-matches in the ApEn calculation.

4.3.4 Multiscale and Composite Multiscale Entropy

While ApEn and SaEn examine the regularity of signals, those methods do not account for the varying time scales within the data. Multiscale entropy (MSE) calculates the SaEn of a signal over multiple time scales to address multiple characteristic time scales ¹⁹. In this analysis, MSE values were calculated for 10 time scales (τ = 1 to 10), corresponding to characteristic timescales from 0.04 to 0.4 seconds, for the COP radius R and angle Ψ. For consistency with SaEn and ApEn methods, the vector length and tolerance were defined as m=3 and r= 20% of the standard deviation. For each data series, complexity indices are computed by calculating the slope of linear least square fit and the area under the MSE versus scale factor curve. The slope represents the change in entropy across increasing time scales, while the area represents the cumulative magnitude of entropy of the signal across multiple time scales. Composite multiscale entropy (CompMSE) is an extension of MSE where, for each time scale τ, there are τ coarse-grained time series ²¹. As such, the corresponding MSE values are obtained by shifting averaging windows from the data point i to i + τ, consecutively. The same parameters and complexity indices used for MSE were used for CompMSE. Both MSE and CompMSE were calculated with the R, Ψ and x, y time series to compare the results of each choice of time series. Both MSE and CompMSE tend to produce very similar results. However, CompMSE tends to provide better estimates at high scale factors because the length of the data series is better preserved than during MSE.

4.3.5 Recurrence Quantification Analysis Entropy

The RQAEn was calculated according to the procedure outline by Ramdani et al. ¹³ using code from Hasson et al. ³⁵. Rather than use individual x and y coordinates, the COP radius, R, and angle, Ψ, were used for RQAEn in order to be consistent across each method. This study used the same parameters as Ramdani et al. ¹³ who examined RQAEn of COP data in elderly fallers and non-fallers. An embedding dimension of m = 8, a time delay of T = 6, and a radius of ε = 30% of the mean of all distances were used for this study to be consistent with previous results ¹³. To correct for the discontinuity in the Ψ time-series, single dimension distances within the reconstructed phase space greater than 2π − ε, indicating a boundary crossing, were transformed back to the unbounded distance by subtracting 2π and taking the absolute value.

4.4 Statistical Analysis

Univariate statistics for each entropy measure (ShanEn, RenyEn, ApEn, SaEn, MSE, CompMSE, RQAEn) and for traditional COP measures (COP area, COP velocity, SD) were calculated for EO and EC conditions and for faller (F) and non-faller (NF) groups. Fallers were designated as individuals who had fallen at least 1 time in the past year. Logistic regression modeled the probability that an individual had their eyes closed during the measurement using either one (R or Ψ) or two independent variables/predictors (R and Ψ). Receiver operating characteristic (ROC) curves were created using the logistic regression probabilities from each regression model. Logistic regression models were also run using the rectangular x, y coordinates’ entropy measures and traditional postural stability measures COP area, COP velocity, x standard deviation, and y standard deviation as predictors. The areas under the curve (AUC) for each ROC curve were compared to determine the predictive ability of each entropy method at differentiating the two conditions, EO and EC. To compare the ability of each method to discriminate F and NF, the process was repeated using only EC data. Logistic regression modeled the probability the individual was a faller based on either one or two predictors, as described above, and the AUC statistics were compared. An AUC statistic of 1 indicates perfect performance at discriminating the two groups, while an AUC close to zero indicates very poor performance ³⁶. An AUC of 0.5 represents the same performance as classifying by random chance, such as a fair coin flip. The AUC represents the probability that a randomly chosen person from group 1 would have a larger test value than a randomly chosen person from group 2³⁶. The entropy methods which resulted in higher AUC values represented better classifiers in these data.

Cumulative entropy classifiers were modeled for the EC/EO and F/NF comparisons using logistic regression with all 16 R, Ψ based entropy measures as predictors/independent variables. An optimal combination was also computed where separate logistic regression models were run for every combinations of entropy measures, and the model with the highest AUC was retained as the optimal combination of predictors for each comparison (EO/EC, F/NF).

5.0 Results

Univariate statistics and AUC values for EO and EC conditions are shown in Table 2. Univariate statistics and AUC values for fallers and non-fallers are shown in Table 3.

Table 2.

Means and standard deviations (SD) for each entropy method for EO/EC conditions. AUC statistics are given for each method.

Method	Measure	EO mean (SD)	EC mean (SD)	AUC (1-Predictor)	AUC (2-Predictors)
ApEn	Ψ	0.20 (0.22)	0.34 (0.24)	0.691	0.674
	R	0.71 (0.40)	0.58 (0.30)	0.513
SaEn	Ψ	0.52 (0.35)	0.36 (0.24)	0.638	0.660
	R	0.62 (0.42)	0.48 (0.31)	0.501
CompMSE	Ψ Area	9.67 (2.14)	8.94 (1.92)	0.606	0.628
	R Area	6.13 (2.75)	6.27 (2.10)	0.569
	Ψ Slope	0.12 (0.04)	0.13 (0.03)	0.604	0.709
	R Slope	0.01 (0.04)	0.03 (0.04)	0.709
	x Area	7.07 (2.69)	5.95 (1.99)	0.555	0.556
	y Area	8.82 (3.06)	8.80 (2.48)	0.520
	x Slope	0.02 (0.05)	0.05 (0.04)	0.719	0.720
	y Slope	−0.01 (0.05)	0.02 (0.04)	0.702
MSE	Ψ Area	9.63 (2.16)	8.95 (1.93)	0.595	0.622
	R Area	6.12 (2.74)	6.26 (2.10)	0.570
	Ψ Slope	0.12 (0.04)	0.13 (0.03)	0.603	0.707
	R Slope	0.00 (0.04)	0.03 (0.04)	0.707
	x Area	7.06 (2.68)	6.95 (2.00)	0.555	0.556
	y Area	8.82 (3.07)	8.79 (2.48)	0.519
	x Slope	0.02 (0.05)	0.05 (0.04)	0.723	0.721
	y Slope	−0.01 (0.05)	0.02 (0.04)	0.705
RQAEn	Ψ	2.30 (0.61)	2.42 (0.53)	0.555	0.561
	R	3.15 (1.68)	3.55 (1.32)	0.530
ShanEn	-	4.76 (1.80)	5.01 (1.51)	0.538	-
RenyEn	-	2.18 (0.55)	2.31 (0.66)	0.559	-
COP Area (cm2)	-	4.12 (3.99)	5.01 (5.65)	0.549	-
COP Vel (cm s−1)	-	2.03 (0.74)	2.78 (1.30)	0.691	-
COP SD (mm)	x	0.07 (0.03)	0.08 (0.04)	0.598	0.5963
	y	0.03 (0.02)	0.04 (0.03)	0.530

Table 3.

Means and standard deviations (SD) for each entropy method for fallers (F) and non-fallers (NF) using only the EC condition. AUC statistics are given for each method.

Method	Measure	NF mean (SD)	F mean (SD)	AUC (1-Predictor)	AUC (2-Predictors)
ApEn	Ψ	0.37 (0.23)	0.30 (0.25)	0.590	0.644
	R	0.52 (0.24)	0.68 (0.36)	0.633
SaEn	Ψ	0.33 (0.23)	0.42 (0.24)	0.650	0.622
	R	0.42 (0.25)	0.57 (0.36)	0.622
CompMSE	Ψ Area	8.41 (1.83)	9.73 (1.80)	0.713	0.776
	R Area	6.74 (2.15)	5.55 (1.82)	0.658
	Ψ Slope	0.13 (0.03)	0.13 (0.03)	0.556	0.753
	R Slope	0.04 (0.04)	0.01 (0.03)	0.716
	x Area	7.29 (1.96)	6.45 (1.97)	0.613	0.620
	y Area	8.85 (2.07)	8.72 (3.02)	0.534
	x Slope	0.07 (0.04)	0.04 (0.03)	0.736	0.739
	y Slope	0.03 (0.04)	0.00 (0.04)	0.731
MSE	Ψ Area	8.43 (1.86)	9.72 (1.79)	0.704	0.767
	R Area	6.74 (2.15)	5.55 (1.83)	0.658
	Ψ Slope	0.13 (0.03)	0.14 (0.03)	0.551	0.757
	R Slope	0.04 (0.04)	0.01 (0.03)	0.716
	x Area	7.29 (1.96)	6.45 (1.98)	0.613	0.618
	y Area	8.85 (2.07)	8.70 (3.02)	0.532
	x Slope	0.07 (0.04)	0.04 (0.03)	0.730	0.744
	y Slope	0.03 (0.04)	0.00 (0.04)	0.747
RQAEn	Ψ	2.54 (0.51)	2.26 (0.53)	0.674	0.700
	R	3.68 (1.18)	3.35 (1.50)	0.567
ShanEn	-	5.04 (1.61)	4.95 (1.37)	0.539	-
RenyEn	-	2.21 (0.52)	2.46 (0.81)	0.596	-
COP Area (cm2)	-	4.51 (5.02)	5.77 (6.51)	0.574	-
COP Vel (cm s−1)	-	2.70 (1.29)	2.91 (1.34)	0.584	-
COP SD (mm)	x	0.07 (0.03)	0.09 (0.05)	0.612	0.617
	y	0.03 (0.02)	0.04 (0.05)	0.591

The cumulative classifiers had AUC’s of 0.796 for the EO/EC paradigm and 0.908 for the F/NF groups. The optimal EO/EC classifier had an AUC of 0.802 and consisted of all entropy measures except MSE_Slope R, and MSE_Slope Ψ, ShanEn. The optimal F/NF classifier had an AUC of 0.911 and consisted of all measures except ApEn R, ApEn Ψ, CompMSE_Area Ψ.

6.0 Discussion

In this paper, different entropy techniques, namely ShanEn, RenyEn, ApEn, SaEn, MSE, CompMSE, and RQAEn, were compared to evaluate the performance of each method at differentiating two different paradigms: eyes open (EO) versus eyes closed (EC) and fallers (F) versus non-fallers (NF). Using the AUC from the ROC curves of each entropy measure, CompMSE and MSE showed the best quality at differentiating both EO from EC and F from NF, likely because MSE and CompMSE use multiple timescales where the other methods were limited to a single timescale of interest.

While several studies have reported statistical differences in various COP entropy measures between fallers and non-fallers, the clinically relevant question is whether these entropy calculations are high-quality discriminators. Though statistical differences between fallers and non-fallers have been reported using ApEn ¹¹, MSE ⁹, and RQAEn ¹³, the present comparison between methods shows MSE can be a slightly better classifier than ApEn. Importantly, the entropy measures outperformed the traditional COP measures of sway area, velocity, and standard deviation for both EO/EC and F/NF comparisons. These results are particularly relevant to researchers and clinicians who wish to develop clinical COP tests which can detect fallers or fall-prone individuals from non-fallers. While several methods can detect significant differences, the best individual classifiers are CompMSE and MSE according to these results.

Notably, every individual measure, including CompMSE and MSE, produced fair to poor classification (AUC < 0.80) results for both EO/EC and F/NF classifications. However, when multiple measures were combined, the discriminatory capability of the optimal classifier exceeded 0.90, an excellent classifier. Even though every measure was calculated from the same data and represented the regularity of the signal, the cumulative combination resulted in an improved logistic regression model. For researchers and clinicians hoping to use nonlinear tools to discriminate patients or populations, this result suggests multiple measures of regularity should be calculated and assessed together, rather than selecting a single entropy method.

For MSE and CompMSE, the entropy values were based on the slope of the linear fit and area under the curve of the linear fit of the complexity indices. While Costa et al. ⁹ used the area under the linear fit, we found that the slope gave considerably better results, particularly when assessing the standard rectangular x,y data. Assessing the entropy based on the slope of the linear fit may therefore be another entropy method for MSE and CompMSE in lieu of the area and worthy of further investigation.

Interestingly, while we predicted the discrimination between EO and EC would be easier than between F and NF, most individual methods performed better discriminating fallers from non-fallers. The primary difference between the EO and EC conditions is the elimination of visual feedback in the EC condition. With no visual feedback, the proprioceptive and vestibular systems are placed under greater demand to maintain stability. Typically, the interruption or elimination of visual feedback (EC condition) results in significantly different COP results compared to the EO condition ²⁵. Conversely, elderly fallers typically experience a degradation, but not elimination, of multiple sensory systems ^{37, 38} which can be more challenging to detect given the varying degrees of degradation. However, previous studies have examined low frequency fluctuations in the COP, as opposed to the relatively high frequencies (2.5 to 25 Hz) examined here. It’s possible the muscle tension or other factors produce a difference in sway in these high frequencies ²⁹.

Additionally, polar coordinates (R and Ψ) may be more suited to detecting this sensory degradation compared to standard x (ML), y (AP) time series. We found the standard AP, ML COP data (slope) and polar R, Ψ data performed similarly when differentiating eyes open and eyes closed postural stability. However, the polar coordinate COP data displayed a slight superiority when discriminating fallers from non-fallers using two predictors. The polar data’s superiority may be indicative of nested correlations between the AP and ML series which are not considered in the x, y entropy analyses. Muscle co-contraction may be a contributing factor. Greater muscle co-contraction between the tibialis anterior and gastrocnemius has been reported in fall-prone elderly compared to healthy elderly ³⁹, and high levels of co-contraction have also been associated with aging ^{40, 41}. These co-contractions may create correlations between the AP and ML data which standard entropy measures cannot address, but polar coordinates, constructed using both AP and ML time series, may retain some of these correlations. While this analysis only explored univariate entropy methods, newer entropy analyses which can consider these multivariate data have been developed and warrant future investigation ⁴².

In the rectangular coordinate data, complexity decreased in fallers for all methods, agreeing with previous studies⁹. However, polar coordinates showed inconsistent results, with increasing complexity in fallers for SaEn, CompMSE, and MSE Ψ timeseries, and decreased complexity for all R entropy measures except ApEn and SaEn. Because of the inconsistent trends, it is difficult to interpret the complexity indices in polar coordinates. Therefore, despite their superior classification, further research must identify and explain the consistent changes before polar coordinate entropy calculations can be recommended, especially when classifying individuals without a priori knowledge of their condition (e.g. predictive fall risk screenings).

ShanEn, and RenyEn, performed the worst when discriminating fallers from non-fallers. In the case of ShanEn and RenyEn, the regularity of the time-series (i.e., the repetition of sequences) is not considered at all. Instead, ShanEn and RenyEn measure the regularity of the state of the signal (i.e. the repetition of values, not sequences). As state entropies, ShanEn and RenyEn appear less suited to distinguishing COP times-series when compared to sequence entropies (ApEn, SaEn, MSE, CompMSE). While RQAEn does not consider the regularity of the time-series itself, it was well-suited to discriminating F from NF, agreeing with results from Ramdani et al. ¹³, who found significant differences between F and NF using RQAEn.

This analysis provides some direction for researchers wishing to choose an entropy analysis for COP data. Both MSE and CompMSE showed the best ability to discriminate fallers from non-fallers suggesting these two methods should be considered first for future COP analyses. Multivariate entropy analyses should also be highly considered for COP analyses to address any correlations between the two data series. However, the increased quality of the cumulative and optimal classifiers suggests that each entropy method should be calculated and considered. Each measure of entropy appears to have its own utility at differentiating the postural control of healthy and fall prone elderly. For researchers and clinicians attempting to create a clinical test to identify fall prone elderly, a cumulative approach should be adopted, with each entropy method included in the decision. Using a combination of multiple forms of entropy, this study successfully differentiated fallers and non-fallers with only 60 seconds of postural stability data; no other clinical metrics (e.g., Activities-specific Balance Confidence score, vision, etc.) were considered. Therefore, each postural stability entropy measure should be considered an important predictor in future fall-risk assessments.

This study had two primary limitations. Primarily, the testing environment of the participants was not identical, nor completely free of distractions. Being a field study, the participants were tested in a community center with noises and other distractions that may have affected the balance during testing. Though the inter-study variation tends to be extremely high in studies reporting fall risk due to methodological variables (time of day, specific population, definition of fallers, instrumentation, analyses parameters) ¹³, the relatively large sample size used in this study removes a limitation of previous work ⁹. The second limitation was that only 60 seconds of postural stability data were collected for each condition due to the difficulties with testing elderly subjects and the possibility of early fatigue. Future work should increase the length of data collection to at least 2 minutes to provide an adequate record length for the entropy analysis ¹⁰. An additional minor limitation was the standardization of foot width. While the standardization did eliminate potential confounds of stance width, it may have placed a small number of participants in an uncomfortable or unnaturally narrow or wide stance. However, this effect was minimized by following the recommended stance width given by McIlroy and Maki ²⁶.