Abstract
We propose a novel multi-atlas based segmentation method to address the segmentation editing scenario, where an incomplete segmentation is given along with a set of existing reference label images (used as atlases). Unlike previous multi-atlas based methods, which depend solely on appearance features, we incorporate interaction-guided constraints to find appropriate atlas label patches in the reference label set and derive their weights for label fusion. Specifically, user interactions provided on the erroneous parts are first divided into multiple local combinations. For each combination, the atlas label patches well-matched with both interactions and the previous segmentation are identified. Then, the segmentation is updated through the voxel-wise label fusion of selected atlas label patches with their weights derived from the distances of each underlying voxel to the interactions. Since the atlas label patches well-matched with different local combinations are used in the fusion step, our method can consider various local shape variations during the segmentation update, even with only limited atlas label images and user interactions. Besides, since our method does not depend on either image appearance or sophisticated learning steps, it can be easily applied to general editing problems. To demonstrate the generality of our method, we apply it to editing segmentations of CT prostate, CT brainstem, and MR hippocampus, respectively. Experimental results show that our method outperforms existing editing methods in all three data sets.
Index Terms: Distance-based voting, interaction-guided editing, label fusion, segmentation editing
I. Introduction
Medical image segmentation is important for many applications, such as image-guided surgery [3], shape analysis [5], disease progression monitoring, and longitudinal studies [6]. With the advances in automatic segmentation tools, now people can more effectively conduct segmentations by first applying these tools, and then manually correcting errors in some parts of the segmentation. The use of automatic tools greatly reduces the burden of slice-by-slice manual segmentation. However, due to various challenges such as unclear target organ boundaries, large appearance variations and shape changes, the current automatic methods often fail to produce reliable segmentation, thereby requiring additional labor-intensive and time-consuming manual editing. If the segmentation errors can be corrected with only a few user interactions (e.g., dots as shown in Fig. 1), the total time to obtain satisfactory segmentation could be significantly reduced.
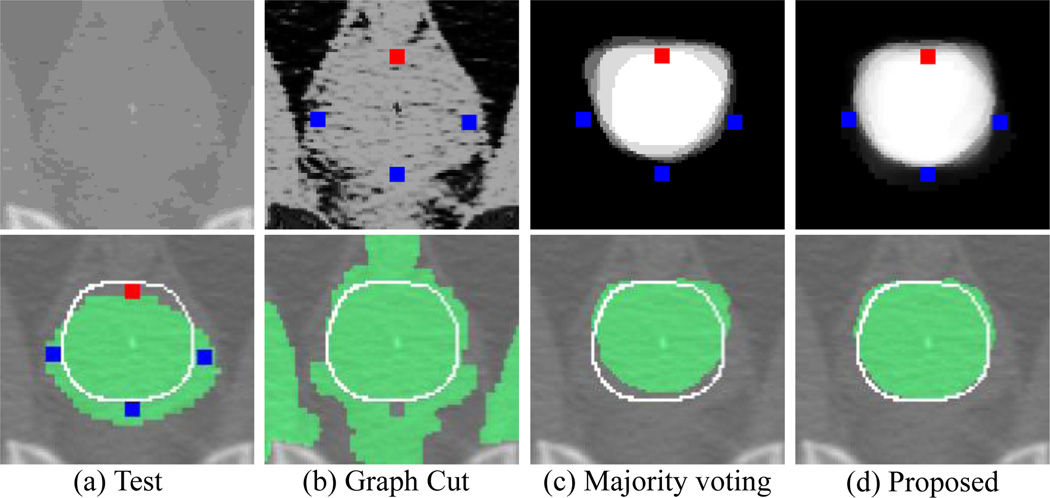
Fig. 1.
Segmentation editing results for three methods: (b) graph cut, (c) majority voting, and (d) proposed method. A test image is shown in the top of (a), and its initial segmentation (green), ground-truth boundary (white line), and user interactions (blue/red dots) are shown in the bottom of (a). Likelihood maps and editing results (green) obtained by three methods are shown in the top and bottom of (b), (c), and (d), respectively. Note that, for the graph cut method (b), the foreground (FG) intensity histogram is constructed from both the FG region of initial segmentation and the voxels annotated as FG. Similarly, the background (BG) histogram is constructed from both the BG region of initial segmentation and the voxels annotated as BG.
Many interactive segmentation methods have been developed for the segmentation editing problem, such as live-wire [7], graph cut [6, 8], and random walk [9]. In these methods, the segmentation is often iteratively updated using accumulated user interactions. Specifically, when additional user interactions are inserted into the erroneous regions, a statistical model is updated by intensities or gradients from new annotated voxels, and then used to update the labels of un-annotated voxels. These methods can improve the segmentation efficiency by using user guidance and simple appearance models, without relying on any expensive learning procedures. However, it is difficult to directly apply these methods to the editing problem, when allowing only a few dots or scribbles as user interactions. Fig. 1(b) gives an example of the editing result using the graph cut [8] with a small amount of interactions on ambiguous parts. In order for these methods to obtain reliable results, a substantial amount of annotations is required.
To address this limitation, we propose a new editing method using high-level information from training data. Specifically, we borrow the idea from multi-atlas based segmentation methods, which often require two steps: (1) searching appropriate atlas labels and (2) label fusion of the selected atlas labels based on their respective voting weights. So far, most multi-atlas based methods have used image appearance features to achieve these two steps, with the assumption that similar images or patches have similar labels. For example, Heckemann et al. [10] and Aljabar et al. [11] aligned training images to the target image and then used the weighted voting of labels of aligned training images to determine the segmentation. Coupe et al. [12] and Rousseau et al. [13] found similar training image patches after the alignment, and then used the non-local weighted voting of the labels of training atlas patches to determine the segmentation. The performance of these patch-based methods can be further improved with some advanced voting weights derived by sparse representation [14, 15] or joint fusion methods [16, 17]. However, it is often easy to find patches with similar appearances, but distinct label patterns, especially for medical images that often include weak boundaries and also the regions with large inter-subject appearance variations. Unlike previous methods depending solely on image appearance, we use the constraints from user interactions to guide both the atlas patch selection and label fusion steps. Specifically, for step (1), we divide user interactions into multiple local interaction combinations, and then locally search the label patches corresponding with each combination. Specially, we introduce a novel label-based similarity to find the atlas label patches that are well-matched with both the interactions and the previous segmentation. For step (2), we introduce a novel distance-based weight map to voxel-wisely fuse the selected label patches to obtain the final segmentation. The advantages of our proposed method, compared to the previous related works, are presented in the following subsections.
A. Related works
Recently, interactive segmentation methods were improved in several ways as briefly introduced below.
Several methods [18–20] have been proposed to effectively use the prior knowledge from user interactions. Specially, Rother et al. [18] proposed grab cut by requiring only a rough bounding box around the target object for interactive segmentation. In this method, a Gaussian mixture model is estimated to summarize the intensity distribution within the bounding box by using the Expectation-Maximization algorithm. Lempitsky et al. [21] further enforced the topological prior of the bounding box into the energy minimization framework. Bai et al. [19] and Criminisi et al. [20] both used geodesic distance from user interactions to encode spatial gradients.
On the other hand, several methods [22–25] consider using more advanced image features and also modeling the relationship between annotated regions and other regions. For example, Kim et al. [22] and Jung et al. [23] divided an image into a set of small regions, and then learned their relationship with a multi-layer graph and a kernel matrix, respectively. Finally, segmentation is conducted by using both the region likelihood and learned inter-region relationship. Gao et al. [25] learned local statistics near user interactions, and then used them to guide active contour evolution within a variational framework.
Active learning based methods [26–28] have also been proposed for efficiently receiving user interactions. Wang et al. [26] and Top et al. [27] measured the uncertainty of either a local region and a 2D plane, and then automatically provided the most ambiguous parts to users. Similarly, Sourati et al. [28] located the ambiguous parts by measuring the uncertainty of pairwise queries.
These methods can generate better segmentations with less user interactions than the early interactive methods [4–7]. However, a number of user interactions are still required since it is difficult to construct a distinct appearance model by using a few dots or scribbles in ambiguous regions. To address this problem, several methods have been proposed to incorporate high-level information from training data. For example, Barnes et al. [29, 30] used the label information of similar image patches from a training set for image completion and reshuffling. The patches were found by random patch selection and propagation methods. Beyond the use of label information, Schwarz et al. [31] further trained the active shape model (ASM) and then incorporated it to assist segmentation editing. Specifically, when any incorrect landmark point is edited by users, the adjacent landmark points are modified accordingly, with the global shape constraint of ASM. However, manual editing of 3D landmarks is inconvenient, and also the ASM with limited training data often fails to capture local shape variations. Recently, Park et al.[1] proposed an editing method based on a structured patch model that utilizes localized classifiers and also the spatial relationship between neighboring patches. In their method, training patches are transferred to appropriate places in the target image by considering the similarity of labels, interactions and the inter-patch spatial relationship. Then, the classifiers trained on the transferred patches are used to guide segmentation. We proposed a semi-supervised learning based method [32] to learn discriminative appearance patterns. Specifically, we first found a small set of atlas label patches that are well-matched with interactions, and then estimated confidence regions in the testing image through majority voting. Finally, a semi-supervised learning algorithm was used to train a classifier by using positive and negative training samples extracted from the confidence regions. The learned classifier is used to label the rest non-confidence regions for updating segmentation. All these previous methods effectively exploit useful image features by using label information. However, since they consider all interactions together for finding the atlas label patches, the number of well-matched atlas label patches is often limited. Thus, it causes the unreliability of either the trained local classifiers or the identified confidence region. Moreover, since editing needs to be sequentially conducted region-by-region, users cannot insert their interactions freely into erroneous regions in the entire image.
B. Contributions
In this paper, we propose a novel editing method, focusing on a reliable estimation of label information without using complex classifiers or training models. There are three main contributions. First, we introduce a new label fusion strategy based on user-guided patch selection and weighted voting for segmentation editing. Since the user-guided constraints are more intuitive and much clearer than simple image appearance information, the atlas label patches and their respective voting weights can be more accurately estimated. Second, our method could consider various local shape variations, even with limited atlas label images, by separately finding atlas label patches for different interaction combinations. Compared to our previous method [22] considering all interactions together, the atlas label patches selected by separate interaction subsets can constrain the abrupt shape changes and also generate more reliable editing results, as illustrated in Figs. 1(c) and 1(d), respectively. Finally, since our proposed method does not need any training image information and expensive learning procedures, it can be easily applied to the editing scenario, when given an incomplete segmentation along with a set of reference label images. We will validate these key contributions on three challenging data sets in our experiments.
II. Multi-atlas based editing
Our proposed editing procedure begins with an initial segmentation obtained by any existing method, a set of existing atlas label images, and user interactions on erroneous parts. To receive the user interactions on erroneous parts, we provide an interface, where user can choose both an appropriate 2D view (among coronal, axial, and sagittal views) and a brush size for interaction. Intuitively, we assume that the foreground (FG) / background (BG) dots or short scribbles are inserted into the erroneous regions near the true object boundary. Specifically, the editing procedure consists of four steps, as described below.
All atlas label images are registered to the previous segmentation Lt−1 for guiding the segmentation update, where t represents the editing round and L0 is the initial segmentation. To enrich the reference label set, we respectively transform each atlas label image to Lt−1 with rigid and affine registrations, and then use the aligned label images as reference atlas label images. In the registration, we extracted the 3D surfaces of both the Lt−1 and binary atlas label images, and then aligned the surface points using the iterative closest point method [2].
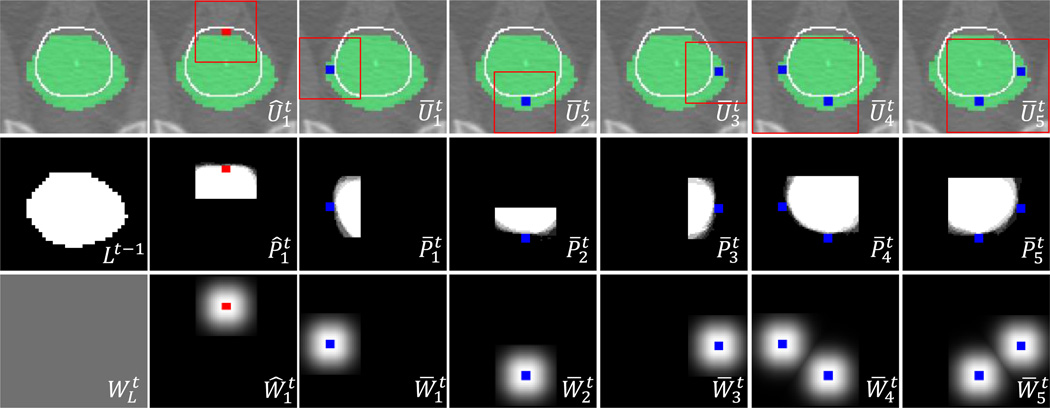
Local interaction combinations (i.e., for FG combination / for BG combination) are extracted from the FG and BG user interactions, respectively, where k is the index of combination. For each combination, a region of interest (ROI) is set as a bounding volume to include the respective interactions with a small margin. Examples of the combinations and their ROIs are shown in the top row of Fig. 2.
For each combination, the appropriate label patches, which are well-matched with both the interactions and previous segmentation in the ROI, are searched from reference label images. The selected patches are averaged to build a local likelihood map (i.e., ). Examples of local likelihood maps are shown in the middle row of Fig. 2.
A global likelihood map Pt in the entire image is determined by the label fusion of the previous segmentation and the local likelihood maps with their respective distance-based weight maps (i.e., for Lt−1 / ). Noting that the local likelihood maps become much more accurate near the interactions, while the previous segmentation is more reliable at a distant voxel v from the interactions, the weight of v is determined by the respective distances to the interactions. The weight maps are shown in the bottom row of Fig. 2. Finally, the segmentation is determined by thresholding the likelihood map Pt.
The above four steps are repeated with the inclusion of additional user interactions, if provided, until the updated segmentation is satisfactory. Note that, when repeating each editing procedure, all accumulated user interactions are considered to find the atlas label patches and derive their respective weight maps. The overall editing procedure is described in Fig. 3. The details of steps 2), 3), and 4) are presented in the following subsections.
Fig. 2.
Interaction combinations and their ROIs (top row), local likelihood maps (middle row), and weight maps (bottom row), obtained from the user interactions shown in Fig. 1(a). The initial segmentation, ground-truth boundary, FG/BG interactions, and ROIs are shown as green, white line, red/blue dots, and red box, respectively. The global likelihood map in Fig. 1(d) is obtained by label fusion of Lt-1 and the local likelihood maps with the weights.
Fig. 3.
Flowchart of our segmentation editing framework. The proposed multi-atlas based editing method is shown in the blue dotted box, where UI denotes the user interactions.
A. Extraction of local interaction combinations
In our method, the segmentation is edited using reference atlas label images that are well-matched with user interactions. If there are many atlas label images well-matched with all provided user interactions, the segmentation can be edited easily by following the user guidance. However, unfortunately, in most situations, there are few globally well-matched atlas label images. Therefore, we separately find the atlas label patches that are well-matched with various local interaction combinations, and then aggregate them to estimate the voxel likelihood. Based on the spatial proximity of separate interactions, we extract three types of local combinations for FG and BG interactions, respectively, as follows: 1) individual interaction such as a dot or scribble, 2) pairwise interaction which includes two individual interactions within a certain distance, and 3) union interaction which includes all neighboring interactions within a certain distance. The interaction combinations are extracted not only from the current interactions, but also from the relevant previous interactions. Specifically, if the previous interactions are located within a certain distance of the current interactions, the combinations between current and previous interactions would be extracted. On the other hand, previous interactions, which are distant from all the current interactions, will not be used in the current editing, since the accurate parts of the updated segmentation do not need to be changed. The distance for defining the pairwise and union interactions was determined with respect to applications by considering the object size. For each kth combination, we set the ROI ( for FG or for BG) as a bounding volume, which covers the interaction combination with a small margin to include possible local variations in the ROI. Since the ROI is set from the annotated voxel positions with a certain margin, its size depends on the interaction combination.
B. Selection of reference label patches with respect to user interactions
For each interaction combination, we find reference label patches that are well-matched with interactions and the previous segmentation Lt−1 in the ROI. Here, the patch size is the same as the ROI size. Since the label images are aligned to Lt−1 without utilizing user interactions in the initial registration step, the registration might be inaccurate, especially for initial segmentation with large errors. To address this issue, we borrowed the idea from non-local patch-based methods [12]. Specifically, we used a novel label-based similarity S defined in Eq. 2 to identify the best well-matched label patch in a local neighborhood of each aligned atlas label image. In our previous work [32], the label-based similarity S is defined as:
| (1) |
where δ is the Kronecker delta, v is a voxel under consideration, M is an aligned atlas label image with values 1 and −1 denoting FG and BG voxels, respectively, Ut is the user interaction map at tth iteration with values 1, −1 and 0 denoting FG, BG and unannotated voxels, respectively, Lt−1 is the previous segmentation at t - 1 iteration with the similar label definitions as M , and φt denotes the ROI including all interactions. In Eq. (1), the first term represents the similarity between an atlas label image and all user interactions, while the second term represents the similarity between an atlas label image and the previous segmentation. γU is a parameter used to control the weight between these two terms. Eq. (1) assumes that a good atlas label patch should be strongly matched with all annotated voxels primarily in a ROI and also matched with the previous segmentation on unannotated voxels. To emphasize the importance of a small amount of annotated voxels, γU was set as a small value (i.e., smaller than 1). However, since all interactions are considered as strong constraints jointly in Eq. (1), the number of well-matched atlas label patches is often limited. Thus, various shape changes cannot be well captured.
To consider local shape variability with a limited number of label images, we separately find similar atlas label patches for each interaction combination, instead of all interactions together. For each interaction combination, we find the atlas label patches 1) tightly matched with interactions in this combination, 2) moderately matched with other interactions, and 3) weakly matched with the previous segmentation. Based on this motivation, we modify our label-based similarity Sk for the kth interaction combination for FG combination or for BG combination) as follows:
| (2) |
where denote the user interactions in kth combination and the other user interactions at tth iteration, respectively. The first, second, and third terms in Eq. (2) represent the similarity of an aligned atlas label image M 1) with the user interactions in the kth combination, 2) with the other user interactions, and 3) with the previous segmentation, respectively. γo and γU denote parameters for balancing these three terms. In our experiment, γo is set as 0.05 to distinguish the strong and moderate constraints for different user interactions. γU is set as 0.005 to represent the weak constraint from the previous segmentation. The more consistent the aligned atlas label image is with and Lt−1 in the ROI , the higher is the similarity obtained in Eq. (2).
For each reference atlas image, the best matched label patch is determined as the one with the highest label-based similarity in the local neighborhood. We repeat this procedure for all reference atlas label images, and then select the np patches with the highest similarities. Finally, the selected label patches are averaged to build a local likelihood map ( for FG, or for BG).
C. Label fusion based on user interactions
In the label fusion step, local likelihood maps are aggregated to build a global likelihood map Pt for the entire image. Since we emphasize the first term in Eq. (2), the local likelihood map is more likely to be accurate near the interaction. In contrast, the confidence of the estimated likelihood for a voxel decreases when its distance from the interactions increases. (E.g., the likelihood becomes small and fuzzy when it is far from the interactions in Fig. 2.) In these low-confidence regions, the previous segmentation is more accurate than the likelihood maps. Therefore, to determine the global likelihood of a voxel, it is natural to emphasize the contribution of the local likelihood maps near user interactions, while emphasizing the contribution of the previous segmentation Lt-1 in distant voxels from interactions. By considering the distance of each voxel from the interaction and also the confidences of local likelihood maps (), Pt is defined as:
| (3) |
where nf and nb are the numbers of FG and BG combinations. The weight for the FG interaction combination is defined as:
| (4) |
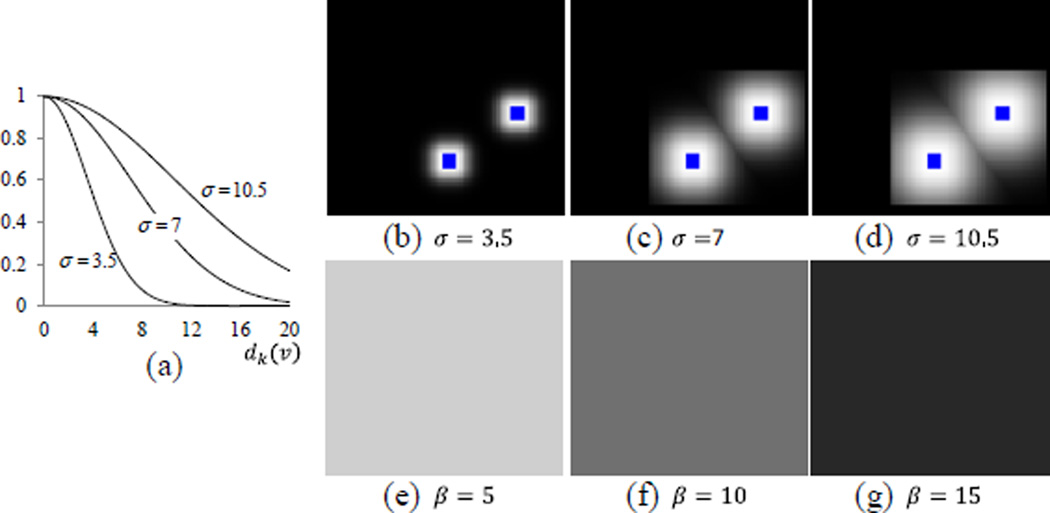
where dk (v) is the shortest distance between a voxel v and the annotated voxels in . If dk (v) is large, decreases and vice versa. σ controls how quickly the emphasis shifts from the local likelihood maps to the previous segmentation as the voxel becomes distant from the interactions. If σ is small, only the region close to the user interactions is affected by the local likelihood maps, while other regions are affected by the previous segmentation. On the other hand, if σ is large, most voxels are affected by the local likelihood maps. αf is the weight for the confidence of voxel likelihood. Note that several likelihood maps obtained by individual or pairwise interaction combinations may be inaccurate due to the strong constraints for a few annotated voxels. To alleviate this effect, we enforce more weights when the likelihood map certainly indicates the voxel as FG or BG. For example, when some local likelihood maps indicate v as BG with low confidence (e.g., ) and some local likelihood maps indicate v as FG with high confidence (e.g., ), we enforce more weight on the latter local likelihood maps. We set αf as largely greater than 1, if ; otherwise 1. The weight of the BG combination is similarly defined as:
| (5) |
where αb is greater than 1, if ; otherwise 1. The weight is defined as:
| (6) |
where β controls the importance of the previous segmentation. If β is small, the result is more affected by the previous segmentation than the local likelihood maps even for voxels near the interactions. On the other hand, if β is very large, the previous segmentation is not considered during label fusion. The weight maps for different σ and β are shown in Fig. 4. Finally, a new segmentation label Lt(v) is set as FG if Pt(v) > 0.5, or v is annotated as FG; otherwise, set as BG.
Fig. 4.
The voting weight maps for different σ and β. The graph of exponential functions with different σ is shown in (a). For the three different values of σ, their respective weight maps are obtained with respect to the distance dk(v) to the user interactions (blue dots) and are shown in (b), (c), and (d), respectively. For three different values of β, their respective weight maps are obtained and shown in (e), (f), and (g), respectively, when using σ = 7.
III. Results
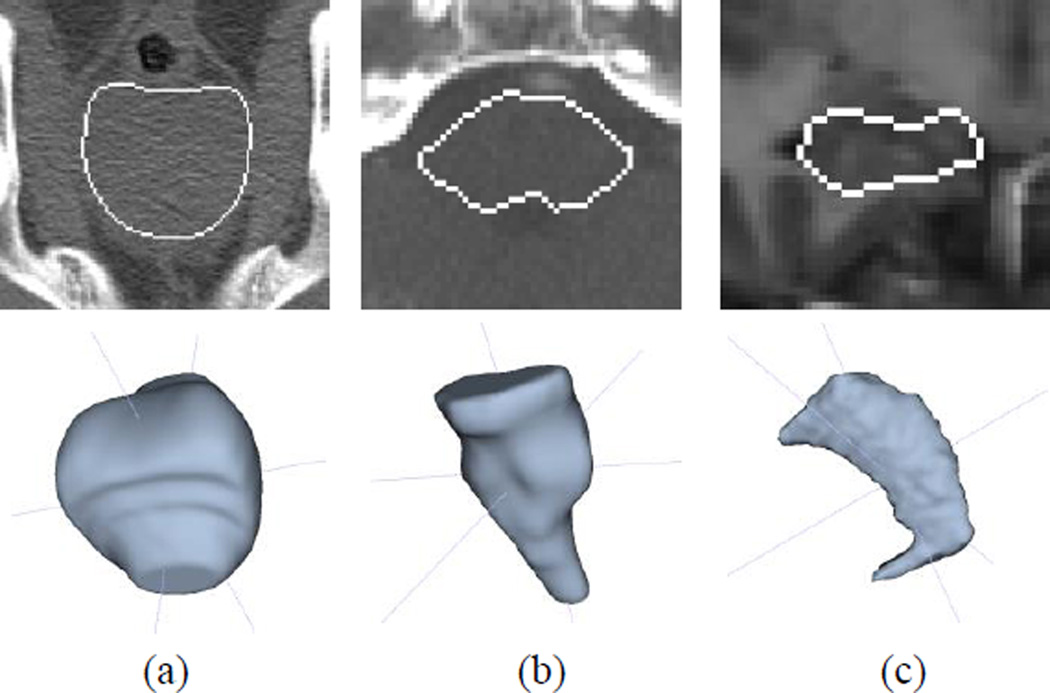
Our proposed editing method was evaluated on three challenging data sets: 1) prostate data set [32] including 73 CT images with dimension 512 × 512 × (61~81) voxel3 and spacing 0.94 × 0.94 × 3.00 mm3, 2) brainstem data set [33] including 40 head & neck CT images with spacing approximately 1.0 × 1.0 × (2.5~3.0) mm3 , and 3) hippocampus data set1 including 35 brain MR images with dimension 256 × 256 × 287 voxel3 and spacing 1.0 × 1.0 × 1.0 mm3 (Fig 5). Although several automatic methods [17, 33–35] have been proposed to address these segmentation problems, inaccurate results were often obtained due to low tissue contrast and large shape and appearance variations. To evaluate editing performances, we first used one of the state-of-the-art automatic methods to generate the initial segmentation, and then applied our editing method to the half of the results with the largest errors. Specifically, for the prostate data set, we randomly divided the data set into four subsets, and then conducted the regression-based segmentation method [34] using four-fold cross validation. Finally, we chose 37 images with the lowest Dice similarity coefficient (DSC) scores. Similarly, for the brainstem data set, we applied the learning-based multi-source integration framework [5] using leave-one-out validation, and then chose 20 images with the worst segmentations. For the hippocampus data set, we applied the joint label fusion method [17] using leave-one-out validation, and then chose 18 images with the worst segmentations. Next, we conducted our editing method with user interactions, inserted in the erroneous parts of selected images. The details of the experimental setting and results are presented in the following subsections.
Fig. 5.
Example of 2D (top) and 3D (bottom) views for (a) prostate, (b) brainstem, and (c) hippocampus data sets. White line represents the target object boundary.
A. Experimental setting
For each of the selected prostate, brainstem, and hippocampus images, the average numbers of 14, 30, and 9 dots were interactively inserted, respectively, depending on the amount of segmentation errors. We first found a reasonable interaction distance value for defining pairwise and union combinations. If the interaction distance value is very small, only individual interactions are used, thus, losing useful middle-level priors, such as those shown in the last two columns of Fig. 2. On the other hand, if the interaction distance value is very large, many distant interactions are considered together. Thus, some irrational atlas label images (well-matched with all combined interactions) cannot well-capture local shape variations. In our experiment, the interaction distance value was empirically set as 40 for the prostate and brainstem due to their relatively large sizes, while 15 for the hippocampus. With these interaction distance values, the average numbers of 48, 111, and 19 interaction combinations were extracted. Since the margin size was also related to the object size, we set the margin as one third of the interaction distance (i.e., 13 for prostate and brainstem, and 5 for hippocampus) so that local variations near interactions could be covered in the ROI. Since the voxel spacing was triple in the z-direction than that in the x- and y-directions for both the prostate and brainstem data sets, the margin sizes were finally set as 13 × 13 × 4 voxel3. On the other hand, the margin size of the hippocampus was set as 5 × 5 × 5 voxel3 because of isotropic image resolution. The rest of the parameters were determined by cross validation. For example, the patch search range is used to compensate for the error of initial alignment. In the validation, the errors of initial alignment usually did not exceed 8 voxels in each direction for the prostate and brainstem, and 4 voxels for the hippocampus. Thus, the patch search range was set accordingly as 8 × 8 × 8 voxel3 for the prostate and brainstem, and 4 × 4 × 4 voxel3 for the hippocampus. The parameters σ and β as the fusion weights need to be determined with respect to the margin size as shown in Fig. 4. We tested the performances with different σ and β values ranged from a quarter to three quarters of the margin size. With different values, the performances could change less than the DSC of 0.007 and the ASD of 0.08mm for the prostate, the DSC of 0.01 and the ASD of 0.15mm for the brainstem, and the DSC of 0.003 and the ASD of 0.01mm for the hippocampus, respectively. Finally, we set σ and β as a half of a margin size and three quarters of a margin size, respectively. Since the remaining parameters np, αf and αb did not significantly affect the performance, the same values such as 7, 5, and 5, respectively, were used for all experiments. The details are presented in Table 1.
TABLE 1.
Experimental setting for three date sets. The numbers of reference label images, user interactions, and interaction combinations, as other parameter values, are provided.
| # of reference label images |
# of interactions |
# of combinations |
Distance for interactions |
ROI margin | Search range | σ | β | |
|---|---|---|---|---|---|---|---|---|
| Prostate | 54 | 6–21 | 10–89 | 40 | 13 × 13 × 4 | 8 × 8 × 8 | 7 | 10 |
| Brainstem | 39 | 7–45 | 25–192 | 40 | 13 × 13 × 4 | 8 × 8 × 8 | 7 | 10 |
| Hippocampus | 34 | 4–13 | 6–31 | 15 | 5 × 5 × 5 | 4 × 4 × 4 | 3 | 4 |
To show the sensitivity of our method to the margin size, we evaluated our method using the above setting, but with different margin sizes: 9×9×3, 13×13×4, 15×15×5, 18 × 18 × 6 voxel3 for the prostate and brainstem, and 3 × 3 × 3, 5×5×5, 7×7×7, 9×9×9 voxel3 for the hippocampus. Even with these different margin sizes, the performance changed less than the DSC of 0.005 and the ASD of 0.05mm for the prostate, the DSC of 0.005 and the ASD of 0.09mm for the brainstem, and the DSC of 0.002 and the ASD of 0.007mm for the hippocampus, respectively.
B. Segmentation performance
Under the same user interactions, our method that uses interaction combinations and weighted voting (namely ICWV) was compared with 1) initial automatic segmentation, 2) a manual editing method, 3) a label fusion method using all interactions in the entire image (namely LFG) for finding the atlas label patches, 4) a label fusion method using all interactions in each local region (namely LFL) for finding the atlas label patches, 5) a method using the structured patch model (namely SPM) [1], and 6) a method using interaction combinations, but with majority voting for label fusion (namely ICMV). Specifically, in the manual editing method, only the labels annotated by users are changed, which is used to estimate the amount of user interactions provided. Except for the manual editing method, the atlas label images are used for all other editing methods. In the LFG method, the labels well-matched with all interactions in the entire image are found with the label-based similarity as defined in Eq. (1). The segmentation is then updated using majority voting on the selected atlas label images. In the LFL and SPM methods, the atlas label patches well-matched with all interactions in each local region are found with respect to Eq. (1). Then, the segmentation is updated by majority voting of the selected atlas label patches in the LFL method, and updated by MRF optimization based on the local classifiers [1] in the SPM method. For these two methods, all interactions are divided into multiple interactions by region, and then the editing is conducted sequentially. In the ICMV method, interaction combinations are used for the atlas label patch selection similarly as the proposed method, but the final segmentation is obtained by equally weighting all local likelihood maps.
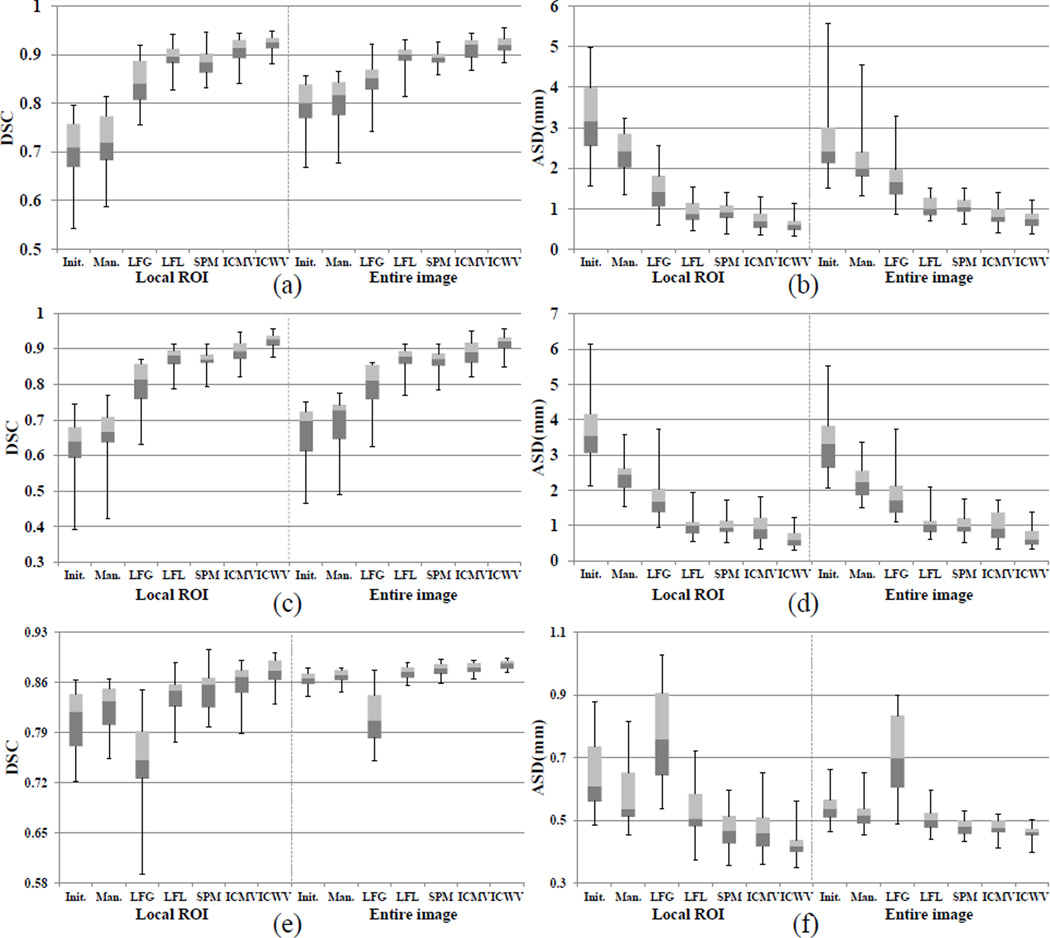
For evaluation, we used the Dice Similarity Coefficient (DSC) and the average surface distance (ASD) between the respective segmentation result Lf and the manual ground-truth Mg. The DSC is computed to measure the overlapping degree: (2 × |Lf ∩ Mg|)/(|Lf| + |Mg|). The ASD is computed by averaging all the symmetric pair-wise closest distances between the surface of Lf and the surface of Mg. The DSC and ASD were measured both in the entire image and the ROI region, because the erroneous regions could be small compared to the entire image. Table 2 and Table 3 show the average and standard deviation of DSC and ASD scores, respectively, for all comparison methods using the aligned atlas label images. Also, the boxplots in Figure 6 show the distributions of DSC and ASD scores. The gain of the manual method was only the DSC of 0.005–0.026 and the ASD of 0.029–1.12mm due to the small amount of user interactions. On the other hand, the methods using existing reference labels gave significantly improved scores, i.e., DSC of 0.01–0.13 and the ASD of 0.043–1.48mm for most cases except the LFG method in the hippocampus data set. Since the hippocampus has a non-convex shape with local variations, the number of label images well-matched with all interactions was very limited. Thus, inaccurate label images, which were often selected, worsened the results (see the last row of Fig. 7 (c)). On the other hand, the LFL and SPM methods had better performances by dividing all user interactions into local parts for finding the well-matched atlas label patches. However, the LFL method could not capture the shape variations near the object boundary due to the limited number of atlas label patches that are tightly matched with all interactions in the ROI. Moreover, since the initial segmentation was not used for computing the likelihood map, the correct parts far from the interactions could be worse by voting from inaccurate label patches. The SPM method has similar problems, due to the patch localization errors and also the low intensity contrast between FG and BG, even though it utilizes the image appearance information. The ICMV method outperformed both the LFL and SPM methods in terms of accuracy, by finding well-matched atlas label patches for multiple interaction combinations. Nonetheless, since several inaccurate local likelihoods, obtained by the individual or pairwise interactions far from the current voxel, can equally contribute to the final label prediction, large standard deviations were obtained compared to our ICWV method. On the other hand, our ICWV method outperformed all other editing methods, in most cases, for both accuracy and robustness (small standard deviation) by using the distance-based fusion weight.
TABLE 2.
The average (standard deviation) of DSC scores for the comparison methods. The DSC scores were measured in both the ROI region and the entire image. Numbers in the most left column represent the numbers of test images. The best DSC scores are highlighted as boldface.
| Initial | Manual | LFG | LFL | SPM | ICMV | ICWV | ||
|---|---|---|---|---|---|---|---|---|
| Prostate (37 images) |
ROI | 0.704 (0.066) | 0.726 (0.061) | 0.84 (0.051) | 0.894 (0.029) | 0.884 (0.028) | 0.91 (0.025) | 0.924 (0.015) |
| Image | 0.794 (0.053) | 0.805 (0.05) | 0.847 (0.04) | 0.895 (0.026) | 0.892 (0.013) | 0.913 (0.023) | 0.921 (0.018) | |
| Brainstem (20 images) |
ROI | 0.623 (0.09) | 0.655 (0.089) | 0.798 (0.07) | 0.875 (0.031) | 0.868 (0.028) | 0.89 (0.037) | 0.92 (0.021) |
| Image | 0.66 (0.084) | 0.686 (0.083) | 0.795 (0.07) | 0.872 (0.033) | 0.868 (0.029) | 0.889 (0.038) | 0.916 (0.026) | |
| Hippocampus (18 images) |
ROI | 0.809 (0.042) | 0.823 (0.036) | 0.749 (0.063) | 0.843 (0.027) | 0.852 (0.033) | 0.858 (0.029) | 0.873 (0.023) |
| Image | 0.864 (0.011) | 0.869 (0.01) | 0.813 (0.041) | 0.874 (0.01) | 0.879 (0.01) | 0.88 (0.008) | 0.885 (0.007) |
TABLE 3.
The average (standard deviation) of ASD scores for the comparison methods. The ASD scores were measured in both the ROI region and the entire image. Numbers in the most left column represent the numbers of test images. The best ASD scores are highlighted as boldface.
| Initial | Manual | LFG | LFL | SPM | ICMV | ICWV | ||
|---|---|---|---|---|---|---|---|---|
| Prostate (37 images) |
ROI | 3.231 (0.897) | 2.407 (0.51) | 1.465 (0.509) | 0.915 (0.274) | 0.927 (0.238) | 0.739 (0.268) | 0.612 (0.202) |
| Image | 2.667 (0.909) | 2.17 (0.636) | 1.686 (0.516) | 1.056 (0.252) | 1.054 (0.22) | 0.84 (0.259) | 0.754 (0.213) | |
| Brainstem (20 images) |
ROI | 3.7 (1.039) | 2.381 (0.504) | 1.864 (0.774) | 0.977 (0.307) | 1.015 (0.32) | 0.951 (0.446) | 0.638 (0.244) |
| Image | 3.383 (0.97) | 2.262 (0.527) | 1.895 (0.771) | 1.009 (0.322) | 1.029 (0.303) | 0.97 (0.447) | 0.668 (0.263) | |
| Hippocampus (18 images) |
ROI | 0.645 (0.121) | 0.58 (0.094) | 0.775 (0.157) | 0.527 (0.09) | 0.475 (0.065) | 0.466 (0.077) | 0.425 (0.053) |
| Image | 0.546 (0.055) | 0.52 (0.045) | 0.703 (0.135) | 0.505 (0.04) | 0.48 (0.03) | 0.478 (0.031) | 0.461 (0.026) |
Fig. 6.
The distributions of DSC and ASD scores in the ROI region and in the entire image, respectively. (a) and (b), (c) and (d), and (e) and (f) represent the results for prostate, brainstem, and hippocampus data sets, respectively. The top, center, and bottom of each box represent the upper quartile, median, and lower quartile scores, respectively, and the whiskers connected to each box represent the maximum and minimum scores, respectively.
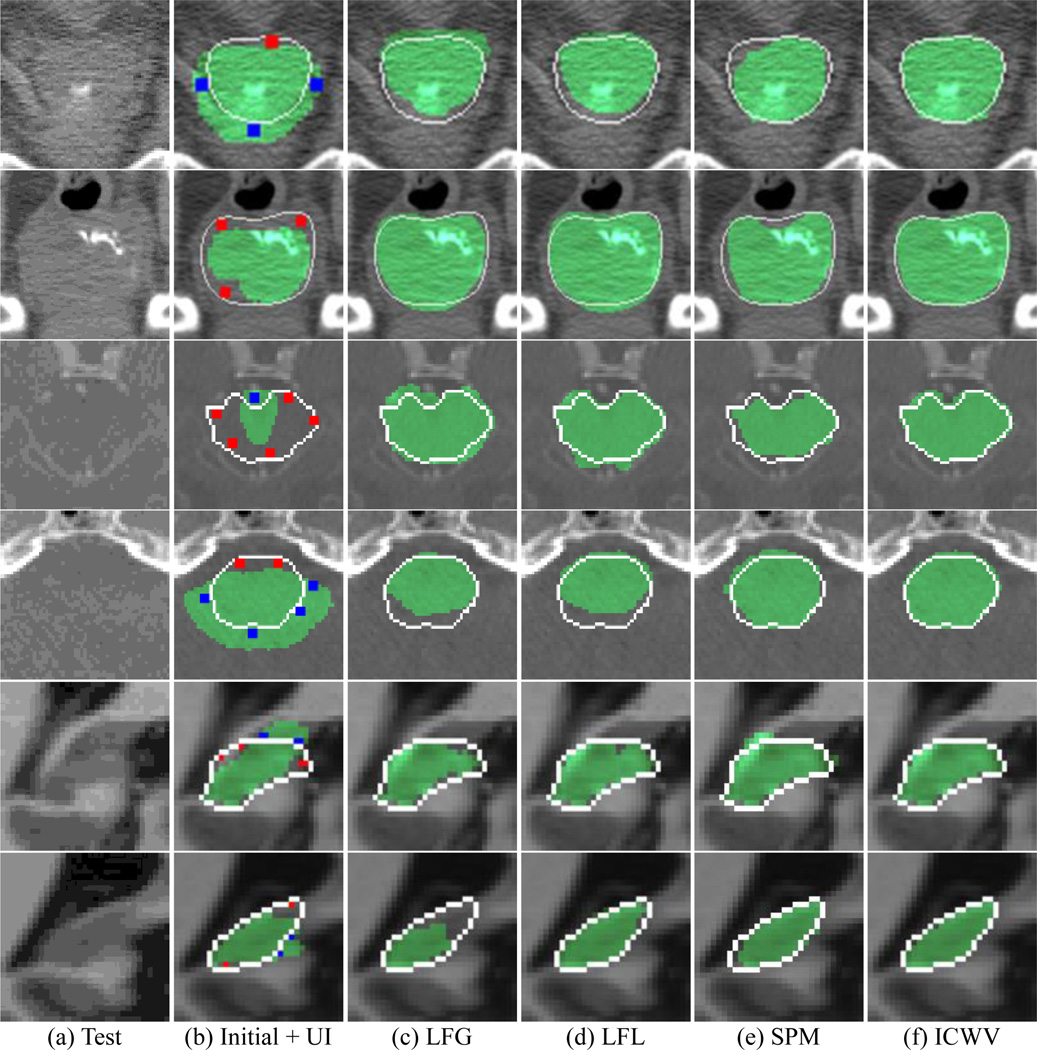
Fig. 7.
Segmentation editing results by LFG, LFL, SPM [1], and ICWV methods (from 3rd to 6th columns). The first column shows the original images, while the 2nd column shows the initial segmentations along with manual interactions. The segmentation results, ground-truth labels, and FG / BG user interactions (UI) are shown as green, white lines, and red / blue dots, respectively. The first two, middle two, and last two rows show the typical slices for 3D prostate, brainstem, and hippocampus images, respectively.
Compared to the other comparison methods, our ICWV method obtained 1–5% DSC gains. Since the erroneous parts are often much smaller than the entire target object, it may look small. However, in clinical application, segmentation improvement for these local errors can be meaningful. For example, hippocampus subfields have recently drawn a lot of attention due to their important role in several neuropsychiatric diseases [36]. The local error can significantly affect the calculation of subfield volume, since its annual change (due to disease) could be as small as 1%. In terms of the prostate, the segmentation is often conducted for radiotherapy [37]. During radiotherapy, high energy X-rays should be accurately delivered to the prostate. Thus, the local error could lead to overdose on nearby healthy tissues, such as the bladder and rectum, since the boundaries of pelvic organs usually touch together.
The qualitative results of comparison methods are described in Fig. 7. Although the LFG, LFL, SPM methods corrected major errors, their correction results still included errors, due to the limited number of well-matched atlas labels. Since the incomplete intermediate result was used for the editing procedure, the errors may have accumulated as the editing procedure was repeated. On the other hand, the segmentation obtained by our proposed ICWV method accurately followed the true object boundary near the user interactions, and also constrained the irregular shape changes in the regions far from the user interactions.
C. Performance for repetitive editing
For the experiments in Sec. III-B, we used all user interactions inserted on erroneous parts in the entire image to perform the segmentation editing. After the first round of editing, the DSC scores of most cases were higher than some inter-rater DSC scores reported in the literature [38–40], and also had no notable qualitative errors. Thus, we usually performed only the first round of editing in this study. However, in a few cases, there were still large errors, especially when the initial segmentation was too bad. Since the atlas label images were initially aligned to the target image based on the initial automatic segmentation, the registration could be inaccurate if the initial automatic segmentation included large errors. In such case, a single round of editing is often insufficient to correct all the segmentation errors, which makes it necessary to repeat the editing steps until obtaining satisfactory results. To demonstrate the effectiveness of our repetitive editing procedure, we selected the 5 worst subjects among 20 brainstem results after the first round of editing, and then conducted the second round of editing with some additional user interactions. Table 4 shows the experimental setting and performances for the five subjects. Since the initial segmentation included relatively large erroneous parts, many user interactions (i.e., 24 dots on average) were inserted in the first round of editing. Accordingly, the performance was significantly improved with a DSC of >0.25 and an ASD of 2.7mm. Since most of the errors were edited during the first round of editing, much less interactions (i.e., 7 dots on average) were inserted in the second round editing. The performance improved again with a DSC of >0.15 and an ASD of 0.43mm. Since the number of interaction combinations was much reduced in the second round of editing, the computational time was also reduced (five times less than that of the first round of editing).
TABLE 4.
The experimental settings and performances for five brainstem subjects during the repetitive editing. The DSC and ASD scores, the numbers of interactions and combinations, and the computational time for each subject are presented.
| subject1 | subject2 | subject3 | subject4 | subject5 | Avg. | ||
|---|---|---|---|---|---|---|---|
| Initial | DSC | 0.578 | 0.466 | 0.707 | 0.734 | 0.691 | 0.635 |
| ASD (mm) | 5 | 5.51 | 2.284 | 2.642 | 3.14 | 3.715 | |
| First editing |
DSC | 0.89 | 0.9 | 0.887 | 0.847 | 0.878 | 0.88 |
| ASD (mm) | 0.839 | 0.86 | 0.864 | 1.387 | 1.082 | 1.006 | |
| # of interactions | 33 | 40 | 27 | 7 | 14 | 24.2 | |
| # of combinations | 127 | 153 | 117 | 25 | 44 | 93.2 | |
| Time (s) | 740 | 869 | 664 | 127 | 226 | 525.2 | |
| Second editing |
DSC | 0.941 | 0.919 | 0.933 | 0.927 | 0.928 | 0.93 |
| ASD (mm) | 0.442 | 0.649 | 0.427 | 0.705 | 0.674 | 0.579 | |
| # of interactions | 8 | 10 | 6 | 9 | 4 | 7.4 | |
| # of combinations | 29 | 32 | 17 | 23 | 10 | 22.2 | |
| Time (s) | 116 | 140 | 76 | 86 | 41 | 91.8 | |
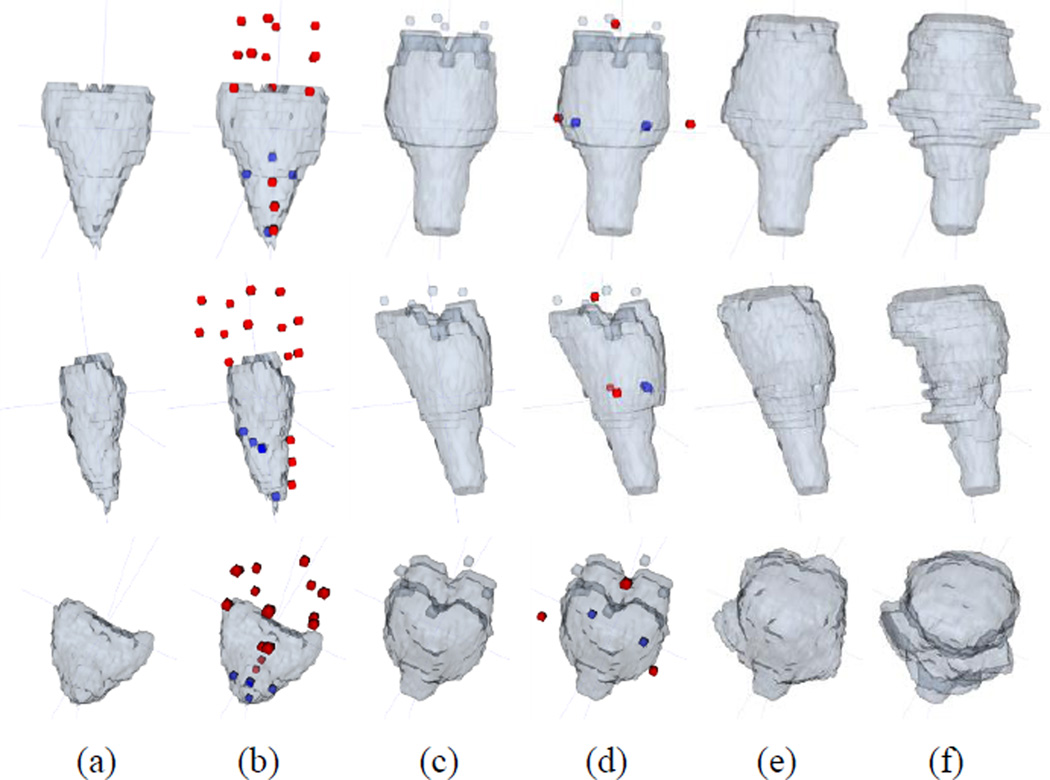
A typical example for the repetitive editing procedure is given in Fig. 8. In this example, the large error occurred in the upper part of the initial segmentation. Thus, there was a lack of good atlas label images that could cover the large shape change, even though the atlas label patches were searched within the local neighborhood. As a result, the intermediate result still included the error on the upper part (Fig. 8(c)). In the next round of editing, we inserted additional user dots, further re-aligned all atlas label images to the intermediate result, and also refined the result with additional interaction combinations near the dots. Since the aligned atlas label images were much more reliable in the second round than in the first round, the possible shape changes for the erroneous part could be covered in the search range of the second round. This allowed the segmentation to be more accurately updated.
Fig. 8.
The procedure of brainstem segmentation update with respect to the repetitive user interactions. (a) Initial segmentation with large errors, (b) initial segmentation with user interactions, (c) intermediate segmentation result based on the interactions shown in (b), (d) intermediate result with some additional user interactions, (e) updated segmentation result based on the interactions shown in (d), and (f) ground-truth segmentation. The red / blue dots represent the FG / BG interactions. Three different views in 3D space are shown in the top, middle, and bottom rows.
D. Validation of label-based registration
The appearance information of the reference image was not used in our editing procedure. Thus, our method can freely use the data sets open to the public or obtained from other modalities as the reference label atlases; which makes our method more useful, especially when only a few reference images with the same modality are available. In addition, the label-based registration usually gave comparable accuracy and less computational complexity than the deformable registration in the editing procedure since the image appearance information was sufficiently considered when the initial segmentations were generated by the state-of-the-art methods [17, 34, 41]. To demonstrate it, we selected the best, median, and worst initial segmentations from each data set, and then conducted our editing method using the reference atlas label images aligned by the ICP registration [2] and the MRF-based deformable registration [4], respectively. The ICP registration is based on labels, while the MRF-based deformable registration is based on image intensities. We measured the DSC scores of the aligned atlas label images with respect to the ground-truth label. The top ten DSC scores were averaged to assess the registration accuracy. We also calculated the final DSC scores using those aligned atlas label images for comparison. Table 5 shows these DSC scores. For both the prostate and brainstem, the initial segmentation gives better guidance than the intensity-based deformable registration since intensity based appearance is ambiguous. Moreover, as the segmentation is improved after the first round of editing, more reliable atlas label images can be obtained in the second round by aligning the atlases to the updated segmentation. On the other hand, the deformable registration is better for the hippocampus, due to its relatively stable position in the brain image. However, in terms of final segmentation accuracy, both registration methods obtain a similar performance as shown in the right two columns of Table 5. This is because we locally search for the similar label patches within a neighborhood, which could overcome a certain amount of registration errors. Therefore, the label-based registration was more efficient in the editing procedure.
TABLE 5.
The registration and editing performances for the label-based affine registration [2] and the intensity-based deformable registration [4], respectively. The column ‘ICP (Iter. 2)’ shows the registration accuracy using the updated segmentation from the first round of editing.
| Registration accuracy | Segmentation accuracy | ||||||
|---|---|---|---|---|---|---|---|
| ICP | Deformable | ICP (Iter. 2) | Initial | Editing with ICP |
Editing with deformable |
||
| Prostate | Best | 0.873 (0.007) | 0.732 (0.051) | 0.895 (0.003) | 0.856 | 0.923 | 0.925 |
| Median | 0.794 (0.006) | 0.705 (0.052) | 0.866 (0.003) | 0.788 | 0.894 | 0.891 | |
| Worst | 0.696 (0.005) | 0.761 (0.036) | 0.908 ( 0.008) | 0.669 | 0.919 | 0.908 | |
| Brainstem | Best | 0.79 (0.034) | 0.735 (0.014) | 0.882 (0.004) | 0.752 | 0.940 | 0.913 |
| Median | 0.642 (0.01) | 0.558 (0.12) | 0.866 (0.007) | 0.691 | 0.878 | 0.866 | |
| Worst | 0.422 (0.009) | 0.799 (0.034 | 0.863 (0.005) | 0.466 | 0.860 | 0.876 | |
| Hippocampus | Best | 0.81 (0.017) | 0.888 (0.006) | 0.822 ( 0.014) | 0.873 | 0.893 | 0.891 |
| Median | 0.772 (0.013) | 0.876 (0.003) | 0.78 ( 0.015) | 0.864 | 0.877 | 0.88 | |
| Worst | 0.748 (0.028) | 0.862 (0.016) | 0.771 (0.022) | 0.841 | 0.878 | 0.878 | |
E. Computational time
The experiments were performed on a PC with a 3.5 GHz Intel quad-core i7 CPU, and 16GB of RAM. The total computational time depended on the number of reference atlas label images, the number of interaction combinations, the ROI margin size, and the search range size. In our experimental settings, the computational time of the first round of editing took 1.5–7 minutes, 2–18 minutes, and 50–80 seconds for the prostate, brainstem, and hippocampus data sets, respectively. Since the editing is conducted with all interactions in the image, our method is unable to promptly produce the intermediate results, like the existing interactive methods [1, 32]. However, the accuracy of our method is much higher than those of the existing methods under the same amount of user interactions. Thus, the total editing time to obtain satisfactory segmentation can be reduced by our method. Specifically, our method allows the batch processing after receiving user interactions for all the erroneous parts. Thus, it will be effective for a scenario in which the incomplete segmentation results need to be edited for multiple images, which is often needed for shape analysis, longitudinal studies, and image-guided surgery. During the second round of editing, the computational time was greatly reduced, compared to the first round (Table 4). As the number of interactions is reduced at the fine-level editing steps, the computational time is further reduced.
IV. Conclusion
We have proposed a novel multi-atlas based segmentation editing method with interaction-guided constraints to find the appropriate atlas label patches and also derive their respective voting weights. Our proposed method can generate robust segmentation editing results without requiring image information and the expensive learning procedures, even in challenging regions. For all three challenging data sets, our method outperformed the other existing editing methods. We expect that our method can help produce accurate segmentations of a large number of 3D medical images, especially for difficult cases that failed in existing automatic methods. Although the simple appearance based deformable registration could not give an improvement in our method, the appearance information can be a useful cue for editing. In the future, we will consider using machine learning techniques, such as [32], to exploit the informative features and then use them for either registration or similarity calculation. Furthermore, we believe that our method can be easily extended to multi-label segmentation editing. Specially, all steps in our method, such as the patch selection step with Eq. (2) and the label fusion step with Eq. (3), can be similarly applied to multiple labels by grouping all labels (except a target label) as background.
Acknowledgments
This work was supported in part by NIH grant CA140413.
Footnotes
Contributor Information
Sang Hyun Park, Department of Radiology and the Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, NC 27599 USA (shpark13135@gmail.com)..
Yaozong Gao, Department of Computer Science and the Department of Radiology, University of North Carolina at Chapel Hill, NC 27599 USA (yzgao@cs.unc.edu)..
Dinggan Shen, Department of Radiology and the Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, NC 27599 USA, and also with the Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, Republic of Korea (dgshen@med.unc.edu)..
Reference
- 1.Park SH, et al. Data-driven interactive 3d medical image segmentation based on structured patch model. presented at the Inf. Process Med. Imaging; 2013. [DOI] [PubMed] [Google Scholar]
- 2.Besl PJ, Mckay ND. A Method for Registration of 3-d Shapes. Ieee Transactions on Pattern Analysis and Machine Intelligence. 1992 Feb;14:239–256. [Google Scholar]
- 3.Gao Y, et al. Prostate segmentation by sparse representation based classification. Medical Physics. 2012;39:6372–6387. doi: 10.1118/1.4754304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Glocker B, et al. Dense image registration through MRFs and efficient linear programming. Medical Image Analysis. 2008 Dec;12:731–741. doi: 10.1016/j.media.2008.03.006. [DOI] [PubMed] [Google Scholar]
- 5.Wang L, et al. Links: Learning-based multi-source Integration framework for Segmentation of infant brain images. Neuroimage. 2015;108:160–172. doi: 10.1016/j.neuroimage.2014.12.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shim H, et al. Knee cartilage: efficient and reproducible segmentation on high-spatial-resolution MR images with the semiautomated graph-cut algorithm method. Radiology. 2009 May;251:548–556. doi: 10.1148/radiol.2512081332. [DOI] [PubMed] [Google Scholar]
- 7.Barrett WA, Mortensen EN. “Interactive live-wire boundary extraction. Med Image Anal. 1997 Sep;1:331–341. doi: 10.1016/s1361-8415(97)85005-0. [DOI] [PubMed] [Google Scholar]
- 8.Boykov Y, et al. Fast approximate energy minimization via graph cuts. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2001 Nov;23:1222–1239. [Google Scholar]
- 9.Grady L. “Random walks for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2006 Nov;28:1768–1783. doi: 10.1109/TPAMI.2006.233. [DOI] [PubMed] [Google Scholar]
- 10.Heckemann RA, et al. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. Neuroimage. 2006 Oct 15;33:115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- 11.Aljabar P, et al. Multi-atlas based segmentation of brain images: Atlas selection and its effect on accuracy. Neuroimage. 2009 Jul 1;46:726–738. doi: 10.1016/j.neuroimage.2009.02.018. [DOI] [PubMed] [Google Scholar]
- 12.Coupe P, et al. Patch-based segmentation using expert priors: application to hippocampus and ventricle segmentation. Neuroimage. 2011 Jan 15;54:940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
- 13.Rousseau F, et al. A Supervised Patch-Based Approach for Human Brain Labeling. Ieee Transactions on Medical Imaging. 2011 Oct;30:1852–1862. doi: 10.1109/TMI.2011.2156806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang D, et al. Sparse Patch-Based Label Fusion for Multi-Atlas Segmentation. Multimodal Brain Image Analysis. 2012:94–102. [Google Scholar]
- 15.Tong T, et al. Segmentation of MR images via discriminative dictionary learning and sparse coding: application to hippocampus labeling. Neuroimage. 2013 Aug 1;76:11–23. doi: 10.1016/j.neuroimage.2013.02.069. [DOI] [PubMed] [Google Scholar]
- 16.Wang HZ, et al. Multi-Atlas Segmentation with Joint Label Fusion. Ieee Transactions on Pattern Analysis and Machine Intelligence. 2013 Mar;35:611–623. doi: 10.1109/TPAMI.2012.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wu GR, et al. A generative probability model of joint label fusion for multi-atlas based brain segmentation. Medical Image Analysis. 2014 Aug;18:881–890. doi: 10.1016/j.media.2013.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rother C, et al. “GrabCut“ - Interactive foreground extraction using iterated graph cuts. ACM Transactions on Graphics. 2004 Aug;23:309–314. [Google Scholar]
- 19.Bai X, Sapiro G. “A geodesic framework for fast interactive image and video segmentation and matting. presented at the IEEE International Conference on Computer Vision.2007. [Google Scholar]
- 20.Criminisi A, et al. GeoS: Geodesic Image Segmentation. Computer Vision - Eccv 2008, Pt I, Proceedings. 2008;5302:99–112. [Google Scholar]
- 21.Lempitsky V, et al. Image Segmentation with A Bounding Box Prior. 2009 Ieee 12th International Conference on Computer Vision (Iccv); 2009. pp. 277–284. [Google Scholar]
- 22.Kim TH, et al. Nonparametric Higher-Order Learning for Interactive Segmentation. presented at the IEEE Conference on Computer Vision and Pattern Recognition.2010. [Google Scholar]
- 23.Jung C, et al. Interactive image segmentation via kernel propagation. Pattern Recognition. 2014 Aug;47:2745–2755. [Google Scholar]
- 24.Panagiotakis C, et al. Interactive image segmentation based on synthetic graph coordinates. Pattern Recognition. 2013 Nov;46:2940–2952. [Google Scholar]
- 25.Gao Y, et al. A 3D interactive multi-object segmentation tool using local robust statistics driven active contours. Medical Image Analysis. 2012 Aug;16:1216–1227. doi: 10.1016/j.media.2012.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang D, et al. Active Learning for Interactive Segmentation with Expected Confidence Change. presented at the ACCV.2013. [Google Scholar]
- 27.Top A, et al. Active Learning for Interactive 3D Image Segmentation. presented at the Medical Image Computing and Computer-Assisted Intervention; 2011. [DOI] [PubMed] [Google Scholar]
- 28.Sourati J, et al. Accelerated Learning-Based Interactive Image Segmentation Using Pairwise Constraints. Ieee Transactions on Image Processing. 2014 Jul;23:3057–3070. doi: 10.1109/TIP.2014.2325783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Barnes C, et al. PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing. ACM Transactions on Graphics. 2009 Aug;28 [Google Scholar]
- 30.Barnes C, et al. The Generalized PatchMatch Correspondence Algorithm. presented at the ECCV.2010. [Google Scholar]
- 31.Schwarz T, et al. Interactive surface correction for 3D shape based segmentation - art. no. 69143O. Medical Imaging 2008: Image Processing, Pts 1–3. 2008;6914:O9143–O9143. [Google Scholar]
- 32.Park SH, et al. Interactive prostate segmentation using atlas-guided semi-supervised learning and adaptive feature selection. Med Phys. 2014 Nov;41:111715. doi: 10.1118/1.4898200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fritscher KD, et al. Automatic segmentation of head and neck CT images for radiotherapy treatment planning using multiple atlases, statistical appearance models, and geodesic active contours. Med Phys. 2014 May;41:051910. doi: 10.1118/1.4871623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gao Y, et al. Learning distance transform for boundary detection and deformable segmentation in CT prostate images. presented at the Machine Learning in Medical Imaging, MICCAI; 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shi Y, et al. Prostate Segmentation in CT Images via Spatial-Constrained Transductive Lasso. presented at the IEEE Conference on Computer Vision and Pattern Recognition; 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wisse LE, et al. A Critical Appraisal of the Hippocampal Subfield Segmentation Package in FreeSurfer. Front Aging Neurosci. 2014;6:261. doi: 10.3389/fnagi.2014.00261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liao S, et al. Sparse patch-based label propagation for accurate prostate localization in CT images. IEEE Trans. Med. Imaging. 2013 Feb;32:419–434. doi: 10.1109/TMI.2012.2230018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Klein S, et al. Automatic segmentation of the prostate in 3D MR images by atlas matching using localized mutual information. Medical Physics. 2008 Apr;35:1407–1417. doi: 10.1118/1.2842076. [DOI] [PubMed] [Google Scholar]
- 39.Iglesias JE, et al. Bayesian segmentation of brainstem structures in MRI. Neuroimage. 2015 Jun;113:184–195. doi: 10.1016/j.neuroimage.2015.02.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Winston GP, et al. Automated hippocampal segmentation in patients with epilepsy: available free online. Epilepsia. 2013 Dec;54:2166–2173. doi: 10.1111/epi.12408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang L, et al. LINKS: Learning-based multi-source Integration framework for Segmentation of infant brain images. Neuroimage. 2014 Dec 22;108C:160–172. doi: 10.1016/j.neuroimage.2014.12.042. [DOI] [PMC free article] [PubMed] [Google Scholar]