Using Active Learning for Speeding up Calibration in Simulation Models

Abstract

Background

Most cancer simulation models include unobservable parameters that determine the disease onset and tumor growth. These parameters play an important role in matching key outcomes such as cancer incidence and mortality and their values are typically estimated via lengthy calibration procedure, which involves evaluating large number of combinations of parameter values via simulation. The objective of this study is to demonstrate how machine learning approaches can be used to accelerate the calibration process by reducing the number of parameter combinations that are actually evaluated.

Methods

Active learning is a popular machine learning method that enables a learning algorithm such as artificial neural networks to interactively choose which parameter combinations to evaluate. We develop an active learning algorithm to expedite the calibration process. Our algorithm determines the parameter combinations that are more likely to produce desired outputs, therefore reduces the number of simulation runs performed during calibration. We demonstrate our method using previously developed University of Wisconsin Breast Cancer Simulation Model (UWBCS).

Results

In a recent study, calibration of the UWBCS required the evaluation of 378,000 input parameter combinations to build a race-specific model and only 69 of these combinations produced results that closely matched observed data. By using the active learning algorithm in conjunction with standard calibration methods, we identify all 69 parameter combinations by evaluating only 5620 of the 378,000 combinations.

Conclusion

Machine learning methods hold potential in guiding model developers in the selection of more promising parameter combinations and hence speeding up the calibration process. Applying our machine learning algorithm to one model shows that evaluating only 1.49% of all parameter combinations would be sufficient for the calibration.

INTRODUCTION

Simulation models have been increasingly used in health policy decision making [1, 2, 3]. Many of these models include a component that describes the natural history of the disease and simulates an individual’s course of health to assess the overall effect of the disease in the population [4, 5, 6, 7]. For example, several models for breast, prostate, colon, and lung cancer have been used to evaluate various cancer screening policies while representing both unobservable and observable portions of the natural history of cancer at an individual level [8, 9, 10, 11, 12, 13, 14]. In particular, natural history components of these simulation models require the use of unobservable parameters such as disease onset and tumor growth rate, which often cannot be estimated from available data sources [13, 15]. One commonly used method for determining these unobservable parameters is calibration [1, 2].

Calibration is an important element of model development and widely used in medical decision making and disease simulation models. Also referred to as “model fitting”, calibration is the process of estimating the values of the unobserved parameters such that simulation model’s output matches the empirical observed data, for example, observed incidence and mortality over time for cancer simulation models [1, 16]. An exhaustive calibration typically involves full exploration of the feasible parameter space of unobservable parameters. Even if the model includes a small number of unobservable parameters, depending on the range of values each unobservable parameter may take, the total number of possible parameter combinations that are evaluated during the calibration process may be very large. The difficulty of the calibration is therefore directly related to the number of unobservable parameters and the range of these parameter values.

Some simulation models employ a grid search approach for the calibration of the unobserved parameters [17, 18]. In this approach, first the maximum and minimum values of each unobserved parameter are determined. Then, the range of values for these unobserved parameters is divided into a regular grid and the output of the simulation model obtained for each grid point is compared to the target outcomes. Another method for searching the parameter space is to use a random search algorithm [19]. In this method, the parameter space is initially sampled randomly. After the first batch of runs, if a parameter combination satisfying the targets is not found, the parameter space is altered by using the information gained from the initial runs and the algorithm continues to sample from the resulting parameter space.

Both calibration methods attempt to find a set of optimal parameter combinations by doing an extensive search in the whole parameter space, which could be a viable option for a simulation model with few unobserved parameters but becomes computationally infeasible as the number of calibrated parameters increases. Furthermore, many established simulation models such as those used in cancer epidemiology can be very complex and even one simulation run may take a long time. Hence, the evaluation of all possible combinations is impractical.

The evaluation of a large number of parameter combinations can be avoided by identifying smaller subsets of the combinations that are more likely to produce desired outputs. Often evaluating only a small subset of input parameter combinations s sufficient for calibration, and the determination of such subsets is of key importance for the identification of natural history parameters. To this end, statistical models such as linear regression or machine learning methods such as artificial neural networks (ANNs) can be used as prediction models to determine promising subsets from the parameter space.

The purpose of this study is to show how machine learning methods, especially ANNs, can be used to expedite the calibration. We develop an active learning algorithm that guides the ANN model to choose which parameter combinations to evaluate during the calibration. We use the University of Wisconsin Breast Cancer Simulation Model (UWBCS), a validated simulation model of the epidemiology of the breast cancer, as a case study to describe our approach and demonstrate its efficacy.

METHODS

Using a Prediction Model for Calibration

We summarize the usage of a prediction model in the calibration process in five steps (see Figure 1). We start with identifying the set of parameter combinations from the parameter space of unobservable parameters. Then, we randomly select a small subset of these possible parameter combinations and evaluate them via simulation to obtain a numerical score, which indicates how closely the output of each parameter combination matches target outcomes. We note that the choice of scoring approach is problem-specific and a generic prediction model performs independently of the scoring scheme. By using this small set of evaluated parameter combinations as our training set, we build a machine learning prediction model, such as an ANN, that predicts the numerical score associated with a given parameter combination. Then, we use this prediction model to find those combinations that have acceptable predicted scores. We refer to a score associated with a parameter combination as an acceptable score only if it falls into a predetermined range for the scores. Those parameter combinations with acceptable predicted scores are more likely to produce desired outputs from the simulation. Finally, we evaluate the parameter combinations with acceptable predicted scores using the simulation and identify the parameter combinations that best correspond to the values of the unobservable parameters.

Figure 1.

Overview of the usage of a prediction model in simulation calibration.

Scores for Parameter Combinations

Scoring the parameter combinations is an important step of the calibration process. The score of a parameter combination is a measure of the difference between the simulation result and target outcome. A scoring scheme is typically model-specific and is affected by how modelers value different targets. A general method to determine the score of a parameter combination is to assign weights to each target and multiply those weights by the absolute or mean squared error between the simulation result and the target outcome. For the simulation models that aim to capture the trends in the observed outcome (e.g., cancer incidence by calendar year or age), an alternative method is to identify acceptance envelopes around these outcomes and determine the scores using these envelopes. Whenever the simulation result corresponding to a target year or age falls outside of the envelope, it is a violation of the closeness measure and the score of the parameter combination is increased by one. Therefore, smaller scores represent the better parameter combinations. Note that the acceptance envelopes are usually formed by determining error margins around the target outcome and can be modified to better capture the trends in a given year or age group.

UWBCS Overview

We use the UWBCS as an example simulation model to assess the efficiency of our approach for calibration. UWBCS is a discrete-event, stochastic simulation model of breast cancer epidemiology in the U.S. female population and has been used to address a variety of breast cancer screening policy questions. The model was designed to match age and stage-specific breast cancer incidence rates and age-specific mortality rates in the U.S. female population between 1975 and 2000. More information about UWBCS can be found elsewhere [19].

UWBCS has four core components: breast cancer natural history, breast cancer detection, breast cancer treatment and non-breast-cancer mortality among the U.S. women. While most of the parameters such as those used in treatment and mortality derived directly from the published studies, several parameters such as those used in natural history are unobservable and cannot be directly estimated from available data sources. Therefore, the UWBCS calibrates these natural history parameters to replicate the observed breast cancer incidence.

There are 10 natural history parameters in UWBCS that govern tumor onset and progression through each individual patient’s lifetime. Each of these parameters can take a wide range of values. Even if we assume that each of these parameters can take only five possible values, there would be approximately 10 million (5¹⁰) combinations, which is computationally infeasible to evaluate using UWBCS. Therefore, the use of accelerated approaches for the calibration of unobservable parameters emerges as a necessity.

Recently, Batina et al. [20] modified the UWBCS and created a race-specific UWBCS for black and white women to investigate the contributions of variations in natural history to the racial disparities in breast cancer outcomes. For this purpose, they first adjusted the model parameters except those relevant to the natural history of breast tumors according to the racial differences in breast cancer screening and treatment. Then, they calibrated the natural history parameters to replicate the observed 1975–2000 race-specific incidence data from Surveillance Epidemiology and End Results (SEER). They tested 378,000 parameter combinations for each race during the calibration process (see Table 1 for the set of calibrated natural history parameters and their corresponding ranges). Considering each simulation run takes 8–10 minutes on a stand-alone 30-core computer, this calibration procedure took more than 70 days.

Table 1.

Breast cancer natural history input parameters used in UWBCS model calibration

Parameter Name	Best fit in the original combined race UWBCS model	Sampled parameter values for the calibration of race-specific model	Number of Parameters
Fraction of LMP tumors	0.42	0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6	7
In situ tumor boundary	0.95	0.95	1
Max LMP size	2	2	1
LMP dwell time	0.5	1, 2, 3	3
Onset proportion	0.9	0.80, 0.85, 0.90, 0.95, 1.00	5
APC lag	3	1, 3, 5, 7	4
Percentage of aggressive tumors	0.01	0.01, 0.05, 0.10, 0.15, 0.20	5
Percentage of highly aggressive tumors	0.02	0.006, 0.010, 0.040, 0.070, 0.100	5
Mean tumor growth	0.12	0.00, 0.01, 0.02, 0.03, 0.04, 0.05	6
Variance tumor growth	0.012	0.00, 0.01, 0.02, 0.03, 0.04, 0.05	6

UWBCS, University of Wisconsin Breast Cancer Simulation; LMP, limited malignant potential; APC age-period-cohort

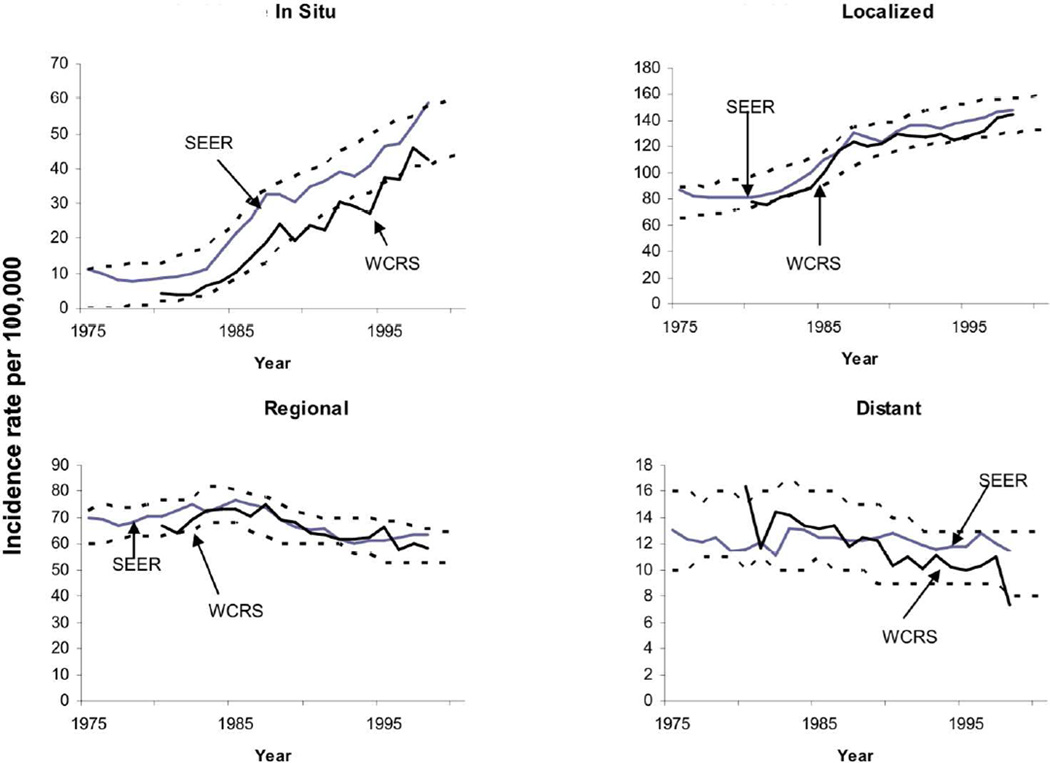
In order to assess the closeness of the output incidence generated by a given natural history parameter combination to the observed breast cancer incidence in the U.S., Batina et al. [20] generated envelopes around the observed incidence, which provide an acceptable error margin (see Figure 2 for these envelopes). Note that the error margins are determined according to the expert opinions and they allow focusing on specific calendar years to capture the trends better for those years. For instance, the envelopes around in situ incidence do not fully cover the Wisconsin Cancer Registry System (WCRS) outcomes, as the modelers put more importance on the SEER data and the difference between SEER and WCRS may become significant for some calendar years. Batina et al. [20] then counted the number of times the output incidence falls outside of these envelopes for each breast cancer stage to assign a score representing the goodness of the output incidence. Because there are 4 incidence values for each cancer stage (in situ, localized, regional, distant) and 26 years between 1975–2000, the worst score for an input parameter is 104. As the smaller scores indicate a better fit to the observed data, the best score is 0, which is obtained when all output incidence values are within the envelopes. Batina et al. [20] assumed that a score less than 10 is an an acceptable match. Note that while we use the scoring scheme described by Batina et al [20], our methods are applicable to other scoring schemes as well.

Figure 2.

Envelopes to score the fit of breast cancer incidence from the simulation model as compared with the SEER Program and the Wisconsin Cancer Reporting System (WCRS).

Artificial Neural Networks as a Prediction Model

One way to build a prediction model is to use a linear regression model, which has the following functional form:

$$f(X)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_n{X}_n,$$ (1)

where X₀,X₁,…, X_n denote n predictor variables (e.g., calibrated natural history parameters of the UWBCS), f(X) denotes the estimated score of a given parameter combination, β₀ is a constant and β₁, β₂, …, β_n are the regression coefficients of the predictor variables X₀,X₁,…, X_n denote n. While linear regression is an easy-to-use prediction method, it will not be able to represent the underlying function accurately if the latter is nonlinear. Therefore, we consider artificial neural networks as a more expressive prediction model that is able to represent nonlinear relationships between the predictor variables. Note that there are also several other nonlinear regression models that consider the interactions between the predictor variables and we use the simple linear regression solely as a benchmark for the performance of other approaches presented in this study.

Artificial neural networks are information processing structures inspired by the function of biological neural networks. They consist of a set of interconnected units where each unit has a transfer function that computes and outputs a function of the values provided by the units that connect to it [21]. Instead of the linear function used in the linear regression for the estimation of scores, ANNs also employ nonlinear functions as transfer functions at some units. The most commonly used transfer functions are sigmoid (logistic) functions, which can be given as follows:

$$g(X)=\frac{1}{1+e^{-x}}.$$ (2)

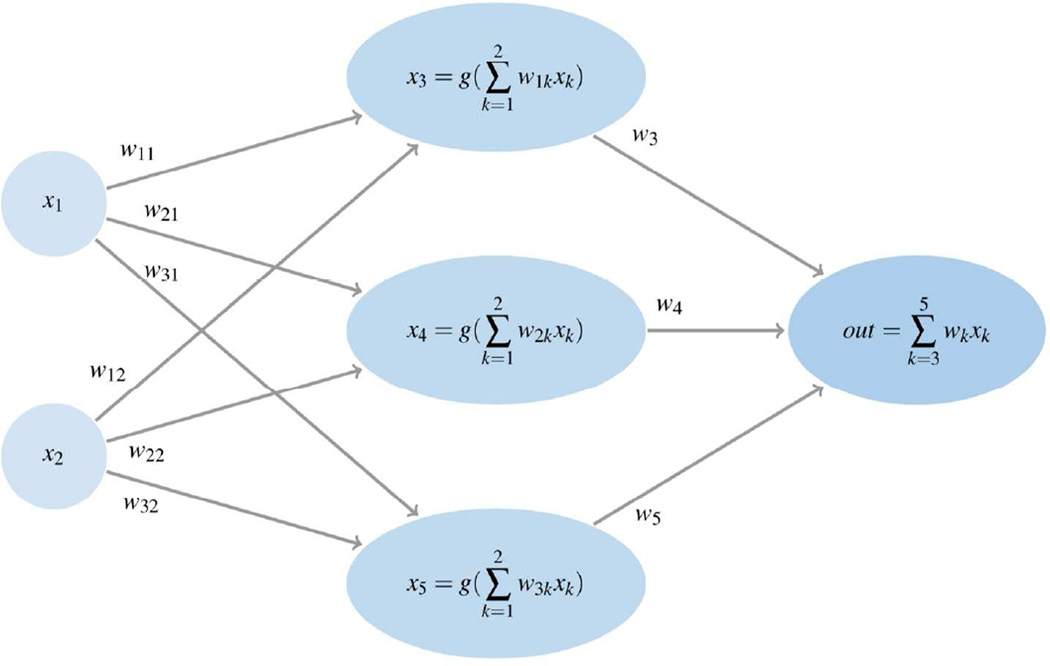
Alternatively, hyperbolic tangent functions or Gaussian functions can be used as transfer functions. Note that single layer ANNs with a linear transfer function f(X) given in equation (1) are equivalent to linear regression models. A graphical representation of a three layer neural network with two inputs and one output is shown in Figure 3.

Figure 3.

An illustrative graph showing a feed-forward ANN with an input layer with 2 inputs, a hidden layer with 3 hidden units, and 1 output unit.

ANNs vary in the way neurons are connected and inputs are processed. In this study, we use a 3-layer feed-forward ANN trained using a backpropagation learning algorithm with a learning rate 0.3 and momentum 0.2 [21]. The layers include an input layer representing the natural history parameters, a hidden layer with 21 hidden units, and an output layer with a single unit generating an estimate for the score. Our ANN model aims to minimize the sum of squared errors between predicted scores and actual scores and it uses the sigmoid function given in equation (2) as the transfer function in the hidden units and a linear transfer function in the output unit. Note that there are no exact rules in determining an ANN model’s parameters. For instance, learning rate and momentum parameters controls the speed of convergence of the backpropogation algorithm and both parameters can take any value between 0 and 1. Choosing higher values for these parameters may lead to divergence of the algorithm, whereas smaller values usually cause a slow convergence. We obtain the final values for such parameters by experimenting with the most commonly used values in the literature.

Ensembles of ANNs

Ensemble methods construct a set of models from the training data where predictions for the new instances are made by using a weight function that combines individual predictions. Bootstrap aggregating (bagging), boosting and stacking are well known approaches for generating ensembles of the prediction models [21]. In addition, some other studies focus on optimal aggregation of the prediction models [22, 23]. There are several successful applications of ensemble learning in healthcare literature. In particular, super learning, a generalization of stacking method where another prediction model is employed to combine the individual predictions, has been used for mortality risk prediction in elderly people and mortality prediction in intensive care units [24, 25].

We observe that using ensembles of ANNs often improve on the performance of a single generic ANN [26]. Our preliminary experiments with frequently-used ensemble methods such as bagging, stacking and additive regression indicate that using bagging to obtain an ensemble of ANNs leads to a prediction model with high predictive accuracy. Different than other ensemble methods, bagging forms several replicates of the training data set by sampling with replacement from the original set and a separate learning model is constructed for each of the replicate samples. Breiman et al. [27] note that bagging may provide substantial gains in accuracy for unstable learning methods such as ANNs where the learning method is significantly affected by the changes in the training set. We refer to the ensemble of ANN models constructed using bagging as bagANN. Also, in keeping with the machine learning terminology, we refer a parameter combination as an instance, and individual input parameters as features. We refer to a parameter combination with an unknown score as an unscored instance.

Active Learning for Calibration

Supervised learning methods such as ANNs use randomly selected instances as training sets to build a prediction model. However, it is often possible to achieve a higher level of predictive accuracy by having the learning method actively sample instances to be included in the training set. The process that interactively samples the instances is known as active learning [28]. The difficulty of obtaining scores via simulation for every parameter combination makes active learning attractive for the calibration problem. Therefore, to increase the prediction power of the bagANN model and to decrease the total number of simulation runs required, we develop an active learning algorithm that iteratively selects promising parameter combinations from the set of all combinations and evaluates only these parameter combinations using the simulation model.

Figure 4 summarizes the active learning approach that is used in this study. First, we train the bagANN model using a small number of evaluated parameter combinations. Then, we use this bagANN model to select a batch of instances with low predicted scores from a large pool of unscored instances and evaluate these instances via the simulation model. If the stopping criterion is not met, we retrain the bagANN model with the selected instances and repeat the process. We use a clustering approach to select the batch of instances with low predicted scores to ensure that the putatively low-scoring instances in the batch represent the different regions of the parameter space. For clustering the instances, we use hierarchical clustering with Euclidean distance and single linkage measures. Moreover, we augment the batch that is used to update the bagANN model with a set of randomly selected parameter combinations. This step further assures that the parameter space is broadly sampled to train the bagANN model. We present a more detailed version of our active learning algorithm in the appendix.

Figure 4.

Flowchart of the simulation-model calibration process using active learning.

An important element of the active learning algorithm is the stopping criterion [29, 30, 31]. For our method, we use a stopping criterion that detects when the active learning process is providing diminishing returns in identifying acceptable parameter combinations. We first determine a warm-up period for the active learning algorithm, which is the minimum number of iterations required to stop sampling. Then, we stop the active learning algorithm when no acceptable instance is added to the training set in k consecutive iterations, where k is a user-defined parameter.

Estimating the Number of Evaluations Required

After training the bagANN model on a randomly selected subset of parameter combinations, we can test the accuracy of the bagANN model on an independently selected test set. This predictive accuracy information serves as a performance measure for our prediction model. In addition, the test set can be used to estimate the total number of simulation runs needed to obtain a reasonably high portion of all good parameter combinations. The following simple procedure summarizes our approach to estimate the number of runs needed.

Algorithm 1.

Calculate Expected Number of Runs

Input: test instances T, all instances S, threshold score δ T′ ← {i ∈ T: l(i) ≤ δ} Δ ← max i ∈ T′{f(i)} ENRuns ← Σi ∈SI{f(i) ≤ Δ}

In this algorithm, l(i) represents the score of each instance in set T, f(i) represents the predicted value for instance i ∈ T, and I is the indicator function. Here, we first form a subset of test instances T′ from the instances in the test set T that have scores lower than the predetermined threshold score δ (e.g., Batina et al. [20] set the threshold value to 10). Then, we find the maximum predicted score Δ for those instances in the set T′. Finally, we count the number of instances with a predicted score lower than Δ in the set S, which is the set consisting of all instances.

Application of our Method to UWBCS

We test the efficiency of our method using the calibration process of the UWBCS. Batina et al. [20] evaluated 378,000 parameter combinations for the black women and another 378,000 parameter combinations for the white women in the U.S. to determine breast cancer natural history parameters for each race. They deemed parameter combinations with scores below 10 as acceptable and reported that they found 69 acceptable parameter combinations for black women and 47 acceptable parameter combinations for white women. Here, we only use the results of the Batina et al. [20]’s experiments with the black female population, as the two calibration processes are very similar. We assume that all of the features (individual parameters of a parameter combination) have nominal values in our experiments. We observe that changing the nominal features to numeric features does not lead to more accurate prediction models, which is also observed in several other studies [32].

In our computational experiments, we first demonstrate the performance of the prediction models in predicting the scores of parameter combinations and then examine the additional benefits of using a prediction model in the active learning setting. Therefore, we first compare the bagANN model with simple linear regression model and conventional ANNs. For this experiment, we start with evaluating 30,000 parameter combinations using the simulation model and use those as our training and test sets according to a 60/40 ratio (i.e. 60% of 30,000 are used for training and 40% of 30,000 are used for testing). As comparison measures, we use mean absolute error and root mean squared error values of the prediction models. We also report the predictive accuracy of the trained models on the instances with low actual scores by only considering the instances in the test set that have actual scores lower than some predetermined value. We use 30 as a threshold score to determine such instances and refer to these instances as low-scored instances. Later, we compare different training sets consisting of 10,000 to 50,000 instances to demonstrate the effect of the training set size. Again, we use a 60/40 ratio to separate these sets into training and test sets.

In our experiments with the active learning algorithm, we start by evaluating 1000 parameter combinations and include these instances in a set L. At each iteration of the algorithm, we add 200 new instances to L. Half of those instances are selected based on predicted scores and hierarchical clustering, and the rest were randomly selected to minimize bias in the prediction model. In order to obtain an estimate of the number of acceptable parameter combinations identified after each iteration of the active learning algorithm, we count the number of acceptable parameter combinations that are in set L and among the set of 1000 instances selected from unscored instances based on their predicted scores. As a stopping criterion in the active learning experiments, we either use a bound on the number of instances in L or use 5 iterations for the warm-up period and k=3 for the number of consecutive iterations without new acceptable instances added to the training set.

We carry out our experiments with the prediction models using the WEKA (version 3.6.5) JAVA library in our implementations. Experiments are run on Intel Xeon 2.27 GHz processor with 12GB RAM running Windows 7.

RESULTS

Table 1 reports the performance of the prediction models in a standard supervised learning setting where we use a single training set to train a model, and then make predictions based on this model. We also report the estimates on the additional number of evaluations required for various prediction models, which are obtained using Algorithm 1. Our results show that the ANNs have significantly better predictive accuracy than linear regression (LinR) as observed in mean absolute error (MAE) and root mean squared error (RMSE) values as well as the number of additional runs required by each model. Besides, improvements in the predictive accuracy are more apparent in MAE and RMSE values obtained for the low-scored instances. We recognize that the simple linear regression model does not account for the interactions between different features. However, ANNs use nonlinear activation functions to overcome this limitation, which also helps ANNs to achieve better predictive accuracy for our problem.

Using bagging to construct ensembles of ANNs further improves predictive accuracy especially in terms of the additional number of runs required by each model. While the ANN model alone suggested that an additional 4626 simulation evaluations would generate all the acceptable parameter combinations, bagANN model achieves the same level of performance through the evaluation of only 2741 additional parameter combinations.

We also demonstrate how bagANN performance varies as a function of the training set size and report the estimates on the additional number of runs required for different threshold values in Table 2. For this purpose, we sample 30 different training sets for each training set size and provide the average values for the performance measures. As the training set size increases, MAE and RMSE improve overall and for the low-scored instances. However, because we randomly select the initial training sets, there exist discrepancies in the reported results. For instance, while training set size of 50,000 leads to the best MAE and RMSE values for the low-scored instances, MAE and RMSE values for the overall instances are worse compared to the training set size of 40,000. Despite these inconsistencies, our results indicate that, as the training set size increases, bagANN model’s predictive accuracy increases at a higher rate for low-scored instances and the number of additional evaluations decreases considerably. On the other hand, increasing the size of the training set beyond 30,000 instances do not lead to significant performance gains. For example, when the training set size is 30,000, by setting the threshold value δ = 15, we obtain 97% of all acceptable instances by performing 1903 additional simulation evaluations, whereas when the training set size is 40,000 and δ = 15, we obtain 99% of all acceptable instances by evaluating 1936 additional parameter combinations.

Table 2.

Comparison of the different prediction models for the UWBCS calibration problem

Training Method	Mean Absolute Error	Root Mean Squared Error	Mean Absolute Error for Instances with Low scores	Root Mean Squared Error for Instances with Low scores	Number of runs required and percentage of acceptable combinations found (δ = 15)	Time (in seconds)
LinR	8.16	10.97	33.45	34.08	78754(99%)	1
ANN	3.26	4.36	7.00	8.42	4626(100%)	290
bagANN	2.26	2.97	5.41	6.46	2741(100%)	2547

LinR, linear regression; ANN, artificial neural networks; bagANN, ensemble of ANN constructed via bagging method

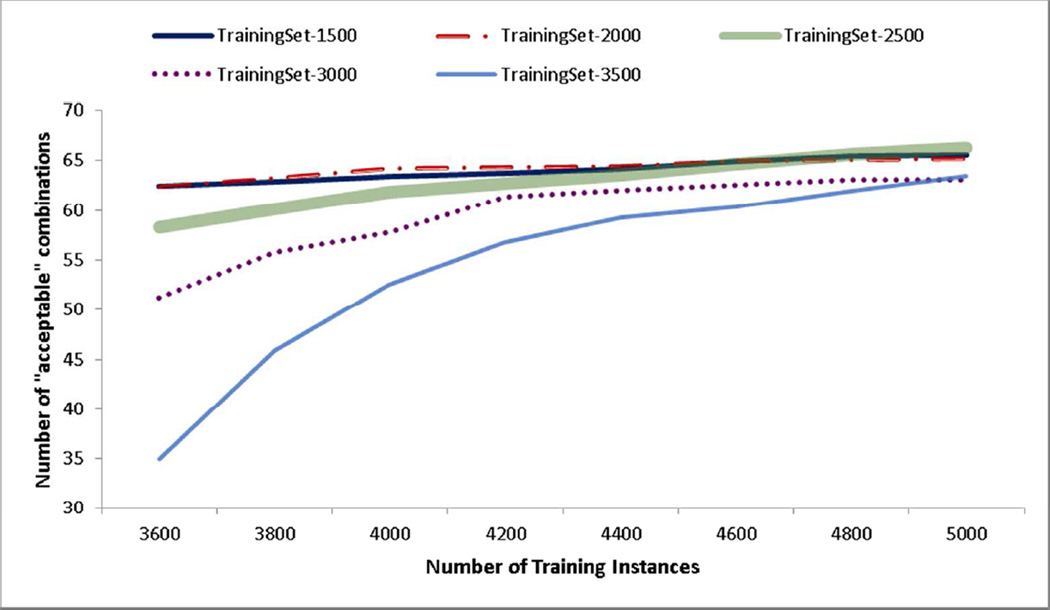
Our next experiment tests the benefit of using an active learning framework to select the instances that are provided to the bagANN for training. In this experiment, we compare our active learning algorithm to a method that randomly selects the instances that are added to the training set. For both cases, we repeat the algorithm for 30 different initial training sets each including 2000 parameter combinations and stop the algorithm when our training set reaches to 5000 instances. Figure 4 shows that the active learning algorithm can locate all acceptable parameter combinations by evaluating only a fraction of all instances whereas the random selection method needs to evaluate significantly more instances to achieve similar performance. In fact, random selection method does not achieve the same level of performance with the active learning algorithm even if we continue sampling instances until the training set reaches 10,000 instances. Error bars in Figure 4 indicate that active learning results are slightly more variable with respect to the initial training set compared to random selection. We also conduct a one-way sensitivity analysis on initial training set size and batch size parameters of the active learning algorithm. Figure 6 shows that the active learning algorithm performs better for the initial training sets with 1500–2000 instances. In addition, Figure 7 shows that although performance of the active learning algorithm is not significantly affected by the choice of the batch size, smaller batch sizes should be more preferable.

Figure 6.

Learning curves for different initial training set sizes.

Figure 7.

Learning curves for different batch sizes used in the active learning algorithm.

In our final experiment, we use the stopping condition based on warm-up period and consecutive number of iterations without new acceptable instances in the training set. We find that, on average, the active learning algorithm stops when the total number of evaluated parameter combinations reaches 5620. These 5620 instances contain all 69 acceptable parameter combinations that were reported by Batina et al. [20], which implies that evaluating only 1.49% of all 378,000 instances would be sufficient to obtain all acceptable parameter combinations. We also perform a one-way sensitivity analysis on the stopping condition parameters of the active learning algorithm. Table 4 shows that while increasing the k value leads to more simulation evaluations, it does not lead to a significant improvement in the number of acceptable parameter combinations. Similar analysis on the length of warm-up period shows that our active learning algorithm is not sensitive to the changes in warm-up period. However, using a limit on the length of warm-up period ensures that active learning algorithm does not terminate prematurely.

Table 4.

Performance of the active learning algorithm for different stopping criterion parameters (k)

	k=2	k=3	k=4	k=5	k=6
avg. # Instances	5340	5620	5820	6200	6640
avg. # Acceptable	65.6	65.6	65.6	66.7	67.9

avg. # Instances, average number of instances (parameter combinations) evaluated via simulation; avg. # Acceptable, average number of instances with acceptable score found by the active learning algorithm

Active learning algorithm requires approximately 2 hours and the evaluation of 5000 parameter combinations takes 22 hours on a 30-core computer. Thus, the total processing duration for the active learning algorithm is 24 hours of CPU time and this is a significant improvement over the time required for evaluation of 378,000 parameter combinations, which is approximately 70 days of CPU time.

DISCUSSION

Simulation models with unobservable parameters frequently resort to calibration, which may require a large number of simulation runs. Finding the best parameter values by evaluating all possible parameter combinations is usually burdensome and requires considerable computational time. In this study, we address the problem of determining the most promising input values so that calibration can be completed by evaluating only a small subset of all parameter combinations. For this purpose, we use several machine learning approaches and provide several key statistics on the predictive accuracy of each method. Our results show that the computational burden of the calibration may be reduced significantly and the calibration is feasible even for complex simulation models.

To the best of our knowledge, the study by Kong et al. [2] is the only calibration work that described a framework to reduce the number of parameter combinations to be evaluated. More specifically, Kong et al. [2] use metaheuristics such as simulated annealing [26] and genetic algorithms [27] to search the parameter space to find the best parameter combination for a lung cancer simulation model. They also provide a method for measuring the closeness of the actual calibration targets and simulation outcomes. While their approach effectively avoids evaluating all parameter combinations, it is able to identify only one (or a small number of) acceptable parameter combination that matches the target outcome without actually assessing the quality of the outputs for other parameter combinations. On the other hand, identifying all or a big portion of acceptable parameter combinations can help guard against non-identifiability problems in calibration. As our approach provides estimations on outcomes of any parameter combination, one can take advantage of all parameter combinations to better understand the effects of parameter uncertainty on model conclusions.

Our computational experiments indicate that an ANN can identify the promising parameter combinations with high accuracy. We further enhance the predictive accuracy of the ANN by using an ensemble method called bagging. Finally, we develop an active learning algorithm that further increases the predictive accuracy of the prediction model while reducing the number of simulation runs required for the calibration. We show that, for the example calibration process given in Batina et al. [20], most of the promising parameter combinations can be obtained by evaluating less than 2% of all parameter combinations. We acknowledge that while the active learning algorithm performs better, stand-alone usage of a prediction model may still be preferable especially considering the complexity of the active learning algorithm. For instance, one may prefer using the stand-alone bagANN model if the objective is not to explore as many acceptable parameter combinations as possible.

Our active learning algorithm and bagANN prediction model do not guarantee finding every acceptable parameter combination and we are able to report the percentage of acceptable parameter combinations found by our method only because Batina et al. [20] reported the number of acceptable parameter combinations in their study. In addition, because the active learning algorithm stops when there are no new acceptable parameter combinations found in k consecutive iterations, the number of acceptable parameter combinations obtained by the active learning algorithm can be used as an estimate on the total number of acceptable parameter combinations in the parameter space. Note that there are no exact procedures for the selection of the warm-up period and the k value and these parameters may significantly affect the performance of the prediction model. For instance, if we increase the length of warm-up period or k, we expect our bagANN model to predict scores more accurately. However, increased values for these parameters also lead to more simulation runs. Therefore, it is important to find the right balance between the prediction model’s predictive accuracy and the total number of simulation runs required to obtain this accuracy. We perform a one-way sensitivity analysis to demonstrate the impact of stopping criteria parameters on the performance of active learning algorithm.

While we demonstrate our method using a previously developed cancer simulation model, it can easily be applied to other simulation models that require the evaluation of a large number of parameter combinations for the calibration. In general, calibration processes of the simulation models require going through similar steps. After deciding on model-specific scoring scheme and determining the set of parameter combinations, modelers can use the two approaches presented in his study. The first approach is summarized in Figure 1 and involves constructing a prediction model using the initial simulation evaluations and estimating the scores of the remaining parameter combinations. While this approach is easier to implement, it is difficult to determine ideal training set size and threshold score δ, which is used to determine which parameter combinations to evaluate. The second approach is to use an active learning algorithm, which starts with a prediction model that is constructed using a very small training set and reconstructs this model by iteratively adding more instances to the training set as shown in Figure 4. As we start with a very small training set and only add those instances to the training set that lead to a better prediction model, active learning approach generally requires significantly less simulation evaluations and also includes a natural stopping criterion. Modelers may choose between these two approaches according to the complexity of their model and available computational resources. In addition, because of the similarities in the calibration processes, we expect our approaches to perform well for other simulation models. However, model-specific features such as the number of unobservable parameters and scoring scheme may affect some parameters of our algorithms (e.g., initial training set size and stopping criteria parameters of the active learning algorithm) as well as the type of the machine learning algorithm used as the prediction model.

Several parameters related to prediction models and the active learning algorithm are determined based on expert opinions and empirical analysis. We conduct numerical experiments to show the effects of some of these parameters such as initial training set size and threshold score δ on model performance. On the other hand, we rely on the most commonly used methods in the literature and our preliminary analysis for the selection of many other parameters such as type of the activation function used in the ANN and type of the clustering approach employed in the active learning algorithm. In addition, we recognize that other prediction models, including different types of regression models and ensemble methods, may perform better than bagANN for a general simulation model. However, determining the best prediction model and comparing the performance of ensemble methods is beyond the scope of this study.

Our study has some limitations. First, it is important to note that training a prediction model using bagANN requires more CPU time compared to using other machine learning methods presented here. However, considering that we use 30,000 parameter combinations as our training and test sets and each simulation evaluation takes 480 seconds, training time for the bagANN is still reasonable for the UWBCS. On the other hand, training bagANN may not be computationally feasible for the simulation models with more unobservable parameters. In such situations, using a conventional ANN as a prediction model could be a viable option as conventional ANNs require significantly shorter training times as shown in our experiments. Secondly, our computational experiments are limited to UWBCS and depending on the simulation model and the scoring approach used, alternative machine learning methods such as support vector machines or Bayesian networks could demonstrate better performance. In any case, our active learning algorithm can easily be used in conjunction with other machine learning methods that are used as prediction models for the calibration problem.

Figure 5.

Learning curves showing the number of acceptable parameter combinations found as a function of the number of training instances: active learning compared with random selection. 254×169mm (72 × 72 DPI)

Table 3.

Performance of the bagANN for different training set sizes

Training Set Size	Mean Absolute Error	Root Mean Squared Error	Mean Absolute Error for Instances with Low Scores	Root Mean Squared Error for Instances with Low scores	Number of runs required and percentage of acceptable combinations found (δ = 10)	Number of runs required and percentage of acceptable combinations found (δ = 15)	Number of runs required and percentage of acceptable combinations found (δ = 20)
10,000	2.70	3.71	6.38	7.57	729(39%)	2504(88%)	6624(99%)
20,000	2.26	3.05	5.13	6.14	754(64%)	1983(95%)	4443(100%)
30,000	2.20	2.94	4.60	5.51	614(76%)	1903(97%)	4086(100%)
40,000	2.12	2.85	4.54	5.45	764(81%)	1936(99%)	4136(100%)
50,000	2.19	2.88	4.53	5.39	677(84%)	2061(100%)	4079(100%)

Appendix

Algorithm 2.

Active Learning for Simulation Calibration

Input:	Scored instances set L, unscored instances set U,
	average number of instances in a cluster k, query batch size B,
	random sample size B’, query strategy φ(·)
	// learn a model using L
	M = train(L)
	repeat
	S = ∅
	for b = 1 to kB
	// select the lowest scored instance
	$x_b^{*}=\text{arg}{\mathit{\text{min}}}_{x\in U-S}$ φ(x)
	$S=S\cup x_b^{*}$
	end
	{C1, …, CB} = cluster(S)
	for b = 1 to B
	// select the lowest scored instance in cluster Cb
	$x_b^{*}=\text{arg}{\mathit{\text{min}}}_{x\in C_b}$ φ(x)
	// evaluate instance to obtain its score
	evaluate$(x_b^{*})$
	$L=L\cup x_b^{*}$
	$U=U-x_b^{*}$
	end
	// select a random sample of size B′ from L
	S′ = select(U, B′)
	// evaluate instances to obtain their scores
	for b′ = 1 to B′
	evaluate(xb′)
	end
	L = L ∪ S′
	U = U − S′
	M = train(L)
	until some stopping criterion;