Abstract
Purpose:
Accurate data regarding linear accelerator (Linac) radiation characteristics are important for treatment planning system modeling as well as regular quality assurance of the machine. The Imaging and Radiation Oncology Core-Houston (IROC-H) has measured the dosimetric characteristics of numerous machines through their on-site dosimetry review protocols. Photon data are presented and can be used as a secondary check of acquired values, as a means to verify commissioning a new machine, or in preparation for an IROC-H site visit.
Methods:
Photon data from IROC-H on-site reviews from 2000 to 2014 were compiled and analyzed. Specifically, data from approximately 500 Varian machines were analyzed. Each dataset consisted of point measurements of several dosimetric parameters at various locations in a water phantom to assess the percentage depth dose, jaw output factors, multileaf collimator small field output factors, off-axis factors, and wedge factors. The data were analyzed by energy and parameter, with similarly performing machine models being assimilated into classes. Common statistical metrics are presented for each machine class. Measurement data were compared against other reference data where applicable.
Results:
Distributions of the parameter data were shown to be robust and derive from a student’s t distribution. Based on statistical and clinical criteria, all machine models were able to be classified into two or three classes for each energy, except for 6 MV for which there were eight classes. Quantitative analysis of the measurements for 6, 10, 15, and 18 MV photon beams is presented for each parameter; supplementary material has also been made available which contains further statistical information.
Conclusions:
IROC-H has collected numerous data on Varian Linacs and the results of photon measurements from the past 15 years are presented. The data can be used as a comparison check of a physicist’s acquired values. Acquired values that are well outside the expected distribution should be verified by the physicist to identify whether the measurements are valid. Comparison of values to this reference data provides a redundant check to help prevent gross dosimetric treatment errors.
Keywords: Linac, reference data, percentage depth dose, small field, IROC
1. INTRODUCTION
Using accurate dosimetry data is an essential part of providing high-quality radiation therapy treatments. This includes both acquiring accurate dosimetry data and constructing an accurate beam model in the treatment planning system (TPS). The challenge in both of these steps has increased as new technologies like intensity-modulated radiation therapy (IMRT) and stereotactic body radiation therapy (SBRT) have become more common because these techniques have increased the necessary dosimetry data and data accuracy required.
One viable solution to help ensure accurate dose delivery is the creation of reference dosimetry data for linear accelerator (Linac) beam data that can be used as a redundant dose verification tool. This dataset can, for example, be compared to commissioning measurements when important reference values are being established. Although dosimetry data for certain models of Linacs have been published, including for multiple machines of the same type, no consistently collected large scale data source is yet available.1–8 This study aims to evaluate and classify Varian Linac models using statistical and clinical metrics. Furthermore, because of the large number of measurements, we provide not just reference dosimetry values for Linacs but distribution characteristics so that physicists can evaluate their dosimetry data in the context of the distribution of similar Linacs.
The Imaging and Radiation Oncology Core-Houston (IROC-H) Quality Assurance Center, formerly named the Radiological Physics Center, was established to ensure that radiation therapy for institutions participating in the National Cancer Institute’s clinical trials is delivered in a comparable, consistent, and accurate manner. IROC-H has examined the dosimetric properties of linear accelerators since its inception. One way this is accomplished is through on-site dosimetry review visits by an IROC-H physicist to participating institutions. One component of the site visit is to acquire Linac characteristics for basic dosimetry parameters.
In this work, we present the measured dosimetry data from site visits for more than 500 Varian accelerators (Varian Medical Systems, Palo Alto, CA). Similarly performing Linac models have been grouped to form representative class datasets. These reference datasets can be used by physicists who might be commissioning a new treatment machine, considering matching different types of Varian machines or as a redundancy check of current baseline values. This work is a substantial expansion of previously published IROC-H photon data;9–11 electron data exist as well but are not addressed here.12 Because a large number of Linacs have been measured, we can provide statistical metrics for each dataset so that a physicist can evaluate their machine’s measurements not against a single value but against a distribution. IROC-H collects data from all types of Linacs, but given the vast amount of data, the analysis in this study was limited to one vendor, Varian.
2. MATERIALS AND METHODS
2.A. Data collection
All dosimetry data were acquired during IROC-H site visits using a 30 × 30 × 30 cm water phantom placed at a 100 cm source-to-surface distance. Point measurements were made with an Accredited Dosimetry Calibration Laboratory (ADCL) calibrated Farmer-type chamber, typically a Standard Imaging Exradin A12 (Standard Imaging, Madison, WI), except for the IMRT and SBRT-style output fields (defined below), which used an Exradin A16 microchamber. Site visits and resulting measurements were performed by all physicists on staff at IROC-H in an approximately equal distribution following a consistent established standard operating procedure that included a detailed review by a second physicist. All measurements were conducted at the effective measurement location of the ion chamber, 0.6rcav upstream of the physical center of the chamber.
Data from more than 500 Varian machines were collected during the period of 2000–2014 and are presented here. The number of measurements at a given point varied slightly as sometimes not every point was measured or recorded for a given parameter, and some parameters, like SBRT-style output factors (OFs), have only relatively recently started being collected.
The following dosimetric data point locations were measured. The percentage depth dose (PDD) was measured in the 6 × 6, 10 × 10, and 20 × 20 cm2 fields at effective depths of 5, 10, 15, and 20 cm; for 10 × 10 cm2 fields, a dmax measurement was also made. Field-size dependent output factors were measured at 10 cm depth. Values were converted to a dmax value based on the ratio of the institution’s PDD values at 10 cm and dmax for 6 × 6, 10 × 10, 15 × 15, 20 × 20, and 30 × 30 cm2 fields. Off-axis factors (OAFs) were measured at dmax at distances of 5, 10, and 15 cm away from the central axis (CAX) in a 40 × 40 cm2 field; at 10 cm off-axis, four measurements were made in the four cardinal directions of the field and averaged. Two sets of small field output factors were measured, both measured at 10 cm depth for the following field sizes: 2 × 2, 3 × 3, 4 × 4, and 6 × 6 cm2. All measurements were normalized to a 10 × 10 cm2 field. The first set of output factors, referred to hereafter as “IMRT-style output factors,” had the jaws fixed at 10 × 10 cm2 and the MLCs moved to the mentioned field sizes; these are so called because they represent approximate segment sizes in an IMRT field. The second set of output factors, referred to hereafter as “SBRT-style output factors,” moved both the jaws and MLCs to the given field size; these represent approximate positions during an SBRT treatment. A representative figure can be seen in the work of Followill et al.9 Wedge factors were measured at a depth of 10 cm in a 10 × 10 cm2 field for 45° and 60° physical and enhanced dynamic wedges (EDW) when applicable; in addition, the 45° wedge was also measured at a depth of 15 cm in a 15 × 15 cm2 field to verify depth and field size dependence of the wedge factor.
Although data have been collected for other energies, 6, 10, 15, and 18 MV are by far the most widely used energies and are thus presented here. Linac models not currently in widespread use were omitted from the analysis. Data were also reviewed for transcription and transfer errors to ensure integrity.
2.B. Data analysis
All data analyses and visualizations were done using the general programming language python. The open-source “pandas” python package was used for data munging and plotting.13 Statistical testing used the “statsmodels” package.14
Varian Linacs have been shown to have comparable dosimetric characteristics for machines of the same model and energy; beyond that, many different models have similar dosimetric properties.1,5,8,14,15 This is understandable because different model names do not necessarily relate to differences in dosimetry—for example, the EX and iX models differ only in the inclusion of an OBI system. IROC-H has measurements from over twenty Varian Linac models. Each model may have multiple energies and produce specialized beams, e.g., flattening-filter free (FFF). If each energy and specialized beam is considered independent, there are over 50 measurement sets. Given the consistent dosimetric values and large number of models, there was a desire to consolidate the different models into dosimetrically distinct groups, or “classes” of accelerator. Thus, models that fall into the same class can be considered dosimetrically equivalent at our criteria levels and our measurement points.
To categorize the different Linac models into classes, two criteria were used to analyze comparability: statistical and clinical. The statistical criterion tested if a model’s mean parameter value [e.g., PDD(6 × 6 cm2, 5 cm)] was significantly different from the comparison model’s mean value using analysis of variance and Tukey’s honest significant difference post hoc analysis (α = 0.05). The clinical criterion tested if the median value of a model’s dataset and the median value of the comparison model dataset had a local difference of less than 0.5%. This value was chosen because it is approximately equal to the overall standard deviation of the IROC-H measurements and these stricter criteria were deemed preferable to a looser ones. If both criteria were not met, the dataset under consideration was rejected from that classification. The clinical criterion was added because statistical differences were occasionally achieved with very small differences in mean values (<0.5%).
Each model and energy combination was considered independent. Thus, using this classification, it could be possible for two models to be dosimetrically equivalent at one energy but not at another energy. Specialized beams like Trilogy SRS and TrueBeam FFF were also independently evaluated. At each energy, the classification that represented the largest number of Linacs was designated the “base” class. The base class was formed by starting with the most populous model dataset for that energy. This method was the most conservative approach since the most populous model had the narrowest confidence interval. The next most populous dataset was compared to the first. If it was within the criteria, that model was also said to be represented by the base class. Each subsequent model dataset was compared to the first. This process was then repeated for model datasets that were not within criteria of the base class, with the most populous remaining dataset forming the start of the next class. This was repeated for each energy until no model datasets remained. Other classifications at the same energy were named as appropriate for the model(s) they represented. It should be noted that alternating the starting model had a negligible impact on the resulting classes. After all the models were assigned a class, the model datasets for a given class were assimilated into one dataset. Statistical metrics were derived from these combined datasets. Discussion of the dataset distributions can be found in the Appendix.
Finally, a comparison of classes was done for each dosimetric parameter at each energy. The 6 MV data are displayed via figures to fully describe the data distribution, while 10, 15, and 18 MV have been described in tables to save space. Quantitative data for all energies can be accessed through the supplementary material, which includes the number of measurements, median, standard deviation, and the 5th and 95th percentile values.15 Because of the large number of data points, the 6 MV figures are plotted in boxplot fashion. The central line within the box represents the median which is robust to outlier influences. The top and bottom of the box represent the 75th and 25th percentiles, respectively, and the whiskers above and below the box represent the 95th and 5th percentile values, respectively. Data are shown here graphically to quickly convey qualitative differences between machine classes and show the entire distribution, but the median value of each class is also given at the top of the plot.
3. RESULTS
3.A. Model comparison
For all energies, the Clinac 21EX model dataset was the most populous. At 6 MV, 17 models were evaluated. Six models were within comparability criteria and were assimilated to form the base class. The remaining classes were generated using the same comparison process, resulting in a total of eight classes. There were 11 models at 10 MV and 12 at 15 MV, which consolidated to three and two classes, respectively. Eleven models were all consolidated to one class at 18 MV. The model classification results are shown in Table I. This table is how a physicist can identify what class their Linac is in. These classes are dosimetric representatives of the listed models. For example, using Table I, a 21iX 10 MV beam is said to be represented by the 10 MV base class, and evaluations of the individual machine should be performed against the results of that class.
TABLE I.
Derived classes with the machine models and/or beams they represent.
| Energy | Class | Represented models/beams |
|---|---|---|
| 6 MV | Base | 21EX (D), 23EX, 21iX, 23iX, Trilogy |
| TB | TrueBeam | |
| TB-FFF | TrueBeam FFF | |
| Trilogy SRS | Trilogy SRS | |
| 2300 | 2300 (C) (CD) | |
| 2100 | 2100 (C) (CD) | |
| 600 | 600 (C) (CD) | |
| 6EX | 6EX | |
| 10 MV | Base | 21EX (D), 23EX, 21iX, 23iX, Trilogy, 2100 (C) (CD), 2300 |
| TB | TrueBeam | |
| TB-FFF | TrueBeam FFF | |
| 15 MV | Base | 21EX, 23EX, 21iX, 23iX, Trilogy, 2100 (C) (CD), 2300 (C) (CD) |
| TB | TrueBeam | |
| 18 MV | Base | 21EX (D), 23EX, 21iX, 23iX, Trilogy, 2100 (C) (CD), 2300 (CD) |
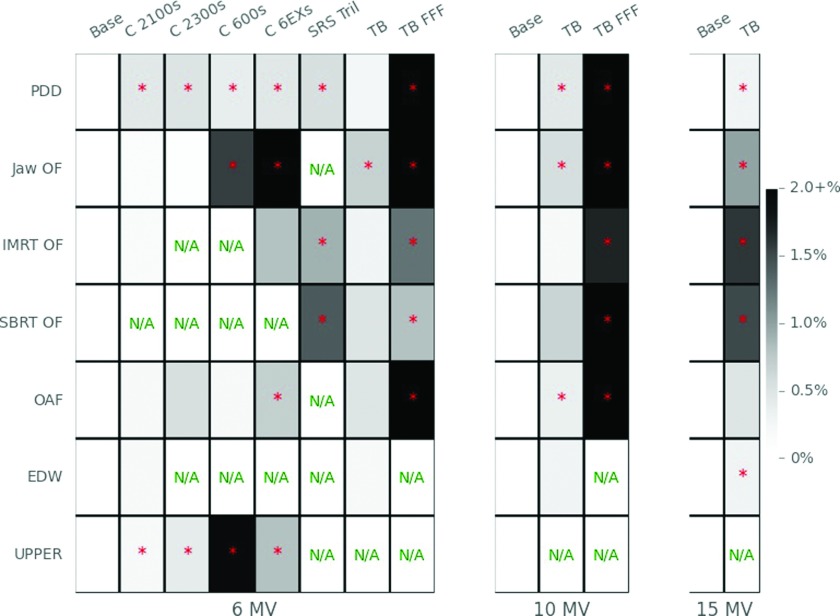
Overall differences between classes of machines were evaluated in Fig. 1. This is clinically important when trying to match machines of different classes, or deciding how many TPS beam models to create. A comparison between the different classes is shown via a heatmap in Fig. 1 relative to the base class. The color of the squares represents the maximum median difference that class had for that parameter in comparison to the base class. Darker squares indicate parameters that have a greater maximum difference than the dosimetric characteristics of the base class while lighter colors indicate smaller maximum differences. An asterisk indicates that the mean value of at least one measurement location is statistically different from the base class’ mean value (α = 0.05). For example, for the PDD, the Clinac 2100 class had at least 1 PDD measurement point that had a clinically and significantly different value as compared to the base class. Although differences and significance are plotted relative to the base class, this does not imply that the base class is a benchmark; it is only meant as a guide in understanding class differences. Since only the maximum differences are plotted, it should be understood that a class may perform similarly to another class except at a single measurement point. For example, two classes’ 5, 10, and 15 cm PDD measurements may agree well but if the 20 cm measurement value is significantly and clinically different, that difference is the value plotted in Fig. 1.
FIG. 1.
Heatmap comparing the maximum difference between parameters for the base class compared to other classes. Parameters include PDD, jaw-based OF (Jaw OF), IMRT-style small field OFs (IMRT OFs), SBRT-style small field OFs (SBRT OF), OAFs, and wedge factors for EDW and “upper” physical wedges (UPPER). Darker color indicates larger maximum differences from the base class. 18 MV is not shown because it only had one class. “N/A” means that measurements were not available for that parameter. An asterisk indicates a statistically different mean value from the base class.
3.B. 6 MV
For 6 MV, and all other energies, data are routinely described in two ways. The difference between classes, called the interclass difference or variability, represents the local difference of the median values. The average interclass difference is the mean of the differences at all the field sizes or depths. Difference can also be described within the class, which we labeled intraclass variability, which is synonymous with the coefficient of variation.
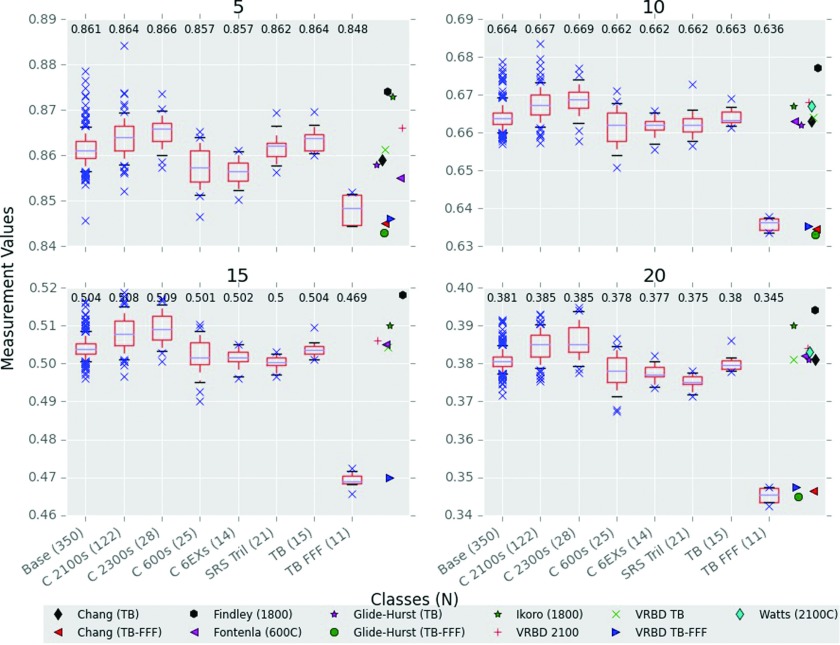
For 6 MV, data are given in figures for visual comparison, but the supplementary material also contains tabular data.15 The measured PDDs of the 10 × 10 cm2 field are shown in Fig. 2 and were normalized to the dmax measurement. Notably, all classes performed consistently with depth; that is, if a class had a higher PDD at 10 cm, it was also almost always higher at 5, 15, and 20 cm. On average, the base class had 0.5% intraclass variability. The 2100 and 2300s classes had consistently harder spectra than the base class, while the 600, 6EX, and Trilogy SRS had softer. The TrueBeam class had a very similar spectrum to the base class, with the largest interclass difference between the two classes being −0.5% at 20 cm. Most previously published PDD data values were similar to our values although deviations are apparent, notably at 5 cm depth. However, the previously published data also have the largest spread in values at 5 cm.
FIG. 2.
6 MV 10 × 10 cm2 depth dose measurements at 5, 10, 15, and 20 cm. Comparisons to other data measurements are from Refs. 2–7; VRBD is Varian representative beam data. Class medians are posted at the top of the respective boxplot and are the central lines in the boxes. N is the number of measurements in a class. The top and bottom of the box represent the 75th and 25th percentiles and the whiskers represent the 95th and 5th percentiles.
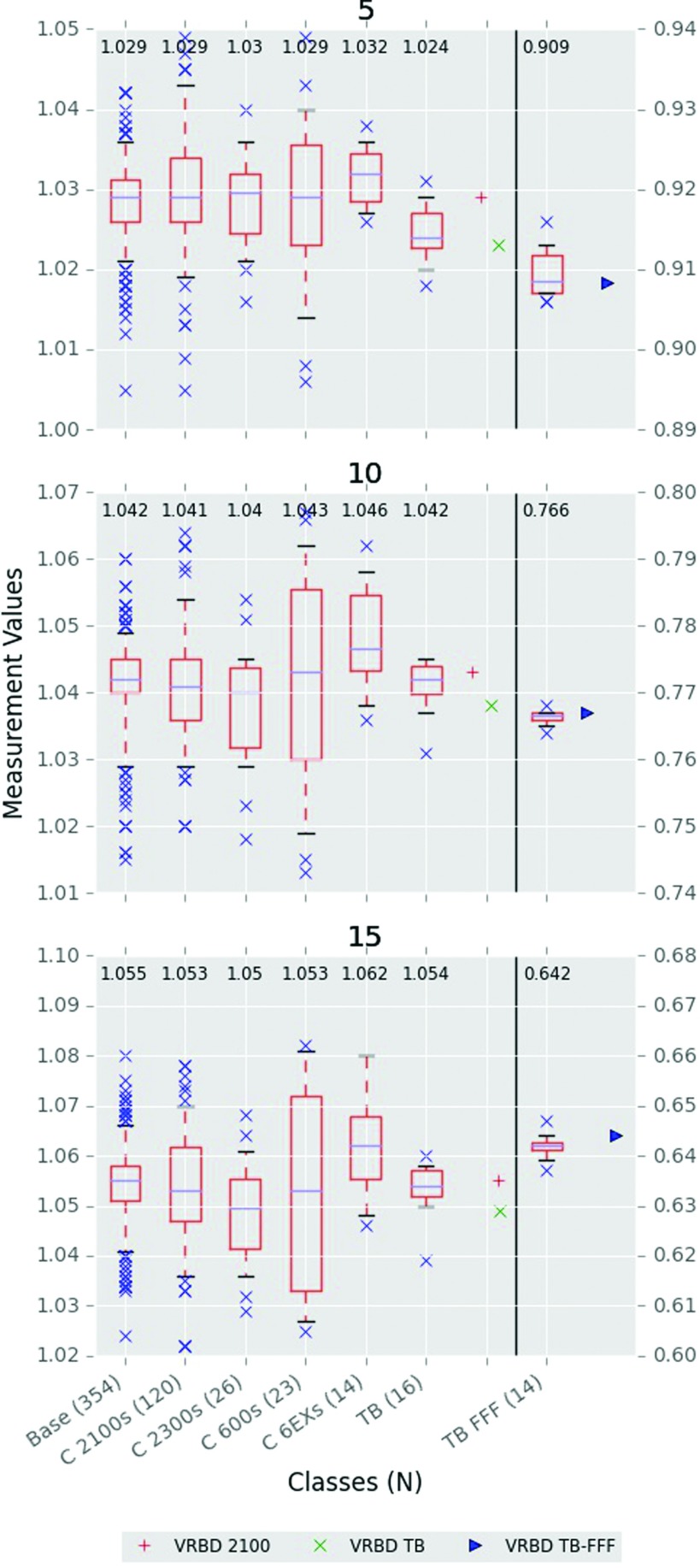
Output factors at dmax for field sizes of 6 × 6, 15 × 15, 20 × 20, and 30 × 30 cm2, normalized to the measurement at 10 × 10 cm2, are shown in Fig. 3. The total range in output factor values across field sizes was largest for the base, 2100s and 2300s classes, which all performed comparably. The 600s, 6EXs, and TrueBeams all had output factors closer to unity at all field sizes (i.e., a flatter slope) although each of them displayed distinctive characteristics. The Trilogy SRS class also showed a similar effect as the latter group for the applicable field sizes (15 × 15 cm2 and smaller; data not shown but are contained in supplementary material).
FIG. 3.
Jaw output factors for 6 MV classes at dmax, normalized to the 10 × 10 cm2 field. Field sizes are above each panel and in cm2. Median class values are also included at the top of each panel. N is the number of measurements in a class.
Off-axis factors were measured at 5, 10, and 15 cm from the CAX (Fig. 4). Agreement of other classes to the base class was closest at 5 cm, but grew apart at further distances from the CAX. The base, TrueBeam, and TrueBeam FFF classes had the smallest interclass variability. The largest interclass variability was from the Clinac 600s, having 1.5% at 15 cm compared to the base class’ 0.6%. On average, the off-axis parameter saw the greatest intraclass variation of all parameters. Interestingly, the inline waveguide machine models (600s, 6EXs) saw the greatest variability.
FIG. 4.
6 MV off-axis factors at the distances indicated (in cm) away from the CAX. TrueBeam FFF data and FFF reference data are aligned to the right axis and are visually separated by the vertical line. N is the number of measurements in a class.
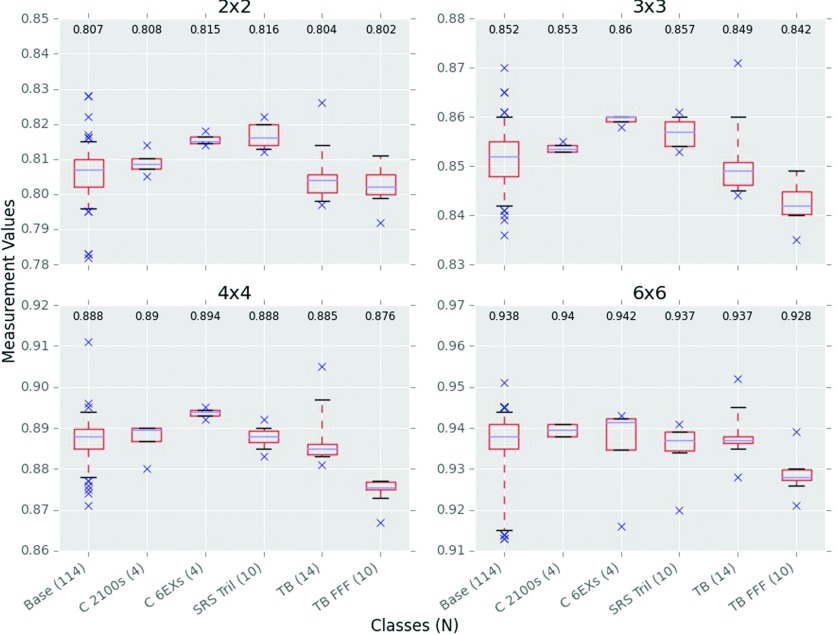
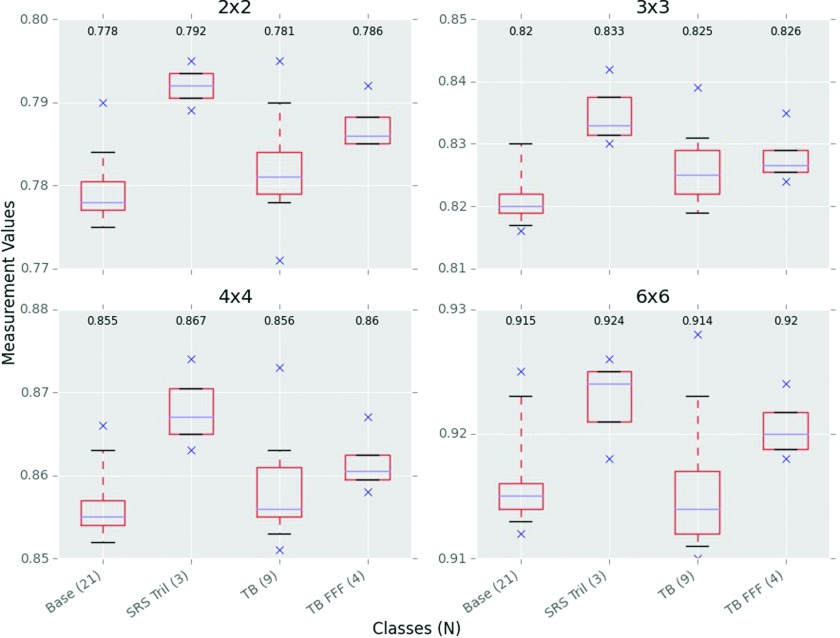
IMRT-style output factors, defined as having fixed jaws at 10 × 10 cm2 and various MLC field sizes, are shown in Fig. 5. No 600, 6EX, 2100, or 2300 class data were available. Collecting small field data is notoriously challenging as results are very sensitive to relatively small setup errors. However, intraclass variability of our measured data was comparable to the other parameters, having an average intraclass variation of 0.5% and a maximum of 0.8%, belonging to the base class. At 6 × 6 cm2, the interclass difference is relatively small, but the differences increase with smaller field sizes. At 2 × 2 cm2, the 6EX and Trilogy SRS classes had at least 1.0% interclass difference compared to the base class.
FIG. 5.
6 MV IMRT-style output factors. Jaws were at 10 × 10 cm2 for all measurements while the MLCs defined the field. Readings were normalized to a field where both the jaws and MLCs were at 10 × 10 cm2. Field sizes are in cm2 and indicate the MLC field. N is the number of measurements in a class.
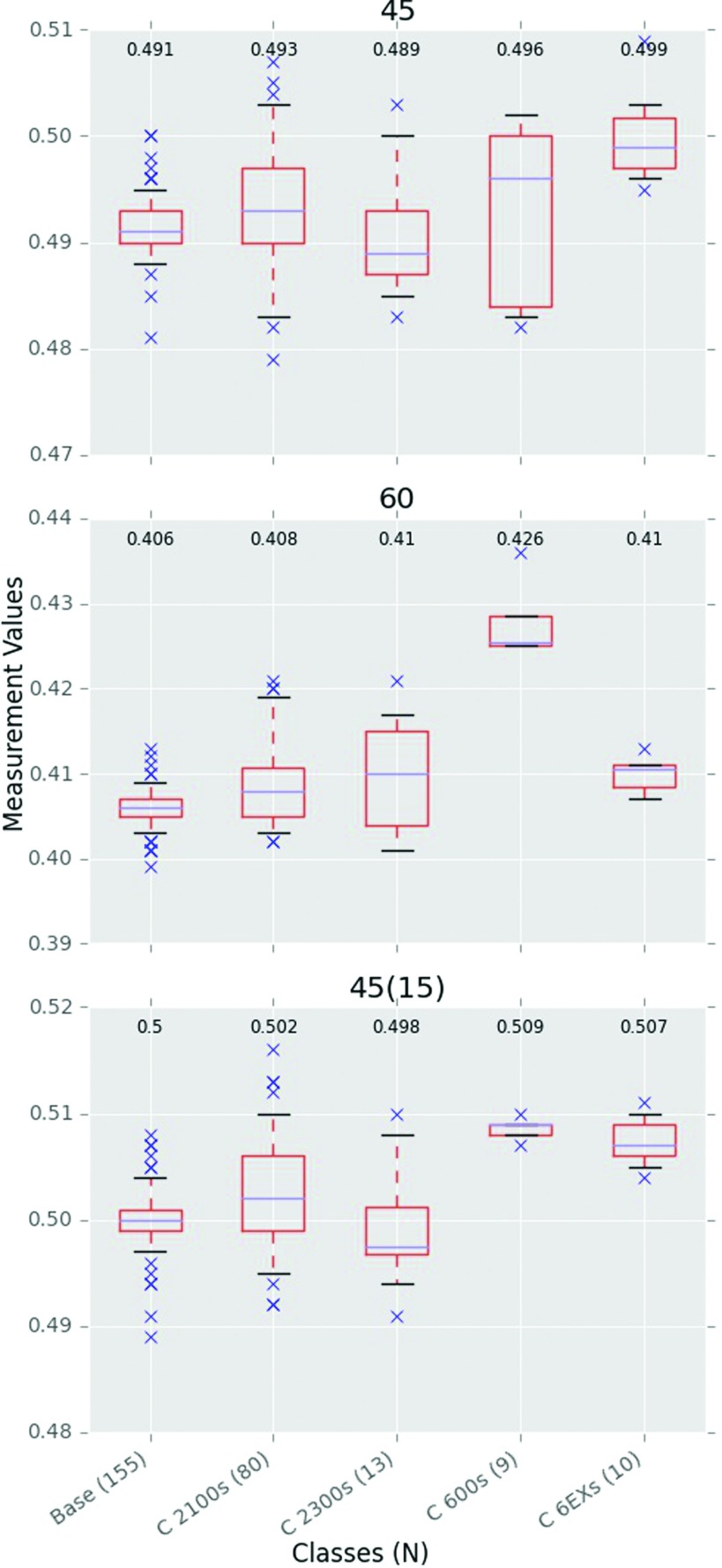
SBRT-style output factors, defined as having both the jaws and MLCs at the given field size, are shown in Fig. 6. SBRT output factors have only recently started being collected by IROC-H; thus, the number of measurements compared to other parameters is fewer. As would be expected, these output factors are smaller than the corresponding IMRT output factors shown above. The base class and TrueBeam performed comparably, having an average interclass difference of 0.25%. The Trilogy SRS class had markedly different values from the base class with an average interclass difference of 1.4%, a difference even greater than the TrueBeam FFF class.
FIG. 6.
6 MV SBRT-style output factors. Jaws and MLCs were both at the indicated field size above the panels. Readings were normalized to a field where both the jaws and MLCs were at 10 × 10 cm2. Fields are in cm2. N is the number of measurements in a class.
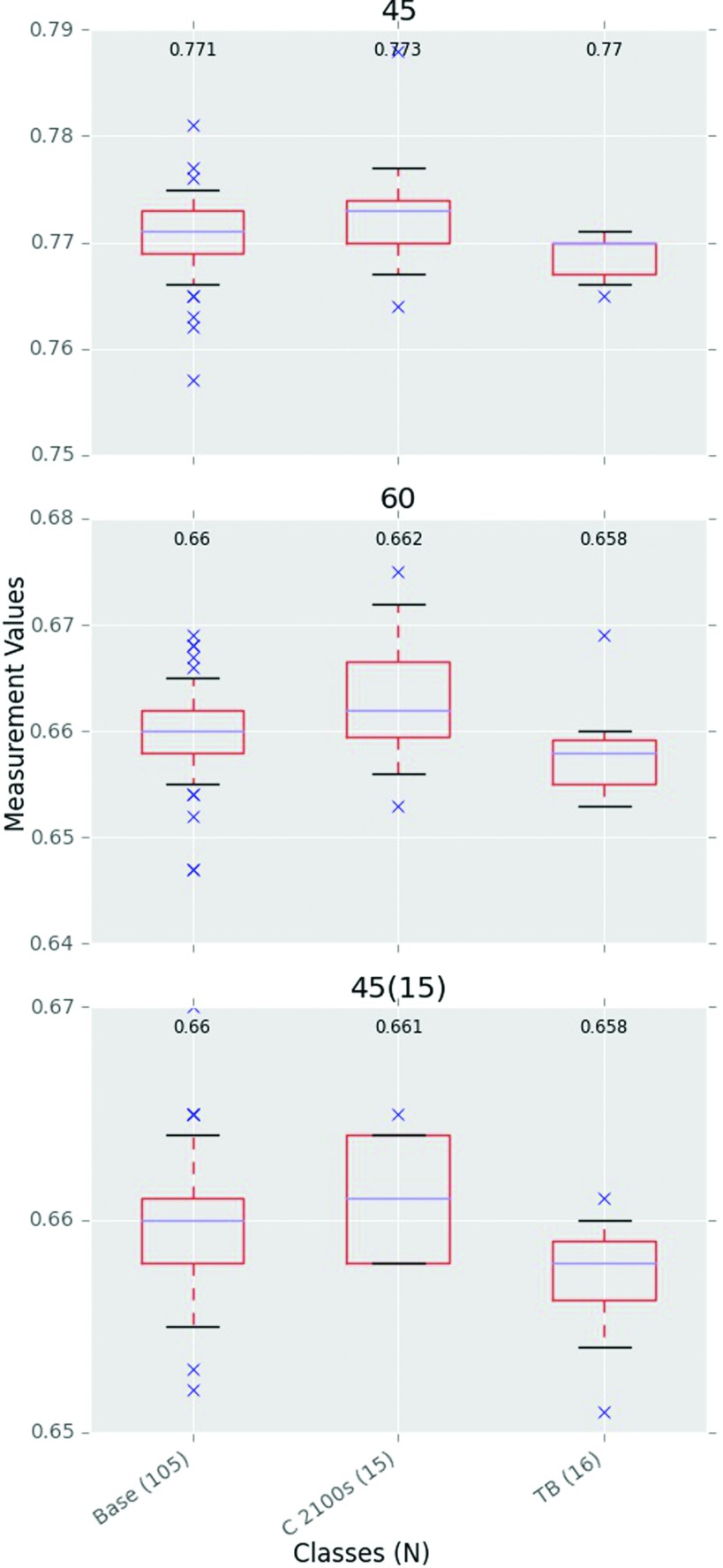
Wedge factors for Varian include both upper physical wedges and enhanced dynamic wedges. The EDW results are shown in Fig. 7 while the physical wedge results are shown in Fig. 8. While only three classes had EDW measurements, both the interclass and intraclass variabilities are small with all classes performing similarly. The physical upper wedges however showed larger interclass variability. The base, 2100, and 2300 classes all had relatively low interclass variability, but the 600 and 6EX classes showed large differences, both interclass and intraclass.
FIG. 7.
6 MV EDW factors. All measurements were at 10 × 10 cm2 and 10 cm depth except the 45(15) measurement, which was at 15 cm depth and 15 × 15 cm2 field size. N is the number of measurements in a class.
FIG. 8.
6 MV “Upper” wedge factors. All measurements were at 10 × 10 cm2 and 10 cm depth except the 45(15) measurement, which was at 15 cm depth and 15 × 15 cm2 field size. N is the number of measurements in a class.
3.C. 10 MV
The results of the 10 MV parameter measurements are shown in Table II for the three identified classes: base, TrueBeam, and TrueBeam FFF. Overall, the base class commonly had a larger intraclass variability than did the TrueBeam and TrueBeam FFF classes. Of interest, deviations between the base and TrueBeam classes were seen that were not present at 6 MV. At 6 MV, the TrueBeam and base class had very similar PDDs. However, at 10 MV, the TrueBeam had a harder beam (an average of +0.6% interclass difference at all depths). The intraclass variability was however comparable to 6 MV, with the base class having the largest average intraclass variability of 0.4%.
TABLE II.
10 MV Varian collected data for the three identified classes. Median values are given with the standard deviation in parentheses. N is the number of measurements.
| Parameter/Class | Base class | TB-flat | TB-FFF | |
|---|---|---|---|---|
| N | 74 | 10 | 10 | |
| PDD | 5 cm | 0.913 (0.003) | 0.918 (0.002) | 0.908 (0.002) |
| 10 cm | 0.733 (0.003) | 0.737 (0.002) | 0.712 (0.001) | |
| 15 cm | 0.582 (0.003) | 0.586 (0.002) | 0.554 (0.001) | |
| 20 cm | 0.460 (0.002) | 0.463 (0.003) | 0.430 (0.001) | |
| Output factors | 6 × 6 cm2 | 0.953 (0.004) | 0.956 (0.003) | 0.980 (0.001) |
| 15 × 15 cm2 | 1.033 (0.004) | 1.032 (0.002) | 1.015 (0.002) | |
| 20 × 20 cm2 | 1.054 (0.005) | 1.053 (0.003) | 1.026 (0.002) | |
| 30 × 30 cm2 | 1.083 (0.007) | 1.077 (0.006) | 1.034 (0.004) | |
| Off-axis factors | 5 cm left | 1.029 (0.006) | 1.029 (0.004) | 0.823 (0.003) |
| 10 cm avg | 1.044 (0.006) | 1.047 (0.003) | 0.632 (0.002) | |
| 15 cm left | 1.053 (0.009) | 1.056 (0.005) | 0.497 (0.003) | |
| N | 21 | 9 | 8 | |
| IMRT output factors | 2 × 2 cm2 | 0.825 (0.007) | 0.823 (0.003) | 0.842 (0.005) |
| 3 × 3 cm2 | 0.881 (0.006) | 0.880 (0.006) | 0.892 (0.004) | |
| 4 × 4 cm2 | 0.918 (0.006) | 0.916 (0.006) | 0.918 (0.003) | |
| 6 × 6 cm2 | 0.959 (0.005) | 0.958 (0.005) | 0.956 (0.002) | |
| N | 4 | 6 | 4 | |
| SBRT output factors | 2 × 2 cm2 | 0.794 (0.004) | 0.790 (0.005) | 0.825 (0.006) |
| 3 × 3 cm2 | 0.846 (0.001) | 0.849 (0.005) | 0.881 (0.003) | |
| 4 × 4 cm2 | 0.877 (0.005) | 0.884 (0.006) | 0.907 (0.003) | |
| 6 × 6 cm2 | 0.929 (0.006) | 0.933 (0.006) | 0.948 (0.004) | |
| N | 17 | 10 | ||
| EDW factors | 45° | 0.803 (0.004) | 0.800 (0.003) | N/A |
| 60° | 0.701 (0.005) | 0.698 (0.004) | ||
| 45° (15 × 15,15) | 0.703 (0.004) | 0.702 (0.003) | ||
| N | 40 | |||
| Upper wedge factors | 45° | 0.525 (0.004) | N/A | N/A |
| 60° | 0.437 (0.003) | |||
| 45° (15 × 15,15) | 0.531 (0.003) |
Jaw output factors showed similar results to 6 MV in that the TrueBeam class showed less range across the field sizes, i.e., a flatter slope, than the base class. The average intraclass variability of the base class was 0.5% compared to 0.3% and 0.2% for the TrueBeam and TrueBeam FFF classes, respectively. Off axis factors were similar between the base class and TrueBeam class, with the TrueBeam-FFF having larger differences, as expected.
IMRT-style output factors had small interclass variability, with the base class and TrueBeam having an average of 0.2%. Notably, the TrueBeam FFF class agreed with the other classes at 4 × 4 and 6 × 6 cm2, but had a larger output factor at smaller field sizes.
SBRT-style factors appeared similar to IMRT output factors, but had less interclass agreement, and the TrueBeam FFF class was consistently higher than the other classes at all field sizes. Whereas the output factors were very close at 6 MV, at 10 MV, the TrueBeam class had an average deviation of +0.3%. The base class had an average intraclass variation of 0.3% compared to the TrueBeam at 0.7%.
EDW factors were very similar for the base and TrueBeam classes, having only 0.3% interclass variation and intraclass variations of 0.6% and 0.4% for the base and TrueBeam classes, respectively. No measurements of upper physical wedges have yet been done for TrueBeam 10 MV.
3.D. 15 MV
Measurements for the 15 MV beams are shown in Table III; the classes determined were the base class and TrueBeam. Some similarities to other energies were seen, but many differences were noted at 15 MV. The interclass differences also had the largest magnitudes at 15 MV.
TABLE III.
15 MV Varian collected reference data. Median values are given with the standard deviation in parentheses. N is the number of measurements.
| Parameter/Class | Base class | TB-flat | |
|---|---|---|---|
| N | 100 | 14 | |
| PDD | 5 cm | 0.943 (0.003) | 0.946 (0.002) |
| 10 cm | 0.767 (0.003) | 0.769 (0.001) | |
| 15 cm | 0.617 (0.003) | 0.620 (0.001) | |
| 20 cm | 0.496 (0.002) | 0.499 (0.001) | |
| N | 97 | 14 | |
| Output factors | 6 × 6 cm2 | 0.959 (0.005) | 0.953 (0.003) |
| 15 × 15 cm2 | 1.030 (0.004) | 1.035 (0.002) | |
| 20 × 20 cm2 | 1.050 (0.006) | 1.060 (0.003) | |
| 30 × 30 cm2 | 1.075 (0.007) | 1.085 (0.005) | |
| N | 100 | 13 | |
| Off-axis factors | 5 cm left | 1.038 (0.008) | 1.036 (0.004) |
| 10 cm avg | 1.049 (0.008) | 1.045 (0.004) | |
| 15 cm left | 1.061 (0.010) | 1.056 (0.004) | |
| N | 18 | 13 | |
| IMRT output factors | 2 × 2 cm2 | 0.831 (0.006) | 0.815 (0.006) |
| 3 × 3 cm2 | 0.893 (0.008) | 0.885 (0.004) | |
| 4 × 4 cm2 | 0.929 (0.008) | 0.924 (0.002) | |
| 6 × 6 cm2 | 0.965 (0.007) | 0.964 (0.002) | |
| N | 7 | 7 | |
| SBRT output factors | 2 × 2 cm2 | 0.799 (0.004) | 0.784 (0.006) |
| 3 × 3 cm2 | 0.865 (0.002) | 0.855 (0.004) | |
| 4 × 4 cm2 | 0.902 (0.003) | 0.892 (0.004) | |
| 6 × 6 cm2 | 0.949 (0.003) | 0.938 (0.003) | |
| N | 27 | 11 | |
| EDW factors | 45° | 0.814 (0.003) | 0.811 (0.002) |
| 60° | 0.716 (0.003) | 0.713 (0.003) | |
| 45° (15 × 15,15) | 0.720 (0.001) | 0.718 (0.003) | |
| N | 44 | ||
| Upper wedge factors | 45° | 0.523 (0.003) | N/A |
| 60° | 0.434 (0.003) | ||
| 45° (15 × 15,15) | 0.529 (0.003) |
Between the two classes, the TrueBeam beam had a consistently harder PDD than that of the base class, as was also seen at 10 MV. The TrueBeam had an average interclass difference of +0.4%.
At 6 and 10 MV, the TrueBeam output factors had a smaller slope across field sizes than the base class; at 15 MV, the opposite was true: the slope was steeper. The TrueBeam had a median difference of −0.6% at 6 × 6 cm2 and +0.9% at 30 × 30 cm2 compared to the base class.
Off-axis factors, similar to the output factors, showed differences between the TrueBeam and base class that were not seen at 6 or 10 MV. At the other energies, the off-axis factors had little interclass variation; at 15 MV, the TrueBeam had −0.4% and −0.6% median difference at 10 and 15 cm off axis, respectively. The base class had an average intraclass variation of 0.8% when compared to 0.3% for TrueBeam.
IMRT output factors also showed marked differences in the two classes compared to other energies. Class medians are nearly the same at 6 × 6 cm2, but the interclass variability increased to nearly 2% at 2 × 2 cm2.
SBRT output factors once again showed differences from the other energies. The TrueBeam consistently had lower median values than the base class for all field sizes. The average interclass difference was −1.3% for the TrueBeam, while the average intraclass variation was 0.4% for both classes.
EDW factors also showed the TrueBeam class as having a consistently lower median than the base class, although the difference was much less than for the IMRT and SBRT output factors and was nearly the same as the average intraclass variation (0.4%). No physical wedges have been measured for the TrueBeam at 15 MV.
3.E. 18 MV
The 18 MV measurement results are shown in Table IV. There was only one resultant class, so no comparison between classes could be done. Intraclass variability of the base class was similar to other energies, however, with an average intraclass variability of 0.45% across all parameters.
TABLE IV.
18 MV Varian collected reference data. Median values are given with the standard deviation in parentheses. N is the number of measurements.
| Parameter/Class | Base class | |
|---|---|---|
| N | 243 | |
| PDD | 5 cm | 0.963 (0.003) |
| 10 cm | 0.793 (0.003) | |
| 15 cm | 0.647 (0.002) | |
| 20 cm | 0.527 (0.002) | |
| Output factors | 6 × 6 cm2 | 0.943 (0.006) |
| 15 × 15 cm2 | 1.041 (0.005) | |
| 20 × 20 cm2 | 1.066 (0.007) | |
| 30 × 30 cm2 | 1.094 (0.010) | |
| Off-axis factors | 5 cm left | 1.029 (0.006) |
| 10 cm avg | 1.044 (0.006) | |
| 15 cm left | 1.054 (0.009) | |
| N | 37 | |
| IMRT output factors | 2 × 2 cm2 | 0.806 (0.005) |
| 3 × 3 cm2 | 0.884 (0.004) | |
| 4 × 4 cm2 | 0.929 (0.004) | |
| 6 × 6 cm2 | 0.970 (0.003) | |
| N | 6 | |
| SBRT output factors | 2 × 2 cm2 | 0.767 (0.003) |
| 3 × 3 cm2 | 0.847 (0.001) | |
| 4 × 4 cm2 | 0.891 (0.000) | |
| 6 × 6 cm2 | 0.942 (0.001) | |
| N | 53 | |
| EDW factors | 45° | 0.824 (0.002) |
| 60° | 0.729 (0.003) | |
| 45° (15 × 15,15) | 0.734 (0.003) | |
| N | 112 | |
| Upper wedge factors | 45° | 0.516 (0.003) |
| 60° | 0.427 (0.002) | |
| 45° (15 × 15,15) | 0.522 (0.003) |
4. DISCUSSION
The IROC-H site visit data for Varian Linacs have been compared, and dosimetrically similar Linac models have been grouped into representative classes at each energy. A base class which represented the most popular models of Linacs was developed for each energy. A total of eight classes were developed for 6 MV and three, two, and one classes for 10, 15, and 18 MV, respectively. The data presented here are the first to show how Varian Linac models perform relative to each other using a systematic approach. Differences between models and classes have been quantified so that physicists can understand how their specific machine performs relative to the community, and also how different Linac models compare dosimetrically to one another.
Previous datasets have been published that describe Varian Linac dosimetric properties. These publications are typically based on a limited number of machines. Data that were taken under the same conditions are presented throughout Figs. 2–4 and in the supplementary material.15 Although other reference datasets exist, the large dataset provided by IROC-H, drawn from hundreds of machines and institutions, allows for statistically robust reference values and metrics, over against a handful of measurements. Most of the values agree, however, so these data are not in opposition—they are well within the range given by our large collection of data. We have added to the robustness of the “average” machine values as well as described the range of values seen from the machines. As well, we have described observed differences between the Linac types.
The parameter with the most numerous comparisons with previously published values is the PDD. As well, the PDD measured by IROC-H occasionally disagreed with previous data in the literature. For example, for the 6 MV base class, IROC-H measured a PDD(10) of 66.4% for the 10 × 10 cm2 field. Most data in the literature, including the Varian Reference Beam Data, describe a value between 66.7% and 67.7%.2,4–6 Although small, this is a notable difference in a core physics parameter. This difference likely arises from the method of measurement. IROC-H, since 2000, has measured PDDs accounting for the effective point of measurement of the ion chamber. Measurements taken before TG-51 or not accounting for the 0.6rcav shift, such as the works of Ikoro et al.4 and Findley et al.,6 were systematically higher than our values because the effective point of measurement was actually upstream of the measurement point. This theory is supported in that PDD(10) data published post-TG-51 (Refs. 1, 2, 5, and 8) agree well with our value of 66.4%.
Output factors also proved noteworthy. At 6 MV, the jaw output factors showed the most interclass variability of all the classes. For 6EXs and TrueBeams, this is the parameter with the greatest mean difference from the base class. Those classes showed less sensitivity to field size, giving a flatter slope of output factors. However, at 15 MV, the differences between the base and TrueBeam class are the opposite. The TrueBeam class shows greater change with field size; at 30 × 30 cm2, the differences are statistically and clinically different from the base class. Beyer1 also concluded that there were output factor differences between the TrueBeam and Clinac 2100, but that the TrueBeams values varied less with field size. Our study confirms this result for 6 and 10 MV but not 15 MV. This difference may lie in our use of many Linac measurements compared to one machine. We have also shown whether these differences are statistically and clinically significant at the given energies.
Two uses of these data are noteworthy. First, the dosimetric properties of an individual Linac can be quantitatively compared directly to these reference data. The goal of quantifying differences is not to match or try to match the class median, but rather to identify the magnitude of those differences and where they lie. Most Linacs should have dosimetric properties that are consistent with the reference data presented here. However, if a machine value is obtained for a particular machine that is different than the one presented here for that machine’s class, this should not necessarily be interpreted as an error as it could be a nonstandard machine. However, such a difference should raise awareness and warrant an investigation to ensure that the difference is justified. Furthermore, differences should be evaluated in context. One value with a large difference may represent a one-off collection or transcription error; many measurements with a systematic difference may represent a setup or collection error. Additionally, machines may truly be different, either through manufacturing or from physicist customization. In any case, awareness of differences can be raised. This can be especially helpful when commissioning a new machine when no prior reference values can be used for comparison. The most important agreement is that of the machine to the treatment planning system. Differences between dosimetry values do not inherently carry clinical impact until modeled. Thus, reference datasets like this study can add a check that the acquired values used in TPS modelling are sufficiently accurate.
A second important use of these data arises when considering the purchase of another machine or trying to match existing machines and the impact it may have. Clinics with multiple Linacs can use one beam model for their TPS only if all the machines have similar dosimetric properties. If machines of different classes are being matched, the clinically acceptable window and therapy type needs to account for the underlying differences in the machine parameters, not including the general uncertainty in the beam model. A useful case for comparison is institutions that have or will transition from older Varian models to the newer TrueBeam platform. An important clinical question is “How similar are these machines?” and therefore “Can I use the same beam model for both?” These differences, including the parameter(s) that are different and the magnitude of difference, are described in this study and an example of comparison to the base class is shown in Fig. 1. In general, the differences between the base and TrueBeam classes were fewer at 6 and 10 MV but had numerous differences at 15 MV. As described above, the output factors were typically the biggest difference between classes. Such data show that the TrueBeam is not dosimetrically similar to prior Linac models at all points. Institutions that have a mixture of Linac classes should be careful in their data acquisition and beam modeling to avoid systematic bias toward one class of machine.
Finally, it should be emphasized that this dataset is not meant to replace machine measurements at a clinic. Conformity to median values is not the goal, which is why the distributions have also been included. This dataset can be consulted to compare a machine or clinic to that of the community at large, understanding that each machine may be slightly unique but that differences should be identified as such.
5. CONCLUSION
Data from the IROC-Houston’s site visits have been analyzed, comparing and classifying Varian Linacs based on dosimetric characteristics. Linac models with comparable dosimetric properties were grouped into classes, and the reference class data, including the underlying distribution, are presented here. Dosimetric characteristics included point measurements of the PDD, jaw output factors, two types of MLC output factors, off-axis factors, and wedge factors. The data can be used as a secondary check of acquired values of a new machine or to understand how a machine performs relative to the community. These reference data can also be used as a guide of how much variability a physicist should expect between different models of linear accelerators.
ACKNOWLEDGMENTS
Many thanks go to Paul Hougin for querying and compiling the site visit data. This work was supported by Public Health Service Grant No. CA180803 awarded by the National Cancer Institute, United States Department of Health and Human Services.
APPENDIX: DATA DISTRIBUTION AND STATISTICAL METRICS
In this appendix, we examine the data distribution of the measurements and reasons for using certain statistical metrics. Measurement distributions with a bimodal distribution would suggest systematic error in the collection of data. Distributions with a relatively large standard deviation may suggest random error, perhaps describing aspects of the Linac that were not as uniform during the manufacturing or operation processes or setup uncertainty.
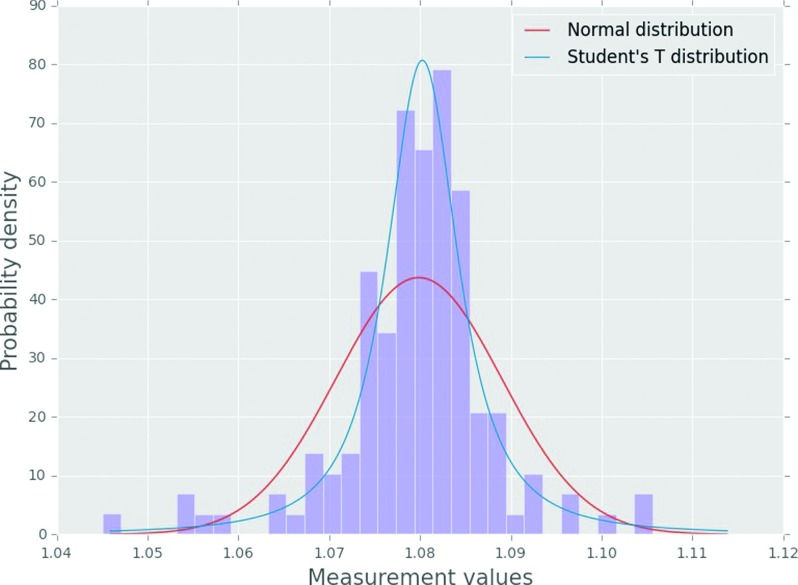
The data for the 30 × 30 cm2 jaw output factor of the Clinac 21EX model, the most populous model, are shown in Fig. 9. The data presented are representative of nearly all the model measurement distributions. A fitted normal distribution and fitted student’s t distribution are also plotted. The fitted normal distribution did not describe the distribution well because of the relatively narrow peak and heavy tails, but the fitted student’s t distribution described the data much better.
FIG. 9.
Measurement histogram for the 6 MV Clinac 21EX 30 × 30 cm2 jaw output factors along with fitted distributions.
A Kolmogorov–Smirnov (K–S) goodness of fit statistical test was also done to test whether the distribution could be said to be derived from either a normal or student’s t distribution. The K–S test quantifies the maximum distance between the measured distribution function and the reference distribution function. The distribution was statistically different than a normal distribution but not a student’s t distribution (α = 0.05). Since the data can reasonably be described by a student’s t distribution, this suggests that data metrics like the mean, median, and standard deviation are valid statistics to describe our observed data.
The use of the median value over the mean was chosen due to the median’s robustness to outliers for small datasets. As Fig. 9 shows, there are a number of outliers in the data. Because the number of measurements per dataset varies, the mean describes large datasets well, but can be influenced by outliers in the smaller datasets. The median however is robust to these influences. For example, for the Clinac 21EX 30 × 30 cm2 jaw output factor shown in Fig. 9, the median and mean, with an N of 141, are both 1.080. However, the TrueBeam SBRT-style 4 × 4 cm2 output factor, with an N of 9, had a median and mean of 0.856 and 0.859, respectively, which is a relative difference of 0.35%.
The spread in the data distributions is likely from three inextricable sources: machine delivery uncertainty, setup uncertainty, and measurement uncertainty. IROC-H maintains strict procedures for equipment setup and measurement, which minimizes as much as possible the contributions from these error sources, while delivery uncertainty is not easily controlled. Given that the distribution is symmetric and unimodal, it is reasonable to assume that systematic error was minimized and the three sources contribute to random error.
REFERENCES
- 1.Beyer G. P., “Commissioning measurements for photon beam data on three TrueBeam linear accelerators, and comparison with Trilogy and Clinac 2100 linear accelerators,” J. Appl. Clin. Med. Phys. 14(1), 273–288 (2013); available at http://www.jacmp.org/index.php/jacmp/article/view/4077/2780). 10.1120/jacmp.v14i1.4077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fontenla D. P., Napoli J. J., and Chui C. S., “Beam characteristics of a new model of 6-MV linear accelerator,” Med. Phys. 19(2), 343–349 (1992). 10.1118/1.596864 [DOI] [PubMed] [Google Scholar]
- 3.Chang Z., Wu Q., Adamson J., Ren L., Bowsher J., Yan H., Thomas A., and Yin F. F., “Commissioning and dosimetric characteristics of TrueBeam system: Composite data of three TrueBeam machines,” Med. Phys. 39(11), 6981–7018 (2012). 10.1118/1.4762682 [DOI] [PubMed] [Google Scholar]
- 4.Ikoro N. C., Johnson D. A., and Antich P. P., “Characteristics of the 6-MV photon beam produced by a dual energy linear accelerator,” Med. Phys. 14(1), 93–97 (1987). 10.1118/1.596113 [DOI] [PubMed] [Google Scholar]
- 5.Watts R. J., “Comparative measurements on a series of accelerators by the same vendor,” Med. Phys. 26(12), 2581–2585 (1999). 10.1118/1.598796 [DOI] [PubMed] [Google Scholar]
- 6.Findley D. O., Forell B. W., and Wong P. S., “Dosimetry of a dual photon energy linear accelerator,” Med. Phys. 14(2), 270–273 (1987). 10.1118/1.596083 [DOI] [PubMed] [Google Scholar]
- 7.Glide-Hurst C., Bellon M., Foster R., Altunbas C., Speiser M., Altman M., Westerly D., Wen N., Zhao B., Miften M., Chetty I. J., and Solberg T., “Commissioning of the Varian TrueBeam linear accelerator: A multi-institutional study,” Med. Phys. 40(3), 031719 (15 pp.) (2013). 10.1118/1.4790563 [DOI] [PubMed] [Google Scholar]
- 8.Sjostrom D., Bjelkengren U., Ottosson W., and Behrens C. F., “A beam-matching concept for medical linear accelerators,” Acta Oncol. 48(2), 192–200 (2009). 10.1080/02841860802258794 [DOI] [PubMed] [Google Scholar]
- 9.Followill D. S., Kry S. F., Qin L., Lowenstein J., Molineu A., Alvarez P., Aguirre J. F., and Ibbott G. S., “The Radiological Physics Center’s standard dataset for small field size output factors,” J. Appl. Clin. Med. Phys. 13(5), 282–289 (2012); available at http://www.jacmp.org/index.php/jacmp/rt/captureCite/3962/2597). 10.1120/jacmp.v13i5.3962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Followill D. S., Kry S., Qin L., Lowenstein J., Molineu A., Alvarez P., Aguirre J. F., and Ibbott G., “Erratum: The Radiological Physics Center’s standard dataset for small field size output factors,” J. Appl. Clin. Med. Phys. 15(2), 356–357 (2014); available at http://www.jacmp.org/index.php/jacmp/article/view/4757). 10.1120/jacmp.v15i2.4757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cho S. H., Vassiliev O. N., Lee S., Liu H. H., Ibbott G. S., and Mohan R., “Reference photon dosimetry data and reference phase space data for the 6 MV photon beam from Varian Clinac 2100 series linear accelerators,” Med. Phys. 32(1), 137–148 (2005). 10.1118/1.1829172 [DOI] [PubMed] [Google Scholar]
- 12.Followill D. S., Davis D. S., and Ibbott G. S., “Comparison of electron beam characteristics from multiple accelerators,” Int. J. Radiat. Oncol., Biol., Phys. 59(3), 905–910 (2004). 10.1016/j.ijrobp.2004.02.030 [DOI] [PubMed] [Google Scholar]
- 13.Mckinney W., “Data structures for statistical computing in Python,” in Proceedings of the 9th Phyton in Science Conference (2010), pp. 51–56. Available at http://conference.scipy.org/proceedings/scipy2010/pdfs/mckinney.pdf. [Google Scholar]
- 14.Seabold S. and Perktold J., “Statsmodels: Economic and statistical modeling with python,” Presented at the python in Science Conference, Austin, TX (2010). [Google Scholar]
- 15.See supplementary material at http://dx.doi.org/10.1118/1.4945697 E-MPHYA6-43-039605 for quantitative data tables of all energies.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1118/1.4945697 E-MPHYA6-43-039605 for quantitative data tables of all energies.