Emergent Global Contractile Force in Cardiac Tissues

Abstract

The heart is a complex organ whose structure and function are intricately linked at multiple length scales. Although several advancements have been achieved in the field of cardiac tissue engineering, current in vitro cardiac tissues do not fully replicate the structure or function necessary for effective cardiac therapy and cardiotoxicity studies. This is partially due to a deficiency in current understandings of cardiac tissue organization’s potential downstream effects, such as changes in gene expression levels. We developed a novel (to our knowledge) in vitro tool that can be used to decouple and quantify the contribution of organization and associated downstream effects to tissue function. To do so, cardiac tissue monolayers were designed into a parquet pattern to be organized anisotropically on a local scale, within a parquet tile, and with any desired organization on a global scale. We hypothesized that if the downstream effects were muted, the relationship between developed force and tissue organization could be modeled as a sum of force vectors. With the in vitro experimental platforms of parquet tissues and heart-on-a-chip devices, we were able to prove this hypothesis for both systolic and diastolic stresses. Thus, insight was gained into the relationship between the generated stress and global myofibril organization. Furthermore, it was demonstrated that the developed quantitative tool could be used to estimate the changes in stress production due to downstream effects decoupled from tissue architecture. This has the potential to elucidate properties coupled to tissue architecture, which change force production and pumping function in the diseased heart or stem cell-derived tissues.

Introduction

To effectively pump blood throughout the body, the heart is organized into laminar sheets of cardiac fibers, myofibrils, which consist of sarcomeres—the main force-producing units of cardiac muscle (1, 2). Ideally, each sarcomere produces a contractile force perpendicular to its z-lines and parallel to the actin and myosin fibrils (3). As a large number of sarcomeres work in synchrony to produce the force necessary for the heart to pump blood, it is essential for them to be properly organized. Accordingly, in the diseased heart, there is evidence of structural remodeling of myofibrils, and thus the force-producing units, which is thought to contribute to poor cardiac function (4, 5, 6). However, the decline in pumping force might not solely be due to changes in force unit organization, but may also be correlated to other downstream effects associated with structural remodeling. Indeed, in vivo studies have revealed a correlation among cardiac remodeling, heart disease, and several other factors such as changes in gene expression (7, 8). The coexistence and interdependence of these factors makes it impossible, with current technologies, to decouple them in vivo. In vitro studies have been shown to be a more practical method to separate each variable and study the relationship between them.

Several in vitro assays have been developed to measure the contractility of engineered cardiac myocyte tissues of varying organization and have the potential to accomplish a decoupling of the factors seen in vivo (9, 10, 11). One such technology is the muscular thin film assay, a device made of synthetic polymer films on which cardiac myocytes of isotropic and globally anisotropic organization have been cultured (12). Through this assay, it has been shown that contractility of the engineered myocardium is related to the sarcomeric organization of the tissue (13). However, the relationship is nontrivial, indicating a presence of other factors that are influencing the dependence. Indeed, other experiments have shown that a change of in vitro cardiac tissue organization is also associated with downstream effects such as changes in electrophysiology, gap junction morphology, distribution, and gene expression levels (13, 14, 15, 16, 17, 18, 19). It is also possible that the registration of the sarcomeric z-lines (i.e., force units) is reduced in disorganized tissues (20). Most of these downstream effects are likely to further affect the contractility of cardiac tissues. It was shown using a very basic model that the amount of force produced by well-organized cardiac monolayers was approximately twice the expected value based on the force measured in isotropic tissues (13). However, this model ignores a large number of cardiac tissue properties, such as the dipole nature of sarcomeres, the viscoelastic properties of the cells, and the nonuniform integrin distribution, which makes it impossible to interpret the model’s results unless it is validated. Therefore, it is not possible to determine how much of the force difference is due to the downstream effects and how much is directly caused by sarcomere reorganization. To address this, it is imperative to create an experimental platform that decouples the change in tissue organization from the associated downstream effects.

We hypothesized that if the cells are locally organized and globally disorganized, most of the inputs that control the downstream effects will match those seen in a globally aligned anisotropic tissue, and the global stress would only depend on the sarcomere organization. Thus, we aimed to design a new tissue pattern with parquets of organized tiles combined to form the desired overall isotropic organization. From these tissues, even though it ignored a host of factors, the basic net force model was tested for predictive capabilities. Furthermore, the parquets were assembled into tissues with a range of global organizations, and the basic model was further validated. The results of this study suggest that we have created a technological platform that can be used to quantitatively determine the contribution of downstream effects to change in force production of engineered muscle tissues at any organization. We were thus able to gain insight into the relationship between global tissue organization and net force production in cardiac tissues. Elucidating these effects has the potential to further current understanding of the consequences of cardiac tissue remodeling in the diseased heart.

Materials and Methods

To accomplish these goals, we utilized a range of experimental approaches detailed below.

Substrate fabrication

For structural and gene-expression studies, round 25 mm glass coverslips were sonicated in 95% ethanol for 30 min and incubated in a 60°C oven for 30 min. PDMS (polydimethylsiloxane; Ellsworth Adhesives, Germantown, WI) was made using a 1:10 base/curing agent, and the clean coverslips were coated in the PDMS and cured overnight in a 60°C oven.

For contractility studies, coverslips were prepared as described by Grosberg et al. (21). Briefly, a large cover glass (Brain Research Laboratories, Newton, MA) was sonicated in 50% ethanol for 30 min. The cover glass was covered with protective film (static cling; Grafix Plastics, Cleveland, OH), which was cut and removed using custom templates to provide 1 cm strips of exposed cover glass. Next, 1 gram of PIPPAm (poly(n-isopropylacrylamide); Polysciences, Warrington, PA) was dissolved in 10 mL of 1-butanol (Macron Fine Chemicals, Center Valley, PA). The PIPPAm was then spin-coated onto the exposed cover glass and allowed to dry at room temperature for at least 15 min. The remaining static cling was carefully removed from the top and the entire cover glass was coated with the PDMS that had been allowed to cure for 5 h. The cover glass was promptly moved to a 60°C oven to cure overnight. Last, the cover glass was cut into individual coverslips using a diamond scriber (Musco Sports Lighting, Oskaloosa, IA) and a custom template for either 6-well or 12-well culture plates.

Extracellular matrix patterning

Stamp patterns were designed using Adobe Illustrator software (Adobe Systems, San Jose, CA). Stamps were made to be 1.5 cm × 1.5 cm to produce FN (fibronectin) lines of 20 μm wide with 5 μm gaps between lines for a globally aligned anisotropic tissue. Parquet patterns were designed to produce 250 μm × 250 μm squares of 20 μm-wide lines of FN with 5 μm spacing between lines. Each square had a varying orientation to control the global organization. Patterns started with lines oriented at 0, 45, 90, 135, and 180° to form the locally organized, globally disorganized (isotropic) tissue. Consecutive stamps were designed for each square to be 5–10° more oriented toward 90° with the second stamp being 10, 50, 90, 130, and 170°. Eight consecutive stamps were designed with the final parquet stamp being 80, 85, 90, 95, and 100° (Fig. S2 in the Supporting Material).

Designs were etched into 5″ × 5″ chrome with soda-lime glass masks by a third-party vendor (FrontRange Photo Mask, Palmer Lake, CO) based on designs created in Adobe Illustrator (Adobe Systems). The glass masks were then used to make silicon wafers via SU-8 deposition in the Bio-Organic Nanofabrication Facility (University of California, Irvine). Next, PDMS stamps were made from the silicon wafer templates. To microcontact print, we utilized a method similar to that used by Tan et al. (22). Briefly, the stamps were sonicated in 50% ethanol for 15 min and were dried in a biosafety cabinet under sterile conditions using compressed nitrogen. Next, stamps were coated with a 0.1 mg/mL concentration of FN (Fisher Scientific Company, Hanover Park, IL) and allowed to incubate at room temperature for 1 h. After 1 h incubation, stamps were dried using compressed nitrogen and stamped onto PDMS coated coverslips that had been exposed to UV light (Jelight Company, Irvine, CA) for 8 min. The stamped coverslips were submerged in solution (5 g Pluronics F-127, dissolved in 500 mL sterile water; Sigma-Aldrich, St. Louis, MO) for 10 min and were immediately rinsed three times with room temperature PBS (phosphate-buffered saline; Life Technologies, Carlsbad, CA).

Isotropic tissue samples were made by coating substrates with a uniform layer of FN, allowing the cardiac myocytes to organize randomly. Substrates were made by incubating PDMS-coated coverslips, which had been exposed to UV light for 8 min, with 300 μL drops of 0.05 mg/mL concentration FN for 10 min. The coverslips were then rinsed three times with PBS. As a result of the difference in preparation, the total area of isotropic tissues is slightly larger than the total area of the anisotropic tissues; however, both are larger than the functional area of the heart-chip, thus this difference has no consequences.

Myocyte harvest, seeding, and culture

Neonatal rat ventricular myocytes were isolated from 2-day-old neonatal rats (Charles River Laboratories, Wilmington, MA) (23). Briefly, ventricular myocardium was excised under sterile conditions in a biosafety cabinet, rinsed in Hanks balanced salt solution buffer (HBSS; Life Technologies), and then incubated in a 1 mg/mL trypsin solution (Sigma-Aldrich, St. Louis, MO) dissolved in HBSS at 4°C overnight (12 h). The trypsin solution was then removed and tissue was neutralized in warmed M199 culture medium (Invitrogen, Carlsbad, CA) supplemented with 10% heat inactivated Fetal Bovine Serum, 10 mM HEPES, 20 mM glucose, 2 mM L-glutamine (Life Technologies), 1.5 μM vitamin B-12 and 50 U/mL penicillin (Sigma-Aldrich). Media was removed without disturbing tissue, which was dissociated through several washes of 1 mg/mL collagenase dissolved in HBSS. Next, collagenase cell solutions were centrifuged at 1200 rpm for 10 min. The supernatant was then aspirated and cells were resuspended in chilled HBSS. The HBSS cell solution was then centrifuged again at 1200 rpm for 10 min. The supernatant was aspirated and cells were resuspended in warm 10% M199 media.

The cell solution was purified through three consecutive preplates of 45, 45, and 40 min in cell culture flasks (BD Biosciences, San Diego, CA) in an incubator. After the final preplate, cells were counted using a disposable hemocytometer (Fisher Scientific, Waltham, MA) and were seeded at a density of 1,000,000 cells per 3 mL.

At 24 h after seeding, dead cells were rinsed from substrates with warmed PBS three times. After washing, warm 10% M199 was added, and substrates were returned to the incubator. Then 24 h later, 10% M199 was replaced with warm 2% M199 media.

Contractility experiments

Heart-on-a-chip experiments were performed four days after seeding in warmed Normal Tyrode’s solution of 5 mM HEPES (Acros Organics, Thermo Fisher Scientific, Bridgewater, NJ); 1 mM magnesium chloride (Santa Cruz Biotechnology, Dallas, TX); and 5 mM glucose, 1.8 mM calcium chloride, 5.4 mM potassium chloride, 135 mM sodium chloride, and 0.33 mM sodium phosphate (Sigma-Aldrich). First, patterned substrates were moved into 60 mm petri dishes with warmed Normal Tyrode’s solution. Then, substrates were cut into thin films using a razor blade as previously described in Grosberg et al. (21). The Tyrode’s solution and substrates were allowed to cool below 37°C to dissolve the PIPPAm and release the films from the cover-glass surface. Substrates were then moved to a 35 mm petri dish containing the Tyrode’s solution inside of an INUL-MS2 Stage Top Incubator (Tokai Hit, Fujinomiya-shi, Shizuoka-ken, Japan) to control for temperature. Customized electrodes were affixed to the 35 mm petri dish and films were paced with 10–12 volts at 2 Hz using a MyoPacer Field Stimulator (IonOptix, Milton, MA).

Contractility experiments were acquired on a model no. SZX-ILLB2 Stereoscope (Olympus America, Center Valley, PA) mounted with a model no. A601f/A602f camera (Basler, Exton, PA). Short video clips were acquired for each sample and then analyzed using custom ImageJ and MATLAB software as previously described in Grosberg et al. (21). Film bending was tracked for each sample, and diastole (defined by the longest projection of each film) and systole (defined by the shortest projection of each film) were automatically detected. Each video was labeled with the original length of each film as indicated by a pink outline and film tracking was indicated by an orange bar. Active stress was defined as the difference between systole and diastole for each film.

Cell and substrate thicknesses are important parameters in the calculation of muscular thin film contractility (24). Cell thicknesses for each tissue type were measured, and the average cell thickness for each tissue type was used in thin film analysis. Substrate thickness was measured for each chip preparation using a DektakXT profilometer (Bruker, Tucson, AZ).

Fixing and immunostaining

Cells were fixed in warm 4% paraformaldehyde (Fisher Scientific, Hanover Park, IL) supplemented with 0.001% Triton X-100 (Sigma-Aldrich) in PBS for 10 min. Next, cells were rinsed three times in room temperature PBS for 5 min each wash.

Cells were immunostained for actin (Alex Fluor 488 Phalloidin; Life Technologies, Carlsbad, CA), sarcomeric α-actinin (Mouse Monoclonal Anti-α-actinin; Sigma-Aldrich), nuclei (4′,6′-diaminodino-2-phenylinodole (DAPI; Life Technologies)), and FN (polyclonal rabbit anti-human fibronectin; Sigma-Aldrich). Secondary staining was done using tetramethylrhodamine- conjugated goat anti-mouse IgG antibody (Alexa Fluor 633 Goat Anti-Mouse, Life Technologies) and tetramethylrhodamine-conjugated goat anti-rabbit IgG antibody (Alexa-Fluor 750 Goat Anti-Rabbit, Life Technologies).

qPCR

Lysate samples were prepared according to the above description. Cells were lysed 72 h after seeding following RNeasy Mini Kit instructions (Qiagen, Valencia, CA). Lysates were then checked for 260/280 absorbance ratios using a DU 730 UV/Vis spectrophotometer (Beckman Coulter, Brea, CA). Only samples with a ratio between 2.1 and 2.2 were accepted. cDNA synthesis was accomplished according to the instructions in an RT² First Strand Kit (Qiagen). Customized arrays for Rat Cardiovascular Disease were run in triplicate for each sample (Array PARN-174Z; Qiagen). Arrays were run in a CFX96 Real-Time System (Bio-Rad, Irvine, CA). Data analysis was completed using RT² Profiler PCR array Data Analysis v. 3.5, an online standardized software (Qiagen).

Imaging and image analysis

Immunostained cells were imaged on an IX-83 inverted motorized microscope (Olympus America, Center Valley, PA) mounted with a digital charge-coupled device camera ORCA-R2 C10600-10B (Hamamatsu Photonics, Hamamatsu City, Japan) using an UPLFLN 40× oil immersion objective (Olympus America). At least 10 fields of view were acquired for each sample. Image processing was done via ImageJ software. Image analysis for orientational order parameter was done using customized MATLAB software (The MathWorks, Natick, MA) as previously described in Feinberg et al. (13) and Grosberg et al. (21).

Local organization was defined by an area of 215 μm × 164 μm at 40× magnification, an area within the 250 μm × 250 μm squares. Global organization was defined by at least 10 fields of view at 40× magnification, totaling an area of ∼3.5 mm², where the total area of patterned tissue was 225 mm² for anisotropic (globally aligned and parquet) patterns and 490 mm² for isotropic tissues.

Cell thicknesses were acquired on an IX-81 Inverted Confocal Microscope (Olympus America) mounted with a model No. EO-4010M camera (Edmond Optics, Barrington, NJ) using a LUCPLanFLN 40×/0.60 objective (Olympus America). Images were acquired using the Fluoview 1200 system with Fluoview Ver. 4.0 software (Olympus America). At least five fields of view were acquired for each sample and were analyzed as previously described using ImageJ software (13) (Fig. S3).

Statistics

To compare the stress and organization of the globally aligned, parquet, and isotropic tissues, we used a one-way ANOVA with the Holm-Sidak test, which is commonly used for pairwise comparison of experimental groups. Significance was considered for an unadjusted p-value less than the critical level, which accounts for the number of comparisons. This was compared against the Tukey Test to confirm significance of outcomes. Gene expression was normalized to isotropic tissue and significance was determined through online software (Qiagen) by a Student’s t-test between the control group and experimental groups. A p-value of <0.05 was considered significant and conversely, a p-value of >0.05 was considered nonsignificant. The confidence interval was calculated using the Confidence function in Excel (Microsoft, Redmond, WA). The 95% confidence limit indicates that if sufficient numbers of samples are collected from the same population, the mean value would be within the limits with a 95% probability.

Results

In this work, we pursued two goals: to create cardiac tissues of a variable global organization with no significant downstream effect differences from maximally anisotropic (i.e., globally aligned) tissues; and to determine whether a basic force-vector addition model (13) could possibly be predictive for the above tissues. As a first step, we formalized the basic model to express the developed stress as a function of tissue organization by making three major simplifications.

First simplification

The probability distribution of the sarcomere complex orientations is assumed to be a uniform probability distribution on the interval $\left[-{\theta }_0,{\theta }_0\right]$ (Fig. S1). This can be written in the following general form:

$$P=\{\begin{array}{cc}0& -\frac{\pi }{2}\le \theta <-{\theta }_0\\ \frac{1}{2{\theta }_0}& -{\theta }_0\le \theta \le {\theta }_0\\ 0& {\theta }_0<\theta \le \frac{\pi }{2}.\end{array}\text{where}{\text{lim}}_{{\theta }_0\to 0}P=\delta \left(\theta =0\right)$$ (1)

The orientational order parameter (OOP) is a very useful metric to describe construct organization (actin fibrils, sarcomeric z-lines, etc.). The OOP is zero for completely disorganized constructs and one for perfectly organized constructs, and it has been extensively used in many fields (21, 25, 26). In this case, the OOP is simply a function of the uniform probability interval $\left({\theta }_0\right)$:

$$OOP=\langle \text{cos}\left(2\theta \right)\rangle ={\int }_{-{\theta }_0}^{{\theta }_0}\frac{1}{2{\theta }_0}\text{cos}\left(2\theta \right)d\theta =\frac{\text{sin}\left(2{\theta }_0\right)}{2{\theta }_0}.$$ (2)

Second simplification

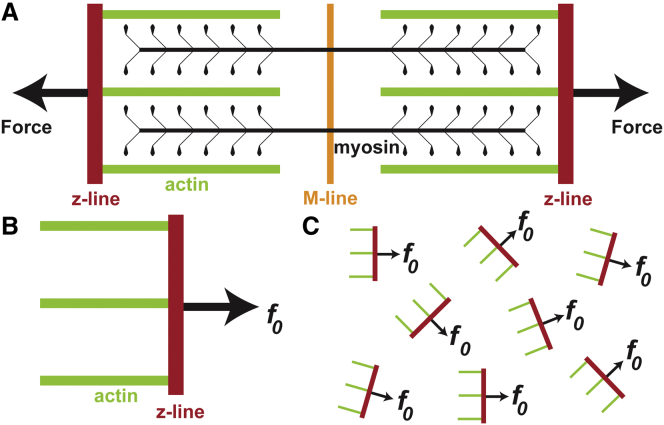
The dipole nature of the sarcomere can be ignored; thus, each sarcomere is assumed to produce some average force $f_0$ in the direction perpendicular to z-lines and parallel to actin fibrils (Fig. 1). Through this assumption, the force vectors became pseudovectors, i.e., symmetric in π, as the choice of positive or negative direction in a sarcomere complex is random. Thus, the average force produced by a single sarcomere in the x direction is also a function of the uniform probability interval $\left({\theta }_0\right)$:

$$\langle f_x\rangle ={\int }_{-{\theta }_0}^{{\theta }_0}{f}_0\times \frac{1}{2{\theta }_0}\text{cos}\left(\theta \right)d\theta =f_0\times \frac{\text{sin}{\theta }_0}{{\theta }_0},$$ (3)

and, the net force developed by the monolayer is:

$$F=N_{\text{sarcomeres}}\times \langle f_x\rangle =N_{\text{sarcomeres}}\times f_0\times \frac{\text{sin}{\theta }_0}{{\theta }_0}=F_0\times \frac{\text{sin}{\theta }_0}{{\theta }_0}.$$ (4)

Figure 1.

The basic model approximation of a sarcomere. (A) A sarcomere is a dipole in which force is produced perpendicular to the z-line and parallel to actin the fibrils. (B) For the model, the sarcomere is simplified to have a single force vector. (C) Within a cardiac tissue, each sarcomere will produce an average force $f_0$ parallel to its actin fibrils. To see this figure in color, go online.

Third simplification

The density of the sarcomeres is the same for all tissue organizations in both the plane and the thickness of the tissue; thus, the stress generated by such a tissue will be proportional to the net force ($\sigma \propto F$), and therefore:

$$\sigma ={\sigma }_0\frac{\text{sin}{\theta }_0}{{\theta }_0}.$$ (5)

In this formulation, ${\sigma }_0$ is the stress that would be produced by the tissue if the sarcomeres were perfectly aligned in the x direction (i.e., $P=\delta \left(\theta =0\right)$). This perfect stress can be calculated as long as both the actual stress and the organization are known and is the single parameter of this basic model:

$${\sigma }_0=\frac{\sigma }{\left(\frac{sin{\theta }_0}{{\theta }_0}\right)}.$$ (6)

Together, these assumptions can be used to predict the stress as a function of organization (OOP) by solving for ${\theta }_0$ from Eq. 2 and inserting the value into Eq. 5. Equation 5 can be reformulated to predict a stress based on a measurement. For example, the stress produced by an isotropic tissue with no downstream effects can be predicted based on the measured stress of the globally aligned tissue and the organizational information for both tissue types (${\theta }_{0,\text{aniso}},{\theta }_{0,\text{iso}}$):

$${\sigma }_{\text{iso,predicted}}={\sigma }_{\text{aniso,measured}}\times \frac{\text{sin}\left({\theta }_{0,\text{iso}}\right)\times {\theta }_{0,\text{aniso}}}{\text{sin}\left({\theta }_{0,\text{aniso}}\right)\times {\theta }_{0,\text{iso}}}.$$ (7)

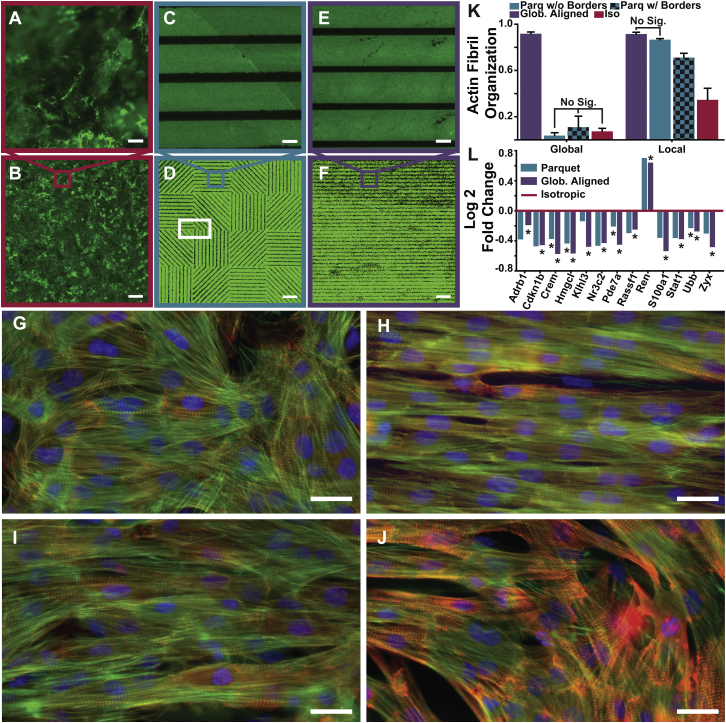
To properly test even this simple model, it was necessary to create tissues where the only dominant variable was the global tissue organization. The classical isotropic tissues were cultured on FN that was disorganized both locally (Fig. 2 A) and globally (Fig. 2 B). We hypothesized that as long as the cells were organized locally, any downstream effects of global disorganization would be muted to the point of being negligible. To achieve this effect, we utilized microcontact printing such that the FN was patterned in 20 μm lines with 5 μm gaps. The locally organized patterns (Fig. 2, C and D) were identical to globally aligned patterns (Fig. 2, E and F) within each parquet (Fig. 2, C and E). The individual parquets (250 × 250 μm) had internal line patterns at 0, 45, 90, and 135°. As a result, the global organization of the parquet FN (Fig. 2 D) matched to the isotropic (Fig. 2 B). Additionally, the images of the sarcomeric z-lines were used to estimate sarcomeric density, which was found to be similar among the tissue types validating the third simplification that lead to Eq. 5.

Figure 2.

Locally organized globally disorganized parquet tissues. (A and B) Isotropic FN. (C and D) The parquet FN pattern. (E and F) The globally aligned anisotropic FN pattern. (A, C, and E) Local scale (96 × 96 μm); (B, D, and F) global scale (1 × 1 mm). (G–J) Immunostain images of actin fibrils (green), sarcomeric z-disks (red), and nuclei (blue) for isotropic tissue (G), globally aligned anisotropic tissue (H), tissues within a parquet tile (I), and tissue from a border region of multiple parquet tiles (J) like the one indicated with the white rectangle in (D). (K) Actin fibril OOP on the global and local scale for each tissue type. Error bars represent the standard deviation of the data. Significance was tested within each group (global, local), and was p < 0.05 unless labeled “No. Sig.” (Table S1). (L) Log twofold change for globally aligned anisotropic (N = 3) and parquet (N = 5) samples normalized to isotropic (N = 3) samples (Table S2). Scale bars, 10 μm (A, C, and E); 100 μm (B, D, and F); 25 μm (G–J). To see this figure in color, go online.

To test the hypothesis and model, neonatal rat ventricular myocytes were seeded on the patterns (Fig. 2, G–J). Qualitatively, the cells followed the parquet patterns, except for small border regions in-between the parquet squares (Fig. 2, white rectangle in D and J). To compare the tissues quantitatively, the OOP was calculated for the actin fibrils (Table S1). Whether the border regions were taken into account or not, the global organization of the parquet tissues was not statistically significantly different from the isotropic tissues (Fig. 2 K; Global). Locally, the internal organization of the parquets matched the globally aligned organization (Fig. 2 K; Local).

When the border regions were taken into account, the local organization of the parquet tissues was reduced, but still significantly higher than isotropic organization. Next, the parquet tissues were compared to the globally aligned and isotropic tissues by quantifying the gene expression levels, which can be seen as measures of some of the downstream effects.

We tested 84 gene expression levels from a Rat Cardiovascular Disease array (Table S2). There was a statistically significant difference in gene expression between isotropic and globally aligned tissues in 13 genes. Conversely, there was only one signal transduction gene (Pde7a), whose expression level was significantly different between globally aligned and parquet tissues. However, Pde7a was also among the four genes that were significantly different between parquet and isotropic tissues. Consequently, the gene expression analysis suggested that the parquet tissues tend to be somewhere in between the isotropic and globally aligned tissues (Fig. 2 L). These results indicated that we were not able to completely eliminate the downstream effects, but they might have been considerably muted. Therefore, if the proposed highly simplified model encompasses all of the dominant properties of the organization-stress production relationship, the stress measured in the parquet tissues should match the prediction given by Eq. 7.

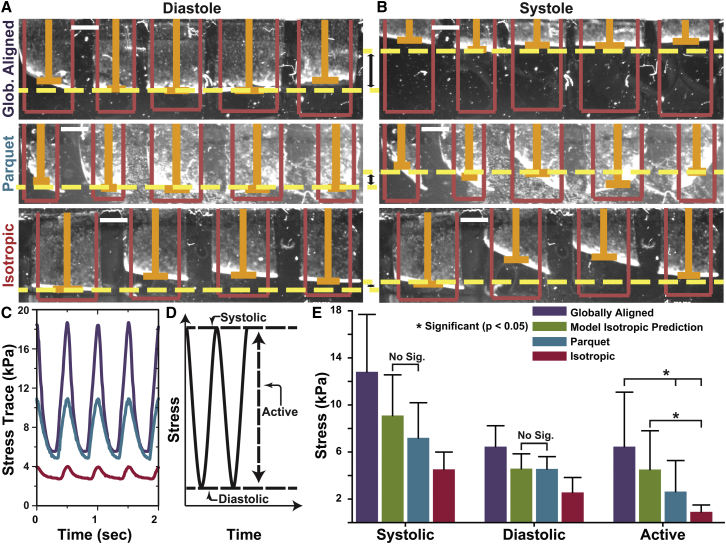
To test this, the heart-on-a-chip assay (21) was utilized with the three tissue types. In this device, each tissue type was cultured on an elastic polymer film that was partially detached from the glass during contractility experiments. The films were imaged from above and the x-projection was measured for every frame (shown: diastole Fig. 3 A and systole Fig. 3 B; Movies S1, S2, and S3). An average x-projection was calculated for films that exhibited off-axis deformation (isotropic and parquet tissues) (13, 21). Samples were paced at 2 Hz for consistency, and stress was calculated using previously established procedures (21, 24) (Fig. 3 C). The systolic-maximum, diastolic-minimum, and active-amplitude stresses were calculated for each film (Fig. 3 D).

Figure 3.

Contractility experiments using heart-on-a-chip assays. (A and B) Sample video frames for the three tissue types showing diastole and systole, respectively. Pink outlines show original film length, orange bars track films’ x-projections, and yellow dashed lines provide a visual cue for the change in contraction between diastole and systole (scale bars, 1 mm). (C) Example stress traces of raw data for anisotropic (top, purple line), parquet (middle, blue line), and isotropic (bottom, red line) tissue from a contractility experiment. (D) Schematic of stresses measured from each stress trace. (E) Comparison of stresses for anisotropic (N = 28), parquet (N = 22), and isotropic (N = 27) tissue versus the basic model prediction (2^nd, green bar). Significance was assumed if p < 0.05 (Table S3). Within systolic and diastolic stress, pairwise comparisons were significant unless labeled with “No. Sig.” Within active stress, pairwise statistical significance is indicated by (^∗). To see this figure in color, go online.

To ensure that we did not bias the conclusions in any way, all results were included in the averages unless there was a clear failure to pattern, the cells were not beating in culture, or the chip substrate was defective. This resulted in a significant biological variability, but data from a large enough number of films was collected to test the statistical significance of the findings (Table S3).

Using Eqs. 2 and 7, the isotropic stress was predicted based on the stress measured for globally aligned tissues and actin fibril organization (Fig. 3 E). As expected from previous works, the prediction was statistically different from the measured isotropic stress. However, there was no statistically significant difference between the model prediction and the three types of stresses measured in the parquet tissues. Therefore, these results collectively lead to two interlinked conclusions: the downstream effects were sufficiently muted that they did not significantly affect force production; and more surprisingly, the very basic model encompasses all the dominant features that relate force production to pure tissue organization in engineered monolayer myocyte tissues.

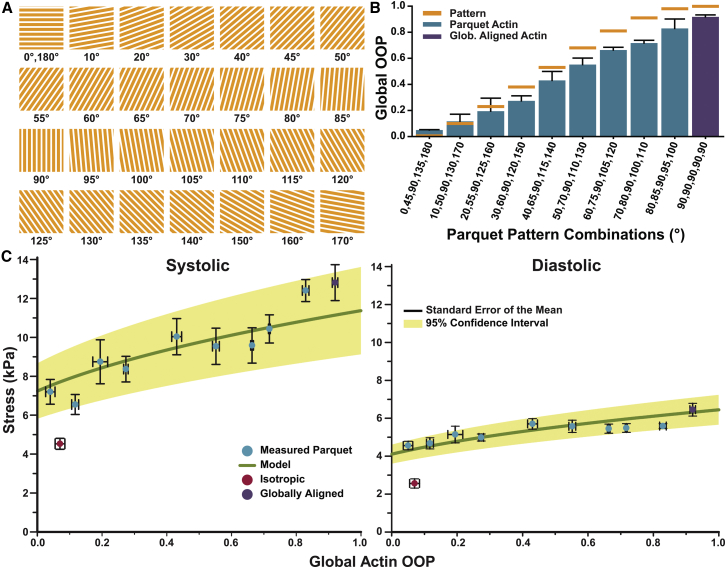
To further test the model and the experimental platform, a range of parquet tissues were created using the tiles depicted in Fig. 4 A. The parquet tiles were combined into blocks (Fig. S2) such that the resultant global OOP varied within the isotropic and anisotropic limits (Fig. 4 B; Table S4). The average systolic stress for the ideal tissue (Eq. 6) was calculated for each film and averaged to arrive at a single value of σ₀ = 11.4 ± 1.2 kPa. Further, the ideal tissue stress was used to predict stress as a function of OOP (Eqs. 2 and 7), and the error was used to derive the 95% confidence limit for the model (Fig. 4 C). Hence, the model predicted that the mean of the experimentally measured systolic and diastolic stresses would fall within the interval bound by the 95% confidence limit. Indeed, the mean systolic and diastolic stresses for each parquet pattern were found to be within the 95% confidence limit of the model while the isotropic mean systolic and diastolic stresses were outside the limits (Fig. 4 C). Thus, the basic model was found to be predictive for the whole range of organizations as long as the downstream effects were muted and negligible.

Figure 4.

Experiment versus model for varying global organization. (A) Various parquet tiles used for tissue design. (B) FN pattern OOP and global actin OOP from all parquet tissues (Table S4). Error bars: standard deviation. (C) Systolic and diastolic stresses as a function of OOP predicted by the model based on calculated parameter ${\sigma }_0$ (thick, green line). The mean systolic stress for each parquet tissue type (light, blue circles) falls within the 95% confidence limit of the model (light brown, shading). The mean systolic and diastolic stresses of the isotropic tissues (dark, red circle) falls outside the confidence limits of the model. Error bars (black) represent standard error of the mean (mean ± SD for all stresses in Table S5). To see this figure in color, go online.

Based on this result, it was possible to quantitatively estimate the contribution of the downstream effects to the reduction of stress in isotropic tissues:

$${\sigma }_{\text{iso,downstream}}={\sigma }_{\text{iso,measured}}-{\sigma }_0\frac{\text{sin}\left({\theta }_{0,\text{iso}}\right)}{{\theta }_{0,\text{iso}}}\approx -3.18\pm 2.61\text{kPa}.$$ (8)

Using the basic model and measured stresses of parquet tissues, it is possible to make this estimate at any organization.

Discussion

The main achievement of this work was the insight into the relationship between global organization of myofibrils and the net-force produced by cardiac tissues. To accomplish this, an experimental platform was designed to measure the developed stress as a function of global tissue organization (Fig. 4 C). The platform is based on tissues cultured on parquet extracellular matrix patterns, which inside the parquet tiles were identical to the pattern used to make globally aligned anisotropic tissues (Fig. 2, A–K). In the parameter space between classical globally aligned anisotropic and isotropic tissues, the parquet tissues were shown to be in-between the two through gene expression levels (Fig. 2 L) and similar to globally aligned tissues through local organization (Fig. 2 K). This was apparently sufficient to mute the downstream effects associated with isotropic tissues. Indeed, they were negligible as illustrated by the experimental results matching the basic net-force model (Figs. 3 E and 4 C). Because of the high biological variability inherent to the contractility measurements (Table S5), it is important to note that the model can only predict mean stresses, not individual film stresses. Thus, if we build a number of tissues with a specified OOP, the model predicts the average systolic stress. Therefore, the new platform can be used to estimate the mean amount of force reduction that can be attributed to downstream effects that might normally be coupled with tissue organization changes.

Common methods of cardiac tissue organization on two-dimensional constructs include microcontact printing, stretch, and topographical cues (13, 17, 18, 19, 27, 28, 29). These methods have been shown to produce globally aligned or isotropic tissues, and have been used to study several factors associated with each tissue type (17, 19, 21, 28). However, in all of these, the reorganization of the tissue also leads to a nontrivial change in functionality. It is possible to create parquet-like organization by providing two perpendicular guidance stimuli such as stretch and patterning, but this introduces stretch to the system, which is also known to affect contractility (17). In contrast, using the parquet tissues, made it possible to decouple the global organization from other factors that might have also affected contractile function. Interestingly, the patches of organized tissues are not foreign to the spontaneous self-assembly of isotropic cardiomyocyte monolayers. This was qualitatively evident in small portions of isotropic tissues (Fig. 2 G) and emerged quantitatively in that OOP_iso,local > OOP_iso,global (Fig. 2 K). It will take further investigation to determine if the downstream effects are contingent on smaller patches of organization in isotropic compared to parquet tissues or if the local patterning changes the self-assembly cascade, which in turn leads to a difference in the downstream effects. Whatever the causes, our parquet tissue is the simplest method to decouple the global organization from downstream effects that can affect contractility.

Modeling cardiac contractility and beating on the scale of the whole organ (30, 31, 32) and at the tissue scale (20, 33, 34) has been extensively pursued. The drastically simplified model presented here could not (and was not meant to) describe all the complexities of the contraction in a cardiac tissue such as the dipole nature of the sarcomeres or the three-dimensional intricate architecture of myofibrils within the heart. Instead, the basic model was designed to work in conjunction with experimental data to provide insight into the causes of change in force production. However, the discovery that the relationship between force production and tissue organization is simple when there is no downstream effect will impact the interpretation of model results and design of future models.

It has been shown that variations in cardiac tissue architecture are linked with changes in gene expression (17, 28). It is not possible to fully understand the effect of these gene expression changes to tissue function without a method by which each can be studied. The proposed platform is a possible remedy to this dilemma. For example, in a comparison study between primary mouse cardiomyocytes and mouse embryonic stem-cell derived cardiomyocyte tissues (ES-tissues), which have very different gene expression profiles, the systolic stresses were found to be ∼17.1 ± 6.1 and 3.4 ± 1.3 kPa, respectively (35). However, it is not clear how much of the difference in stress was due to the stem-cell origin of the cells as the tissue organization was also different (OOP_primary ≈ 0.71 ± 0.03 and OOP_stem ≈ 0.35 ± 0.03) (35). Using the method developed here, it is possible to estimate that the primary cells would have produced 9.1 ± 0.9 kPa systolic stress at the ES-tissue organization. Thus, we can show that −5.7 ± 2.2 kPa of stress difference was due to some factors inherent to the stem-cell derived nature of the ES-tissues. This illustrates the power of our experimental platform and the validated basic model.

In this work, the parquet tiles were of a constant size—a size that allowed for the downstream effects to be muted. It is obvious that tissues with larger tiles, similar in size to the heart-chip films, will perform similarly to globally aligned tissues. Likewise, there must exist a minimum parquet tile size where the border effects (Fig. 2 J) will overwhelm the tiles, and the tissue will be essentially isotropic. These various length-scales will point to the underlying mechanisms of the various downstream effects (such as sarcomeric z-line registration), and will be an interesting area of study.

Conclusions

In this work, it was shown that in the absence of downstream effects caused by local tissue organization, the global organization of the myofibrils is related to the net force produced by a cardiac tissue through an analytical force-vector addition model. Consequently, it is now possible to estimate the contribution to force production of other factors that would normally be coupled to tissue organization. These results will lead to better models of the heart in health and disease. Additionally, it is now possible to quantitatively analyze differences in various tissues, such as stem cell-derived cardiac monolayers, decoupled from the effect of their altered tissue organizations. As more studies are performed on cardiac tissues, our results and the technological platform can be used to explore the functional implications of a variety of biological factors; thus, elucidating the mechanisms involved in heart development and disease.

Author Contributions

M.B.K., L.A.M., and A.G. performed experiments; M.B.K., N.K.D., and A.G. performed data analysis and modeling; A.G. designed research; and M.B.K. and A.G. wrote the article.

Editor: Andrew McCulloch.