Shape Transformations of Epithelial Shells

Abstract

Regulated deformations of epithelial sheets are frequently foreshadowed by patterning of their mechanical properties. The connection between patterns of cell properties and the emerging tissue deformations is studied in multiple experimental systems, but the general principles remain poorly understood. For instance, it is in general unclear what determines the direction in which the patterned sheet is going to bend and whether the resulting shape transformation will be discontinuous or smooth. Here these questions are explored computationally, using vertex models of epithelial shells assembled from prismlike cells. In response to rings and patches of apical cell contractility, model epithelia smoothly deform into invaginated or evaginated shapes similar to those observed in embryos and tissue organoids. Most of the observed effects can be captured by a simpler model with polygonal cells, modified to include the effects of the apicobasal polarity and natural curvature of epithelia. Our models can be readily extended to include the effects of multiple constraints and used to describe a wide range of morphogenetic processes.

Introduction

Regulated deformations of epithelial sheets play important roles during tissue morphogenesis and can be driven by a variety of mechanisms, the simplest of which rely on spatial patterns of apical cell contractility (1, 2, 3). These prepatterns are commonly established by upstream signaling processes, which upregulate the activity of the actomyosin networks on the apical surfaces or apical edges in a subset of cells within the epithelium (4, 5). Intracellular nonuniformities in contractility trigger shape changes of individual cells, leading to three-dimensional (3D) deformations, such as localized tissue invaginations. This sequence of processes, from patterning of apical contractility, to spatially restricted cell shape changes, to 3D tissue deformations has been documented in a wide range of experimental systems (6, 7, 8, 9, 10).

A canonical example is provided by the early stages of mesoderm invagination in Drosophila, where apical constriction of cells on the ventral side of the embryo transforms a convex epithelial shell into a more complex shape with an Ω-like cross section (11). In this system the apical surfaces of epithelial cells are facing toward the rigid membrane surrounding the embryo. In another well-studied experimental model—the developing Drosophila egg chamber—the epithelium has opposite polarity, with the apical surfaces oriented toward the oocyte, which is enclosed by the epithelial sheet (8, 12). In this case, a two-dimensional (2D) patch of the follicle cells evaginates, bending in the direction of the membrane surrounding the egg chamber. This deformation is thought to be guided, at least in part, by the embedded contour of apically constricting epithelial cells.

The general principles governing 3D deformations induced by patterns of apical contractility remain poorly understood. It is in general unclear what determines the direction in which the patterned sheet is going to bend and whether the resulting deformation will be discontinuous or smooth. Several mathematical and computational models have been proposed to explore these questions, but none of them is sufficiently versatile for analyzing the interplay of multiple physical and geometrical factors (6, 7, 10, 13, 14, 15, 16, 17, 18). For instance, multiple models have been used to describe the invaginations in the early embryos (6, 7, 10, 18). However, most of these models consider only a 2D cross section of the epithelial shell, which limits the class of shape transformations that can be analyzed.

Here we provide what appears to be a minimal, yet physically realistic computational framework that enables systematic exploration of epithelial deformations induced by spatial patterns of active and passive cell properties. Our approach is based on the recently proposed energy formulation in which every cell is modeled as a prism with apical, basal, and lateral surfaces that can have different properties (19). We use this model to construct epithelial shells enclosing a fluid-filled volume and surrounded by a hard membrane, mimicking a scenario encountered in developing tissues and tissue organoids. We then use numerical continuation algorithms to explore how these model epithelial shells deform in response to the prepatterns of apical contractility. We find that, for most cases, the deformations are smooth, i.e., they happen without bifurcations, when viewed as a function of the amplitude that characterizes the spatial pattern of apical contractility. We also demonstrate that a simpler 2D model (in which epithelial shells are constructed from polygonal cells) can describe the effects predicted by the 3D model and can be used to explore a wide range of morphogenetic processes.

Materials and Methods

3D vertex model

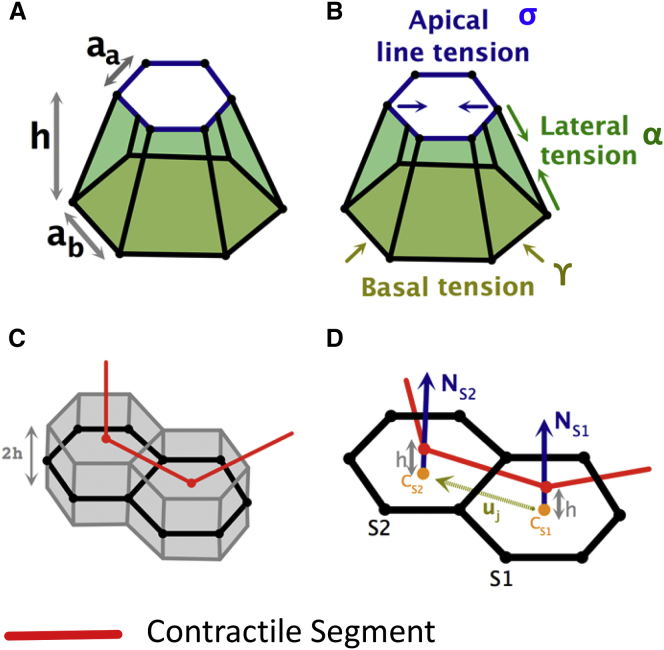
Vertex models constructed from 3D cells have been proposed to study epithelial morphogenesis in multiple experimental systems (19, 20, 21, 22, 23). Based on these previous studies, we used the following energy functional to model an epithelial monolayer constructed from cells with distinct apical and basal surfaces (Fig. 1, A and B):

$$E_{3D}=\sigma \sum _e{l}_e+\alpha \sum _l{S}_l+\gamma \sum _b{S}_b+B\sum _c{\left(V_c-V_c^0\right)}^2.$$ (1)

Figure 1.

Schematic representation of our vertex models. (A and B) Schematic representation of the 3D model. (A) A model 3D cell with distinct apical, basal, and lateral surfaces. (B) Schematic highlighting different tension terms in the 3D vertex model. (C) Schematic explanation of the modified 2D vertex model. The modified 2D model idealizes the epithelial sheet as the midsurface (shown in black) of an epithelial monolayer with finite thickness 2h and assumes that a contractile segment (shown in gray) joins the centers of the apical faces. (D) The figure shows two adjacent 2D cells S1 and S2 with shared edge j, cell centers (C_S1, C_S2), and unit outward normals (N_S1, N_S2), pointing toward the outer shell. The value ${\mathit{u}}_{j^{\prime }}$ is the unit vector joining the cell centers and h is the offset parameter. See text for more details. The red line highlights a contractile segment that is offset by a distance from the surface along the cell normals. To see this figure in color, go online.

In this expression, the first term sums over all apical edges e, the second term sums over lateral surfaces l, the third term sums over basal surfaces b, and the last term sums over cells c. The first term corresponds to the line tension along the apical edges of neighboring cells; l_e is the edge length and σ is the apical line tension coefficient. The second and third terms correspond to the contributions from lateral and basal tensions, which are proportional to the lateral and basal surface areas (S_l, S_b) with coefficients α and γ, respectively. These coefficients model the resistance to deformation due to the cytoskeletal meshwork that underlies the surface. The last term penalizes the deviation of the cell volume, V_c, from its target value, $V_c^0$, with compression modulus B to approximate cytoplasmic incompressibility. For more details, see Section S1 in the Supporting Material.

In our 3D model, we define prepatterned apical edges to represent a contractile ring $R$ embedded in the apical surface (shown in red in Fig. 2 A1 and Fig. 3 A1) or an apically constricting patch of cells P (shown in red in Fig. 2 B1 and Fig. 3 B1). The first pattern is motivated by the embedded compressive cable observed in follicle cells during Drosophila appendage formation and early sea urchin embryo, which displays localization of the motor protein myosin (8, 24). The second pattern is motivated by biological settings in which a group of cells is influenced by uniform actomyosin constriction across the apical surface (2, 25, 26). Apical edges belonging to the contour or the patch are assigned an apical line tension (σ + Γ), which is larger than the apical line tension σ of the other nonpatterned edges. This is implemented through an additional energy term for the prepatterned edges

$$E_{\Gamma }=\Gamma \sum _{i\in RorP}{l}_i,$$ (2)

where the index i runs over all edges belonging to the apical ring R or apical patch P.

Figure 2.

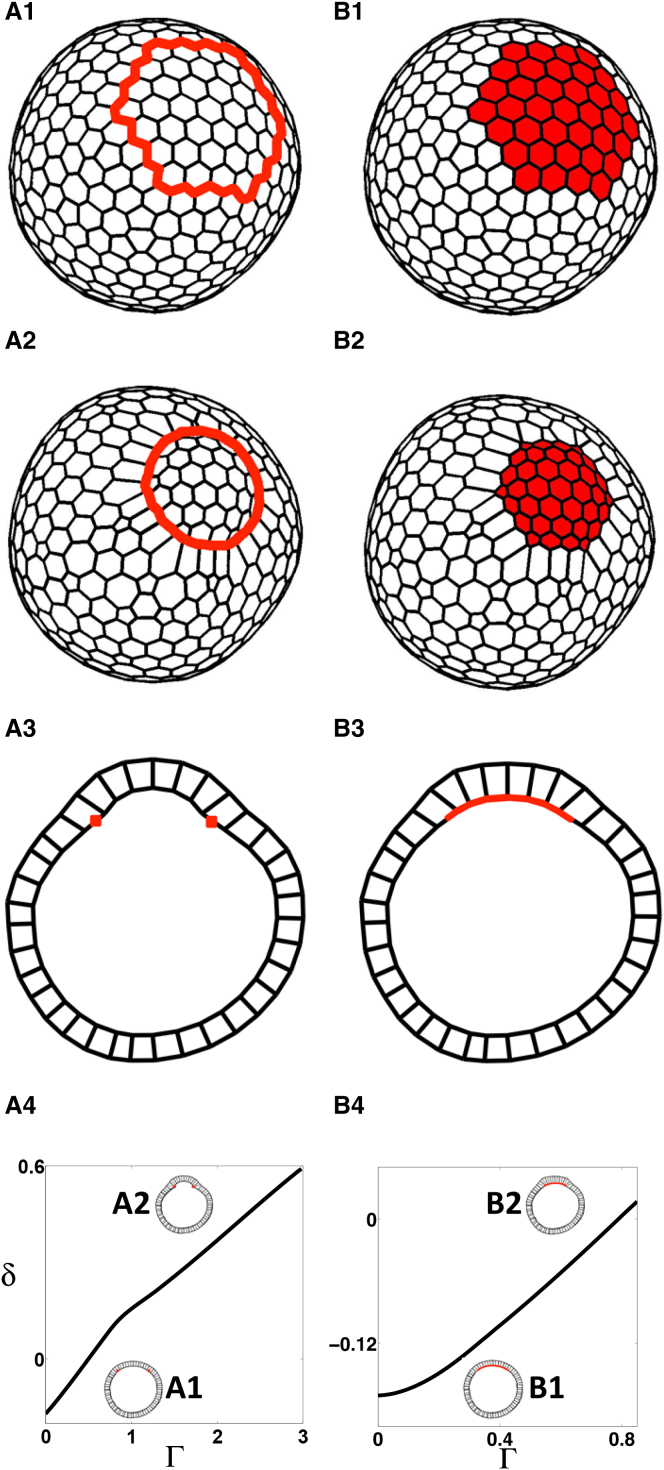
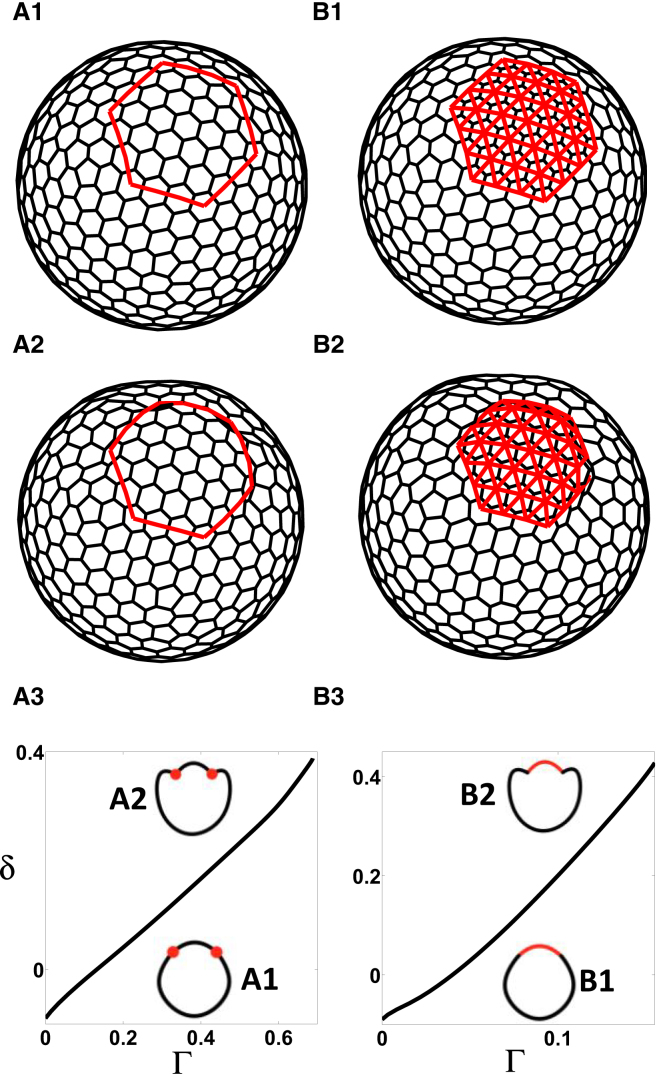
3D deformations induced by prepatterns of line tension in a model with 3D cells for the apical-in case; see text for details. (A1 and B1) Initial configurations, showing the inner surface (i.e., apical side and omitting the outer basal surface) of the shell, with different heterogeneities: (A1) Contractile ring. (B1) Patch of apically constricting cells. (A2 and B2) Representative evaginated states, showing the inner surface, where the enclosed patch bends outward (positive deflection, δ > 0, as defined in Fig. S3). (A3 and B3) Cross-section representation of equilibrium shapes (A2 and B2), respectively. (A4 and B4) Steady-state diagrams showing deflection δ with increasing parameter Γ. (Solid line) Stable steady states. Cross sections of representative steady states (A1, B1, A2, and B2) are shown as insets. Parameter values are listed in Table S2 in the Supporting Material. To see this figure in color, go online.

Figure 3.

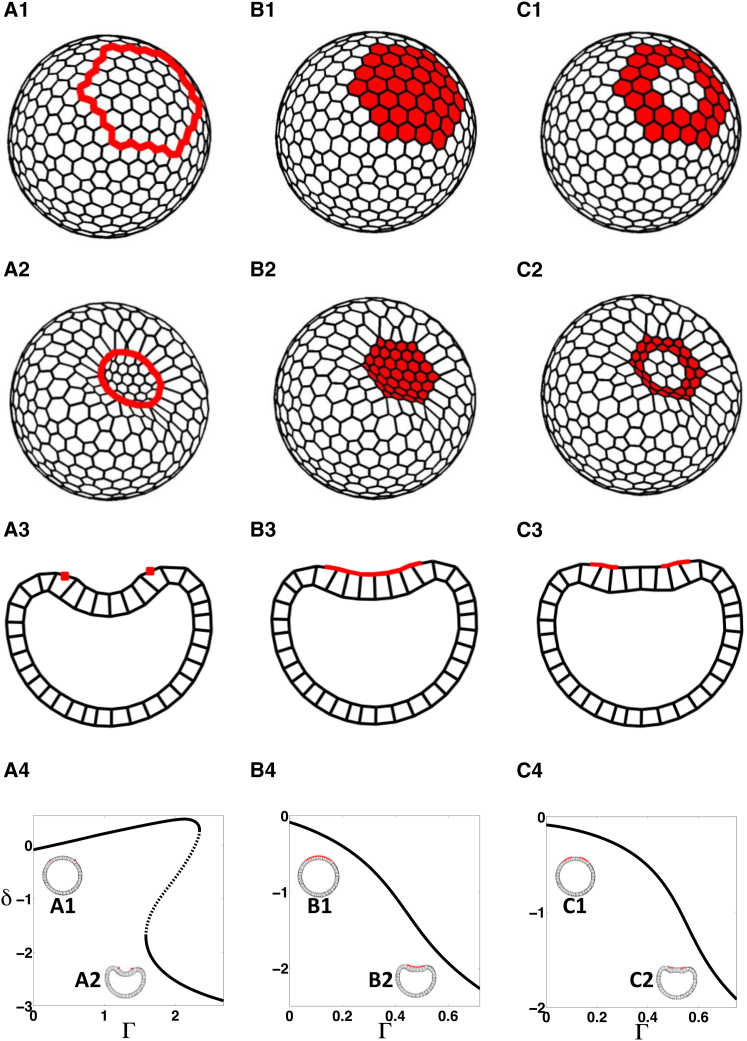
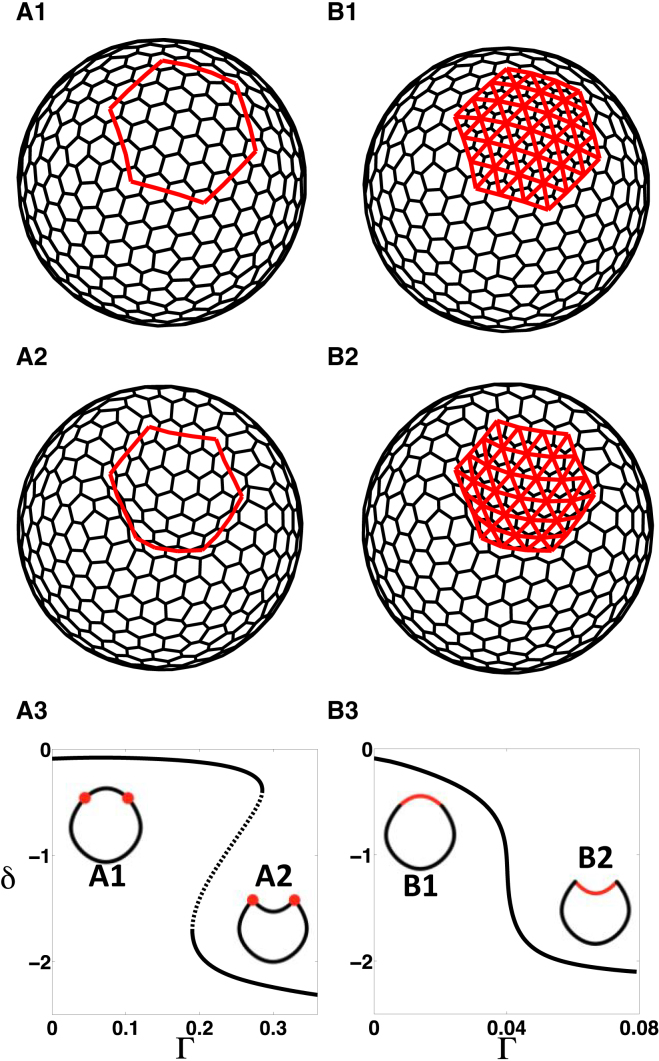
3D deformations induced by prepatterns of line tension in a model with 3D cells for the apical-out case; see text for details. (A1–C1) Initial configurations, showing the outer surface (i.e., apical side) of the shell, with different heterogeneities: (A1) Contractile ring. (B1) Patch of apically constricting cells. (C1) A ring of apically constricting cells, two cells wide. (A2–C2) Representative invaginated states, showing the outer surface, where the enclosed patch bends inward (negative deflection, δ < 0 as defined in Fig. S3). (A3–C3) Cross-section representation of equilibrium shapes (A2–C2), respectively. (A4–C4) Steady-state diagrams showing deflection δ with increasing parameter Γ. (Solid lines) Stable states; (dashed lines) unstable steady states. Cross sections of representative steady states (A1–C1 and A2–C2) are shown as insets. Parameter values are listed in Table S2. To see this figure in color, go online.

2D vertex model

Most of the previously published 2D vertex models were used to describe the dynamics of epithelia constrained to two spatial dimensions (27, 28, 29). More recently, we have used these models to explore 3D deformations induced by prepatterning of cell properties (8, 9, 30)Fig. 4). We extended these models so that they can account for the natural curvature of the sheet, and, importantly, for the intrinsic apicobasal polarity of epithelial cells. The energy in this model is defined in the following way:

$$E_{2D}=\mu \sum _c{\left(A_c-A_c^0\right)}^2+\sigma \sum _j{l}_j+\beta \sum _{j^{\prime }}\left(\left(1-{\mathit{N}}_{s2\left(j^{\prime }\right)}\cdot {\mathit{N}}_{s1\left(j^{\prime }\right)}\right)+k_{j^{\prime }}\left({\mathit{N}}_{s2\left(j^{\prime }\right)}-{\mathit{N}}_{s1\left(j^{\prime }\right)}\right)\cdot {\mathit{u}}_{j^{\prime }}\right).$$ (3)

Figure 4.

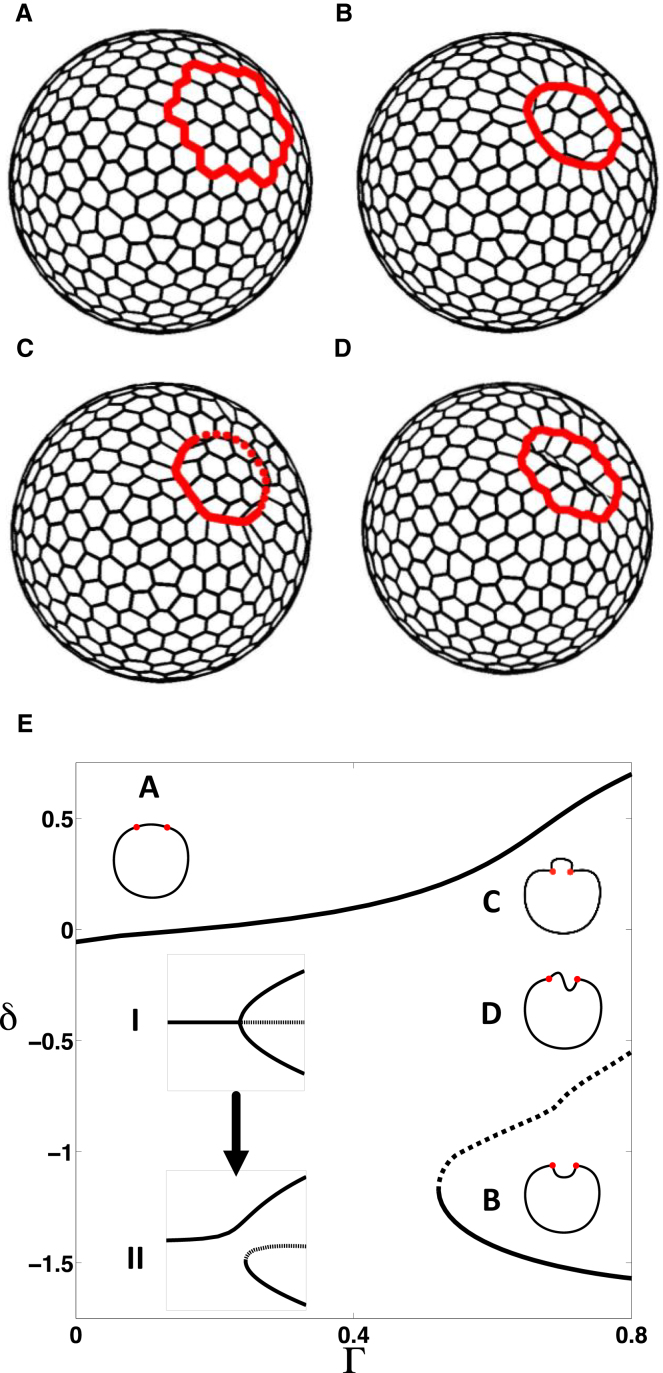
3D bending of closed epithelial shells in the naturally planar 2D vertex model due to the embedded contractile ring. (A) Initial equilibrium configuration with the contractile ring (shown in gray). (B) Representative invaginated state, where the enclosed patch bends inward (negative deflection, δ < 0). (C) Representative evaginated state, where the enclosed patch bends outward (positive deflection, δ > 0). Dashed red line represents patterned edges that lie behind the evaginated patch. (D) Representative unstable equilibrium configuration. (E) Steady-state diagram showing deflection δ with increasing parameter Γ. (Solid lines) Stable states; (dashed lines) unstable steady states. Insets (I) and (II) highlight the breakup of the pitchfork bifurcation in the naturally planar 2D vertex model due to curvature (discussed more in Fig. S1). Cross sections of representative steady states (A–D) are shown as insets. Parameter values are listed in Table S3. To see this figure in color, go online.

The first term sums over all cells c, the second term sums over all edges j, and the last term sums over all interior edges $j^{\prime }$, i.e., edges shared by two adjacent cells $s1\left(j^{\prime }\right)$ and $s2\left(j^{\prime }\right)$. The first term corresponds to sheet elasticity, where A_c is the area of cell c, $A_c^0$ is its target area, and μ is the stretching modulus. The second term captures intercellular interactions in the form of tensile forces along cell-cell edges, where l_j is the length of the edge j and σ is the line tension coefficient. The last term represents the bending energy term, where β is the bending elasticity coefficient and $k_{j^{\prime }}$ represents the local natural curvature of the shell ($k_{j^{\prime }}$ is roughly the rest value of the dihedral angle between the faces adjacent to edge $j^{\prime }$, and it scales like the natural curvature of the midsurface times the typical cell size; see Section S2.1 for details). Here ${\mathit{N}}_s$ denotes the outward unit normal to a cell s (i.e., the normal vector of each cell points toward the outside of the closed shell). The value ${\mathit{u}}_{j^{\prime }}$ is the unit vector joining the cell centers (Fig. 1, C and D),

$${\mathit{u}}_{j^{\prime }}=\frac{{\mathit{C}}_{s2\left(j^{\prime }\right)}-{\mathit{C}}_{s1\left(j^{\prime }\right)}}{|{\mathit{C}}_{s2\left(j^{\prime }\right)}-{\mathit{C}}_{s1\left(j^{\prime }\right)}|},$$ (4)

where ${\mathit{C}}_{s2\left(j^{\prime }\right)}$ and ${\mathit{C}}_{s1\left(j^{\prime }\right)}$ are cell centers, defined as the mean position of the nodes belonging to the cells s1 and s2, respectively (Fig. 1, C and D). The bending energy term defines an at-rest value of the angle between the normals of adjacent cells, which depends on $k_{j^{\prime }}$ (and is proportional to $k_{j^{\prime }}$ for small $k_{j^{\prime }}$) and hence implements the notion of natural curvature. For more details, see Section S2.

In our 2D model, we idealize the epithelial sheet as the midsurface of a 3D epithelial monolayer (Fig. 1 C). We proceed to show how we mimic the effect of the prepatterns in our 2D model that are present on the apical surface of an epithelium (Fig. 1 D). From now on, we will refer to this representation of prepatterns as being offset from the midsurface. Such prepatterns include a contractile ring R (Fig. 5 A1) and a constricting patch P (Fig. 5 B1): a contractile ring R is defined by a closed path joining the centers of a ring of adjacent cells (Fig. 5 A1), while a constricting patch P represents a subset of the mesh and is implemented by adding a line tension along all segments joining the adjacent cell centers that are contained within this subset (Fig. 5 B1). Segments belonging to either type of prepattern are assigned a line tension Γ and an offset parameter h, and an additional energy term is considered:

$$E_{\Gamma }=\Gamma \sum _{i\in RorP}\left(|{\mathit{C}}_{s2\left(i\right)}-{\mathit{C}}_{s1\left(i\right)}|-h\left({\mathit{N}}_{s2\left(i\right)}-{\mathit{N}}_{s1\left(i\right)}\right)\cdot {\mathit{u}}_i\right),$$ (5)

where the index i runs over all edges belonging to the apical ring R or apical patch P, and h is one-half the thickness of the real tissue.

Figure 5.

3D deformations induced by prepatterns of line tension in a model with 2D cells for the apical-in case; see text for details. (A1 and B1) Initial configurations with different heterogeneities: (A1) contractile ring; (B1) constricting patch. Both are implemented as subsets of the dual mesh, which is used to offset contractile patterns; see text for details. (A2 and B2) Representative evaginated states. (A3–B3) Steady-state diagrams showing deflection δ with increasing parameter Γ corresponding to the prepatterning defined in (A1) and (B1), respectively. (Solid line) Stable steady states. Cross sections of representative steady states (A1–B1 and A2–B2) are shown as insets. Parameter values are listed in Table S4. To see this figure in color, go online.

The key feature of Eq. 5 is that it represents the line tension of segments that are offset by a distance h from the midsurface (see Section S2 for details), but does so by using solely the degrees of freedom of the 2D model, namely the positions of the nodes lying onto the midsurface. The line tension parameter Γ acts in two ways: it brings the cell centers closer together and, when h ≠ 0, it bends the surface so that the end points of the normal vectors come close together (h > 0) or further apart (h < 0). Note that the line tension prepatterning parameter $\Gamma$ in the model with 3D cells has qualitatively similar effects.

In the special case $k_{j^{\prime }}$ and h = 0, this model reduces to the 2D vertex model that has been used in the literature to understand epithelial deformations for flat epithelial sheets in different contexts (8, 9, 28, 30). Hereafter, we will refer to that particular case as the naturally planar 2D vertex model (because $k_{j^{\prime }}=0$, the bending energy term corresponds to a naturally flat sheet). Note the new terms that we introduce in this work, namely the one proportional to $k_{j^{\prime }}$ in Eq. 3 and the one proportional to h in Eq. 5; both depend on the nodal positions through the same expression $\left({\mathit{N}}_{s2\left(i\right)}-{\mathit{N}}_{s1\left(i\right)}\right)\times {\mathit{u}}_i$. As a result, both terms have a similar numerical implementation.

Modeling the effects of constraints

To study the effects of epithelial shell curvature, i.e., a fluid-filled inner cavity and an outer stiff membrane during epithelial bending, we consider an initial homogeneous spherical configuration and include additional terms in the energy functions:

$$E=B_Y{\left(V_Y-V_Y^0\right)}^2+ϵ\sum _k\frac{1}{{\left(R_C-R_k\right)}^n}+E_{2D/3D}+E_{\Gamma }.$$ (6)

Here, the first term penalizes deviations from the initial volume of the inner cavity. $V_Y$ is the volume enclosed by the closed surface, $V_Y^0$ is the initial volume, and $B_Y$ is a compression modulus. The second term corresponds to the outer membrane stiffness (16, 18) that runs over all vertices on the outer surface of the shell and restricts the radial motion of vertices within a sphere of radius $R_C$. This sphere is concentric with the homogeneous spherical configuration from which the system is initialized. The center of the initial spherical configuration acts as a reference center to calculate the radial distance of the vertices. The term $R_k$ denotes the radial distance of the vertex k, and hence $R_k-R_C$ represents the membrane thickness near that vertex. The value ε is a membrane stiffness parameter, and n is the exponent of the repulsive potential term that models the effects of the outer stiff membrane.

Numerical methods

To find an equilibrium shape for a typical configuration in the 3D vertex model, we solved the system of nonlinear algebraic equations that correspond to vanishing of the gradient of the energy with respect to node positions by Newton-Raphson iteration. The number of equations was halved for the corresponding configurations in the 2D vertex model. Initial guesses were obtained by direct forward Euler integration following overdamped gradient dynamics. In some cases, rotational and translational symmetries had to be factored out through appropriate pinning conditions, as described in Section S3. Pseudo-arc-length continuation (31, 32) was used to follow solution branches in parameter space and to go around turning points. The eigenvalues of the Jacobian upon convergence quantify the stability of the computed equilibrium shapes. Branches were terminated when equilibrium solutions featured vertices too close to each other (edge length < 0.01). The merging of vertices and the rearrangement of cell neighbors were not considered here. We used the Armadillo, a C++ linear algebra library, to solve the linear systems of equations and calculate leading eigenvalues (33).

Homogeneous configurations and model parameters

In all cases considered below, we start with a system with spatially uniform cell properties at a mechanical equilibrium. This equilibrium configuration is then used as a starting point for numerical continuation that analyzes the effects of spatial patterns of cell properties, with the amplitude of the pattern chosen as continuation parameter. To construct the initial equilibrium states for our model epithelial shells, we analyzed an idealized system sheet with uniform cell properties. For the 2D vertex model, we considered a shell constructed from regular hexagons (Fig. 1 D). For the 3D model, we considered a shell constructed from a lampshade shape with hexagonal apical/basal surfaces (Fig. 1 A). In both these cases, one can analyze the explicit expressions for the overall energy as a function of the geometric and model parameters. The geometric parameter for the 2D model is the edge length of the unit hexagonal cell. For the 3D model, the geometric parameters are the edge length of the hexagonal apical and basal surfaces and the height of the unit cell. The minima of such functions provide a relationship between equilibrium cell shape and tissue properties.

Once the parameters were found for an idealized sheet at an equilibrium, we used DistMesh to realize an epithelial shell with a finite number of cells tiling a closed surface (34). This meshing package builds triangular tessellations on a sphere for the given edge length. As an input geometry for the 2D vertex model, we used these tessellations to construct polygonal cells by considering centers of triangular mesh elements as vertices of epithelial cells. To construct the 3D vertex model input geometry, we first constructed the inner surface of the epithelial shell using the 2D model input geometry approach and then extended the vertices radially to a given height to form 3D cells. This produces a globally curved epithelial shell with a finite number of 3D lampshade-shaped cells, i.e., cells with asymmetric apical and basal surfaces. Further details are provided in Section S6.1.

Results

Three-dimensional vertex model

Three-dimensional vertex models have previously been used to study dynamic tissue morphogenesis for cell aggregates and spatially uniform cell sheets (21, 22, 27). Recently, Hannezo et al. (19) extended a similar framework to model different shapes of epithelial cells. Here, we use a simplified 3D vertex model (Eq. 1), along with the additional term for prepatterns (Eq. 2), to numerically find equilibrium shapes in an epithelial monolayer induced by the in-plane prepatterns of apical contractility. We also analyze the effects of a fluid-filled cavity and an outer membrane (Eq. 6) on out-of-plane deformations induced by such prepatterns. All of these factors are present in different developmental contexts, including Drosophila appendage formation (12, 35) and the blastula-to-gastrula transition in different species (6, 7, 10, 18, 36, 37).

To understand the effect of model parameters on cell morphology and to provide good initial guesses for the numerical calculation of equilibrium shapes, we calculated equilibrium shapes for flat as well as curved homogeneous epithelial monolayers. The analysis was performed for ideal cases where apical and basal surfaces were approximated as hexagons. For the 3D vertex model with planar cells, increasing the lateral tension coefficient (α) makes the equilibrium cell shape more columnar, whereas increasing the basal tension coefficient (γ) makes the cell more squamous (Fig S4, C and D). We discuss the effects of basal and lateral tension coefficients in greater detail in Section S6.1. We use this information to construct the initial homogeneous configuration (Γ = 0) with given model parameters (see Materials and Methods) and then apply different prepatterns (Γ > 0) and solve for the equilibrium shapes.

We started with a closed shell monolayer of 3D cells, which had polarity similar to the cells in the follicular epithelium in the developing Drosophila egg, where the apical side forms the inner surface of the epithelium (apical-in case, Fig. S1 D (8)). Consistent with recent observations (38), we kept the value of the cell-volume compression modulus B large, to make sure that the deviation from the initial cytoplasmic volume of each cell was small. We then introduced spatial patterns of apical contractility. We considered two prepatterns of apical constriction in different settings: (I) an embedded contractile ring (Fig. 2 A1) and (II) a patch of apically constricting cells (Fig. 2 B1). As mentioned before, the first prepattern is motivated by the study of Drosophila appendage formation (8). The second prepattern is found in diverse developmental settings in which a group of cells undergoes apical constriction driving localized tissue bending (2, 25, 26).

We found one continuous branch of stable equilibria in which the epithelium bent in the basal direction (evagination) for both apical contractility prepatterns (Fig. 2, A4 and B4). Due to cytoplasmic incompressibility, a patch of cells undergoing apical constriction leads to the expansion of the basal surface and thus causes the sheet to bend in the apical-to-basal direction. Inclusion of an outer membrane term kept the configuration more spherical (Fig. S8), and increasing the inner-fluid compression modulus (B_Y) decreased deflection without affecting the qualitative nature of the equilibrium shapes (Fig. S9).

We then considered a scenario in which the apical side forms the outer surface of the shell (apical-out case, Fig. S1 C) by reversing the polarity and keeping the energy formulation the same. A similar scenario is observed during the blastula-to-gastrula transition in many species, such as sea urchin (24) and Drosophila (37). We introduced similar prepatterns of apical contractility as before (Fig. 3, A1 and B1) and found one continuous branch of stable steady states for the case of a patch of apically constricting cells in which the epithelial shell formed an invagination (Fig. 3 B4). However, in the case of prepatterning with a contractile ring, we observed bistability in the shapes of shells (Fig. 3 A4). This shape bistability was not present in configurations with smaller shell curvature (Fig. S12) or with a one-cell-wide ring (Fig. S11). We also considered a prepattern of line tension in the form of a two-cell-wide ring of apically constricting cells, which was inspired by the pattern of actomyosin localization during primary invagination in the sea urchin embryo (24, 39). Here, as well, we found one continuous branch of stable invaginated shapes (Fig. 3 C4).

To summarize, in response to most of the analyzed patterns of apical contractility, the 3D model predicts a smooth transition to the evaginated state when the apical surface forms the inner surface and to the invaginated states when the apical surface forms the outer surface of the shell.

Naturally planar 2D vertex model

Naturally planar 2D vertex models provide a computationally simpler framework to model epithelial deformations, while still incorporating the essential physical features of the apical surface of the epithelium that drive such transformations. In this section we determine what aspects of the 3D model can be captured with a naturally planar 2D vertex model. We use the model presented by Murisic et al. (30) as our starting point. This model can be viewed as a special case of the 2D model introduced here (h = 0; $k_{j^{\prime }}=0$).

Similar to our analysis of the model with 3D cells, we examined the case of a closed shell with different prepatterns of apical cell contractility. In contrast to the 3D model, the naturally planar model showed no out-of-plane deformations for a constricting patch prepattern. However, for a contractile ring, we found two disconnected branches of steady-state solutions (Fig. 4). Equilibrium shapes with cells deflecting outward (the evaginated state) formed a continuous branch of steady states from an initially homogeneous configuration, whereas solutions with cells deflecting inward (the invaginated state) formed a disconnected branch (Fig. 4 E).

This steady-state diagram can be traced back to the pitchfork bifurcation observed by Murisic et al. (30) in the presence of contour forces for flat configurations. However, the pitchfork bifurcation here is imperfect, as the sheet curvature breaks the symmetry present in the flat configuration case (Fig. S5). We observed that the turning point of the branch of invaginated states shifts to the right as the curvature of the initial homogeneous configuration is increased. This is consistent with the past analysis of buckling in Elastica (a thin strip of elastic material) with imperfections, such as preferred curvature or misaligned axial load (40, 41, 42).

The presence of an outer membrane term tends to keep the configuration more spherical (Fig. S6, A and B). As expected, increasing the inner-fluid compression modulus $\left({\beta }_Y\right)$ and bending elasticity coefficient (β) made it more difficult to bend the epithelium. It decreased the deflection of evaginated shapes for a given value of $\Gamma$ and shifted the limit point to the right (Fig. S6, D and E). We observed similar imperfect pitchfork bifurcations for different stretching moduli μ.

In sum, we observed a typical imperfect pitchfork bifurcation for the closed shell configuration. The addition of an inner fluid-filled cavity and outer membrane term does not affect the qualitative response of the naturally planar 2D vertex model, influencing only the domain of shape bistability. The results of the naturally planar 2D vertex model suggest that the initially curved and homogeneous epithelium can smoothly bend, due to contour forces, only in the outward direction, which is similar to the response of the apical-in case of the 3D model to a contractile ring. Thus, this model does not capture all of the effects predicted by the 3D model, particularly the deformations driven by an apically constricting patch.

2D vertex model

As noted above, the naturally planar 2D vertex model cannot capture different aspects of the 3D model, including apicobasal polarity, natural curvature of the sheet, and a smooth transition from homogeneous configuration to invaginated states in the presence of an apical constriction pattern. Here we show that the 2D model with natural curvature, as introduced in Eqs. 3–5, is fully consistent with the 3D model responses to different prepatterns, while maintaining the simpler framework of the 2D model. The model includes additional terms making the sheet naturally curved and incorporates apicobasal polarity by offsetting the prepatterns away from the sheet’s midsurface such that they lie on the apical side of the shell.

Similar to previous sections, we considered two prepatterns of apical contractility: a contractile ring (Fig. 5 A1) and a constricting patch (Fig. 5 B1), now offset from the 2D sheet. We started with a homogeneous closed shell configuration at equilibrium, for which we set the value of $k_{j^{\prime }}$ equal to the average angle between the normals of the adjacent cells (see Section S2.1 for details). We then introduced the prepatterns of constriction in two settings corresponding to apical-in (h < 0) and apical-out (h > 0) cases (note that we defined the cell normals in both cases such that they always point outwards with respect to the shell). For the apical-in case, we found that each prepattern produces a continuous branch of equilibrium shapes as we increased Γ in which the epithelium bent in the outward direction (the evaginated state) (Fig. 5, A3 and B3). For the apical-out case, the constricting patch prepattern produces one continuous branch of equilibrium shapes with the epithelium bending in the inward direction (the invaginated state; Fig. 6 B3). However, we observed bistability in the shapes of shells in the case of the contractile ring prepattern (Fig. 6 A3). Increasing the inner-fluid compression modulus $\left(B_Y\right)$ decreased deflection without affecting the qualitative nature of the steady-state diagram (Fig. S10). Thus, the results obtained with the 2D vertex model are qualitatively similar to results from the 3D vertex model, suggesting that the additional terms can effectively capture the features of the complete 3D description of the epithelial sheet and its responses to different patterns of apical cell contractility.

Figure 6.

3D deformations induced by prepatterns of line tension in a model with 2D cells for the apical-out case; see text for details. (A1 and B1) Initial configurations with different heterogeneities: (A1) contractile ring; (B1) constricting patch. (A2 and B2) Representative invaginated states. (A3 and B3) Steady-state diagrams showing deflection δ with increasing parameter Γ. (Solid lines) Stable states; (dashed lines) unstable steady states. Schematic cross sections of representative steady states (A1, B1, A2, and B2) are shown as insets. Parameter values are listed in Table S4. To see this figure in color, go online.

Discussion

We used vertex models to explore how the spatial patterns of cell contractility lead to 3D deformations of epithelial shells. Previous studies of such deformations used appropriately modified elastic shell theories to make connections between biophysical descriptions of epithelia and a large body of tools and ideas from continuum mechanics (15, 17, 43, 44). Although these studies can mimic a number of canonical processes, including vertebrate neurulation, they are difficult to adapt to different biological systems, such as morphogenesis driven by cell rearrangements, directed migration, or cell proliferation (36). Furthermore, the spatial patterns of apical contractility that drive 3D epithelial deformations are commonly fine-grained. For instance, the early stages of sea urchin gastrulation are triggered by a contractile ring that is only two cells wide (24). These observations provide a clear motivation for models that can resolve individual cells.

A number of cell-based models, similar to the vertex models used in our work, have been used to describe deformations in 2D cross-sections of epithelial tissues (6, 7, 29, 30). The most extensive work has been done to model the formation of the ventral furrow in the early Drosophila embryo (10, 37). We extended these models to three dimensions, making it possible to investigate deformations induced by a broader class of spatial patterns of apical contractility. Our results can be summarized as follows: Model epithelia constructed from 3D cells, with distinct apical and basal properties, can readily generate both invaginated and evaginated shapes. The direction of bending is dictated by the apicobasal orientation of the epithelium: cells with increased apical contractility bend out of the sheet in the apical-to-basal direction. In contrast, naturally planar 2D vertex models predict that two different equilibrium shapes (invaginated and evaginated) coexist for the same set of parameters. The invaginated state exists as an isolated branch, which cannot be reached by continuous changes in the parameters of the spatial prepatterns; this is in contrast to the predictions of the 3D model. It also lacks the ability to include the apicobasal polarity or the natural curvature of the epithelial monolayer.

To address these issues, we proposed a modified 2D vertex model that better accounts for the 3D nature of the epithelium. This was accomplished by incorporating additional terms into the energy function. These terms effectively offset contractile patterns from the sheet and include the natural curvature of the epithelium. The modified model can readily capture the full effects of the 3D model. Most importantly, it can generate both evaginated and invaginated shapes depending on the apicobasal polarity of the epithelial shell. This suggests that the modified 2D vertex model can be used to describe shape transformations in a broader class of systems, especially those in which 3D deformations are driven by asymmetric apical contractility patterns, while maintaining the computational simplicity of the 2D framework. In our current work, we are using these models to explore shape transformations that include cell rearrangements and directed cell migration.

Author Contributions

M.M., B.A., I.G.K., and S.Y.S. designed the research; M.M. performed the research; and M.M., B.A., I.G.K., and S.Y.S. wrote the article.

Editor: Leah Edelstein-Keshet.