Density-Dependent Differentiation of Bacteria in Spatially Structured Open Systems

Abstract

Bacterial quorum sensing is usually studied in well-mixed populations residing within closed systems. The latter do not exchange mass with their surroundings; however, in their natural environment, such as the rhizosphere, bacteria live in spatially structured open systems. Here, we tested the hypothesis that trapping of bacteria within microscopic pockets of an open system triggers density-dependent differentiation. We designed a microfluidic device that trapped swimming bacteria within microscopic compartments. The geometry of the traps controlled their diffusive coupling to fluid flow that played a dual role as nutrient source and autoinducer sink. Bacillus subtilis differentiates into a state of competence in response to quorum sensing and nutrient limitation. Using a mutant strain with a high differentiation rate and fluorescent reporters for competence, we found that the cell density required for differentiation was 100-fold higher than that required in closed systems. A direct comparison of strongly and moderately coupled reservoirs showed that strong coupling supported early differentiation but required a higher number of bacteria for its initiation. Weak coupling resulted in retardation of growth and differentiation. We conclude that spatial heterogeneity can promote density-dependent differentiation in open systems, and propose that the minimal quorum is determined by diffusive coupling to the environment through a trade-off between retaining autoinducers and accessing nutrients.

Introduction

Bacteria can detect the presence of other bacteria by secreting and detecting small molecules. Once the concentration of these small molecules, called autoinducers, exceeds a threshold, bacteria change their gene-expression pattern. Various evolutionary benefits of autoinducer sensing have been proposed. A widely accepted idea holds that bacteria use quorum sensing (1) to check whether the population is large enough for a specific group behavior to be beneficial. This idea neglects the fact that bacteria in their environment usually reside within open systems where the autoinducers are transported away from their source by diffusion or other mechanisms of transport. For this reason, a different function of autoinducer production, namely, diffusion sensing, was proposed. The idea is that bacteria produce small molecules (at low cost) to sample for diffusive transport (2). When the local concentration of autoinducers exceeds a threshold concentration, it is beneficial for the bacterium to produce and secrete molecules that are associated with a high cost. It has been demonstrated experimentally that individual cells can secrete enough autoinducers to trigger the quorum response (3, 4). The efficiency sensing theory combines both functions, taking spatial structures of the environment into account (5). Spatial structures are important for diffusive transport in the natural environment of bacteria. For example, bacteria residing within the rhizosphere are likely to accumulate within microscopic grooves, depressions, or pockets. Quorum and efficiency sensing in structured environments are poorly characterized.

Bacillus subtilis is a gram-positive bacterial species that employs quorum sensing and nutrient limitation to control cellular differentiation (6). In particular, differentiation into a state of competence for transformation is mediated by multiple cellular factors that report cellular crowding, in particular cell density and nutrient limitation (7). At the center of the regulatory network is ComK, a master regulator for the proteins required for transformation. Through a nonlinear autocatalytic feedback, comK expression reveals switch-like behavior (8, 9). Noise in the expression level of comK in conjunction with temporal regulation of basal ComK levels generates bimodal behavior, i.e., within a population of cells only a fraction will differentiate into a state of competence (10, 11, 12, 13, 14). Deletion of rok, a repressor of comK, leads to nearly all cells of the population differentiating into a state of competence (14). The major autoinducer that affects comK expression is a peptide called ComX (15). At sufficiently high extracellular concentrations, ComX activates a two-component system that increases the basal ComK concentration. Another autoinducer, competence-stimulating factor (CSF), or PhrC, stimulates competence at low concentrations and inhibits competence at high concentrations (16). Furthermore, expression of comK is fine-tuned by multiple Rap proteins and their cognate Phr peptides (17). Moreover, GTP acts as a nutritional signal for competence development (18). So far, competence development has been investigated using well-mixed bacteria growing in closed containers. However, both the autoinducers and the nutrients are subject to diffusion, and it is tempting to speculate that spatial structures affect the differentiation dynamics.

Soft lithography and related microfluidic techniques have been used recently to study the influence of local geometries on bacterial behavior (19, 20). At the single-cell level, engineered microscopic landscapes have been used to control the motility of crawling (21, 22) and swimming bacteria (23). The use of heart-shaped microfluidic channels has been explored for sorting Escherichia coli cells with respect to their length (24), trapping bacteria, and generating rotation of microscopic objects (25). Furthermore, microfabricated ratchet structures have been used as concentrator arrays for studying cell-to-cell communication (26, 27).

Microstructures have been designed for studying quorum sensing. By generating small isolated volumes within nanostructured droplets, researchers showed that a single cell was able to trigger quorum sensing (3, 4). Various experiments systematically addressed the spatial range over which quorum signals could be detected (28, 29, 30, 31). In particular, within biofilms, gradients of autoinducers were formed that were detected as far as 8 mm away from the producer. In a different approach, traps were generated that were permeable for small molecules but prevented bacteria from leaving (32). These experiments, together with a set of experiments that examined quorum sensing in microcolonies (33), demonstrated that quorum sensing is dependent not only on cell density but also on the flow conditions.

Here, we addressed the question of whether local trapping of bacteria within an open (microfluidic) system initiates quorum-sensing responses. We investigated whether the differentiation dynamics differs from that of well-mixed populations in closed environments. To this end, we designed a microfluidic device that allowed gradual diffusional decoupling of the traps from fluid flow carrying a high concentration of nutrients and low concentration of autoinducers. We estimated diffusional coupling using finite-element analysis and visualized differentiation using a fluorescence reporter of the master regulator of competence, comK. We found that motile B. subtilis were efficiently trapped. Within traps, B. subtilis differentiated into a state of competence. The timing and average number of cells required for a half-maximal response were dependent on the diffusional coupling strength between the trap and the reservoir. We conclude that local trapping of motile bacteria in structured environments promotes density-dependent differentiation. In our experimental system, the local concentration of bacteria had to exceed the concentration in closed systems by orders of magnitude.

Materials and Methods

Bacterial strains and preculture growth conditions

The B. subtilis strain Bs076 (his leu met, rok::kan, P_comKgfp) was derived from strain BD630. The rok gene was deleted by insertion of an antibiotic resistance cassette (V01547 from Enterococcus faecalis) that confers resistance against kanamycin. The strain was transformed with chromosomal DNA of BD2711 (8), introducing the reporter for comK expression. Cells were pregrown in LB medium overnight at 37°C and 200 rpm in a shaking flask, and subsequently diluted in liquid competence medium (34) supplemented with glucose (0.5%), L-histidine, L-leucine, L-methionine (50 μg/mL) at 37°C and 200 rpm in a shaking flask, and grown from OD₆₀₀ 0.08 to a mid-exponential phase OD₆₀₀ of 0.24. Before they were inserted into the microstructures, the cells were diluted to OD₆₀₀ 0.001 in fresh competence medium.

We note that the timing of competence initiation was subject to day-to-day variation because it was dependent of the age of the preculture. Since the process of assembling the flow chamber was time consuming, the age of the preculture varied by ∼1 h. Since the side channels with strong and medium coupling emanated from the same main channel, all experiments performed with these structures were directly comparable in terms of timing of competence initiation. Accordingly, all examples shown in Figs. 4, a and b, 5, a and b, 6, a and b, and 7, b and c, were acquired from the same flow chamber. The side channel with the weakly coupled trap extended from a different side channel on the silicon master, and the respective experiments were performed on different days.

Figure 4.

Dynamics of growth and differentiation within traps. (a–c) Time-lapse image of competence development using a P_comKgfp reporter in traps with (a) strong, (b) medium, and (c) weak coupling. Brightfield and fluorescence images were merged. Since the cells were not fixed, time elapsed between acquisitions of the brightfield and fluorescence images, and therefore the overlap is not always perfect. To see this figure in color, go online.

Figure 5.

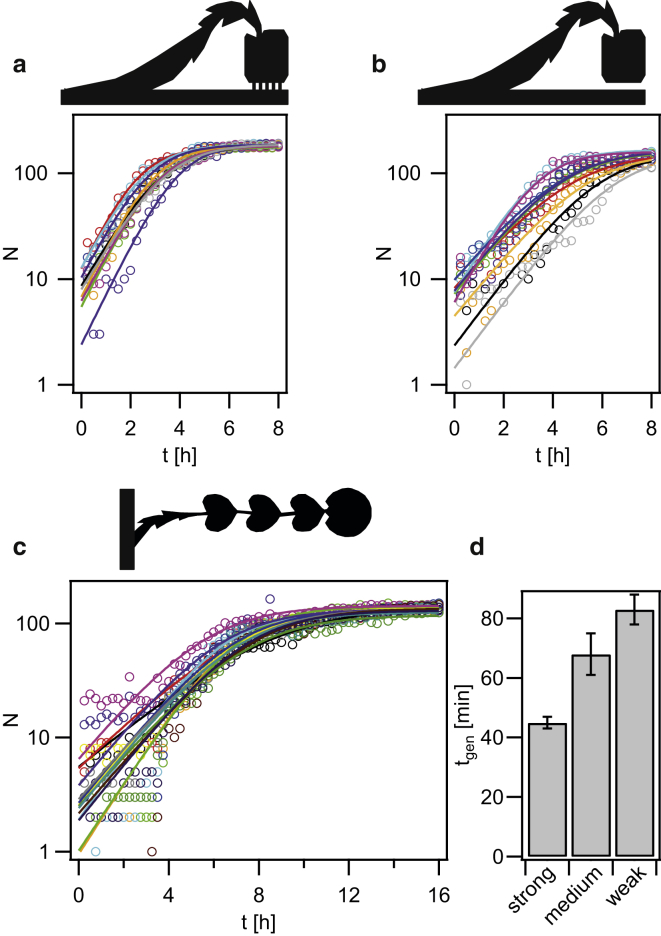
Growth dynamics within traps. (a–c) Number of cells within a single trap as a function of time for (a) strong, (b) medium, and (c) weak coupling. Each line depicts a single trap. The full lines are fits to the logistic function. (d) Generation times determined from the fits in (a–c). Error bars: standard error for 18–35 traps for each condition. To see this figure in color, go online.

Figure 6.

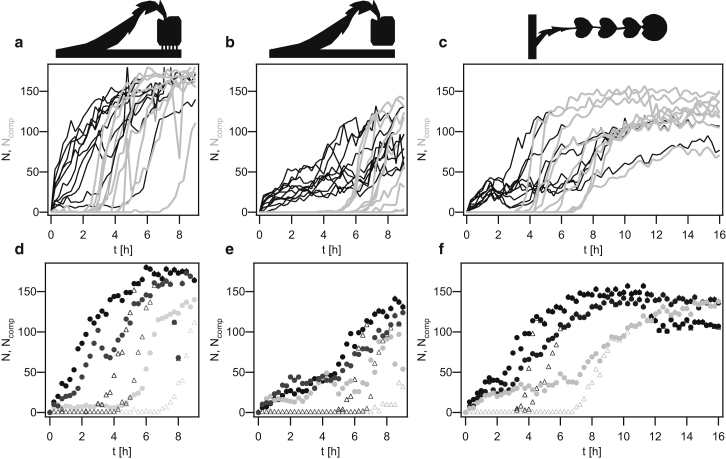
(a–c) Differentiation dynamics within traps, showing (a) strong, (b) medium, and (c) weak coupling. Each line depicts the cell number N (black) and number of competent cells N_comp (gray) within a single trap as a function of time. (d–f) Selected examples (from a–c) of growth and competence development for (d) strong, (e) medium, and (f) weak coupling. Equal grayscales depict the same trap. Solid circles: number of cells within one trap, N; open triangles: number of competent cells within the respective trap, N_comp.

Figure 7.

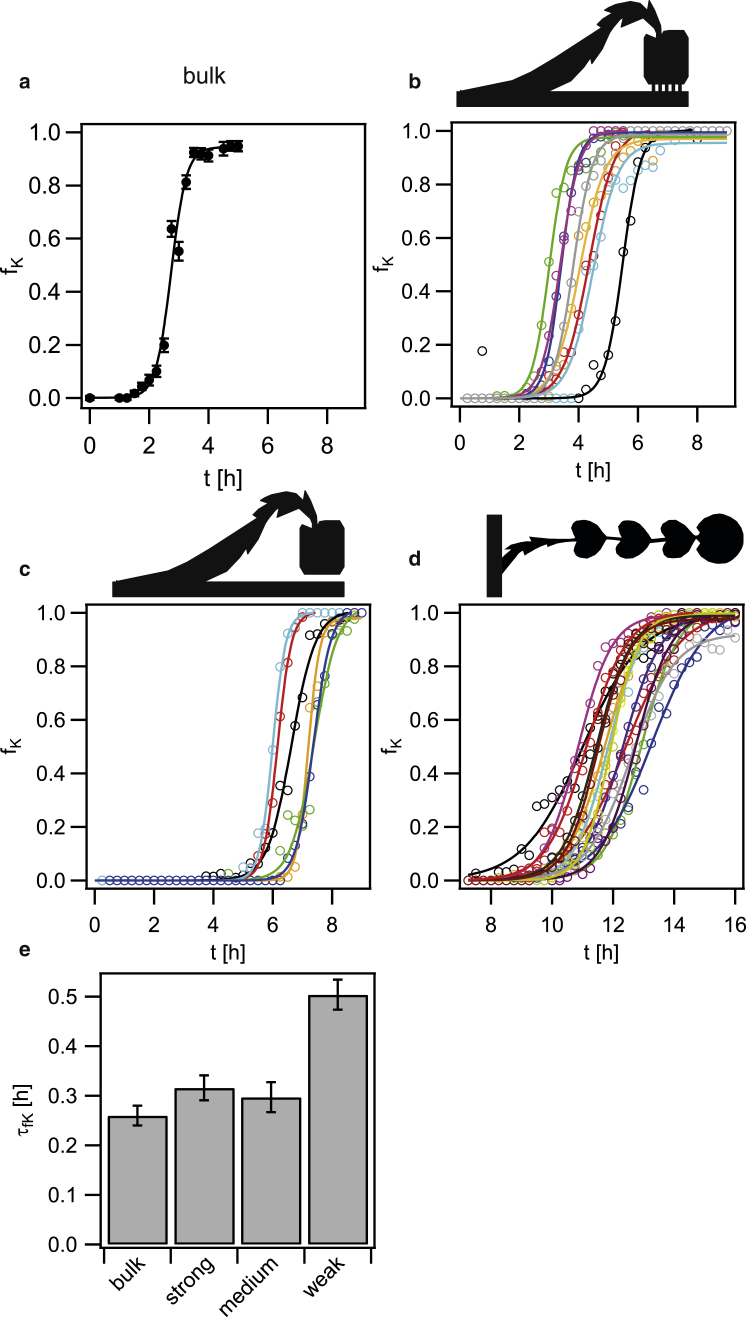
The differentiation dynamics is slower in weakly coupled traps. (a–d) The fractions of competent cells as a function f_K of time were determined in a shaking flask (a) and within strongly (b), medium (c), and weakly (d) coupled traps as a function of time. The data in (a) were adapted from (12). In (b–d), the line depicts a single trap. The full lines are fits to a sigmoidal equation. (e) Average characteristic time of the sigmoidal fits. The error bars depict standard errors over >100 cells for the bulk condition and 14–35 traps for each condition within the flow chambers. To see this figure in color, go online.

Microfabrication and assembly of the microfluidic device

The microstructures were generated by soft lithography (35) using a custom design for the photo mask. The masks were fabricated by Deltamask (Twente, The Netherlands). The masks were designed to have a main channel and more than 20 side channels of different design branching off (Fig. 1). This design allowed simultaneous monitoring of differentiation dynamics within multiple traps. We designed a teflon mount for the microscope that allowed direct casting of polydimethylsiloxane (PDMS; Sylgard 184, Dow Corning, Auburn MI; 1:10) onto the wafer (Fig. S1 a in the Supporting Material). The PDMS was cured at 60°C for at least 12 h. The depth of the channels was 2.5 μm, which chosen to allow bacterial swimming while enabling detection and analysis of individual cells. The depth of the main channel and the feeding channel was manually increased to 200 μm. Subsequently, the PDMS structure was sealed with a cover slide (28 × 32 mm²; Roth) by oxygen plasma treatment for 20 min and then incubation at 80°C for 20 min. The flow cells were stored for at least 48 h at room temperature before usage.

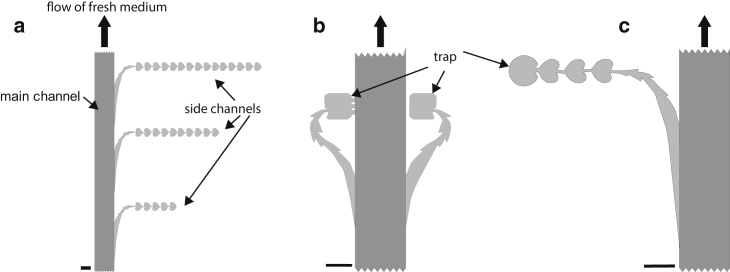
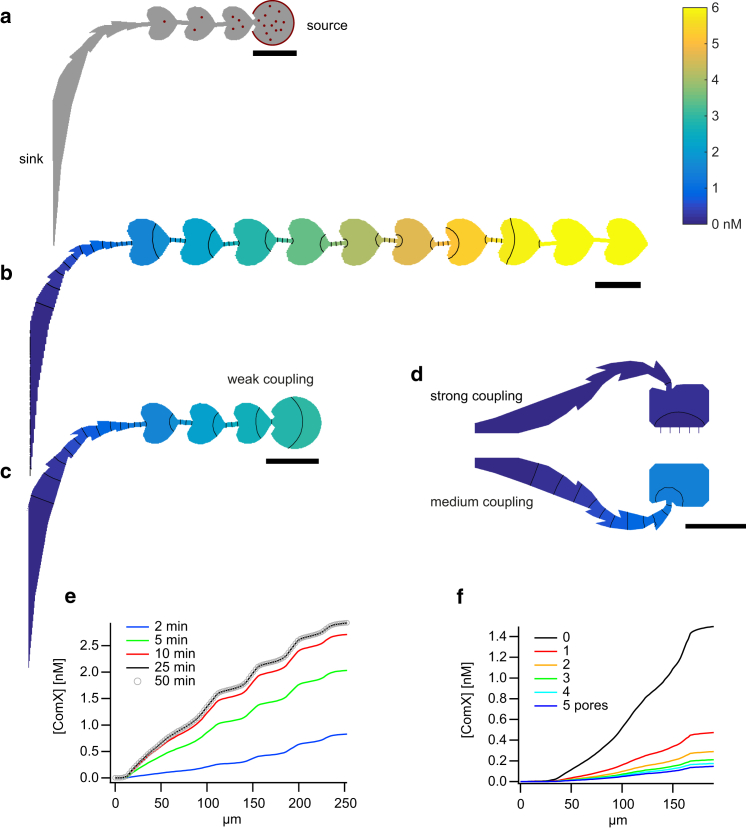
Figure 1.

Scheme of the microfluidic setup, depicting the side-channel designs. Fresh medium is continuously supplied through the main channel (depth 200 μm). The arrows denote the flow direction during image acquisition. The side channels (depth 2.5 μm) ratchet motile bacteria into the traps formed by the dead ends of the channel. (a–c) Side-channel geometry with (a) very weak diffusive coupling, (b) strong (left) and medium (right) coupling, and (c) weak coupling. Scale bars, 50 μm.

Before each experiment, cleaned tubing (Carl Roth, Karlsruhe, Germany; 9554.1 with an inner diameter of 0.5 mm) was connected to the flow cell. Subsequently, the flow cell was mounted onto the microscope and flushed with competence medium containing 0.8% bovine serum albumin. The outlet was closed for 5–30 s to avoid formation of air bubbles. The bacteria were supplied at OD₆₀₀ 0.001 in 1 μL fresh competence medium through the main channel (Fig. S1 b). To avoid contamination of the feeding channel, medium flow was applied during the filling process using a syringe pump (Legato 111; KD Scientific, Holliston, MA). During this process the main channel was monitored using microscopy. Once cells were detected, the inlet was sealed and bacteria were able to swim into the side channels during a period of 1–5 min. Once enough bacteria had settled within the side channels, the flow direction within the main channel was reversed by closing the former outlet of the main channel (Fig. S1 b). The former inlet of the main channel served as outlet during the experiment (Fig. S1 b). A constant flow rate of 250 nL/s was maintained throughout the experiment. With an effective volume of the main channel of ∼500 nL, the high flow rate ensured that the entire volume was replaced every 2 s. Although bacteria that remained within the flow channel were transported out of the channel at a high rate, it was unavoidable that eventually bacteria stuck to the walls of the channel. Therefore, after ∼5 h, bacteria were sometimes observed within the main channel. The high flow rate ensured that the autoinducers produced by these bacteria were rapidly transported out of the channel. Therefore, they did not affect quorum sensing within the side channels.

Microscopy

We acquired images using an inverted fluorescence microscope with a 100× objective (Eclipse-Ti; Nikon, Düsseldorf, Germany). We used an automatic stage to screen an area of ∼3 mm² containing the main channel and up to multiple side channels. Brightfield and fluorescence images were acquired at Δt = 15 min time intervals. The Perfect Focus System (Nikon) ensured that the sample remained in focus for up to 16 h. We corrected for a shift in the x-y plane using a MATLAB (The MathWorks, Natick, MA) routine based on a cross-correlation algorithm. Fluctuations in the brightfield illumination were homogenized by normalizing the total brightfield image intensities to the initial image.

Image processing and cell detection

To determine the total number of cells within a trap, we wrote a cell-detection routine using MATLAB. The cell-detection algorithm used the brightfield images. In the first step, it was essential to distinguish between changes in intensity arising from the side channels from signals associated with bacteria. To this end, we aligned a mask of the side channel with each image, excluding the pronounced signal by the PDMS structure. The reference image acquired at t = 0 was smoothed with a 3 pixel (312 nm) Gaussian kernel, reducing background fluctuations. This reference image was used as a background image and subtracted from each image acquired at later time points, eliminating the signal associated with the PDMS structures. Subsequently, a Laplace filter was applied to enhance the contrast of the cellular contours and a threshold was used for cell detection. Local maxima were generated via a distance transformation, and a watershed algorithm was applied to distinguish cells. Detected patches >0.5 μm² were registered. Potential adjacent cells whose centers of mass were <2 μm apart were discarded provided that their image contrast was comparable, since the brightfield illumination pattern of a cell was sometimes registered as well. As the height of the side channels is 2.5 μm, theoretically, multiple layers of cells can form. The algorithm worked most reliably up to a cell count of N = 180 cells within the trap with an area of 1800 μm². Furthermore, B. subtilis forms filaments during exponential growth. We note that the total number of cells determined by the algorithm is associated with a large error at high cell densities. However, we applied the cell-detection routine using the same parameters for all routines, and therefore the results are comparable. The carrying capacity per trap determined from the logistic fits in Fig. 5 is likely to be biased by the detection limit of the algorithm. The important parameter of this fit is the growth rate, and we verified the latter by considering growth during the exponential phase only. Finally, for comparison with the predicted number of cells necessary for initiation of the quorum response (Fig. 3), the relevant number of cells is <100.

Figure 3.

Finite-element simulation of ComX diffusion in side channels. (a) Boundary conditions of the simulation. The source of ComX is located at the circumferences of the traps (red). The main channel is modeled as a perfect sink for ComX. (b–d) Simulated steady-state concentration profiles of the ComX concentration, assuming a constant cell number of N = 50 for different geometries of the side channels. (e) Concentration profile along a polygon running through the center of the side channel shown in (c). Different colors correspond to different time points after the start of ComX production. (f) Steady-state ComX concentration profiles running along a polygon through centers of the side channels shown in (d). Different colors correspond to different numbers of pores connecting the trap to the main channel. Scale bars, 50 μm. To see this figure in color, go online.

Characterization of differentiation dynamics

The bacteria expressed gfp under the control of the promoter of the master regulator of competence, comK (P_comKgfp). The transition from a vegetative to a competent state shows switch-like behavior whereby the fluorescence intensity of individual cells increases to saturating levels within ∼1.5 h (14). We monitored competence development by acquiring fluorescence images every 10–15 min. Under the experimental conditions found in a shaking flask, nearly all Δrok cells switch eventually, but they do not switch simultaneously. To count the number of competent cells, we determined a threshold fluorescence intensity beyond which cells are considered competent. This threshold was chosen to exceed the basal level of fluorescence (in the undifferentiated state) threefold.

Simulation of [ComX] gradients

We used MATLAB routines to perform a finite-element simulation of the concentration gradient of a molecule within the side channels. The simulated output was the local concentration of ComX, c(x,y,t), for a constant number of cells, N. The diffusion equation

$$\frac{\partial c\left(x,y,t\right)}{\partial t}-D\Delta c\left(x,y,t\right)=0$$

was solved in two dimensions. We estimated a diffusion constant of D_ComX = 2.9 × 10⁴ μm²/min using the Stokes-Einstein formula with a radius of ComX of r = 0.7 nm.

To account for the geometric boundary conditions, polygons were generated directly from the design files of the silicon master of the flow chamber. Apart from the source and sink, reflecting boundary conditions were used. The polygon boundary of the trap (see Fig. 3 a) represented the source with an influx g. The influx g was determined by the average production rate of ComX. This value has not been measured directly, and we used an estimated value of $g={10}^{-21}molecel{l}^{-1}{h}^{-1}$ (36). The production rate was consistent with an estimate obtained using the concentration of half-maximal activity, and the fact that switching typically begins at approximately T₀ (15, 36, 37). We assume that the production rate increases linearly with the number of cells in a trap. The outlets of the side channels into the main channel were modeled as perfect sinks with an absorbing boundary condition.

Results

Design of the microfluidic device for varying diffusional coupling strength

Our goal was to elucidate the effect of microscopic structures on bacterial differentiation dynamics. In particular, we hypothesized that quorum sensing is affected by microscopic dead ends that capture motile bacteria. To address this issue, we designed a microfluidic device in which fresh medium was continuously supplied through a main channel (Fig. 1). From this main channel, multiple side channels branched off. The main channel had a depth of ∼200 μm to ensure a continuous supply of nutrients. Moreover, the main channel served as a sink for autoinducers. The flow rate within the main channel was adjusted to 250 nL/s, ensuring that the total fluid was replaced every 2 s. The side channels had a depth of 2.5 μm to enable image analysis at the single-cell level. We designed the side channels as ratchets for motile bacteria with a dead end in which bacteria accumulated. Henceforth, these dead ends will be called traps. By varying the geometry of the side channels, we intended to vary the diffusive coupling strength of the bacteria trapped in the trap to the main channel. We expected that with decreasing coupling, autoinducers produced by the bacteria would accumulate and nutrients would be depleted. This approach allowed us to correlate the coupling strength with the dynamics of B. subtilis differentiating into a state of competence. The latter is triggered by a combination of autoinducer accumulation and nutrient depletion (6).

Motile B. subtilis are efficiently trapped at the dead ends of the side channels

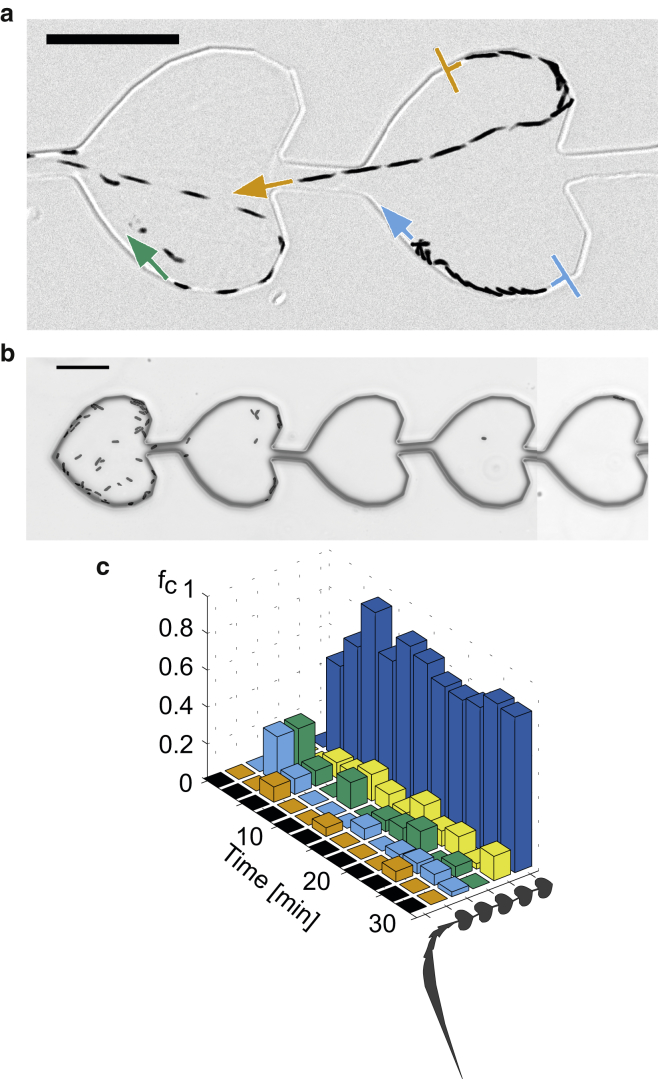
It was previously demonstrated for E. coli that heart-like structures are efficient for ratcheting swimming bacteria (24). We verified that this method worked well for B. subtilis. Within the side channels, individual cells swam preferentially along the walls (Fig. 2 a). We measured the probability of leaving the heart-shaped chamber at both openings. The probability of leaving the heart-shaped chamber at the tip (left side of Fig. 2 a) was p = 0.84 ± 0.04 (N = 700). After several minutes, a gradient of cell density formed along the side channel (Fig. 2 b). The fraction of cells in the most distant heart-shaped chamber remained constant at 80% after 5 min of exposure (Fig. 2 c). Importantly, the number of nonmotile cells that entered the side channels was negligible. Thus, swimming motility is a prerequisite for the experiments performed in this study. We conclude that our microfluidic device works well for ratcheting motile B. subtilis.

Figure 2.

Trapping efficiency for motile bacteria. Motile bacteria were applied to the main channel. A time-lapse image of the side channels was recorded. (a) Overlay of multiple time points of brightfield images. Bacteria are shown in black. Blunt arrows denote the start of the trajectories and pointed arrows denote the direction of swimming. Total time, 2.5 s; scale bar, 25 μm. (b) Typical image of a side channel after 20 min. (c) Spatiotemporal dynamics of the concentration gradient of swimming bacteria. f_c denotes the fraction of bacteria residing within the heart-shaped chamber shown on the right side of the graph. To see this figure in color, go online.

Simulation of diffusive coupling strength

We intended to test the hypothesis that local confinement of B. subtilis triggers a quorum-sensing response, inducing competence for transformation. We assume that each bacterium within the trap produces autoinducers at a constant rate. In a classic experiment, namely, bacteria growing within a closed shaking flask, autoinducers accumulate continuously and eventually the concentration of autoinducers is high enough to trigger quorum-dependent gene expression. Here, the bacteria are confined to a space (the trap) that is coupled to a reservoir containing fresh medium without autoinducers through diffusion. We hypothesize that a given number of cells will produce a steady-state concentration of autoinducers within the trap, and that the number of cells required for quorum depends on the strength of diffusional coupling.

To quantify the strength of diffusional coupling, we performed finite-element simulations of the diffusion of a small molecule the size of ComX. ComX is the most important autoinducer that triggers differentiation in the state of competence. Since bacteria accumulate efficiently within the trap, we assume an autoinducer source located at the circumference of the trap (Fig. 3 a). The main channel is modeled as a perfect sink for the autoinducer. We assume that the production rate increases linearly with the number of cells within the trap N. The volumes of the traps are ∼4.5 × 10³ μm³. The volume of B. subtilis is 0.3 μm³. Further below, we will show that the relevant number of cells per trap is on the order of N = 100. Therefore, the volume reduction of a trap through the bacteria should be negligible. Although swimming motility was important for entering the side channel and reaching the trap, the bacteria settled down within the trap (Movies S1, S2, and S3). Therefore, flow generated by bacteria swimming within a trap was neglected in the simulation. We estimate a diffusion constant for ComK of D_ComK ≈ 4.5 × 10⁴ μm² min⁻¹. Furthermore, we assume that the estimated rate of ComX production is k = 167 nM cell⁻¹ min⁻¹ or k’ = 10⁻²¹ mole cell⁻¹ h^{− 1} (36). Using the geometry of the side channels as boundaries, we simulated the concentration profile of ComX within side channel of different geometries. In the following text, the steady-state concentration of ComX in the trap will be used as a measure for the diffusive coupling strength between the trap and the main channel. The higher the steady-state concentration within the trap, the lower is the coupling strength (Fig. 3). Nutrients are depleted by bacteria within the traps and are resupplied through diffusion from the main channel. Thus, it is reasonable to assume that the nutrient concentrations within the side channels form gradients with inverted sign.

The ComX concentrations along four different side channels were simulated for N = 50 bacteria residing within the trap (Fig. 3). The concentration of ComX decreased with the distance from the source of autoinducer production. For the side channel consisting of 10 heart-shaped chambers, the concentration in the most distal heart-shaped chamber containing the source was [ComX] ≈ 6 nM (Fig. 3 a). The concentration jumped to lower values for each heart-shaped chamber that was located closer to the main channel. For the side channel with three heart-shaped chambers connected to a distal circle (trap), the simulation predicts [ComX] ≈ 3 nM within the trap (Fig. 3 b). For this structure, the steady-state concentration profile was reached within 25 min (Fig. 3 e), i.e., on a timescale well below the generation time within this structure (see Fig. 5 d). The geometries in Fig. 3 d were designed to trap bacteria while maintaining strong coupling to the main channel. Fig. 3 d shows the steady-state concentration profiles of traps whose coupling strength was determined through both the side channel and pores that connect the trap directly to the main channel containing nutrient-rich, autoinducer-poor medium. Since we observed that bacteria were able to elongate from the trap into the pores, we expect that not all pores were open throughout the experiment. To account for this effect, we determined the concentration for variable numbers of pores (Fig. 3 f). The steady-state concentrations increased from [ComX] ≈ 0.15 nM for five pores to [ComX] ≈ 1.5 nM for zero pores. Importantly, even for a single pore, the steady-state ComX concentration was reduced threefold compared with the trap without pores. The steady-state concentration profiles were reached within 10 min and 2 min for the structures with zero and five pores, respectively. Owing to the different steady-state concentrations within the traps, the side channel shown in Fig. 3 c will be called the weakly coupled trap, and traps with and without pores will be characterized by strong and medium coupling strengths (Fig. 3 d), respectively. The volumes of the three traps are comparable, with V ≈ 4500 μm³.

With purified ComX autoinducer, the half-maximal response has been determined at [ComX] ≈ 3 nM (15). We therefore predict that the number of cells necessary for differentiation in the strongly coupled traps is on the order of hundreds of cells. Moreover, we predict that fewer cells are required for differentiation within the traps with medium and weak coupling.

Dynamics of growth within traps

Next, we monitored the growth dynamics in the four different traps shown in Fig. 3 (Fig. 4). Cells were injected into the main channel (Fig. S1; Materials and Methods). The density of bacteria within the side channels was monitored using time-lapse microscopy. Once each side channel contained between 1 and 30 cells, the flux within the main channel was reversed (Fig. S1).

We found that the growth rate decreased with decreasing diffusive coupling to the main channel (Figs. 4 and 5). To quantify the number of cells within the traps as a function of time, we detected individual cells as described in the Materials and Methods section. The maximum number of cells per trap that the algorithm could resolve was N ≈ 180.

The growth curves within single traps were consistent with a sigmoidal behavior, as expected for an exponentially growing population with a limited carrying capacity K (Fig. 5, a–c). To obtain the generation times, we fitted the solution of the logistic equation, $N\left(t\right)=K{N}_0{e}^{rt}/\left(K+N_0\left(e^{rt}-1\right)\right)$, where r is the growth rate and N₀ is the initial number of bacteria within the trap. Within the strongly coupled traps, the average generation time was t_gen^strong = (45 ± 2) min. When only the exponential part of the curves was considered, the resulting generation time was comparable, t′_gen^strong = (44 ± 4) min, indicating that the detection limit of N ≈ 180 did not affect the measurement of the generation time. The generation time agrees with the generation time of an exponentially growing shaking culture of t_gen = 45 min, indicating that growth was not inhibited within the strongly coupled trap. The average generation time was lower in the traps with medium coupling, t_gen^medium = (68 ± 7) min. Although the values are variable in this geometry, the difference from the strongly coupled traps is statistically significant. Within the weakly coupled traps, the generation time was t_gen^weak = (83 ± 5) min. Within the long side channels containing 10 or more heart-shaped chambers (Fig. 3 b), no growth was observed, and therefore this geometry is not considered in the following text.

We note that the initial numbers of bacteria were different for each trap. Due to exponential growth during the first hours of the experiment, the time points at which the half-maximal cell number was observed were highly variable. This effect was observed for multiple side channels emanating from the same main channel within the same flow chamber (Fig. 5). The spread was even more pronounced when the results of different experiments (each using a different cast of the flow chamber) were compared. Therefore, Figs. 5, a–c, 6, and 7, a and b, show data from single experiments. Each of these data sets is representative of multiple experiments. All statistically analyzed data (containing error bars) are average numbers over multiple experiments. We note that the generation times are independent of N₀ and thus are reproducible between different experiments and flow chambers.

We conclude that each local subpopulation localized within a trap shows logistic growth. The growth rate decreases with decreasing diffusive coupling to the nutrient-rich main channel.

Dynamics of differentiation within traps

To monitor differentiation into the competent state, we used the strain P_comKgfp Δrok, which expressed gfp under the control of the comK promoter. This strain was used as a reporter for switching to a state of competence at the single-cell level. To increase the probability of switching, we used a strain in which the major repressor of comK, rok, was deleted. The comK expression dynamics of the Δrok strain is qualitatively similar to that of the wild-type (12, 14). The major quantitative difference is a higher expression rate of comK in the Δrok strain. As a consequence, nearly all cells switch to a state of competence, a property that simplifies the analysis of switching. The half-maximal fraction of competent cells is reached only slightly earlier (relative to entry into the stationary phase) for the Δrok cells (12). This suggests that the population densities that trigger differentiation into a state of competence are similar.

Bacteria were able to differentiate into a state of competence within the traps (Fig. 4). The subpopulations residing within the traps were transiently bimodal in terms of fluorescence intensity. This transient bimodality occurred in all traps but at different time points, most likely because the initial number of cells was not strictly controlled. In Fig. 4 a, the first differentiated cells (showing strongly elevated levels of fluorescence intensity) were detected at t = 4.5 h (Movie S1). The number of competent cells increased as a function of time. After several hours, cells occurred sometimes within the main channel. It is important to note that cells residing within the main channel did not show the fluorescence signal associated with differentiation into the competent state. The only exceptions were competent cells that grew from the trap through the pores into the main channel (Fig. 4 a, 6.25 h). Within the traps that contained no pores to the main channel, the onset of competence development tended to occur at later time points compared with the strongly coupled trap (Fig. 4, b and c; Movies S2 and S3). We note that this counterintuitive result can be explained by different growth rates and will be addressed in more detail in Fig. 8. Most importantly, bacteria within the traps of varying coupling strength differentiated, whereas bacteria in the main channel did not, indicating that local trapping was necessary for competence development.

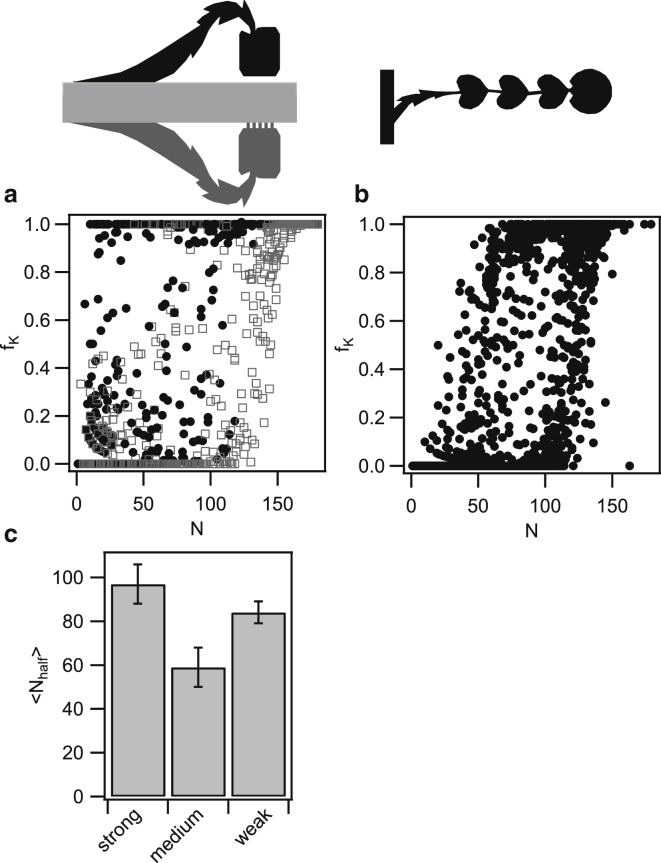
Figure 8.

Correlation between the fraction of competent cells and the total number of cells within trap. (a) Fraction of competent cells f_k versus total number of cells N per trap. The data were collected from traps with strong (gray) and medium (black) coupling branching off the same main channel. (b) Fraction of competent cells f_k versus total number of cells N per trap for weak coupling. (c) Average number of cells per trap at half-maximal competence <N_half>. Error bars: standard error of 18–35 traps for each condition.

To quantify the number of competent cells at each point in time, we measured the fluorescence intensities of individual cells. During competence development, the fluorescence intensity of individual cells increases during ∼1.4 h (14). Therefore, we set a fluorescence intensity threshold to determine whether cells were counted as competent (see Materials and Methods). The number of competent cells as a function of time showed sigmoidal behavior (Fig. 6). The midpoints of the sigmoid curves were shifted to later time points as compared with the growth curves (Fig. 6, a–c). Traps that started with a high number of cells and subsequently reached the carrying capacity early on also showed an early onset of competence differentiation (Fig. 6, d–f).

Next, we assessed how the diffusive coupling strength between the main channel and the traps affected the dynamics of differentiation. Previously, we showed that in a shaking flask the fraction of competent cells as a function of time, $f_K\left(t\right)=f_K^{max}/\left(1+e^{-\left(t-T\right)/\tau }\right)$ (where $f_K^{max}$ is the saturating fraction of competent cells, T is the time at $1/2f_K^{max}$, and τ is the characteristic time) had a sigmoidal shape (12). The characteristic time was τ = (0.26 ± 0.02) h (Fig. 7 a). In other words, between f_K(t) = 0.5 and f_K(t) = 0.73, the elapsed time was ∼15 min. We found that within individual traps, the function f_K(t) was also sigmoidal (Fig. 7, b–d). Interestingly, the characteristic times for cells residing within the traps with strong and medium coupling were comparable to the characteristic time in the bulk experiments (Fig. 7 e). For the weakly coupled trap, the characteristic switching time was significantly higher (Fig. 7 e), i.e., the differentiation dynamics was slowed down. For all experiments, the saturating fractions of competent cells were $f_K^{max}\approx 1$. Nearly all cells eventually switched to a state of competence.

We conclude that spatial trapping of motile B. subtilis triggers differentiation into a state of competence. The differentiation dynamics in traps with strong and medium diffusive coupling is comparable to the results obtained with a shaking flask in which autoinducers accumulated continuously. Within the weakly coupled traps, the switching dynamics is slowed down.

The number of cells required for half-maximal differentiation depends on the diffusive coupling strength

The fact that the midpoints of the growth curves and the switching curves are correlated in time for individual traps (Fig. 6, d and e) suggests that a minimal number of cells are necessary to initiate the differentiation dynamics. Furthermore, the simulations of ComX concentrations predict that the number of cells required for competence differentiation will decrease with decreasing diffusive coupling (Fig. 3).

We assessed these hypotheses by plotting the fraction of competent cells f_K versus the total number of cells N (Fig. 8, a and b). We found that f_K(N) increased as a function of N. Even though the data show considerable scatter, Fig. 8 a shows that on average, more cells are necessary to elicit the half-maximal fraction of competent cells within the strongly coupled traps compared with traps with medium coupling. Since both side channels with medium and strong coupling emanate from the same main channel, this difference is independent of day-to-day variance. Using sigmoidal fits to individual traps (Fig. S2), we determined the average number of cells required to elicit the half-maximal fraction of competent cells, N_half (Fig. 8 d). An average number of N_half^medium = (59 ± 9) cells agrees well with the prediction that the steady-state concentration is [ComX] = 1.8 nM (Fig. 3, d and f) and that the ComX concentration required for half-maximal response is [ComX] = 3 nM (15). The average number of N_half^strong = (97 ± 9) cells was higher for the strongly coupled traps than for the traps with medium coupling strength. This result is again qualitatively consistent with our preditionspredictions based on simulations of the ComX concentration (Fig. 3, d and f). Quantitatively, the value of N_half^strong was expected to be higher. For the weakly coupled traps, we found an average number of N_half^weak = (84 ± 5) cells. Our simulations predict a steady-state [ComX] = 5 nM for 84 cells (Fig. 3, c and e). This number is again close to [ComX] = 3 nM (15). However, we predicted that the number of cells required to elicit the half-maximal fraction of competent cells would be lower in the weakly coupled trap than in the trap with medium coupling. The latter prediction was not confirmed by the experiment.

In summary, we found that the number of cells required to elicit differentiation within the weakly and medium coupled traps agrees remarkably well with the value predicted by the simulation of the ComX concentration profile within the trap. Contrary to the prediction by the same model, we found that the number of cells required for half-maximal differentiation was lowest within the traps of medium coupling strength.

Discussion

Relation among the differentiation dynamics, growth dynamics, and quorum

In this study, we tested the hypothesis that the efficiency of quorum sensing correlates with diffusional coupling to a reservoir that acts as a sink for autoinducers. Finite-element simulations predicted the steady-state concentrations of a small, diffusible molecule the size of the autoinducer ComX for the different geometries of the side channels. The simulations made qualitative predictions about the relative strengths of diffusive coupling of the different traps to the reservoir and quantitative predictions about the total number of cells required for a half-maximal response. The production rate of ComX assumed in our simulations is a very rough estimate (36) and has not been measured so far. Apart from ComX, other secreted peptides act as autoinducers. Multiple Phr peptides (including PhrC, PhrF, and PhrH) affect competence development in a concentration-dependent manner (38, 39, 40). Since the latter are similar in size to ComX and are likely to be produced at a similar rate (36), it is reasonable to assume that they form similar concentration gradients. The half-maximal response of competence development in bulk experiments was observed at a concentration of [ComX] = 3 nM (15). In the experiment, we found that ∼60 cells elicited the half-maximal response (Fig. 8). Our simulations predict that the steady-state concentration within the trap is [ComX] = 1.8 nM. Taking the uncertainties of the production rates into account, this result agrees remarkably well with the predictions.

As predicted, the number of cells required for the half-maximal response was lower in the strongly coupled traps than in the traps with medium coupling. However, quantitatively, our simulations predict a steady-state concentration of only [ComX] = 0.3 nM within the strongly coupled trap containing ∼100 cells. This value is lower by an order of magnitude than the expected value of [ComX] = 3 nM (15). Most likely, bacteria clogging the pores affect the exchange rate of ComX between the trap and the reservoir.

Unexpectedly, the weakly coupled traps required a higher number of cells for a half-maximal response than the traps with medium coupling. Concomitantly, the population dynamics of differentiation was slowed down. When the fraction of competent cells was measured as a function of time, the differentiation rates within the traps with strong and medium coupling were comparable to the rate in the bulk experiment (12). However, the rate in the weakly coupled trap was lower, suggesting interference with competence development. Moreover, growth was inhibited within the weakly coupled traps. It is reasonable to assume that the reduced diffusive flux also reduces the rate at which nutrients are replenished and that a gradient of nutrients forms within the side channels. Our observation that the growth rate was reduced is in agreement with growth-limiting nutrient concentrations within the traps. Since the competence medium is a rich and chemically undefined medium, it is impossible to predict the concentration profile of the growth-limiting component. However, the trend of the growth rate is unambiguous: within the strongly coupled traps the growth rate agrees with the bulk conditions, the growth rate decreases with decreased diffusive coupling of the traps (Figs. 3 and 5), and growth is prohibited within very weakly coupled traps (Fig. 3 b). One possible explanation for the high quorum in weakly coupled traps could be a reduced rate of autoinducer secretion in slowly growing cells.

Taken together, we propose that an optimum diffusive coupling strength exists. At this optimum strength, the quorum is at its minimum. This optimum most likely results from a trade-off between retaining autoinducers and replenishing nutrients.

Quorum, diffusion, and efficiency sensing

Initially, the term “quorum sensing” was proposed to describe the “minimum behavioral unit as a quorum of bacteria” required to elicit a transcriptional response of the population (1). The function of quorum sensing is to check whether the population is large enough for a specific group behavior to be beneficial. The method of secreting autoinducers and measuring their concentration works well when the population is confined to a defined volume and well mixed. This setup corresponds to standard laboratory conditions. However, in their natural environment, such as the rhizosphere in the case of B. subtilis, bacteria reside within open systems that contain sinks for autoinducers. Therefore, the mass transfer of autoinducers caused by diffusion and convection has to be taken into account. For this reason, a different function of autoinducer production, namely, diffusion sensing, was proposed. The idea is that bacteria produce small molecules (at low cost) to sample for mass transport (2). When the local concentration of autoinducers exceeds a threshold concentration, it is beneficial for the bacterium to produce and secrete molecules that are associated with a high cost. In this case, an individual bacterium would profit from the production of autoinducers. The efficiency sensing theory combines both functions, taking spatial structures of the environment into account (5).

In this study, we have demonstrated that spatial structures severely affect density-dependent differentiation. It is interesting to compare the cell densities that are required for triggering differentiation. Competence classically develops in the stationary growth phase, where the shaking flask contains a cell density of $\left[cells\right]\approx 2\cdot {10}^{8}cellsm{l}^{-1}$. Within the traps, the density is higher by 2 orders of magnitude, with $\left[cells\right]\approx 2\cdot {10}^{10}cellsm{l}^{-1}$. This finding demonstrates clearly that diffusive transport of autoinducers increases the quorum, i.e., the density of cells required to produce the threshold concentration of autoinducers. On the other hand, the cell density required for differentiation did not depend as strongly on diffusive coupling as predicted. Clustering of cells may affect the concentration of autoinducer required to elicit the response. If the binding affinity of the cells for the autoinducer was high, free diffusion of autoinducers from the trap to the reservoir was hindered. Along these lines, a recent report demonstrated that rationally designed polymers were able to control quorum sensing in Vibrio harveyi by forming cellular clusters and sequestering the autoinducer molecules (41).

Conclusions

We have shown that local trapping of bacteria enables density-dependent differentiation in an open system, enabling mass transport. The quorum within the diffusively coupled traps is higher by 2 orders of magnitude than in closed systems. Within closed systems, the conditions vary as a function of time, since the concentration of autoinducers increases continuously, and as a consequence density-dependent differentiation can occur only during a temporally limited window of opportunity (10, 12, 42). The system designed here has the potential to permit investigations of quorum sensing under nearly steady-state concentrations of autoinducers.

Author Contributions

Designed research, analyzed data, and wrote the manuscript: J.R. and B.M. Performed research: J.R.

Editor: Zemer Gitai.

Supporting Material

Movie S1. Growth and Differentiation at Strong Diffusive Coupling

Δt = 15 min. Hot orange: fluorescence from P_comKegfp.

Movie S2. Growth and Differentiation at Medium Diffusive Coupling

Δt = 15 min. Hot orange: fluorescence from P_comKegfp.

Movie S3. Growth and Differentiation at Weak Diffusive Coupling

Δt = 15 min. Hot orange: fluorescence from P_comKegfp.