Exploratory Study of 4D Versus 3D Robust Optimization in Intensity-Modulated Proton Therapy for Lung Cancer

Abstract

Background

To compare the impact of uncertainties and interplay effect on 3D and 4D robustly optimized intensity-modulated proton therapy (IMPT) plans for lung cancer in an exploratory methodology study.

Methods

IMPT plans were created for 11 non-randomly selected non-small-cell lung cancer (NSCLC) cases: 3D robustly optimized plans on average CTs with internal gross tumor volume density overridden to irradiate internal target volume, and 4D robustly optimized plans on 4D CTs to irradiate clinical target volume (CTV). Regular fractionation (66 Gy[RBE] in 33 fractions) were considered. In 4D optimization, the CTV of individual phases received non-uniform doses to achieve a uniform cumulative dose. The root-mean-square-dose volume histograms (RVH) measured the sensitivity of the dose to uncertainties, and the areas under the RVH curve (AUCs) were used to evaluate plan robustness. Dose evaluation software modeled time-dependent spot delivery to incorporate interplay effect with randomized starting phases of each field per fraction. Dose-volume histogram indices comparing CTV coverage, homogeneity, and normal tissue sparing were evaluated using Wilcoxon signed-rank test.

Results

4D robust optimization plans led to smaller AUC for CTV (14.26 vs. 18.61 (p=0.001), better CTV coverage (Gy[RBE]) [D_95% CTV: 60.6 vs 55.2 (p=0.001)], and better CTV homogeneity [D_5%–D_95% CTV: 10.3 vs 17.7 (p=0.002)] in the face of uncertainties. With interplay effect considered, 4D robust optimization produced plans with better target coverage [D_95% CTV: 64.5 vs 63.8 (p=0.0068)], comparable target homogeneity, and comparable normal tissue protection. The benefits from 4D robust optimization were most obvious for the 2 typical stage III lung cancer patients.

Conclusions

Our exploratory methodology study showed that, compared to 3D robust optimization, 4D robust optimization produced significantly more robust and interplay-effect-resistant plans for targets with comparable dose distributions for normal tissues. A further study with a larger and more realistic patient population is warranted to generalize the conclusions.

INTRODUCTION

Lung cancer is the leading cause of cancer death. Passive scattering proton therapy (PSPT) has been shown effective for lung cancer treatment (1,2). Recently, scanning beam proton therapy, which uses magnetic steering of a narrow proton beam (beamlet) and modulates the weight of individual beamlets (intensity-modulated proton therapy [IMPT]), has been shown to outperform intensity-modulated x-ray therapy (IMRT) and PSPT (3–5).

The presence of heterogeneous tissue in lung cancer makes IMPT especially vulnerable to patient setup and range uncertainties (uncertainties) (6). Although robust optimization has been found to be effective to make IMPT more resilient in the face of uncertainties (5,7–13), the existence of the respiratory motion in lung cancer may lead to range mismatch and may make 3D robust optimization less effective in mitigating the impact of uncertainties (14). A 4D robust optimization method is needed to further reduce the impact of uncertainties in IMPT to treat lung cancer.

Unfortunately, in addition to the uncertainties in lung cancer, the interference between dynamic beamlet delivery and intrafractional respiratory motion (interplay effect) may severely degrade the quality of the resulting dose distribution (15–26). Therefore, it is also essential to minimize this effect to take full advantage of IMPT to treat lung cancer. Many approaches have been proposed to mitigate this effect, including range-adapted internal target volume (ITV) (27–29), breath hold, gating, tumor tracking, and 4D treatment planning. Previous studies (15,19,21,22,24,25) on interplay effect in IMPT were limited by the use of IMPT plans derived by 3D planning without robust optimization. Liu et al. (14) studied the influence of respiratory motion on the 3D robustly optimized IMPT plans to treat lung cancer. They found that 3D robust optimization can partially account for respiratory motion (14).

4D treatment planning has been proposed in photon therapy for years (30–46). Only a few studies in 4D optimization have been published in particle therapy (47–50). In the aforementioned literature, phase-specific plans, or the so-called 4D raster treatment plans (RST) (51), which describe which beam spots are to be delivered to which motion phase, are generated. For this approach to be effective, perfect synchronization between the spot delivery and the 4DRST is needed. This is expensive and difficult to implement clinically. A 4D optimization strategy without the need of synchronization is desired, even though it may not be the optimal solution for all patients. Graeff (47) has proposed one method without the need for synchronization in 4D treatment planning for particle therapy. Unfortunately, the plan robustness was not considered.

Both uncertainties and interplay effect may lead to geometric misses of the target, thereby leading to local disease recurrence. In this exploratory methodology study we aimed to combine both robust optimization and 4D treatment planning to implement a 4D robust optimization method without the requirement of perfect synchronization. A single, non–phase-specific plan was constructed for all 4D motion phases. We hypothesize that this new 4D robust optimization method will make the target dose distribution more resilient to uncertainties and simultaneously mitigate the target underdosage resulting from interplay effect in IMPT for lung cancer. We found that the target coverage was significantly better for 4D robust optimization compared to 3D robust optimization.

METHODS AND MATERIALS

Patient Data and Treatment Planning

We retrospectively evaluated treatment plans for 11 non–small cell lung cancer (NSCLC) patients who had been treated at XXXX and re-planned them for IMPT using 3D and 4D robust optimizations. The spot sizes (σ) in air at the isocenter were 6–14 mm, depending on energy. The patients were not randomly selected according to the true patient population statistics, but rather were selected to represent varying tumor stages, tumor volumes, and respiratory motion patterns (Table 1) to see the performance of our method in extreme cases. Regular fractionation scheme was used (i.e., 66 Gy[RBE] were delivered in 33 fractions). 3D and 4D robustly optimized plans for each fractionation scheme were created for each patient with identical dosimetric goals using our in-house developed treatment planning system (10). The number of spots and their positions before optimization were the same for both 3D and 4D robust optimization.

Table 1.

Tumor Location, Stage, CTV Volume (TV), and Respiratory Motion Amplitude (RMA)

Patient	Tumor Location	Tumor Stage	TV (cm3)	RMA (mm)
1	Right upper	III	103.77	4.9
2	Right upper	II	219.12	8.2
3	Right	III	565.97	4.0
4	Right lower	III	747.16	15.0
5	Left lower	III	666.09	8.5
6	Right hilar	III	312.93	13.0
7	Left upper	III	334.51	6.0
8	Right upper	III	484.94	2.0
9	Right middle	III	1247.96	3.0
10	Right upper	IV	396.57	3.5
11	Left upper	III	556.32	5.0

TV: clinical target volume; RMA: respiratory motion amplitude

Modeling of Range and Patient Setup Uncertainty

The interfractional patient setup uncertainties were simulated by shifting the isocenter of the patient in the antero-posterior (A-P), superior-inferior (S-I), and right-left (R-L) directions by 5 mm, yielding 6 dose distributions and the corresponding “influence matrices” (i.e., beamlet dose distributions per unit intensity). Range uncertainties were simulated by scaling the stopping power ratios by ±3.5% (52, 53) to generate 2 additional dose distributions and influence matrices corresponding to minimum and maximum proton ranges, respectively. The total number of uncertainty scenarios was 9 and indicated by a superscript m. Both 3D and 4D robust optimization explicitly accounted for range and patient setup uncertainties in optimization algorithms.

3D Robust Optimization

Our 3D robust optimization approach for lung cancer treatment is based on PSPT planning for lung cancer (54). In PSPT planning for lung cancer, internal gross target volume (IGTV) is formed to encompass the extent of gross target volume (GTV) motion in all phases using 4D computed tomograms (CTs), and an internal target volume (ITV) is formed by expansion of IGTV by a margin of 8 mm (14). In 3D robust optimization we generated plans on average CTs with IGTV density overridden (54) and the delivery of prescribed dose to ITV. We derived the worst-case dose distribution by choosing the smallest dose among the nine doses (8 perturbed dose distributions plus the nominal dose distribution) for each voxel in the ITV and the largest dose for each voxel outside the ITV (55). The resulting worst-case dose distribution was then used in 3D robust optimization. Our approach used the voxel-based worst-case method and differed from the objective wise and composite worst-case methods discussed in Fredriksson and Bokrantz (56). For a comprehensive description of 3D robust optimization, we refer to Liu et al. (14).

4D Robust Optimization

The 4D robust optimization plans were constructed by optimizing the clinical target volume (CTV) dose on all phases of the 4D-CTs. The CTV was generated in each breathing phase by expanding the GTV by an 8-mm margin.

We considered the dose distribution, $D_{i_k}^m={\sum }_{j}I{M}_{i_k,j}^m{\omega }_j^2$, where ${\omega }_j^2$ represented intensity weight of beamlet j. The influence matrix $I{M}_{i_k,j}^m$ described the contribution of beamlet j in breathing phase k to voxel i_k in uncertainty scenario m, where i_k was the corresponding voxel on the phase k 4D-CT of the voxel i on the reference CT (the end-expiration phase). Therefore, $I{M}_{i_k,j}^m$ modeled the target motion and dynamically changing ranges in different uncertainty scenarios by relating each voxel to its corresponding voxel in the reference breathing phase (57). Then, the accumulated doses $\langle D_i^m\rangle$ with the mth uncertainty scenario were summed onto the reference phase averaged by the number of phases (i.e., $\langle D_i^m\rangle ={\sum }_k{D}_{i_k}^m/10$). This assumes that the patient spends equal time in all 10 breathing phases (44). The resulting dose was termed the “accumulated dose” for each uncertainty scenario m thereafter (58). The 4D dose accumulation was carried out using a symmetric force demon registration software (59).

We derived the worst-case dose distribution by choosing the smallest dose among the nine doses (eight perturbed dose distribution plus the nominal dose distribution) for each voxel $({\langle D_i\rangle }_{\mathit{\text{min}}}={\text{min}}_m\langle D_i^m\rangle )$ in the CTV of each phase for 4D robust optimization and the largest dose for each voxel outside the CTV $({\langle D_i\rangle }_{\mathit{\text{max}}}={\text{max}}_m\langle D_i^m\rangle )$ (55). We then used a standard quadratic objective function to design IMPT plans using aforementioned accumulated doses as follows:

$$F^{4D}({\omega }_j)=\sum _{i\in CTV}{p}_{CTV,\mathit{\text{min}}}{({\langle D_i\rangle }_{\mathit{\text{min}}}-D_{0,CTV})}^2+\sum _{i\in CTV}{p}_{CTV,\mathit{\text{max}}}{({\langle D_i\rangle }_{\mathit{\text{max}}}-D_{0,CTV})}^2+\sum _{i\in OARs}{p}_{OARs}H({\langle D_i\rangle }_{\mathit{\text{max}}}-D_{0,OARs}){({\langle D_i\rangle }_{\mathit{\text{max}}}-D_{0,OARs})}^2,$$ (1)

where p denotes the penalty weight of the corresponding term and D₀ denotes the prescribed dose for the corresponding organ. Dose-volume constraints were incorporated in eq. (1) by additional terms not shown here (60).

It is worth noting here that the intensity map ${\omega }_j^2$ does not have a subscript k, unlike the N_jk in eq. 1 of Graeff (47), i.e., the intensity map resulting from this method is not phase specific.

Plan Normalization

The doses of both 3D and 4D robustly optimized plans were recalculated on the averaged CTs with IGTV density override. The resulting dose was termed the “static dose” thereafter (58). In the static dose, the 3D robustly optimized plan was normalized to have the same ITV D_95% (the dose covering 95% of the structure’s volume) as the 4D robustly optimized plan for fair comparison. The static dose for all plans was checked to ensure that the institutional dose-volume constraints were met (Table 2).

Table 2.

Dose Volume Constraints

Critical structure	Dose limits (Gy)
Planning target volume	> 99% volume receiving > 95% of 66 Gy[RBE]
Brachial plexus	Minimum dose to 2 cc highest dose volume < 60 Gy[RBE]
Esophagus	1/3 volume < 65 Gy[RBE]; 2/3 volume < 55 Gy[RBE], as low as reasonably achievable
Liver	Mean dose to liver < 25 Gy[RBE]; 1/3 liver < 35 Gy[RBE]
Total lung	Mean lung dose < 20 Gy[RBE], V20 < 37% of volume; mean lung dose < 22 Gy[RBE] and V20 < 40% are acceptable as minor deviations
Spinal cord	Maximum dose to 2 cc highest dose volume < 50 Gy[RBE]
Heart	1/3 volume < 60 Gy[RBE]; 2/3 volume < 45 Gy[RBE]; mean heart dose < 30 Gy[RBE], as low as reasonably achievable

4D Robustness Quantification

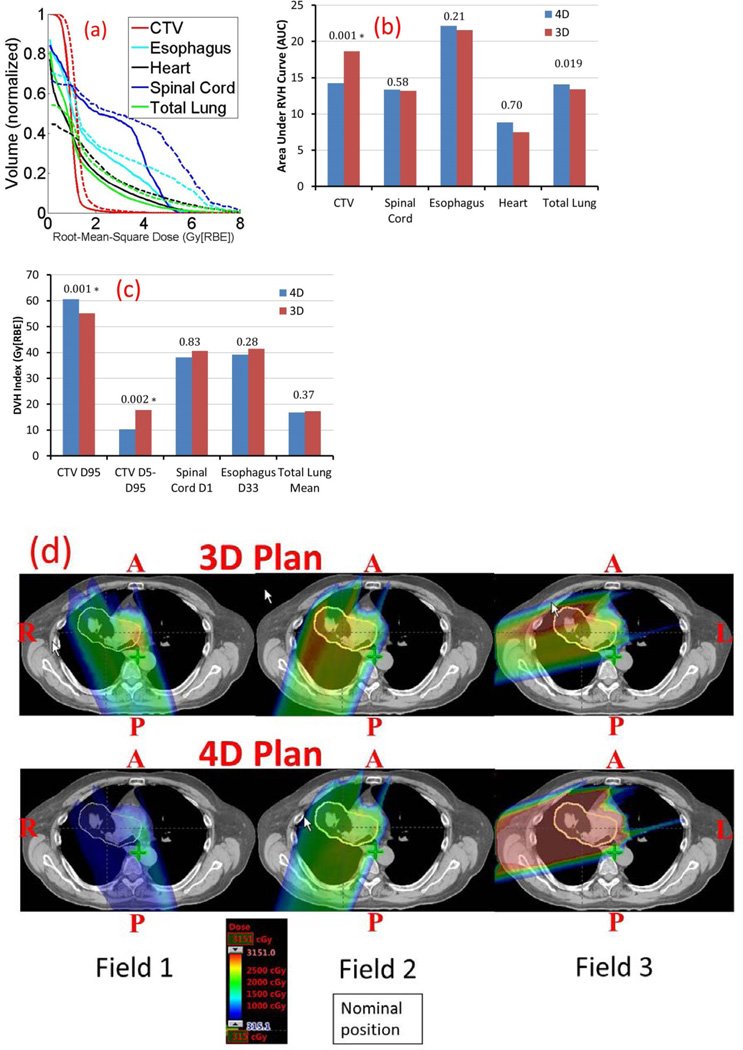
We used root-mean-square dose (RMSD) per voxel as a measure of plan robustness (61, 62). With 21 uncertainty scenarios considered, i.e., for each of nominal, minimum, and maximum proton range, the isocenter of the patient is at the nominal position and rigidly shifted in the A-P, S-I, and R-L directions, respectively, yielding 21 dose distributions (7 per proton range). Then the 21 accumulated doses were used to construct the RMSD-volume histograms (RVH) (Figure 1A). The area under the RVH curve (AUC) gives a numerical index summarizing plan robustness similar to the way that equivalent uniform dose summarizes a dose-volume histogram (DVH): the smaller AUC value indicates better plan robustness.

Figure 1.

A, Comparison of RVHs from 4D (solid) and 3D (dashed) robust optimization; B, comparison of the averaged AUCs of different structures for 11 lung cancer cases; C comparison of the averaged target D_95% and D_5%–D_95% dose, organ sparing in the worst-case scenario. D, Dose distributions per field in the transverse plane for patient 8 illustrate that robust 4D optimization considerably reduces high dose gradients within each of the three fields on the accumulated dose distribution. Blue arrows in some of the panels indicate beam directions. Clinical Target Volume (CTV): yellow.

*p values are statistically significant after Bonferroni correction of 0.05/10 tests = 0.005.

Dose Calculation With Interplay Effect

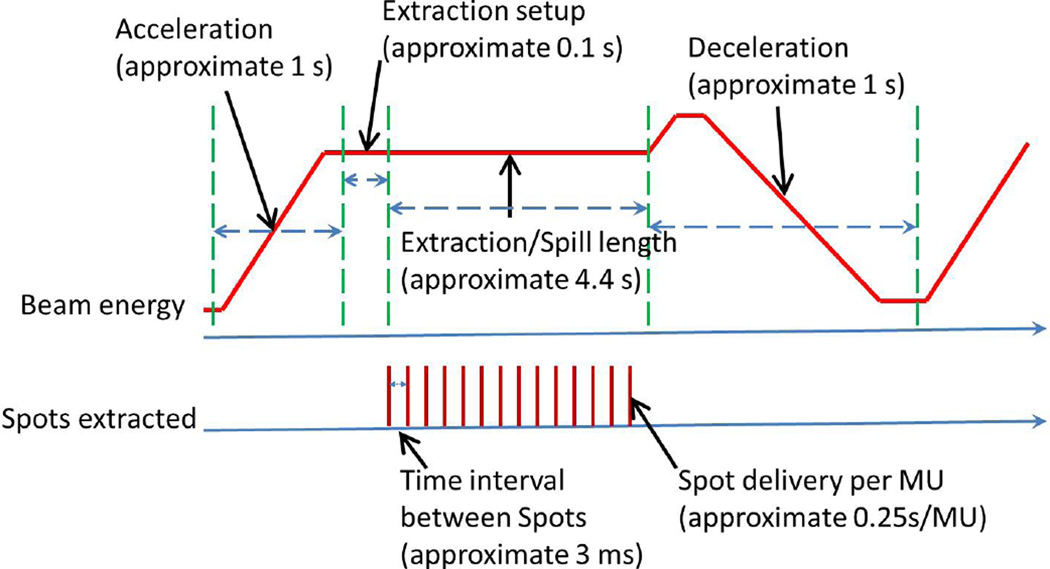
Software was developed to assess a plan’s ability to retain dose volume objectives under the influence of interplay effect following the methods in previous literature (23,51,63). We call a dose calculated with interplay a “dynamic dose” (58). The dose calculation software used proton beam therapy delivery system parameters (Figure 2), 4D-CTs, and the time spent in each respiratory phase acquired from a real-time position management system (Varian Medical System, Palo Alto, CA) during CT simulation (44,64,65) to realistically estimate the dose to a patient with interplay effect. In the dose calculation with interplay effect considered, no uncertainties were considered due to the technical difficulties.

Figure 2.

Beam spot delivery sequence of our machine.

Plan Quality Evaluation

We used the accumulated dose to compare the impact of uncertainties, and the dynamic dose to compare the impact of interplay effect. The conventional DVHs were derived from the above dose distributions.

D_95% and D_5% (the dose covering 5% of the structure’s volume) were derived from the CTV DVH. CTV D_95% and D_5%–D_95% were used to assess CTV dose coverage and homogeneity. The dose covering a percentage of the structure’s volume (D_%) was compared for organs at risk (OARs). We used D_1% dose for the spinal cord and D_33% dose for the esophagus. In addition, we used the mean dose (D_mean) for the total normal lung.

To estimate the treatment outcome, the tumor control probability (TCP) of 2-year local control rate (2y-LC) was calculated as proposed by Willner et al (γ₅₀ = 3.52 and D₅₀ = 74.5) (66).

The starting phase of each field per fraction was randomized to minimize the influence of starting phases. For all patients, 5 runs with randomized starting phases were conducted for both 3D and 4D robustly optimized plan to see the influence of the randomized starting phases for two fractionation schemes (in total, 220 runs). The results of the DVH indices are presented using average values of the corresponding DVH indices (from 5 runs) with error bars. The error bars indicate maximum and minimum values of the corresponding DVH indices from 5 runs.

Statistical Analysis

We performed statistical comparison analyses of the results from 3D and 4D robustly optimized plans. All evaluation metrics were compared with the non-parameter Wilcoxon signed rank test, using JMP Pro 10 software (SAS Institute Inc., Cary, North Carolina). A p value of <0.05 was considered statistically significant. The means of all metrics were also calculated. In post-hoc analysis, the Bonferroni correction was computed in a conservative fashion based on the number of multiple tests conducted.

RESULTS

Study of Impact of Uncertainties Using Accumulated Doses

We discussed the impact of uncertainties using the accumulated doses. The means of the computed AUCs of the targets and OARs for the 11 patients are shown in Figure 1B, with p values shown at the tops of the columns. Compared to 3D robust optimization, 4D robust optimization was significantly less affected by uncertainties for CTV (14.26 vs. 18.63 [p=0.001]) and total lung (14.05 vs. 15.15 [p=0.019]), while the robustness for esophagus (22.15 vs. 24.22 [p=0.21]), heart (8.84 vs. 8.83 [p=0.70]), and spinal cord (13.34 vs. 14.65 [p=0.58]) is comparable.

In the worst-case scenario with uncertainties, compared to 3D robust optimization, 4D robust optimization led to significantly better target dose coverage (unit: Gy[RBE]) [D_95% CTV: 60.64 vs. 55.22 (p=0.001)], significantly better target homogeneity [D_5%–D_95% CTV: 10.29 vs. 17.74 (p=0.002)], and comparable normal tissue protection [D_1% spinal cord: 38.14 vs. 40.56 (p=0.83), D_mean total lung: 16.78 vs. 17.22 (p=0.37), D_33% esophagus: 39.17 vs. 41.42 (p=0.28)] (Figure 1C). This translated to the reduction of TCP of 2y-LC by as much as 5.32% (patients 5 and 6) from 4D to 3D robust optimization.

Figure 1D shows the per-field accumulated dose distributions on an axial CT slice for patient 8, with results from 3D robust optimization at the top and 4D robust optimization at the bottom. This figure illustrates that 4D robust optimization considerably reduced high-dose gradients within each of the three fields on the accumulated dose distribution compared to 3D robust optimization. Interestingly, 4D robust optimization reduced the contributions from Field 1, whose direction mostly was perpendicular to the tumor motion direction, and enhanced the contribution from Field 3, whose direction mostly aligned with the tumor motion direction in the transverse plane. This greatly improved the 4D plan robustness in the face of uncertainties (9,10), and at the same time helped to mitigate interplay effect (see discussion below).

Study of Impact of Interplay Effect Using Dynamic Doses

We found that, given randomized initial phase per field per fraction, all the relevant DVH indices from 5 runs converged with limited differences among different runs. This demonstrated that the influence of initial phase had been sufficiently minimized by the randomization (Figure 3A).

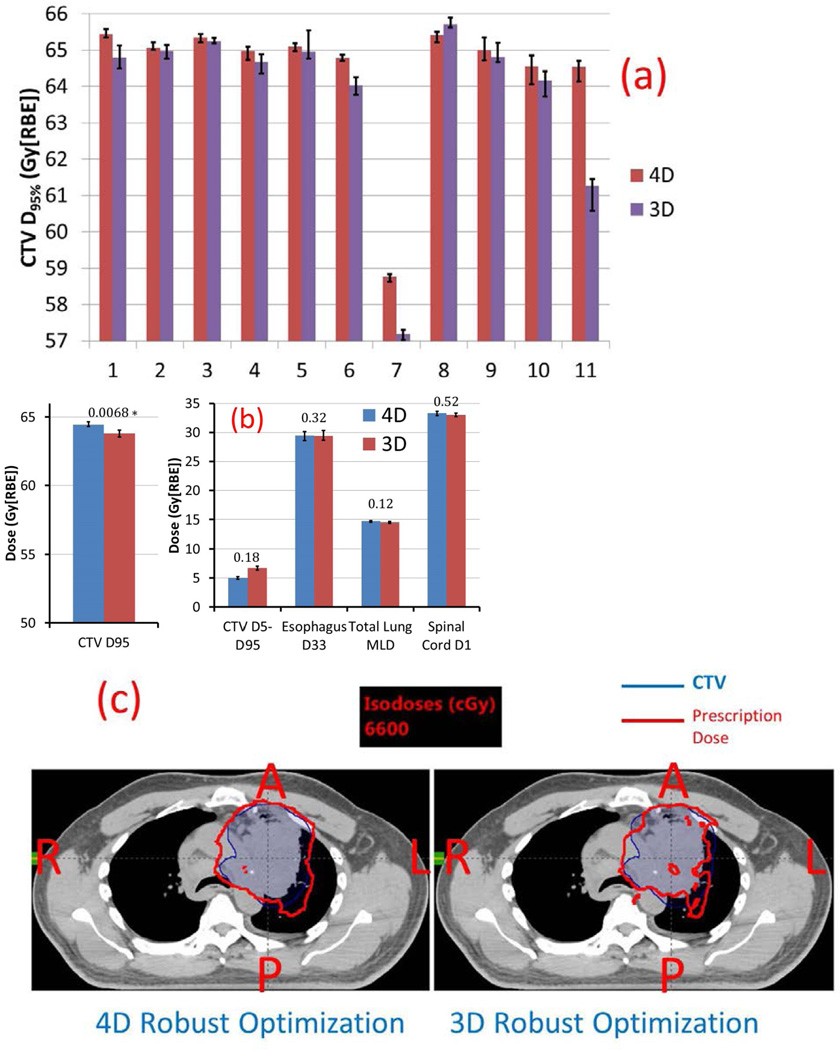
Figure 3.

A, Comparison of 11 patients’ CTV D_95% of the dynamic doses of 4D (red) and 3D (purple) robust optimization. Error bars indicate maximum and minimum values of D_95% among 5 runs. B, Comparison of averaged target D_95%, D_5%–D_95%, spinal cord D_1%, total normal lung mean dose D_mean, and esophagus D_33%. Numbers at the top of the columns are P values. C, Dose distributions in the transverse plane illustrate that the 4D robust optimization plan (left) was less affected for patient 11 by interplay effect than the 3D robust optimization plan (right).

*p values are statistically significant after Bonferroni correction of 0.05/5 tests = 0.01.

Figure 3A shows 11 patients’ CTV D_95% of the dynamic dose distributions (red [4D] and purple [3D]). The target coverage with interplay effects considered was improved for almost all patients (except patient 8). The improvement of the target coverage was the most obvious for patients 7 and 11. Please note that those two patients were actually the typical patients in the true patient population for stage III lung cancer (more discussions in the Discussion section).

4D robust optimization produced plans with significantly better target coverage with interplay effect considered (Figure 3B) (unit: Gy[RBE]) [D_95% CTV: 64.5 vs. 63.8 (p=0.0068)], comparable target homogeneity [D_5%–D_95% CTV: 5.0 vs. 6.7 (p=0.18)], and normal tissue protection [D_1% spinal cord: 29.4 vs. 29.4 (p=0.32), D_mean total lung: 14.7 vs. 14.5 (p=0.12), D_33% esophagus: 33.3 vs. 33.0 (p=0.52)]. This translated to the reduction of TCP of 2y-LC by as much as 5.24% (patient 11) from 4D to 3D robust optimization.

Figure 3C depicts doses in the presence of interplay effect on an axial CT slice for patient 11. Prescription isodose lines (red) in the 3D robustly optimized plan (right) were affected by interplay effect to a greater degree than in the 4D robustly optimized plan (left), leading to more cold spots in the CTV.

Mitigation of Interplay Effect vs. Respiratory Motion Amplitude and Target Volume

There is no obvious relationship between the magnitude of interplay effect and respiratory motion amplitude (RMA) and/or CTV volume (TV) (Table 3). For example, we observed a small impact of interplay effect in patients with small RMA (patient 9) and large RMA (patient 4). We also observed a large impact of interplay effect on patients with small RMA (patient 10) and large RMA (patient 6). And we observed a small impact of interplay effects on patients with small TV (patient 2) and large TV (patient 9). We also observed a large impact of interplay effects on patients with small TV (patient 1) and large TV (patient 11). These findings were consistent with the findings of Kardar et al. (25) and Li et al. (24). Our study confirmed that respiratory motion alone may not be a good measure of interplay effect.

Table 3.

Improvement of Plan Robustness in the Face of Uncertainties and CTV Under-dosage Due to Interplay Effect vs. the Dimensionlessless Ratio of the Cube of Respiratory Motion Amplitude (RMA) Over CTV Volume (TV)

Patients	RMA3/(TV×10−4)	CTV Plan Robustness Improvement (%) (AUC3D−AUC4D)/ AUC3D	Improvement of Mitigation of Interplay Effect on CTV (D95%,4D−D95%, 3D)/ D95%,3D (%)
1	11.34	14.59	1.01
2	25.16	24.75	0.15
3	1.13	4.47	0.15
4	45.17	9.98	0.47
5	9.21	39.57	0.19
6	70.21	17.53	1.19
7	6.46	24.01	2.77
8	0.16	50.62	−0.47
9	0.22	12.20	0.29
10	1.08	26.12	0.59
11	2.25	14.44	5.37

TV: Clinical Target Volume; RMA: respiratory motion amplitude; AUC: Area under RVH curve; RVH: root-mean-square dose volume histogram

However, we found some interesting trends: The effectiveness of 4D robust optimization to mitigate interplay effects compared to 3D robust optimization seemed to be largest for patients 7 and 11, who have the dimensionless ratios defined as the cube of RMA over $\mathrm{T}\mathrm{V}(\frac{RM{A}^3}{TV\times {10}^{-4}})$ to be 6.46 and 2.25, respectively. Other patients either have a ratio below 2 or above 7 (Table 3).

DISCUSSION

The present analysis of this exploratory methodology study with non-randomly selected patients reveals that 4D robust optimization significantly improves the 4D plan robustness of targets to uncertainties with respiratory motion considered, compared to 3D robust optimization. In the presence of interplay effects, 4D robust optimization is also significantly superior to 3D robust optimization in terms of the target dose coverage. The reduction of CTV underdosage due to better mitigation of interplay effect from 4D to 3D robust optimization is clinically important, resulting in the increase of TCP of 2y-LC as much as 5.24% for some patients. The starting phase has limited influence, which is consistent with Grassberger et al. (22).

Unlike the 4D optimization methods proposed in the previous literature (except equation 3 of Graeff [47]), this 4D robust optimization method does not need synchronization. This idea might sound implausible (at least in photon therapy due to the static dose cloud nature of photon therapy); fortunately, in IMPT, the dose distribution could be easily perturbed by respiratory motion and uncertainties due to the high-range dependence. This sensitivity actually provides additional freedom to optimizers (9,10), which makes the 4D optimization without the need for synchronization possible in IMPT. The same logic has been successfully applied to robust optimization to mitigate the uncertainties compared to PTV-based conventional optimization (9,10). This method considerably eases the delivery hardware requirement (the same 3D delivery facility) at the sacrifice of possible plan quality. This method also greatly reduces the size of robust optimization problems by 10 times, and we can easily achieve a clinically acceptable 4D robustly optimized plan for lung cancer patients within 40 minutes.

Our method was also different from the method related to equation 3 of Graeff (47). In the method related to eq. 3 of Graeff et al 2014 (47), the summation over the phase number k is outside the summation over the voxel number i, i.e., they are trying to optimize the dose distribution of each phase to be homogeneous among the targets. However, in our methods, the summation over the phase number k is inside the summation over the voxel number i, i.e., we are trying to optimize the 4D accumulated dose distribution to be homogeneous among the targets while the dose distribution of each phase could be inhomogeneous among the targets. Therefore, our methods have relatively more flexibility compared to their methods. Also, the initial spot positions are based on the scanning target volume (STV), i.e., PTV plus a penumbra margin. The water equivalent path length (WEPL)-ITV proposed by Graeff et al. (29) is not used.

The improvement of target dose coverage in the dose distribution evaluated with uncertainties and/or interplay effect provides more confidence in the doses delivered during treatment, and may reduce the chance of local failure. It was found that the uncertainties underdose the target more than interplay effect (lower CTV D_95% from the impact of uncertainties than from the impact of interplay effect; compare Figure 1C and Figure 3B). This might be due to smoothing out of interplay effect from multiple fractionations. Some patients’ plans cannot meet the target coverage threshold with interplay effect considered, even after 4D robust optimization. Target coverage of those patients might be further improved using repainting techniques (17,19,25,28,67,68).

Although 4D robust optimization doesn’t explicitly account for interplay effect, it produces more interplay-effect-resistant plans in terms of better target coverage compared to 3D robust optimization, possibly because respiratory motion (thus correct range changes) is explicitly modeled in 4D robust optimization algorithms. Moreover, it appears that the requirement to improve plan robustness with respiratory motion steers the optimizer toward a solution with shallower per-field 4D accumulated dose gradients (Figure 1D) (9). Also, since 4D robust optimization had respiratory motion modeled in the optimization algorithm, it adjusts the contributions of beams from different directions to have more contributions from the beams with their directions parallel to the tumor motion direction. Both greatly help improve 4D plan robustness and mitigate interplay effect. This outperformance of 4D over 3D is another example of how making treatment more robust to one type of uncertainty (e.g., range or setup) leads to greater robustness to other sources of uncertainty (e.g., interplay). (14)

The tumor coverage improvement seems to be largest for some patients (patients 7 and 11 in our study, for example). We want to emphasize that this study was an exploratory methodology study, and in order to see how well our method performed in some extreme cases, the patients were not randomly selected based on the true patient population. According to Li et al. (24), among 112 stage III non–small-cell lung cancer patients, their CTVs ranged from 26 to 1360 cc (median, 336 cc), whereas their center-to-center CTV motions (i.e., difference between centers of mass) ranged from 0.2 to 16.6 mm (median, 3.3 mm). Most of stage III lung cancer patients actually had a ratio as defined: $(\frac{RM{A}^3}{TV\times {10}^{-4}})$ to be close to patient 7 (6.46) and patient 11 (2.25). We speculate that if we randomly select a large number of stage III lung cancer patients, the advantage of our 4D robust optimization method would clearly stand out over the 3D robust optimization method. This will be done in a larger randomly selected patient-population clinical study.

The 4D optimization has certain limitations. The deformable image registration software, though extensively used clinically, can introduce errors. So far we have assumed in 4D robust optimization that patients’ respiratory patterns during the treatment course are exactly the same as in simulation. However, patients’ respiratory patterns may vary from day to day (65). Also, potential instabilities in spot delivery are not considered (69). Additionally, we emphasize that the above conclusions may be valid only for our patient cohort and machine parameters. We recommend that each institution conduct institution-specific analyses of interplay effect before enacting institution-specific protocols (24, 25).

The new proton scanning beam machines have significantly smaller spot sizes. It would be interesting to perform 4D robust optimization of IMPT to treat lung cancer patients and evaluate the impact of uncertainties and interplay effect with smaller spot sizes. Also, it is very interesting to see the performance of our 4D robust optimization method in hypofractionated proton therapy. We intend to address these issues in future work.

Summary.

To mitigate uncertainties and interplay effects in optimizing intensity-modulated proton therapy for lung cancers, we used 4D robust optimization that generated plans on 4D-CTs with the clinical target volume of individual phases receiving non-uniform doses to achieve a uniform cumulative dose. Compared to 3D robust optimization, 4D robust optimization provided more robust target dose distribution to uncertainties and led to better target coverage, comparable dose homogeneity, and normal tissue protection with interplay effects considered.