Clinical evaluation of a model-updated image-guidance approach to brain shift compensation: experience in 16 cases

Abstract

Purpose

Brain shift during neurosurgical procedures must be corrected for in order to reestablish accurate alignment for successful image-guided tumor resection. Sparse-data-driven biomechanical models that predict physiological brain shift by accounting for typical deformation-inducing events such as cerebrospinal fluid drainage, hyperosmotic drugs, swelling, retraction, resection, and tumor cavity collapse are an inexpensive solution. This study evaluated the robustness and accuracy of a biomechanical model-based brain shift correction system to assist with tumor resection surgery in 16 clinical cases.

Methods

Preoperative computation involved the generation of a patient-specific finite element model of the brain and creation of an atlas of brain deformation solutions calculated using a distribution of boundary and deformation-inducing forcing conditions (e.g., sag, tissue contraction, and tissue swelling). The optimum brain shift solution was determined using an inverse problem approach which linearly combines solutions from the atlas to match the cortical surface deformation data collected intraoperatively. The computed deformations were then used to update the preoperative images for all 16 patients.

Results

The mean brain shift measured ranged on average from 2.5 to 21.3 mm, and the biomechanical model-based correction system managed to account for the bulk of the brain shift, producing a mean corrected error ranging on average from 0.7 to 4.0 mm.

Conclusions

Biomechanical models are an inexpensive means to assist intervention via correction for brain deformations that can compromise surgical navigation systems. To our knowledge, this study represents the most comprehensive clinical evaluation of a deformation correction pipeline for image-guided neurosurgery.

Introduction

Image-guided neurosurgery relies on preoperative images to provide visualization and facilitate surgical navigation within the brain. However, routine neurosurgical presentation and access lead to deformation of the brain cortical surface as well as subsurface resection targets [1]. The amount of brain shift depends on a number of factors including the extent of the craniotomy, retraction, tumor resection, drainage of cerebrospinal fluid (CSF) and drugs administered during surgery. Cortical shifts of up to 20 mm and subsurface shifts of up to 7 mm result in persistent misalignment between the patient’s brain structures and their preoperative image counterparts [1–5]. To improve the fidelity and utility of image-guided neurosurgery systems, the shift experienced in the brain must be taken into account to reestablish alignment accuracy.

One readily apparent solution is to re-image the brain during the surgery using intraoperative imaging systems. These intraoperative images typically have poorer soft-tissue contrast than those images taken preoperatively with an intact cranium. In order to preserve image quality and coregister other preoperatively acquired images (T1, T2, fMR, DTI, etc), the high-resolution preoperative images are often nonrigidly registered to the intraoperatively acquired MR images typically using either image-based or physics-based methods [6]. Although a powerful framework, intraoperative imaging systems are costly (represent large infrastructural commitment in cost-conscious healthcare system), occupy a significant portion of operating room space, and are likely not widely adoptable by most medical centers. While intraoperative tomographic imaging may be key for the most critical cases, a perhaps more cost-effective, complementary, and more widely adoptable solution is to make use of the exposed cortical surface to record brain shifts and use the measured surface displacements to drive a comprehensive biomechanical model of the brain. The computed deformation could then be used to update the preoperative images. While there have been many proposed sparse data solutions with encouraging results in phantom, animal, and human studies, the work is largely based on a limited number of samples [7–15]. This study evaluated the robustness and accuracy of a biomechanical model-based brain shift correction system developed for tumor resection surgery in a larger number of clinical cases, encompassing various patient ages, brain tumor sizes, locations, and degrees of brain shift.

Methods

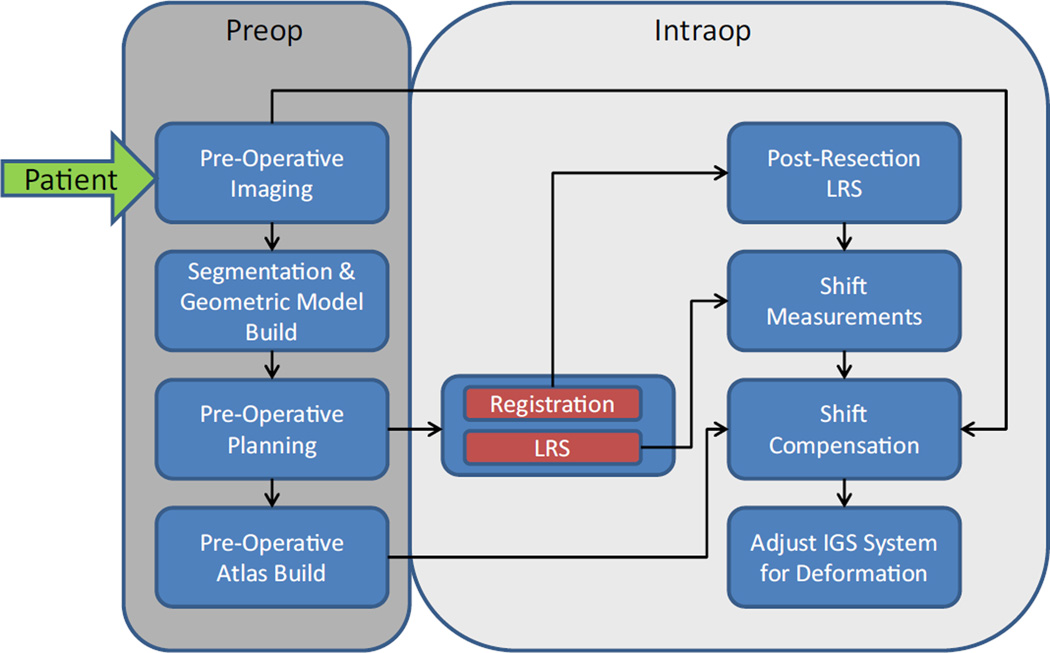
A semiautomated, preoperative and intraoperative computational processing pipeline for brain shift correction has been realized for use and is illustrated in Fig. 1. Briefly, preoperative magnetic resonance (MR) images were acquired a day or more prior to surgery from which the patient’s brain, tumor, and intracranial support structures, falx and tentorium cerebri, were segmented. A patient-specific finite element mesh was generated from the segmented brain and tumor images, while locations of the falx and tentorium are used to define associated boundary conditions in the mesh. A preoperative planning graphical user interface (GUI) was used by neurosurgeons to establish the approximate head orientation as well as size and location of the craniotomy. Based on the preoperative plan, a suite of boundary conditions that describe many possible brain shifts was created from an automatic generator and a distribution of possible deformation solutions was created by solving a series of finite element models [9].

Fig. 1.

A workflow illustrating the preoperative and intraoperative computational processing steps involved in producing an updated brain shift image. The inputs are preoperative MR images, face laser range scan (LRS) for registration, and pre- and postresection cortical brain surface LRS to drive the inverse modeling

A commercially available LRS system (Pathfinder Therapeutics, Inc., Nashville, TN, USA) integrated with an optical tracking system (Polaris Spectra, Northern Digital Inc., Ontario, Canada) was used to collect the patient’s face data and cortical surface data. The face LRS (using orbital and forehead geometric information) was used to register patient space to image space using our custom-made Registration GUI, while the cortical surface LRS was used to drive the inverse model based on the atlas using our custom-made Correction GUI. The patient’s brain image data are subsequently deformed using the optimum solution to reflect the current state of the brain’s shape.

MR imaging and segmentation

Sixteen patients scheduled to undergo brain tumor resection surgery were processed through the preoperative and intraoperative pipelines. For each patient, one gadolinium-enhanced set and one non-enhanced set of T1-weightedMRimage volumes were acquired from a conventional clinical MR scanner (Table 1). All patients provided written consent prior to this Vanderbilt Institutional Review Board-approved procedure. All procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1975, as revised in 2008 [5].

Table 1.

Patient information and tumor details

No.	Age (years)	Sex	Location of tumor	Size (cm3)	No. of points	Basis	Measured (mm)	Predicted (mm)	Error after correction (mm)
1	19	F	RT	4.8	52	Wcp	9.3 ± 1.4 (13.0)	8.6 ± 0.3 (9.2)	3.1 ± 1.4 (7.5)
2	38	F	LF	1.3	13	Wcp	9.0 ± 1.6 (10.8)	8.3 ± 1.2 (9.9)	3.3 ± 1.2 (5.1)
3	63	F	LT	25.1	18	C	12.8 ± 2.4 (17.7)	12.1 ± 0.9 (13.0)	4.0 ± 2.2 (8.2)
4	51	F	LT	27.2	16	C	21.3 ± 3.5 (28.2)	21.1 ± 3.2 (26.1)	2.6 ± 1.1 (5.8)
5	28	F	RF	7.6	11	C	11.2 ± 2.2 (14.7)	10.6 ± 1.1 (12.1)	3.3 ± 1.5 (5.2)
6	63	M	LF	29.2	4	C	3.2 ± 0.9 (4.4)	3.2 ± 0.4 (3.7)	0.7 ± 0.4 (1.2)
7	68	F	LT	16.1	213	Wcp	2.5 ± 1.0 (4.9)	2.0 ± 0.2 (2.5)	1.6 ± 0.8 (3.7)
8	42	F	RP	100.2	20	C	7.1 ± 4.8 (22.3)	6.1 ± 4.9 (25.3)	2.5 ± 1.3 (6.7)
9	64	F	RF	10.2	3	C	4.9 ± 0.2 (5.1)	4.7 ± 0.7 (5.5)	1.2 ± 0.4 (1.5)
10	84	M	LF	47.3	13	C	6.8 ± 4.8 (17.0)	6.5 ± 2.2 (10.4)	3.3 ± 1.8 (7.5)
11	48	F	RT	6.2	26	C	12.7 ± 2.8 (18.8)	12.7 ± 0.9 (13.6)	3.3 ± 1.3 (5.5)
12	46	M	RT	56.8	17	C	15.0 ± 3.6 (22.1)	13.2 ± 3.5 (17.4)	3.7 ± 3.2 (13.6)
13	22	F	LF	48.2	10	C	20.0 ± 4.3 (26.5)	18.6 ± 2.9 (21.3)	3.9 ± 2.5 (9.1)
14	58	M	LP	23.1	12	C	6.3 ± 2.0 (10.3)	5.7 ± 1.1 (7.3)	1.9 ± 1.2 (4.3)
15	77	M	LT	8.9	7	C	6.3 ± 0.5 (6.7)	6.1 ± 0.1 (6.3)	1.5 ± 0.7 (2.6)
16	75	F	LT	21.8	22	C	13.0 ± 2.1 (15.9)	10.3 ± 0.8 (11.3)	3.7 ± 1.8 (6.9)

The measured, predicted, and corrected brain shift results (mean ± SD with maximum in parenthesis) for all 16 cases. With respect to location (L-left, R-right, T-temporal, F-frontal, P-parietal). With respect to basis, ‘C’ indicates that corresponding points drove the correction, while ‘Wcp’ indicates sparse corresponding points were used to directionally weight additional closest point distances were employed

Each brain was isolated from the images using an automated atlas-based segmentation that relies on both contrast and non-contrast MR images [16]. The segmented brains were visually verified for accuracy, and when needed, manual editing of the automatically segmented brain was performed. Manual segmentation was performed for the tumor volume from the gadolinium-enhanced brain image volume. In addition, the framework used an automated approach to deploying patient-specific dural septa (falx cerebri and tentorium cerebelli), which has been shown to provide important structural support [17].

Surgical planner

Several factors influence the amount of brain shift to include orientation with respect to gravity, location, and size of craniotomy. An a priori estimate of these three variables will help in constraining the extent of our deformation atlas and can be provided by the neurosurgeon during preoperative planning. To achieve, a user-interactive surgical planner GUI has been developed to assist the neurosurgeon in quantifying those variables. Brain and tumor surface models are created from segmented brain and tumor images, respectively, and are rendered in the GUI where the neurosurgeon can manipulate the orientation of the brain to anticipated surgical presentation. Once complete, the software records the transformation, and then, the surgeon moves on to planning the craniotomy. The center of the craniotomy is selected by the anticipated path to the tumor and is designated by picking a point on the brain surface. The craniotomy size is then determined using a slide bar tool to adjust an intersecting sphere to estimate craniotomy size (Fig. 2a). These 3 variables are then exported to routines that define the boundary conditions for the model (Fig. 2b) and deformation atlas-building procedure.

Fig. 2.

a Preoperative GUI planner with craniotomy location and size tool demonstrated, and b boundary conditions automatically generated from preoperative planning tool with (left) showing fixed brain stem nodes in red, stress-free nodes in green, cranially constrained but lateral freedom in black, with dural septa nodes of falx and tentorium shown in magenta, and tumor shown in blue on the left image. On the (right), drainage conditions are specified with drainage allowed on regions of the brain open to atmosphere in blue with nondraining nodes in red

Biomechanical model

Biot’s theory of consolidation is employed to represent the brain mathematically in this framework. This biphasic model (solid and liquid phases) represents the brain to something reminiscent of a saturated sponge. More specifically, as force is applied to the tissue, the solid matrix supports the load as fluid drains from the tissue. Over time, the deformation is allowed to communicate deeper into the matrix as the tissue continues to drain interstitial fluid from the pores of the tissue. This is a very common representation of soft tissue and has been pursued by several investigators [18,19].

For each patient, a patient-specific finite element model is generated from the MR images. These models typically consist of approximately 20,000 vertices with approximately 100,000 tetrahedral elements. Brain elements were divided into white and gray matter based on an image intensity threshold which is designed to preserve the volumetric ratio of white-to-gray matter in the patient-specific brain. Tumors are manually designated. Each material can be prescribed different mechanical and hydraulic properties. With respect to material property values, the work in [20] was followed.

Atlas generation

Boundary conditions to the brain mesh were defined according to physiological conditions following the work of [21]. At and around the craniotomy where brain shift is largely present, the nodes on the brain boundary were set as stress free. The skull encloses the rest of the nodes on the brain boundary such that movement is limited to only the tangential direction along the cranial wall; hence, slip boundary conditions were assigned. Slippage was also designated on the nodes at the rigid dural septa. The nodes at the brainstem were fixed since the brainstem does not move. The CSF level in the brain affects the pressure boundary conditions in the brain. The nodes above the fluid level were exposed to atmospheric pressure and as such were set as a Dirichlet boundary condition, while Neumann no flux boundary conditions were assigned to the nodes below the fluid level. Figure 2b is an example of boundary condition designation.

In addition to the general boundary conditions described above, more specialized conditions were assigned based on the three main causes of brain deformation: (1) gravity-induced brain shift, (2) brain volume reduction due to administration of hyperosmotic drugs such as mannitol, and (3) brain swelling due to edema around the tumor. For gravity-induced deformation, three different CSF levels associated with different amounts of CSF drainage were modeled, while three different capillary permeability values were used for mannitol-induced deformation. A more complete description of the automatic boundary condition generation process is described in the work of Dumpuri et al. [10]. To account for changes in patient positioning during the procedure due to head tilt variations, and surgical table adjustments, 60 head orientations ranging incrementally over a conical capture range of ±20° from the base head orientation determined from the preoperative surgical planner were added. Tumor resection was modeled by decoupling the tumor nodes from brain nodes, thereby negating their biomechanical effects. Lastly, swelling variations were simulated with three different capillary permeability values and three different craniotomy sizes (75, 100, and 125% of planned size) to account for any deviations from the planner. Altogether, for each patient, there were 729 total brain shift possibilities, gravity- and mannitol-induced deformations each had 360 possibilities (60 head orientations × 3 CSF or permeability values × 2 resected or not), and swelling had 9 possibilities. The 729 finite element models were solved for displacement and pressure using an open-source Portable Extensible Toolkit for Scientific Computation (PETSc) package (http://www.mcs.anl.gov/petsc). While the solution creating this atlas could be determined in a one-day preplanning procedure, in recent work [22], the sampling extent in this atlas was shown to be unnecessary, and atlas construction could take place as a day-of-surgery procedure (e.g., 2.2 ± 0.6 h average atlas build [22]).

Physical-to-image space registration

In the operating room, an optically tracked laser range scanner is used to acquire patient face data before the craniotomy. The Registration GUI facilitates physical-to-image space alignment by using the patient’s face LRS and the extracted MR image counterpart surface mesh. The manual segmentation tool in the LRS acquisition software is used to remove extraneous points in the face scan, such as hair, intubation tubes, and drapes. After loading the segmented face LRS into the GUI, three homologous points on the face scan and head surface mesh are selected using a 3D interactive viewer. The points are used to provide an initial alignment which then moves on to a standard iterative closest point algorithm to complete the rigid registration process. It has been found that face-based alignment is equivalent to traditional synthetic fiducial alignment in [23].

Brain shift correction

After the craniotomy and with the dura opened, the LRS of the exposed cortical brain surface is acquired. Again, the scanner’s manual segmentation tool is used to remove extraneous information from the textured point cloud data, isolating just the brain surface. After tumor resection, a second cortical brain surface is acquired. In our experience, this second LRS is taken near the conclusion of surgery and it is usually when the surgeon wishes to examine and confirm spatial information regarding removal of the tumor. With respect to the second LRS, because the LRS is tracked in physical space, the preresection LRS information can be used as a mask to automatically segment the postresection LRS. Some manual interaction can still be needed to discard outlier points due to specular issues.

In the Correction GUI [20], these two LRS scans (before and after resection) are used to provide sparse measurements of brain shift. More specifically, the 2D pre- and postresection bitmaps associated with LRS data are used for the selection of homologous points. The homologous points were chosen using vessel bifurcations that could be identified in both LRS texture maps. As each bitmap pixel can be associated with a 3D position from their respective LRS surfaces, they represent a distinct 3D displacement that can be used to constrain model-updating approaches. It should also be noted that brain shift can occur immediately after dural opening. To accommodate for this first shift, the initial brain position is based on the brain boundary mesh nodes that are closest to the preresection scan. This closest point field is used as an initial measurement of shift upon dural opening.

An additional novel feature added to our framework manages the eventuality when only a very small handful of homologous points is available for measurement. In this instance, the approach is to initiate a process of determining shift measurements using a closest point distance between the postresection LRS and corresponding initial brain position but then using the corresponding distances to weight the directionality from the few manually selected points. For three patients in this study, this feature was used due to a limited number of easily identifiable homologous points.

Once brain shift measurements have been calculated, the correction was computed using an inverse modeling approach based on the atlas and constrained by the measured displacement shift vectors on the cortical surface. Details of the inverse model approach can be found in the work in [9,17]. Briefly, the least-squared error between the measured shift vectors and predictions from the deformation atlas were minimized by solving the following equations for the weighing coefficients, w,

$$\text{min }{\Vert Mw-u\Vert }^2\exists w_i\ge 0\text{ and }\sum _{i=1}^m{w}_i\le 1$$

where u are the measured shift vectors on the brain’s surface as determined by the above methods, and M is the atlas matrix containing the precomputed deformation solutions at the selected measurement points on the computer model. The series of homologous model points used to comprise M were selected via the closest point operator between the model boundary nodes and the nodes for the measured shift vectors in the preresection LRS data. The first constraint ensures only positive regression coefficients, and the second constraint prevents extrapolations of the solution. Ultimately, the constraints enforce that the optimal volumetric solution is comprised of a deformation field that is within the bounds of the series of model solutions that is used to generate the atlas. While less constrained objectives can be used, we have found this particular form of objective function to demonstrate good correction accuracy while maintaining a robust applicability across subjects [9,10,17].

Once a nonnegative constrained least-squares optimal solution is found to the surface-matching problem, the same combination of coefficients, w, is used to generate the 3D volumetric shift over the entire volume. The 3D volume of displacements is then used in a fast trilinear interpolation scheme to generate a deformed image volume that is more representative of the intraoperative scene.

Results

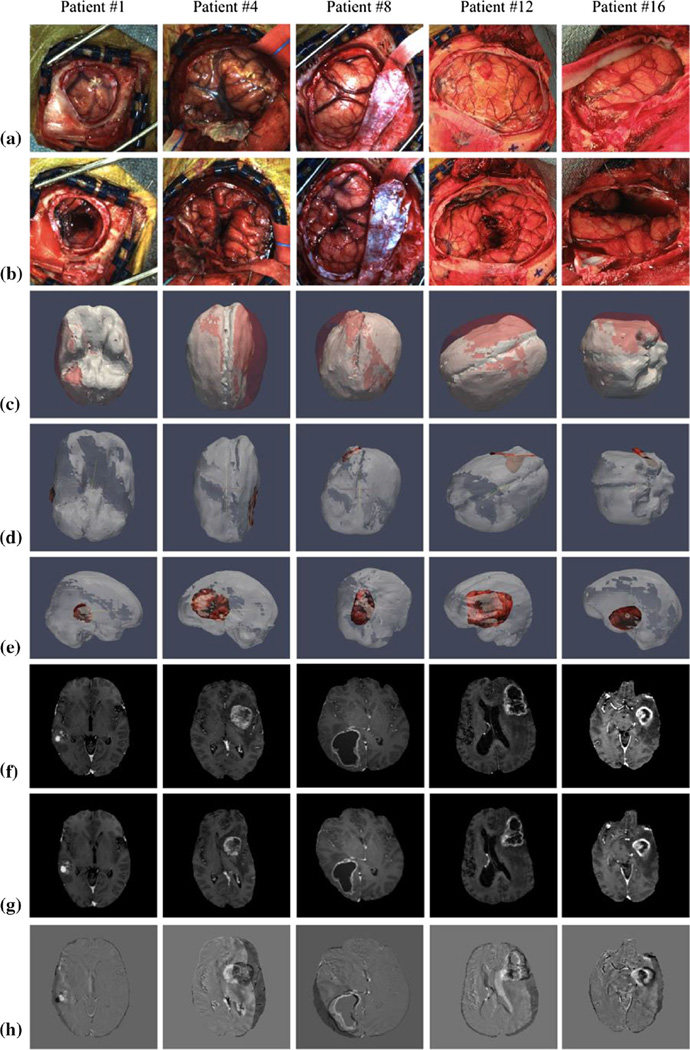
A summary of the measured, predicted, and corrected brain shift results for all 16 patients is shown in Table 1 to include the number of homologous points employed. For 3 patients (Patients #1, #2 and #7), there was a lack of corresponding blood vessels between the pre- and post-resection bitmaps and our custom weighted closest points approach was used in the calculation of the shift vectors. The mean measured shift magnitudes ranged from 2.5 to 21.3 mm, while the mean predicted shift magnitudes ranged from 2.0 to 21.1 mm. The mean corrected error magnitude ranged from 0.7 to 4.0 mm. Overall, looking across the 16 patients, approximately 70 ± 12% of error due to shift was corrected. To be clear, the percentage correction for any individual patient represents the amount of corrected error given the extent of shift for that particular patient (e.g., two separate patients that experience 10 and 20 mm average shift during their surgery, respectively, would both represent 80% correction results if the remaining average error after correction was 2 and 4 mm, respectively). Figure 3 shows example results in 5 cases. We should note that in the deformed MR image (Fig. 3g) the tumor has not been removed despite being driven by brain shift data after resection. While our atlas contains solutions both with and without the tumor-enhancing regions (for latter, nodal equations are decoupled and surrounding tissue is stress free), we chose to interpolate the tumor shape based on the surrounding displacement field. Observing patient 8 results and comparing (f) and (g), one can easily see the interpolated lesion shape change.

Fig. 3.

For patients #1, 4, 8, 12, and 16, illustrated are a preresection field of view bitmap (FOVBMP), b post-resection FOVBMP, c brain shift as observed by the overlay of deformed (white) and undeformed (red) brain mesh, d top view and e side view of the deformed brain mesh overlaid with the postresection LRS scans, f original MR image, g deformed MR image, and h image difference between original and deformed MR images

Discussion

This study evaluated the robustness and accuracy of a biomechanical model-based brain shift correction system for tumor resection surgery in 16 clinical cases. The distribution of patient tumor sizes, locations, types, and degree of shift were all consistent with standard tumor resection interventions. Looking across the clinical cases, the average surface shift is approximately 1 cm, which is consistent with previous literature, and the model-based methodology corrected on average 70% of the deformation. To our knowledge, this is the most extensive testing of a correction pipeline. As we look across the results, patient 7 has the worse % correction with the framework performing at 37% correction. However, the magnitude of shift in this case is on the order of measurement accuracy (i.e., 2.5 mm). Furthermore, when using Dixon’s Q two-sided test to determine the existence of an outlier, this patient is the only considered outlier, P = 0.005. This likely suggests that shifts at the scale of our measurement accuracy do not need correction. It is also interesting to note that among the 16 cases, the 5 worst performers (corrections ranging from 37 to 67%) used the custom weighted closest point operator approach. These cases are effectively among those with the worst correspondence, obviously indicating a need for continued improvement in shift measurement fidelity.

While the evaluation presented involves a description of the ability of the deformation correction pipeline to perform correction and updated guidance information after the resection procedure has been completed, it is important to note that the proposed correction pipeline is capable of providing updated guidance information at other time points during the surgical procedure. The rate limiting step in providing updated guidance at other time points primarily revolves around the acquisition of additional cortical surface data and determining the cortical surface displacements to drive the inverse model. While the use of the LRS to achieve this end has been well documented in the literature [24,25], other groups have focused on the use of stereo-pair reconstruction to acquire textured cortical surface digitizations [20]. Similarly, Kumar et al. [26] presented efforts toward the realization of a robust, real-time stereo-vision system using the surgical microscope with the novel addition of an accuracy comparison between stereo-reconstruction and LRS-generated results. The realization of a robust and accurate stereo-vision system using the surgical microscope should facilitate amore seamless platform for cortical surface digitization throughout the surgical procedure.

As of yet, extensive subsurface validations have not been achieved. In a previous study by Dumpuri et al. [9], MR images were taken with 12–24 h of surgery and used within a subsurface validation study. In this study, corresponding MR surface points between pre- and post-operative scans drove the correction and subsurface target positions were compared. The average surface shift used to drive the approach was 7.8 ± 1.4 mm. The average subsurface feature shift was 3.0 ± 1.4 mm. Over all 8 patients, approximately 85% of the shift on average was corrected. While encouraging, the magnitude of driving surface shifts is a typical and not the 1 cm reported clinically. That work was extended by Chen et al. [17] where intraoperative shift differed from the Dumpuri et al.’s experience by as much as 35–65%, emphasizing the need for intraoperative validation studies. More recently, work by Simpson et al. [27] summarizes clinical experience with conoscopic holography for digitizing tumor resection cavities. The tumor resection cavity digitizations were then used to validate the deformation correction pipeline presented previously [17,20]. While these studies shed light on performance, an extensive iMR validation of this candidate pipeline is clearly needed, and work towards this is underway. Nevertheless, the experiences reported here are encouraging, especially when one considers the repeated consistency of the results in the light of previously realized work.

Conclusions

To our knowledge, this work is the most extensive experience in using this model-based correction pipeline to account for deformations during guided surgery. Our results are encouraging and await further comparisons that include: (1) detailed intraoperative MR validation, (2) workflow analysis, and (3) optimal forms of data visualization.