Individual spatial aggregation correlates with between-population variation in fine-scale genetic structure of Silene ciliata (Caryophyllaceae)

Abstract

Fine-scale genetic structure (FSGS) can vary among populations within species depending on multiple demographic and environmental factors. Theoretical models predict that FSGS should decrease in high-density populations and increase in populations where individuals are spatially aggregated. However, few empirical studies have compared FSGS between populations with different degrees of individual spatial aggregation and microhabitat heterogeneity. In this work, we studied the relationship between spatial and genetic structure in five populations of alpine specialist Silene ciliata Poiret (Caryophyllaceae). We mapped all individuals in each population and genotyped 96 of them using 10 microsatellite markers. We found significant FSGS consistent with an isolation-by-distance process in three of the five populations. The intensity of FSGS was positively associated with individual spatial aggregation. However, no association was found between FSGS and global population density or microhabitat heterogeneity. Overall, our results support theoretical studies indicating that stronger spatial aggregation tends to increase the magnitude of FSGS. They also highlight the relevance of characterizing local plant distribution and microhabitat to better understand the mechanisms that generate intraspecific variation in FSGS across landscapes.

Introduction

Fine-scale spatial genetic structure (FSGS) is defined as the nonrandom spatial distribution of genotypes within plant populations. This pattern influences evolutionary parameters and processes like biparental inbreeding, kin competition, effective population size and local adaptation that in turn affect individual and population fitness (Linhart and Grant, 1996; Leblois et al., 2006). FSGS results from the complex interaction between limited gene flow through seed and pollen dispersal, genetic drift and local selection (Ennos, 1994; Vekemans and Hardy, 2004). Restricted gene dispersal in a continuous plant population theoretically leads to local inbreeding and the build-up of family structures across generations. In the absence of homogenizing selection, this phenomenon is expected to result in the nonrandom spatial organization of genotypes or FSGS (Ennos, 1994; Vekemans and Hardy, 2004).

A common form of FSGS is genetic isolation by distance (IBD), that is, a positive relationship between genetic and geographic distances among individuals (Wright, 1943). IBD patterns are usually measured by the rate of decrease in the probability of gene identity with spatial distance, which has been shown to be determined by the product of the effective gene dispersal rate, σ_e, and effective population density, D_e (‘neighbourhood size' Nb, sensu Wright, 1943; Rousset, 2000). As σ_e and D_e can vary among species and populations, FSGS patterns should show variation at both hierarchical levels.

Most empirical studies on plant FSGS patterns have focused on the influence of interspecific life-history variation, and particularly on the IBD patterns of species with different life forms, mating systems, and seed and pollen dispersal strategies (Vekemans and Hardy, 2004; Hardy et al., 2006; Hamrick and Trapnell, 2011). The determinants of intraspecific variation in FSGS remain comparatively underexplored, although intraspecific competition, microenvironmental selection and historic events such as founder effects or other demographic disturbances have been cited (Linhart et al., 1981; Tero et al., 2005; Chung et al., 2007). Differences in FSGS among populations may partly arise from variation in population density and spatial aggregation of individuals generated by the above-mentioned determinants. The magnitude of FSGS is expected to be higher in low-density populations characterized by a low D_e (Leblois et al., 2004; Vekemans and Hardy, 2004). In addition, for a given population density, several numerical simulation studies have shown that the spatial aggregation of adult plants generally increases the magnitude of FSGS compared with random or regular distributions (Doligez et al., 1998; Leblois et al., 2004; Robledo-Arnuncio and Rousset, 2010). Recent empirical studies have also shown that plant populations in fragmented habitats exhibit stronger FSGS than in continuous habitats (see, for example, Valbuena-Carabaña et al., 2007; Wang et al., 2011; but see Born et al., 2008). However, empirical studies examining variation in FSGS among populations with different densities and degrees of spatial aggregation remain scarce (Hamrick and Trapnell, 2011), and FSGS has not been analysed together with the spatial distribution of individuals and microhabitat heterogeneity (but see Chung et al., 2007; Jacquemyn et al., 2009; Van Heerwaarden et al., 2010). Further comparative studies of FSGS across populations with different demographic and microhabitat characteristics are needed to better understand the mechanisms generating intraspecific variation in FSGS across different landscapes (see, for example, Born et al., 2008; Wang et al., 2011).

The alpine specialist Silene ciliata Poiret (Caryophyllaceae) constitutes a suitable system to study the demographic and environmental determinants of intraspecific variation in FSGS. The low effective seed dispersal distance of this species (Lara-Romero et al., 2014) and the possibility of selfing (García-Fernández et al., 2012) may yield substantial FSGS. Previous studies have shown strong variation in demographic structure (for example, density and spatial aggregation of individuals) and physical environment (for example, microhabitat heterogeneity and water availability) among populations (Gimenez-Benavides et al., 2007, 2008; Lara-Romero et al., 2014). In this study, we described the spatial genetic structures of five demographically stable but spatially heterogeneous populations of S. ciliata and assessed whether FSGS intensity increases in populations with low plant density and high spatial aggregation. We addressed three main questions: (1) Do S. ciliata populations have FSGS? (2) Does the intensity of FSGS vary among populations? (3) If so, is this variation associated with differences in demographic structure (that is, population density and individual spatial aggregation) and/or microhabitat heterogeneity?

Materials and methods

Study region and species

S. ciliata Poiret (Caryophyllaceae) is a perennial cushion plant that occurs in the Mediterranean mountain ranges of southern Europe. It is self-compatible, although autogamy is restricted by pronounced protandry (García-Fernández et al., 2012). It blooms in late summer (Gimenez-Benavides et al., 2007) and its flowering stems reach 15 cm in height and have 1–5 flowers. S. ciliata is pollinated at night by Hadena consparcatoides Schawerda (Lepidoptera, Noctuidae) but can also be pollinated by diurnal insects (Gimenez-Benavides et al., 2007). Fruit capsules contain up to 100 seeds that are wind dispersed in August–September. Average effective seed dispersal distances are relatively invariant across populations (mean±s.e.: 0.40±0.08 m, Lara-Romero et al., 2014).

This study was carried out in the Sierra de Guadarrama, a mountain range located in central Spain. S. ciliata grows locally at altitudes from 1900 to 2430 m in dry cryophilic pastures dominated by Festuca curvifolia Lag ex Lange and other perennial plants that are interspersed in a shrub matrix characterized by Cytisus oromediterraneus Rivas Mart. et al. and Juniperus communis subsp. alpina (Suter) Čelak. Mean annual precipitation (40° 46′N, 4° 19′W; 1860 m above sea level) is 1330 mm with a pronounced dry season (<10% of total annual rainfall) from May to October. Mean annual temperature is 6.3 °C, with mean monthly temperatures ranging from −1 °C in January to 16 °C in July (www.aemet.es). Although S. ciliata presents variable ploidy levels in natural populations, all individuals from the studied Guadarrama populations are diploid (2n=24, García-Fernández et al., 2012).

Study plots

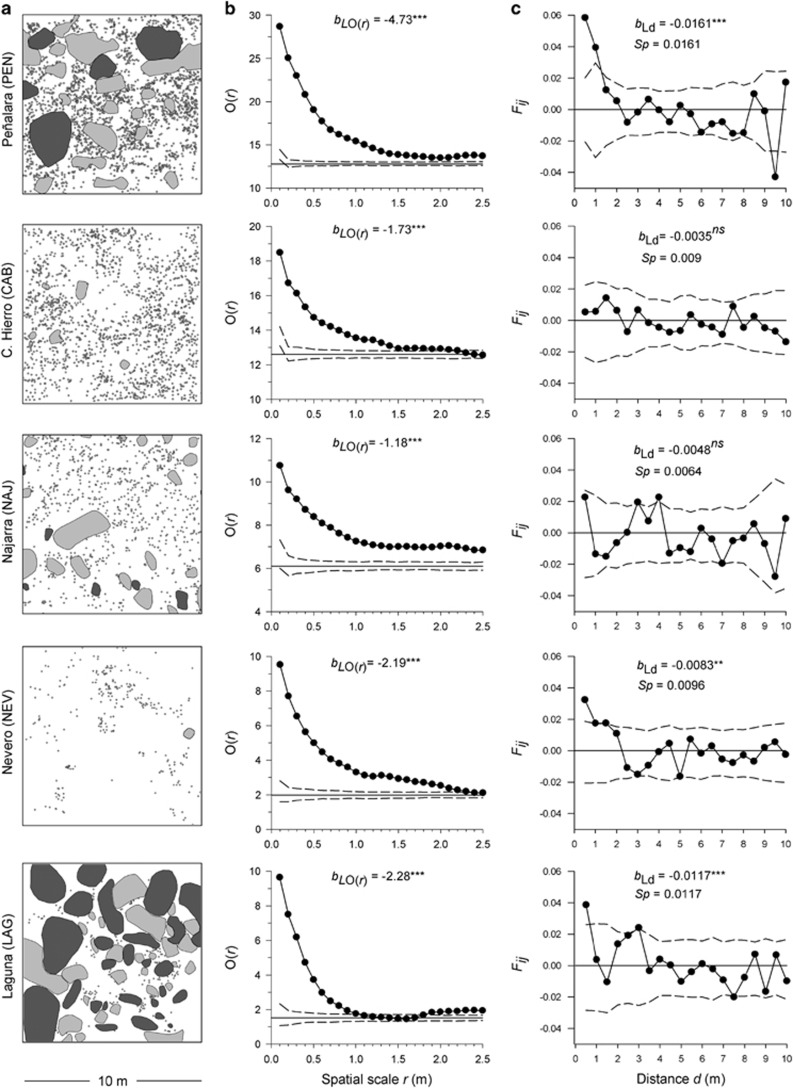
In August and September 2010, we established one 10 × 10 m plot in each of five S. ciliata populations distributed along the Sierra de Guadarrama (Figure 1a and Table 1). Additional information on the selected populations can be found in Lara-Romero et al., 2014. Based on the low human intervention in the area and long-term demographic monitoring of two of the populations (Peñalara (PEN) and Laguna (LAG)), we expected these populations to be at equilibrium. Genetic tests for detecting past changes in effective population size support the demographic stability of the populations (Appendix 1 in Supplementary Information). We mapped all adult S. ciliata individuals in each study plot using two high-resolution Differential Global Navigation Satellite System (DGNSS) receivers (Viva GS15, Leica, Switzerland) with an absolute accuracy of 5 cm for x and y coordinates. We also mapped the spatial position and contour of all neighbouring C. oromediterraneus and J. communis shrubs, rocky outcrops and rocks >50 cm in diameter that are unsuitable microhabitats for S. ciliata (Figure 1a). We then used this information to estimate global density (D) and to characterize the spatial distribution of the adult plants in each study plot (that is, O-ring statistic, see below), as well as microhabitat heterogeneity, calculated with the shape index (SI). SI is widely used in landscape ecology as a measure of landscape complexity and fragmentation (Berry, 2007). It has a value of one when the patch is a perfect circle/square and increases as the patch becomes more irregular (Berry, 2007). The five populations spanned a gradient in adult density (D) and had different degrees of microhabitat heterogeneity (Table 1).

Figure 1.

Spatial distribution of adult plants (a), spatial demographic structure (b) and spatial genetic structure (c) in Silene ciliata study plots. (a) Spatial distribution of adult plants (small circles), rocks (grey) and shrubs (dark grey) in each study plot of S. ciliata. (b) Spatial demographic structure: b_LO(r) denotes the slope of the regression of the O ring statistic, O_(r) on the logarithm of the spatial distance, ln(r); the thin solid line indicates average intensity of the point pattern (that is, plant density) and dashed lines indicate 95% confidence envelopes under the null hypothesis of random spatial structure. Note that y axes show different scales for clarity. (c) Spatial genetic structure: b_Ld denotes the slope of the regression of kinship coefficient values (F_ij) on the logarithm of the spatial distance, ln (d_ij); dashed lines represent 95% confidence envelopes constructed under the null hypothesis (no genetic autocorrelation exists). **P<0.01, ***P<0.001.

Table 1. Description of sampling sites and genetic diversity estimates in Silene ciliata populations.

Population	Abbreviation	UTM coordinates (m)		D	De	SH (%)	SI	N	A	HO	HE	FIS
Peñalara	PEN	419427	4522814	12.8	3.57	71.3	1.91	96	10	0.39	0.50	0.15*
Cabezas de Hierro	CAB	421169	4516859	12.6	3.34	96.8	1.14	94	10	0.41	0.55	0.23*
Najarra	NAJ	430196	4518886	6.10	1.64	86.2	1.42	95	9	0.36	0.53	0.21*
Nevero	NEV	428863	4537167	1.99	0.54	99	1.11	96	12	0.39	0.55	0.19*
Laguna	LAG	419931	4521082	1.52	0.40	48.8	2.40	93	11	0.34	0.53	0.26*

Abbreviations: A, average number of alleles per locus; D, census plant density (individuals per m²); D_e, effective plant density; F_IS, average inbreeding coefficient; H_O and H_E, expected and observed heterozygosities; N, sample size; SH, proportion of suitable habitat; SI, shape index of suitable habitat; UTM, x, y geographical coordinates.

Significance level: *P<0.001.

DNA extraction and microsatellite genotyping

We collected leaf material from ∼96 adult plants per plot for genetic analysis (Table 1). To increase the sample size of shorter interindividual distances for autocorrelation analysis, plants were selected using a clustered random sampling design (sensu Storfer et al., 2007). Namely, we randomly selected 24 sample locations in each plot, where we collected leaf material from four adult individuals located in close proximity to one other. The minimum sample distance ranged between 10 cm (Nevero (NEV)) and 28 cm (Cabezas de Hierro (CAB)). We collected large individuals of similar rosette size to prevent sampling individuals belonging to different age classes (that is, parents and offspring).

DNA was extracted using the DNeasy Plant minikit (QIAGEN, Valencia, CA, USA) with 10–20 mg of dried S. ciliata tissue. Ten microsatellite loci previously used in genetic studies of S. ciliata were selected for genotyping: Sci1224, Sci1208, Sci0106, Sci1443, EST-2HTS, EST-8HTS, EST-37HTS, EST-X4-3, EST-G34D06 and EST-G47A02 (García-Fernández et al., 2012). Specifications of PCR reactions and amplification are described in García-Fernández et al. (2012). Samples were run on an automated DNA sequencer (ABI PRISM 3730, Applied Biosystems, Foster City, CA, USA) in Parque Científico de Madrid (Madrid, Spain). Fragment size was determined using GeneMarker version 1.85 (SoftGenetics, State College, PA, USA).

We evaluated genotyping accuracy by re-amplifying and re-scoring a random subset of samples. We also estimated the occurrence of null alleles, large-allele dropout and stuttering using the software MICRO-CHECKER (Van Oosterhout et al., 2004). We discarded loci Sci1443 and EST-SSR X4-3 because of inconsistent allelic scoring. Locus Sci1224 showed signs of potential null alleles because of an excess of homozygotes in some allele size classes. Subsequent analysis produced the same results and conclusions irrespective of whether or not this locus was included, except for the fixation index (F_IS). Therefore, locus Sci1224 was excluded from the calculation of F_IS (see below). Selected loci were found to be statically independent (P>0.05: Log-likelihood ratio G statistic based on 5000 permutations performed in GENEPOP v. 4.2, http://genepop.curtin.edu.au/).

Spatial distribution of adult plants within populations

We employed the noncumulative O-ring statistic O(r) (Wiegand and Moloney, 2004) to characterize the spatial distribution of adult plants in the five study populations. O(r) gives the expected number of points (that is, plants) in a ring at distance r from an arbitrary point (Wiegand and Moloney, 2004). We calculated O(r) considering concentric rings of a constant width of 0.1 m. To avoid estimation bias, O(r) was calculated between r=0.10 and 2.5 m, that is, up to a quarter of plot width (Baddeley and Turner, 2005). We used Ripley's isotropic correction (Baddeley and Turner, 2005) to correct for edge effects. To assess the existence of significant spatial aggregation within populations, we generated 95% simulation envelopes associated to the null model of complete spatial randomness using the tenth lowest and tenth highest value of 399 Monte Carlo simulations of the complete spatial randomness-null model. O(r) values above and below the envelope indicate significant spatial aggregation and repulsion compared with a complete spatial randomness pattern, respectively (Wiegand and Moloney, 2004).

Finally, to compare the overall strength of aggregation among populations, we calculated the slope (b_LO(r)) of the linear regression of O(r) on the logarithm of the spatial distance r for each population. Associated s.d. was also estimated and used to perform pairwise t-tests to determine whether b_LO(r) significantly differed among populations. All statistical analyses were performed in the open source software R v 3.0.2 using the package ‘spatstats' (Baddeley and Turner, 2005).

Population genetic analyses

We used GENEPOP to calculate standard population genetic measures, including total number of alleles (A), observed (H_O) and expected (H_E) heterozygosity, and inbreeding coefficients (F_IS). We used per-locus values to test for statistical differences in genetic measures across populations using the nonparametric Friedman rank sum test. Deviations from Hardy–Weinberg equilibrium within each population were tested using Fisher's exact test implemented in GENEPOP.

Characterization of FSGS

Bayesian clustering analysis

Within-population spatial heterogeneity could limit gene movement between individuals separated by physical obstacles (for example, shrub, rock and so on) or growing in a different environment (that is, gene flow is limited because of selection acting against locally maladapted migrant genes and individuals) (Storfer et al., 2007). When abiotic and/or biotic discontinuities remain static across generations, genetic diversity could be geographically clustered in each plot. To address this possibility, we used a Bayesian clustering method implemented in the R package ‘Geneland' version 4.0.3 (Guillot et al., 2005). This approach uses Markov chain Monte Carlo procedures to estimate the number of genetic clusters that is treated as an unknown parameter. Five independent runs of the spatial D-model were performed with 100 000 Markov chain Monte Carlo iterations, of which every hundredth one was saved.

Spatial genetic autocorrelation analysis

To assess FSGS resulting from IBD, we used the spatial autocorrelation approach implemented in SPAGeDi version 1.4 (Hardy and Vekemans, 2002). In each population, we estimated the genetic similarity between every pair of individuals i and j with Loiselle's kinship coefficient (F_ij, Loiselle et al., 1995). We then regressed the obtained values on the spatial distance between individuals and its natural logarithm (d_ij and ln(d_ij), respectively) and reported the regression slopes (b_d and b_Ld, respectively) for each type of regression. The s.e. values for F_ij, b_d and b_Ld were estimated by jackknifing over loci. We addressed the significance of the spatial variation of F_ij by computing the average pairwise F_ij over a set of distance intervals (d) comprising between 0.5 and 10 m and comparing these values with those expected under the null hypothesis of absence of IBD (that is, F_ij and d_ij or ln(d_ij) are uncorrelated). The confidence interval associated to the null hypothesis was constructed by performing 9999 random permutations of genotypes among spatial positions.

To compare FSGS intensity among populations, we calculated the statistic Sp for each population (Vekemans and Hardy, 2004). We used the formula Sp=– b_Ld/(1–F₁), where F₁ is mean F_ij at the smallest distance interval d. Mean Sp and s.e. were calculated for each population over all loci, and the approximate 95% confidence intervals (CIs) were obtained as ±1.96 times the s.e. estimates obtained across loci. As before for b_LO(r), we carried out pairwise t-tests to determine the statistical significance of the differences found between populations.

We also used the software SPAGeDi to estimate Wright's neighbourhood size (Nb, Wright, 1943) and effective gene dispersal rate (σ_e) of each population.

Under Wright's IBD model, Nb can be estimated in two-dimensional populations as (Vekemans and Hardy, 2004):

where b_r is the restricted regression slope (b_Ld) of F_ij on ln(d_ij) in the range σ_e<d<20 σ_e. The expected relationship between Nb and σ_e is given by (Rousset, 2000):

where D_e is effective population density, which can be conveniently approximated as D_e=D × N_e/N. Following the approach suggested by Vekemans and Hardy (2004), we estimated the ratio N_e/N from Equation 3 and used this estimation to calculate D_e

where V corresponds to the variance of lifetime reproductive success among individuals (Kimura and Crow, 1963; see Appendix 2 in Supplementary Information for further details).

In populations where we detected significant FSGS consistent with IBD, we computed Nb (Equation 1) and used estimated values of D_e to compute σ_e (Equation 2), applying the iterative procedure implemented in SPAGeDi.

Approximate 95% CIs around Nb estimates were computed as (F₁–1)/(b_r+2s.e._b) and (F₁–1)/(b_r–2s.e._b), respectively, where s.e._b is the standard error of b_r estimated by jackknifing over loci. When b_r>2s.e., the upper bound was reported as infinite (Fenster et al., 2003; Hardy et al., 2006). The 95% CI of σ_e was obtained using an analogous procedure.

Following Crawford (1984), we decomposed σ_e into effective seed (σ_e,s) and pollen (σ_e,p) gene dispersal rates:

We used contemporary (Crawford, 1984) field estimates of mother–seedling axial square dispersal distance (σ_s) obtained through inverse modelling (Lara-Romero et al., 2014) as a rough approximation of σ_e,s. We then used estimated σ_e and σ_e,s values to approximate the value of σ_e,p using Equation 4.

Association between demographic structure, microhabitat heterogeneity and FSGS

O(r) shares the ring-based approach with spatial genetic autocorrelation, making the results of our spatial demographic and genetic analyses directly comparable (Chung et al., 2007, 2011). Hence, to quantify the strength of the association between individual spatial aggregation and FSGS, we conducted a correlation analysis between b_Ld and b_LO(r) (Chung et al., 2007). We also assessed the correlation between Sp and adult density (D) and the heterogeneity of suitable microhabitat (SI).

Results

Spatial distribution of adult plants within populations

The O-ring statistic O(r) showed significant individual spatial aggregation at small scales in all of the studied populations (Figure 1b). PEN showed the strongest overall aggregation, with a slope of the O-ring statistic of b_LO(r)=–4.73 (95% CI: –5.22, –4.24). LAG and NEV exhibited intermediate patterns (b_LO(r)=–2.28, 95% CI: –2.71, –1.85 and b_LO(r)= –2.19, 95% CI: –2.35, –2.03, respectively), whereas CAB and Najarra (NAJ) showed the flattest functions (b_LO(r)=–1.73, 95% CI: –1.87, –1.59 and b_LO(r)=–1.18, 95% CI: –1.30, –1.06, respectively). Pairwise t-tests showed significant differences in b_LO(r) values between all studied population pairs except between NEV and LAG (Supplementary Information and Supplementary Table S1).

Population genetic analyses

We scored a total of 144 alleles across 8 loci in 474 individuals (Table 1), with a mean (±s.e.) number of 10 (±0.8) alleles per locus. All five populations contained similar levels of genetic diversity and inbreeding (Table 1). All populations showed significant departures from Hardy–Weinberg equilibrium towards heterozygote deficiency, according to global tests across loci. Detailed genetic diversity estimates for each marker and population are provided as Supplementary Information (Supplementary Table S2).

Characterization of fine-scale genetic structure

All five independent runs of Geneland gave a single genetic group for each population, indicating that there were no genetic discontinuities or spatially structured gene pools within populations.

No significant relationship was found between genetic kinship (F_ij) and geographic distance between individuals in CAB and NAJ (b_L and b_Ld were not statistically different from 0, Figure 1c and Supplementary Table S3). However, the slopes of the linear regressions between F_ij and both geographic distance and the logarithm of geographic distance were significantly negative in PEN, NEV and LAG (Figure 1c and Supplementary Table S3), as expected under IBD. In all three populations, the decrease in F_ij with distance fitted a logarithmic relationship better than a linear relationship (R²_dL>R²_d) (Supplementary Table S3), as expected for two-dimensional populations. The three populations with significant IBD showed significantly positive F_ij values in the first distance class (d≤0.5 m), rapidly declining and becoming nonsignificant in the second or third distance classes (Figure 1c). The Sp statistic confirmed the existence of among-population variation in FSGS intensity (Figure 1c and Supplementary Table S3). PEN showed the strongest FSGS with Sp=0.0161 (95% CI: 0.0127, 0.0221), followed by LAG and NEV, Sp=0.0117 (0.029, 0.0205) and Sp=0.0096 (0.0033, 0.0159), respectively. The lowest Sp values were found in NAJ and CAB with Sp=0.0064 (0.0015, 0.0113) and Sp=0.0009 (0, 0.0054), respectively. Pairwise t-tests indicated that Sp at PEN was significantly greater than at NAJ and CAB (t=2.27, P<0.05 and t=2.70, P<0.01; respectively).

Wright's neighbourhood size (Nb) and effective gene dispersal rate (σ_e) were assessed in the three populations that had a FSGS consistent with IBD. Estimates of neighbourhood size were Nb=158 individuals (95% CI: 121, 195) for PEN, Nb=103 individuals (91, ∞) for LAG and Nb=106 individuals (81, ∞) for NEV. Nb values for PEN were ∼10% of the total number of individuals in the plot, whereas in NEV and LAG they accounted for ∼40% and 60% of total plot size, respectively. The ratio of effective to census population sizes (N_e/N) was estimated at 0.279, 0.265, 0.268, 0.272 and 0.261, in PEN, CAB, NAJ, NEV and LAG, respectively. These N_e/N ratios yielded effective densities D_e ranging from 0.40 to 3.57 ind m⁻² (Table 1). Using these D_e estimates, we obtained a notably lower σ_e estimate for PEN (1.94 m, 95% CI: 1.74, 2.14) than for NEV (σ_e=3.9 m, 95% CI: 3.69, ∞) and LAG (σ_e=4.65 m, 95% CI: 4.17, ∞). The decomposition of σ_e into effective seed (σ_e,s) and pollen (σ_e,p) gene dispersal rates showed that among-population differences in σ_e seemed to be mainly mediated by differences in pollen–mediated gene dispersal. In particular, σ_e,s estimates were similar in all populations (0.27, 0.21 and 0.20 m for PEN, NEV and LAG, respectively), whereas the estimate of σ_e,p for PEN was 1.35 m, less than half of those for NEV and LAG (2.75 and 3.28 m, respectively).

Association between demographic structure, microhabitat heterogeneity and FSGS

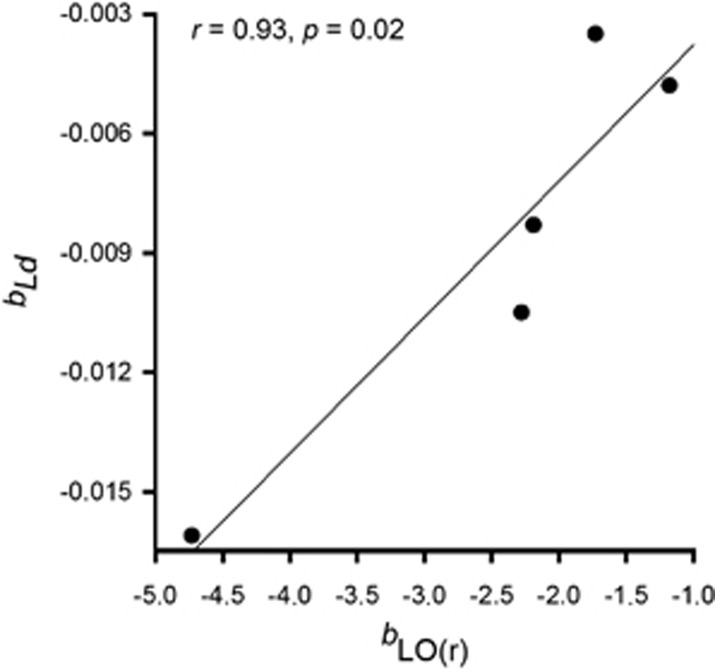
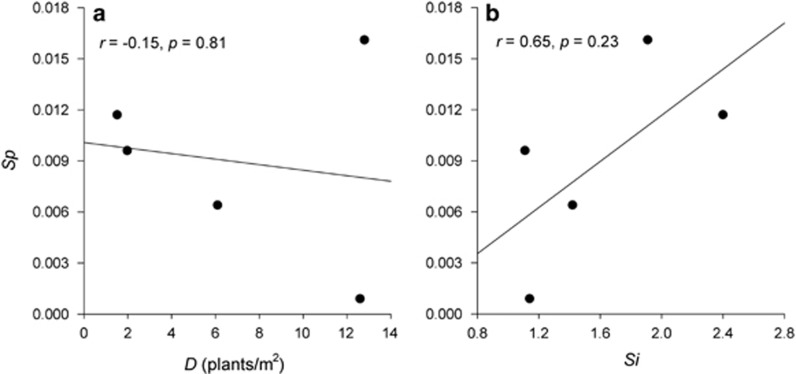
We found a significant strong association between spatial autocorrelation measures of genetic structure (b_Ld) and individual spatial aggregation (b_LO(r)) (Figure 2; Pearson's product-moment correlation: r=0.93, P=0.02). The correlation between Sp and microhabitat heterogeneity (SI) was high but not significant (Figure 3b: r=0.69, P=0.20). No correlation was found between Sp and adult density (D) (Figure 3a; r=−0.15, P=0.81).

Figure 2.

Association between spatial autocorrelation measures of fine-scale genetic structure (b_Ld) and individual spatial aggregation (b_LO(r)); ‘r' indicates Pearson's product-moment correlation.

Figure 3.

Association between the fine-scale spatial genetic structure (Sp) and (a) adult density (D) and (b) microhabitat heterogeneity (SI); ‘r' indicates Pearson's product-moment correlation.

Discussion

This study found significant FSGS, consistent with IBD, in three of the five studied populations of S. ciliata, as well as significant among-population variation in the intensity of FSGS. Spatial aggregation of individuals and FSGS were positively correlated, supporting the influence of fine-scale aggregation of plants on intraspecific FSGS variation. The populations that did not exhibit significant IBD corresponded to those with the lowest spatial aggregation. On the other hand, FSGS was not significantly correlated with global population density or microhabitat heterogeneity.

Assuming dispersal–drift equilibrium, the observed differences in FSGS among the studied populations, as measured by Sp, should mainly result from differences in the product between effective gene dispersal and effective population density (that is, the genetic neighbourhood size, inversely related to Sp: Wright, 1943; Rousset, 2000; Vekemans and Hardy, 2004). Effective gene dispersal σ_e is defined as the (long-term) asymptotic mean-square dispersal distance of gene lineages across generations, akin to a diffusion rate of genes in the landscape (Wright, 1943; Rousset, 2000; Vekemans and Hardy, 2004). Thus, the magnitude of σ_e and its ensuing effects on Sp depend on both the dispersal rate over a single generation (σ) and the permeability of the landscape to the long-term diffusion of gene lineages (Robledo-Arnuncio and Rousset, 2010). If favourable habitat is not continuous, and especially if the discontinuities remain static across generations, some gene lineages may remain on the edges of a favourable habitat patch over several generations until an interpatch dispersal event occurs. This resistance to gene diffusion may result in σ_e values substantially lower than σ (Robledo-Arnuncio and Rousset, 2010). Furthermore, σ itself may be lower in spatially aggregated populations, if plant clustering reduces seed or pollen dispersal vector mobility, for instance if the proportion of intrapatch pollinator flights tends to increase with spatial aggregation (Morris, 1993; Cresswell and Osborne, 2004). Overall, FSGS is expected to be stronger in spatially aggregated populations than in continuous populations, even if, on average, σ remains unchanged.

Consistent with this prediction, we found a positive correlation between the spatial aggregation of individuals and FSGS, as well as the lowest value of σ_e estimated for the population with the strongest individual spatial aggregation and FSGS. This suggests that variation in the spatial distribution of individuals generates intraspecific variation in FSGS for the study species, even if average seed dispersal distances are largely invariant across populations (Lara-Romero et al., 2014). The positive correlation between spatial aggregation and FSGS would not be expected in plant species or populations where the scale of seed and/or pollen dispersal was large relative to the distance between favourable patches, nor if individual aggregation resulted from habitat heterogeneities that change rapidly over generations (Robledo-Arnuncio and Rousset, 2010). In future, it would be of interest to empirically assess potential associations between spatial and genetic population structure as a function of the dispersal ability of species and temporal habitat dynamics.

Although previous empirical studies have suggested that spatial heterogeneity could be a potential determinant of variation in FSGS (Valbuena-Carabaña et al., 2007; Born et al., 2008; Wang et al., 2011), its association with spatial aggregation and its ensuing effects on effective gene dispersal rates have rarely been measured. The few studies that aimed to quantify both the local distribution of individuals and genetic structure across plant populations found positive associations between the level of FSGS and spatial aggregation (Jacquemyn et al., 2009; Chung et al., 2011). However, these studies compared continuous stable populations with expanding and senescing spatially aggregated populations, or seedlings to adult plants within the same population. As far as we know, this is the first empirical study reporting evidence of a possible relationship between the spatial aggregation of plants and FSGS in equilibrium populations.

Contrary to our expectations, the correlation between the intensity of FSGS and global population density was not significant. This could have resulted from the low statistical power of the design because, with only 5 populations, an observed value of r>0.81 is required for statistical significance at the 5% level. If PEN population is considered an outlier and removed from the analysis (for example, on the basis of having experienced a different demographic history than the rest of the populations), then there is a clear trend of decreasing Sp with D, as the theory predicts (Leblois et al., 2004; Vekemans and Hardy, 2004). However, our results suggest a common history of all studied populations. Rather than reflecting a statistical issue, the lack of a significant association between Sp and global population density could also be explained by at least two different biological processes. First, it could result from the interacting effects of D_e and spatial aggregation on FSGS. Indeed, even if increasing D_e is expected to decrease FSGS, this effect can be masked by the opposite (positive) effect of a high level of spatial aggregation on FSGS. This is likely the case in this study, because both D_e and the levels of spatial aggregation vary among populations. Such an effect could explain why the two populations with the highest, similar, densities (the weakly aggregated population CAB and the strongly aggregated PEN) exhibited contrasting levels of FSGS (with larger Sp in PEN). Second, pollinator behaviour could invert the direction of the relationship between D_e and FSGS. Namely, global density is assumed to cause a reduction in FSGS through decreased gene identity probabilities; however if pollinators flew longer distances (that is, increased σ_e) in low- than in high-density populations (as found in several empirical studies, see, for example, Tero et al., 2005; Barluenga et al., 2011), this effect could result in stronger genetic structure in high-density populations. This effect could explain why Sp was not significantly different in high-density PEN than in low-density LAG and NEV. It is also consistent with the inferred effective pollen gene dispersal rate σ_e,p that was less than half of the values calculated for NEV and LAG (2.75 and 3.28 m, respectively) in PEN (1.35 m).

Conclusions

This study shows that variation in the fine-scale spatial distributions of individuals can be associated with intraspecific variation in FSGS, even if average seed dispersal distances are invariant across populations. These findings support theoretical studies indicating that stronger individual spatial aggregation generally increases the magnitude of FSGS (Doligez et al., 1998; Barton and Keightley, 2002; Robledo-Arnuncio and Rousset, 2010). No linear association was found between global plant density, or microhabitat heterogeneity, and FSGS. These results are difficult to interpret because of the low statistical power of our analysis; however, they suggest that individual spatial aggregation is more relevant than global plant density and microhabitat heterogeneity in determining variation in FSGS among S. ciliata populations. Additional research is required to confirm our findings and to evaluate their generality in a wider range of taxa and environments. This study highlights the importance of combining spatial analyses of genotypes, individuals and microhabitats to better understand the mechanisms generating intraspecific variation in FSGS across landscapes.

Data archiving

The data sets used for this study including the location of each S. ciliata adult plant within the study plots and microsatellite data are available at the institutional repository of Rey Juan Carlos University (BURJC-Digital, http://eciencia.urjc.es/handle/10115/12500).

The authors declare no conflict of interest.