Ab Initio Calculation of Rate Constants for Molecule–Surface Reactions with Chemical Accuracy

Abstract

The ab initio prediction of reaction rate constants for systems with hundreds of atoms with an accuracy that is comparable to experiment is a challenge for computational quantum chemistry. We present a divide‐and‐conquer strategy that departs from the potential energy surfaces obtained by standard density functional theory with inclusion of dispersion. The energies of the reactant and transition structures are refined by wavefunction‐type calculations for the reaction site. Thermal effects and entropies are calculated from vibrational partition functions, and the anharmonic frequencies are calculated separately for each vibrational mode. This method is applied to a key reaction of an industrially relevant catalytic process, the methylation of small alkenes over zeolites. The calculated reaction rate constants (free energies), pre‐exponential factors (entropies), and enthalpy barriers show that our computational strategy yields results that agree with experiment within chemical accuracy limits (less than one order of magnitude).

Predicting the rate of chemical reactions is a fundamental problem in chemistry. For gas‐phase reactions that do not involve too many atoms, such as H+CH₄→H₂+CH₃, this has now been possible from first principles for thermal rate constants “with an accuracy comparable to (or even exceeding) experimental precision” for almost a decade.2 Evidence has also been provided that for temperatures above 400 K, classical transition‐state theory3 can safely be applied without tunneling corrections. However, for large chemical systems, such as those encountered in heterogeneous catalysis, where adequate models typically include several hundred atoms, the “chemical accuracy” (4 kJ mol⁻¹ for the energy barriers, one order of magnitude for the pre‐exponential factors) required for useful predictions is not attained. The exponential scaling with the system size of both the electronic structure methods (potential energy surface) and the nuclear motion problem (vibrational partition function) limits the applicable method to density functional theory (DFT) for the potential energy surface and the harmonic approximation for the vibrations.4, 5, 6, 7, 8 Depending on the functional, energy barriers may be in error by 10–20 kJ mol⁻¹, and the harmonic approximation is most problematic for low‐frequency modes, which are known to make the largest contribution to the partition functions.9

Instead of calculating vibrational partition functions, the potential energy surface can be sampled using molecular dynamics or Monte Carlo simulations. As converged results require the calculation of millions of points in configuration space, even DFT becomes computationally too expensive, and this approach is limited to systems for which reliable force fields are available. This is often the case with biomolecular systems, for example, enzymes,10 but not for systems involving inorganic materials.

Herein, we provide a divide‐and‐conquer strategy that yields energy barriers, pre‐exponentials, and rate constants within chemical accuracy limits for systems with simulation cells of the order of 1000 atoms. We demonstrate this for the reactions of methanol with ethene, propene, and trans‐2‐butene catalyzed by an acidic zeolite (H‐MFI), for which reliable experimental data are available.11, 12 This is the key reaction of the hydrocarbon pool mechanism,13 which has been postulated for the industrially relevant14 conversion of methanol into olefins by acidic zeolites.

We started from a DFT potential‐energy surface and proceed in two ways: 1) To obtain improved energies for stationary points (reactant and transition structures), we applied a hybrid high level–low level quantum method that combines DFT for the full periodic system with second‐order Møller–Plesset perturbation theory (MP2) for the reaction site.15 To determine whether MP2 is accurate enough, we calculated coupled cluster (CC) corrections for sufficiently small models of the reaction site.16 2) We stayed with the DFT potential energy surface to calculate the normal modes and harmonic vibrational energies. We reduced the scaling of the 3N dimensional (N=number of atoms) anharmonic vibrational problem from exponential to linear by solving 3N one‐dimensional Schrödinger equations for each normal mode independently of all others.17 As finite‐size distortions are needed to calculate the one‐dimensional potentials, the rectilinear normal coordinates need to be represented in curvilinear internal coordinates.18 For example, this ensures that when rotating a molecule relative to the surface, its bond distances and bond angles do not change. This approach has proven to be chemically accurate in predicting equilibria for the adsorption of small alkanes in zeolites19 and of methane on MgO(001).17

For direct comparison with experiment, apparent barriers were considered, that is, the energy difference between the transition structure and the methanol–catalyst complex with the alkene molecule in the gas phase, and the computational protocol proposed in Refs. 17 and 19 was applied. Figure 1 shows the crystallographic unit cell of the above zeolite with the transition structure for the methylation of ethene (a×b×c=20.16×20.03×13.47 ų), which contains about 300 atoms. Periodic boundary conditions were applied to the DFT calculations, which used plane waves20 and applied the PBE functional21 with Grimme's semi‐empirical “D2” dispersion term.22 The subtractive scheme was used to obtain single‐point energies at the hybrid MP2/CBS:PBE+D2 level of theory.19 High‐level (MP2) calculations were performed on the cluster models shown in the Supporting Information, Figure S1 with the TURBOMOLE code.23 Gaussian basis sets with complete basis set (CBS) extrapolation were applied. Counterpoise corrections were made to account for the basis‐set superposition error, and Table S2 shows the individual energy contributions. The difference between the CCSD(T) coupled‐cluster and MP2 energies were evaluated for the smaller models shown in Figure S2.

Figure 1.

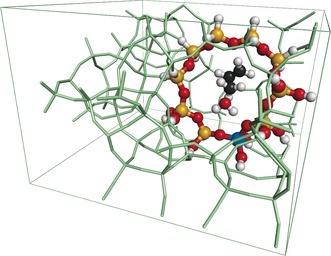
Unit‐cell view of the H‐MFI zeolite showing the embedded cluster used for the QM/QM calculations with the transition structure for the methylation of ethene at the active site. Aluminum blue, hydrogen white, oxygen red, silicon yellow. Non‐embedded framework atoms are shown in green.

Figure 2 and Figure 3 show the results for the enthalpy barriers, the pre‐exponentials, and the rate constants as a function of the alkene length at a pressure of 10⁻⁴ MPa and a temperature of 623 K. The labels “Anharm‐Hybrid” and “Harm‐Hybrid” refer to the anharmonic and harmonic vibrational energies, respectively, which were obtained by using finite‐difference normal‐mode distortions in internal coordinate representation.17 Comparison will also be made with previous results of Svelle and co‐workers,1 which differ from the present one in the following respect: In Svelle's report, the structures had been optimized and the harmonic frequencies had been calculated with PBE without including dispersion, whereas in the present study, PBE+D2 was used. Moreover, Svelle et al. used finite differences of Cartesian distortions to obtain the harmonic force constants and limited this to some of the atoms of the whole system (“partial Hessian”), whereas in the present study, the anharmonic and harmonic frequencies were calculated including all atoms. Unlike Svelle et al., who used a two‐point formula for the finite difference, the harmonic force constants of the present work were obtained from finite differences using all eight points of the curvilinear sampling of the normal mode.17

Figure 2.

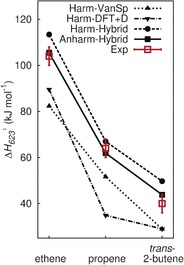
Calculated heats of activation (623 K) for ethene, propene, and trans‐2‐butene compared to experiment (“Exp”).11, 12 “Harm‐Hybrid” and “Anharm‐Hybrid” results were obtained from the hybrid MP2:DFT+D energies and the harmonic and anharmonic vibrational frequencies, respectively. The DFT+D results obtained with harmonic vibrational frequencies in this study (“Harm‐DFT+D”) and those obtained for a cluster of 46 tetrahedra by Van Speybroeck et al.5 (“Harm‐VanSp”) are also shown.

Figure 3.

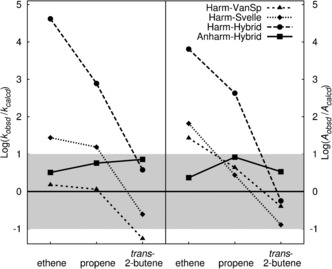
Logarithm of the observed/calculated ratios for the rate constants (left) and pre‐exponentials (right). “Anharm‐Hybrid” and “Harm‐Hybrid” refer to results calculated with anharmonic and harmonic frequencies, respectively, whereas “Harm‐Svelle” refers to harmonic frequencies obtained for a part of the system.1 The “Harm‐VanSp” results5 were obtained with a 46 tetrahedra cluster model. The gray region represents a deviation of ±1 order of magnitude from the observed values.

The experimental values for the enthalpy barriers, ΔH ₆₂₃ ^≠, in Figure 2 are the Arrhenius activation energies minus RT (see the Supporting Information).9 Table S2 shows the different contributions to ΔH ₆₂₃ ^≠. As expected,24 PBE+D2 underestimates the energy barriers by about 20 kJ mol⁻¹, which corresponds to a factor of about 50 in the rate constant at 623 K. For the hybrid MP2:PBE+D2 results, including anharmonicity lowers the barrier by a small, but significant amount (7, 4, and 3 kJ mol⁻¹ for ethene, propene and trans‐2‐butene, respectively), and brings them into agreement with experiment within chemical accuracy limits (±4 kJ mol⁻¹, indicated by vertical bars in Figure 2).

Figure 3 shows the ratios between the observed and calculated rate constants and pre‐exponentials (see the Supporting Information for working equations) obtained with the different methods. A deviation of a factor of ten reflects the experimental uncertainty5, 25 and is considered “accurate”. This is indicated by the gray region in the logarithmic plot of Figure 3. Our anharmonic results, together with the hybrid MP2:DFT+D method for the energies, yield uniformly good agreement for both the pre‐exponentials and rate constants. For all three systems studied, the observed/calculated ratios are between 3.3 and 7.3 for the rate constants, and between 3.4 and 8.4 for the pre‐exponentials (see also Table S3). Effects such as barrier re‐crossing are ignored in our TST approach, and remaining uncertainties about the reaction coordinate do not seem to affect the results beyond chemical‐accuracy limits.

For all harmonic models, the observed/calculated ratios of the pre‐exponential vary with the size of the alkene molecule over several orders of magnitude. This shows that the amazing agreement with experiment for particular cases, here for propene, is due to fortuitous error cancellation. Among the harmonic models, the variation is largest for the present calculations, which consider all 3N vibrations, whereas “Harm‐Svelle”1 and “Harm‐VanSp”5 consider only a limited number of vibrational degrees of freedom.

We conclude that the development of quantum‐mechanical methodology, computational algorithms, and computer technology has made it possible to rigorously and chemically accurately predict rate constants for large systems (of the order of 1000 atoms), and thus to contribute significantly to our atomistic understanding of relevant problems, for example in heterogeneous catalysis.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

G. Piccini, M. Alessio, J. Sauer, Angew. Chem. Int. Ed. 2016, 55, 5235.