Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Mar 8;16(4):2407–2412. doi: 10.1021/acs.nanolett.5b05211

Transition from Reconstruction toward Thin Film on the (110) Surface of Strontium Titanate

Z Wang †,*, A Loon ‡, A Subramanian ‡, S Gerhold †, E McDermott §, J A Enterkin ∥, M Hieckel †, B C Russell ⊥, R J Green #, A Moewes #, J Guo ∇, P Blaha §, M R Castell ⊥, U Diebold †, L D Marks ‡
PMCID: PMC4834633  PMID: 26954064

Abstract

graphic file with name nl-2015-05211a_0005.jpg

The surfaces of metal oxides often are reconstructed with a geometry and composition that is considerably different from a simple termination of the bulk. Such structures can also be viewed as ultrathin films, epitaxed on a substrate. Here, the reconstructions of the SrTiO3 (110) surface are studied combining scanning tunneling microscopy (STM), transmission electron diffraction, and X-ray absorption spectroscopy (XAS), and analyzed with density functional theory calculations. Whereas SrTiO3 (110) invariably terminates with an overlayer of titania, with increasing density its structure switches from n × 1 to 2 × n. At the same time the coordination of the Ti atoms changes from a network of corner-sharing tetrahedra to a double layer of edge-shared octahedra with bridging units of octahedrally coordinated strontium. This transition from the n × 1 to 2 × n reconstructions is a transition from a pseudomorphically stabilized tetrahedral network toward an octahedral titania thin film with stress-relief from octahedral strontia units at the surface.

Keywords: Surface structure, reconstruction, thin film nanostructures, epitaxy, DFT

The increasing interest in SrTiO3 as a functional ceramic material is due to its broad variety of optical, electrical, and chemical properties. The surfaces and interfaces are particularly important in the field of oxide electronics where it is used both as a substrate and an active material (e.g., refs (1−4)), and the electronic properties can be modulated through tailored epitaxial film growth (e.g., refs (5−7)). The surfaces also have interesting properties for applications such as model catalytic supports.8−10 Although strontium titanate is the prototype perovskite, its surface structures make most other materials seem simple with a very large number of different reconstructions on the (001)11 and (111)12 surfaces, many of which are unsolved.

The surface reconstructions of simple binary oxides under oxidizing conditions involve only atomic rearrangements, but ternary oxides such as SrTiO3 are more complex. There is an additional degree of freedom associated with changes in the surface composition, and all the reconstructions solved to date are known to be TiO2 rich. The (110) surface of SrTiO3 displays a range of different reconstructions (see ref (13) and references therein). The first set of structures to be decoded was a family of n × 1 surface reconstructions containing corner-shared tetrahedral TiO4 units arranged in a homologous series of valence neutral reconstructions.13 The structural details have been refined by STM.14 While many features are now known, for instance, the role of strontium at domain-boundaries,15 these are not the only structures that form on this surface. Of particular relevance here, the n × 1 reconstructions can coexist with small regions of 1 × n surface structures, which STM images indicate occur near surface steps.

The n × 1 reconstructions are not simply a minor adjustment of the atomic positions; instead, there is a complete change in the local titanium co-ordination. The local band gap is substantially larger, and all local properties will be quite different so they should be considered as a monolayer of a different phase at the surface, that is, heteroepitaxial growth of an oxide on an oxide. A subtle issue is how does the surface/thin film structure develop as the surface excess of TiO2 increases toward the limit at high excess of a heteroepitaxial TiO2 thin film. Does the initial one or two atomic layers reconstruction template further layers? Does the (110) surface transform back from the unusual tetrahedral co-ordination of the n × 1 structures to a more standard octahedral structure? It is established that local bonding considerations matter for the monolayer thickness surface reconstructions13,16 but as the excess TiO2 increases will the system start to be dominated by the energetics of conventional epitaxial growth theory with, for instance, misfit dislocations and stress relief rather than local bonding dominating the thermodynamics?

These issues have recently become of increasing interest for oxides following the observation that for optimal growth of certain oxides by molecular beam epitaxy (MBE) the deposition order that is required is different to that of the final desired material.17−19 This is analogous to many other types of growth, for instance conventional MBE of III–V semiconductors where the best results require a surface rich in the V compound and the excess acts as a surfactant. A similar role for surfactants has also been recently found for the SrTiO3 (001) surface where optimal growth of low defect material by hybrid MBE occurs when in reflection high-energy electron diffraction a c(4 × 4) structure is present during growth,20 this reconstruction being one which contains chemisorbed water21,22 which presumably acts as the surfactant. While phenomena such as surfactant controlling growth are well established for epitaxial growth, one does not often consider a surface reconstruction as a surfactant–but clearly the c(4 × 4) acts as one and this could be a general phenomena. For oxides, are surface structures, epitaxy and growth always intimately linked or is there an evolution from one to another in controlling the final material?

We report here a step toward a better understanding of how oxide systems evolve from the monolayer to multilayer, from monolayer surface reconstruction toward multilayer heteroepitaxial thin film. This is done through an analysis of the high TiO2 coverage 2 ×n reconstructions on the (110) SrTiO3 surface from scanning tunneling microscopy, transmission electron diffraction and density functional theory calculations complemented by X-ray absorption spectroscopy. The adjustment of surface structures is performed in the following two ways: by vapor-depositing appropriate amounts of Ti and Sr and annealing in O2 at moderate temperatures as reported earlier,23 and by simple oxygen anneal at high temperatures. While the STM images of the external surface imply a structure similar to lepidocrocite titania nanosheets,24−26 electron diffraction data show that it is more complicated with partial occupancy and disorder of the second-layer titanium sites, which is a conclusion verified by DFT energetics. The surface switches from tetrahedral TiO4 coordination to a double layer of edge-shared TiO6 octahedra with bridging units of octahedral strontium, which play the role of stress relaxation defects with the transformation dominated by stress considerations. This transition toward more conventional epitaxial growth occurs for about 2.75 monolayers excess of TiO2. There is still strain in the system with stress relief taking place at the top surface rather than at the interface with issues of local bonding also important. The data indicate that it will only be after more than 3.5 monolayers that the system will start to approach a conventional thin film structure with conventional epitaxial terms dominant.

Methods

The SrTiO3 (110) samples were studied in several different laboratories by various techniques. The two types of surface reconstructions, n × 1 and 2 × n, could be reproducibly obtained using two different approaches; these are referred to as low-temperature and high-temperature samples.

The high-temperature samples were used for the TEM studies as well as some STM imaging. As described previously,13 they were prepared by ion-beam sputtering followed by annealing in the temperature range 950–1100 °C in 1 atm of O2 for ∼1 h as well as as part of a more extensive study as a function of time and temperature.27 In all cases high purity single crystal SrTiO3 (110) wafers (MTI Corporation) were prepared using mechanical polishing and dimpling then annealed with slower cooling rates (∼0.25 K/sec). Electron diffraction data were collected using a Hitachi H8100 at 200 kV with the intensities extracted using the edm code.28

The low-temperature samples were used for the STM (Figure 1) and for the XAS measurements and were checked with LEED in both cases (see Figure S1). Nb-doped (0.5 wt %) SrTiO3 (110) single crystal samples were purchased from MaTecK, Germany. In the low-temperature approach, the surfaces were initially sputtered and annealed at moderate temperature. By further deposition of Sr or Ti, followed by annealing at moderate temperatures in O2, the surface structure could be precisely tuned according to the surface phase map shown in Figure S2 in Supporting Information and ref (23). Here the surface stoichiometry, and thus structure, was adjusted until a desired monophased surface was observed via STM and/or a sharp low-energy electron diffraction (LEED) pattern was present.29,30 For the results shown in Figure 1, the clean 4 × 1 surface was obtained by cycles of Ar+ sputtering followed by annealing in 2 × 10–6 mbar oxygen at 900 °C for 1 h,31 and the 2 × 5 surface was obtained by depositing Ti at 600–700 °C in 6 × 10–6 mbar O2. STM images were obtained in a SPECS UHV system with a base pressure of 1 × 10–10 mbar. XAS was performed at room temperature at the I311 beamline at Max-lab,32 and structures were ascertained by LEED. A Scienta electron analyzer was used to measure the integrated intensity of the surface-sensitive Ti LM,M Auger lines with the detector in a surface-grazing orientation, as well as the more bulk-sensitive total secondary electron yield. The Ti L2,3 spectra were analyzed using the CTM4XAS code.33

Figure 1.

Figure 1

Open in a new tab

STM images of the 4 × 1 (a) and two kinds of 2 × 5 surfaces (b,c). The arrows in between indicate that these structures can be switched reversibly by depositing Ti/Sr followed by annealing. The Sr single adatom on the 4 × 1 surface is labeled by an arrow. The insets in (b,c) show magnified views, superimposed with simulated STM images of 2 × 5b in (b) and 2 × 5a in (c).

Remarkably, both the high- and the low-temperature approaches gives the same types of surface reconstructions. This is clear from the evolution of the electron diffraction patterns and also from the fact that the STM images of 4 × 1 structure, observed on low-temperature samples, are in remarkably good agreement with the structural model proposed based on TEM results obtained for high-temperature samples. The XAS data shown below further confirm the 4 × 1 model, which is based on tetrahedral building blocks as a structural motif. In addition, STM data described in ref (34), which was collected using higher-temperature annealing for comparable times, are comparable to our low-temperature STM results.

DFT calculations were performed with the all-electron augmented plane wave + local orbitals WIEN2K code.35 The surface in-plane lattice parameters were those of the DFT optimized bulk cell with ∼1.2 nm of vacuum. STM images were simulated using the Tersoff-Hamann approximation.36 Technical parameters were muffin-tin radii of 1.6, 2.36, and 1.75 Bohrs for O, Sr, and Ti, respectively, a min(RMT)*Kmax of 6.25, Brillouin-zone sampling equivalent to a 6 × 4 in-plane mesh for a (110) 1 × 1 cell with a Mermin functional. The electron density and all atomic positions were simultaneously converged using a quasi-Newton algorithm37 to better than 0.01 eV/1 × 1 surface cell. Crystallographic Information Format (CIF) files for all the converged structures are in the Supporting Information. The PBEsol38 generalized gradient approximation as well as the revTPSSh method39 were used with 0.5 on-site exact-exchange based on earlier work.40 The surface enthalpy per (1 × 1) surface unit cell (Esurf) was calculated as Esurf = (Eslab – ESTO*NSTO – ETO*NTO)/(2*N1×1), where Eslab is the total enthalpy of the slab, ESTO fis or one bulk SrTiO3 unit cell, NSTO is the number of bulk SrTiO3 unit cells, ETO is bulk rutile TiO2, NTO is the number of excess TiO2 units, and (N1×1) is the number of (1 × 1) cells. Consistency checks indicated an error in the energies of approximately 0.1 eV/1 × 1 cell (∼76 mJ/m2, 10 kJ/mol).

Results

Surface Structural Transition

Depending upon the surface cation coverage, the SrTiO3 (110) surface exhibits two distinct series of reconstructions, n × 1 and 2 × n. These reconstructions were obtained reversibly by depositing Ti/Sr followed by annealing (see Figure 1 and Figure S2), and the two reconstructions can coexist.13 The n × 1 structures are a homologous series composed a single layer of tetrahedrally coordinated TiO4 residing directly on bulk truncated SrTiO3 (110),13 appearing as quasi-one-dimensional stripes along the [11̅0] direction (see the STM image of the 4 × 1 in Figure 1a). The 2 × n (n = 4,5) structures show wider stripes along the [001] direction, separated by trenches with bright protrusions often, but not always, in every other row, leading to a 2× periodicity along the [001] direction. We note for later that this doubling was not observed for the STM images of samples prepared at high temperatures. Excluding the trench structure, the STM images are similar to published data for lepidocrocite titania nanosheets.24−26

The possibility exists that for some tip conditions the (0,0,2) repeat might not be observable and appears as a smeared (0,0,1) repeat. A careful analysis showed that there were regions where both repeats occurred, as shown in Figure S3. This verifies that there are two types of ordering although they are only local and the system is better considered as a surface-solution of different compositions, similar to a bulk solid solution.

X-ray Absorption Spectroscopy

To clarify the structural transition, we performed XAS measurements using the Auger electron yield (AEY) and the secondary electron yield (SEY), which provide fingerprints of the local coordination environments for Ti atoms in the near-surface region. In AEY, the X-ray beam excites a photoelectron for a specific state; and the Auger electron emitted when the state decays are detected. As electrons with a kinetic energy of several hundred electronvolts strongly interact with solids, their inelastic mean free path (IMFP) is short.41 For the specific case of Ti LM,M transitions (450 eV) in grazing exit we estimate the IMFP as 1 nm. This makes XAS-AEY a very surface sensitive technique, where monolayers are easily detectable.42 In contrast, in SEY the photoelectrons emitted are detected as secondaries leaving the surface in an energy window of 0–20 eV, that is, with a somewhat larger IMFP. Thus, this mode probes layers deeper in the bulk.43

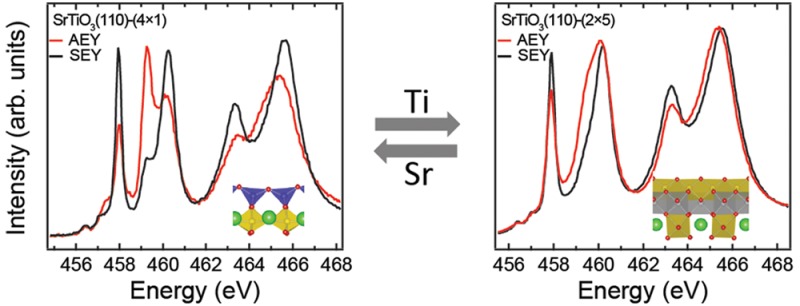
Striking differences were observed between the AEY and SEY on the 4 × 1 surface (see Figure 2a). Two main peaks located at 458 and 460 eV correspond to Ti 2p3/2→3d transitions, while an additional shoulder appears at 459 eV in the SEY (see the black curve in Figure 2a). The shoulder becomes pronounced and the two main peaks are significantly weakened in the AEY (see the red curve in Figure 2a). Similar effects were present in the Ti L2 spectra (2p1/2→3d transitions).43

Figure 2.

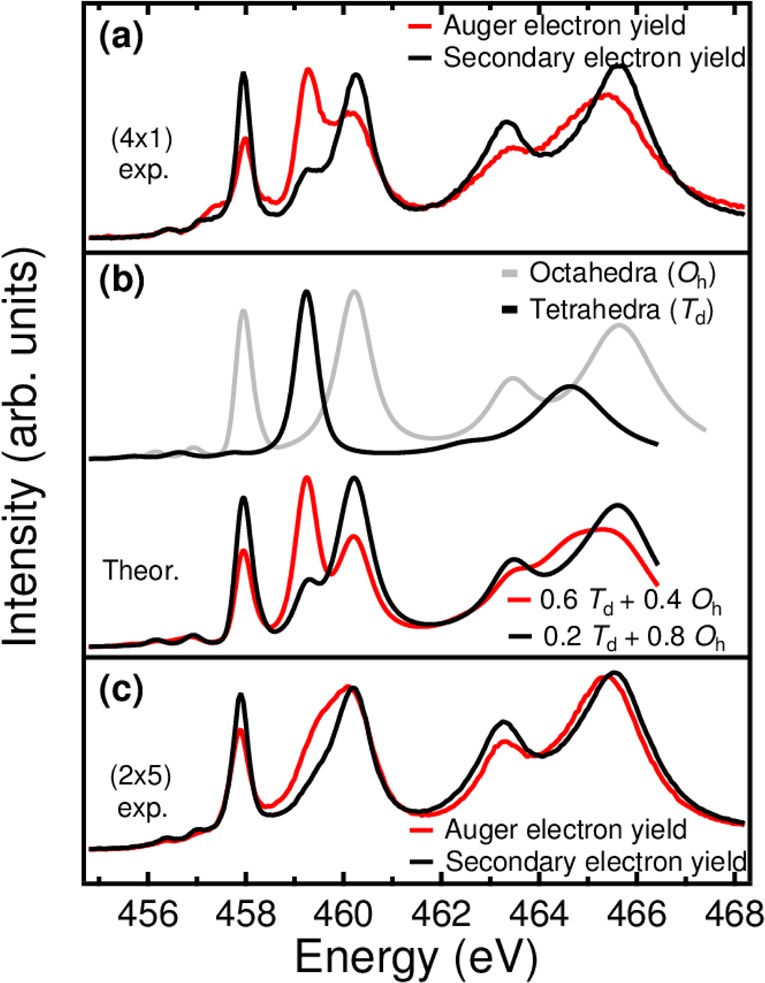
Figure 2

Open in a new tab

Ti L2,3 XAS on the 4 × 1 and 2 × 5 surface. (a) Experimental Ti L2,3 XAS measured with AEY (red curve) and SEY (black curve) mode, respectively. (b) Simulated Ti L2,3 XAS of Ti ions in octahedra (Oh) (gray) and tetrahedra (Td) (black) coordination. The low panel shows the spectra with combination of Oh and Td. (c) Experimental Ti L2,3 XAS measured with AEY (red) and SEY (black) electron yield on the 2 × 5 surface.

To understand the Ti L2,3 spectra, we performed crystal-field multiplet calculations of a Ti4+ ion in octahedral (Oh) and tetrahedral (Td) symmetry using the CTM4XAS code.33,44 As shown in Figure 2b the simulated spectra of Ti in Oh and Td symmetry agree well with previously published experimental spectra for BaTiO3 and Ba2TiO4 with octahedrally and tetrahedrally coordinated Ti ions, respectively.45 Very good agreement is achieved between the simulated combination spectra of Oh and Td and experimental AEY and SEY spectra (see Figure 2b). These results verify that the 4 × 1 surface is composed of tetrahedrally coordinated TiO4 units.

The Ti L2,3 XAS spectra on the 2 × 5 surface show differences between the AEY and SEY data, and significantly differ from the spectra of the 4 × 1 surface, indicating that the Ti coordination environment changes when the surface structure changes. We note that the spectrum measured with the surface sensitive AEY mode resembles that of a lepidocrocite-like titania nanosheet46 implying some structural similarity. Furthermore, both valence band and core-level photoemission spectra indicate that the valence of Ti is 4+ and the 2 × 5 surface is insulating (see Figure S4), which is in line with a surface prepared in an oxygen atmosphere.

Structural Model

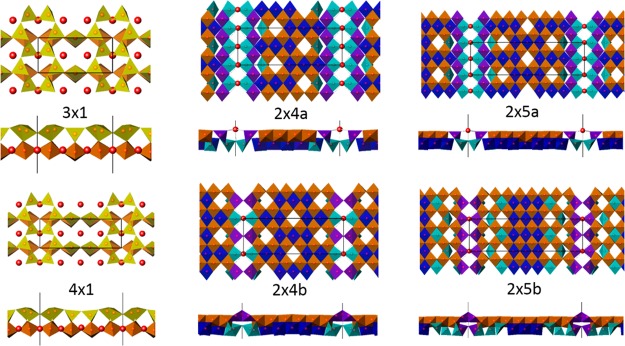
Upon the basis of a structure similar to lepidocrocite, we now turn to an identification of the bright feature in the rows, as well the structure below the outermost layer that is invisible to STM. With full occupancy of all the Ti sites in the second layer, the surface would be a metallic conductor, similar to previous reports of lepidocrocite-like titania as cited earlier. Reducing the second-layer occupancy of titanium leads to a valence-neutral and insulating surface. From Sr deposition experiments, there was a circumstantial link between the bright features and the presence of extra Sr atoms. From a detailed DFT analysis of different occupancies, and coupling this with refinements against the diffraction data, we isolated two homologous series of 2 × n structures as shown in Figure 3, together with the 3 × 1 and 4 × 1 for reference. The first, 2 × na, contains two Sr atoms in the trench every unit cell along the “2” direction with a separation of (0,0,1), while the second 2 × nb contains one every other with a (0,0,2) spacing and a bridging TiOx unit. Both are strictly 2 × n structures, although the 2 × na family will not appear so in STM images. Careful analysis of the diffraction data (see Figure S5) indicated that the “2×” component was disordered. Because of this disorder, the Shelx code47 was used to refine the diffraction data against a combination of either 2 × 4a,b or 2 × 5a,b, that is, statistical fractional occupancy, yielding a crystallographic R1 of 15% with ∼1/4 coverage of 2 × 4a, and an R1 of 22% with 56 measurements for the 2 × 5 with also ∼1/4 coverage of 2 × 5a, see Tables S1 and S2. While these are high for a bulk structure, they are good numbers for a surface indicating that one can have confidence in the structures.40 For completeness, the DFT calculations indicate the possibility of additional higher-TiO2 coverage structures without any Sr in the trenches but because we have no diffraction data to confirm this we will not pursue these further here.

Figure 3.

Figure 3

Open in a new tab

Polyhedral representations of the structures (color online), top normal to the surface and below from the side. The 3 × 1 and 4 × 1 octahedra are brown and tetrahedra are golden; in all the others, octahedra in the outermost layer are brown, dark blue are in the 2nd layerm while TiO5[] are purple in the top layer and light green in the second layer.

The DFT convex-hull is shown in Figure 4 with error-bars of 0.1 eV/1 × 1 cell. This is a conventional representation of the energetics versus composition, and here the enthalpy versus surface excess of TiO2. The lower envelope describes the single or two-phase coexistence regimes as a function of surface composition. The 2 × na family occur at lower surface excess of TiO2, consistent with coexistence with n × 1 reconstructions for the high-temperature samples.13 At the high TiO2 coverage (right) of the convex hull both 2 × n families are converging to a straight line to a nominal 2 × ∞ structure (see Supporting Information CIF file). For a straight line, one expects extensive coexistence of structures due to the entropy of mixing similar to that found for the (111) surface,12 which is consistent with the experimental results.

Figure 4.

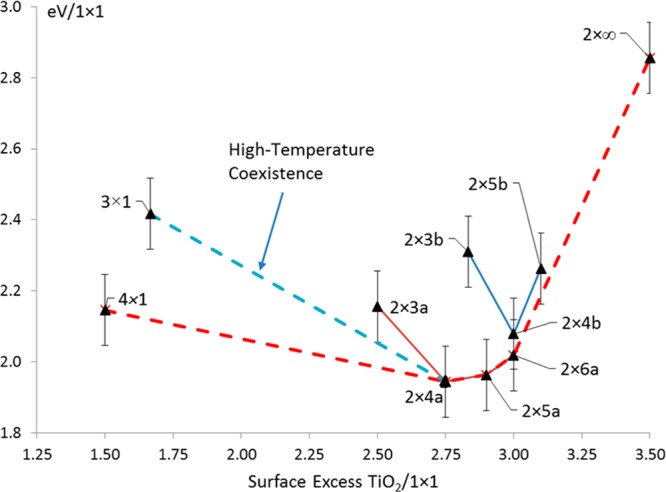
Figure 4

Open in a new tab

Convex-hull construction (red) of the surface enthalpies in eV/1 × 1 (y-axis) for different TiO2 excess per 1 × 1 unit cell (x-axis), revTP SSh functional. Error bars are 0.1 eV/1 × 1 cell. Lines are shown for the 2 × na and 2 × nb families, as well as the 2-phase coexistence (blue dashes) between the 3 × 1 and 2 × 4a structures observed for the samples prepared at higher temperatures.13

Turning to the structures, all the atomic coordinates are available in the Supporting Information as CIF files. The 2 × n surface structures are good insulators with a network of Oh coordinated TiO6 or TiO5[] (where [] is either a very long Ti–O distance or a vacant site) obeying bond-valence criteria.16 The arrangement of Ti in the second layer follows bonding considerations. In the top layer (visible in the STM images) all the available titanium Oh sites are filled except at the origin, but there is only partial occupancy in the second layer. Upon the basis of exploring all the different possibilities, the occupancies follow some simple rules: (i) all the oxygen sites are filled; (ii) the total number of occupied sites is that to yield valence neutrality of the overall structure; (iii) vacant sites do not want to be adjacent along either the long axis of the structure, or the short axis; (iv) vacant sites want to be as far apart as possible.

Somewhat unusual are the octahedral SrO5[] units, which have coordination similar to that in bulk SrO but with longer bond lengths. Using as a reference the bond-valence sum (BVS) for bulk SrO of 1.73, the Sr atoms at the surface are slightly under-bonded for the structures with only one Sr per 2 × n cell with BVS of 1.56 (2 × 4a) and 1.62, 1.69 (2 × 5a); and severely underbonded with double Sr occupancy with BVS of 1.18 (2 × 4b), 1.21 (2 × 5b). However, the oxygens to which they are bonded all have reasonable BVS numbers of 1.6–1.8. We note that the strontium is a hard Sr2+ ion and is present mainly to satisfy ionic neutrality rather than having true covalent bonding, whereas the oxygens have valence electrons and their reasonable BVS numbers are indicative of appropriate coordination and accommodation of the 2p valence electrons, a necessary condition for a stable surface.

Discussion

To understand the difference between the low-temperature and high-temperature experiments, we note that ordering can be relatively slow. While oxygen atoms can diffuse relatively fast, the activation energy barriers for Ti/Sr cation migration is higher. STM is a local probe whereas the electron diffraction measurements are statistical averages over the microns coherence width of the electron beam. There is sufficient disorder in the STM images for the low-temperature samples that diffraction data would show streaking rather than sharp spots. Without diffraction data to delineate what is below the outermost surface for some of the probably metastable surfaces seen by STM in the low-temperature samples, we will not speculate about their detailed structure. With the higher-temperature experiments, the convex-hull energies are consistent with the experimental data.

The reason the surface switches from tetrahedral to octahedral coordination is stress- and packing density-driven. The tetrahedral coordination in the n × 1 reconstructions is stabilized by large tensile strains13 which can occur for a single monolayer with a low TiO2 coverage. This is comparable to pseudomorphic growth where the substrate drives the structure of a thin film, here it is driving stabilization of tetrahedral co-ordination. With a higher coverage of TiO2 the stresses and strain energy required to maintain tetrahedral co-ordination become excessive, and the lower energy octahedral coordination will be favored, although this is still strained as evidenced by the underbonding apparent in the BVS numbers. Because of the higher coordination numbers of the oxygen atoms at the surface, the Ti–O bond lengths in the surface plane are longer with approximate spacings along the “n” direction in fractional coordinates of (0,1/7) and (0,1/9) for the 2 × 4 and 2 × 5 structures, respectively, with the outermost Ti at the positions (0,m/14) and (0,m/18) respectively, with m even and the second layer partially occupied sites at odd values, leading to a net compressive strain. Stress relief occurs via the formation of a discontinuous essentially 1D reconstruction with a long repeat along the n direction with additional Sr atoms to satisfy valence neutrality as well as to coordinate with the oxygen atoms at the edges of the rows. These bridging units play the same role of stress relief of the overlayer with respect to the underlying bulk SrTiO3 as misfit dislocations would in classic epitaxial strained layer growth. At higher coverages (>4 monolayers) the STM images suggest a transition to a metallic structure closer to lepidocrocite titania nanosheets.24−26 We suspect there are misfit dislocations at the buried interface although the exact Ti atom distribution below the outermost layer accessible to STM imaging is unclear so we will not speculate further here.

These results indicate that the evolution of an oxide thin film from a reconstruction toward a multilayer epitaxial thin film can involve a sequence of structures with competing energetics. This phenomenon probably occurs in many other thin oxide films such as those of interest for oxide electronics. As mentioned in the introduction there is already evidence that controlling these surface structures can be more important than how layers of an oxide structure are deposited by MBE.17−19 There may well be many complex structural issues which will merit attention as interest develops in producing oxide multilayers with more complex structures with high reproducibility for commercial applications. There are already other indications of this in the literature; for instance, how heteroepitaxial oxide films grown on SrTiO3 (001) can depend upon the initial surface structure48,49 as can homoepitaxy.20

Acknowledgments

L.D.M. acknowledges funding by the DOE on Grant DE-FG02-01ER45945; A.L. and A.S. funding by the NSF on Grant DMR-1206320; J.E. support from Northwestern University Institute for Catalysis in Energy Processes (ICEP) on Grant DOE DE-FG02-03-ER15457; B.C.R., M.R.C., and L.D.M. by the NSF on Grant DMR-0710643. S.G. and E.M. acknowledge funding from the Austrian FWF under Project W1243 (Solids4Fun). Z.M. and S.G. acknowledge support by the Austrian Science Fund (FWF), project F45-07 (FOXSI), and U.D. acknowledges support by the ERC Advanced Grant “OxideSurfaces”. U.D. and M.R.C. acknowledge support from COST Action CM1104. A.M. acknowledges support by the Natural Sciences and Engineering Council of Canada (NSERC) and the Canada Research Program. R.J.G. acknowledges support by NSERC. The authors acknowledge useful discussions with J. Redinger and F. Mittendorfer, Vienna University of Technology, and help with the XAS measurements by Karina Schulte, MAX IV Laboratory, Lund University.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b05211.

  • LEED patterns, surface structure diagram, X-ray photoemission spectra, transmission electron diffraction pattern and two tables supporting the conclusions presented in the main text. (PDF)

  • (CIF)

  • (CIF)

  • (CIF)

  • (CIF)

  • (CIF)

  • (CIF)

  • (CIF)

  • (CIF)

  • (CIF)

  • (CIF)

The authors declare no competing financial interest.

This paper was published on the Web on March 11, 2015, with minor errors in the last sentence of the caption for Figure 1. The corrected version was reposted on April 13, 2016.

Supplementary Material

nl5b05211_si_001.pdf (1.2MB, pdf)
nl5b05211_si_002.cif (4.4KB, cif)
nl5b05211_si_003.cif (4.5KB, cif)
nl5b05211_si_004.cif (5.1KB, cif)
nl5b05211_si_005.cif (5.6KB, cif)
nl5b05211_si_006.cif (2.9KB, cif)
nl5b05211_si_007.cif (3.3KB, cif)
nl5b05211_si_008.cif (6.5KB, cif)
nl5b05211_si_009.cif (6.6KB, cif)
nl5b05211_si_010.cif (7.2KB, cif)
nl5b05211_si_011.cif (2.4KB, cif)

References

  1. Ohtomo A.; Hwang H. Y. Nature 2004, 427 (6973), 423–6. 10.1038/nature02308. [DOI] [PubMed] [Google Scholar]
  2. Santander-Syro A. F.; Copie O.; Kondo T.; Fortuna F.; Pailhes S.; Weht R.; Qiu X. G.; Bertran F.; Nicolaou A.; Taleb-Ibrahimi A.; Le Fevre P.; Herranz G.; Bibes M.; Reyren N.; Apertet Y.; Lecoeur P.; Barthelemy A.; Rozenberg M. J. Nature 2011, 469 (7329), 189–193. 10.1038/nature09720. [DOI] [PubMed] [Google Scholar]
  3. Meevasana W.; King P. D.; He R. H.; Mo S. K.; Hashimoto M.; Tamai A.; Songsiriritthigul P.; Baumberger F.; Shen Z. X. Nat. Mater. 2011, 10 (2), 114–8. 10.1038/nmat2943. [DOI] [PubMed] [Google Scholar]
  4. Wang Z.; Zhong Z.; Hao X.; Gerhold S.; Stoger B.; Schmid M.; Sanchez-Barriga J.; Varykhalov A.; Franchini C.; Held K.; Diebold U. Proc. Natl. Acad. Sci. U. S. A. 2014, 111 (11), 3933–7. 10.1073/pnas.1318304111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Mannhart J.; Schlom D. G. Science 2010, 327 (5973), 1607–11. 10.1126/science.1181862. [DOI] [PubMed] [Google Scholar]
  6. Zubko P.; Gariglio S.; Gabay M.; Ghosez P.; Triscone J. M. Annu. Rev. Condens. Matter Phys. 2011, 2 (1), 141–165. 10.1146/annurev-conmatphys-062910-140445. [DOI] [Google Scholar]
  7. Hwang H. Y.; Iwasa Y.; Kawasaki M.; Keimer B.; Nagaosa N.; Tokura Y. Nat. Mater. 2012, 11 (2), 103–13. 10.1038/nmat3223. [DOI] [PubMed] [Google Scholar]
  8. Lin Y.; Wen J.; Hu L.; Kennedy R. M.; Stair P. C.; Poeppelmeier K. R.; Marks L. D. Phys. Rev. Lett. 2013, 111, 156101. 10.1103/PhysRevLett.111.156101. [DOI] [PubMed] [Google Scholar]
  9. Enterkin J. A.; Poeppelmeier K. R.; Marks L. D. Nano Lett. 2011, 11 (3), 993–7. 10.1021/nl104263j. [DOI] [PubMed] [Google Scholar]
  10. Enterkin J. A.; Setthapun W.; Elam J. W.; Christensen S. T.; Rabuffetti F. A.; Marks L. D.; Stair P. C.; Poeppelmeier K. R.; Marshall C. L. ACS Catal. 2011, 1 (6), 629–635. 10.1021/cs200092c. [DOI] [Google Scholar]
  11. Newell D. T.The Surface Structure and Reconstructions of SrTiO3(001); University of Oxford: Oxford, U.K., 2007. [Google Scholar]
  12. Marks L. D.; Chiaramonti A. N.; Rahman S. U.; Castell M. R. Phys. Rev. Lett. 2015, 114 (22), 226101. 10.1103/PhysRevLett.114.226101. [DOI] [PubMed] [Google Scholar]
  13. Enterkin J. A.; Subramanian A. K.; Russell B. C.; Castell M. R.; Poeppelmeier K. R.; Marks L. D. Nat. Mater. 2010, 9 (3), 245–8. 10.1038/nmat2636. [DOI] [PubMed] [Google Scholar]
  14. Li F.; Wang Z.; Meng S.; Sun Y.; Yang J.; Guo Q.; Guo J. Phys. Rev. Lett. 2011, 107 (3), 036103. 10.1103/PhysRevLett.107.036103. [DOI] [PubMed] [Google Scholar]
  15. Wang Z.; Li F.; Meng S.; Zhang J.; Plummer E. W.; Diebold U.; Guo J. Phys. Rev. Lett. 2013, 111 (5), 056101. 10.1103/PhysRevLett.111.056101. [DOI] [PubMed] [Google Scholar]
  16. Enterkin J. A.; Becerra-Toledo A. E.; Poeppelmeier K. R.; Marks L. D. Surf. Sci. 2012, 606 (3–4), 344–355. 10.1016/j.susc.2011.10.018. [DOI] [Google Scholar]
  17. Wu C.; Kruska K.; Castell M. R. Surf. Sci. 2013, 618, 94–100. 10.1016/j.susc.2013.08.019. [DOI] [Google Scholar]
  18. Lee J. H.; Luo G.; Tung I. C.; Chang S. H.; Luo Z.; Malshe M.; Gadre M.; Bhattacharya A.; Nakhmanson S. M.; Eastman J. A.; Hong H.; Jellinek J.; Morgan D.; Fong D. D.; Freeland J. W. Nat. Mater. 2014, 13 (9), 879–83. 10.1038/nmat4039. [DOI] [PubMed] [Google Scholar]
  19. Nie Y. F.; Zhu Y.; Lee C. H.; Kourkoutis L. F.; Mundy J. A.; Junquera J.; Ghosez P.; Baek D. J.; Sung S.; Xi X. X.; Shen K. M.; Muller D. A.; Schlom D. G. Nat. Commun. 2014, 5, 4530. 10.1038/ncomms5530. [DOI] [PubMed] [Google Scholar]
  20. Kajdos A. P.; Stemmer S. Appl. Phys. Lett. 2014, 105 (19), 191901. 10.1063/1.4901726. [DOI] [Google Scholar]
  21. Becerra-Toledo A. E.; Castell M. R.; Marks L. D. Surf. Sci. 2012, 606 (7–8), 762–765. 10.1016/j.susc.2012.01.008. [DOI] [Google Scholar]
  22. Becerra-Toledo A. E.; Enterkin J. A.; Kienzle D. M.; Marks L. D. Surf. Sci. 2012, 606 (9–10), 791–802. 10.1016/j.susc.2012.01.010. [DOI] [Google Scholar]
  23. Wang Z. M.; Yang F.; Zhang Z. Q.; Tang Y. Y.; Feng J. G.; Wu K. H.; Guo Q. L.; Guo J. D. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83 (15), 155453. 10.1103/PhysRevB.83.155453. [DOI] [Google Scholar]
  24. Orzali T.; Casarin M.; Granozzi G.; Sambi M.; Vittadini A. Phys. Rev. Lett. 2006, 97 (15), 156101. 10.1103/PhysRevLett.97.156101. [DOI] [PubMed] [Google Scholar]
  25. Vittadini A.; Casarin M. Theor. Chem. Acc. 2008, 120 (4–6), 551–556. 10.1007/s00214-008-0425-8. [DOI] [Google Scholar]
  26. Atrei A.; Ferrari A. M.; Szieberth D.; Cortigiani B.; Rovida G. Phys. Chem. Chem. Phys. 2010, 12 (37), 11587–95. 10.1039/c0cp00173b. [DOI] [PubMed] [Google Scholar]
  27. Loon A.Reconstructions on Strontium Titanate (110) Surfaces at Various Annealing Conditions; Northwestern University: Evanston, IL, 2011. [Google Scholar]
  28. Kilaas R.; Marks L. D.; Own C. S. Ultramicroscopy 2005, 102 (3), 233–7. 10.1016/j.ultramic.2004.10.004. [DOI] [PubMed] [Google Scholar]
  29. Wang Z.; Hao X.; Gerhold S.; Novotny Z.; Franchini C.; McDermott E.; Schulte K.; Schmid M.; Diebold U. J. Phys. Chem. C 2013, 117 (49), 26060–26069. 10.1021/jp407889h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wang Z.; Hao X.; Gerhold S.; Mares P.; Wagner M.; Bliem R.; Schulte K.; Schmid M.; Franchini C.; Diebold U. J. Phys. Chem. C 2014, 118 (34), 19904–19909. 10.1021/jp506234r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wang Z. M.; Wu K. H.; Guo Q. L.; Guo J. D. Appl. Phys. Lett. 2009, 95 (2), 021912. 10.1063/1.3180701. [DOI] [Google Scholar]
  32. Nyholm R.; Andersen J. N.; Johansson U.; Jensen B. N.; Lindau I. Nucl. Instrum. Methods Phys. Res., Sect. A 2001, 467-468, 520–524. 10.1016/S0168-9002(01)00399-0. [DOI] [Google Scholar]
  33. Stavitski E.; de Groot F. M. Micron 2010, 41 (7), 687–94. 10.1016/j.micron.2010.06.005. [DOI] [PubMed] [Google Scholar]
  34. Russell B. C.; Castell M. R. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77 (24), 245414. 10.1103/PhysRevB.77.245414. [DOI] [Google Scholar]
  35. Tran F.; Blaha P.; Schwarz K.; Novak P. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74 (15), 155108. 10.1103/PhysRevB.74.155108. [DOI] [Google Scholar]
  36. Tersoff J.; Hamann D. R. Phys. Rev. Lett. 1983, 50, 1998–2001. 10.1103/PhysRevLett.50.1998. [DOI] [Google Scholar]
  37. Marks L. D. J. Chem. Theory Comput. 2013, 9 (6), 2786–800. 10.1021/ct4001685. [DOI] [PubMed] [Google Scholar]
  38. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Phys. Rev. Lett. 2008, 100 (13), 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  39. Staroverov V. N.; Scuseria G. E.; Tao J.; Perdew J. P. J. Chem. Phys. 2003, 119 (23), 12129–12137. 10.1063/1.1626543. [DOI] [Google Scholar]
  40. Kienzle D. M.; Becerra-Toledo A. E.; Marks L. D. Phys. Rev. Lett. 2011, 106 (17), 176102. 10.1103/PhysRevLett.106.176102. [DOI] [PubMed] [Google Scholar]
  41. Seah M. P.; Dench W. A. Surf. Interface Anal. 1979, 1 (1), 2–11. 10.1002/sia.740010103. [DOI] [Google Scholar]
  42. Diebold U.; Shinn N. D. Surf. Sci. 1995, 343 (1–2), 53–60. 10.1016/0039-6028(95)00780-6. [DOI] [Google Scholar]
  43. Stöhr J.NEXAFS Spectroscopy; Springer-Verlag: Berlin, 1992. [Google Scholar]
  44. Green R. J.; Zatsepin D. A.; Hunt A.; Kurmaev E. Z.; Gavrilov N. V.; Moewes A. J. Appl. Phys. 2013, 113 (10), 103704. 10.1063/1.4795262. [DOI] [Google Scholar]
  45. Brydson R.; Garvie L. A. J.; Craven A. J.; Sauer H.; Hofer F.; Cressey G. J. Phys.: Condens. Matter 1993, 5 (50), 9379–9392. 10.1088/0953-8984/5/50/018. [DOI] [Google Scholar]
  46. Walle L. E.; Agnoli S.; Svenum I. H.; Borg A.; Artiglia L.; Kruger P.; Sandell A.; Granozzi G. J. Chem. Phys. 2011, 135 (5), 054706. 10.1063/1.3623271. [DOI] [PubMed] [Google Scholar]
  47. Sheldrick G. M. Acta Crystallogr., Sect. A: Found. Crystallogr. 2008, 64 (1), 112–22. 10.1107/S0108767307043930. [DOI] [PubMed] [Google Scholar]
  48. Hitosugi T.; Shimizu R.; Ohsawa T.; Iwaya K. Chem. Rec. 2014, 14 (5), 935–43. 10.1002/tcr.201402041. [DOI] [PubMed] [Google Scholar]
  49. Ohsawa T.; Shimizu R.; Iwaya K.; Hitosugi T. ACS Nano 2014, 8 (3), 2223–9. 10.1021/nn405359u. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl5b05211_si_001.pdf (1.2MB, pdf)
nl5b05211_si_002.cif (4.4KB, cif)
nl5b05211_si_003.cif (4.5KB, cif)
nl5b05211_si_004.cif (5.1KB, cif)
nl5b05211_si_005.cif (5.6KB, cif)
nl5b05211_si_006.cif (2.9KB, cif)
nl5b05211_si_007.cif (3.3KB, cif)
nl5b05211_si_008.cif (6.5KB, cif)
nl5b05211_si_009.cif (6.6KB, cif)
nl5b05211_si_010.cif (7.2KB, cif)
nl5b05211_si_011.cif (2.4KB, cif)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES