Asynchronous Replica Exchange Software for Grid and Heterogeneous Computing

Abstract

Parallel replica exchange sampling is an extended ensemble technique often used to accelerate the exploration of the conformational ensemble of atomistic molecular simulations of chemical systems. Inter-process communication and coordination requirements have historically discouraged the deployment of replica exchange on distributed and heterogeneous resources. Here we describe the architecture of a software (named ASyncRE) for performing asynchronous replica exchange molecular simulations on volunteered computing grids and heterogeneous high performance clusters. The asynchronous replica exchange algorithm on which the software is based avoids centralized synchronization steps and the need for direct communication between remote processes. It allows molecular dynamics threads to progress at different rates and enables parameter exchanges among arbitrary sets of replicas independently from other replicas. ASyncRE is written in Python following a modular design conducive to extensions to various replica exchange schemes and molecular dynamics engines. Applications of the software for the modeling of association equilibria of supramolecular and macromolecular complexes on BOINC campus computational grids and on the CPU/MIC heterogeneous hardware of the XSEDE Stampede supercomputer are illustrated. They show the ability of ASyncRE to utilize large grids of desktop computers running the Windows, MacOS, and/or Linux operating systems as well as collections of high performance heterogeneous hardware devices.

1. Introduction

Many physiochemical processes, such as phase transitions[1] and the folding and binding of proteins, occur on time scales difficult to access even with the fastest supercomputers available.[2, 3, 4] Enhanced conformational sampling algorithms have been developed to accelerate the modeling of these processes so that they can be studied in reasonable time frames.[5, 6, 7, 8] An important class of methods are based on the imposition of thermodynamic or mechanical biasing forces which can speed up, often by many orders of magnitude, conformational interconversions otherwise too rare to be observed in traditional simulations.[9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20] Results produced by biased sampling methods are typically analyzed using post-processing to recover true (unbiased) thermodynamic observables.[21, 22, 23, 24, 25, 26]

Replica Exchange (RE) algorithms[27, 28] are recognized as among the most powerful enhanced conformational sampling tools available,[29, 30, 31, 32, 33, 34] yielding converged results orders of magnitude faster than conventional approaches.[7] RE methods are based on replicating the system across combinations of thermodynamic and potential energy parameters[35] (in this work primarily alchemical receptor-ligand coupling λ and temperature T), each evolving independently with the exception of occasional exchanges of thermodynamic parameters between replicas. Hence, each replica travels in conformational space as well as in thermodynamic space. Accelerated conformational sampling is achieved because conformational transitions can occur at the thermodynamic state where they are most likely, rather than only at the thermodynamic state of interest, where they may be rare.[36]

Because RE is inherently a parallel sampling algorithm, it is particularly suited for large high performance computing (HPC) clusters. In conventional synchronous implementations of RE, parameter exchanges occur simultaneously for all replicas after, for example, the completion of a given number of MD steps. Synchronous RE is a suitable algorithm for dedicated High Performance Computing (HPC) clusters where MD threads can efficiently execute in parallel at equal speeds for extended periods of time without failures. In these cases exchanges among replicas are implemented using inter-process communication libraries, such as the Message Passing Interface (MPI). On HPC resources a high rate of exchanges, which is beneficial for sampling efficiency,[37, 38] can be achieved with minimal overhead.

However, unlike methods based on swarms of independent trajectories,[39, 40, 41] traditional synchronous RE approaches are not well suited to distributed and dynamically allocated resources, such as those available on computational grids.[42] In these environments direct communication across compute nodes is typically not available, and the pool of compute nodes varies unpredictably. Synchronous RE is also not well suited to heterogeneous HPC environments, such as the XSEDE Stampede cluster, which are increasingly becoming common place. Typically these clusters provide large computational throughput by utilizing highly parallel co-processors (many-core integrated co-processors, MIC’s, or general programmable graphic processing units, GPGPU’s) attached to conventional CPU nodes. Effective use of these computing devices is challenging due to their wide range of performance profiles and modes of operation. Legacy MD packages for biomolecular modeling often lack the ability to exploit multiple heterogeneous computing devices concurrently; in part because of the large diversity of hardware configurations that would need to be supported.

Finally, conventional synchronous RE implementations require that computational resources be secured for all of the replicas before the simulation can begin execution, and that these are maintained until the simulation is completed. This effectively precludes the use of general computing resources, such as farms of office desktops, that may be too small to run large RE applications all at once. Conversely, zero fault tolerance complicates the deployment of multi-dimensional RE algorithms, employing hundreds to thousands of replicas, on HPC resources.

The replica exchange method itself does not impose the restriction that exchanges should necessarily occur synchronously across all processors.[43] In particular the RE method itself does not require that all of the replicas be running at the same time. There are therefore no obstacles in principle preventing the deployment of asynchronous RE algorithms over distributed and heterogeneous computing infrastructures. Previous efforts have showed that the asynchronous prescription has significant advantages over the conventional synchronous implementation in terms of scalability and flexibility in the choice of exchange schemes.[44]

Towards the goal of filling the current gap in availability of RE software tools capable of harnessing the latent computational power of distributed and heterogeneous computing resources, in this work we present an asynchronous replica exchange software framework, named ASyncRE, based on the idea of avoiding centralized synchronization steps by allowing replicas to progress at different rates and enabling parameter exchanges among arbitrary sets of replicas independently from other replicas. As illustrated here, the proposed ASyncRE framework is sufficiently flexible to drive RE molecular simulations on high end heterogeneous supercomputers, such as the XSEDE Stampede cluster, as well as on distributed computing grids, such as those built around the BOINC software platform. Campus computational grids that utilize existing general computing resources, such as those in student PC labs, when they would be otherwise idle, are attractive research computing alternatives to HPC clusters. It would be very beneficial to extend the domain of applicability of RE to campus-wide distributed computing grids and much larger collections of computers such as the World Community Grid (worldcommunitygrid.org).

To achieve these goals, while addressing as generally as possible the computational challenges described above, a number of design choices were made. For optimal flexibility, ASyncRE is implemented as a managing agent of the underlying MD engine, rather than being integral part of it. To ensure resiliency, ASyncRE issues MD executions of replicas in discrete chunks, typically lasting from a few minutes to several hours, after which the replica is checkpointed on a coordination server. Executions can be launched on a diverse pool of computing devices ranging from parallel co-processors to user desktops. Parameter exchanges are performed by the coordination server by manipulating output and input files of the replicas currently checkpointed, thereby avoiding synchronization bottlenecks and the need for direct communication links between computing devices. The specific algorithms and techniques used to achieve these characteristics are described in detail below, followed by illustrative applications of the software to the study of supramolecular and macromolecular complexes. The ASyncRE software is freely available at https://github.com/ComputationalBiophysicsCollaborative/AsyncRE

2. Methods

2.1. Replica Exchange Conformational Sampling

The objective of equilibrium molecular simulations is to efficiently sample the canonical distribution, exp[−βU(x; θ)], where x represents a molecular conformation, β = 1/k_BT is the inverse temperature, and U(x; θ) is the potential energy function, dependent on a set of parameters collectively denoted by θ. Collecting sample sets of sufficient quality is often very challenging due to the high dimensionality of the sampling space and the ruggedness of the potential. General-purpose sampling algorithms such as Monte Carlo (MC) and Molecular Dynamics (MD) often remain trapped into metastables conformations isolated by high potential energy barriers which are crossed only rarely at standard conditions. Sampling can be accelerated by performing biased sampling at higher temperatures (small β) or at suitable values of potential energy parameters, at which the likelihood of trapping is decreased.[45, 46, 47, 48] The problem of correcting the probabilities of samples so that they reflect the experimental conditions of interest is addressed using thermodynamic reweigthing techniques.[24, 25]

In replica exchange the potential energy parameters and/or the temperature are sampled across a discrete set of values, which include those of interest, together with molecular conformations in such a way that the canonical distribution is sampled at each choice of parameters and temperature. Defining the reduced potential energy function as

$$u(x;s)=\beta U(x;\theta ),$$ (1)

where in the most general case s = (β, θ) denotes a joint thermodynamic and mechanical state of the system, the Replica Exchange (RE) algorithm involves simulating M replicas of the system at states s_i = (β_i, θ_i). Conformational sampling of each replica at fixed s_i is performed using standard MD. A replica can change its thermodynamic/mechanical state (hereafter referred to simply as a “state”) by exchanging its current state with that of another replica. The probability of exchange is regulated to ensure microscopic reversibility, that is equilibration towards the canonical distribution at every value of s_i = (β_i, θ_i).

Formally, the RE ensemble distribution

$$p_{\text{RE}}(x_1,x_2,\dots ,x_M\mid \{s\})=exp\left[-\sum _{i=1}^{M}u(x_i;s_i)\right]/Z_{\text{RE}}$$ (2)

is introduced, where x_i is the molecular configuration of replica i and s_i is the state assigned to it, which is taken from a discrete set (s₁, s₂, …, s_M) of M possible states. Z_RE is the partition function of the RE ensemble to ensure normalization. The symbol {s} denotes one of the M! permutations of the assignment of states to replicas. RE algorithms seek to sample both molecular conformations and state permutations, that is they are designed to sample the joint distribution p_RE(x₁, x₂, …, x_M, {s}).

The RE joint distribution is commonly sampled by means of a Markov chain alternating between updates of molecular configurations of replicas at a fixed state and updates of state assignments to replicas (permutations) at fixed molecular conformations. The simplest variation of the latter is a long series of parameter swapping attempts among randomly selected pairs of replicas accepted according to the well-known Metropolis-Hastings acceptance probability[49]

$$p_{s{s}^{\prime }}=min\left\{1,\frac{p_{\text{RE}}(\{s^{\prime }\}\mid x_1,x_2,\dots ,x_M)}{p_{\text{RE}}(\{s\}\mid x_1,x_2,\dots ,x_M)}\right\}=min\left\{1,exp\left[-\sum _{i=1}^{M}u(x_i;s_i^{\prime })+\sum _{i=1}^{M}u(x_i;s_i)\right]\right\},$$ (3)

where {s′} is the proposed state permutation and {s} the current one. As observed,[50, 51] it is beneficial to perform as many exchanges as possible at each set of molecular configurations as they are produced until a fast exchange limit is reached. To facilitate this, it is convenient to pre-compute the M × M reduced potential energy matrix

$$u_{ij}=u(x_i;s_j)$$ (4)

that is the reduced potential energy of each replica i at each thermodynamic state s_j.

2.2. ASyncRE Algorithm

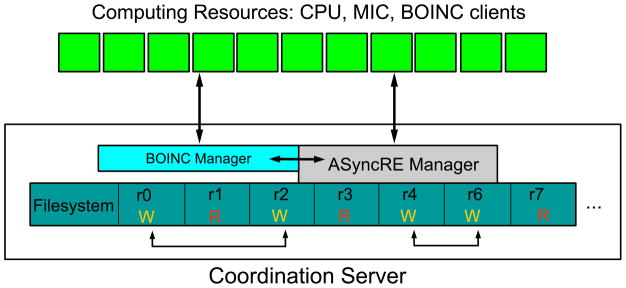
Replicas are implemented as independent executions (or “cycles”) of the MD engine for a predetermined amount of simulation time. Each replica lives in a separate sub-directory of a server (see Fig. 1) running the ASyncRE Manager daemon (see below). A state is assigned to each replica. The ASyncRE Manager maintains a record of the mapping between replicas and states. MD engine input files are then prepared for each replica according to the assigned parameters and the RE scheme under consideration. A randomly chosen subset of eligible replicas are submitted for execution and enter the running (’R’) state. Replica executions are restarted from checkpoint files generated by the previous execution. Typically, coordinates and velocities are extracted from checkpoint files, while state parameters are reset to the newly assigned values.

Figure 1.

Schematic diagram of the design of ASyncRE. The ASyncRE Manger runs on a coordination server which also hosts the filesystem where replicas are stored. Each cell represents a replica which can be either in a waiting (“W”) state or running (“R”) state. Replicas in the waiting state can exchange state parameters as illustrated by the arrows at the bottom of the diagram. The ASyncRE manager issues replica executions on a variety of computing devices (top) either directly, or through the BOINC grid Manager.

When a replica completes a cycle, it enters a waiting (’W’) state, making it eligible for exchange with other replicas and the initiation of a new cycle. Periodically, permutations of thermodynamic parameters (see below) are performed restricted to only the pool of replicas in the waiting state. Exchanges are conducted based on the appropriate reduced energies depending on the RE scheme being employed. This entails, see below, extracting energetic information from the MD engine output files and computing the relevant reduced energies u(x, s) [see Eq. (1)]. Exchanges ultimately result in a new set of MD engine input files ready to begin a new execution cycle.

In the algorithm outlined above exchanges occur asynchronously, that is for example they occur for some waiting replicas while other running replicas are undergoing MD. The algorithm does not require a direct network link between the compute nodes as all exchanges are managed and conducted by the manager. Furthermore the algorithm is resilient in terms of loss of computing nodes. That is, for example, failure to send a replica execution to a computing device does not cause termination of the ASyncRE calculation. The job is simply submitted to another available device.

2.3. ASyncRE Software Framework

The software implementation of the asynchronous RE algorithm described above consists of a set of Python classes and scripts organized in a package called ASyncRE (https://github.com/ComputationalBiophysicsCollaborative/AsyncRE). Different classes are assembled, depending on the application, to implement an ASyncREManager daemon. Each simulation is associated with an individual instance of the ASyncRE Manager daemon. Multiple instances of the ASyncRE Manager daemon can run concurrently on one managing server. Only the ASyncRE Manager requires access to the filesystem (see Fig. 1). This software framework, as illustrated by the applications described here, is capable of supporting large-scale and flexible execution of RE calculations with hundreds of replicas on standard and heterogeneous computing clusters and grid resources. The framework supports different coupling schemes between the replicas (including multi-dimensional RE schemes, see below) using a modular design that is conducive to fast prototyping to experiment with new RE schemes. The modular design is extended to the interaction with the underlying MD engine (IMPACT[52] in this case) and with different computing resources, such as HPC clusters and BOINC computational grids. The main module classes are categorized as follows:

1. Core coordination module. This module implements, often abstractly, the main asynchronous RE algorithm outlined above calling subroutines in attached modules to perform specific tasks, such as submitting replicas, reading output files, evaluating energies and performing exchanges.

2. RE schemes modules. These modules assemble the energies and thermodynamic parameters of each replica (calling the MD engine module functions below) and compute the reduced potential energy matrix u(x; s) relevant to the selected RE scheme to conduct parameter exchanges.

3. MD engine module. This module collects utility functions to write input files for the MD engine and reads output files to, for example, extract potential energy values required for parameter exchanges. As part of this task this module determines the validity of a replica run and issues resubmissions as necessary. This module also performs the specific task of submitting replicas executions to the attached job transport mechanism.

4. Job transport modules. These modules acquire replica execution submissions and dispatch them to physical computing resources. Two job transport mechanisms are supported, SSH and BOINC, described below. The first is suitable for general heterogeneous collections of computers, including HPC clusters, and the second for computing grids managed by the BOINC grid software.

Below we describe the design of some of the modules outlined above.

2.3.1. Core coordination module

The ASyncRE software is modularized taking advantage of the object-oriented capabilities of the Python language (class inheritance and method overrides). The core module performs general tasks common to RE, such as job staging and coordinating exchanges of parameters among replicas using independence sampling algorithms (see below). The core module often calls specialized routines defined in lower modules. For example the matrix of reduced energies used by the exchange algorithms are computed by one of the RE schemes modules (such as the λ-BEDAM module) and MD engine file I/O is accomplished by calling specific MD engine module subroutines. This is accomplished by having the core module class interact with generic routines which are specialized by subclasses of the core class. By importing the core class and an arbitrary set of subclasses, a large variety of ASyncRE manager applications can be built. For example, by importing the core class, and the IMPACT MD engine, the temperature replica exchange, and the BOINC transport subclasses, an ASyncRE job manager capable of running temperature RE simulations (also known as parallel tempering) with the IMPACT MD engine on a BOINC distributed grid is constructed. The modular design of the software library is designed for extensibility to arbitrary replica exchange modalities and MD engines. To add support for a new modality only a handful of specialized routines need to be provided. The main ones are those that write MD engine input files and extract information from output files and those that calculate the reduced potential energy matrix.

The core module keeps track of states by generic identifiers; user modules maintain data structures linking these identifiers to the list of temperature, potential energy parameters, etc. used to compose input files and compute the reduced potential energy matrix. The association between replicas and their thermodynamic states is saved periodically to a checkpoint file which is loaded as needed to restart an ASyncRE simulation. The core module also implements the main loop of the program which consists of updating the list of running and waiting replicas and of the number of running cycles completed by each replica, issuing parameter exchange attempts, generating new input files and submitting replicas for execution for the next cycle. A minimum number of replicas (typically from one quarter to a half of the total) is maintained in the waiting list to ensure that sufficient exchanges can occur within this set. The main loop is executed on a tunable period (referred to as the “cycle time”) of typically a few minutes, chosen to be a small fraction of the running time of a replica.

As described in a recent report,[50] due to the infrequent opportunities for exchanges in asynchronous RE (especially when deployed on a distributed grid) it is essential to perform as many parameter exchanges as possible. Efficient independence sampling algorithms have been proposed for this purpose.[49, 53] These methods seek to sample the state permutation ensemble as thoroughly as feasible without having to recompute energies of molecular configurations. To maintain generality and facilitate automation, we have not considered for implementation algorithms which require prior definition of neighboring states. This information may not be easily obtainable by the user, especially for multi-dimensional RE schemes. ASyncRE implements the Metropolis-based Independence Sampling (MIS) algorithm proposed by Chodera & Shirts,[49] which consists of a long series of parameter exchange attempts among randomly selected pairs of replicas accepted according to Eq. (3). The MIS algorithm does not rely on supplied information about neighboring states, which is a key feature for an algorithm to be employed in a general-purpose RE engine with minimal user input. ASyncRE also implements a variation of the MIS algorithm which offers some additional advantages in terms of code performance. In this variation, we call Sequential Gibbs, a permutation update is the result of the evaluation of the probability of multiple state permutations in parallel (ASyncRE uses numpy for vectorization) choosing one of them based on a single generated random number. This strategy reduces the CPU footprint of the algorithm, which is important to run many copies of the ASyncRE manager on a single server.

2.3.2. Replica exchange schemes modules

These are modules that implement specific RE schemes (temperature, alchemical, etc.), including multidimensional combinations of these. One key function of modules implementing RE schemes is the computation of the reduced potential energy matrix u_ij = u(x_i; s_j) in Eq. (4). This information is passed to the core module which, together with the list of waiting replicas, conducts exchanges using independence sampling algorithms. User-provided RE modules can be added to support a variety of exchange schemes.

Currently, modules for temperature-RE and BEDAM λ-RE alchemical binding free energy calculations are implemented. The binding free energy of the complex between two molecular species (for example a protein receptor and a ligand, or a molecular host and its guest) is a quantity expressing the affinity of the two molecules to bind each other.[54] Computational methods aimed at predicting and rationalizing binding affinities find applications in such areas such as medicinal chemistry, biophysics, and chemical engineering.[55, 56, 57] RE methods are known to significantly accelerate binding free energy calculations.[7, 58] The reduced potential energy corresponding to the multi-dimensional RE binding free energy model with the BEDAM method is: [59, 60, 61, 62]

$$u(x;\beta ,\lambda )=\beta [U_0(x)+\lambda b(x)]$$ (5)

where β is the inverse temperature, and λ is an alchemical progress parameter ranging from 0, corresponding to the uncoupled state of the complex, to 1, corresponding to the coupled state of the complex. U₀(x) is the potential energy of the complex when receptor and ligand are uncoupled, that is as if they were separated at infinite distance from each other. The quantity b(x), called the binding energy, is defined as the change in effective potential energy of the complex for bringing the receptor and ligand rigidly from infinite separation to the given conformation x of the complex.

Eq. (5) is evaluated given the state parameters β and λ and the energies U₀(x) and b(x) of a given replica extracted from the main IMPACT output file. The same data is subsequently processed using UWHAM analysis as described (http://cran.r-project.org/web/packages/UWHAM)[25] to yield the binding free energy of the complex. Other routines place the currently assigned state parameters β and λ into the input file of a replica to ready it for execution. The standard one-dimensional version of BEDAM is implemented by fixing the temperature and assigning to each replica set values of λ between 0 and 1. Similarly, in the two-dimensional version of BEDAM both λ and β are exchange parameters. As illustrated in the applications, the purpose of the sampling along λ is to enhance mixing of conformations along the alchemical pathway while high temperatures enhance sampling of internal molecular degrees of freedom at each alchemical stage. A standard temperature-RE module, which formally corresponds to Eq. (5) with fixed λ and varying β, is also available.

2.3.3. MD engine module

This module collects routines to prepare input files for the MD engine to launch executions, to inspect output files to detect failures, and to extract data from output files needed to evaluate the reduced potential energy matrix. (A module for the IMPACT MD engine is available. User-provided modules can add support to a variety of MD engines.) The generation of input files is triggered by the core module while RE modules invoke specific MD engine routines to extract data from output files. Another important function of the MD engine module is to submit the replicas for execution. This entails assembling a job dictionary specifying typically the cycle number and the replica to run, the required input files, the expected output files, and the location of the executable. This job dictionary is then passed to the attached job transport module which handles the actual execution on remote resources. The core module, after being notified by the job transport module of a completion of a replica run, calls a routine of the MD engine module responsible for validating the output. Typically a series of checks ranging from the existence of output files to whether they contain readable information is conducted. If the run is deemed failed the replica cycle is not advanced and the replica is placed back into the waiting list and eventually relaunched.

2.3.4. Job transport modules

The core coordination module launches replica executions by issuing a call to the MD engine module which prepares the job and submits it to the attached job transport module. Two job transport mechanisms are currently supported. The mode of interaction between the core module and job transport modules is based on our earlier work with the BigJob transport mechanism.[63, 44]

SSH transport

The SSH job transport module is capable of dispatching job executions on any remote computing node reachable from the coordination server by means of the widely available Secure Shell (SSH) protocol. The mechanism does not require that the coordination server and the compute node share a common filesystem and user domain, nor that they have compatible operating systems and architectures. The only requirement is the availability of a remote user accessible by public key authentication (to avoid manual entering of a password). Information about remote computing nodes is acquired from a “nodefile” containing qualified names and the corresponding remote user name, temporary job directory, architecture and operating system. On HPC clusters the nodefile is typically assembled automatically by the job submission script from the node list assigned by the queuing system prior to the launching of the ASyncRE manager (which typically runs on the first node).

A replica run consists of the transfer of input files and executable files, as assembled by the MD engine module, to the designated temporary job directory on the remote computing node followed by the remote launching of the executable. Job monitoring is implemented by maintaining a constant link with the remote process under which the replica runs. This is accomplished by issuing remote commands (using the paramiko Python modules) under a child process (using the multiprocess Python module) of the ASyncRE job manager. Upon return of the MD engine remote execution command, the child process transfers back output files into the appropriate replica directory on the coordination server and exits. Failures are caught by the MD engine validation mechanism described above.

An important feature of the SSH transport mechanism is the use of a job queue (implemented using the standard queue Python module) to hide latencies involved in the management of replica exchanges and preparation. That is, ASyncRE submits replica runs to the SSH job transport in excess of the available compute resources. Hence, the submission of a replica for execution does not, in general, imply that it is immediately launched. Rather, the replica job is inserted by the transport module into the queue ready to begin execution as soon as resources become available, without having to wait for the core module to prepare and submit new replicas.

BOINC transport

BOINC is a popular grid computing software framework. Some of the best known volunteer computing projects such as IBM’s World Community Grid (worldcommunitygrid.org) and SEti@Home (setiathome.berkeley.edu) are based on BOINC. A BOINC grid consists of a (possibly very large) network of computers running the BOINC client application. The BOINC client software is available for a wide variety of architectures. The clients connect to a central server via the HTTP protocol to download work units, consisting of the application executable and input files, and return output files upon completion of a work unit. The BOINC server component runs on a Linux server. The central element of the BOINC server is a MySQL database which stores, among others, work unit and client information. Daemons running on the server communicate with the MySQL database to submit and retrieve work units. The BOINC server also interfaces with an Apache web server to communicate with clients.

While sufficiently powerful to support large world-wide volunteer computing communities, BOINC is also a promising platform for campus computational grids. The attractive feature of computing grids of this kind is that they use general computing resources of the institution, such as student PC labs, when they are idle. For suitable applications, a campus computational grid can effectively supplement local HPC resources with minimal hardware investment.

The BOINC transport mechanism shares some of the features of the SSH transport mechanism, except that it interacts with the remote computing devices only through the BOINC framework. In our implementation the ASyncRE manager and BOINC run on the same server. A replica run submission is performed by calling the create_work utility of the BOINC server software and ultimately results in the placement of a suitable work unit entry into the BOINC MySQL database. The work unit entry specifies the executable (IMPACT in this case) which is packaged into a BOINC application format which allows BOINC to automatically select the executable version compatible with the receiving client. The work unit information contains input/output file information similar to the SSH transport mechanism described above, as well as metadata concerning such things as the deadline by which clients are expected to return results. Upon completion, clients return results to the BOINC server. These undergo an assimilation process that, in this case, consists of storing output files in the replica filesystem structure expected by ASyncRE. The ASyncRE BOINC transport module also implements, through MySQL queries to the BOINC database, a facility to query the status of replica runs, such as whether they have completed. This information is used by the core and MD engine modules to validate the results and prepare the subsequent replica run cycle.

In addition to the implementation of the BOINC transport module, a substantial amount of effort went into the set up of the BOINC server software and of the client desktops. On the client side we received the generous help of university IT staff at Temple University and Brooklyn College who automated the installation of the BOINC client application on hundreds of desktop computers and ensured propagation of the set up across OS and hardware upgrades. Tuning of the grid of clients included the implementation of the schedule of availability, such as dedicated use during overnight hours and the rules to stop and resume computations depending on student interactive usage of the client machine. A variety of issues were pinpointed and addressed, for example we found it necessary to tune CPU usage limits on Windows clients to avoid failures under heavy load. The set up of the BOINC server software also required substantial amount of thought and effort. Some of the BOINC utilities, such as the assimilator and the file staging tools, were customized for ASyncRE. As part of this work the IMPACT MD package was ported to the Windows OS. BOINC requires that the executable interfaces in a particular way with the BOINC application on the client. As an alternative to placing explicit BOINC calls in the MD code, we opted for running IMPACT under a provided wrapper utility.

Overall the implementation and system administration tasks related to BOINC accounted for a significant component of the work. As a guide to others, we have prepared a detailed step-by-step tutorial, based on our experience, on how to set up a BOINC server for a campus grid. A version of the tutorial is available on the project site https://github.com/ComputationalBiophysicsCollaborative/AsyncRE.

3. Illustrative Applications

3.1. Validation and Benchmarking: Host-Guest Binding

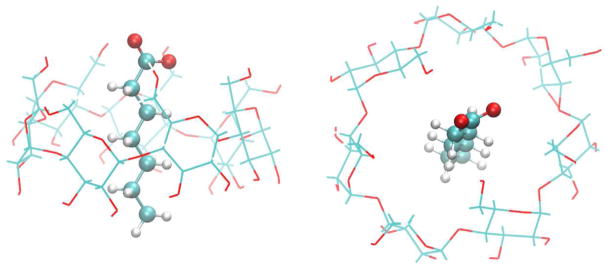
To validate and benchmark the ASyncRE software we employed a small host-guest chemical system, Fig. 2, investigated in our previous work.[64, 65] The goal of the calculations is to estimate the binding free energy of the host-guest complex in water. We first gathered a solid reference benchmark from a long (1.152 μs aggregated simulation time) standard 1D Synchronous BEDAM simulation on a HPC cluster. This simulation employed 16 replicas at λ values (0.0, 0.001, 0.002, 0.004, 0.01, 0.04, 0.07, 0.1, 0.2, 0.4, 0.6, 0.7, 0.8, 0.9, 0.95, and 1.0) at 300K and an exchange period of 0.5 ps. This and other calculations employed OPSL-AA[66, 67] force field model: and the AGBNP2 implicit solvent model.[68] For this and later applications in this work binding free energy analysis has been conducted with the UWHAM library in the R statistical package.[25] The reference binding energy distribution at λ = 1.0 and the binding free energy profile are shown in Fig. 3b. The binding energy distribution displays a mixture of modes corresponding to different orientations of the guest within the host cavity.[64, 65] Reproducing the relative populations of these modes represents a strict test of the new algorithms.

Figure 2.

Side and top view of β-cyclodextrin-heptonoate complex

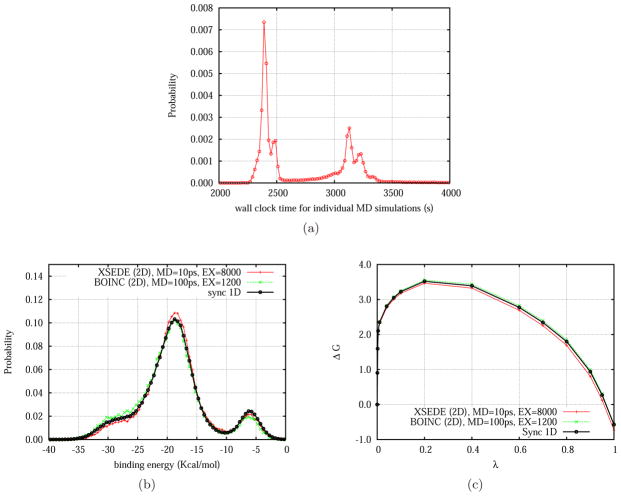
Figure 3.

2D asynchronous REMD results from the BOINC distributed network at Temple University and XSEDE HPC resources: (a) distribution of wall clock times for individual 100ps MD simulations; (b) binding energy distributions; (c) binding free energies at different λ values.

2D ASyncRE REMD validation simulations were performed in both environments targeted by the software: an HPC cluster (XSEDE’s Stampede cluster) using SSH transport and the BOINC distributed computing networks at Temple University and at Brooklyn College of CUNY. The 2D asynchronous REMD simulations were conducted for 30 ns per replica, and have the same 16 λ values as the 1D Sync case multiplexed over fifteen temperatures (200, 206, 212, 218, 225, 231, 238, 245, 252, 260, 267, 275, 283, 291, 300K), resulting in a total of 16 × 15 = 240 replicas with 240 different pairs of (λ, β) values. The ASyncRE simulations employed the Metropolis Independence Sampling exchange algorithm with an MD cycling time of 100ps per replica.

As shown in Fig. 3b the 2D ASyncRE simulations on XSEDE and BOINC grid resources returned results nearly indistinguishable from the 1D Sync REMD reference. The location and intensities of the modes of the binding energy distribution at λ = 1, the value at which the distribution is most difficult to converge, are nearly identical. In addition, the binding free energy estimates obtained are all within statistical uncertainty of each other. Hence, these validation tests confirm consistency and correctness of all aspects of the novel ASyncRE methodology: the computing environment, the software implementation, and the multidimensional RE scheme.

While equivalent in terms of results, the ASyncRE simulations progressed quite differently from each other and from the synchronous reference. The nature of the file-based asynchronous algorithm and the SSH and BOINC job transport mechanisms prevents parameter exchanges as frequent as in the MPI synchronous setup. In these benchmarks the period of exchanges in the asynchronous simulations was set to 100 ps, or 200 times longer than for the synchronous MPI simulation. Analysis of convergence behavior, reported in detail elsewhere,[50] reveals that despite the fewer opportunities for parameter exchanges, independence exchange sampling allows ASyncRE to achieve similar convergence rates as synchronous RE, while enjoying the benefits of greater robustness and applicability to a wider array of computing devices. The reason for the similar convergence rates despite the much smaller frequency of exchange attempts in ASyncRE compared to synchronous RE is the slow conformational relaxation of replicas relative to the rate of exchanges. For additional discussion of this point see reference [50].

In contrast to synchronous MPI and AsyncRE simulations on HPC clusters, the replica execution times on the BOINC grid varied considerably. As shown in Fig. 3a, replica execution times on the 500-cores grid at teaching laboratories at Temple University, exhibited relatively short (first peak in Fig. 3a) or much longer execution times (second peak) depending on the delay patterns due to the programmed halting and resumption of BOINC client activity due to intermittent student usage. This behavior negatively affects throughput, however it is unavoidable on CPU scavenging facilities such as this and it is similar to that observed below for ASyncRE simulations of protein-ligand systems on the Brooklyn College BOINC grid.

3.2. Binding Free Energy-Based Drug Screening on a Campus Computational Grid

We have conducted benchmarks to evaluate the feasibility of conducting replica-exchange (RE) protein-ligand binding free energy drug screening calculations on campus computational grids. The architecture and mode of operation of such facilities does not allow for frequent and synchronous communication between replicas. It is therefore of interest to test the ability of the AsyncRE algorithm coupled to the BOINC job transport to overcome these limitations. We have selected as test systems five ligand candidates as LEDGF inhibitors of the integrase enzyme of the HIV virus. This system has been previously investigated by us as part of the international SAMPL4 blind challenge using synchronous MPI-based exchanges on XSEDE HPC clusters.[61] It is therefore a useful point of comparison between the HPC and distributed computing approaches. In that work hundreds of parallel binding free energy calculations were performed on a series of computer clusters with the goal of screening experimentally confirmed binders (unknown to us) from a large pool of inactive molecules. Our model was judged as among the most accurate in this respect.[69] The five ligands selected for this work are composed of two true positives (correctly identified binders) and three false negatives (binders incorrectly identified as non-binders) from the SAMPL4 study. See Table 1. The inclusion of both successful and unsuccessful cases realistically probes the reproducibility of the calculations.

Table 1.

BEDAM binding free energies of five HIV integrase candidate inhibitors computed using the ASyncRE framework on the Brooklyn College BOINC grid, compared to previous results obtained on XSEDE clusters using MPI communication.

Ligand id	Ligand Structure	$\mathrm{\Delta }{G}_b^{\circ }$a (this work)	$\mathrm{\Delta }{G}_b^{\circ }$a (reference 61)
AVX17556_3		−8.1 ± 0.7	−8.2 ± 0.8
AVX40911_0		−5.6 ± 0.8	−4.4 ± 0.2
AVX38780_0_1		−1.7 ± 0.9	0.7 ± 0.3
AVX38783_1_1		0.9 ± 0.6	1.3 ± 0.2
AVX38789_1_1		2.2 ± 0.5	−1.3 ± 0.3

^aIn kcal/mol.

The protein-ligand system was prepared as previously reported.[61] Briefly, a truncated model of the ligand binding domain of HIV integrase was derived from a known crystal structures (PDB id 3NF8). The model includes residues 68–90 and 158–186 of chain A and residues 71–138 of chain B. This truncated model contains at a minimum all receptor residues with at least one atom closer than 12 Å of any atom of the ligand in the 3NF8 crystal structure. Additional residues were included to minimize the number of chain breaks. Chain terminals were capped by acetyl and N-methylacetamide groups. Ligands were prepared using the LigPrep workflow (Schrödinger, LLC). The same initial structures as those for the SAMPL4 study, which were obtained by docking as described, were employed. Docked structures of the two true positives turned out to agree with crystal structures of the complexes[70] significantly better than those of the three false negatives.

BEDAM binding free energies were conducted on the BOINC computational grid at the WEB student computer lab at the Brooklyn College of the City University of New York. The computer lab, administered by the Information Technology Service office of Brooklyn College, hosts a computing grid of approximately 290 desktop computers running the Windows 7 OS. With approximately 1,200 CPU cores, the facility has a theoretical throughput of 4.5 Teraflops, comparable to a typical campus computing cluster. In the current setup the WEB computers are available for computing only when the lab is closed to the public (nights, weekends and holidays). An off-site server runs the BOINC coordination server, dispatches jobs to desktops and collects the results. Job preparation and replica exchanges are performed by the ASyncRE application running on the BOINC coordination server for each binding free energy calculation as described above.

The results of the BEDAM ASyncRE calculations on the BOINC grid are summarized in Table 1, compared to estimates previously obtained for the SAMPL4 challenge.[61] Overall the agreement between the two sets is satisfactory. The ligands judged as true positives in the SAMPL4 work remained so in the present analysis. Similarly, the binding free energies of the three false negatives remained above the −4 kcal/mol cutoff used to discriminate likely binders from non-binders. Quantitative agreement is obtained for the two true positives (AVX17556_3 and AVX40911_0) and for one false negative (AVX38783_1_1). Deviations were larger for the false negatives presumably reflecting their inferior level of convergence. We have indeed confirmed that the cause of the misprediction in the false negative set has been slow convergence due to their incorrect initial structure from docking. Calculations starting from crystallographic structures correctly predicted them as binders (data not shown).

The present calculations with ASyncRE on the computational grid yielded almost twice the amount of data collected for SAMPL4 of 1.1 ns per replica. Here, due to the random nature of the ASyncRE protocol, the amount of data collected varied from one replica to another depending on the number of times that the replica was selected for execution and the additional (and variable) time for clients to return results (see below). The aggregate simulation time for each complex ranged from 39 to 44 ns, or 2.0 to 2.2 ns per replica. The contribution of individual replicas had a larger spread. For example for AVX17556_3 replica 13 provided only 1.8 ns of simulation time compared to replica 6, the most productive, with 2.5 ns of simulation time.

While the overall CPU time cost was similar (approximately 3,000 CPU hours per complex per nanosecond), the wall-clock time involved in the grid and cluster calculations was very different. It took about 3 weeks for each complex to collect from the grid the same amount of data that was collected in only three days on XSEDE computing clusters with MPI communication. This is due to a variety of factors. MD executions on clusters, which utilized a multithreaded version of the IMPACT MD engine, ran approximately four times as fast than calculations on grid clients, which were not multithreaded due to OS limitations. In the asynchronous simulations a maximum of approximately 70% of the replicas was allowed to run at any one time to ensure that a fraction of the replicas was checkpointed to disk and available for parameter exchanges. In contrast, in the synchronous MPI RE simulations all of the replicas executed concurrently. Finally it took additional time for the BOINC clients to return results after execution. The latter was one of the dominating factors limiting throughput, in particular when clients failed to return results because of detachment from the grid (such as when turned off or placed back into service for student use). In these occasions the server waited for a period of time (set to 24 hours) to receive results from the client before declaring a failure and issue a new replica execution. During this time an affected replica was effectively idle and unavailable for exchanges. Due to this behavior, illustrated by Fig. 3a for the host-guest benchmark, the majority of replica cycle times, defined as the time elapsed from issuing a replica execution to the receipt of valid results, are clustered around the execution time. However few, corresponding to client outages discussed above, were, in this case, as long as two days. The effect of these outliers was substantial; they raised the average cycle time from approximately two and half hours to more than four hours.

Overall, these experiments showed that the ASyncRE framework can make effective use of campus grid computing resource for free energy-based drug screening. While further optimizations are possible, the power of these computational resources clearly resides primarily in their computational throughput capacity over a long period of time rather than raw speed. On the 1,000 CPU cores Brooklyn College grid for example few hundreds protein-ligand complexes of the kind tested here could be screened in a period of a few weeks, which is comparable to the throughput we achieved on multiple high-end cluster resources for the SAMPL4 blind challenge.[61]

3.3. Study of a Peptide Dimerization Equilibrium on Heterogeneous Parallel Computing Resources

In this section we illustrate the use of the ASyncRE framework to carry out multi-dimensional replica exchange BEDAM calculations for a challenging macromolecular complex on heterogeneous high-performance computing resources. The biological system in question is the leucine zipper domain of the General Control Nonderepressible (GCN4) transcription factor (Fig 4). The coiled-coil structure of this domain is typical of many structural proteins and proteins involved in mechanical work, such as the muscle protein myosin. They are also frequently found as multimerization domains in proteins, such as the GCN4 protein itself.[71] The binding propensities of GCN4-derived peptides have been studied extensively.[72] Binding affinity is provided by appropriately spaced hydrophobic residues at the interface between the two α-helices whereas polar aminoacids line the external surfaces (Fig. 4).

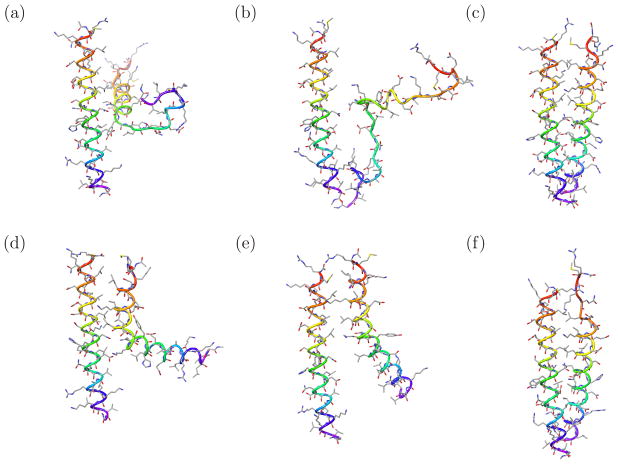
Figure 4.

Illustrative conformations of the GCN4 leucine zipper dimer from the 2D BEDAM simulations. (c) and (f) are representative of bound and folded conformations. (a,b,c) Replicas at λ = 1 and, respectively, 417, 397, and 362 K at the end of the simulation. Replicas at λ = 1 above 362 K tend to be dissociated and unfolded. (d,e,f) A replica undergoing a folding and binding event at λ = 1 and 379 K in 0.54 ns (time progresses left to right).

While understood at a qualitative level, the quantitative prediction of the binding propensities of this and other macromolecular complexes is very challenging. This is because the binding free energy is the result of a large compensation between the favorable average interaction energy between the folded monomers and the unfavorable free energy of folding, both of which are strongly dependent on aminoacid composition. Using computational methods to reliably predict binding free energies of peptide-peptide and protein-peptide complexes would be very helpful in many applications such as protein engineering and the rational development of biological medicines.

In this experiment we have employed the BEDAM method to estimate the free energy of dimerization of the GCN4 leucine zipper peptide using 2D replica exchange conformational sampling in alchemical and temperature space. The inclusion of high temperature replicas is necessary to activate intramolecular degrees of freedom involved in monomer folding. We utilized 144 replicas with all possible combinations of 18 λ values distributed between 0 and 1, and 8 temperatures distributed between 300 and 417 K. UWHAM analysis was employed.[25] The RE simulation was started from the 2ZTA crystallographic structure[73] and lasted 7.5 ns per replica on average, or 1.1 μs of simulation. To mimic the conditions relevant for a protein-peptide binding free energy calculations, here one of the two (identical) monomers was restrained in the native α-helical conformation by means of (ϕ,ψ) dihedral angle flat-bottom harmonic restraints. A dimer was defined as any conformation in which the Cα atoms of the central Asn16 residues (2ZTA numbering) of the two monomers were within a distance of 7 ± 4 Å.

The calculations were conducted on the Stampede XSEDE cluster. Calculations of such magnitude consume thousands of hours of CPU time and it is important to use the hardware at maximum capacity. In addition to a standard complement of CPU’s, the nodes of the Stampede cluster are equipped with a many-core co-processor (MIC). A substantial fraction of the computing capacity of each node resides in the co-processor, however it is not straightforward to design software to optimally utilize these heterogeneous hardware resources in concert. The ASyncRE framework is particularly suited for this purpose. For this application we have ported the Impact MD engine to the MIC and utilized the SSH job transport feature of ASyncRE to launch replica executions on either the CPU or the MIC simultaneously. We observed that the co-processor can run concurrently a larger number of replicas than the CPU’s but at a lower speed (Table 2). In practice this is not a significant issue because ASyncRE performs parameter exchanges asynchronously so that, unlike traditional synchronous algorithms, replicas can progress at different rates to utilize all hardware resources at maximum capacity. We observed an overall throughput of ASyncRE/BEDAM of 130 ns/day, a third of which is accounted by the co-processor (Table 2).

Table 2.

Throughput achieved with ASyncRE on 6 CPU/MIC heterogeneous nodes of the Stampede cluster for the dimerization free energy simulation of GCN4.

Device	speeda	#replicas per device	#devicesb	throughputc	%throughput
CPU (4 threads)	27.1	4	24	84.3 ns/day	64.7%
MIC (24 threads)	5.9	10	6	45.9 ns/day	35.3%
All				130.2 ns/day	100%

^aAverage speed in MD/steps per second.

^bEach Stampede node utilized has four CPU’s with 4 cores each, and one MIC co-processor with 240 threads.

^cComputed from average speed with a 1.5 fs MD timestep and number of concurrent replicas on device.

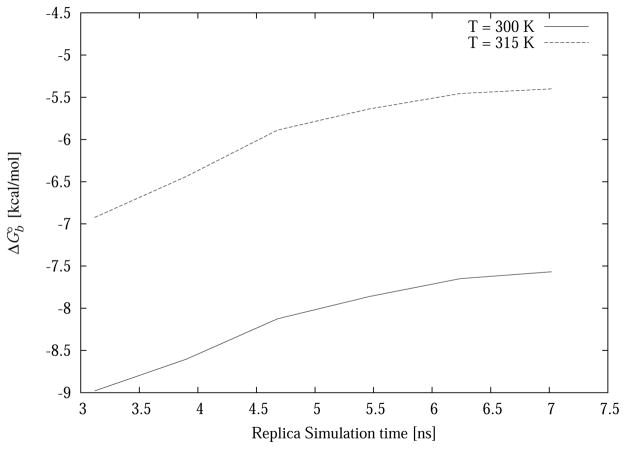
The computed dimerization binding free energy increases as a function of simulation time (Fig. 5). This is due to migration away from the dimeric structure of replicas at high temperatures and low values of λ. Thermodynamically, the simulation is progressively including conformational reorganization effects, which oppose binding. The role of high temperatures is key in this case to trigger fast dissociation of the dimer and monomer unfolding, and enhance of sampling of the unbound state. Illustrative examples of conformations sampled from high temperature replicas are illustrated in Fig. 4. In some cases a replica that underwent dissociation reformed a bound dimer (Fig 4). The binding free energy estimate appears to converge to approximately −7.5 kcal/mol at 300 K and −5.4 kcal/mol at 315 K. However slow drifting to higher free energies can not be ruled out. Longer simulations are needed to reliably estimate the binding free energy. The experimental binding free energy is −8.5 kcal/mol based on temperature-driven unfolding measurements.[72, 74]

Figure 5.

Computed dimerization free energy of the GCN4 peptide at two temperatures as a function of simulation length. Values correspond to a window of 3.1 ns per replica (80 RE cycles) ending at the time indicated.

An additional advantage of simulating the binding at multiple temperature is the availability of the conformational entropy of binding as the temperature derivative of the binding free energy. As shown in Table 3, conformational entropy changes are negative, implying, as expected, an entropic penalty due to the loss of conformational freedom of the binding partners. Together with the reorganization free energy values average binding energy values, it is then possible to then extract the energy component of the reorganization energy for binding, ΔE_reorg in Table 3, which measures the change in intramolecular energy of the binding partners upon folding. The reorganization energy is significantly smaller than the entropic component (7.3 kcal/mol vs. 46.4 kcal/mol), indicating that relatively little intramolecular potential energy is expended to fold the monomers into helical conformations. The sum of energetic and entropic penalties is smaller than the average interaction energy gain (53.8 kcal/mol vs −61.4 kcal/mol) resulting in a favorable, but much reduced, net dimerization free energy. From these values it can be appreciated how mutations affecting only slightly the interaction between monomers or energetic and entropic penalties, can significantly shift the equilibrium for or against dimerization. We intend to employ further this novel computational platform to study protein-peptide binding equilibria.

Table 3.

Computed thermodynamic parameters of the dimerization of the GCN4 dimer at 300 K.

$\mathrm{\Delta }{G}_b^{\circ }$ a	ΔEbb	$\mathrm{\Delta }{G}_{\mathit{rearg}}^{\circ }$ c	ΔEreorgd	$-T\mathrm{\Delta }{S}_b^{\circ }$ e
−7.5 ± 0.3	−61.4 ± 0.9	53.8 ± 1.0	7.3 ± 1.0	46.4 ± 0.4

All values in kcal/mol.

^aUncertainty estimated as the change in computed binding free energy in the second half of the trajectory, see Fig. 5.

^bAverage effective interaction energy between the two monomers at λ = 1; the uncertainty is the standard error of the mean.

^c $\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }=\mathrm{\Delta }{G}_b^{\circ }-\mathrm{\Delta }{E}_b$; uncertainty computed by error propagation.

^d $\mathrm{\Delta }{E}_{\text{reorg}}=\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }-T\mathrm{\Delta }{S}_b^{\circ }$; uncertainty computed by error propagation.

^e $\mathrm{\Delta }{S}_b^{\circ }$ computed by finite difference from the binding free energies at 300 and 315 K; uncertainty computed by error propagation.

4. Conclusions

We have presented the ASyncRE software for asynchronous replica exchange molecular simulations on volunteered computing grids and heterogeneous high performance computing clusters and illustrated its deployment on heterogeneous high performance clusters and BOINC distributed computational grids. In the first case ASyncRE enhanced the throughput of the calculation by accessing CPU and co-processor resources in concert with minimal coordination overhead. In the second, ASyncRE enabled the use of large distributed computational grids of computers that, while providing abundant resources, are notoriously unfriendly to coupled parallel simulations such as replica exchange. Both cases illustrate the wider array of computing resources that ASyncRE opens to replica exchange applications. These advancements have been made possible by the adoption of simple general-purpose software design choices, and the application of recent algorithmic advances in replica exchange schemes. The ASyncRE software is coded in an accessible and modular manner to encourage the community to adopt it and extend it based on individual needs. The software is freely available for download at https://github.com/ComputationalBiophysicsCollaborative/AsyncRE